Первый слайд презентации: Применение производной к построению графиков функций»
практическое применение знаний и умений
Слайд 2: Цель работы на уроке
обобщить знания связанные с производной, а также расширить алгоритм исследования функции; оценить свои знания по теме; развивать умение работать в паре; развивать логическое мышление; формировать навыки контроля и самоконтроля.
Слайд 3: План урока
Повторение основных понятий и определений; Работа с графиками функции и производной; Применение полной схемы исследования функции, построение графиков функций; Практическое применение умения строить графики функций с помощью производной
Слайд 4: Правила поведения в паре
Активно участвуй в совместной работе. Внимательно выслушай собеседника. Не перебивай собеседника, пока он не закончит свой рассказ. Выскажи свою точку зрения по данному вопросу, будь при этом вежлив. Не смейся над чужими ошибками и недостатками в работе, но тактично укажите на них. Поблагодари партнера за совместную работу.
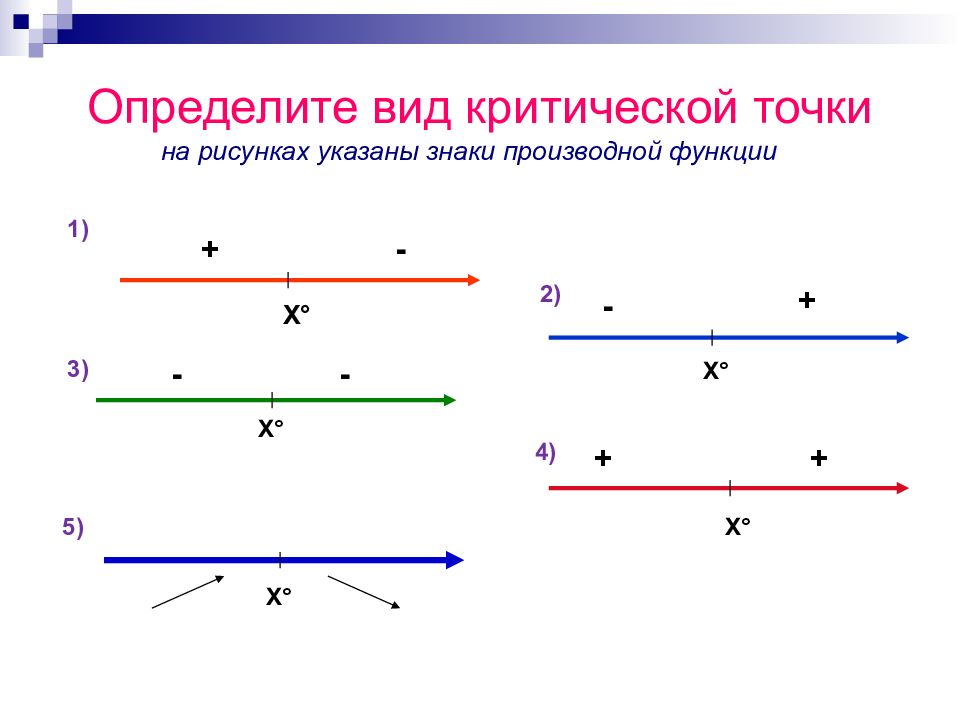
Х ° Х ° Х ° Х ° Х ° - + - - + + 1 ) 2 ) 3) 4 ) 5) + -
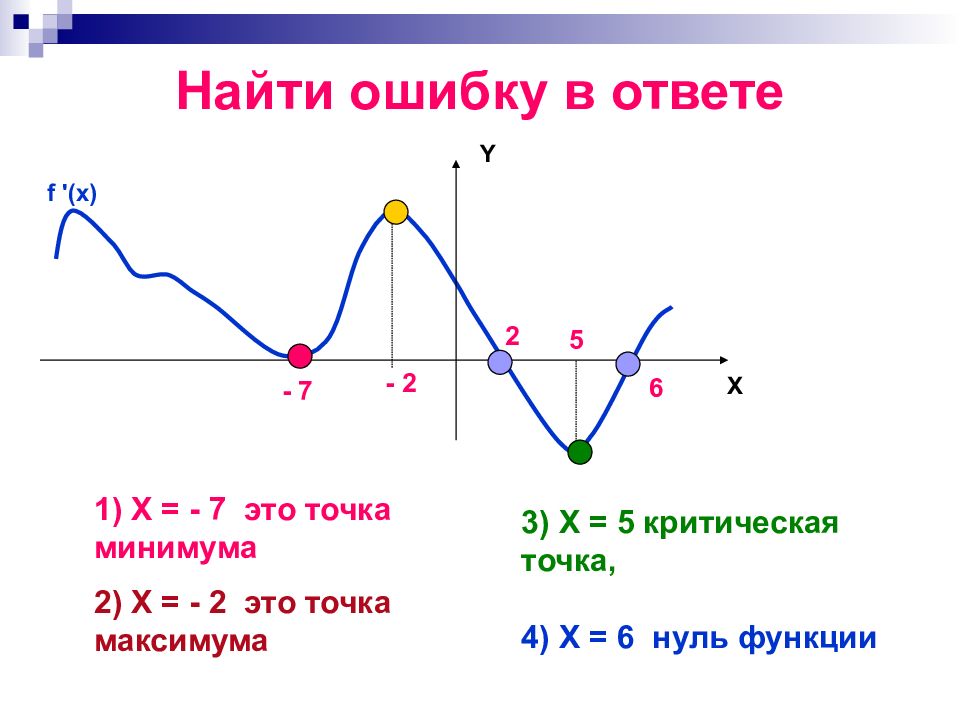
Слайд 7: Найти ошибку в ответе
Ученик, определяя по графику точки экстремума, допустил некоторые ошибки. Зная определение критических точек и точек экстремума, проанализируйте ответ и найдите ошибки!
Слайд 8: Найти ошибку в ответе
5 - 7 f '(x) - 2 6 1) X = - 7 это точка минимума 2) X = - 2 это точка максимума 3) X = 5 критическая точка, 4) X = 6 нуль функции X Y 2
Слайд 9: Установите соответствие
1. f '(x) меняет знак в точке х о с "+" на "-". А. В точке х о экстремума нет. 2. f '(x) меняет знак в точке х о с "-" на "+". Б. В точке х о минимум. 3. f '(x) не меняет знак. В. В точке х о максимум. Установите соответствие.
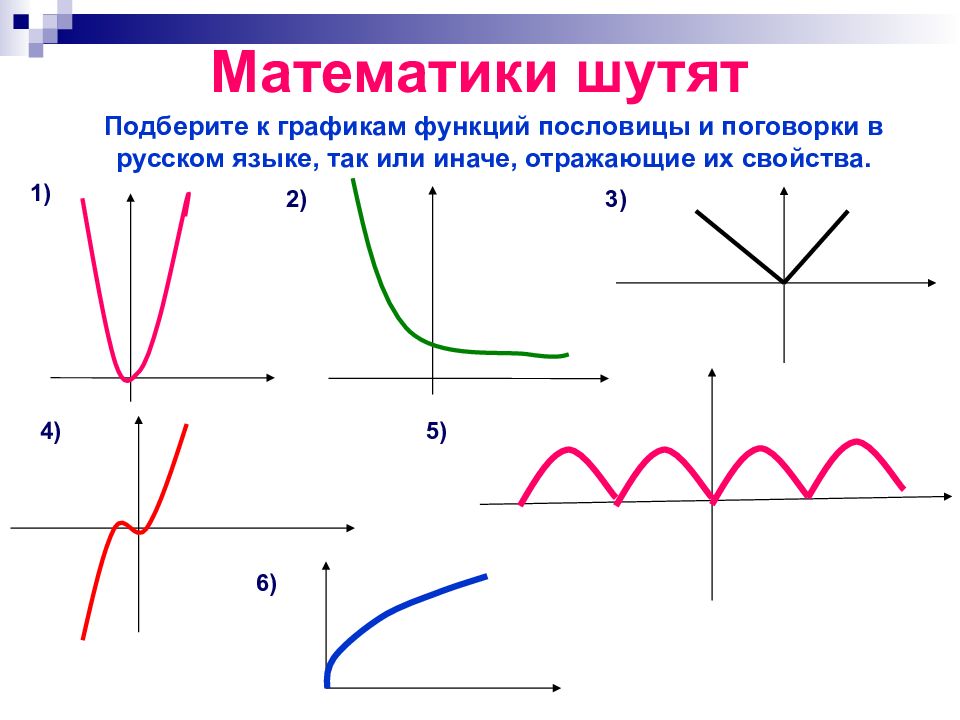
Слайд 10: Математики шутят
Подберите к графикам функций пословицы и поговорки в русском языке, так или иначе, отражающие их свойства. 1) 2) 3) 4) 5) 6)
Слайд 11: Математики шутят
Как аукнется, так и откликнется; (четность) № 1, № 3, № 5 Тише едешь, дальше будешь; (убывание) № 2 Повторенье – мать ученья; (периодичность) № 5 Чем дальше в лес, тем больше дров; ( возр-ие ) № 4, № 6 Любишь кататься, люби и саночки возить; (убывание, возрастание, четность)
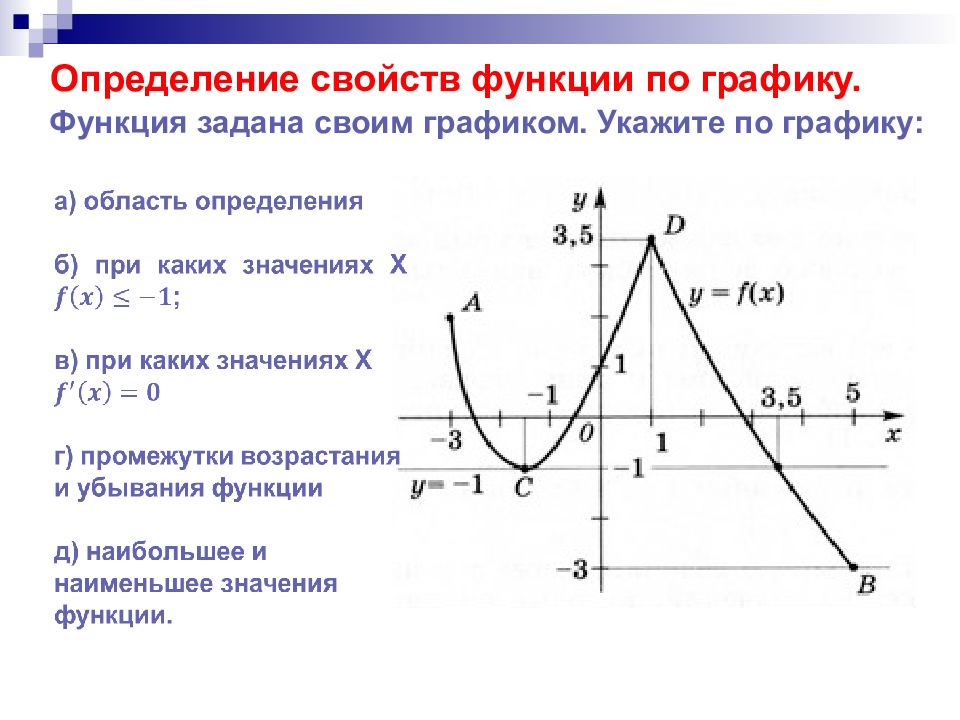
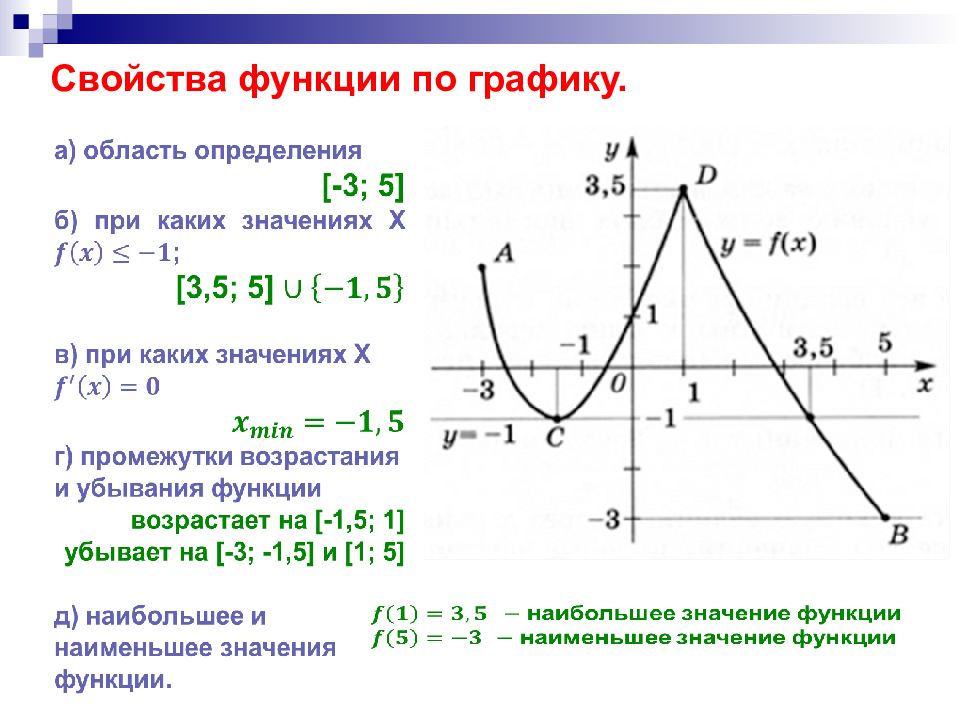
Слайд 12: Определение свойств функции по графику
Функция задана своим графиком. Укажите по графику:
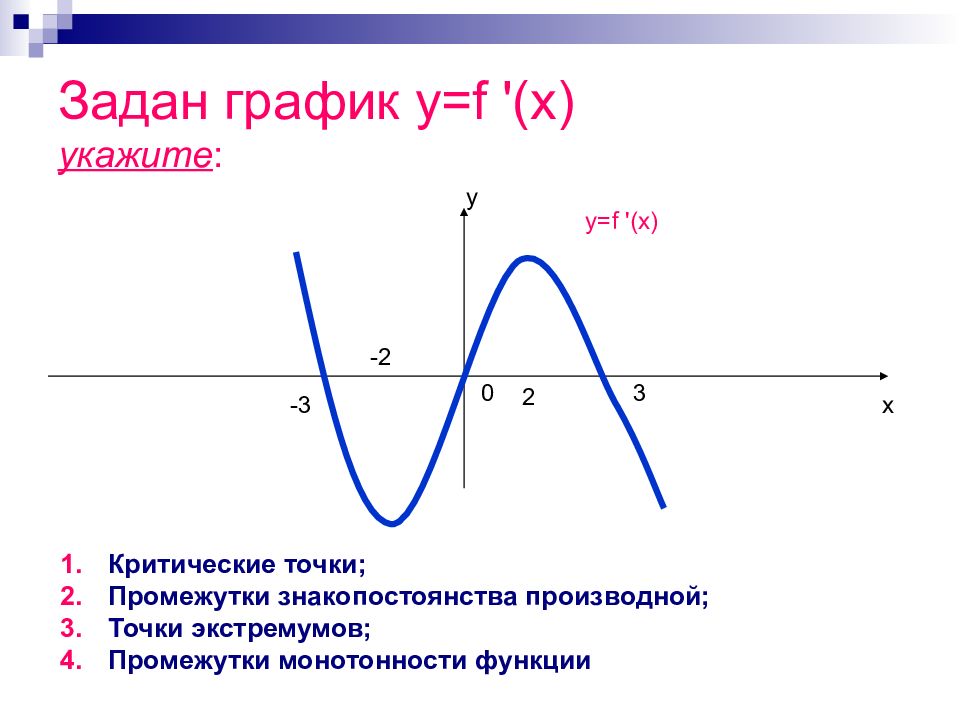
Слайд 14: Задан график y=f '(x) укажите :
у х y=f '(x) -3 0 3 -2 2 Критические точки; Промежутки знакопостоянства производной; Точки экстремумов; Промежутки монотонности функции
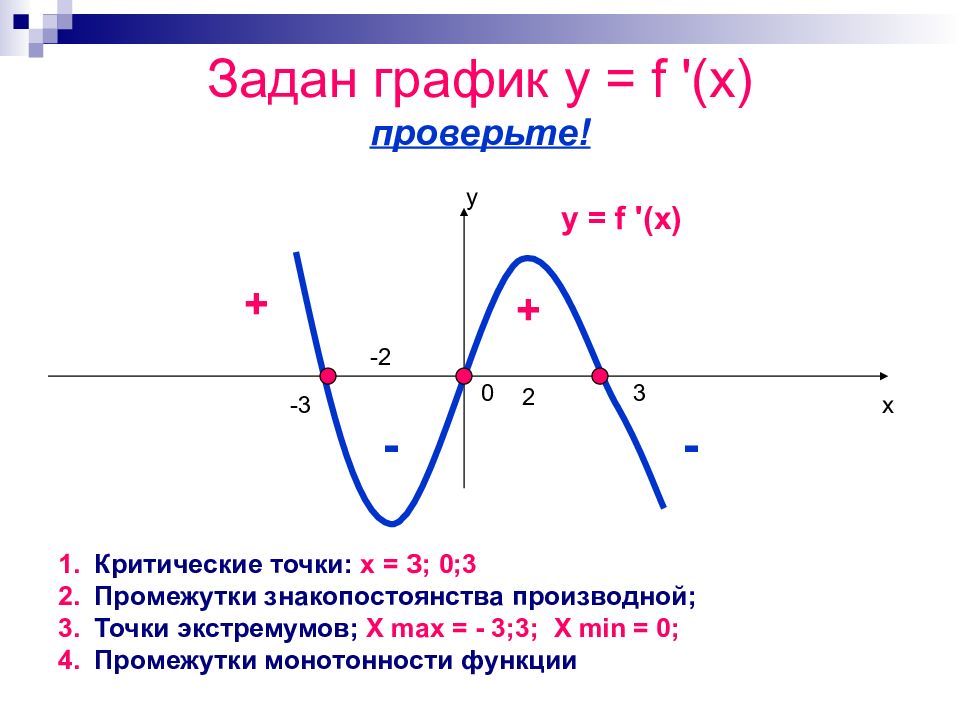
Слайд 15: Задан график y = f '(x) проверьте!
Критические точки: x = З ; 0;3 Промежутки знакопостоянства производной; Точки экстремумов; X max = - 3;3; X min = 0 ; Промежутки монотонности функции х у y = f '(x) -3 0 3 -2 2 + + - -
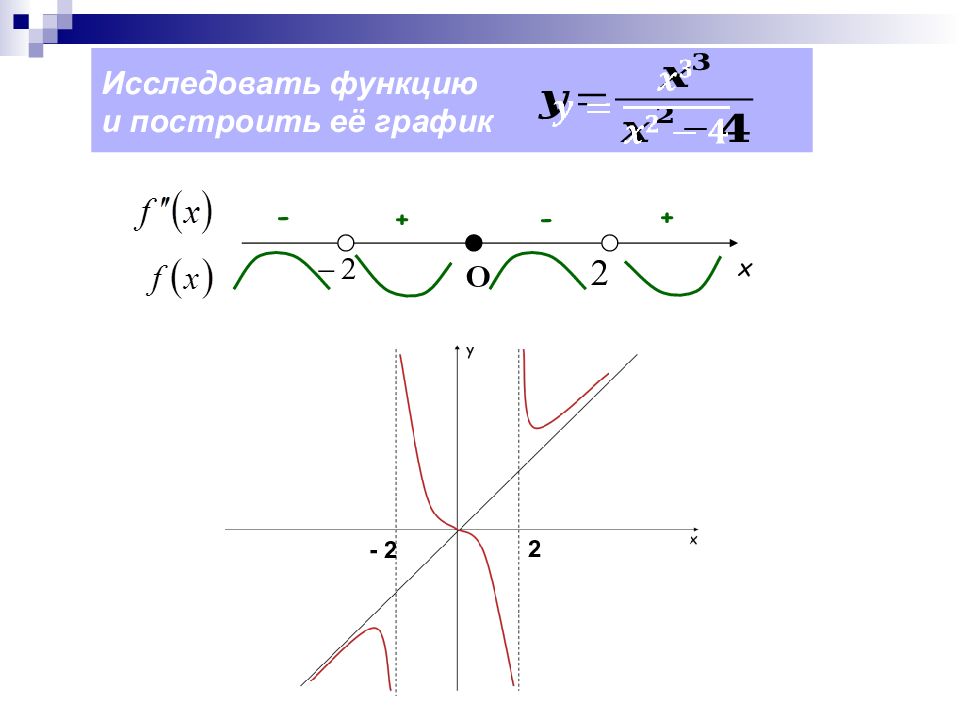
Слайд 17: Схема исследования функции
Алгоритм исследования функции с помощью производной: Область определения функции. Четность. Периодичность. Точки пересечения графика с осями координат. Производная, критические (стационарные) точки. Монотонность функции, экстремумы функции. Асимптоты. Таблица исследования функции. Направление выпуклости графика функции, точки перегиба. Контрольные точки.
Последний слайд презентации: Применение производной к построению графиков функций»: ИТОГ урока:
М.В. Ломоносов сказал: «Математику уже затем учить надо, что она ум в порядок приводит…» Мы постарались привести в порядок все знания о производной функции… Мы оценили свои умения, выработанные при её изучении, Мы ещё раз убедились в важности изученной темы…