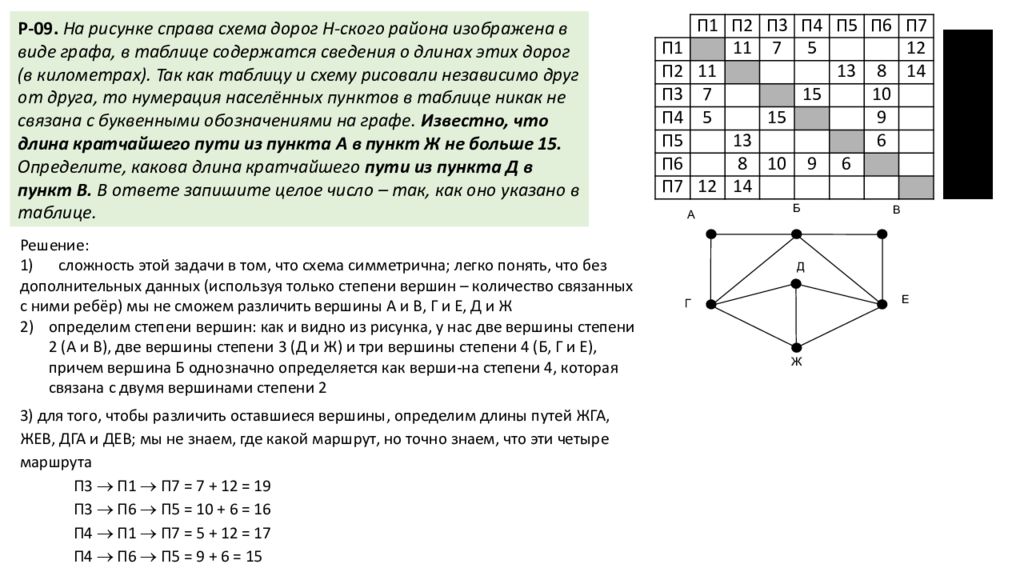
В А Е Д Г Ж Б Решение: 1) сложность этой задачи в том, что схема симметрична; легко понять, что без дополнительных данных (используя только степени вершин – количество связанных с ними ребёр ) мы не сможем различить вершины А и В, Г и Е, Д и Ж определим степени вершин: как и видно из рисунка, у нас две вершины степени 2 (А и В), две вершины степени 3 (Д и Ж) и три вершины степени 4 (Б, Г и Е), причем вершина Б однозначно определяется как верши-на степени 4, которая связана с двумя вершинами степени 2 П1 П2 П3 П4 П5 П6 П7 Г, Е П1 11 7 5 12 4 Б П2 11 13 8 14 4 Д, Ж П3 7 15 10 3 Д, Ж П4 5 15 9 3 А, В П5 13 6 2 Г, Е П6 8 10 9 6 4 А, В П7 12 14 2 3) для того, чтобы различить оставшиеся вершины, определим длины путей ЖГА, ЖЕВ, ДГА и ДЕВ; мы не знаем, где какой маршрут, но точно знаем, что эти четыре маршрута П3 П1 П7 = 7 + 12 = 19 П3 П6 П5 = 10 + 6 = 16 П4 П1 П7 = 5 + 12 = 17 П4 П6 П5 = 9 + 6 = 15
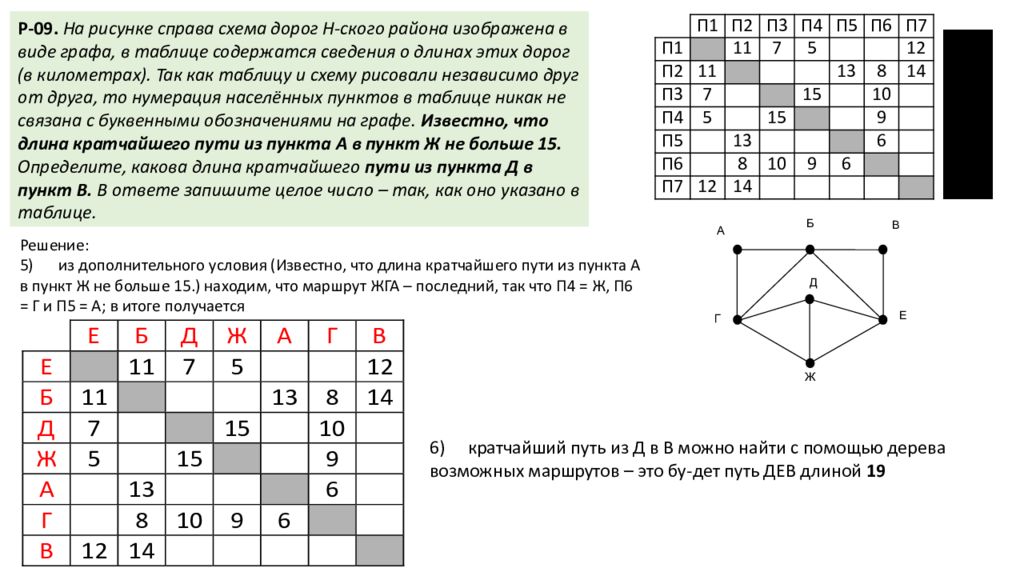
В А Е Д Г Ж Б Решение: 5) из дополнительного условия (Известно, что длина кратчайшего пути из пункта А в пункт Ж не больше 15.) находим, что маршрут ЖГА – последний, так что П4 = Ж, П6 = Г и П5 = А; в итоге получается П1 П2 П3 П4 П5 П6 П7 Г, Е П1 11 7 5 12 4 Б П2 11 13 8 14 4 Д, Ж П3 7 15 10 3 Д, Ж П4 5 15 9 3 А, В П5 13 6 2 Г, Е П6 8 10 9 6 4 А, В П7 12 14 2 6) кратчайший путь из Д в В можно найти с помощью дерева возможных маршрутов – это бу -дет путь ДЕВ длиной 19
Решение: сначала представим себе, что двоек в строке не было вообще: в этом случае сумма цифр была бы равна 10, что не подходит по условию; если к этим 10 единицам добавить 2 и сделать замену «21» на 5, то сумма станет равной (10-1+5) = 14, то есть каждое добавление двойки с заменой увеличит сумму на 4 нам нужно добавить 34 – 10 = 24, то есть в цепочке должно быть 6 двоек, каждая из которых стоит перед единицей; в результате работы программы все 6 пар «21» должны быть заменены на 5. Ответ: 6.
объём музыкального файла вычисляется по формуле I = r * ƒ * t * k при повышении разрешения (количества битов на хранения одного отсчёта) в 2 раза объём файла (при прочих равных условиях) увеличивается в 2 раза, поэтому время тоже увеличится в 2 раза при снижении частоты дискретизации (количества хранимых отсчётов за 1 секунду) в 1,5 раза объём файла (при прочих равных условиях) уменьшается в 1,5 раза, поэтому время тоже уменьшится в 1,5 раза при увеличении пропускной способности канала связи (здесь это то же самое, что и скорость передачи данных) в 4 раза время передачи (при прочих равных условиях) уменьшится в 4 раза поэтому исходное время передачи файла нужно а) умножить на 2 б) разделить на 1,5 в) разделить на 4 получается 30 · 2 / 1,5 / 4 = 10 секунд Ответ: 10.
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 50 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 5 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 6 раз выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 3 раза выше и частотой дискретизации в 2 раз меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 12 секунд; пропускная способность канала связи с городом Б в 5 раз выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город A? В ответе запишите только целое число, единицу измерения писать не нужно. Ответы: 1) 5; 2) 40
Решение. Такую задачу начинаем рассматривать с конца. Размер конечного файла – 6 Мб и это 40% от исходного. V исх = = 15 Мб. – Этот объем уже преобразованного файла, но без сжатия. Необходимо проделать обратную процедуру: 15 * 4 * 3 /2,5 = 72 Мб – размер файла при начальной записи.
любой канал связи имеет ограниченную пропускную способность (скорость передачи информации), это число ограничивается свойствами аппаратуры и самой линии (кабеля) объем переданной информации вычисляется по формуле Q = q*t, где q – пропускная способность канала (в битах в секунду или подобных единицах), а t – время передачи
1)вспомним, что 1 Мбайт = 210 Кбайт = 220 байт = 223 бит 2)время передачи несжатого файла (по варианту Б): 40 * 223 / 223 = 40 с 3)время передачи файла по варианту А: 16 + 0,9 * 40 + 2 = 18 + 36 = 54 с 4)таким образом, быстрее вариант Б на 54 – 40 = 14 с Ответ: Б14.
98)Сколько единиц в двоичной записи числа 8 4024 – 4 1605 + 2 1024 – 126? 99)Сколько единиц в двоичной записи числа 8 1234 – 4 234 + 2 1620 – 108? 100)Сколько единиц в двоичной записи числа 8 2341 – 4 342 + 2 620 – 81? 101) Сколько единиц в двоичной записи числа 8 1341 – 4 1342 + 2 1343 – 1344?
Задание типа 16 Что нужно знать : для того, чтобы задать рекурсивную функцию, нужно определить условие окончания рекурсии, то есть значения параметров функции, для которых значение функции известно или вычисляется без рекурсивных вызовов; рекуррентную формулу (или формулы), с помощью которых значение функции для заданных значений параметров вычисляется через значение (или значения) функции для других значений параметров (то есть, с помощью рекурсивных вызовов) задачи, в которых требуется найти значение заданной рекурсивной функции при известных значениях параметров можно решать с помощью ручных вычислений, используя электронные таблицы или с помощью своей программы; последние два способа обычно более эффективны
Алгоритм вычисления функции F ( n ) задан следующими соотношениями: F ( n ) = 1 при n = 1 F ( n ) = n + F ( n – 1), если n чётно, F ( n ) = 2· F ( n – 2), если n > 1 и n нечётно. Чему равно значение функции F (26) ? Решение (ручной счёт от последнего значения): чтобы вычислить F (26), используем формулу для чётных n : F (2 6 ) = 2 6 + F (2 5 ) нам неизвестно значение F (25), поэтому, применяя формулу для нечётных n, находим F (2 5 ) = 2 F (2 3 ) далее так же придётся написать формулы для вычисления F (23), F (21), …, F (3), и в конце мы получим F (3) = 2 F (1) значение F (1) = 1 нам задано, подставляя его в предыдущую формулу, находим F (3) = 2 F (1) = 2 теперь значение подставляем в формулу для F (5), потом найденное значение F (5) – в формулу для F (7), и т.д. после продолжительных вычислений получим F (26) = 2074 Ответ: 4122.
Алгоритм вычисления функции F ( n ) задан следующими соотношениями: F ( n ) = 1 при n = 1 F ( n ) = n + F ( n – 1), если n чётно, F ( n ) = 2· F ( n – 2), если n > 1 и n нечётно. Чему равно значение функции F (26) ? программа на языке Python : def F( n ): if n == 1: return 1 if n % 2 == 0: return n + F(n-1) else: return 2 * F(n-2) print( F(26) ) программа на языке С++: #include < iostream > using namespace std ; int F( int n ) { if( n == 1 ) return 1; if( n % 2 == 0 ) return n + F(n-1); else return 2 * F(n-2); } int main() { cout << F (2 6 ); }
Python C++ def F( n ): print( 2*n ) if n > 1: print(n-5) F(n-1) F(n-2) void F( int n ) { cout << 2*n << endl ; if( n > 1 ) { cout << n-5 << endl ; F(n-1); F(n-2); }} def F ( n ): global s # если не объявить s глобальной – ошибка! # print(2*n) s += 2*n if n > 1: # print(n-5) s += n - 5 F(n-1) F(n-2) можно попробовать изменить программу так, чтобы сумма выводимых чисел считалась автоматически: добавим в программу глобальную переменную s и будем увеличивать её при выводе каждого числа на значение этого числа; при этом для ускорения (значительного!) работы программы сразу закомментируем вывод чисел на экран: 2) можно оформить поиск нужного значения n в виде цикла, например, так: n = 0 while True : n += 1 # первое значение n = 1 s = 0 # нужно обнулять сумму перед каждым вызовом F ( n ) # подсчитали сумму if s > 500000: break ; # если нашли, выход из цикла print ( n, s ) # вывод результата
Python C++ def F( n ): print( 2*n ) if n > 1: print(n-5) F(n-1) F(n-2) void F( int n ) { cout << 2*n << endl ; if( n > 1 ) { cout << n-5 << endl ; F(n-1); F(n-2); }} решение на языке C++ (строки с выводом чисел закомментированы): #include < iostream > using namespace std ; int s; void F( int n ) { // cout << 2*n << endl ; s += 2*n; if( n > 1 ) { // cout << n-5 << endl ; s += n - 5; F(n-1); F(n-2); } } int main() { int n = 0; do { n += 1; s = 0; F(n); } while( s <= 500000 ); cout << n << " " << s; }
