Системы счисления. Перевод чисел из одной системы счисления в другие.
C истемы счисления Система счисления – это совокупность символов, используемых для изображения чисел. Система счисления включает в себя: алфавит, т. е. набор символов для записи чисел, способ записи чисел, способ чтения чисел. Они делятся на два класса: позиционные и непозиционные Позиционные системы счисления – это системы, в которых величина цифры определяется ее положением (позицией) в числе. Позиция цифр называется разрядом числа. Позиционные системы счисления различают по их основаниям, где о снование – это число цифр, используемых в системах счисления. Например: двоичная система счисления ( А 2 ), восьмеричная система счисления ( А 8 ) т.д. Непозиционные системы счисления – это системы, в которых величина цифры не определяется ее положением (позицией) в числе. Например: римская система счисления ( II, V, XII )
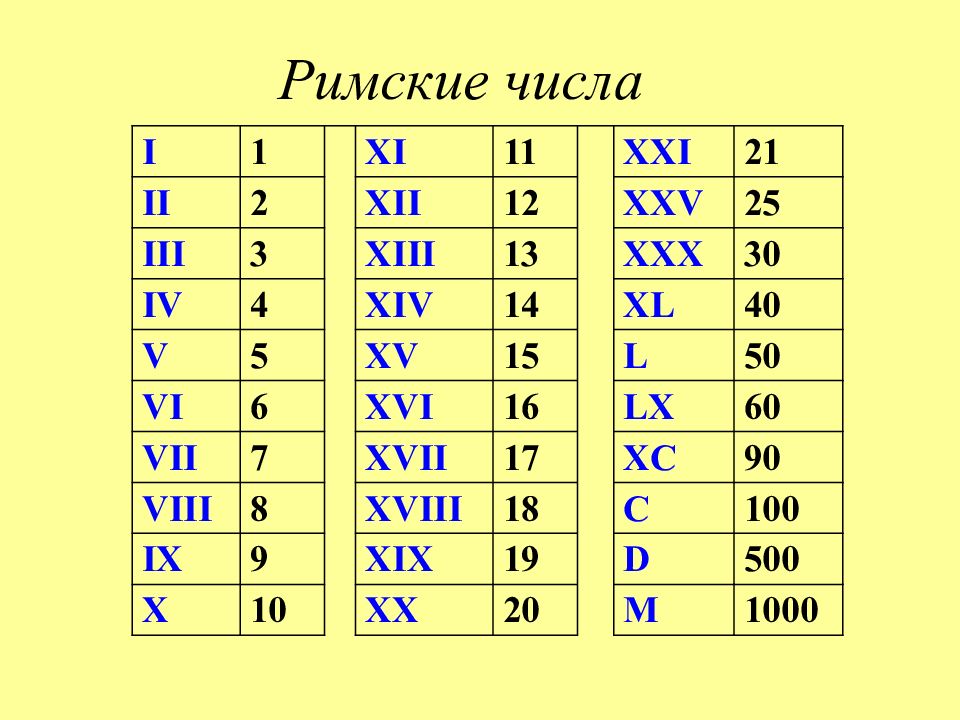
I 1 XI 11 XXI 21 II 2 XII 12 XXV 25 III 3 XIII 13 XXX 30 IV 4 XIV 14 XL 40 V 5 XV 15 L 50 VI 6 XVI 16 LX 60 VII 7 XVII 17 XC 90 VIII 8 XVIII 18 C 100 IX 9 XIX 19 D 500 X 10 XX 20 M 1000 Римские числа
Правила записи и чтения римских чисел Буква, повторяющаяся дважды или трижды, удваивает или утраивает свое значение (СС - 200). Одна или более букв, помещенных после другой большего значения, увеличивает это значение на величину более мелкой ( XI – 11, DCC - 700). Буква, помещенная перед другой буквой большего значения, уменьшает это значение на величину этой буквы ( XC – 90, XL – 40). Горизонтальная черта, помещенная над буквой, повышает ее значение в 1000 раз.
Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. Алфавит двоичной системы счисления состоит из 0 и 1 Достоинства 2 с/с: Простота кодирования; Простота арифметических действий; Простота записи, хранения и передачи техническими средствами. Недостатки 2 с/с: Много места занимает запись числа; Трудоемкость перевода в 10 с/с и наоборот. Основание м, служит цифра 2 Двоичная система счисления
Восьмеричная система счисления Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 Основание м является цифра 8 Шестнадцатеричная система счисления Алфавит:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Основание м является цифра 16 8 10 =10 8 Например: 276 8 16 10 =10 16 Например: 26 A7 16
Рассмотрим, для примера, десятичное число 3745. Его можно записать несколькими способами, не изменяя его количества. А 10 = 3745 А 10 = 3000 + 700 + 40 + 5 А 10 = 3 x 1000 + 7 x 100 + 4 x 10 + 5 А 10 = 3 x 10 3 + 7 x 10 2 + 4 x 10 1 + 5 x 10 0 (любое число в степени 0 равно 1) Последнюю запись называют разложением по степеням основания. Формула разложения числа по степеням основания
Формула разложения по степеням основания показывает, что число можно представить в виде суммы цифр, которые в свою очередь, равны произведению цифры на основание в степени, равной номеру разряда. При разложении целых чисел нумерация разрядов идет справа налево, начиная с « 0 ». А р = а n р n + … +а 1 р 1 +а 0 p 0
Алгоритм перевода чисел из десятичной системы счисления в любую позиционную систему счисления с основанием q (2, 8, 16). Делим число на основание системы счисления нацело (остаток должен быть меньше основания). Если частное больше основания системы счисления, то повторить шаг 1. Если частное меньше основания, то записываем число из остатков, начиная с последнего частного, справа налево.
Алгоритм перевода целого числа из системы счисления с основанием q (2, 8, 16) в десятичную систему счисления. 1. Определяем разряд каждой цифры в числе (разряды выставляются строго над цифрами справа налево, начиная с нуля) 2. Умножаем цифру числа на основание в степени, равной номеру разряда. 3. Суммируем все произведения.
1. Чтобы число 124 перевести из 10 с\с в 2 с\с надо это число делить на 2 (основание с\с ) до тех пор, пока остатком деления не окажется число меньше 2 (1 или 0). 124 2 62 124 0 2 62 31 0 2 15 30 1 2 7 14 1 2 3 6 1 2 1 1 2 2. Выписываем все остатки (справа налево) начиная с частного, следовательно 124 10 1 1 1 1 1 0 0 2 =
1. Для того, чтобы перевести число из 2 с\с в 10 с\с, надо представить его в виде суммы п роизведени й цифры на основание в степени, равной номеру разряда. (п ри разложении целых чисел нумерация разрядов идет справа налево, начиная с « 0 » ) 1 1 0 0 1 = 4 3 2 1 0 1х2 4 + 1х2 3 + 0х2 2 + 0х2 1 + 16+ = 8+ 1 = 25 10 Получаем, что 11001 2 = 25 10 1х2 0 =
1.Чтобы число 124 перевести из 10 с\с в 8 с\с надо это число делить на 8 (основание с\с ) до тех пор, пока остатком деления не окажется число меньше 8 (0, 1, 2, 3, 4, 5, 6, 7). 124 120 8 15 4 8 1 8 7 2. Выписываем все остатки (справа налево) начиная с частного, следовательно 124 10 = 1 7 4 8
1. Для того, чтобы перевести число из 8 с\с в 10 с\с, надо представить его в виде суммы п роизведени й цифры на основание в степени, равной номеру разряда. (п ри разложении целых чисел нумерация разрядов идет справа налево, начиная с « 0 ») 6 1 3 2 1 0 = 6 x 8 2 + 1 x 8 1 + 3 x 8 0 = = 384 + 8 3 + = 395 10 2. Получаем, что 613 8 = 395 10
1.Чтобы число 395 перевести из 10 с\с в 16 с\с надо это число делить на 16 (основание с\с ) до тех пор, пока остатком деления не окажется число меньше 16 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F ). 395 16 384 11 24 16 1 16 8 2. Выписываем все остатки (справа налево) начиная с частного, следовательно 395 10 = 1 8 B 16
Для того, чтобы перевести число из 16 с\с в 10 с\с, надо представить его в виде суммы п роизведени й цифры на основание в степени, равной номеру разряда. (п ри разложении целых чисел нумерация разрядов идет справа налево, начиная с « 0 ») А 7 F 5 16 = Ax16 3 + 7x16 2 + 3 2 1 0 Fx16 1 + + 5x16 0 = 10x4096 + + 7x256 + 15x16 + 5x1 = 42997 10 2. Получаем, что A7F5 16 = 42997 10
4) 489 10 1 ) 124 10 а) 1111100 2 б) 1010101 2 г) 1101100 2 в) 1111001 2 2 ) 543 10 а) 1111100 11 2 в) 10 000 111 11 2 б) 1111001 001 2 г) 1101100 010 2 3) 131 10 а) 1111100 1 2 а) 111110 11 0 2 б) 10 0 0 0 01 1 2 б) 101010 10 1 2 г) 11110 10 01 2 в) 1111001 0 2 в) 1101100 00 2 г) 1 0 101100 2
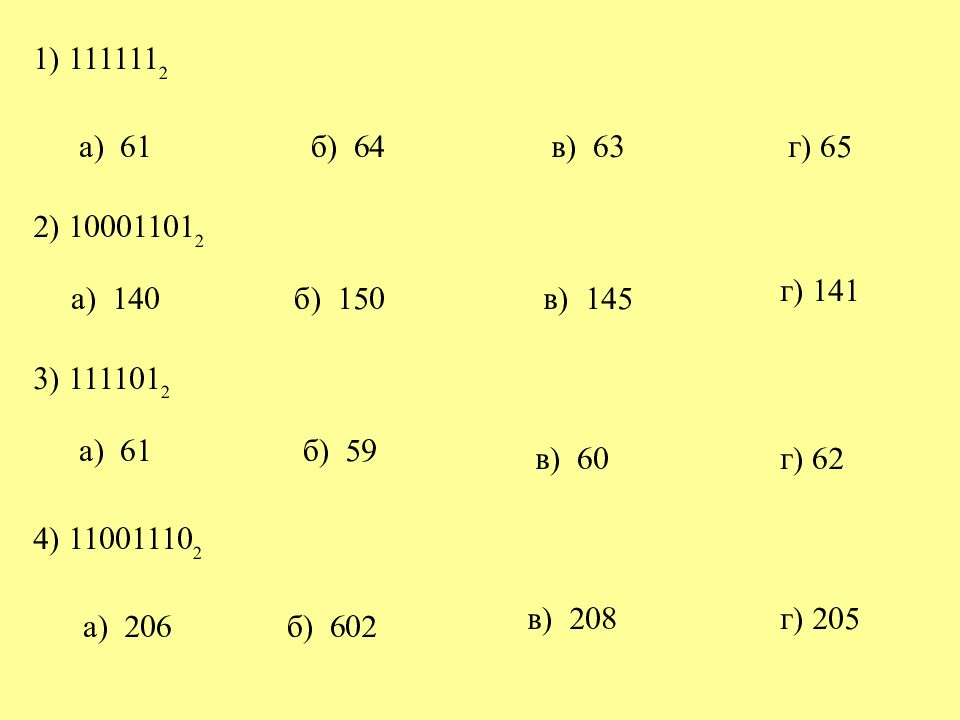
4) 11001110 2 1) 111111 2 а) 61 в) 63 г) 141 2) 10001101 2 а) 140 б) 64 б) 150 в) 145 3) 111101 2 а) 61 а) 206 б) 59 б) 602 в) 60 в) 208 г) 62 г) 65 г) 205
1) 613 8 а) 359 10 б) 395 10 в) 358 10 г) 360 10 2 ) 24 8 3 ) 100 8 4 ) 154 8 а) 20 10 а) 56 10 а) 117 10 б) 25 10 б) 100 10 б) 198 10 в) 30 10 в) 64 10 в) 104 10 г) 36 10 г) 68 10 г) 108 10
1 ) A7F5 16 2 ) 10 16 3 ) B0E 16 4 ) 120 16 а) 43959 10 б) 42997 10 в) 34779 10 г) 45360 10 а) 8 10 а) 2830 10 а) 300 10 б) 12 10 б) 1865 10 б) 267 10 в) 23 10 в) 2967 10 в) 288 10 г) 16 10 г) 2525 10 г) 280 10
1 ) 12 10 2 ) 235 10 3 ) 1768 10 4 ) 895 10 а) 16 8 б) 14 8 а) 535 8 а) 3416 8 а) 1577 8 в) 15 8 г) 20 8 б) 314 8 б) 2314 8 б) 1304 8 в) 134 8 в) 3350 8 в) 1532 8 г) 353 8 г) 2780 8 г) 1520 8
1 ) 54 10 2 ) 125 10 3 ) 3758 10 4 ) 52167 10 а) 36 16 б) 46 16 в) 26 16 г) 56 16 а) A2 16 а) AEE 16 а) ABF5 16 б) 7D 16 б) BCB2 16 б) DA1 16 в) 5F 16 в) 7BBA 16 в) EAE 16 г) 59 16 г) CA1 16 г) CBC7 16
