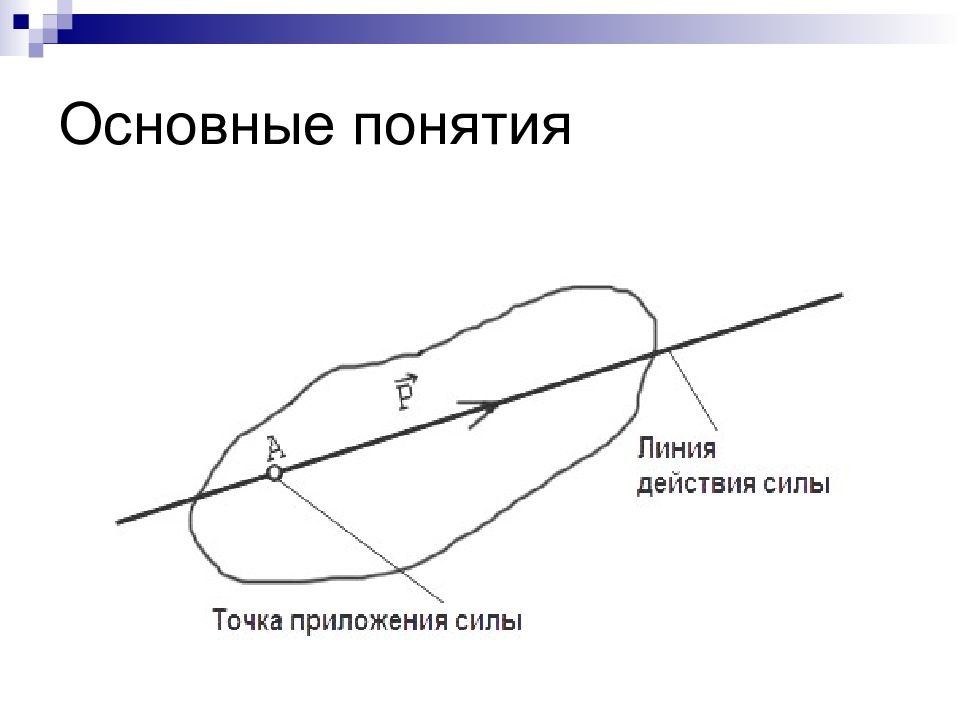
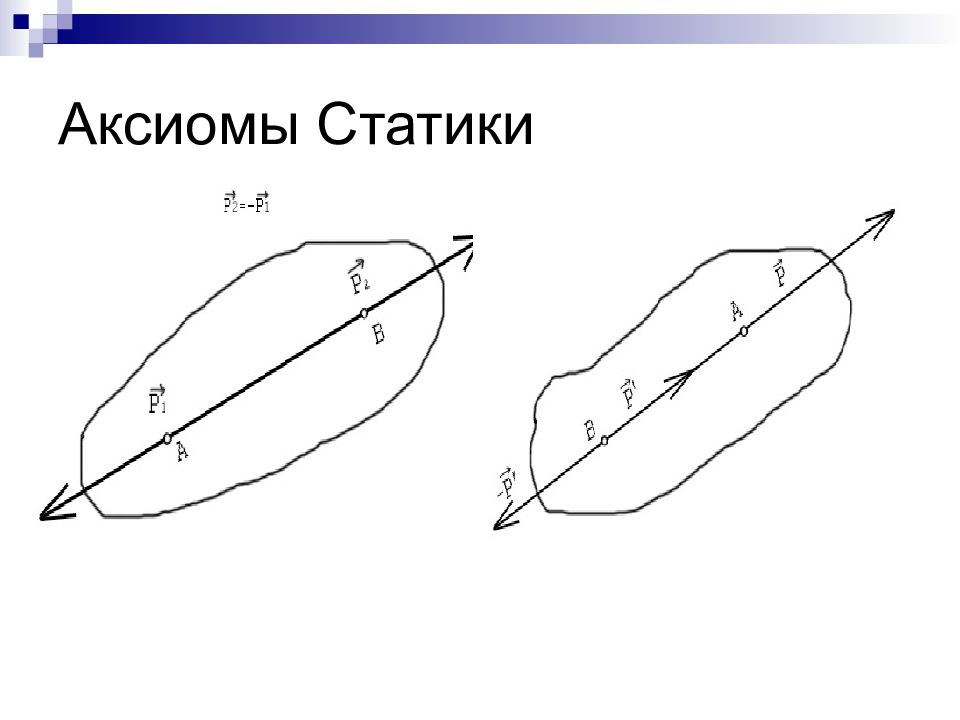
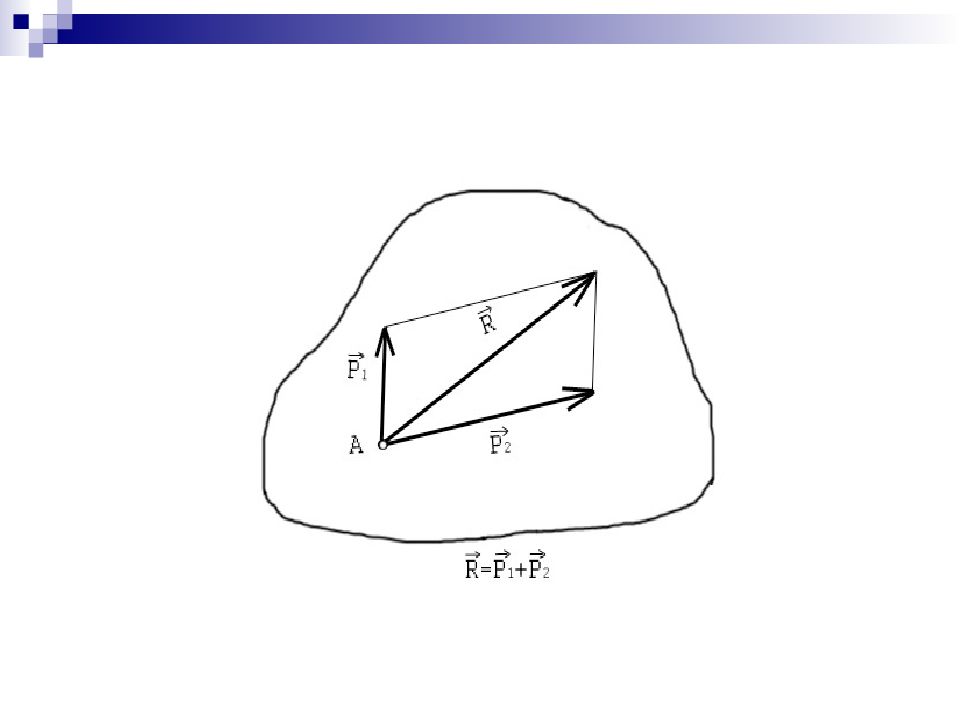
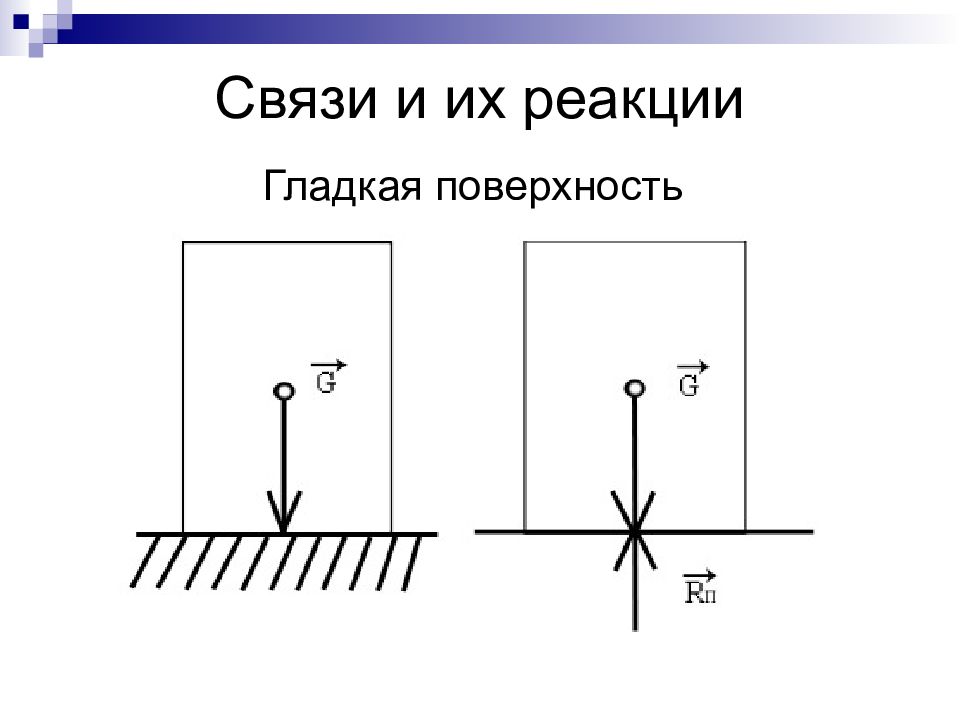
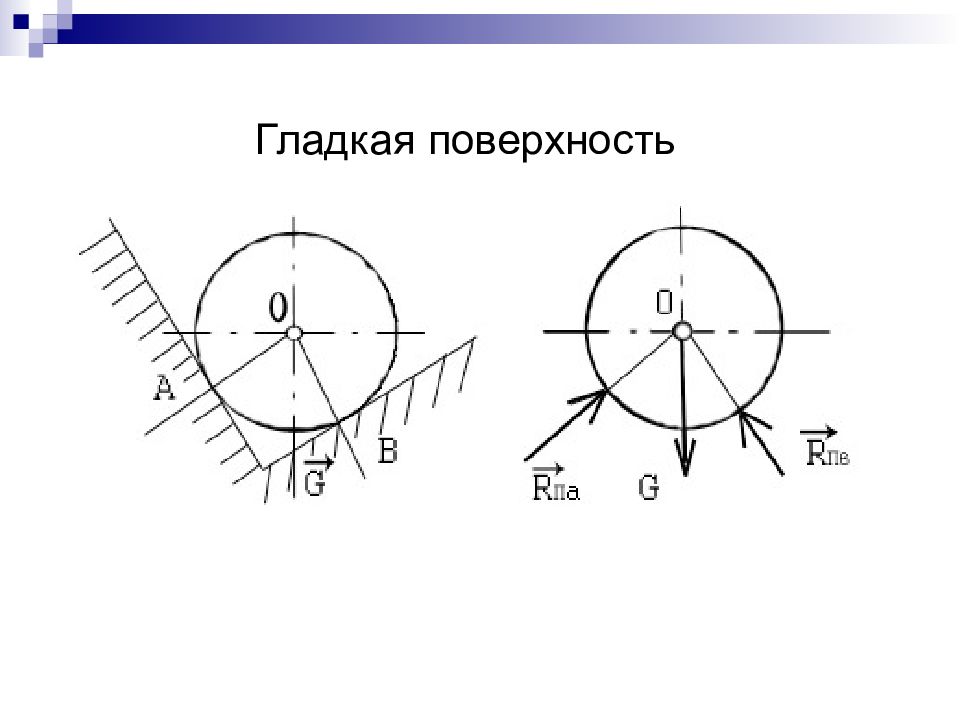
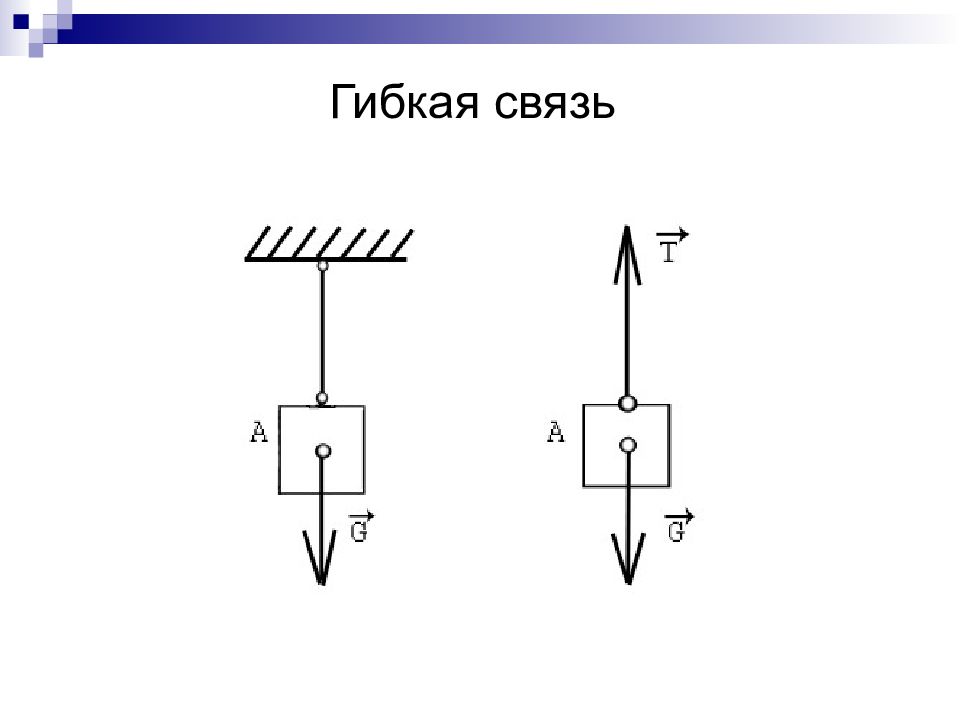
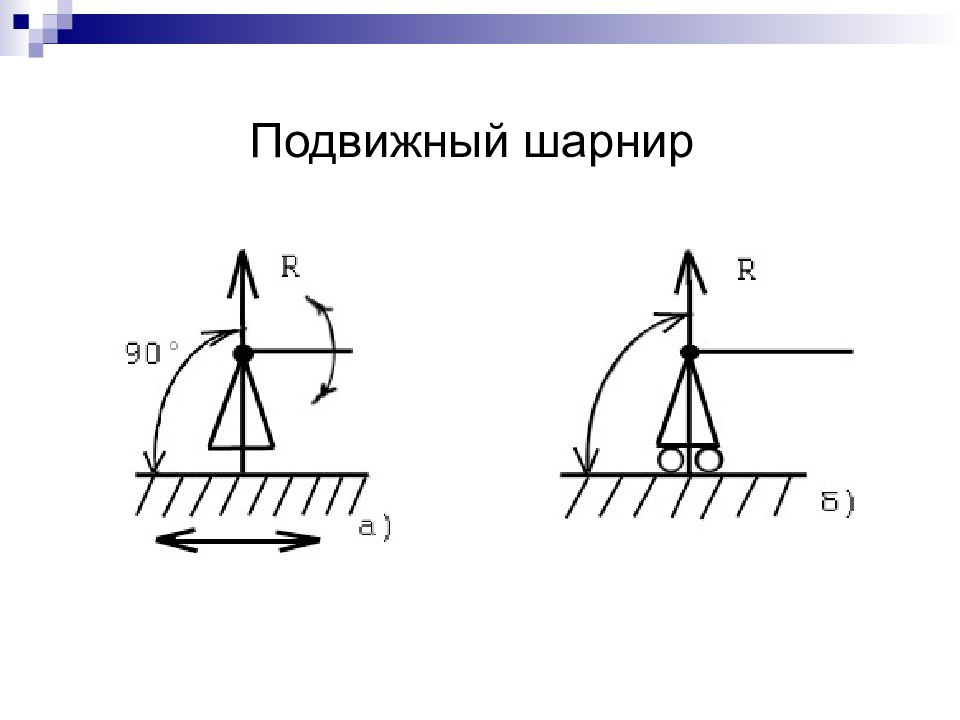
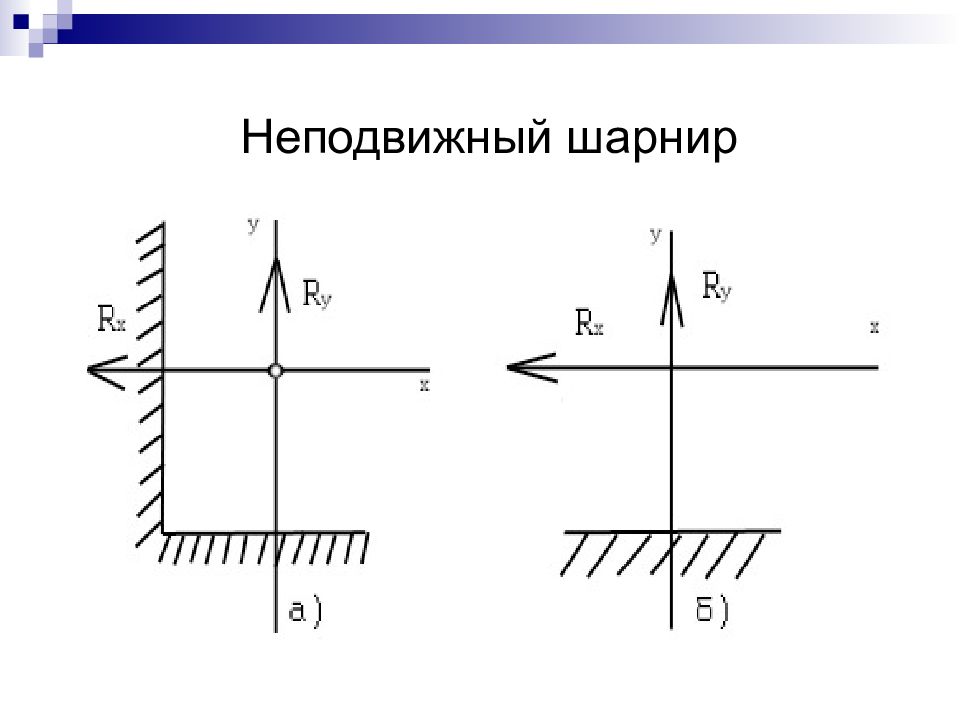
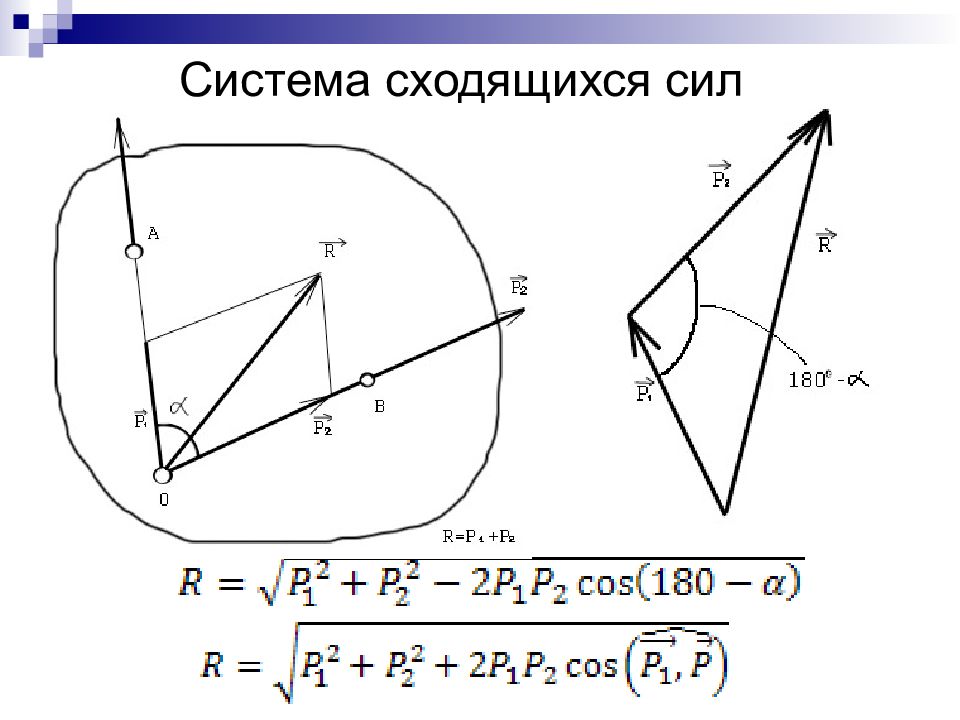
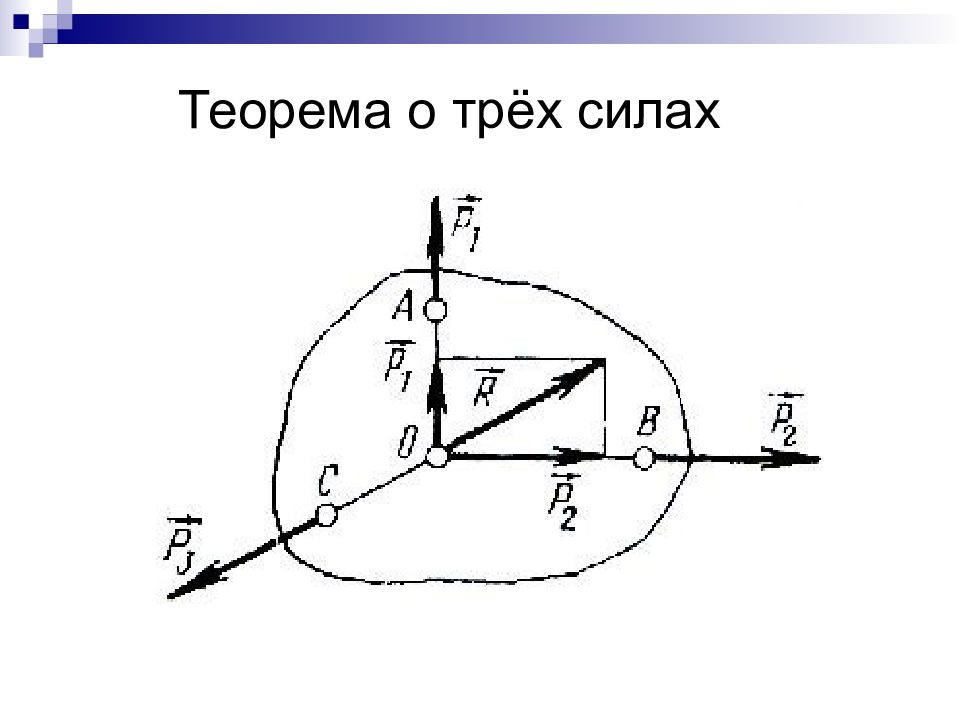
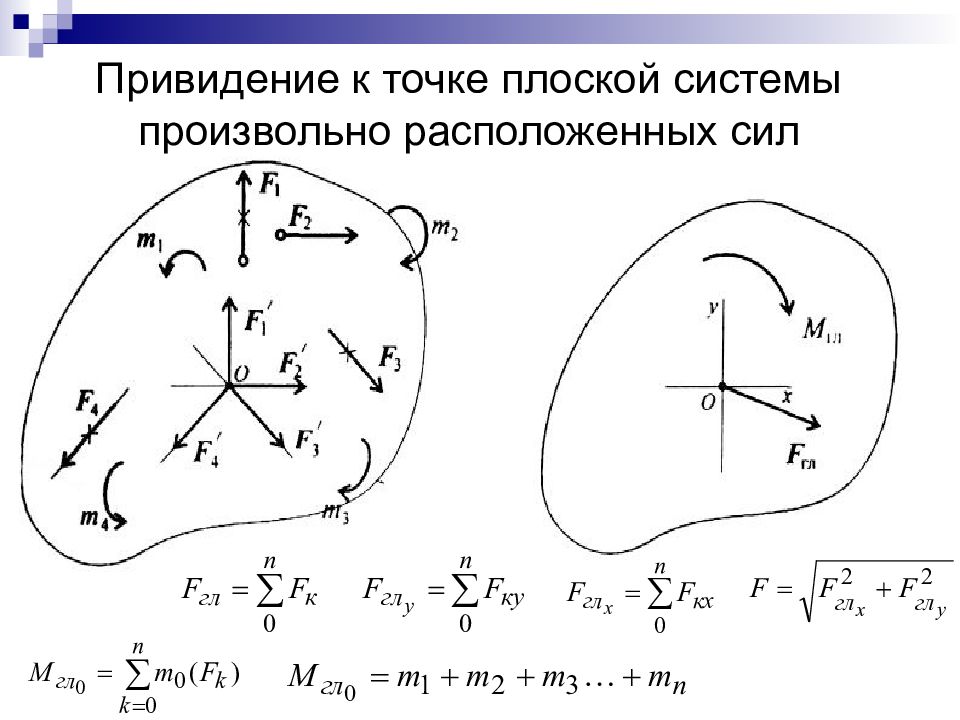
Слайд 12: Система сходящихся сил
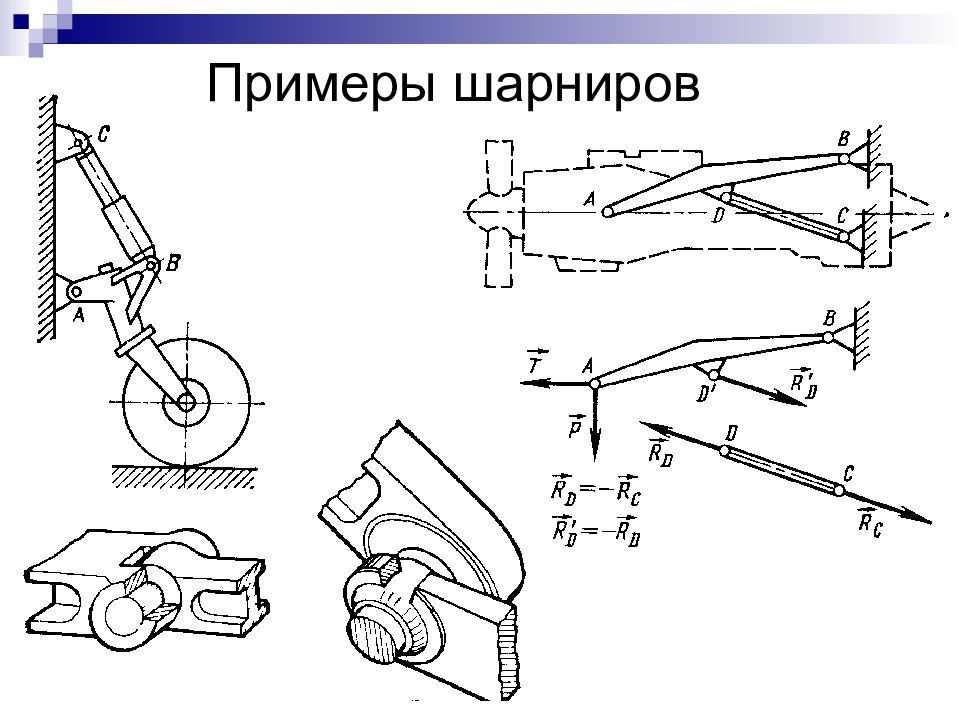
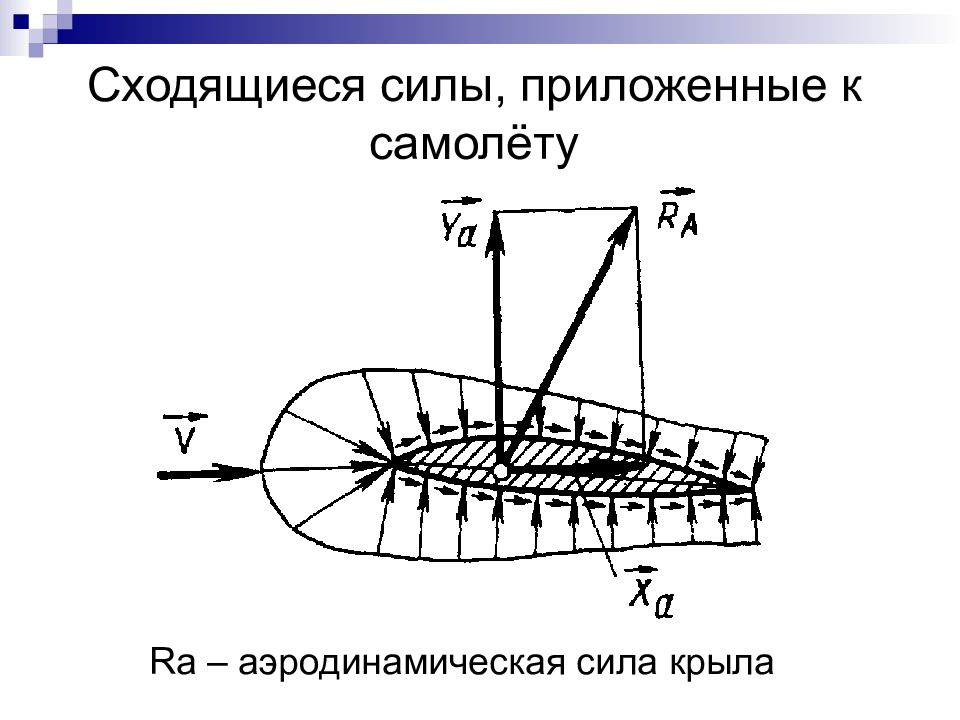
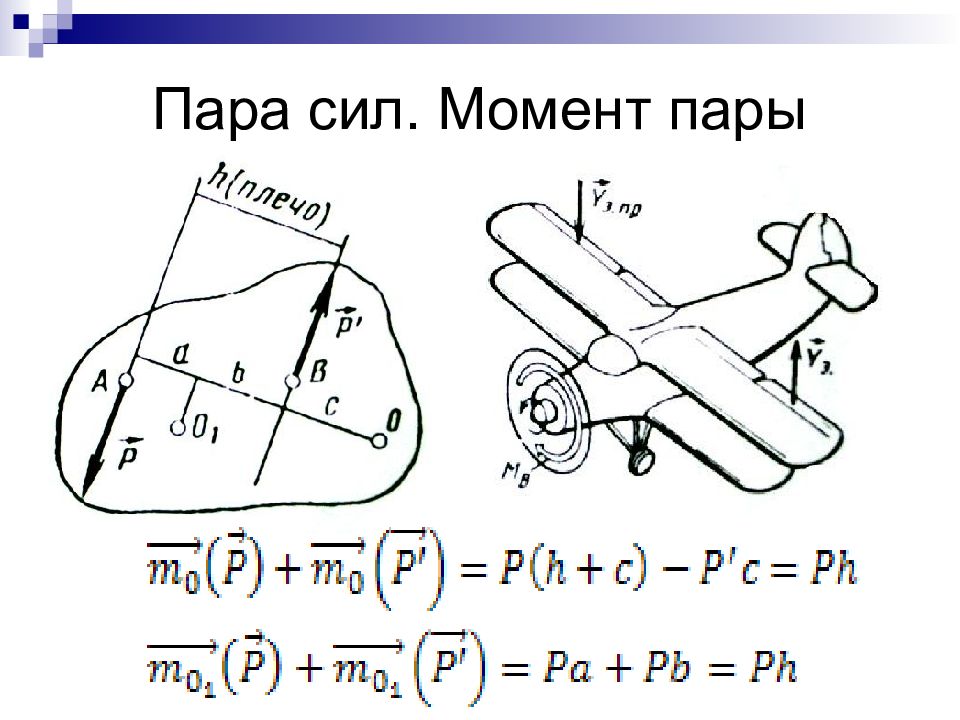
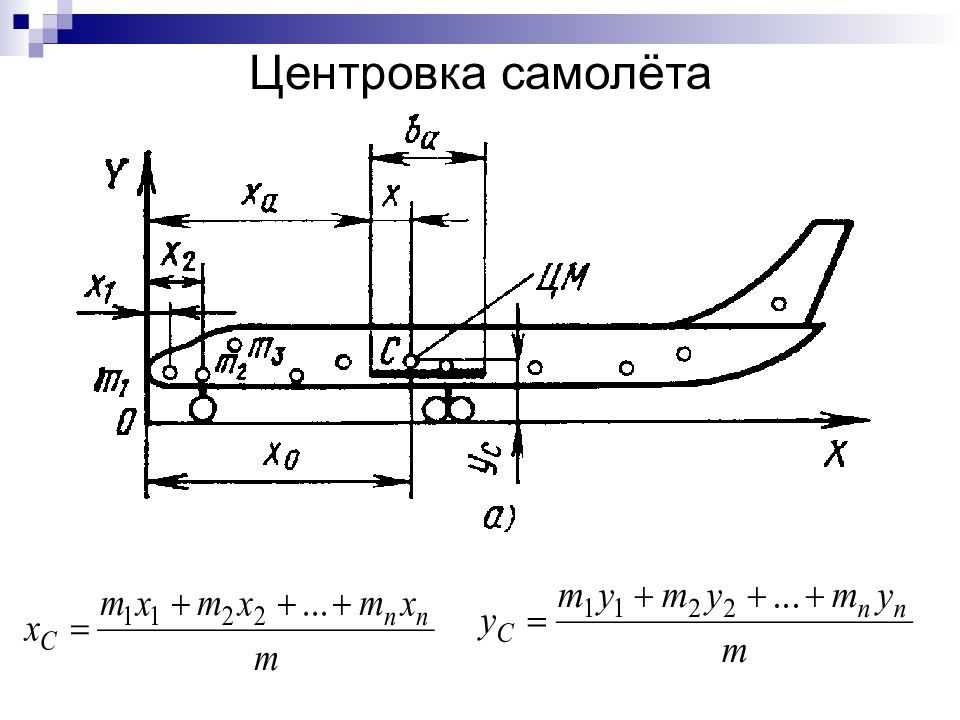
Слайд 17: Сходящиеся силы, приложенные к самолёту
Ra – аэродинамическая сила крыла
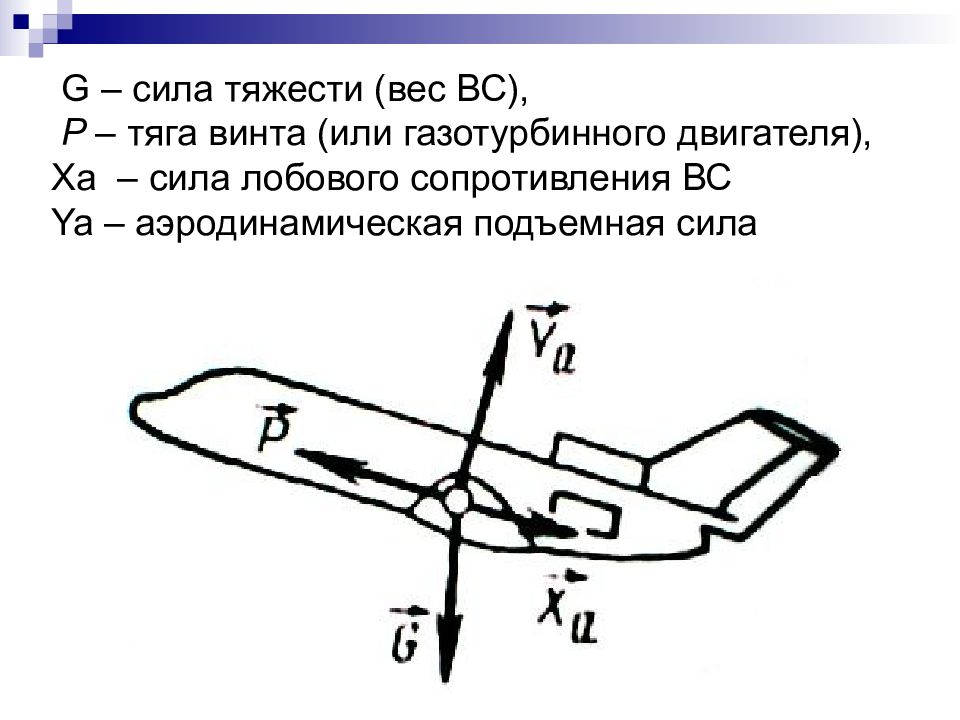
Слайд 18: G – сила тяжести (вес ВС), P – тяга винта (или газотурбинного двигателя), Xa – сила лобового сопротивления ВС Ya – аэродинамическая подъемная сила
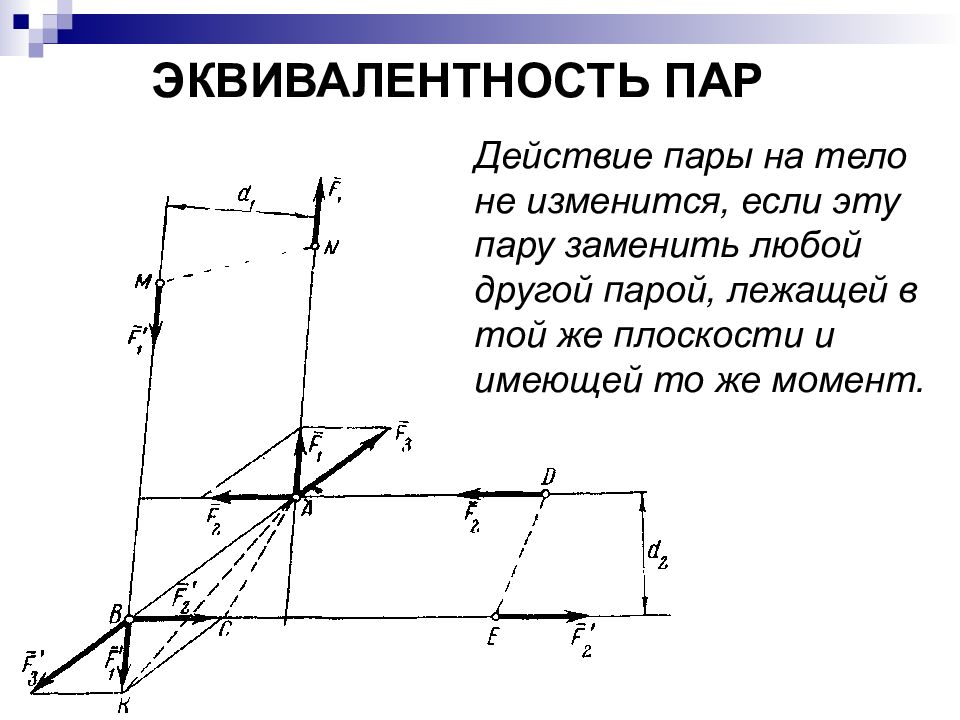
Слайд 25: ЭКВИВАЛЕНТНОСТЬ ПАР
Действие пары на тело не изменится, если эту пару заменить любой другой парой, лежащей в той же плоскости и имеющей то же момент.
Слайд 26
Свойства пары сил: 1. Действие пары на тело не изменится, если переместить пару в другое положение в плоскости ее действия. 2. Действие пары на тело не изменится, если одновременно изменить модуль сил пары и величину ее плеча, сохраняя при этом численное значение и знак, момента пары.
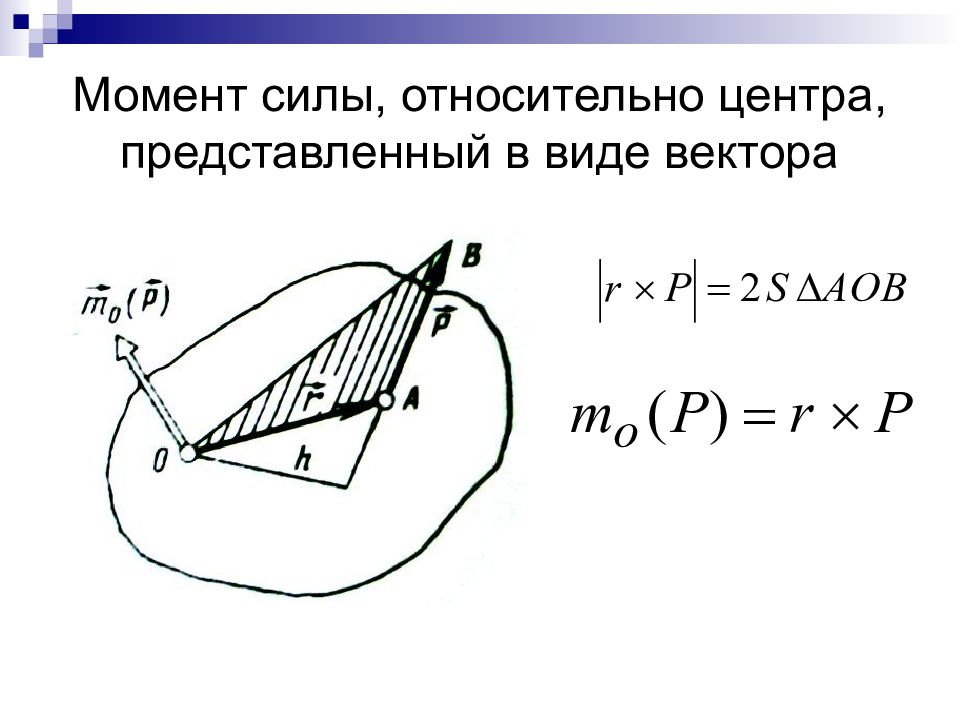
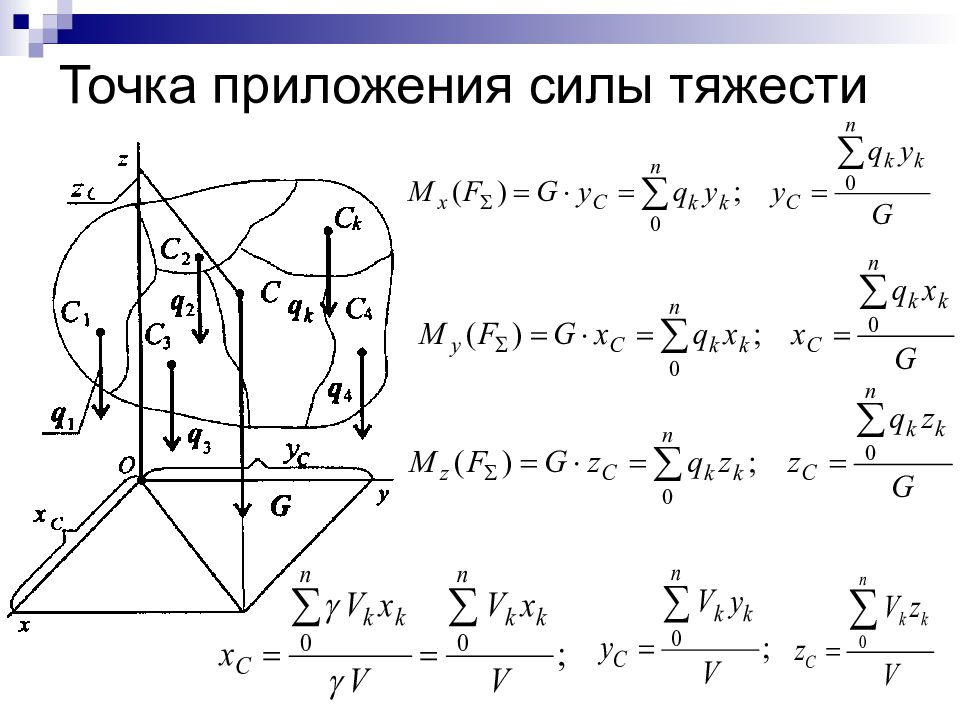
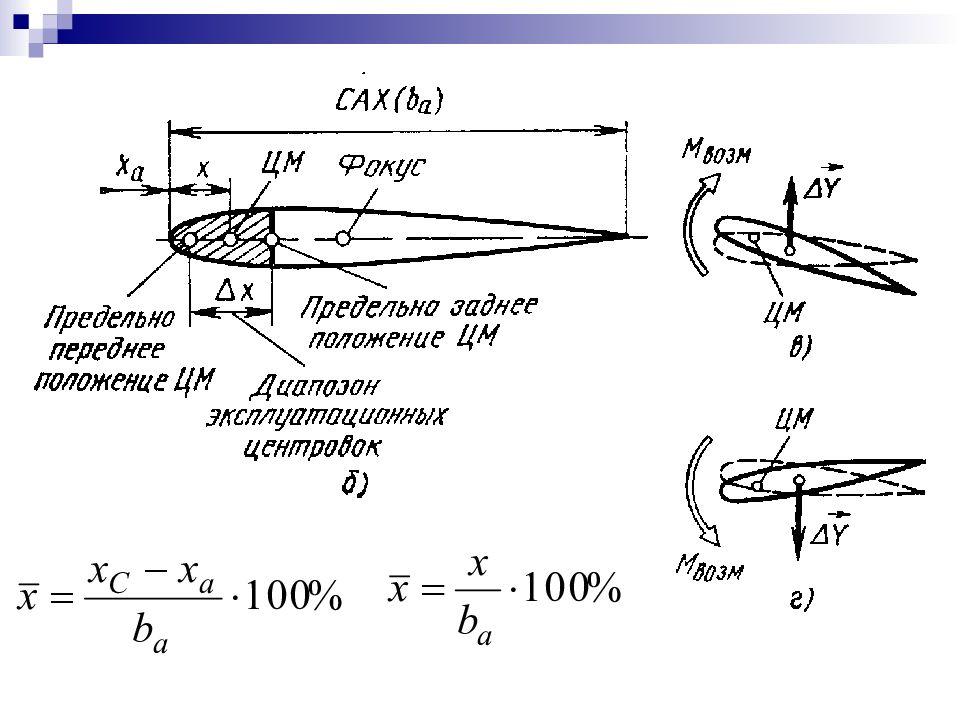
Слайд 29: Точку приложения равнодействующей можно определить по формуле
где d – расстояние от выбранной точки приведения до точки приложения равнодействующей; М гл – величина главного момента относительно выбранной точки приведения; F гл – величина главного вектора системы сил.
Слайд 32
Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил
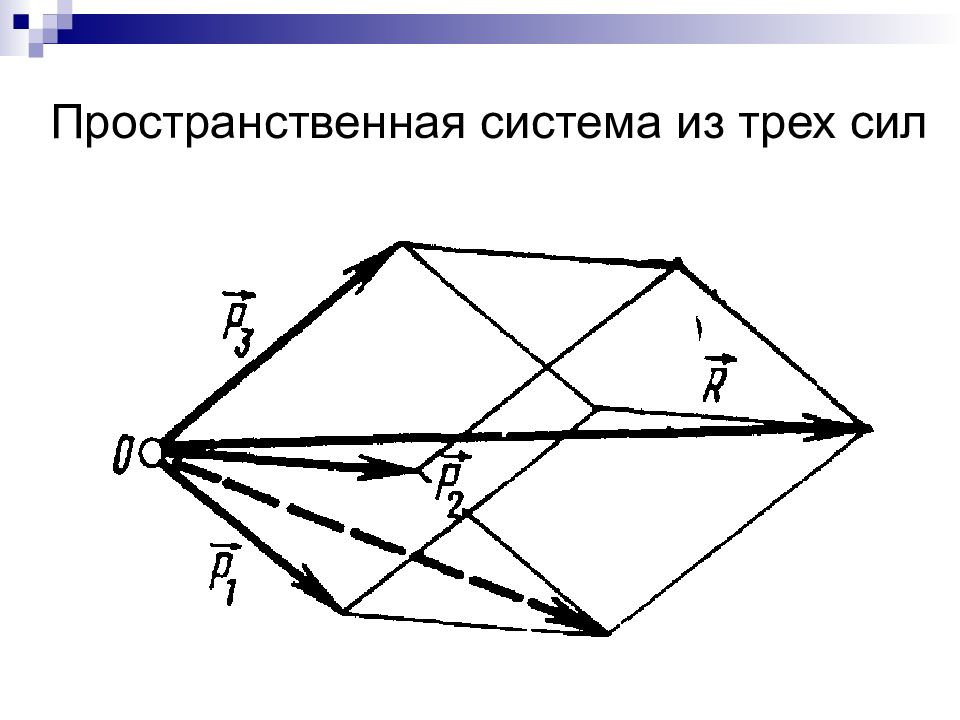
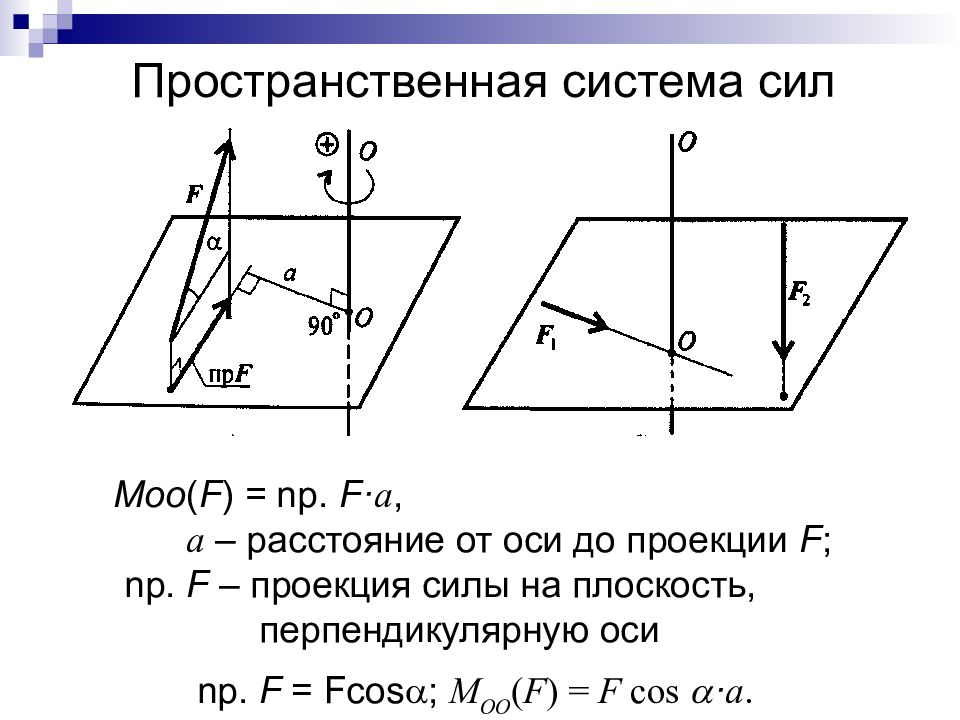
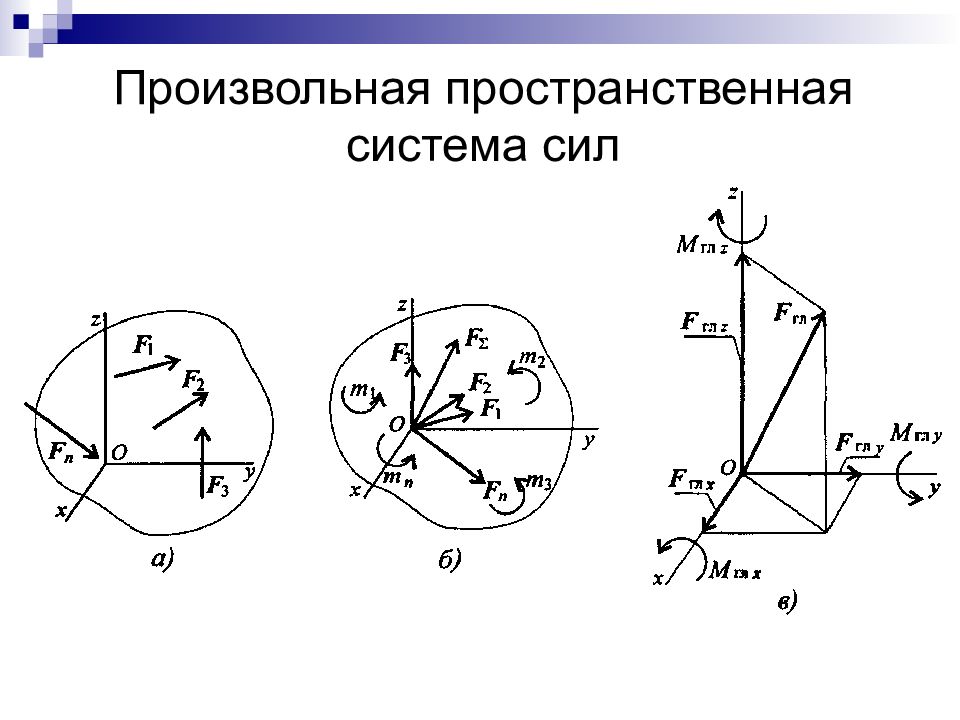
Слайд 33: Пространственная система сил
Moo ( F ) = np. F · a, a – расстояние от оси до проекции F ; np. F – проекция силы на плоскость, перпендикулярную оси np. F = Fcos ; М ОО ( F ) = F cos · a.
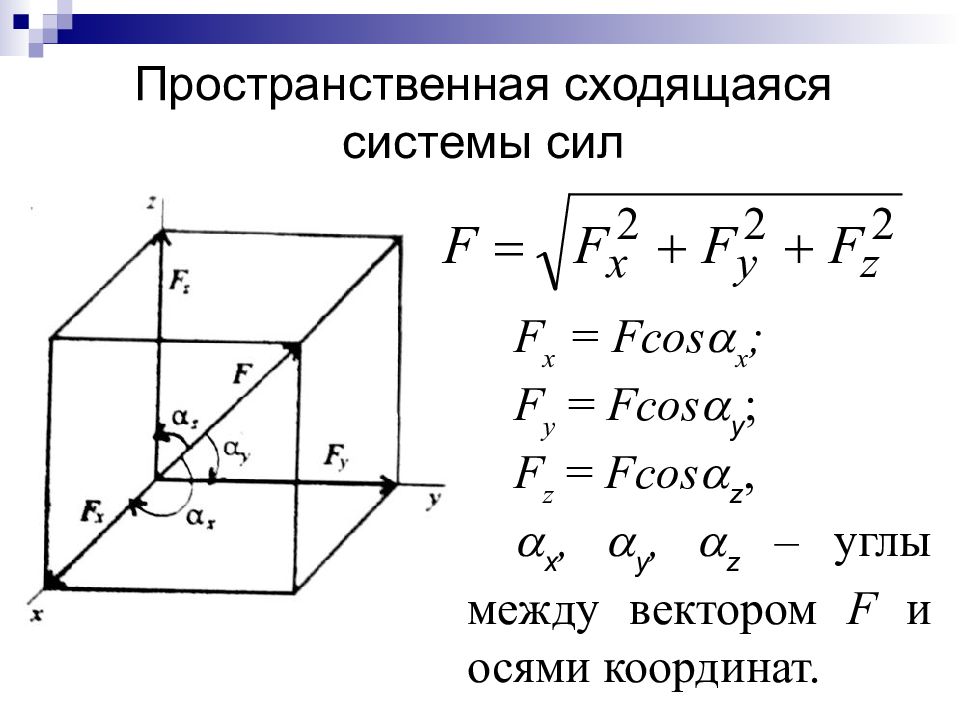
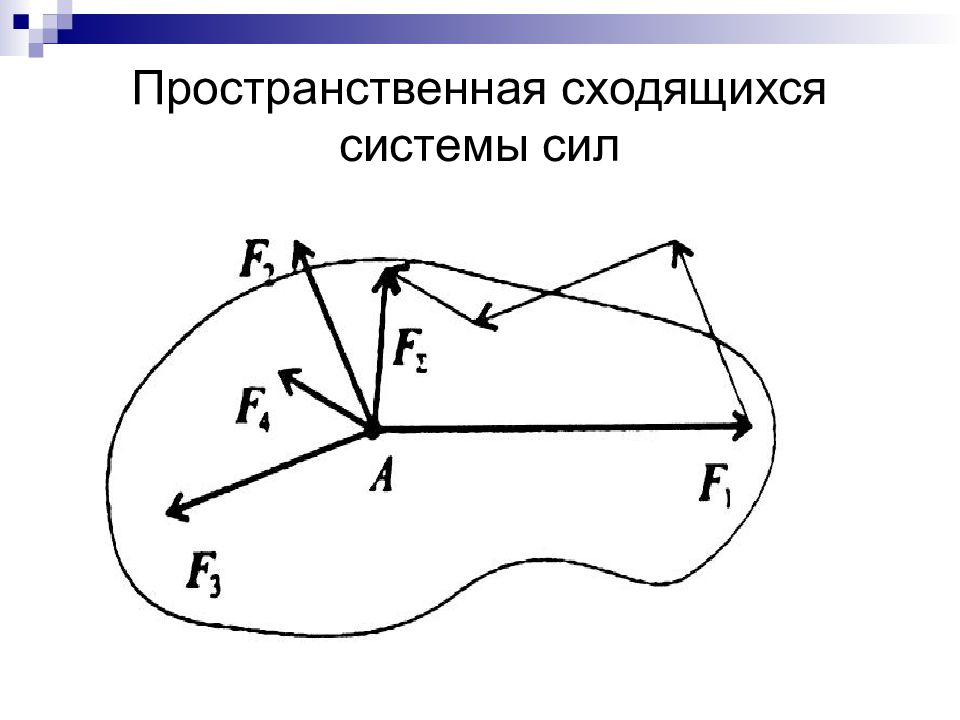
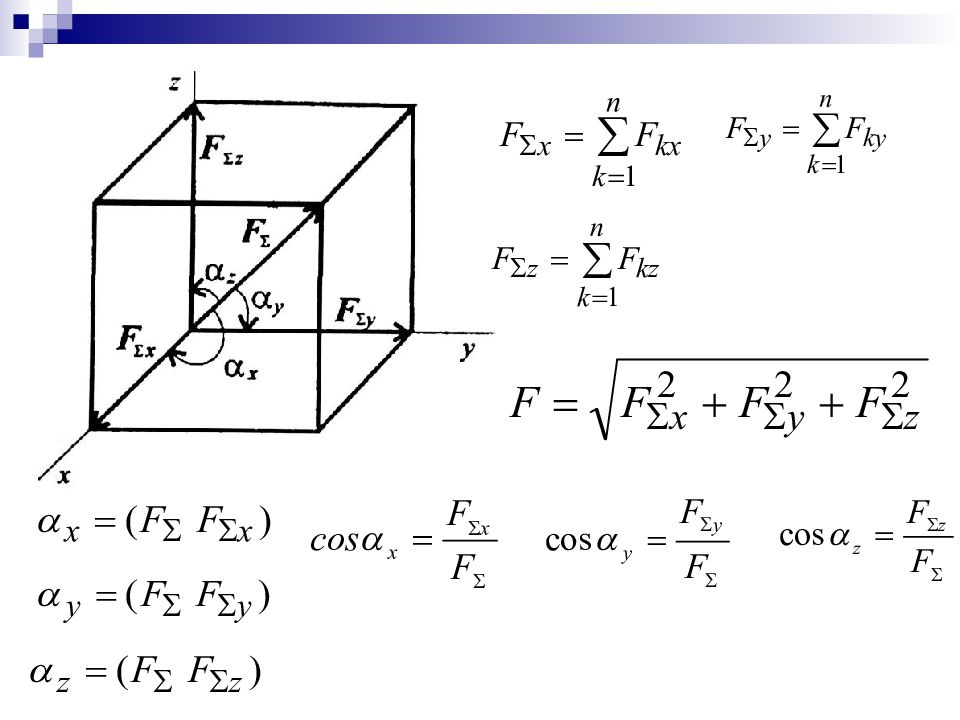
Слайд 34: Пространственная сходящаяся системы сил
F x = Fcos x ; F y = Fcos y ; F z = Fcos z, x, y, z – углы между вектором F и осями координат.
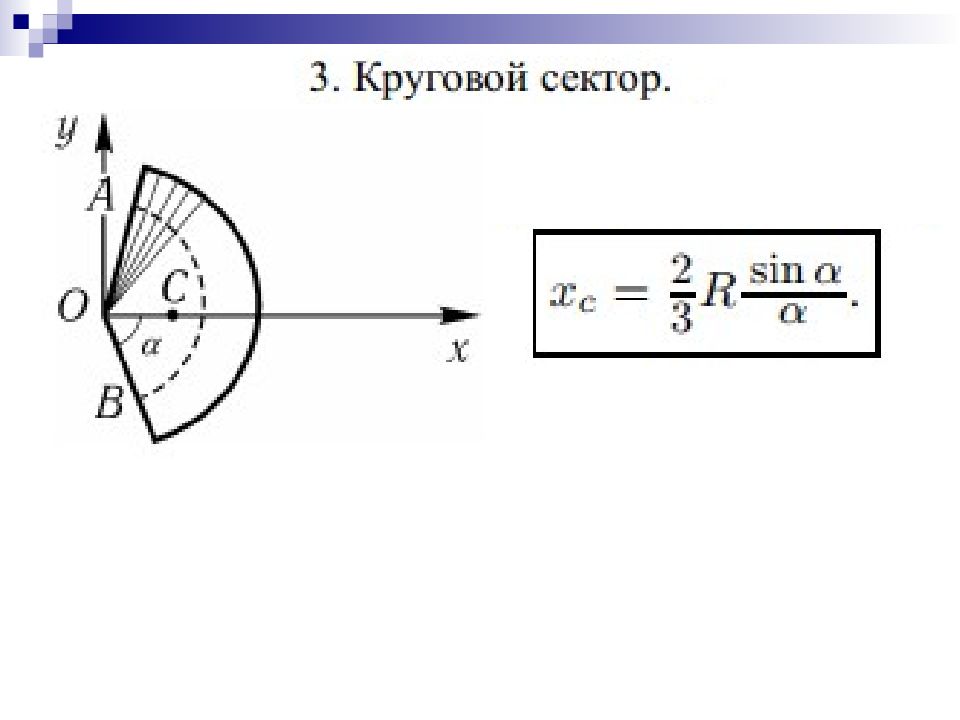
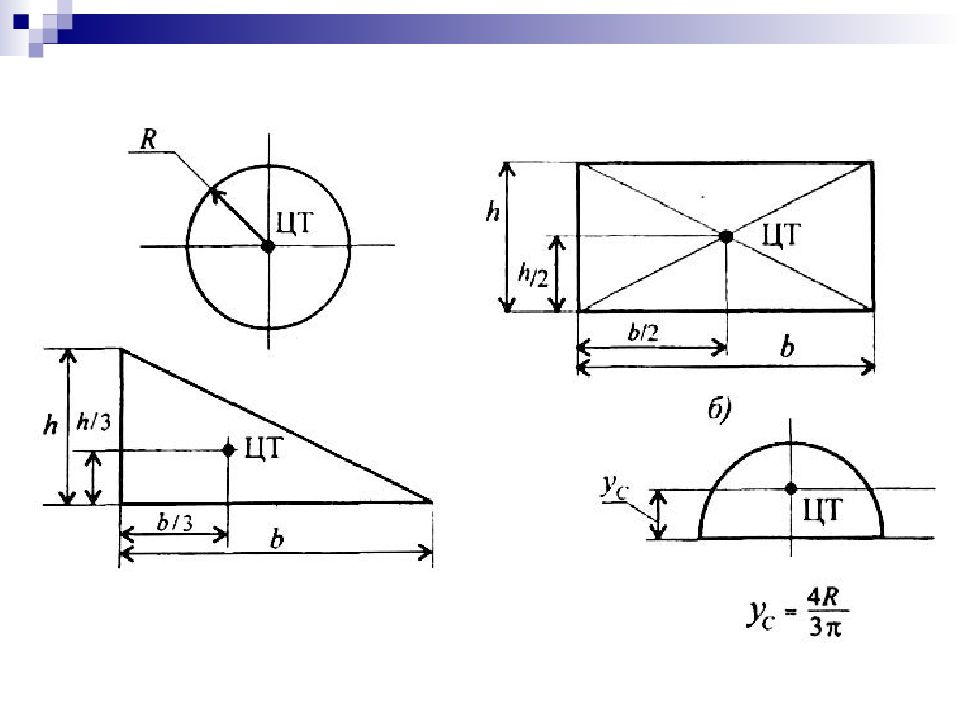
Слайд 42: Определение координат центра тяжести плоских фигур
Для плоских тел: V = Ah, где А – площадь фигуры, h – ее высота Определение координат центра тяжести плоских фигур Координаты центра тяжести сечения можно выразить через статический момент:
Слайд 46
При решении задач используются следующие методы: 1) Аналитический (интегрированием)
Слайд 47
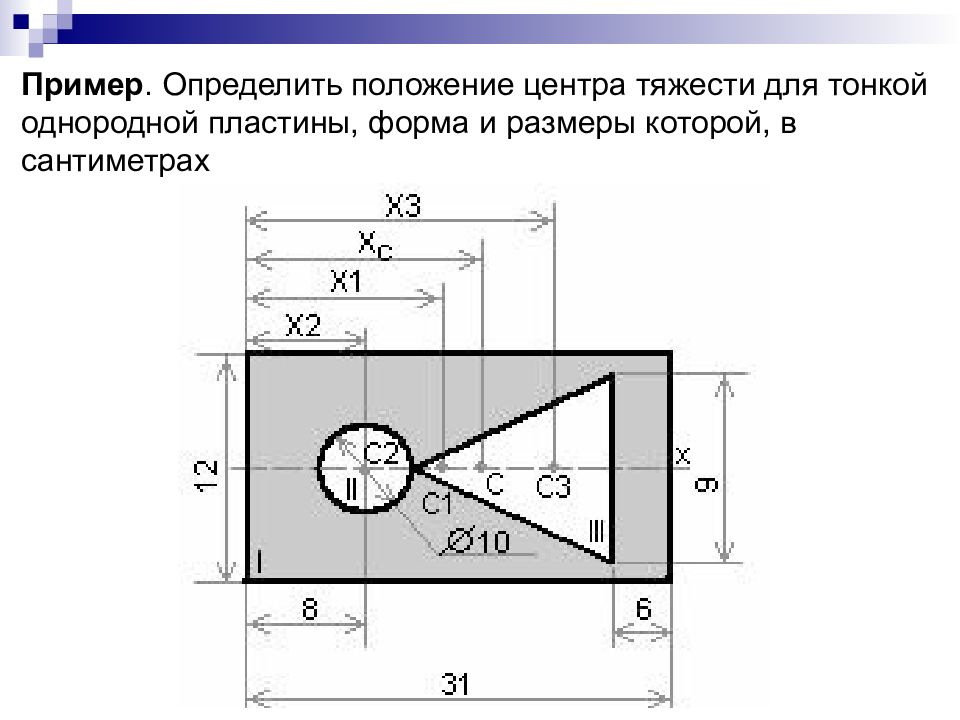
Пример. Определить положение центра тяжести для тонкой однородной пластины, форма и размеры которой, в сантиметрах
Слайд 48
Решение. Данную фигуру представляем состоящей из трех простых фигур: 1 – прямоугольник, 2 – круга, 3 – треугольника. Площади кругового и треугольного отверстий вводим в расчет со знаком минус, а площадь прямоугольника – без учета имеющихся в нем отверстий. Площади простых фигур: Высота треугольника
Слайд 49
Координаты центра тяжести простых фигур: х 1 =31/2=15,5 см, х 2 =8см, х 3 =31-6-12/3=21см, где 12/3 – расстояние от центра тяжести треугольника до его основания, равное 1/3 высоты. Координата центра тяжести заданной фигуры
Слайд 55
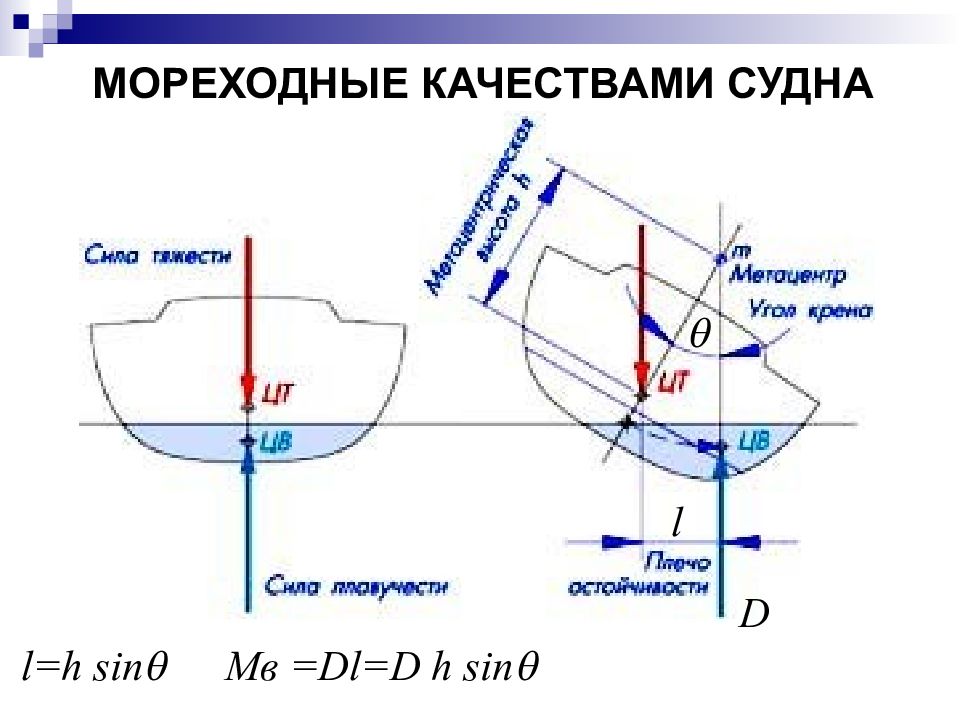
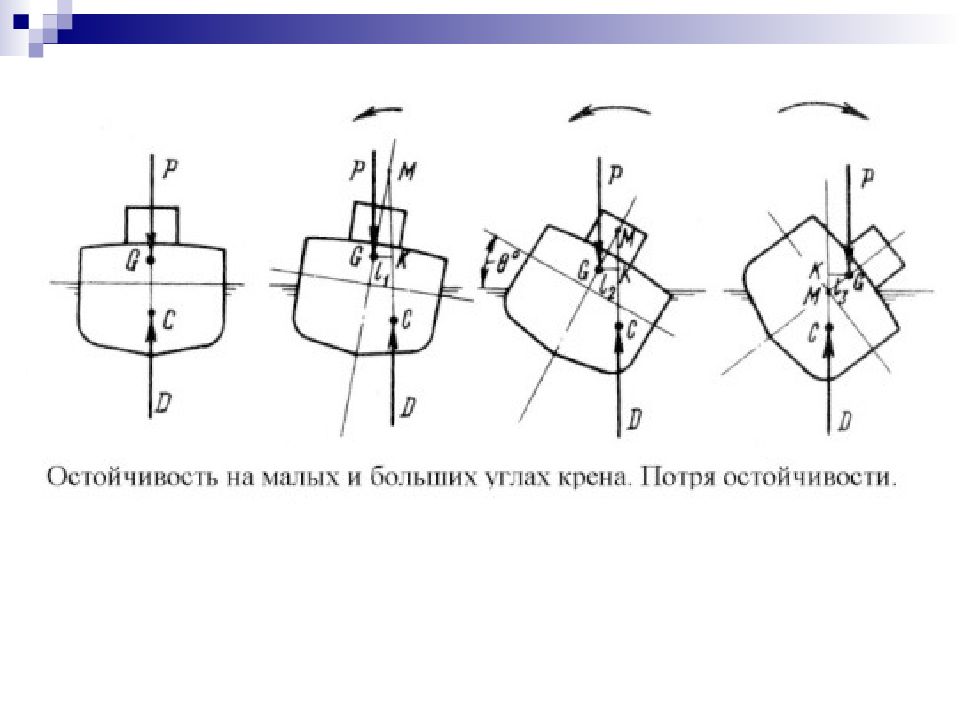
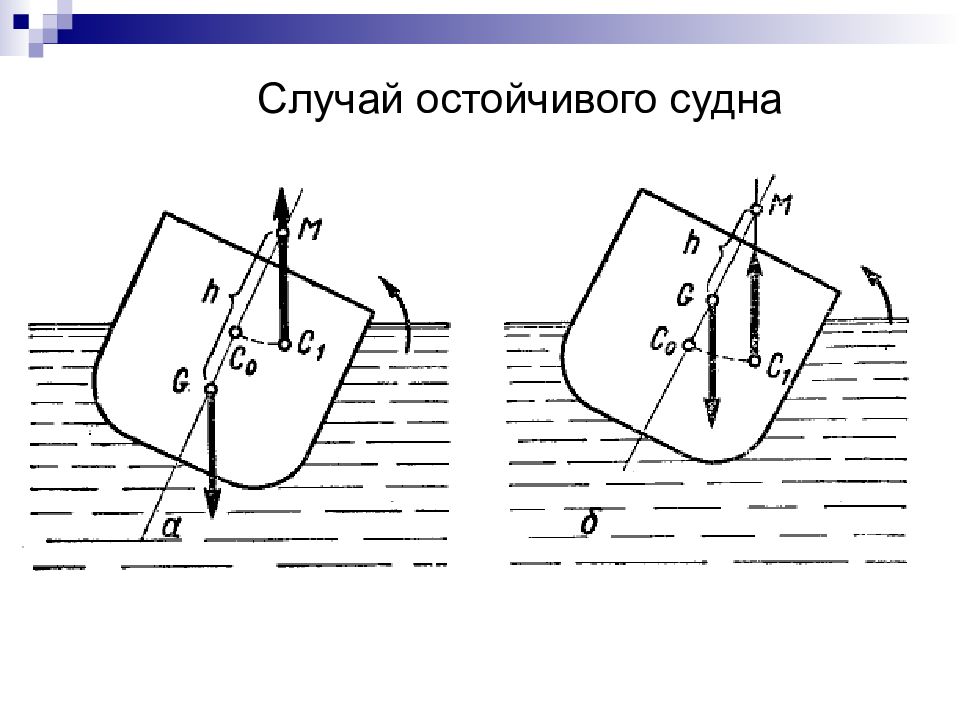
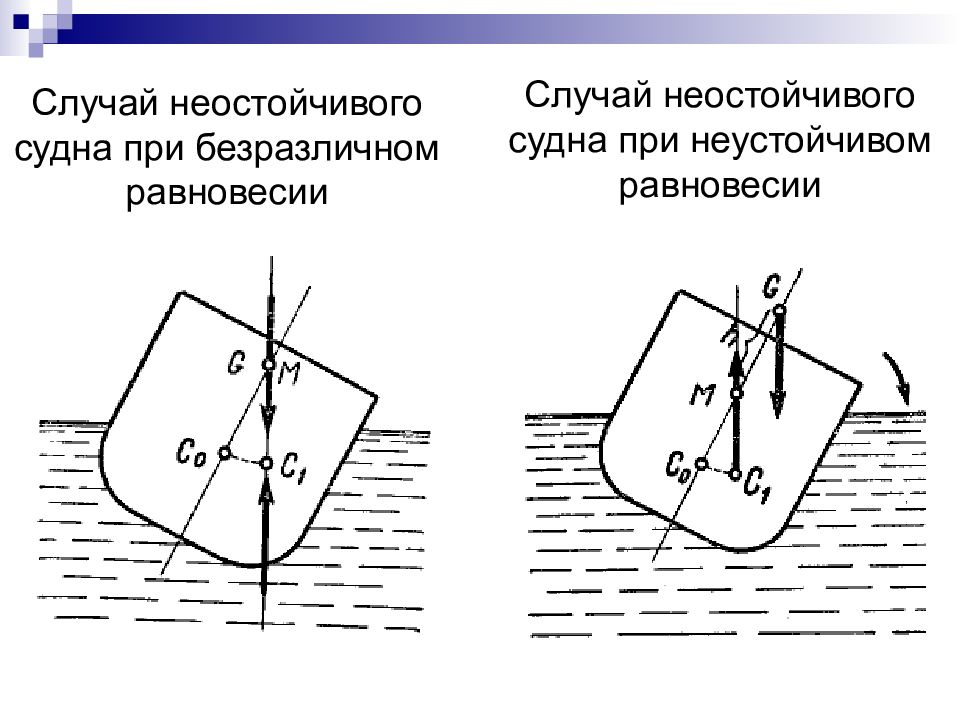
Случай неостойчивого судна при безразличном равновесии Случай неостойчивого судна при неустойчивом равновесии
Слайд 56
Для классической яхты “Contessa 32” потеря остойчивости наступает только при крене 155°
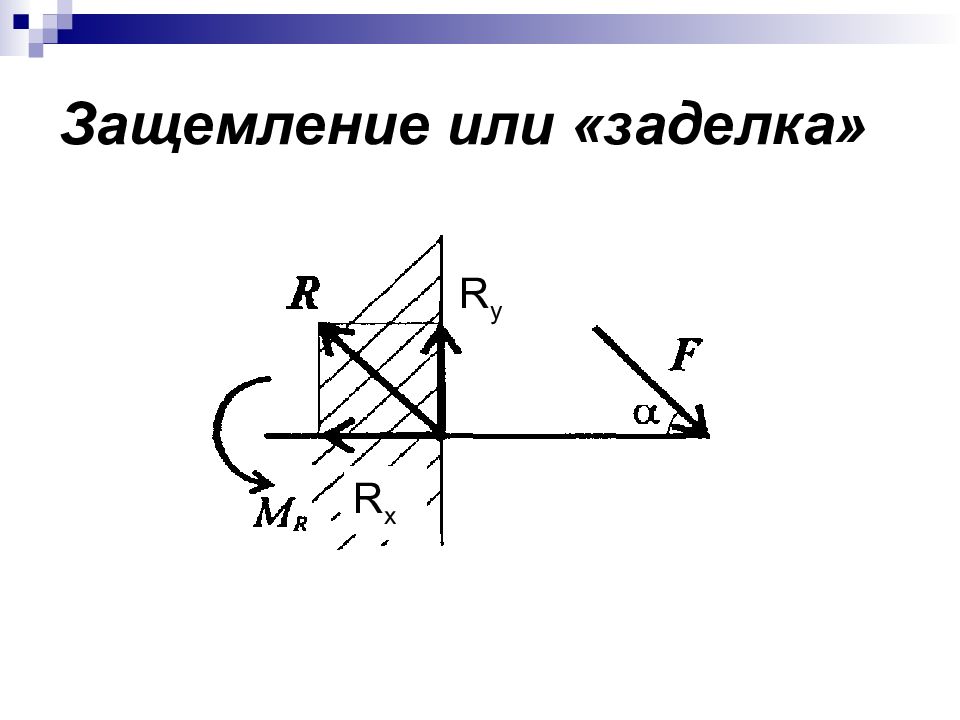
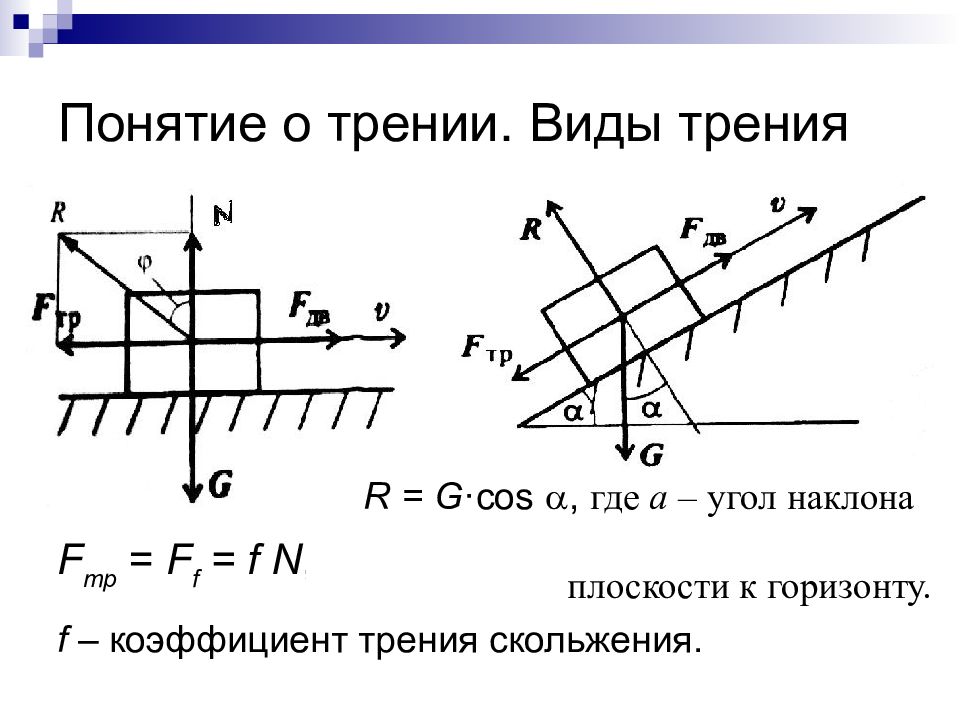
Слайд 57: Понятие о трении. Виды трения
F тр = F f = f N, f – коэффициент трения скольжения. R = G · cos , где а – угол наклона плоскости к горизонту.
Слайд 58
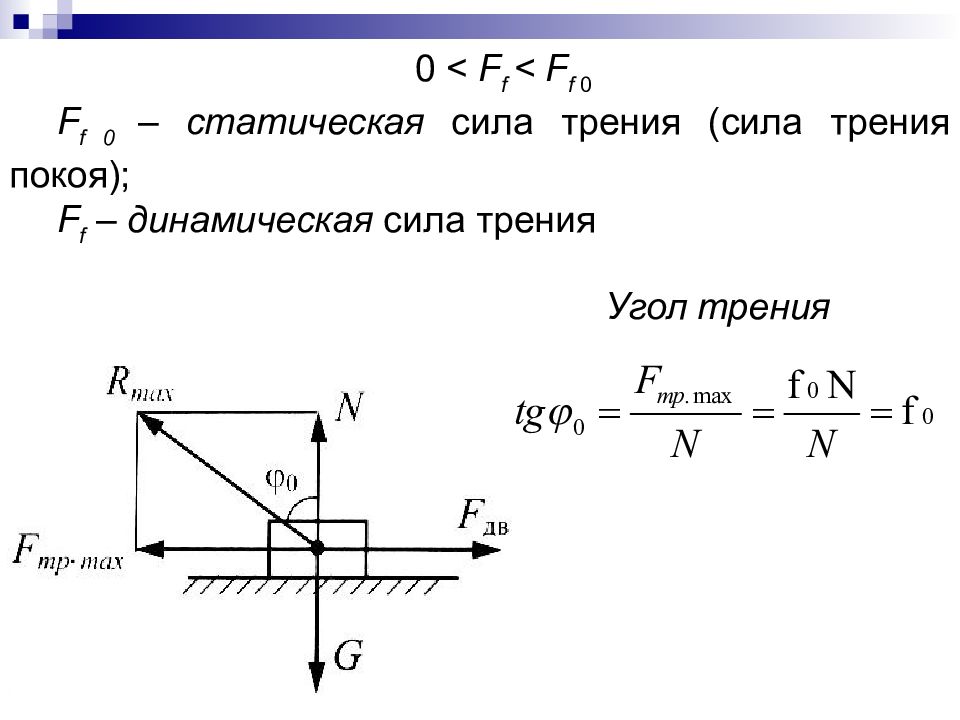
0 < F f < F f 0 F f 0 – статическая сила трения (сила трения покоя); F f – динамическая сила трения Угол трения
Слайд 59
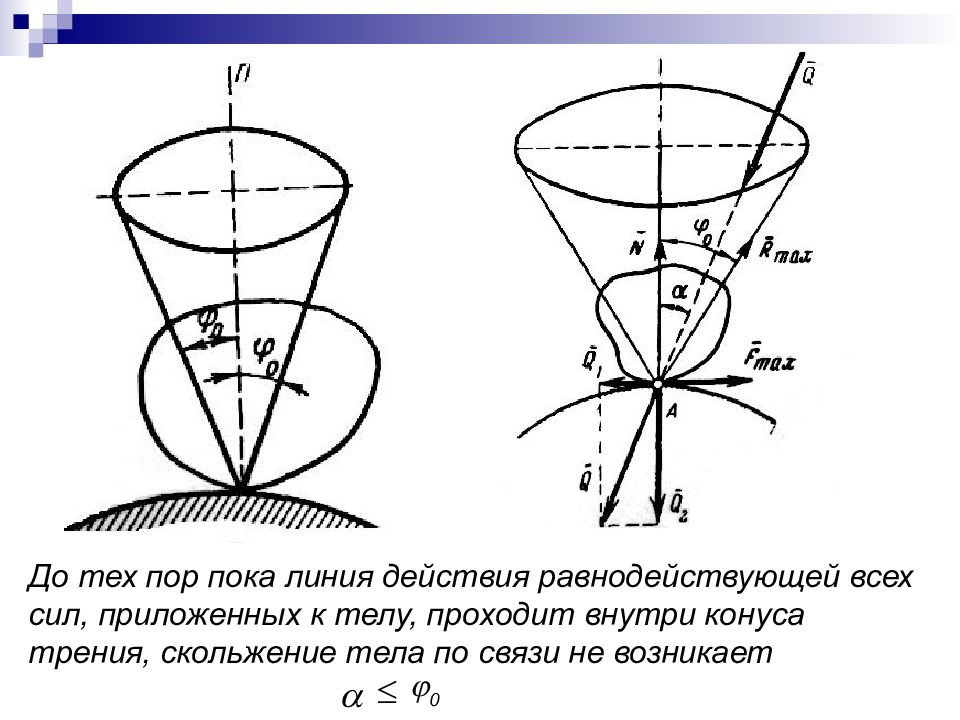
До тех пор пока линия действия равнодействующей всех сил, приложенных к телу, проходит внутри конуса трения, скольжение тела по связи не возникает 0
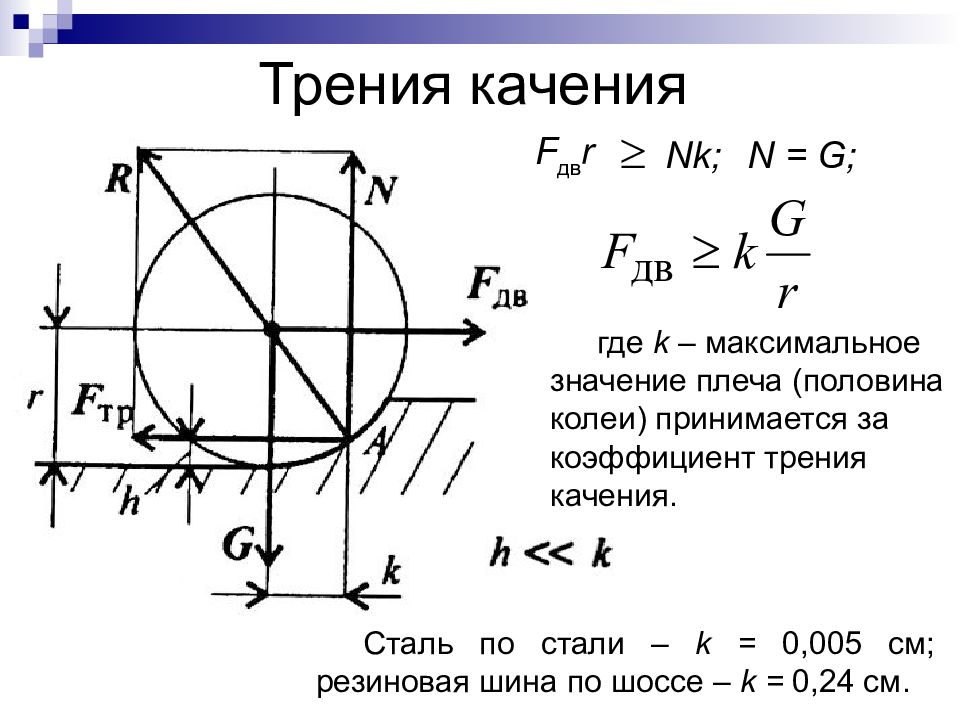
Последний слайд презентации: СТАТИКА: Трения качения
Nk; Трения качения F дв r где k – максимальное значение плеча (половина колеи) принимается за коэффициент трения качения. N = G ; C таль по стали – k = 0,005 см; резиновая шина по шоссе – k = 0,24 см.