Первый слайд презентации: СВОЙСТВА И ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
(9 класс) Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной
Слайд 2: Содержание
Схема исследования функций Постоянная функция (у = с) Линейная функция (у = k х+в) Квадратичная функция (у = k · х ² ) Функция обратной пропорциональности ( у = k /х) Функция корня (у = √ х) Функция модуля (у = | х | ) Функция (у = ах ² + вх + с) Другие функции
Слайд 3: Схема исследования функций
Область определения D(f). Множество значений Е (f) Нули функции ( у=0) Интервалы знакопостоянства (у > 0 ; у < 0) Промежутки монотонности (возрастания, убывания) Набольшее и наименьшее значения функции Ограниченность функции Непрерывность функции Выпуклость функции Четность функции
Слайд 4: Постоянная функция У=С
у =С СВОЙСТВА: 1) D(f) = R 2) Е (f) = множество, состоящее из единственного числа С 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: не определена 8) Непрерывность функции: непрерывна 9) Выпуклость функции: 10) Четность функции: четная 0 х у С
Слайд 5
Графиком функции является прямая и Если к > 0 Если к < 0 СВОЙСТВА: 1) D(f) = R 2) Е (f) = R 3) Нули функции: у=0 при х = х 1 4) Интервалы знакопостоянства: у > 0 при х Є… (для каждого графика свое) у < 0 при х Є… (для каждого графика свое) 5) Промежутки монотонности: У возрастает при к > 0 У убывает при к < 0 6) У наиб.= нет У наим. = нет 7) Ограниченность функции: не ограничена 8) Непрерывность функции: непрерывна 9) Выпуклость функции : ( нет смысла) 10) Четность функции: (нет смысла) Линейная функция у=кх+в х у в 0 х у В О у=кх+в у=кх+в х 1 х 1
Слайд 6: у = k · х ²
Графиком функции является парабола с вершиной в начале координат и если к > 0, то: СВОЙСТВА: 1) D(f) = R или (- ∞; + ∞ ) 2) Е (f) = [ 0; + ∞ ) 3) Нули функции: у=0 при х= 0 4) Интервалы знакопостоянства: у > 0 при х Є ( - ∞; 0 ) U (0; + ∞ ) 5) Промежутки монотонности: У возрастает при х Є [ 0; + ∞ ) У убывает при х Є ( - ∞; 0 ] 6) У наиб. - нет У наим. = 0 7) Ограниченность функции: ограничена снизу 8) Непрерывность функции: непрерывна 9) Выпуклость функции: выпукла вниз 10) Четность функции: четная Квадратичная функция 0 Х У У=КХ ²
Слайд 7: у = k · х ²
Графиком функции является парабола с вершиной в начале координат и если к < 0, то: СВОЙСТВА: 1) D(f) = R или (- ∞; + ∞ ) 2) Е (f) = ( - ∞;0 ] 3) Нули функции: у=0 при х=0 4) Интервалы знакопостоянства: у < 0 при х Є ( - ∞; 0 ) U (0; + ∞ ) 5) Промежутки монотонности: У возрастает при х Є ( - ∞; 0 ] У убывает при х Є [ 0; + ∞ ) 6) У наиб.= 0 У наим. – не сущ. 7) Ограниченность функции: ограничена сверху 8) Непрерывность функции: непрерывна 9) Выпуклость функции: выпукла вверх 10) Четность функции: четная Квадратичная функция 0 Х У У=КХ ²
Слайд 8: у = k /х
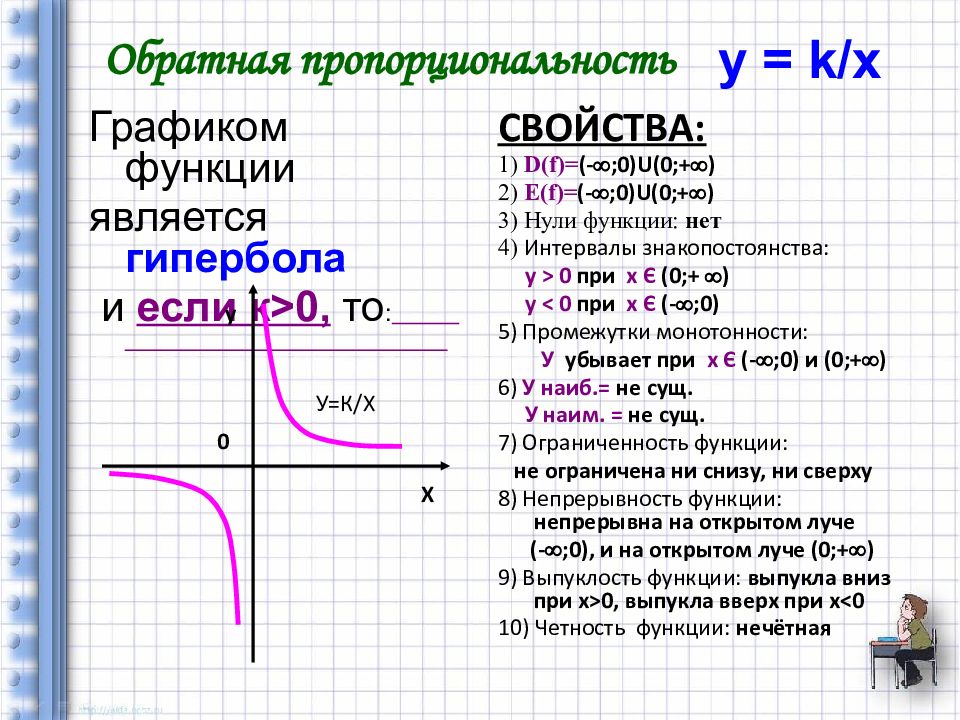
Графиком функции является гипербола и если к > 0, то : СВОЙСТВА: 1) D(f) = (- ;0) U (0;+ ) 2) Е (f) = (- ;0) U (0;+ ) 3) Нули функции: нет 4) Интервалы знакопостоянства: у > 0 при х Є (0;+ ) у < 0 при х Є (- ;0) 5) Промежутки монотонности: У убывает при х Є (- ;0) и (0;+ ) 6) У наиб.= не сущ. У наим. = не сущ. 7) Ограниченность функции: н е ограничена ни снизу, ни сверху 8) Непрерывность функции: н епрерывна на открытом луче (- ;0), и на открытом луче ( 0 ;+ ) 9) Выпуклость функции: в ыпукла вниз при x>0, выпукла вверх при x<0 10) Четность функции: н ечётная Обратная пропорциональность Х у 0 У=К/Х
Слайд 9: у = k /х
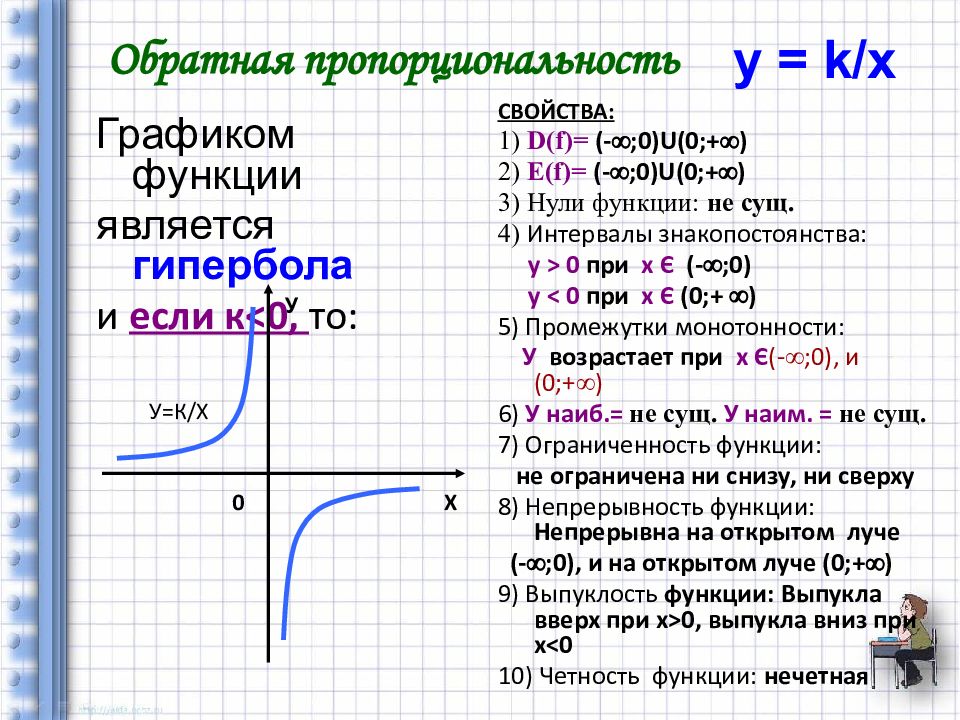
Графиком функции является гипербола и если к < 0, то: СВОЙСТВА: 1) D(f) = (- ;0) U (0;+ ) 2) Е (f) = (- ;0) U (0;+ ) 3) Нули функции: не сущ. 4) Интервалы знакопостоянства: у > 0 при х Є (- ;0) у < 0 при х Є (0;+ ) 5) Промежутки монотонности: У возрастает при х Є (- ;0), и ( 0 ;+ ) 6) У наиб.= не сущ. У наим. = не сущ. 7) Ограниченность функции: н е ограничена ни снизу, ни сверху 8) Непрерывность функции: Непрерывна на открытом луче ( - ;0), и на открытом луче ( 0 ;+ ) 9) Выпуклость функции: Выпукла вверх при x>0, выпукла вниз при x<0 10) Четность функции: нечетная Обратная пропорциональность Х У 0 У=К/Х
Слайд 10: у = √ х
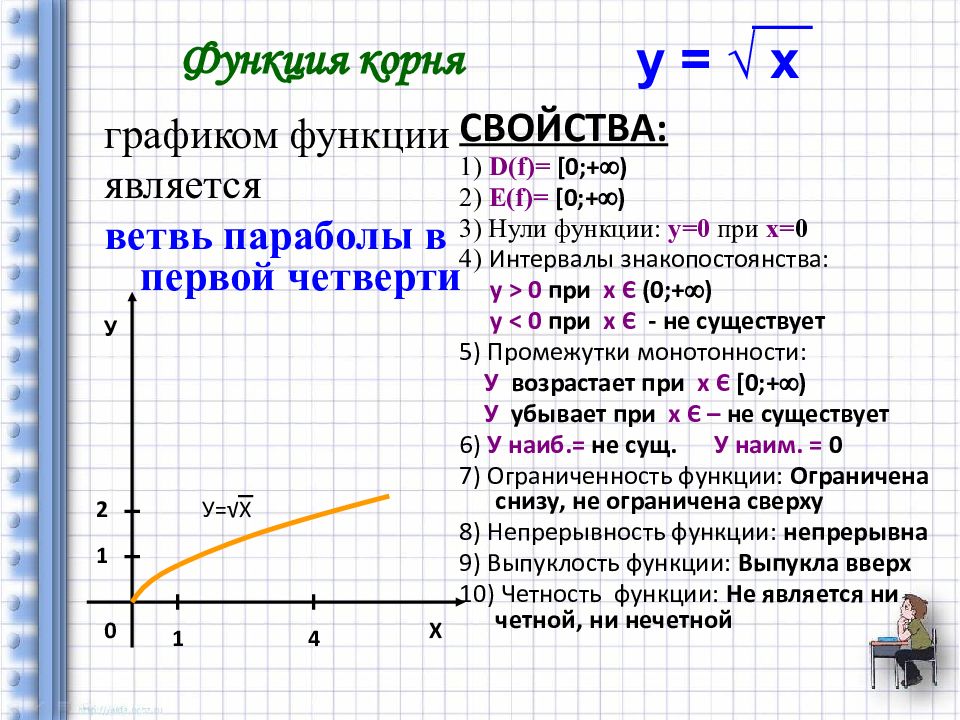
графиком функции является ветвь параболы в первой четверти СВОЙСТВА: 1) D(f) = [0 ;+ ) 2) Е (f) = [0; + ) 3) Нули функции: у=0 при х= 0 4) Интервалы знакопостоянства: у > 0 при х Є ( 0; + ) у < 0 при х Є - не существует 5) Промежутки монотонности: У возрастает при х Є [0 ;+ ) У убывает при х Є – не существует 6) У наиб.= не сущ. У наим. = 0 7) Ограниченность функции: Ограничена снизу, не ограничена сверху 8) Непрерывность функции: непрерывна 9) Выпуклость функции: Выпукла вверх 10) Четность функции: Не является ни четной, ни нечетной Функция корня Х У 0 1 4 1 2 У=√Х
Слайд 11
Графиком функции является объединение двух лучей : у=х, х≥0 и у=-х, х≤0. СВОЙСТВА: 1) D(f) = (- ;+ ) 2) Е (f) = [0; + ) 3) Нули функции: у=0 при х= 0 4) Интервалы знакопостоянства: у > 0 при х Є (- ; 0) U ( 0; + ) у < 0 при х Є – не существует 5) Промежутки монотонности: У возрастает на луче [0 ;+ ) У убывает на луче (- ;0 ], 6) У наиб.= не сущ. У наим. = 0 7) Ограниченность функции: Ограничена снизу, не ограничена сверху 8) Непрерывность функции: Непрерывна 9) Выпуклость функции: можно считать выпуклой вниз 10) Четность функции: Чётная Функция модуля y = | x | Х У 0 У = | х |
Слайд 12: Функция у = ах ² + вх + с
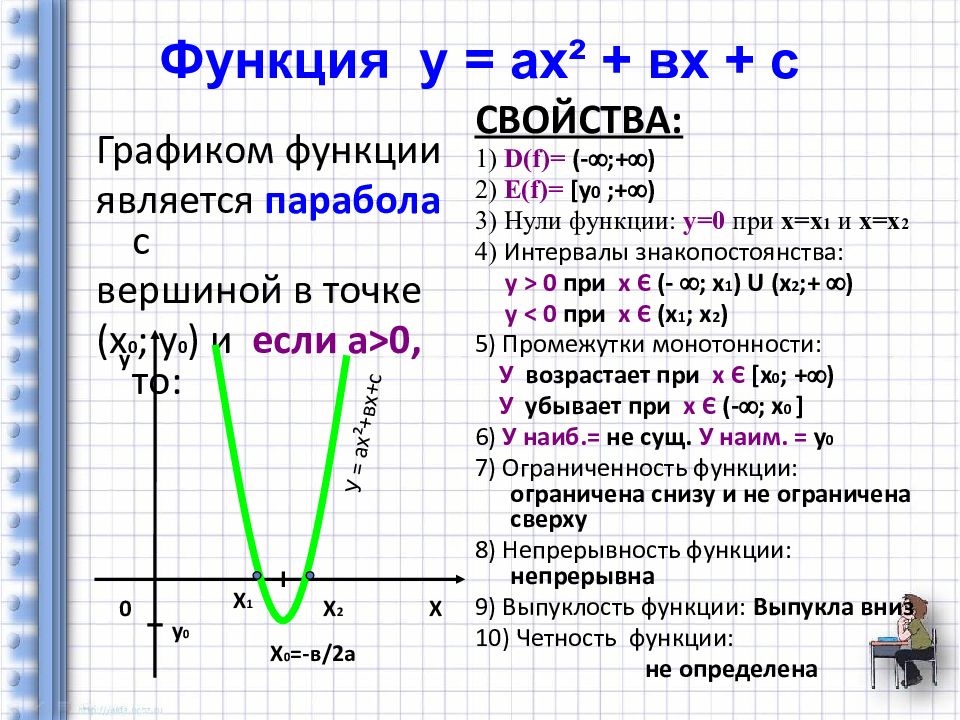
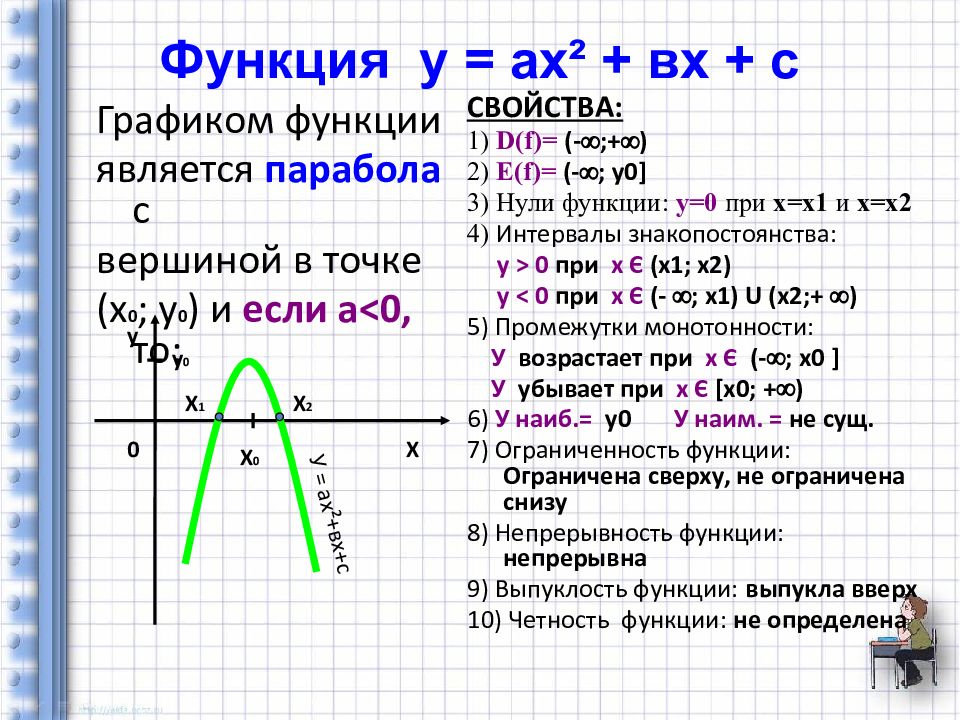
Графиком функции является парабола с вершиной в точке (х 0 ; у 0 ) и если а > 0, то: СВОЙСТВА: 1) D(f) = (- ;+ ) 2) Е (f) = [y 0 ; + ) 3) Нули функции: у=0 при х=х 1 и х=х 2 4) Интервалы знакопостоянства: у > 0 при х Є (- ; х 1 ) U ( х 2 ;+ ) у < 0 при х Є ( х 1 ; х 2 ) 5) Промежутки монотонности: У возрастает при х Є [ х 0 ; + ) У убывает при х Є (- ; х 0 ] 6) У наиб.= не сущ. У наим. = у 0 7) Ограниченность функции: ограничена снизу и не ограничена сверху 8) Непрерывность функции: непрерывна 9) Выпуклость функции: Выпукла вниз 10) Четность функции: не определена Х у 0 Х 0 =-в/2а у 0 У = ах ² +вх+с Х 1 Х 2
Слайд 13: Функция у = ах ² + вх + с
Графиком функции является парабола с вершиной в точке (х 0 ; у 0 ) и если а < 0, то: СВОЙСТВА: 1) D(f) = (- ;+ ) 2) Е (f) = (- ; y 0 ] 3) Нули функции: у=0 при х=х1 и х=х2 4) Интервалы знакопостоянства: у > 0 при х Є ( х1 ; х2) у < 0 при х Є (- ; х1) U ( х2 ;+ ) 5) Промежутки монотонности: У возрастает при х Є (- ; х0 ] У убывает при х Є [ х0; + ) 6) У наиб.= у0 У наим. = не сущ. 7) Ограниченность функции: Ограничена сверху, не ограничена снизу 8) Непрерывность функции: непрерывна 9) Выпуклость функции: выпукла вверх 10) Четность функции: не определена Х у 0 у 0 Х 0 У = ах ² +вх+с Х 1 Х 2
Слайд 14: вспомним
Аналитичес кая формула Название функции Название графика Схематический рисунок у=кх+в линейная прямая у=кх прямая пропорциональность прямая у=к/х обратная пропорциональность гипербола у= ах ² квадратичная парабола у= ах ² +вх+с квадратичная парабола у= √х корень из х ветвь параболы у= | х | модуль х объединение двух лучей
Слайд 15: Функция у = - √ х
графиком функции является ветвь параболы. СВОЙСТВА: 1) D(f) = 2) Е (f) = 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: 8) Непрерывность функции: 9) Выпуклость функции: 10) Четность функции: у Х 0 1 4 -1 -2
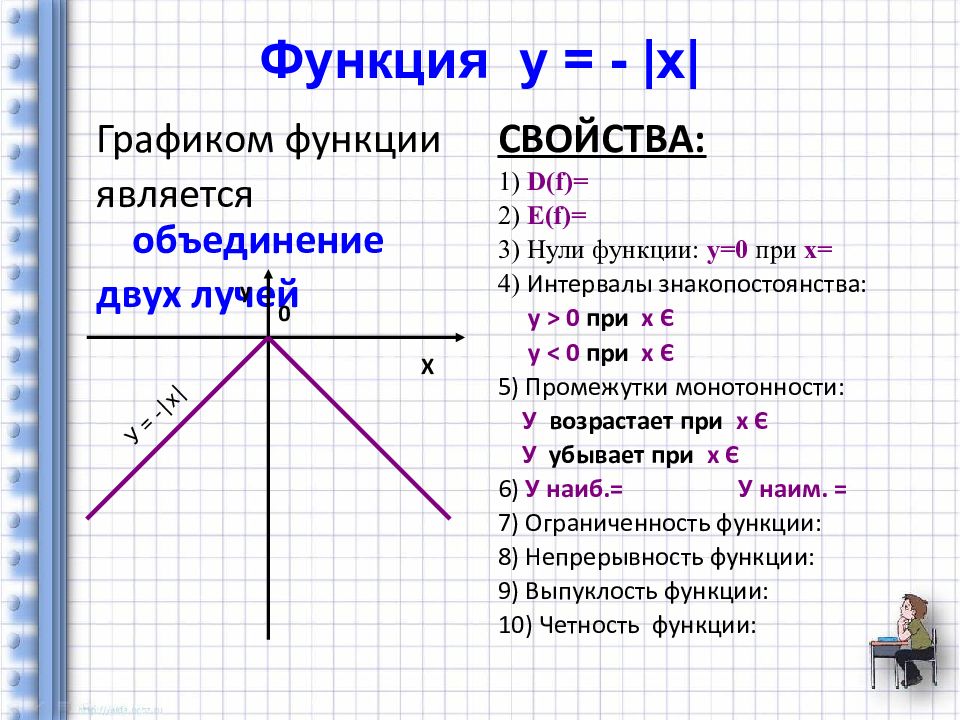
Слайд 16: Функция у = - | х |
Графиком функции является объединение двух лучей СВОЙСТВА: 1) D(f) = 2) Е (f) = 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: 8) Непрерывность функции: 9) Выпуклость функции: 10) Четность функции: Х у 0 У = - | х |
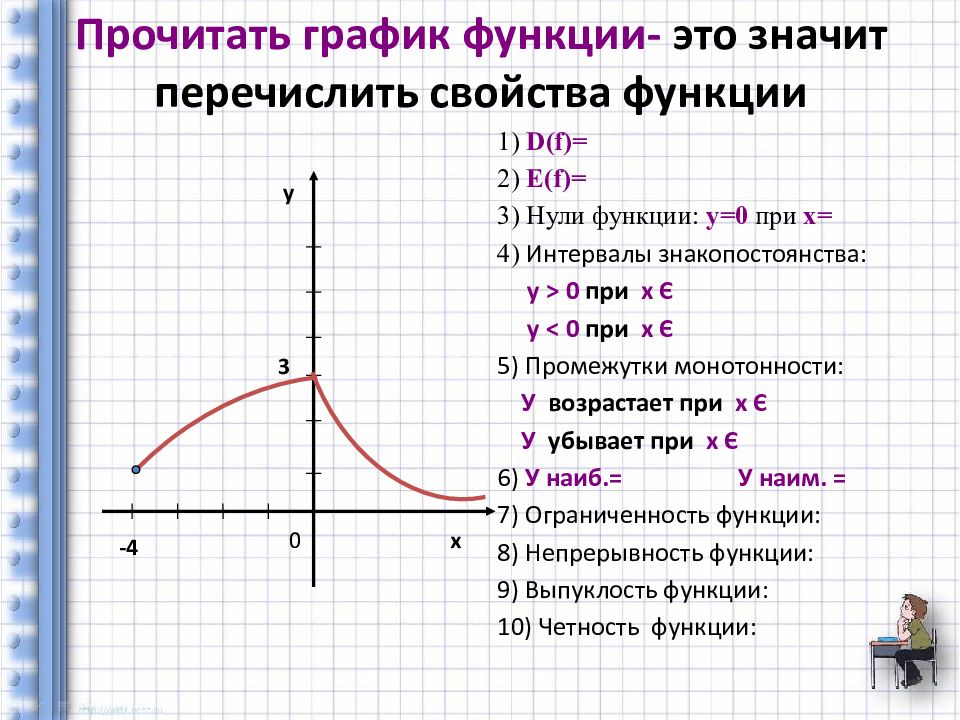
Слайд 17: Прочитать график функции- это значит перечислить свойства функции
1) D(f) = 2) Е (f) = 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: 8) Непрерывность функции: 9) Выпуклость функции: 10) Четность функции: 0 х у -4 3
Слайд 18: Прочитать график функции- это значит перечислить свойства функции
1) D(f) = 2) Е (f) = 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: 8) Непрерывность функции: 9) Выпуклость функции: 10) Четность функции: у х 1 1
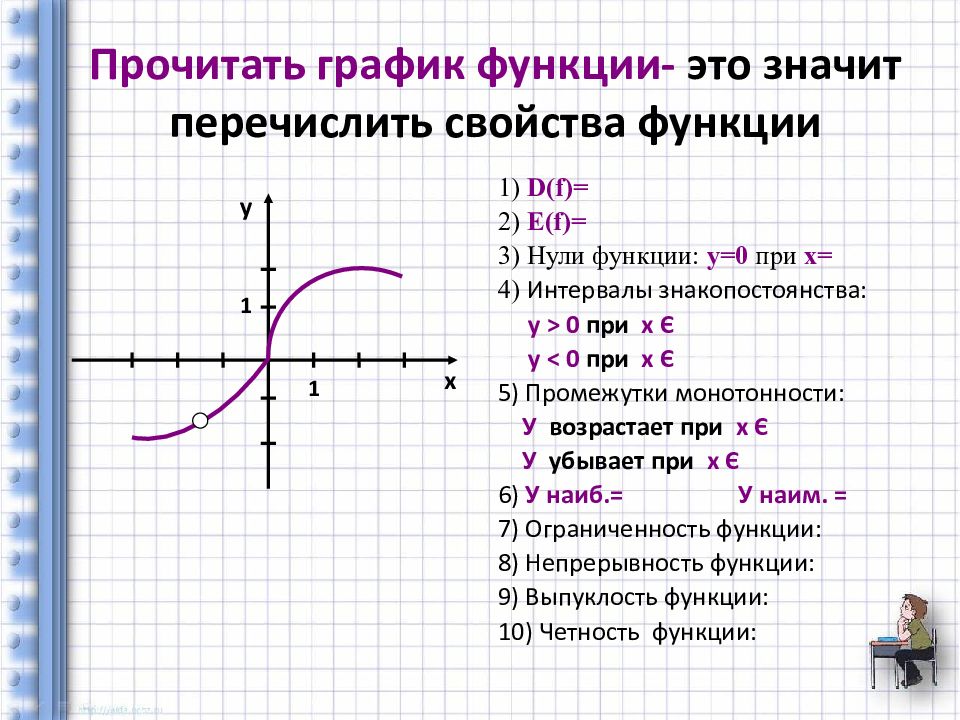
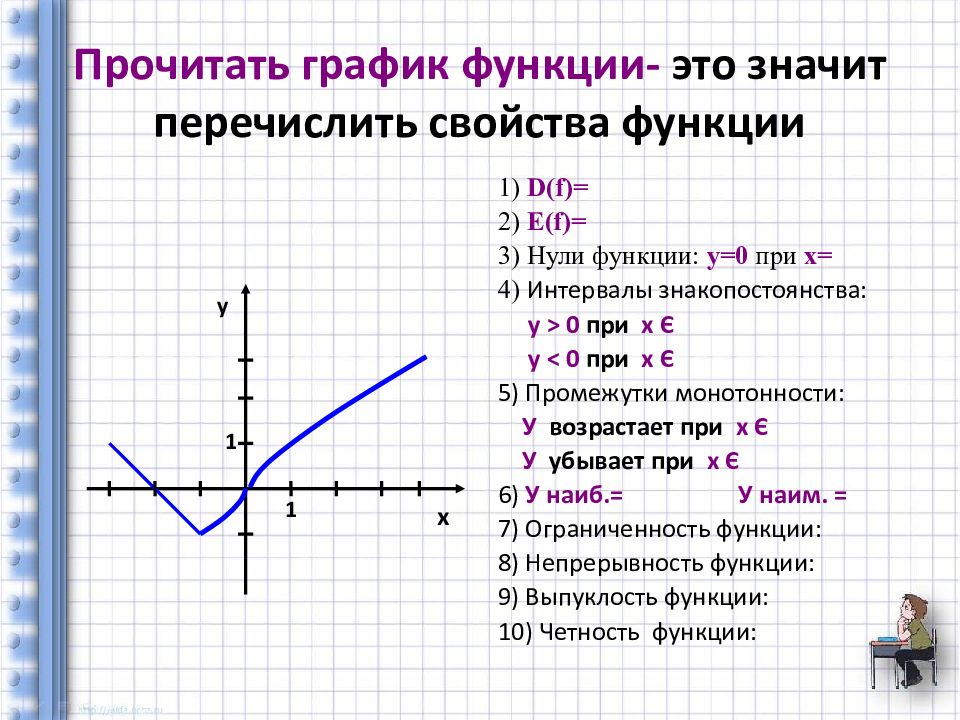
Слайд 19: Прочитать график функции- это значит перечислить свойства функции
1) D(f) = 2) Е (f) = 3) Нули функции: у=0 при х= 4) Интервалы знакопостоянства: у > 0 при х Є у < 0 при х Є 5) Промежутки монотонности: У возрастает при х Є У убывает при х Є 6) У наиб.= У наим. = 7) Ограниченность функции: 8) Непрерывность функции: 9) Выпуклость функции: 10) Четность функции: 1 1 х у