Первый слайд презентации: Тема: Картографический метод исследования
1 /( 17 ) Тема: Картографический метод исследования
Слайд 2
2 /( 17 ) Совмещение очертаний материков Африки и Ю.Америки (по изобате 200 м) Обнаружено сходство очертаний восточного побережья Ю.Америки и Африки. В результате возникла теория дрейфа континентов и глобальной тектоники плит (Вегенер, 1912 г.); В древние времена картографические рисунки использовались лишь для узкопрактичных целей: ориентирования, указания соседних поселений, дорог и т.п. Затем по картам стали измерять площади и расстояния. В средние века карты использовались для мореплавания, путешествий, ведения военных действий. С XVIII-XIX вв. карты стали использовать в научных целях : по картам были открыты многие закономерности, выявлены взаимосвязи явлений, предсказаны еще не открытые объекты.
Слайд 3
3 /( 17 ) Группы приемов анализа карт: описания; графические приемы; графоаналитические приемы; приемы математико-картографического моделирования. По уровню механизации и автоматизации исследования по картам делятся на визуальный анализ (чтение карт, глазомерное сопоставление и зрительная оценка изучаемых объектов); инструментальный (применение для измерений циркулей, транспортиров и т.д.); компьютерный анализ ( выполняется в автоматическом или интерактивном режиме с использованием специальных программ или ГИС). Картографический метод исследования - это метод использования карт для изучения изображенных на них явлений.
Слайд 4
4 /( 17 ) Графические приемы включают построение по картам графиков, профилей, диаграмм, роз-диаграмм, получение изображений при различных действиях с поверхностями (их сложение; вычитание, умножение на число и т.д. ) Розы-диаграммы передают преобладающую ориентировку линейных объектов. где L i - длина луча розы-диаграммы i -го азимута, l ij - длина j -го линейного элемента i -ого азимута, п - число таких элементов, k - масштабный коэффициент. Элементы гидрографии (спрямленные) и построенная по ним роза-диаграмма Описание - прием, основанный на визуальном анализе карт. Цель - выявить изучаемые явления, особенности их размещения и взаимосвязи. Приемы анализа карт
5 /( 17 ) Графоаналитические приемы ( картометрия, морфометрия ) предназначены для измерения и вычисления по картам показателей размеров, формы и структуры объектов. Картометрия - измерения по картам: географических и прямоугольных координат; длин прямых и извилистых линий, расстояний; площадей, объемов участков поверхностей; углов. Морфометрия - вычисление показателей формы и структуры объектов на основе картометрических данных, в том числе: формы объектов; кривизны линий; плотности и концентрации объектов; горизонтального и вертикального расчленения поверхностей. Система приемов анализа карт
Слайд 6: Вычисление некоторых морфометрических показателей:
6 /( 17 ) Показатель формы f=P 2 /4 S, где P - периметр объекта, S - его площадь. Для простых фигур f равен: круг - 1 квадрат - 1,27 равносторонний треугольник - 1,65. Чем больше отклонение формы объекта от круга, тем выше f. Оценка кривизны извилистых линий относительная извилистость = l/s, где l - длина линии со всеми извилинами, s - длина огибающей; извилистость общих очертаний = s/d, где d - длина замыкающей; Вычисление некоторых морфометрических показателей: Графоаналитические приемы
Слайд 7: Вычисление морфометрических показателей:
7 /( 17 ) Вычисление морфометрических показателей: Плотность объектов - отношение их числа п к площади участка S, на котором они расположены ( характеризует встречаемость объектов на карте): Q= n/S. Концентрация объектов - отношение суммы их площадей s i к общей площади участка S ( характеризует относительную площадь объектов на карте): K = s i /S. Горизонтальное расчленение рельефа - отношение суммарной длины l i расчленяющих линий ( например, длина рек) к площади участка S, на котором они расположены: H= l i /S, Вертикальное расчленение - разность максимальной и минимальной высот в пределах какой-то территории (например в речном бассейне): A=z max - z min Графоаналитические приемы
Слайд 8
8 /( 17 ) Приемы математико-картографического моделирования Картографируемое явление можно представить либо как функцию z = F(x,y), где X и Y - координаты точки, либо как поле случайных величин. В зависимости от этого представления при анализе карт используют методы: математического анализа ( аппроксимация ); математической статистики: построение гистограмм и получение статистики; теория корреляции; факторный анализ; теории информации. Система приемов анализа карт
9 /( 17 ) Приемы математико-картографического моделирования 1. Аппроксимация - замена сложной или неизвестной функции другой, более простой, свойства которой известны. Любую сложную поверхность можно представить ( аппроксимировать) в виде z=f(x, y ) + , где f( х,у) - некая аппроксимирующая функция, - остаток, не поддающийся аппроксимации. Для ее нахождения с карты снимают ряд значений z i и составляется система уравнений, решаемая способом наименьших квадратов: i 2 = [ z i - f( х i, у i ) ] 2 = min. Аппроксимирующие функции: алгебраические многочлены, тригонометрические функции и др. При анализе карт аппроксимацию используют: для описания поверхностей, изображенных на картах, и выполнения с ними различных действий (суммирования, вычитания...), для подсчета объемов, ограниченных этими поверхностями, для разложения поверхностей на составляющие - выделения нормальных и аномальных факторов явлений.
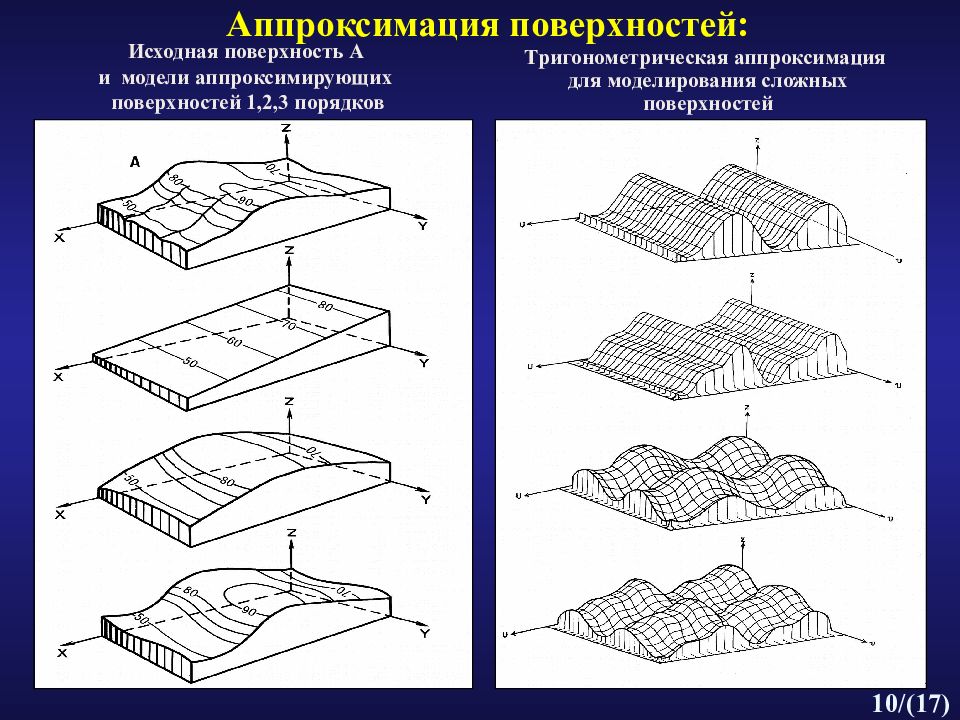
Слайд 10: Аппроксимация поверхностей:
10 /( 17 ) Тригонометрическая аппроксимация для моделирования сложных поверхностей Аппроксимация поверхностей: Исходная поверхность A и модели аппроксимирующих поверхностей 1,2,3 порядков
Слайд 11
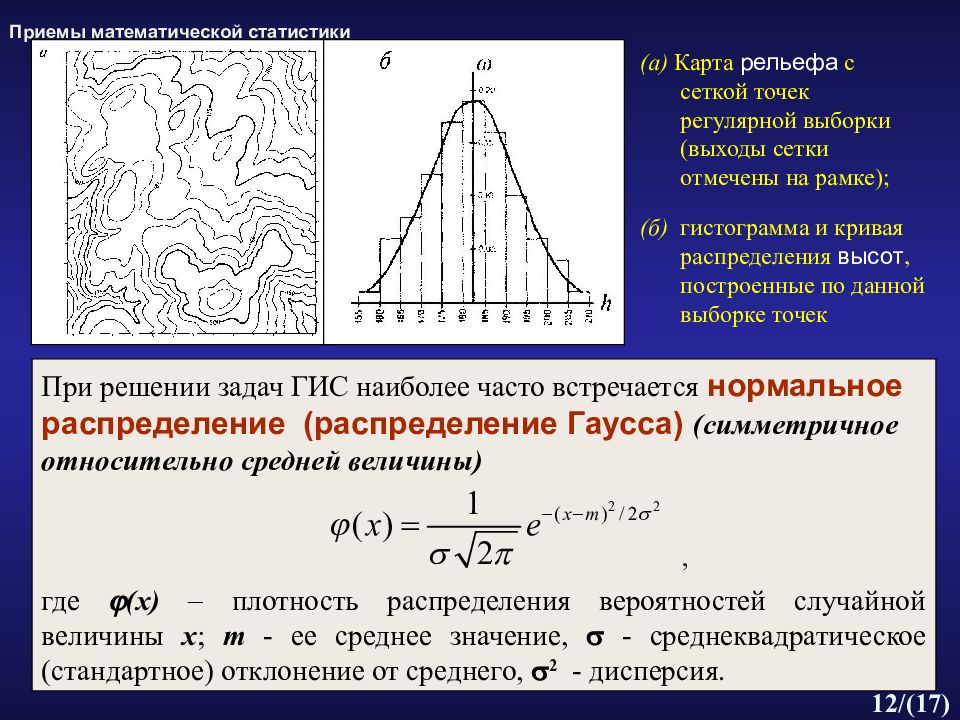
11 /( 17 ) Приемы математико-картографического моделирования 2. Приемы математической статистики а) Построение гистограмм и получение статистик - для изучения характеристик и функций распределения явления В основе статистического исследования карты лежит выборка - подмножество однородных величин а i, снятых с карты : по регулярной сетке точек ( систематическая выборка), в случайно расположенных точках ( случайная выборка), на ключевых участках ( ключевая выборка), по районам ( районированная выборка). Выборочные данные группируются по интервалам, затем составляются гистограммы распределения и вычисляются статистики - количественные показатели, характеризующие распределение явления (среднее значение, среднеквадратическое отклонение, дисперсия и др).
Слайд 12
12 /( 17 ) При решении задач ГИС наиболее часто встречается нормальное распределение (распределение Гаусса) (симметричное относительно средней величины) , где (x) – плотность распределения вероятностей случайной величины x ; m - ее среднее значение, - среднеквадратическое (стандартное) отклонение от среднего, 2 - дисперсия. (а) Карта рельефа с сеткой точек регулярной выборки (выходы сетки отмечены на рамке); (б) гистограмма и кривая распределения высот, построенные по данной выборке точек Приемы математической статистики
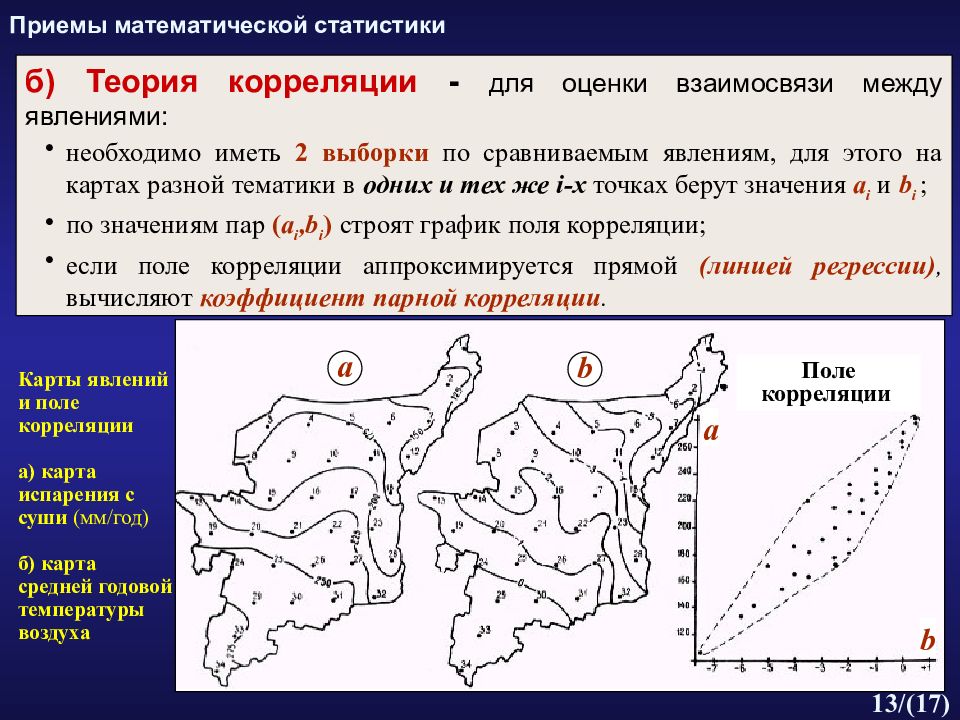
13 /( 17 ) Карты явлений и поле корреляции а) карта испарения с суши (мм/год) б) карта средней годовой температуры воздуха б) Теория корреляции - для оценки взаимосвязи между явлениями: необходимо иметь 2 выборки по сравниваемым явлениям, для этого на картах разной тематики в одних и тех же i -х точках берут значения а i и b i ; по значениям пар ( а i,b i ) строят график поля корреляции; если поле корреляции аппроксимируется прямой (линией регрессии), вычисляют коэффициент парной корреляции. Приемы математической статистики b a a b Поле корреляции
Слайд 14
14 /( 17 ) Коэффициент парной корреляции : где а i и b i - выборочные данные, полученные по картам А и В; п - объем выборки; m a и m b - средние значения: a и b - среднеквадратические отклонения от среднего: Свойства R: R [-1,+1 ]. При R = ±1 между явлениями существует прямая или обратная линейная связь. Если R 0 - связь между явлениями отсутствует. При R > |0.7| связь считается существенной. Приемы математической статистики: теория корреляции
Слайд 15
15 /( 17 ) Приемы математической статистики в) Факторный анализ - для выделения основных факторов, определяющих развитие и размещение явления. Позволяет свести большие совокупности исходных показателей, характеризующих сложное явление, к 3 - 4 главным факторам. Уравнение факторного анализа в общем виде : а i - исходные показатели; f r - выделенные главные факторы, l ir - “вес” каждого фактора; е i - остаток, характеризующий неучтенные отклонения. Применение: создание синтетической (например, климатической) карты, показывающей районы, однородные по всему комплексу показателей.
Слайд 16
16 /( 17 ) 3. Приемы теории информации служат для оценки степени однородности / неоднородности явления, изучаемого по карте; совпадения контуров явлений (что является показателем их взаимосвязи). Для оценки неоднородности картографического изображения используется энтропия - основная функция теории информации. Энтропия Е(А) некоторой системы А - это сумма произведений вероятностей p i различных состояний этой системы на логарифмы вероятностей, взятая с обратным знаком: В картографическом анализе вероятность p i заменяется i - долей контуров, соответствующих i -ому состоянию ( отношением площади контуров в i -ом состоянии S i к площади всех n контуров на карте): Приемы математико-картографического моделирования , где
Последний слайд презентации: Тема: Картографический метод исследования
17 /( 17 ) Свойства функции энтропии: Е(А) >=0 ; Е(А) =0 при n =1 - на карте изображен только один контур (или только одно состояние) - изображение в этом случае совершенно однородно ; Оценка степени неоднородности с помощью функции энтропии с увеличением п энтропия возрастает от 0 до , т.е. увеличивается неоднородность явления; при фиксированном n величина неоднородности зависит от относительных площадей контуров (долей i ) и достигает max при равных долях 1 = 2 =…= n =1/n : Увеличение энтропии Е (А) с возрастанием числа контуров на карте (а) и изменением соотношения их площадей (б). E(A 1 ) < E(A 2 ) < E(A 3 ) <… < E(A n ) ) E(A 1 ) < E(A 2 ) < E(A 3 ) < E(A 4 ) = max