Первый слайд презентации: Тема: Математическая основа карт
1 /(67) Тема: Математическая основа карт Элементы математической основы: эллипсоид масштаб проекция, координатные сетки
Слайд 2
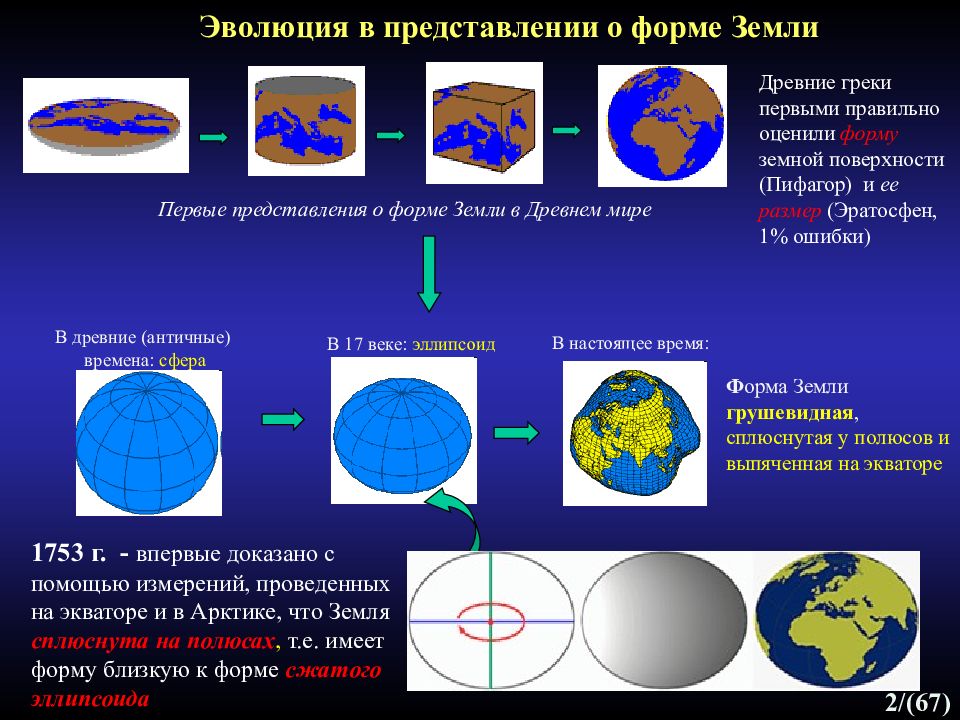
2 /(67) Первые представления о форме Земли в Древнем мире Эволюция в представлении о форме Земли Древние греки первыми правильно оценили форму земной поверхности (Пифагор) и ее размер (Эратосфен, 1% ошибки) 1753 г. - впервые доказано с помощью измерений, проведенных на экваторе и в Арктике, что Земля сплюснута на полюсах, т.е. имеет форму близкую к форме сжатого эллипсоида В древние (античные) времена: сфера В 17 веке: эллипсоид Ф орма Земли грушевидная, сплюснутая у полюсов и выпяченная на экваторе В настоящее время:
Слайд 3
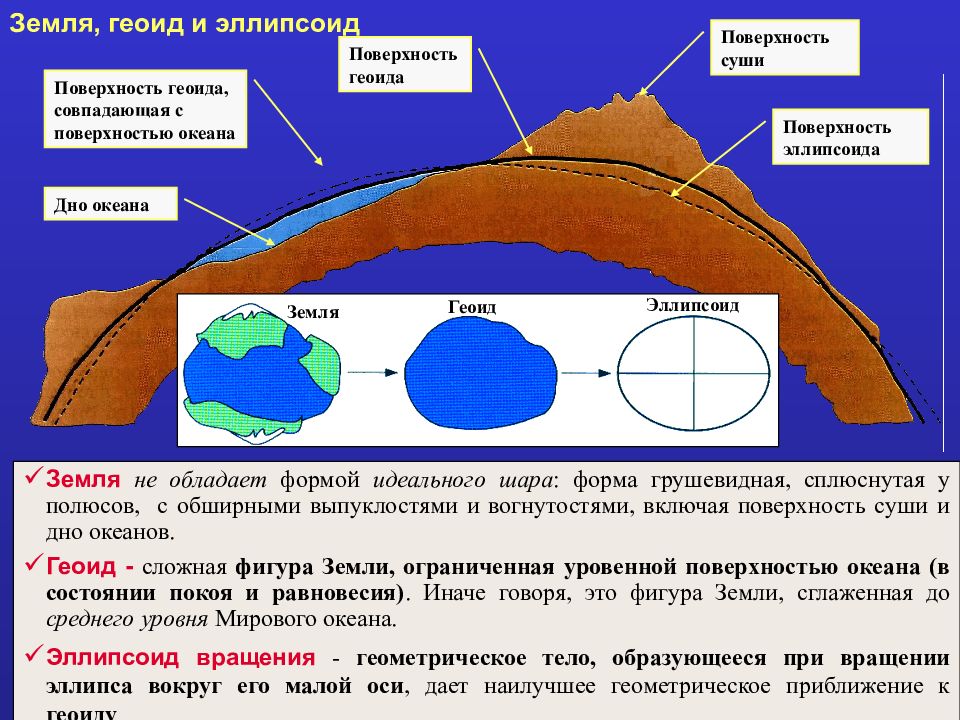
3 /(67) Поверхность геоида, совпадающая с поверхностью океана Поверхность эллипсоида Дно океана Поверхность суши Поверхность геоида Земля, геоид и эллипсоид Земля не обладает формой идеального шара : форма грушевидная, сплюснутая у полюсов, с обширными выпуклостями и вогнутостями, включая поверхность суши и дно океанов. Геоид - сложная фигура Земли, ограниченная уровенной поверхностью океана (в состоянии покоя и равновесия). Иначе говоря, это фигура Земли, сглаженная до среднего уровня Мирового океана. Эллипсоид вращения - геометрическое тело, образующееся при вращении эллипса вокруг его малой оси, дает наилучшее геометрическое приближение к геоиду. Земля Геоид Эллипсоид
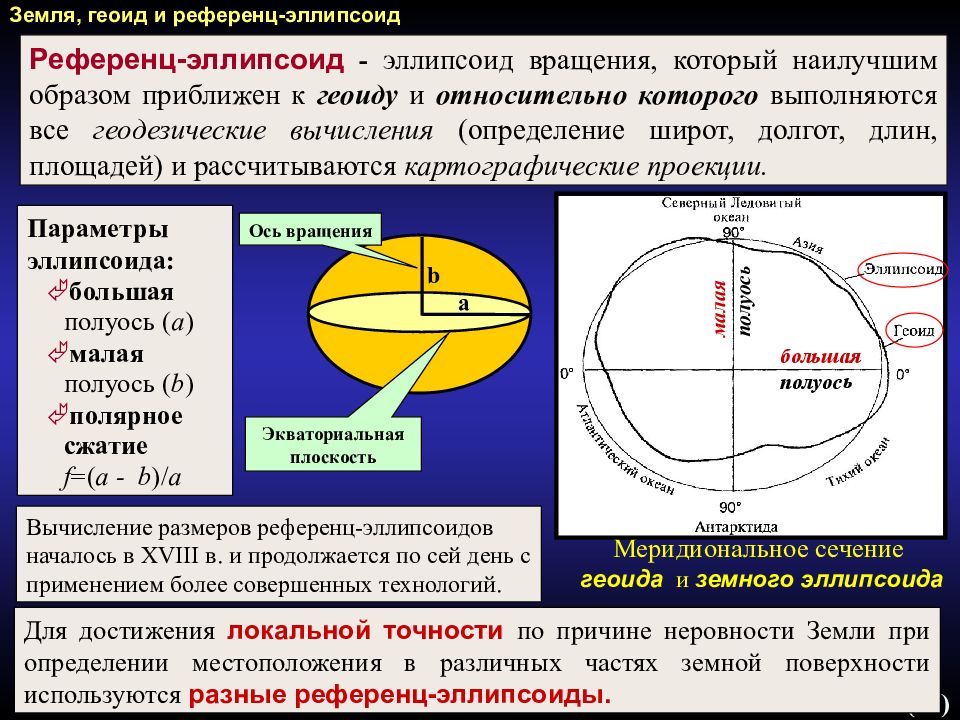
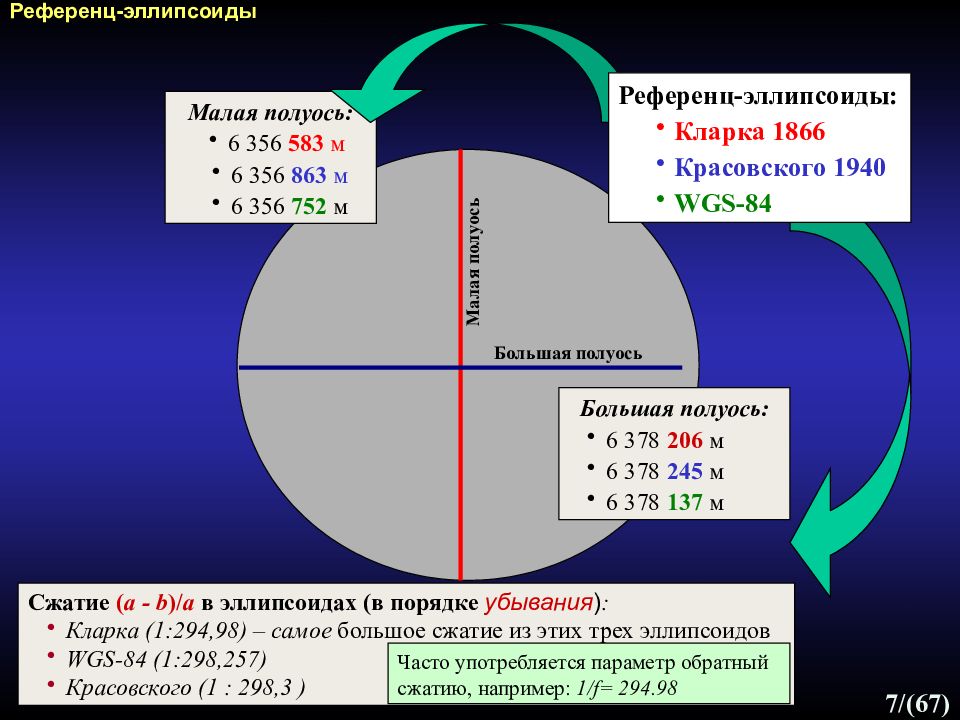
4 /(67) Референц-эллипсоид - эллипсоид вращения, который наилучшим образом приближен к геоиду и относительно которого выполняются все геодезические вычисления (определение широт, долгот, длин, площадей) и рассчитываются картографические проекции. Земля, геоид и референц-эллипсоид Меридиональное сечение геоида и земного эллипсоида Параметры эллипсоида: большая полуось ( а ) малая полуось ( b ) полярное сжатие f = ( а - b )/ а a b Ось вращения Экваториальная плоскость Вычисление размеров референц-эллипсоидов началось в X VIII в. и продолжается по сей день с применением более совершенных технологий. Для достижения локальной точности по причине неровности Земли при определении местоположения в различных частях земной поверхности используются разные референц-эллипсоиды. большая полуось малая полуось
Слайд 5
5 /(67) Разница между большой и малой полуосями земных эллипсоидов незначительна и составляет меньше 0.34 %, около 22 км (для эллипсоида Красовского а = 6 3 78 245; b = 6 3 56 863 м; ) Референц-эллипсоиды глобальные геоцентрические эллипсоиды - наилучшим образом согласуются с поверхностью геоида в целом, служат основой для измерения местоположений во всем мире : в 1984 г. на основе более точных спутниковых измерений вычислен международный эллипсоид WGS -84 (World G e odetic System 1984). GPS измерения основаны на данном эллипсоиде. Существуют: локальные эллипсоиды - наилучшим образом согласуются с геоидом на ограниченной части его поверхности: в России принят эллипсоид Красовского (1940 г. ) ( на его основе составлены крупномасштабные карты в России), отклонение от геоида на территории Росси не превышает 150 м; в США и Канаде - эллипсоид Кларка (1866г.); Глобальный геоцентрический эллипсоид Локальный эллипсоид ГЕОИД
Слайд 6
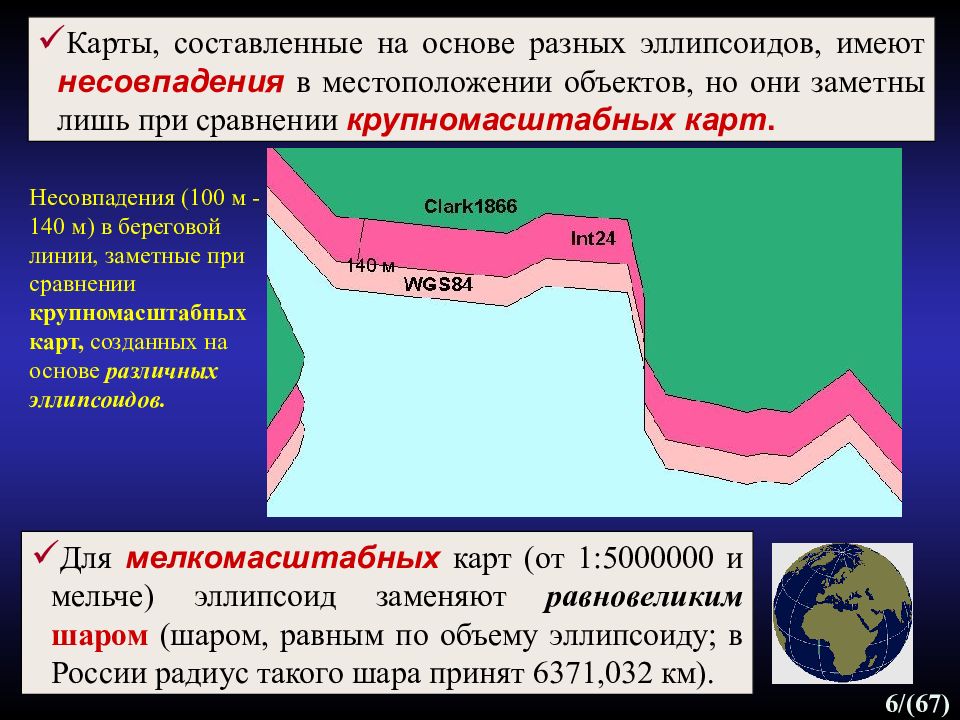
6 /(67) Несовпадения (100 м -140 м) в береговой линии, заметные при сравнении крупномасштабных карт, созданных на основе различных эллипсоидов. Карты, составленные на основе разных эллипсоидов, имеют несовпадения в местоположении объектов, но они заметны лишь при сравнении крупномасштабных карт. Для мелкомасштабных карт (от 1:5000000 и мельче) эллипсоид заменяют равновеликим шаром ( шаром, равным по объему эллипсоиду; в России радиус такого шара принят 6371,032 км ).
Слайд 7
7 /(67) Большая полуось: 6 378 206 м 6 378 245 м 6 378 137 м Малая полуось: 6 356 583 м 6 356 863 м 6 356 752 м Большая полуось Малая полуось Сжатие ( а - b )/ а в эллипсоидах (в порядке убывания ) : Кларка (1:294,98) – самое большое сжатие из этих трех эллипсоидов WGS-84 (1:298,257) Красовского ( 1 : 298,3 ) Референц-эллипсоиды: Кларка 1866 Красовского 1940 WGS-84 Референц-эллипсоиды Часто употребляется параметр обратный сжатию, например: 1/ f= 294.98
Слайд 8
Масштаб карт - cтепень уменьшения объектов на карте относительно их размеров на земной поверхности (эллипсоиде). Масштаб на плоской карте изменяется от места к месту из-за неизбежных деформаций, связанных с переходом от сферической поверхности Земли к плоскости карты ( чем больше территория, показанная на карте, тем больше изменения масштаба ). Плоскость карты Земная поверхность Различают: Главный масштаб - показывает во сколько раз линейные размеры на карте уменьшены по отношению к эллипсоиду (шару). Подписывается на карте, но справедлив он лишь для отдельных линий и точек, где искажения отсутствуют, т.е. это масштаб исходного уменьшенного эллипсоида, развертыванием которого в плоскость и получена карта. Частный масштаб - показывает соотношение размеров объектов на карте и эллипсоиде (шаре) в данной точке. Выделяют: частный масштаб длин - зависит от точки на карте и от направления в данной точке, может быть больше или меньше главного; частный масштаб площадей. 8 /(67)
Слайд 9
9 /(67) На карте (в основном) указывается главный масштаб, относящийся к линиям, где нет искажений. Виды подписей масштаба на карте: численный - в виде дроби с единицей в числителе ; показывает, во сколько раз длины на карте меньше соответствующих длин на местности ( чем меньше знаменатель, т.е. чем больше дробь, тем крупнее масштаб ). Например, 1:100 000 ; Линейный (графический) - в виде линейки, разделенной на равные части, с подписями, означающими соответствующие расстояния на местности. Именованный масштаб - в виде подписи, указывающей, какое расстояние на местности соответствует одному сантиметру на карте. Например, в 1 см- 1 км. Значения частных масштабов длин на карте ( M ) измеряют в долях ( или процентах ) от главного масштаба карты, например M>1, M<1, M=1. Чем мельче масштаб карты и обширнее территория, тем сильнее различия между главным и частным масштабами. Масштаб
Слайд 10
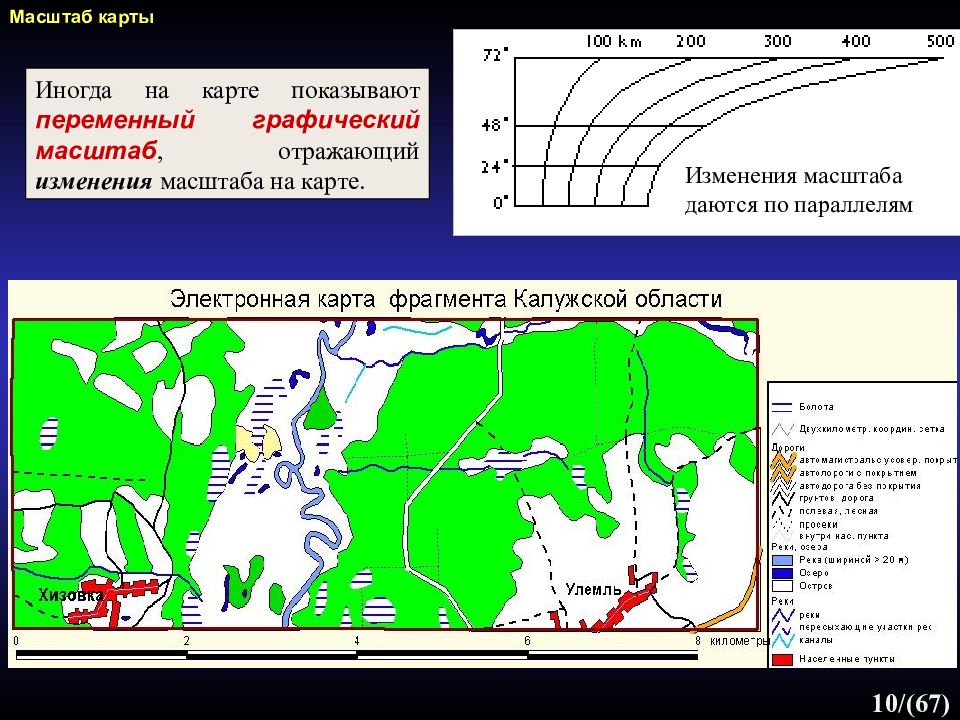
10 /(67) Иногда на карте показывают переменный графический масштаб, отражающий изменения масштаба на карте. Изменения масштаба даются по параллелям Масштаб карты
Слайд 11
11 /(67) Предельная точность масштаба Любой объект на карте ( бумажной ) можно изобразить и измерить с точностью не более 0,1 мм. Это предельная графическая точность, соответствующая минимально возможной толщине линии на карте. Масштаб карты Предельная графическая точность (0,1 мм или 10 -2 см или 10 -4 м на карте ), выраженная в масштабе карты, называется предельной точностью масштаба (ПТМ): ПТМ=10 -4 *Масштаб (м) Примеры, для карт в масштабе: 1:5000 ПТМ= 50 см, 1:100 000 ПТМ= 10 м.
Слайд 12
12 /(67) Системы координат, используемые для определения местоположения на земной поверхности: географические (геодезические) системы координат, в которых положение точки на земной поверхности определяется географическими координатами (широтой , долготой ). прямоугольные спроектированные системы координат с плоскими координатами XY.
Слайд 13
13 /(67) Географические координаты (широта и долгота) - это угловые величины, определяющие положение точки на земной поверхности. Измеряются в градусах, минутах, секундах. Широта - это угол между отвесной линией (нормалью) в данной точке и плоскостью экватора. Изменяется от 0 (экватор) до 90 0 на полюсах: “северные” (+), “южные” (-). Долгота - это угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана (проходит через Гринвич, вблизи Лондона, принят в 1884 г.). Изменяется от 0 до 360 0 с запада на восток или в обе стороны от 0 до 180 0: “восточная” (+), “западная” (-). Географические системы координат M Экватор
Слайд 14
14 /(67) На глобусах и картах широты и долготы показываются с помощью параллелей и меридианов: меридиан линия, все точки которой имеют одну и ту же долготу; линия сечения земной поверхности плоскостью, проходящей через С. и Ю. полюсы (т.е. через ось вращения Земли) и выбранную точку на земной поверхности. Сетка меридианов и параллелей на земном эллипсоиде, шаре, глобусе называется географической сеткой, а ее изображение на карте - картографической сеткой. Географические координаты (долгота) (широта) Параллель Меридиан (в. д.) (с. ш.) параллель - линия, все точки которой имеют одну и ту же широту; - линия сечения земной поверхности плоскостью, параллельной плоскости экватора.
Слайд 15
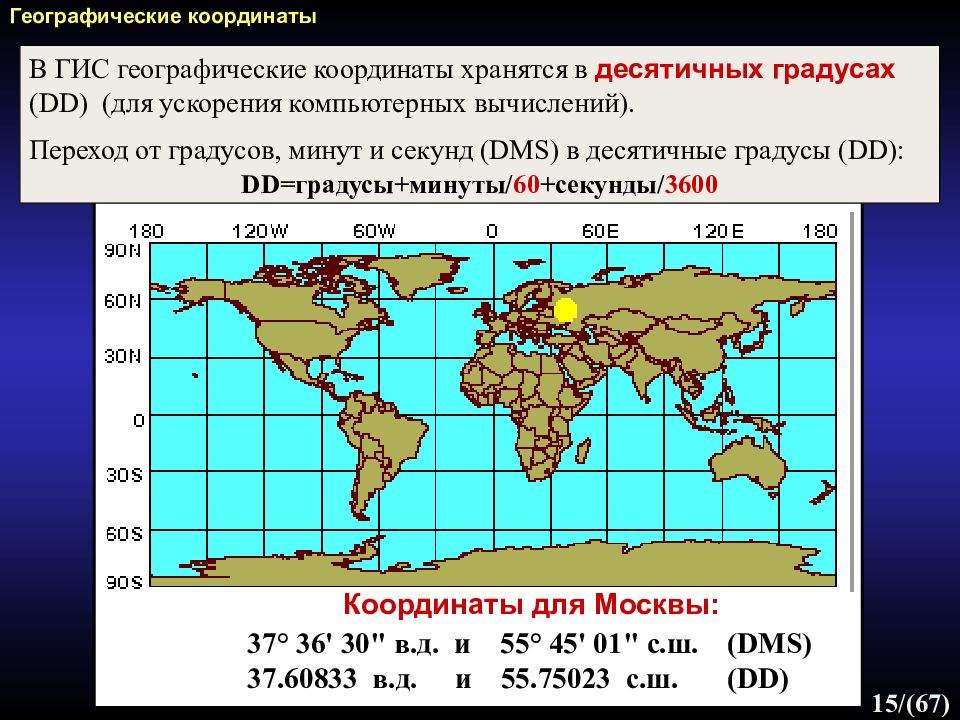
15 /(67) Координаты для Москвы: 37 ° 36 ' 30 " в.д. и 55 ° 45 ' 01 " с.ш. (DMS) 37.60833 в.д. и 55.75023 с.ш. ( DD) В ГИС географические координаты хранятся в десятичных градусах ( DD) (для ускорения компьютерных вычислений). Переход от градусов, минут и секунд (DMS) в десятичные градусы (DD) : DD= градусы + минуты / 60 + секунды / 3600 Географические координаты
Слайд 16
Географические системы координат Географические системы координат (ГСК ) строятся на основе: эллипсоида (или сферы), используемых для моделирования геоида, а также положения эллипсоида относительно центра Земли и его ориентации ( Datum) ; ГСК бывают локальными (местными) и геоцентрическими. В локальной ГСК центр эллипсоида сдвинут относительно центра Земли, в геоцентрической совпадает с центром масс Земли. В геоцентрической системе координат размеры эллипсоида, его ориентация и положение центра выбираются так, что: объем эллипсоида предполагается равным объему геоида; среднеквадратичное отклонение поверхности эллипсоида от поверхности геоида минимально по всей территории земного шара; большая полуось эллипсоида лежит в плоскости экватора геоида; малая полуось направлена по оси вращения Земли. В национальной (локальной) системе координат эллипсоид выбирается и располагается так, чтобы для некоторой заданной территории среднеквадратичное отклонение поверхности эллипсоида от поверхности геоида было минимальным. При этом отклонения в других местах Земли может быть сколь угодно велико.
Слайд 17
17 /(67) Геоид Геоцентрическая ГСК WGS -84: построена на основе эллипсоида WGS -84, начало которо го совпадает с центром масс Земли Л окальная ГСК NAD27 : основана на эллипсоиде Кларка ( используется для Сев. Америки) центр масс Земли Локальная ГСК Пулково-42 (СК-42): основана на эллипсоиде Красовского (используется для России, СНГ), начало координат смещено относительно центра масс на расстояние около 100 м Примеры GCS : Пулково-42 (СК-42) С развитием спутниковой навигации проблема перехода из универсальной ГСК WGS84, используемой приборами GPS, в другие системы координат, например СК-42, встает особенно явно. Обычная разница между одними и теми же координатами в разных системах составляет порядка 150 метров.
Слайд 18
18 /(67) ГСК можно изобразить на плоскости в виде сетки с ячейками одинакового размера: по оси ординат Y – значения широты, по оси абсцисс X – долготы, размер сетки : 360˚ по долготе, 180˚ по широте. Такое представление ГСК иногда называют географической проекцией. Географические координаты (ГК) при этом показываются, как если бы они были плоскими, но это не так - величина градуса по долготе в метрах меняется в зависимости от широты. В результате такого «плоского» представления ГСК на карте возникают сильные деформации. «Плоский» способ отображения ГК неудобен для измерений длин, площадей, определения пространственных отношений, поэтому данные из угловых географических координат ( , ) переводят в прямоугольные спроектированные координаты ( XY). Московская область в географической системе координат, показанной на плоскости Деформации в географической системе координат, показанной на плоскости Московская область в спроектированной системе координат – в проекции UTM эллипсы искажений Географические системы координат
Слайд 19: Спроектированные системы координат
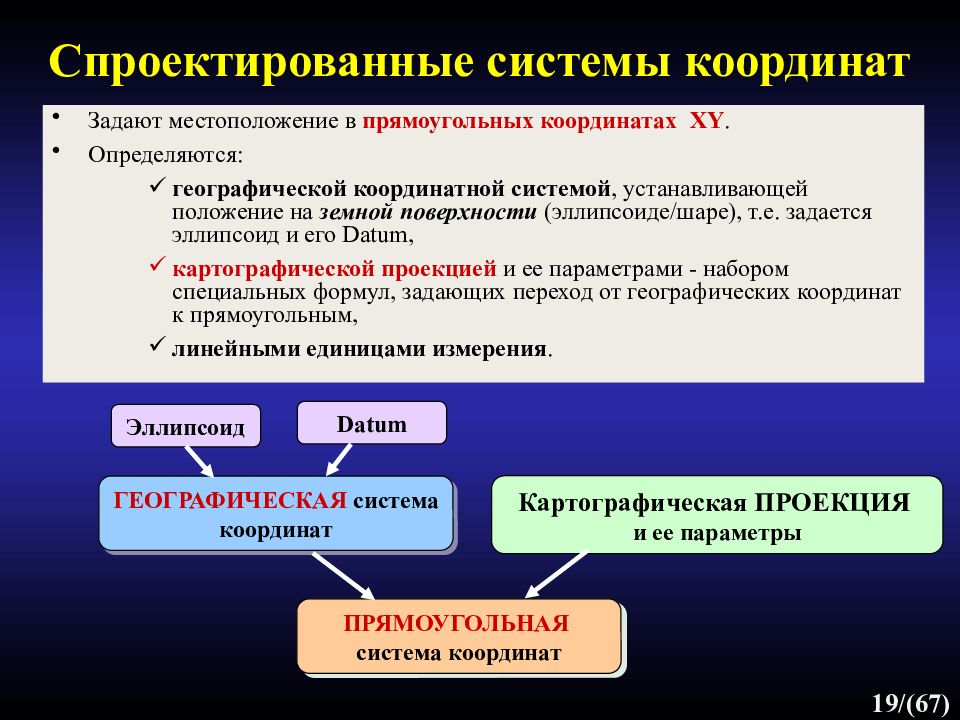
19 /(67) Спроектированные системы координат Задают местоположение в прямоугольных координатах XY. Определяются: географической координатной системой, устанавливающей положение на земной поверхности (эллипсоиде/шаре), т.е. задается эллипсоид и его Datum, картографической проекцией и ее параметрами - набором специальных формул, задающих переход от географических координат к прямоугольным, линейными единицами измерения. Эллипсоид Datum ГЕОГРАФИЧЕСКАЯ система координат Картографическая ПРОЕКЦИЯ и ее параметры ПРЯМОУГОЛЬНАЯ система координат
Слайд 20
20 /(67) Картографическая проекция - математически определенное отображение поверхности эллипсоида (шара) на плоскость карты. Проекция устанавливает однозначное соответствие между географическими координатами точек (широтой и долготой ) и их прямоугольными координатами ( X,Y) на карте и задается математическими уравнениями. Уравнения проекции в общем виде: X= 1 ( , ); Y= 2 ( , ). Картографические проекции Сетка географической системы координат (географическая сетка) на сферической поверхности Сетка плоской системы координат
Слайд 21
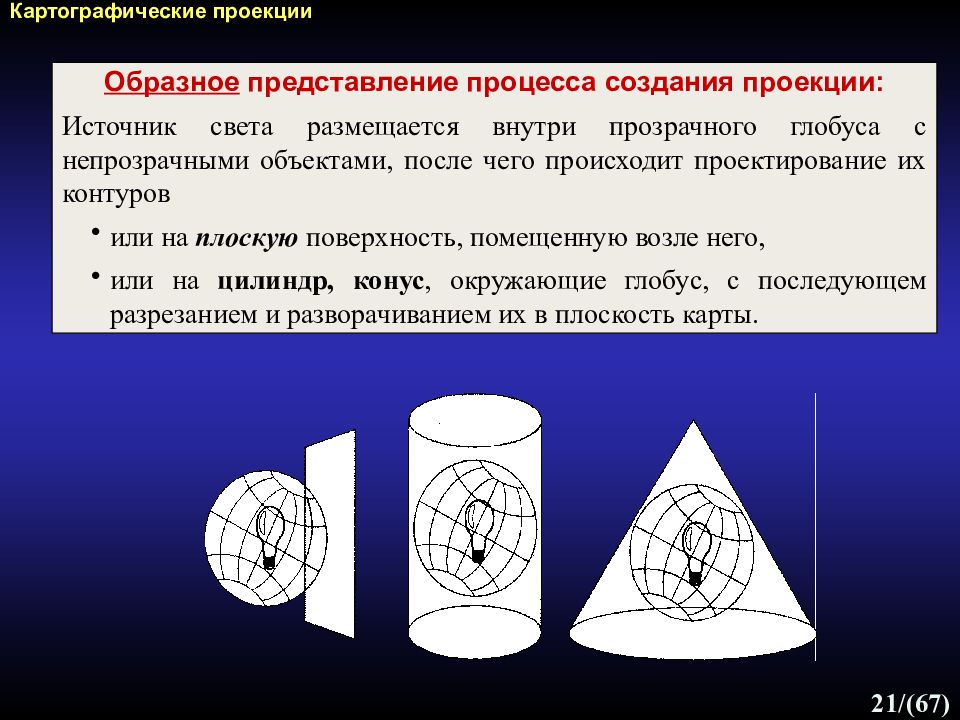
21 /(67) Образное представление процесса создания проекции: Источник света размещается внутри прозрачного глобуса с непрозрачными объектами, после чего происходит проектирование их контуров или на плоскую поверхность, помещенную возле него, или на цилиндр, конус, окружающие глобус, с последующем разрезанием и разворачиванием их в плоскость карты. Картографические проекции
Слайд 22
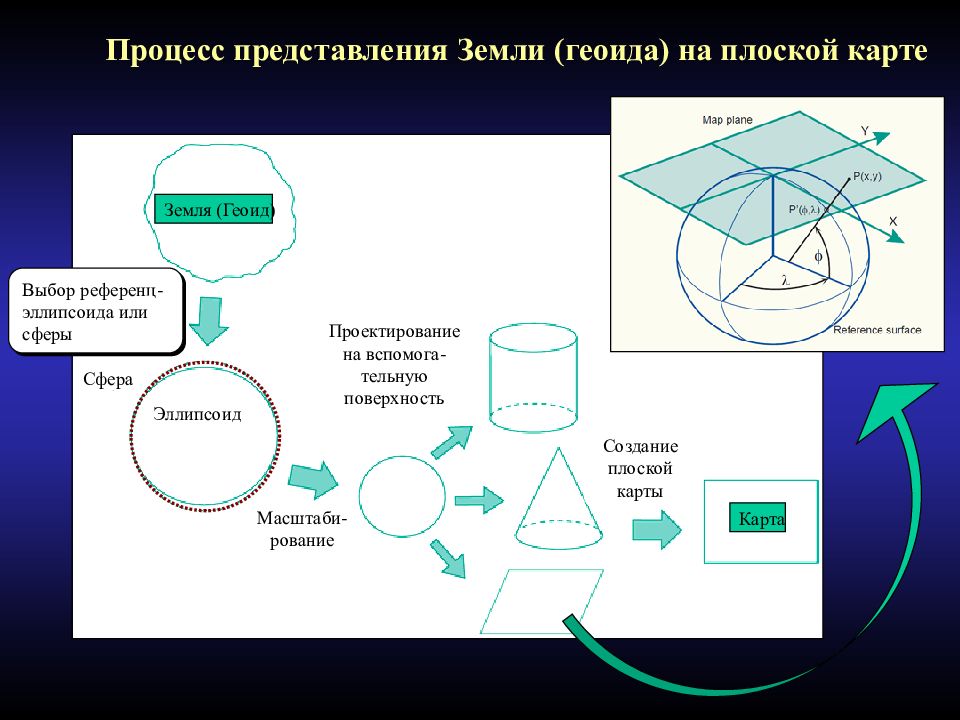
Процесс представления Земли (геоида) на плоской карте Выбор референц- эллипсоида или сферы Масштаби-рование Проектирование на вспомога-тельную поверхность Создание плоской карты Карта Земля (Геоид) Эллипсоид Сфера
Слайд 23
23 /(67) Виды искажений в картографических проекциях: искажения длин - масштаб длин непостоянен в разных точках карты и по разным направлениям; искажения площадей (связаны с искажением длин) - масштаб площадей различен в разных точках карты, что приводит к нарушению размеров объектов; искажения углов - углы между направлениями на карте искажены относительно тех же углов на местности; искажения форм (связаны с искажениями углов) - фигуры на карте деформированы и не подобны фигурам на местности. Картографические проекции Сферическую поверхность земного эллипсоида (шара) нельзя развернуть на плоскости карты без искажений - неизбежны сжатия и растяжения, различные по величине и направлению (отсюда непостоянство масштабов длин и площадей на карте). Все картографические проекции деформируют объекты в процессе их трансформации со сферической поверхности на плоскость!
Слайд 24
24 /(67) При проектировании любая бесконечно малая окружность на шаре (эллипсоиде) с радиусом 1 переходит на карте в бесконечно малый эллипс - эллипс искажений. Служит для показа распределения искажений на карте : его размеры и форма в некоторой точке карты отражают искажения длин, площадей и углов в этой точке; большая ось отражает направление наибольшего масштаба длин в данной точке, малая ось – направление наименьшего масштаба длин (это главные направления - взаимно перпендикулярные направления, по одному из которых масштаб длин имеет наибольшее, а по другому - наименьшее значение ) Эллипс искажений (индикатрисса Тиссо ) Линии или точки нулевых искажений - это линии или точки, где искажения отсутствуют и сохраняется главный масштаб ( M=1 ). Изоколы - линии равных искажений (длин/площадей/углов/форм). Параллель a b Меридиан r=1 Эллипс искажений на карте Элементарная окружность на шаре
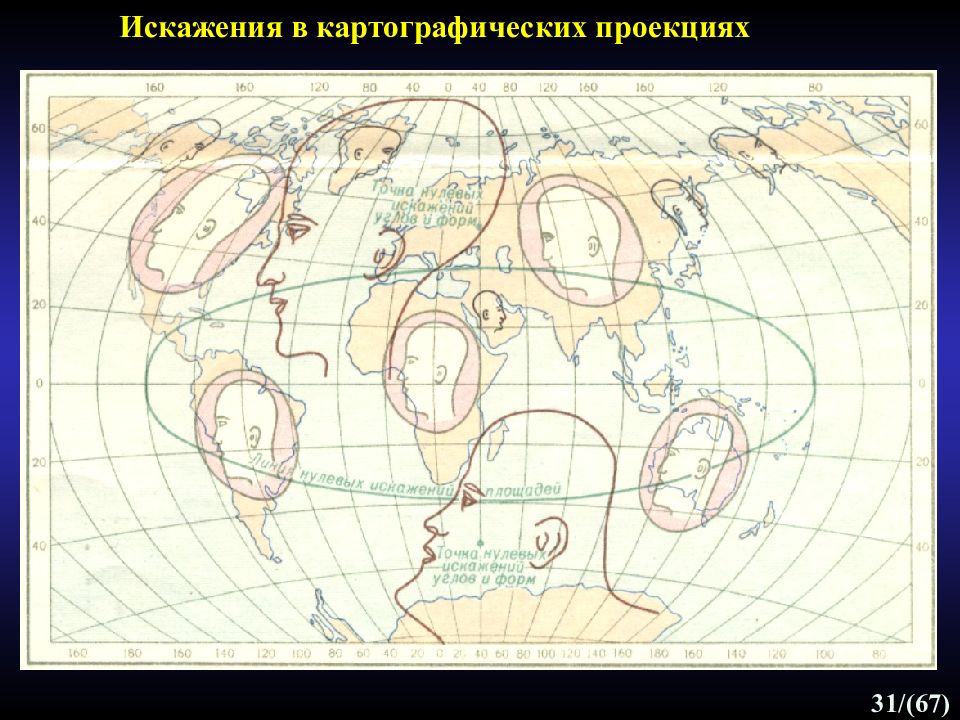
Слайд 25: Контуры России в разных проекциях
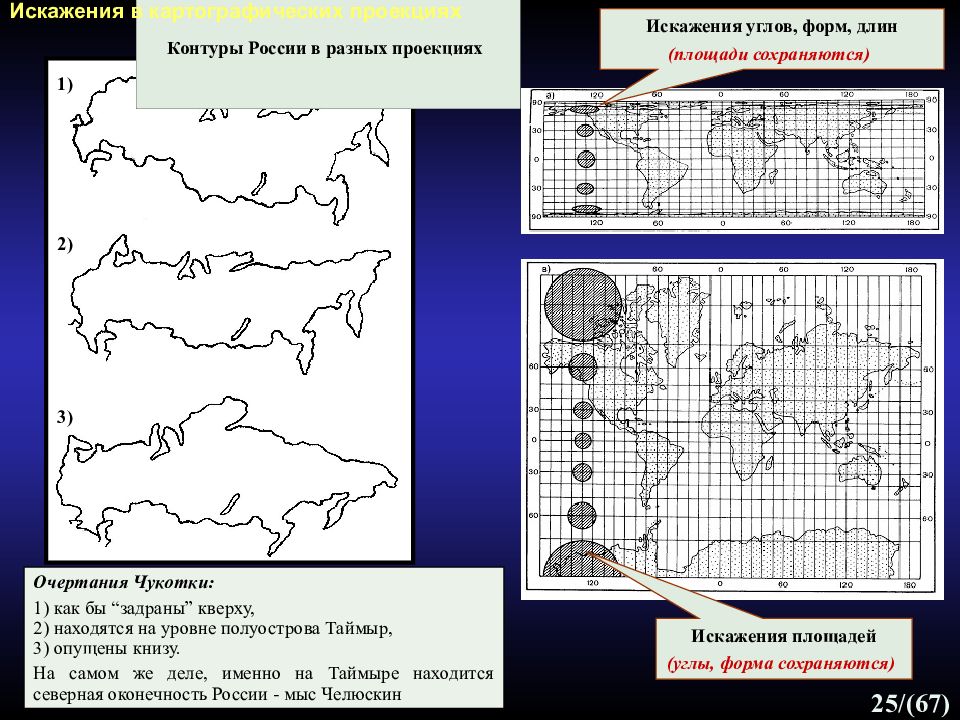
25 /(67) Контуры России в разных проекциях Искажения в картографических проекциях Очертания Чукотки: 1) как бы “задраны” кверху, 2) находятся на уровне полуострова Таймыр, 3) опущены книзу. На самом же деле, именно на Таймыре находится северная оконечность России - мыс Челюскин Искажения углов, форм, длин (площади сохраняются) Искажения площадей (углы, форма сохраняются) 1) 2) 3)
Слайд 26: Равновеликая цилиндрическая проекция ( эллипсы искажений характеризуют искажения углов, форм, длин)
26 /(67) Классификация проекций по характеру искажений : Равновеликие проекции - сохраняют площади, но искажают углы и формы. Удобны для измерения площадей объектов, но приполярные области выглядят сильно сплющенными. В такой проекции изображаются экономические, почвенные и др. карты. Равновеликая цилиндрическая проекция ( эллипсы искажений характеризуют искажения углов, форм, длин). Все множество проекций классифицируют как по типу искажений, так и по виду картографической сетки.
Слайд 27: Равноугольная цилиндрическая проекция (размеры окружностей характеризуют искажения площадей)
27 /(67) Классификация проекций по характеру искажений: Равноугольные проекции ( конформные ) - нет искажений углов и локальных форм контуров (элемен.окружность остается окружностью), но есть значительные искажения площадей : картографическая сетка ортогональна ( нормальная ), масштабы длин в каждой точке не зависят от направлений, удобны для определения направлений, используются на навигационных картах. Равноугольная цилиндрическая проекция (размеры окружностей характеризуют искажения площадей). Ни одна проекция не может сохранять одновременно форму и площадь объектов! Уменьшение искажения одного из них влечет увеличение искажения другого.
Слайд 28
28 /(67) Равнопромежуточные проекции - произвольные проекции, в которых искажения длин отсутствуют только по одному из главных направлений (различают равнопромежуточные по меридианам и по параллелям ). Классификация проекций по характеру искажений: Произвольные проекции - это проекции, в которых в той или иной степени содержатся все искажения (длин, площадей, углов, форм). При их построении стремятся найти наиболее выгодное для конкретного случая распределение искажений. Например, минимальные искажения - в центральной части карты, а все сжатия и растяжения "сбрасываются" к её краям.
Слайд 29
29 /(67) Простая (квадратная) Plate Carree : касательный цилиндр, ячейки картографической сетки – квадраты Искажения в равнопромежуточной цилиндрической проекции, показанные эллипсами искажений Прямоугольная Plate Carree : секущий цилиндр, ячейки картографической сетки - одинаковые прямоугольники
Слайд 30: Искажения в картографических проекциях
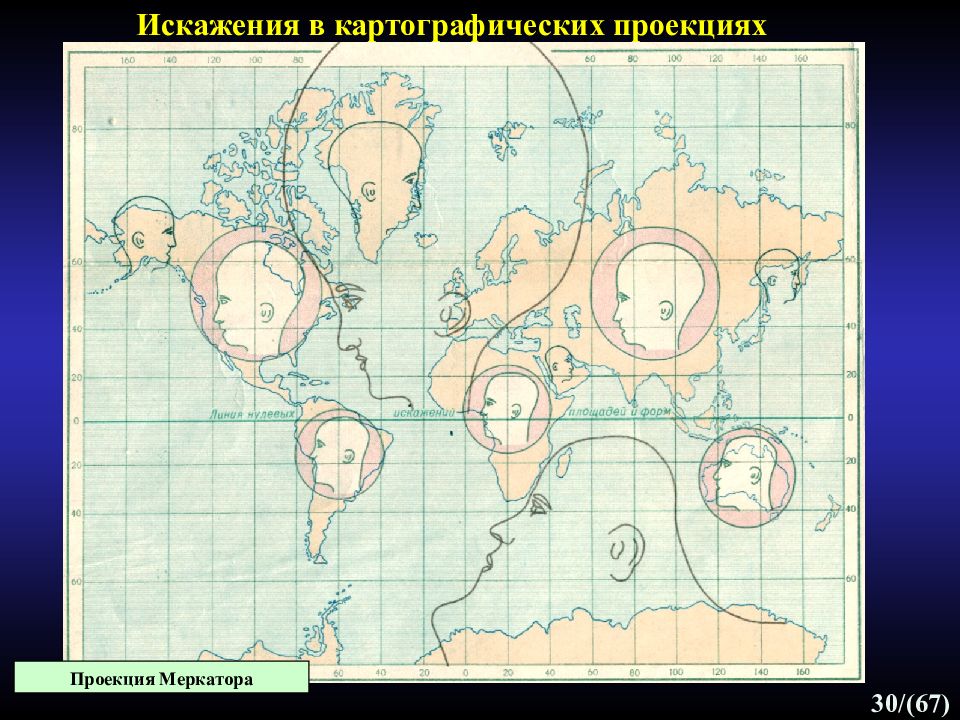
30 /(67) Искажения в картографических проекциях Проекция Меркатора
Слайд 31: Искажения в картографических проекциях
31 /(67) Искажения в картографических проекциях
Слайд 32: Искажения в картографических проекциях
32 /(67) Искажения в картографических проекциях Поликоническая проекция
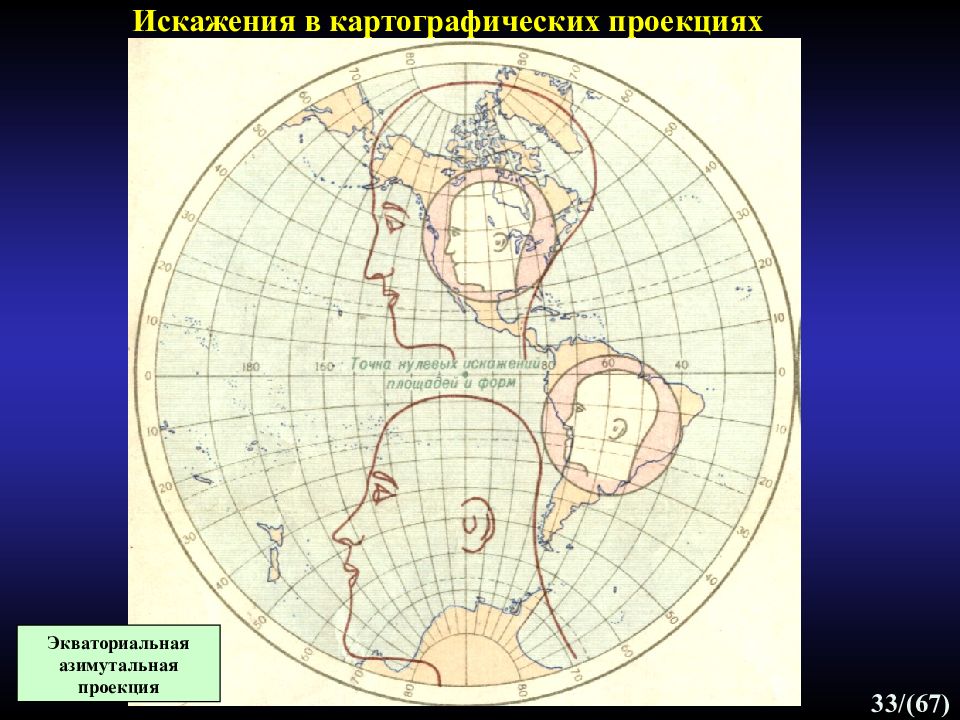
Слайд 33: Искажения в картографических проекциях
33 /(67) Искажения в картографических проекциях Экваториальная азимутальная проекция
Слайд 34
34 /(67) Основными вспомогательными поверхностями при переходе от эллипсоида (шара), моделирующих геоид, к карте являются цилиндр, конус ( разворачивающиеся поверхности ) и плоскость. В зависимости от используемой вспомогательной поверхности и виду получаемой картографической сетки проекции подразделяются на: Цилиндрические Конические Азимутальные Условные Вид картографической сетки Классификация проекций по виду картографической сетки (по сетки меридианов и параллелей)
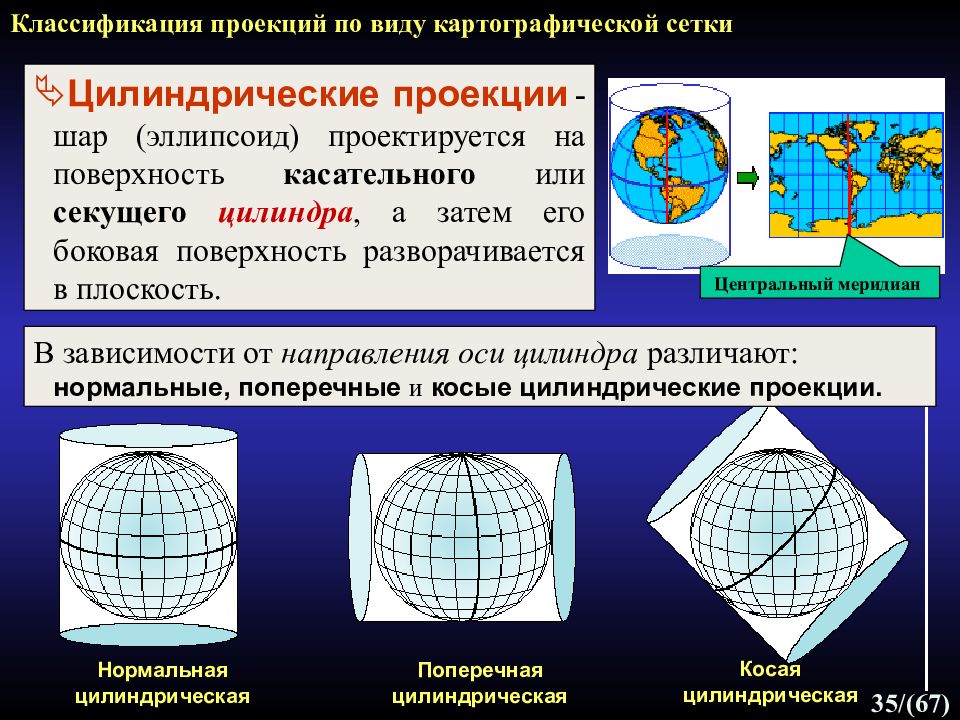
Слайд 35: Классификация проекций по виду картографической сетки
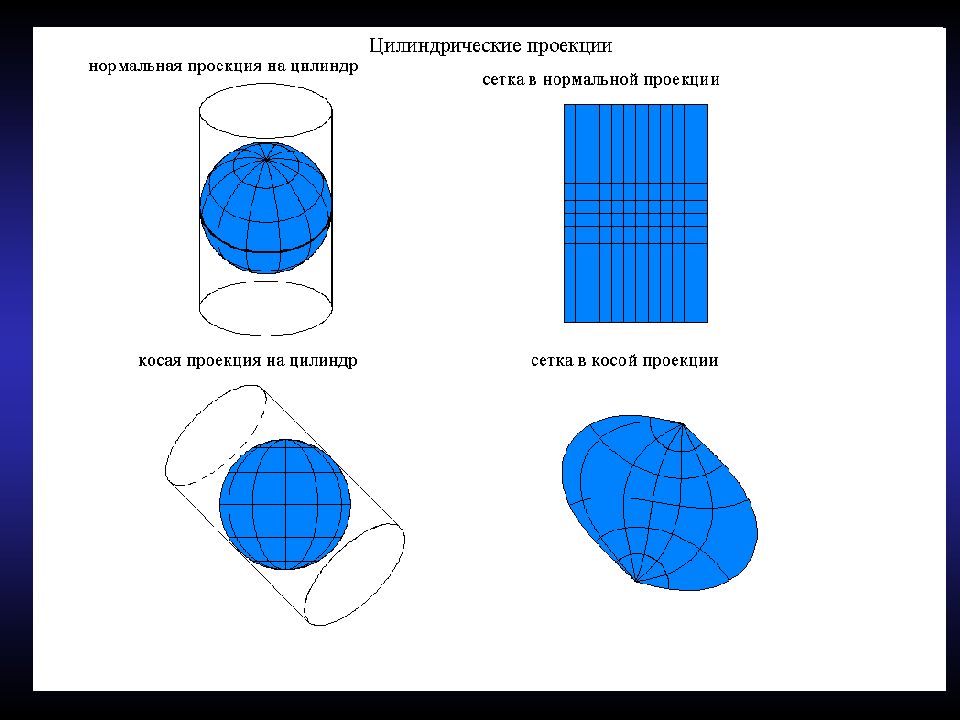
35 /(67) Классификация проекций по виду картографической сетки Цилиндрические проекции - шар (эллипсоид) проектируется на поверхность касательного или секущего цилиндра, а затем его боковая поверхность разворачивается в плоскость. Нормальная цилиндрическая Поперечная цилиндрическая Косая цилиндрическая В зависимости от направления оси цилиндра различают: нормальные, поперечные и косые цилиндрические проекции. Центральный меридиан
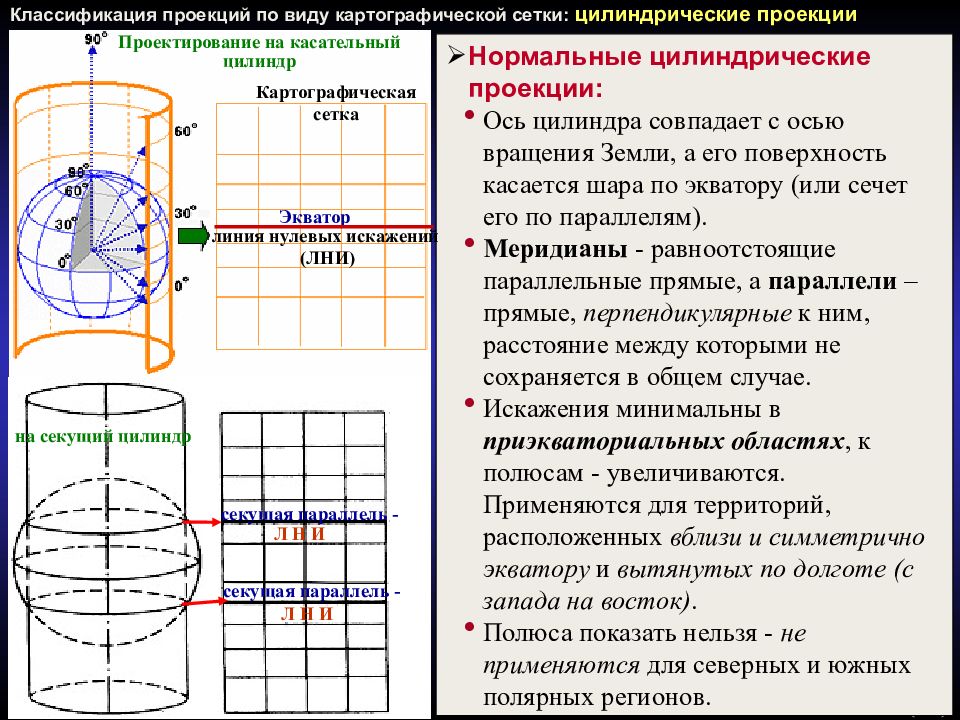
Слайд 36: Классификация проекций по виду картографической сетки: цилиндрические проекции
36 /(67) Классификация проекций по виду картографической сетки: цилиндрические проекции Нормальные цилиндрические проекции: Ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору (или сечет его по параллелям). Меридианы - равноотстоящие параллельные прямые, а параллели – прямые, перпендикулярные к ним, расстояние между которыми не сохраняется в общем случае. Искажения минимальны в приэкваториальных областях, к полюсам - увеличиваются. Применяются для территорий, расположенных вблизи и симметрично экватору и вытянутых по долготе (с запада на восток). Полюса показать нельзя - не применяются для северных и южных полярных регионов. Проектирование на касательный цилиндр на секущий цилиндр Экватор Л Н И Картографическая сетка Л Н И линия нулевых искажений (ЛНИ) секущая параллель - секущая параллель -
Слайд 37: Классификация проекций по виду картографической сетки: цилиндрические
37 /(67) Классификация проекций по виду картографической сетки: цилиндрические Поперечные цилиндрические проекции Ось цилиндра расположена в плоскости экватора. Цилиндр либо касается шара по меридиану, поэтому искажения вдоль него отсутствуют, либо сечет по двум линиям, параллельным центральному меридиану, на равных расстояниях от него. Центральный меридиан и экватор – прям ые, остальные линии сетки - кривые. Проекция становится неопределенной при удалении от центрального меридиана более, чем на 90 °. И скажения увеличиваются с расстоянием от центрального меридиана. Поэтому проекция применяется для территорий, вытянутых с севера на юг и удаленных в обе стороны от центрального меридиана не более, чем на 15 ° - 20 °. Поперечная цилиндрическая проекция ЛНИ Центральный меридиан Искажения в поперечной цилиндрической проекции
Слайд 38: Классификация проекций по виду картографической сетки: цилиндрические
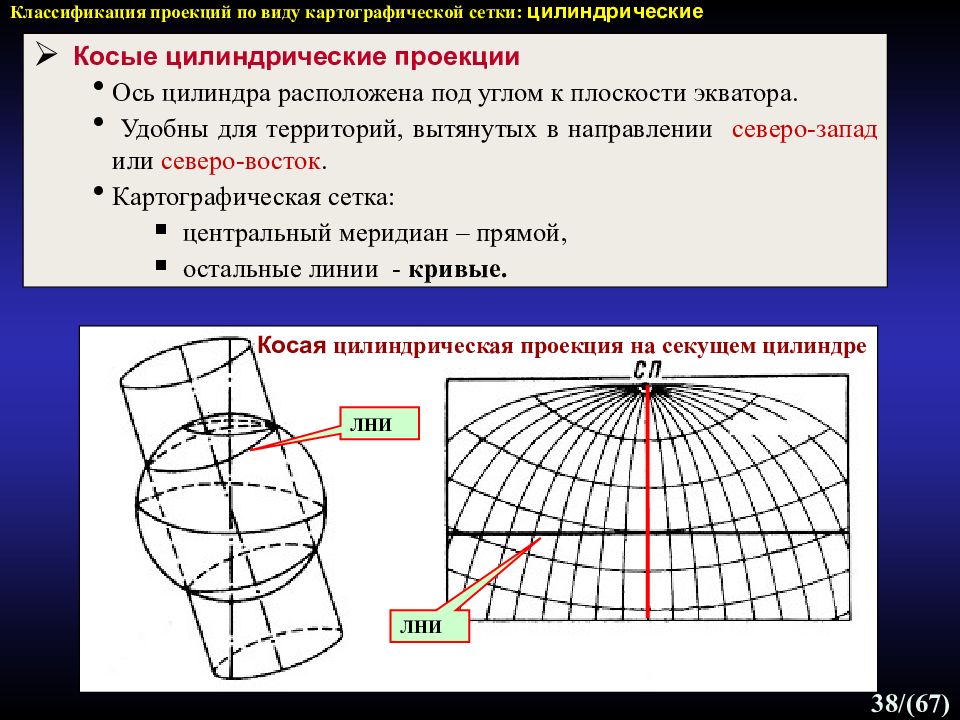
38 /(67) Классификация проекций по виду картографической сетки: цилиндрические Косые цилиндрические проекции Ось цилиндра расположена под углом к плоскости экватора. Удобны для территорий, вытянутых в направлении северо-запад или северо-восток. Картографическая сетка: центральный меридиан – прямой, остальные линии - кривые. Косая цилиндрическая проекция на секущем цилиндре ЛНИ ЛНИ
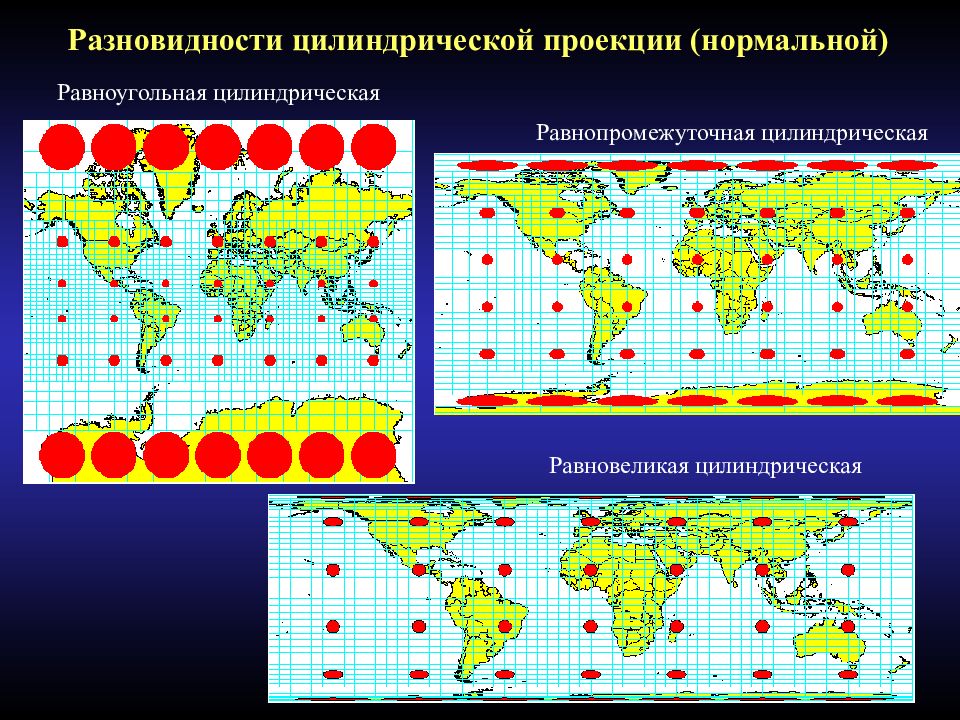
Слайд 40: Разновидности цилиндрической проекции (нормальной)
Равноугольная цилиндрическая Равнопромежуточная цилиндрическая Равновеликая цилиндрическая
Слайд 41
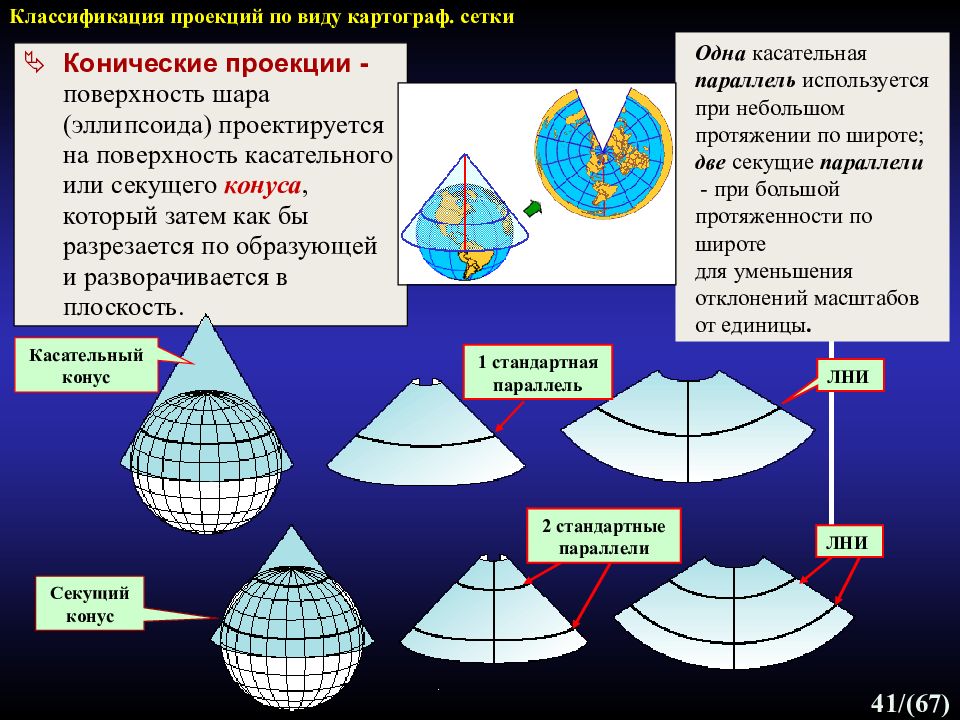
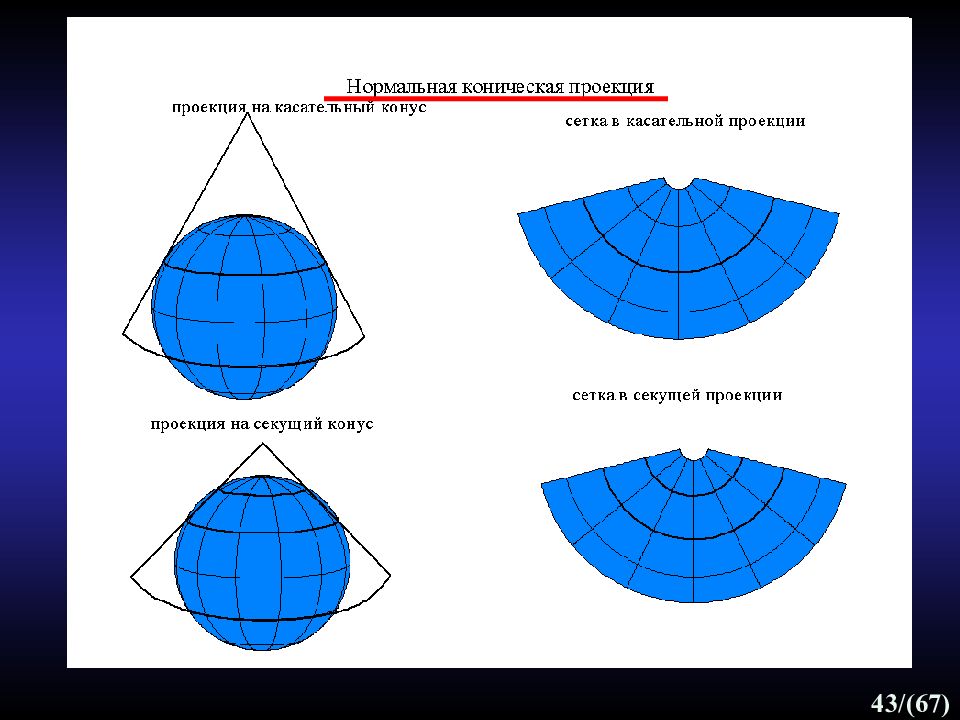
41 /(67) Конические проекции - поверхность шара (эллипсоида) проектируется на поверхность касательного или секущего конуса, который затем как бы разрезается по образующей и разворачивается в плоскость. Классификация проекций по виду картограф. сетки Касательный конус Секущий конус ЛНИ ЛНИ 2 стандартные параллели 1 стандартная параллель Одна касательная параллель используется при небольшом протяжении по широте; две секущие параллели - при большой протяженности по широте для уменьшения отклонений масштабов от единицы.
Слайд 42
42 /(67) Различают: нормальную (прямую) коническую проекцию - ось конуса совпадает с осью вращения Земли; поперечную коническую - ось конуса лежит в плоскости экватора; косую коническую - ось конуса наклонена к плоскости экватора. Классификация проекций по виду картографической сетки: конические проекции Секущий конус и картографическая сетка. Касательный конус В нормальной конической проекции: меридианы - прямые, расходящиеся из точки полюса; параллели - дуги концентрических окружностей с центром в этой точке; картографируют территории России, Канады, США, вытянутые с запада на восток в средних широтах. Искажения сильно увеличиваются к полюсам, поэтому на многих картах, основанных на данной проекции, полярные области удаляются.
Слайд 44
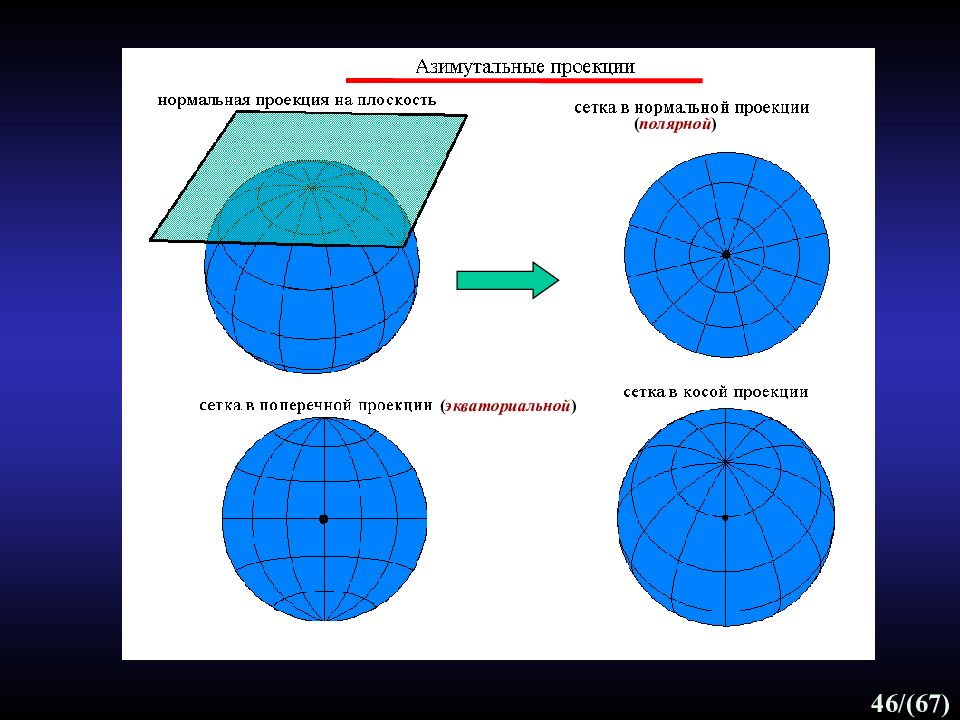
44 /(67) Классификация проекций по виду картографической сетки Азимутальные проекции - поверхность земного шара (эллипсоида) переносится на касательную или секущую плоскость : Нормальная (полярная) азимутальная - плоскость перпендикулярна к оси вращения Земли. Используется для карт полярных областей. Поперечная (экваториальная) азимутальная - плоскость проекции перпендикулярна к плоскости экватора. Используется для карт полушарий. Косая азимутальная - плоскость находится под любым углом к плоскости экватора. Нормальная азимутальная Поперечная азимутальная Косая азимутальная
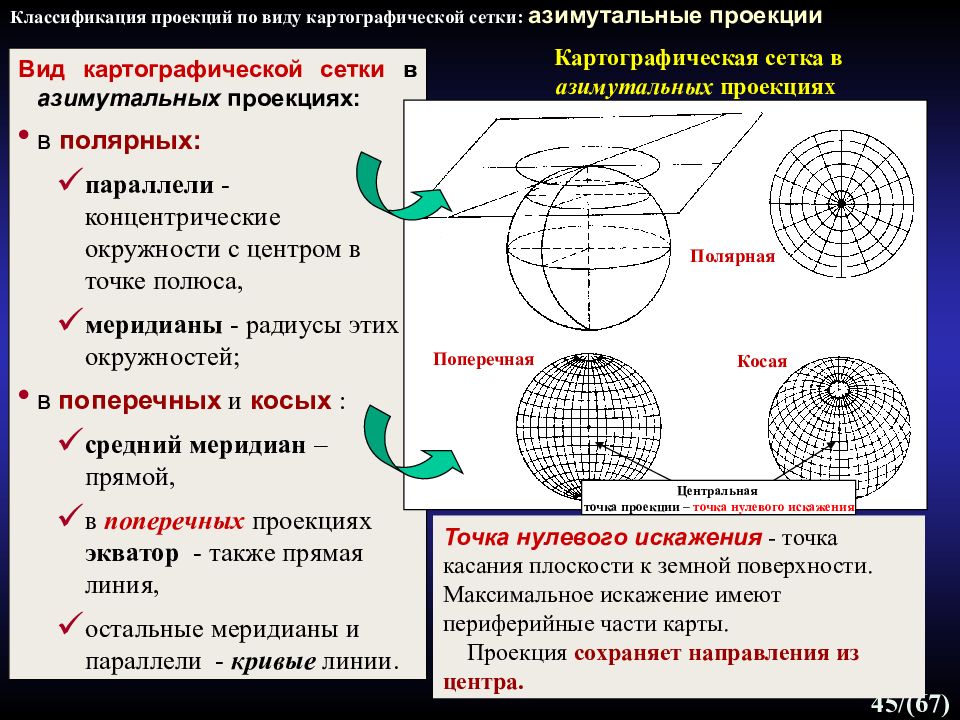
Слайд 45
45 /(67) Вид картографической сетки в азимутальных проекциях: в полярных: параллели - концентрические окружности с центром в точке полюса, меридианы - радиусы этих окружностей; в поперечных и косых : средн ий меридиан – прямой, в поперечных проекциях экватор - также прямая линия, остальные меридианы и параллели - кривые линии. Картографическая сетка в азимутальных проекциях Классификация проекций по виду картографической сетки: азимутальные проекции Центральная точка проекции – точка нулевого искажения Полярная Поперечная Косая Точка нулевого искажения - точка касания плоскости к земной поверхности. Максимальное искажение имеют периферийные части карты. Проекция сохраняет направления из центра.
Слайд 47
47 /(67) К ним относятся: Псевдоцилиндрические : параллели - прямые линии, средний меридиан - перпендикулярная им прямая, остальные меридианы - кривые, симметричные относительно среднего меридиана с увеличивающейся кривизной. Классификация проекций по виду картографической сетки Условные (производные) проекции - проекции, для которых нельзя подобрать простых геометрических аналогов. С троятся путем преобразования вышеперечисленных проекций, исходя из заданных условий ( желательного вида сетки или распределения искажений на карте),. Вид картографической сетки в условных проекциях ( нормальных ) Псевдоконические : параллели - дуги концентрических окружностей, средний меридиан - прямая линия, остальные меридианы - кривые, симметричные относительно среднего меридиана с увеличивающейся кривизной. Коническая ( нормальная ) Псевдо-коническая Цилиндрическая ( нормальная ) Псевдо-цилиндрическая
Слайд 48
48 /(67) Классификация проекций по виду картографической сетки: условные проекции Псевдоазимутальные : параллели - концентрические окружности, меридианы - кривые линии, симметричные относительно двух прямых меридианов. Коническая ( нормальная ) Поликоническая Поликонические : проектирование шара (эллипсоида) ведется на множество конусов; параллели - дуги эксцентрических окружностей с центрами на среднем прямом меридиане, остальные меридианы - кривые, симметричные относительно среднего меридиана и экватора. Азимутальная ( нормальная ) Псевдо- азимутальная Вид картографической сетки в условных проекциях ( нормальных )
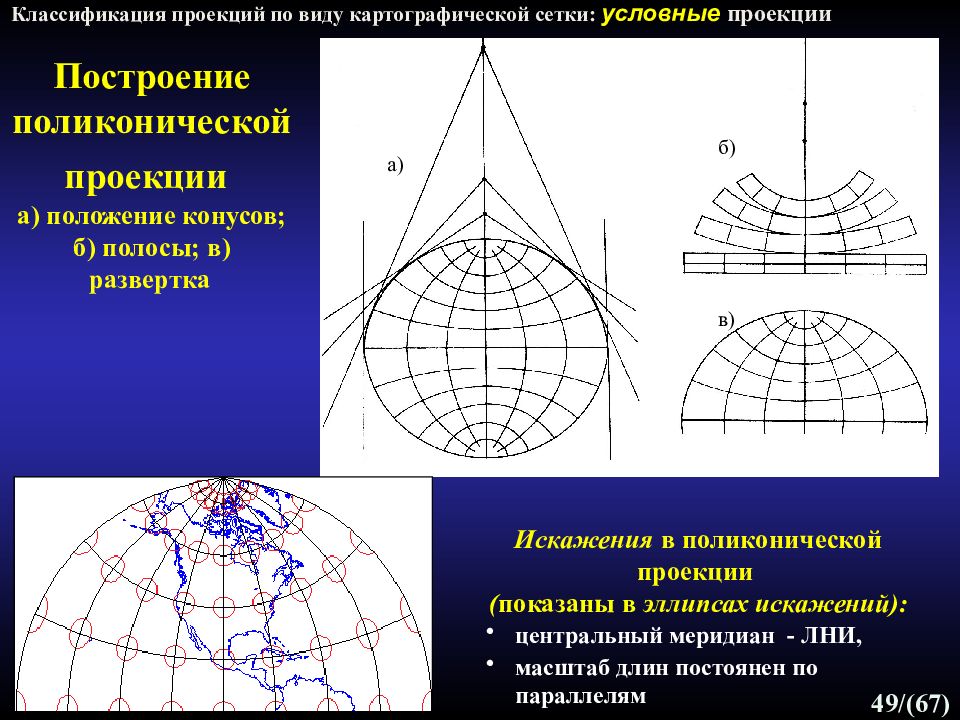
Слайд 49: Построение поликонической проекции а) положение конусов; б) полосы; в) развертка
49 /(67) Построение поликонической проекции а) положение конусов; б) полосы; в) развертка б) а) в) Классификация проекций по виду картографической сетки: условные проекции Искажения в поликонической проекции ( показаны в эллипсах искажений): центральный меридиан - ЛНИ, масштаб длин постоянен по параллелям
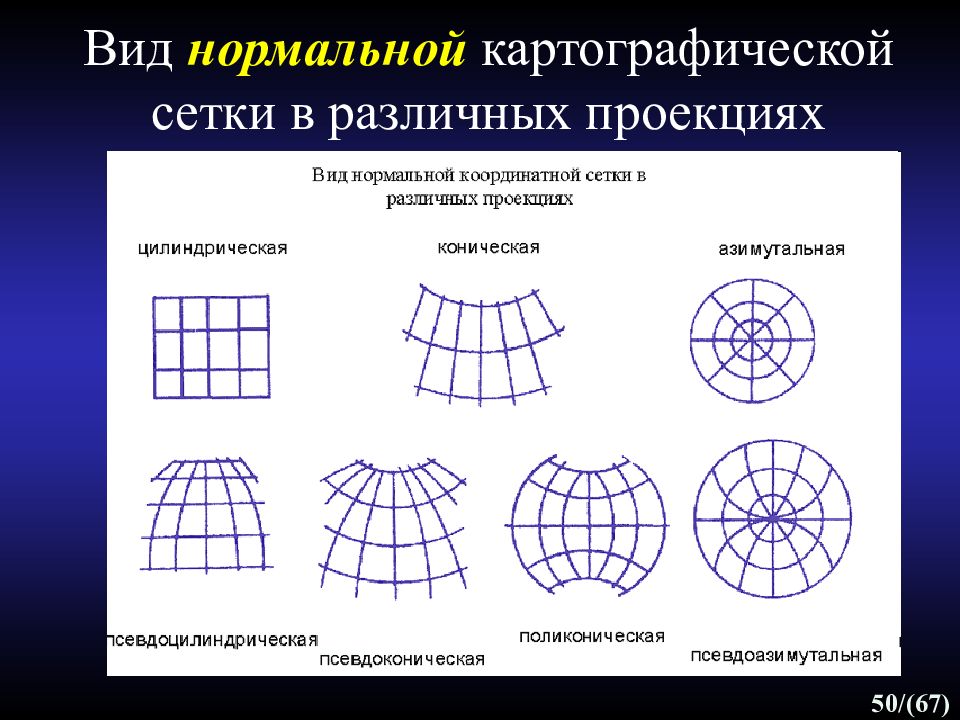
Слайд 50: Вид нормальной картографической сетки в различных проекциях
50 /(67) Вид нормальной картографической сетки в различных проекциях
Слайд 51
51 /(67) Факторы, влияющие на выбор проекции: географические особенности территории (ее положение, размеры и конфигурация); масштаб; тематика карты; задачи, которые будут решаться по карте; требования к точности результатов измерений; особенности самой проекции - искажения длин, площадей, углов, их распределение по территории. Знать проекцию карты (установить ее название, класс) необходимо для того, чтобы иметь представление о ее свойствах, распределении и величине искажений. З ная проекци ю пространственных данных, их можно перепроектировать в другую проекцию, т.к. со вместное использование данных в ГИС (например, их наложение) возможно, только если они находятся в одной системе координат, в одной проекции. Файл описания проекции Проекция данных записывается в специальный файл ( с расширением prj ), в котором указывается система координат, проекция, единицы измерения и др. Этот файл позволяет ГИС определить проекцию данных, осуществить их пространственную привязку и при необходимости перевести данные в другую проекцию. (- v)
Слайд 52
PROJCS ["WGS_1984_UTM_Zone_36N", GEOGCS ["GCS_WGS_1984", DATUM ["D_WGS_1984", SPHEROID ["WGS_1984",6378137.0,298.257223563]], PRIMEM ["Greenwich",0.0], UNIT ["Degree",0.0174532925199433]], PROJECTION ["Transverse_Mercator"], PARAMETER ["False_Easting",500000.0], PARAMETER ["False_Northing",0.0], PARAMETER ["Central_Meridian",33.0], PARAMETER ["Scale_Factor",0.9996], PARAMETER ["Latitude_Of_Origin",0.0], UNIT ["Meter",1.0]] GEOGCS ["GCS_North_American_1927", DATUM ["D_North_American_1927", SPHEROID ["Clarke_1866",6378206.4,294.9786982]], PRIMEM ["Greenwich",0], UNIT ["Degree",0.0174532925199433]] Примеры файлов с описаниями проекций (*. prj) Зная ГСК, проекцию и ее параметры, файл prj можно создать, как правило, в любой настольной ГИС или вручную.
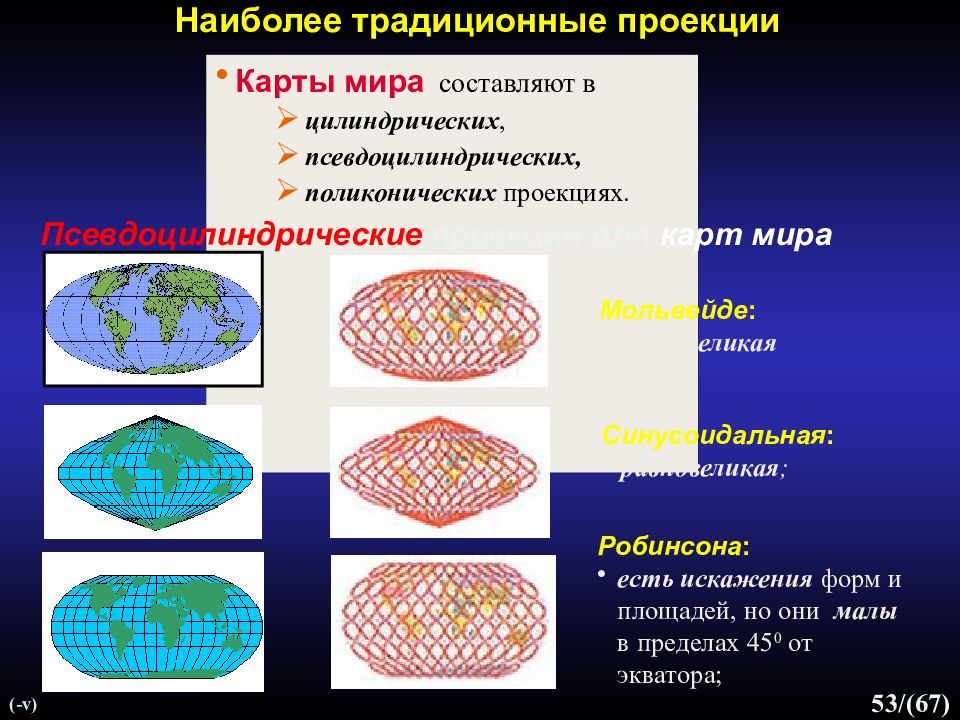
Слайд 53: Наиболее традиционные проекции
53 /(67) Наиболее традиционные проекции Карты мира составляют в цилиндрических, псевдоцилиндрических, поликонических проекциях. (- v) Робинсона : есть искажения форм и площадей, но они малы в пределах 45 0 от экватора; Мольвейде : равновеликая Псевдоцилиндрические проекции для карт мира Синусоидальная : равновеликая ;
Слайд 54
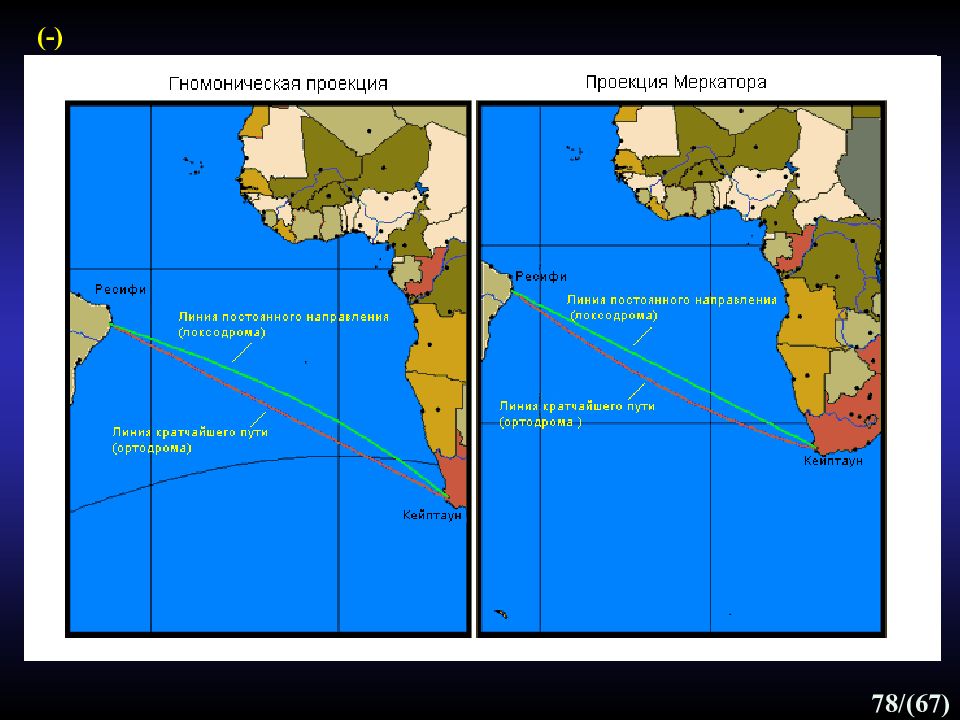
54 /(67) (- v) Цилиндрическая проекция Меркатора (16 в.) - нормальная цилиндрическая проекция с касательным цилиндром (ось цилиндра совпадает с осью вращения Земли), равноугольная, меридианы - равноотстоящие параллельные прямые, параллели - перпендикулярны меридианам, но расходятся в направлении полюсов ; по люса показать нельзя ; меридианы ограничены 80 º с.ш. и ю. ш, экватор – линия нулевых искажений, искажения площадей возрастают в направлении к полярным обл. Проекция преувеличивает площади на параллели 60° в 4 раза, а на параллели 80° более чем в 30 раз. ( Африка выглядит меньше Северной Америки и Гренландии, хотя это 2-й по величине материк ), ис пользование - морские навигационные карты, воздушные перелеты, равноугольные карты мира, картографирование экваториальных районов. 80 ° с.ш. 60 ° с.ш.
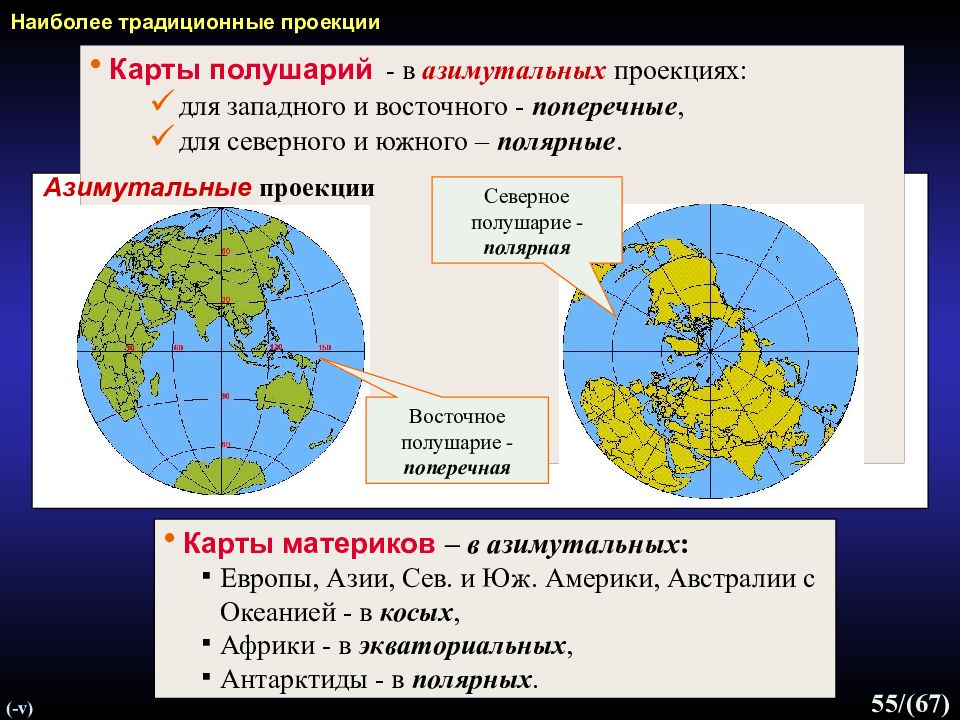
Слайд 55: Наиболее традиционные проекции
55 /(67) Наиболее традиционные проекции Карты полушарий - в азимутальных проекциях: для западного и восточного - поперечные, для северного и южного – полярные. Азимутальные проекции Восточное полушарие - поперечная Северное полушарие - полярная (- v) Карты материков – в азимутальных : Европы, Азии, Сев. и Юж. Америки, Австралии с Океанией - в косых, Африки - в экваториальных, Антарктиды - в полярных.
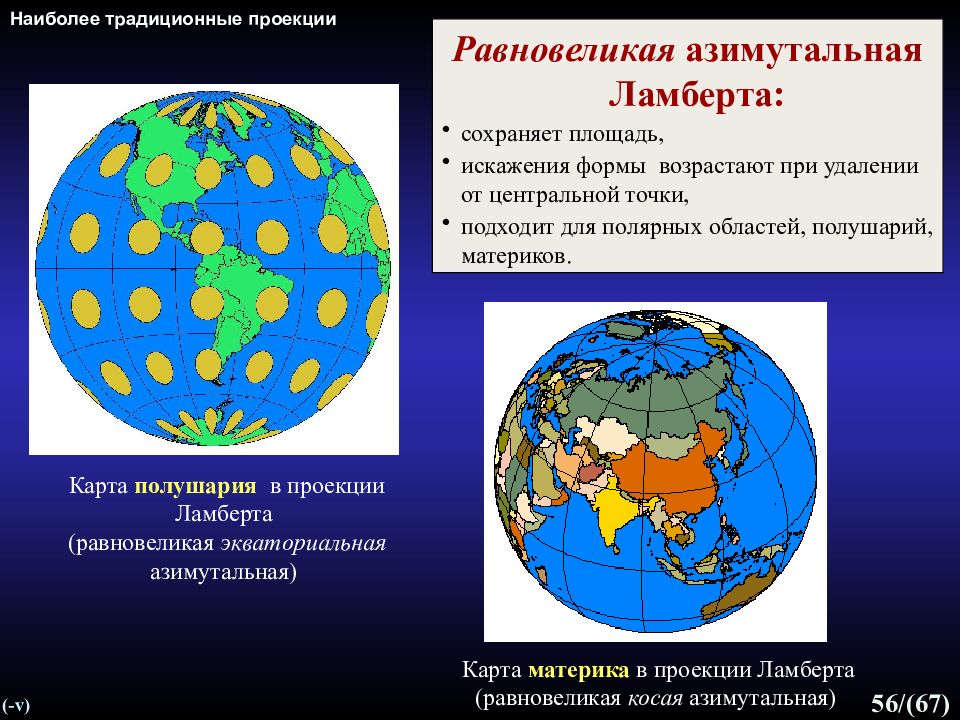
Слайд 56: Наиболее традиционные проекции
56 /(67) Наиболее традиционные проекции (- v) Равновеликая азимутальная Ламберта: сохраняет площадь, искажения формы возрастают при удалении от центральной точки, подходит для полярных областей, полушарий, материков. Карта материка в проекции Ламберта (равновеликая косая азимутальная) Карта полушария в проекции Ламберта (равновеликая экваториальная азимутальная)
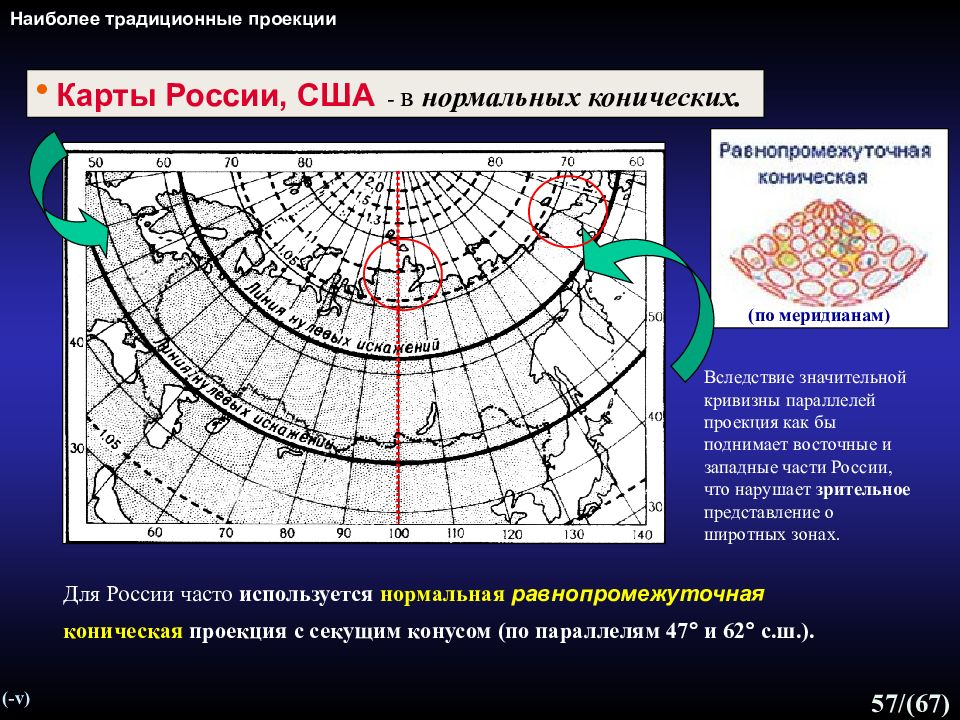
Слайд 57: Наиболее традиционные проекции
57 /(67) Наиболее традиционные проекции (- v) Для России часто используется нормальная равнопромежуточная коническая проекция с секущим конусом (по параллелям 47 и 62 с.ш.). (по меридианам) Карты России, США - в нормальных конических. Вследствие значительной кривизны параллелей проекция как бы поднимает восточные и западные части России, что нарушает зрительное представление о широтных зонах.
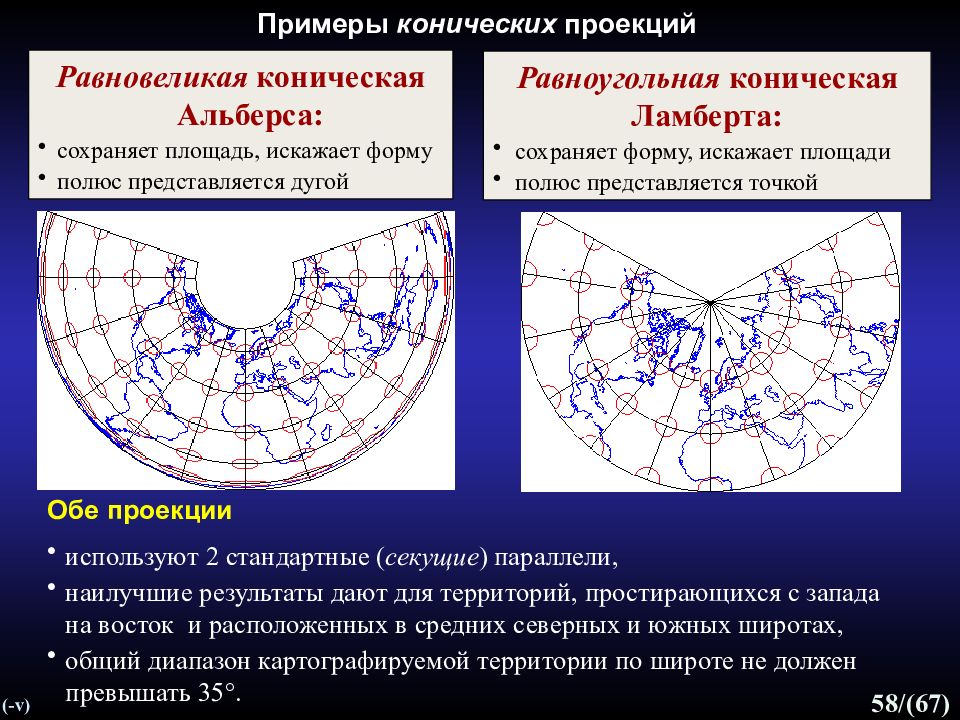
Слайд 58
58 /(67) Примеры конических проекций Равноугольная коническая Ламберта: сохраняет форму, искажает площади полюс представляется точкой Равновеликая коническая Альберса: сохраняет площадь, искажает форму полюс представляется дугой (- v) Обе проекции используют 2 стандартные ( секущие ) параллели, наилучшие результаты дают для территорий, простирающихся с запада на восток и расположенных в средних северных и южных широтах, общий диапазон картографируемой территории по широте не должен превышать 35 °.
Слайд 60: Наиболее традиционные проекции
60 /(67) Наиболее традиционные проекции Морские и аэронавигационные карты - в нормальной равноугольной цилиндрической проекции Меркатора. Топографические карты в России - в проекции Гаусса – Крюгера, в США и запад. странах - в UTM ( универсальная поперечно-цилиндрическая проекция Меркатора, U niversal Transverse Mercator), одна из самых распространенных проекций в ГИС.
Слайд 61
61 /(67) Свойства UTM и Гаусса – Крюгера: очень близки по своим характеристикам; обе строятся на основе поперечно-цилиндрической проекции Меркатора (Transverse Mercator, равноугольной ) ; являются многополосными - делят земную поверхность на 60 зон по 6 º долготы ( с целью уменьшения искажений для каждой зоны цилиндр поворачивается вокруг земного шара с шагом 6 º по долготе). (- v) Поверхность эллипсоида, отображаемая в проекции UTM и Гаусса-Крюгера по меридианным зонам Проекции UTM и Гаусса – Крюгера
Слайд 62: Свойства проекций Гаусса - Крюгера и UTM :
62 /(67) Свойства проекций Гаусса - Крюгера и UTM : для UTM поперечный цилиндр сечет земную поверхность по двум линиям, параллельным центральному меридиану, каждая на расстоянии 180 км от него ( являются линиями нулевых искажений, на этих линиях M =1, на центральном меридиане M = 0.9996 ), для Гаусса–Крюгера цилиндр касается земной поверхности по центральному меридиану (является линией нулевых искажений, M=1 ). Картографическая сетка для UTM и Гаусса-Крюгера : центральный меридиан и экватор - прямые, остальные меридианы и параллели – кривые, симметричные относительно центрального меридиана и экватора с малой кривизной. Параллели Меридианы
Слайд 63: Наиболее традиционные проекции: UTM
63 /(67) Наиболее традиционные проекции: UTM единица измерения длины - метр ; земная поверхность делится на 60 вертикальных зон шириной по 6 o долготы (для UTM от 80 о ю.ш. до 84 о с.ш., для Гаусса-Крюгера – до полюсов); зоны нумеруются с запада на восток числами от 1 до 60 (для UTM - начиная с 180 о в.д, для Гауса-Крюгера - от 0-го меридиана); в UTM каждая зона делится еще на полосы по 8 о широты (самая северная - 12 о ); начало прямоугольных координат каждой зоны - в точке пересечения центр. меридиана для этой зоны с экватором; для исключения отриц. Х-координат применяется сдвиг на восток 500000 м, для Гауса-Крюгера, кроме сдвига на восток на 500000 м, перед х-ой координатой часто указывается также номер зоны. Например, Х = 30 766 000 м означает, что точка находится в 30-й зоне и отстоит от начала координат по оси X на расстоянии 266 000 м. для исключения отриц. Y -координат для южного полушария применяется сдвиг на север 1 0 000 000 м. 12 Свойства проекций UTM и Гаусса - Крюгера :
Слайд 64
64 /(67) Сетка зон UTM для карты мира В настоящее время эллипсоид WGS84 используется в качестве основной модели Земли в системе координат UTM
Слайд 65: Наиболее традиционные проекции: UTM
65 /(67) Наиболее традиционные проекции: UTM Внутри каждой зоны Гаусса - Крюгера и UTM : углы сохраняются – проекции равноугольные (комформные); локальные формы подобны ; искажения площади минимальны ; ошибки масштаба длин не более 0,1 процента; на центральном меридиане каждой зоны частный масштаб длин ( scale factor ): для UTM М=0.9996 ; для Гаусса-Крюгера М=1. Ошибки и искажения увеличиваются для территорий, охватывающих более чем одну зону UTM и Гаусса-Крюгера. Свойства проекций Гаусса - Крюгера и UTM :
Слайд 66
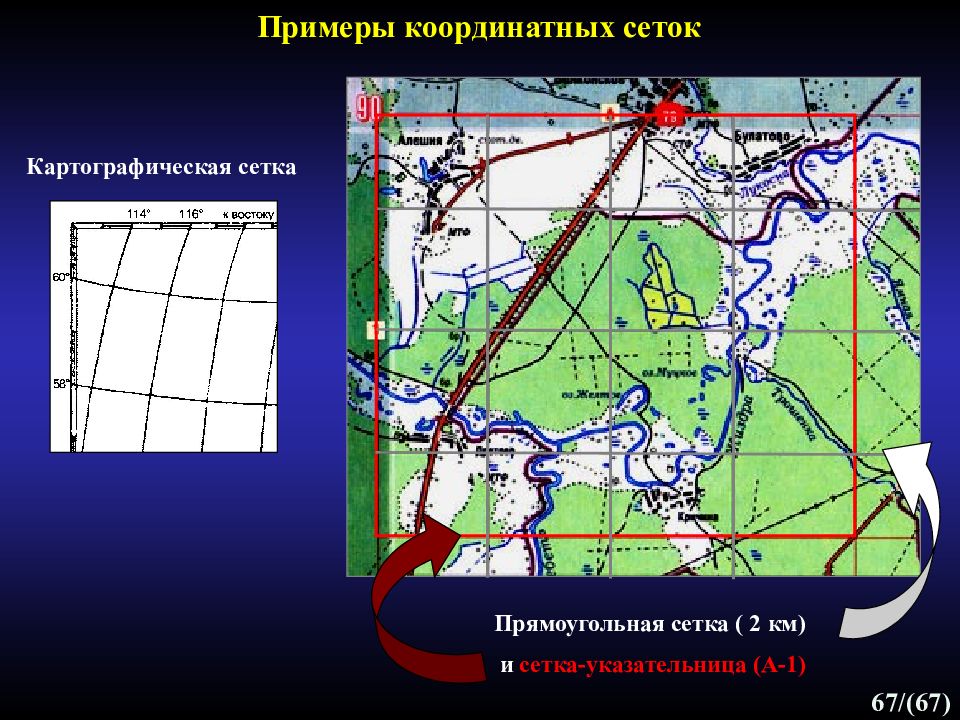
66 /(67) Виды координатных сеток: Картографическая сетка - линии меридианов и параллелей на карте. Прямоугольная сетка - сетка плоских прямоугольных координат в данной картографической проекции. Километровая сетка (частный случай прямоугольной сетки) – квадратная координатная сетка, линии которой проведены на карте параллельно экватору и осевому меридиану через интервалы, соответствующие определенному числу километров. Сетка-указательница - сетка на карте, предназначенная для указания местоположения и поиска объектов по указателю географических названий. Ячейки такой сетки обозначаются буквами и цифрами ( В-3). Координатные сетки - элемент математической основы карт: необходимы для ориентирования по карте, нанесения новых объектов и снятия координат; позволяют судить о масштабе карты, виде проекции и искажениях в ней. Координатные сетки
Слайд 67
67 /(67) Картографическая сетка Прямоугольная сетка ( 2 км) и сетка-указательница (А-1) Примеры координатных сеток
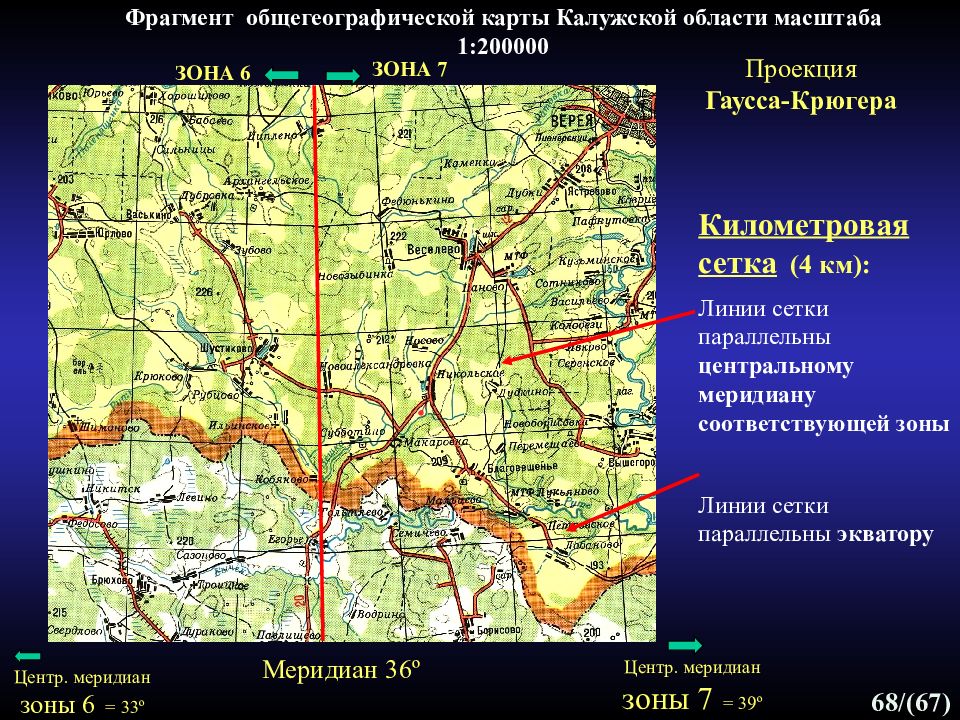
Слайд 68
68 /(67) ЗОНА 6 ЗОНА 7 Километровая сетка (4 км): Линии сетки параллельны центральному меридиану соответствующей зоны Линии сетки параллельны экватору Проекция Гаусса-Крюгера Фрагмент общегеографической карты Калужской области масштаба 1:200000 Центр. меридиан зоны 7 = 39 º Меридиан 36 º Центр. меридиан зоны 6 = 33 º
Слайд 70: Разграфка и номенклатура топографических карт
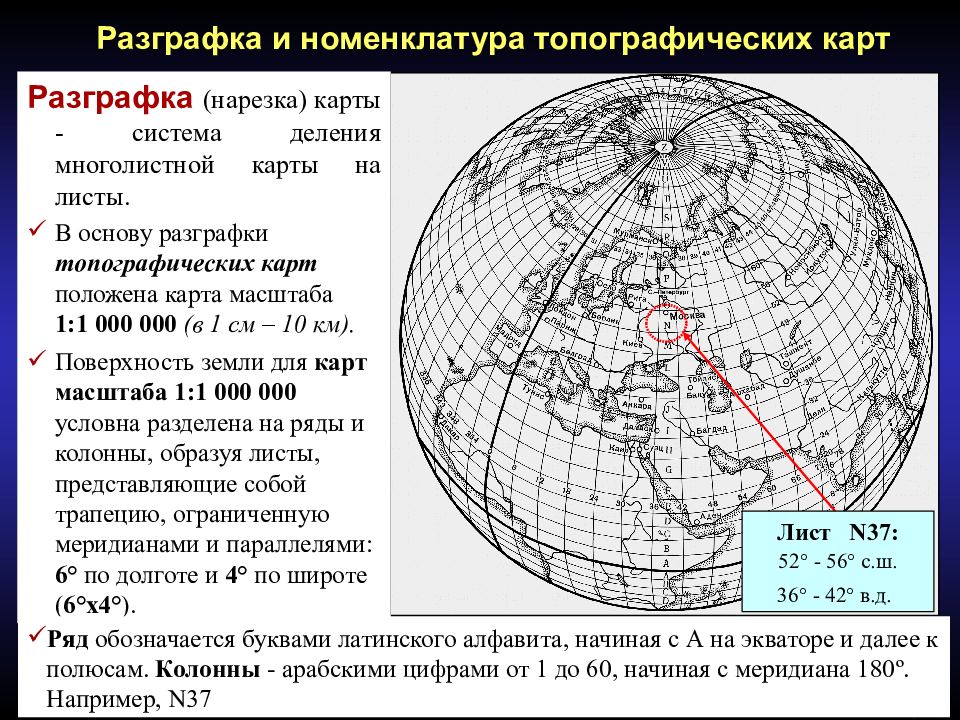
70 /(67) Разграфка и номенклатура топографических карт Разграфка (нарезка) карты - система деления многолистной карты на листы. В основу разграфки топографических карт положена карта масштаба 1:1 000 000 (в 1 см – 10 км). Поверхность земли для карт масштаба 1:1 000 000 условна разделена на ряды и колонны, образуя листы, п редставляющие собой трапецию, ограниченную меридианами и параллелями: 6° по долготе и 4° по широте ( 6° x 4° ). Ряд обозначается буквами латинского алфавита, начиная с А на экваторе и далее к полюсам. Колонны - арабскими цифрами от 1 до 60, начиная с меридиана 180 º. Например, N37 Лист N 37: 52 ° - 56° с.ш. 36° - 42° в.д.
Слайд 71: Разграфка и номенклатура топографических карт
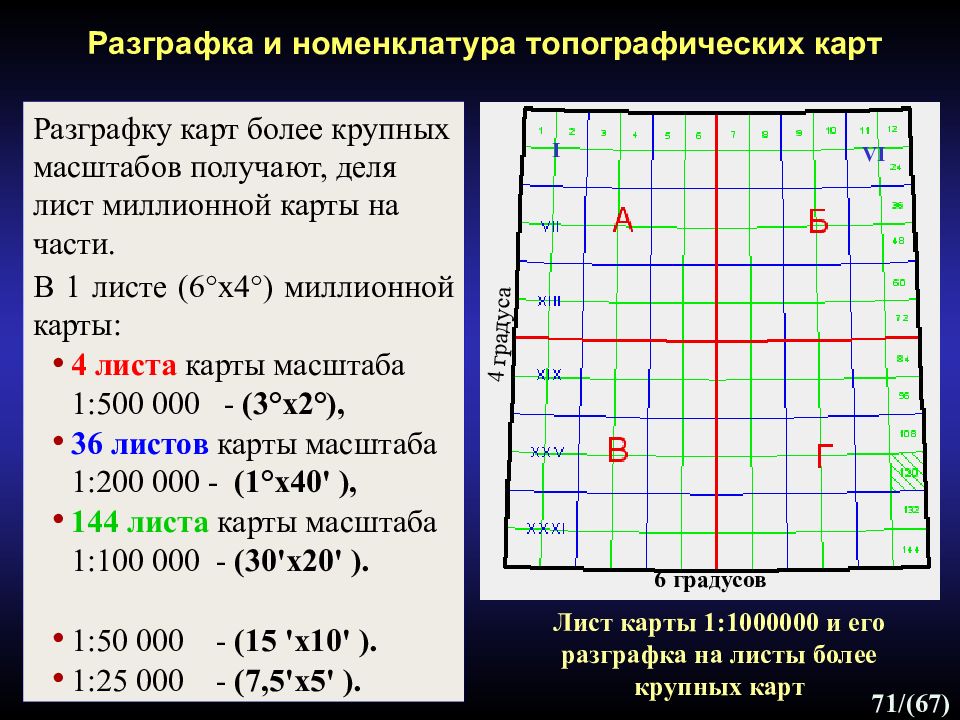
71 /(67) Разграфка и номенклатура топографических карт Разграфку карт более крупных масштабов получают, деля лист миллионной карты на части. В 1 листе (6° x 4°) миллионной карты: 4 листа карты масштаба 1:500 000 - (3°х2°), 36 листов карты масштаба 1:200 000 - (1°х40' ), 144 листа карты масштаба 1:100 000 - (30'х 2 0' ). 1:50 000 - (15 'х10' ). 1:25 000 - (7,5'х5' ). 6 градусов 4 градуса I VI Лист карты 1:1000000 и его разграфка на листы более крупных карт
Слайд 72: Номенклатура топографических карт
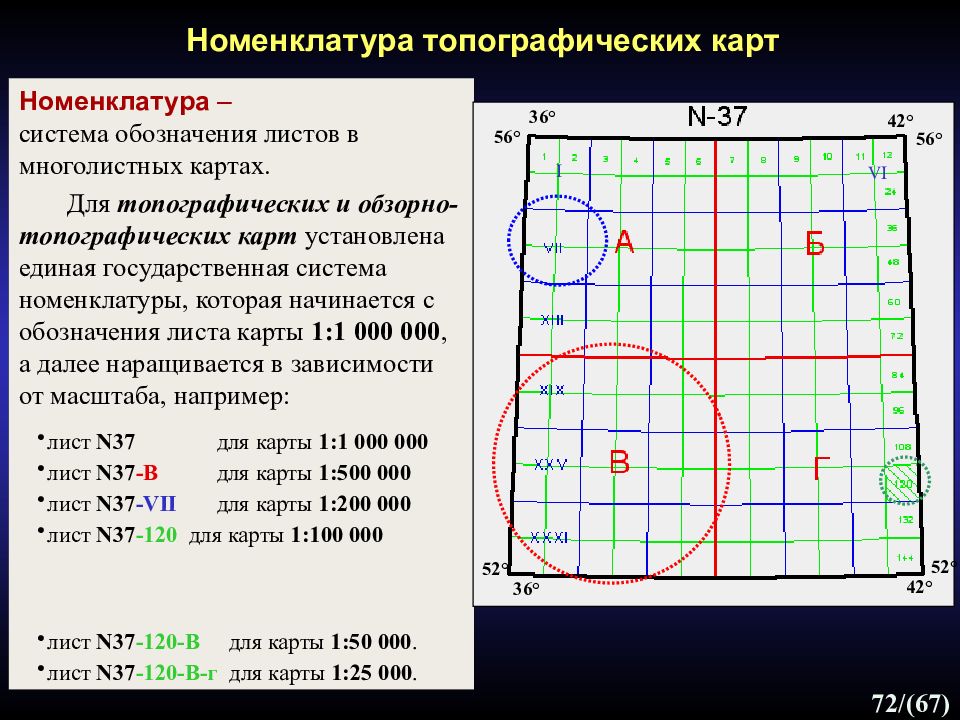
Номенклатура – система обозначения листов в многолистных картах. Для топографических и обзорно-топографических карт установлена единая государственная система номенклатуры, которая начинается c обозначения листа карты 1:1 000 000, а далее наращивается в зависимости от масштаба, например: лист N3 7 для карты 1: 1 0 00 000 лист N3 7 - В для карты 1:500 000 лист N3 7 -VII для карты 1:200 000 лист N3 7 - 120 для карты 1: 1 00 000 лист N3 7 - 120- B для карты 1: 5 0 000. лист N3 7 - 120- B -г для карты 1: 25 000. 72 /(67) Номенклатура топографических карт I VI 36 ° 52 ° 42 ° 56 ° 42 ° 36 ° 56 ° 52 °
Слайд 73: Разграфка и номенклатура карт в России
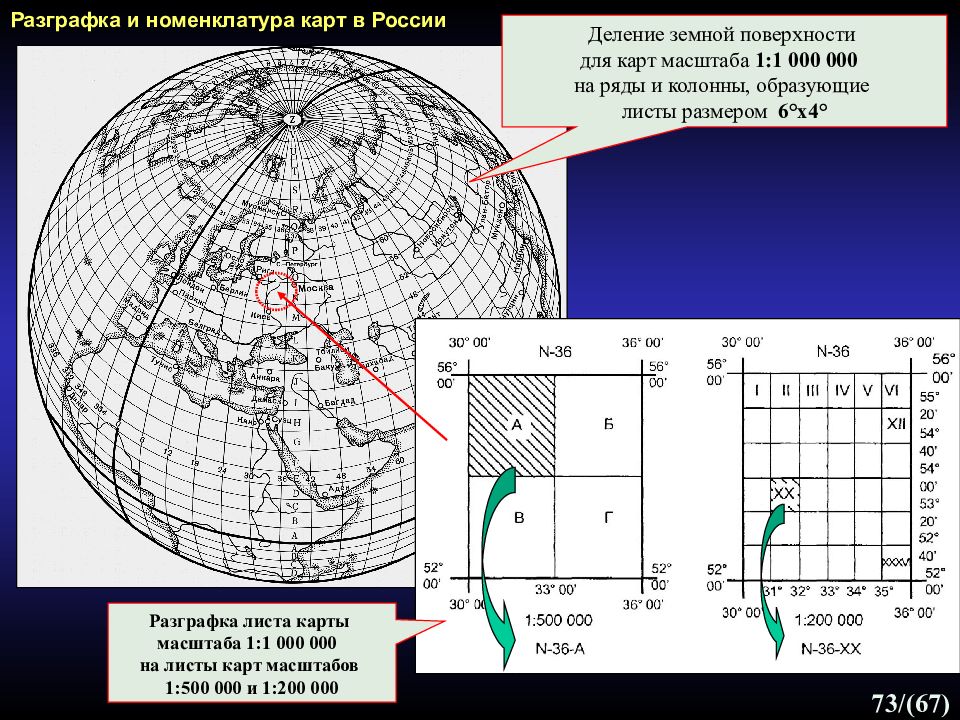
73 /(67) Разграфка и номенклатура карт в России Деление земной поверхности для карт масштаба 1:1 000 000 на ряды и колонны, образующие листы размером 6° x 4° Разграфка листа карты масштаба 1:1 000 000 на листы карт масштабов 1:500 000 и 1:200 000
Слайд 74
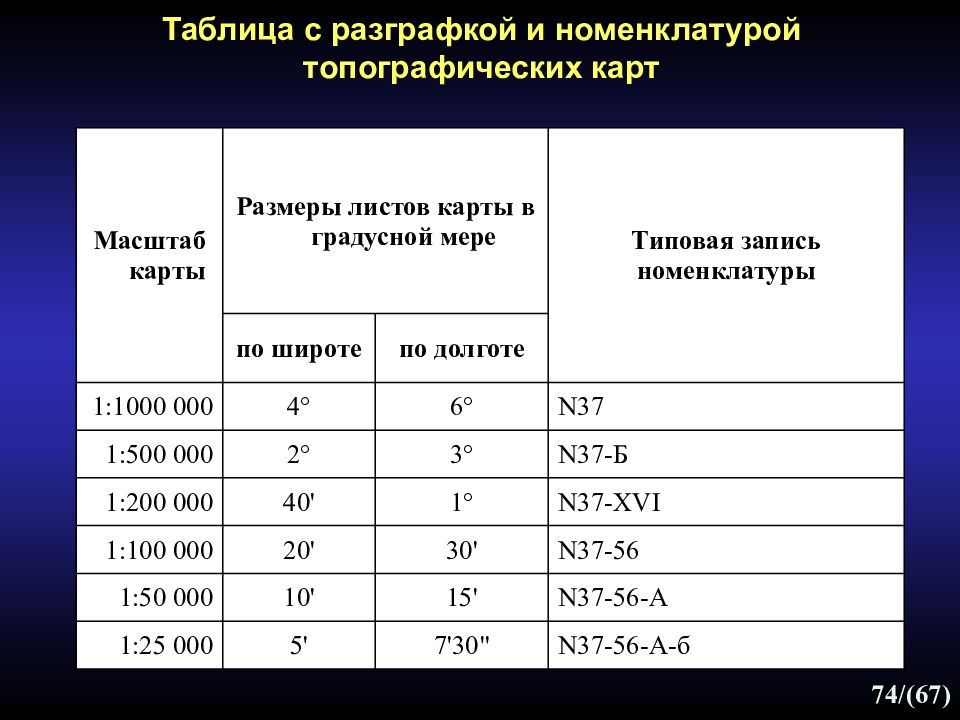
Масштаб карты Размеры листов карты в градусной мере Типовая запись номенклатуры по широте по долготе 1:1000 000 4° 6° N37 1:500 000 2° 3° N37-Б 1:200 000 40' 1° N37-XVI 1:100 000 20' 30' N37-56 1:50 000 10' 15' N37-56-A 1:25 000 5' 7'30" N37-56-A-б Таблица с разграфкой и номенклатурой топографических карт 74 /(67)
Слайд 75: Проекции с разрывами
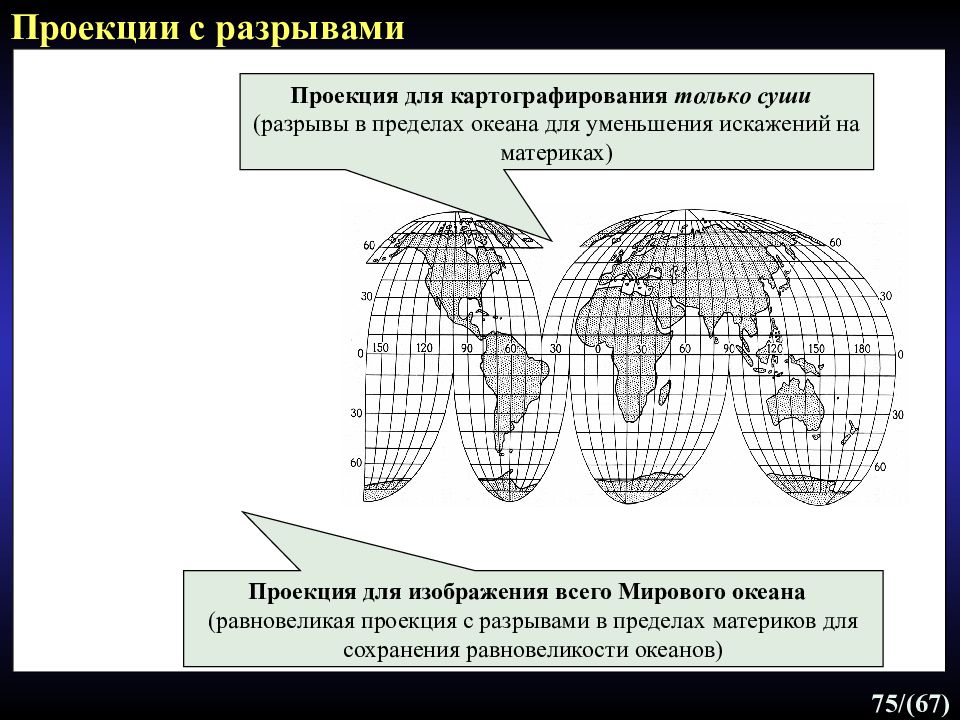
75 /(67) Проекции с разрывами Проекция для изображения всего Мирового океана (равновеликая проекция с разрывами в пределах материков для сохранения равновеликости океанов) Проекция для картографирования только суши ( разрывы в пределах океана для уменьшения искажений на материках)
Слайд 76
76 /(67) Получаются перспективным проецированием точек поверхности шара на плоскость. В зависимости от того, где расположен центр проецирования на луче, перпендикулярном плоскости проецирования и проходящем через центр шара, различают: Гномонические проекции - проецирование из центра шара, в этой проекции все большие круги (экватор, меридианы в том числе) – прямые линии, меньше половины сферы можно спроецировать на карту. Стереографические – проецирование с поверхности шара. Проекция определена на всей сфере за исключением точки проецирования; я вляется азимутальной равноугольной. Перспективные проекции (-)
Слайд 77
77 /(67) Внешние - центр проецирования находится за пределами шара на конечном расстоянии от него. Ортографические - проецирование из бесконечности параллельными прямыми лучами, может отобразить до полусферы. Форма и углы искажаются, особенно вблизи краев, но расстояния сохраняются вдоль параллелей. Перспективные проекции (-)