ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА
2 ПЛАН ЛЕКЦИИ Цель лекции Кинетическая энергия материальной системы и способы её вычисления Кинетическая энергия твердого тела Закон сохранения полной механической энергии материальной системы Пример решения задачи Ознакомиться с теоремой об изменении кинетической энергии системы. Научится считать кинетическую энергии и работу для ряда специальных случаев.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ ТЕОРЕМА КЕНИГА Пусть M k одна из точек материальной системы массы Введем подвижную систему координат O 2 x 2 y 2 z 2 перемещающуюся поступательно относительно неподвижной системы координат O 1 x 1 y 1 z 1 3
4 - скорость центра масс С относительно подвижной системы отсчета Ox 2 y 2 z 2 - масса системы - кинетическая энергия относительного движения 4 ТЕОРЕМА КЕНИГА
5 Если начало подвижных осей О совпадает с центром масс С системы, то Кинетическая энергия механической системы равна сумме кинетических энергий поступательного движения системы вместе с центром масс и движения системы относительно центра масс ТЕОРЕМА КЕНИГА
6 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА Кинетическая энергия поступательно движущегося тела Скорости всех точек тела одинаковы и равны v M – масса тела Поступательное движение
7 КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ПРИ ВРАЩЕНИИ ОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ОСИ Z O – момент инерции тела относительно оси вращения z 7 Вращение относительно неподвижной оси
Введем поступательно движущуюся систему координат С x 2 y 2 z 2 с началом в центре масс C тела. По теореме Кёнига Движение тела относительно подвижной системы координат – вращение с угловой скоростью ω и поэтому 8 Плоскопараллельное движение КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА ДВИЖУЩЕГОСЯ ПЛОСКОПАРАЛЛЕЛЬНО - момент инерции тела относительно оси
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ работа внешних сил системы, действующих на n- ю точку работа внутренних сил системы, действующих на n -ю точку Учтём, что -кинетическая энергия системы 9 Теорема об изменении кинетической энергии
Изменение кинетической энергии системы точек на некотором перемещении равно сумме работ внешних и внутренних сил системы на этом же перемещении 10 Теорема об изменении кинетической энергии ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
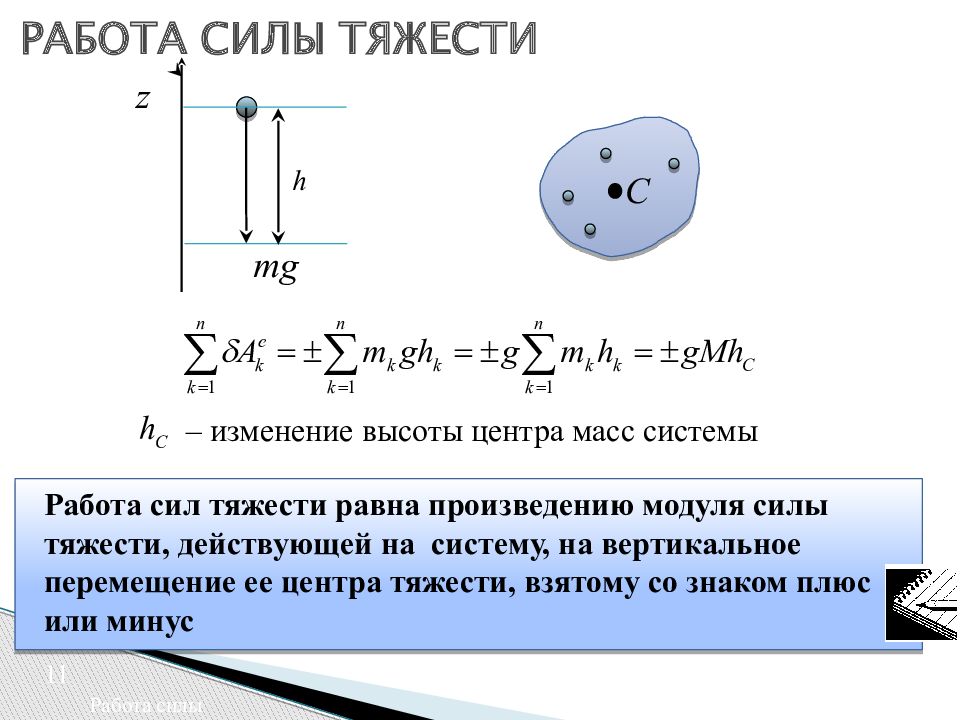
Работа сил тяжести равна произведению модуля силы тяжести, действующей на систему, на вертикальное перемещение ее центра тяжести, взятому со знаком плюс или минус – изменение высоты центра масс системы 11 Работа силы РАБОТА СИЛЫ ТЯЖЕСТИ
Сумма работ всех внутренних сил абсолютно твердого тела на любом его перемещении равна нулю и – внутренние силы взаимодействия точек B и D твердого тела Теорема о проекциях: 12 Работа силы РАБОТА ВНУТРЕННИХ СИЛ ТВЁРДОГО ТЕЛА
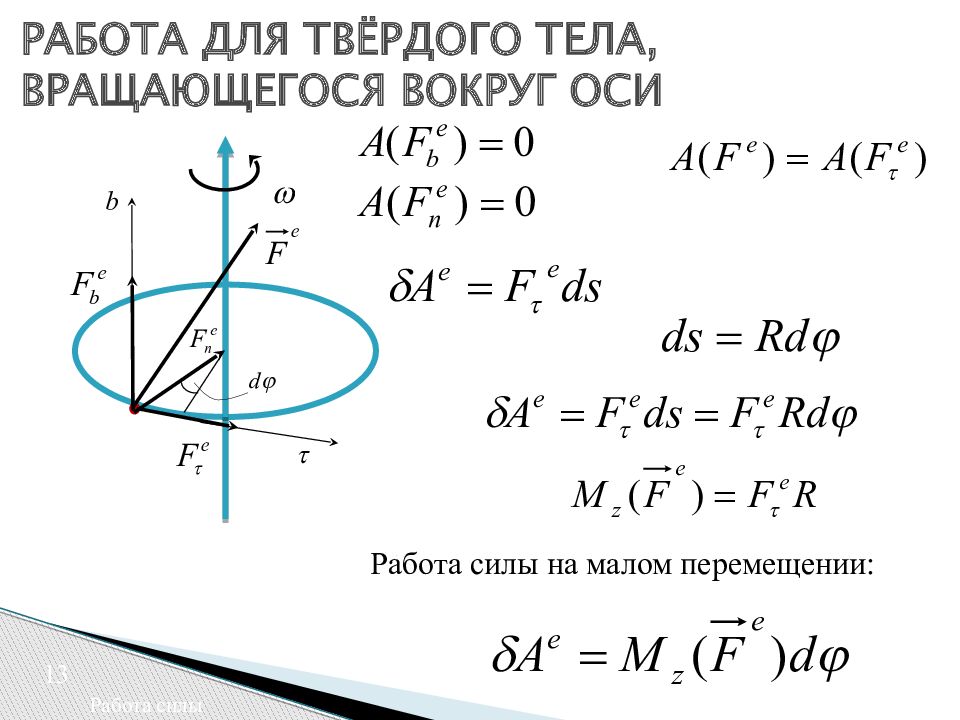
Работа силы на малом перемещении: 13 Работа силы РАБОТА ДЛЯ ТВЁРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ ОСИ
Если то Работа силы на конечном перемещении: 14 Работа силы РАБОТА ДЛЯ ТВЁРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ ОСИ
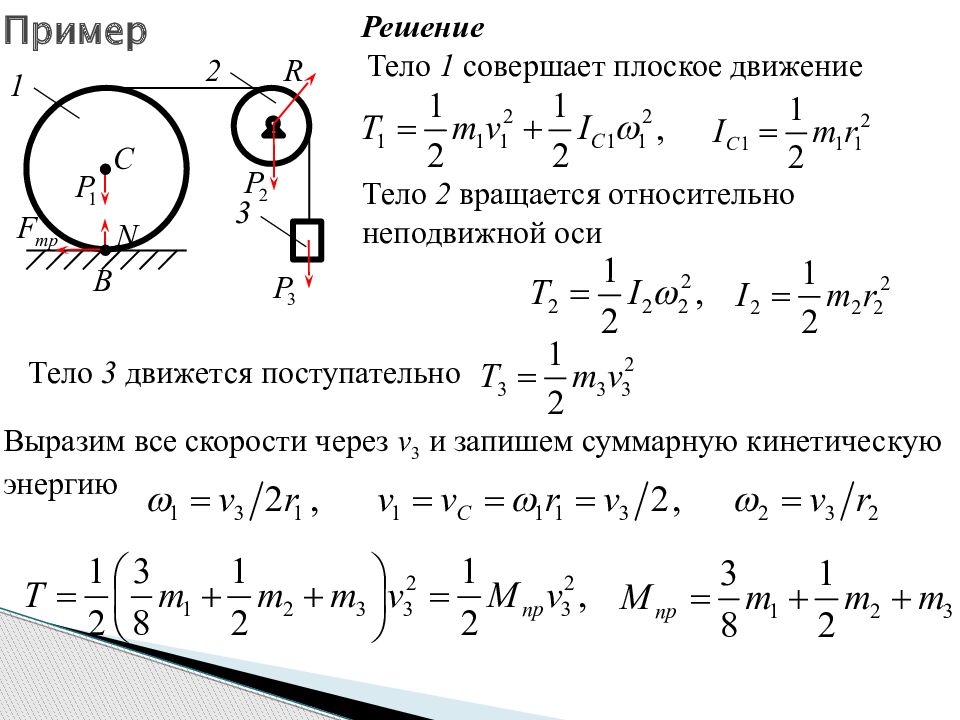
Материальная система состоит из трех тел. Груз 3 под действием силы тяжести опускается вниз из состояния покоя. Определить скорость груза 3 при опускании его на высоту h. Массы тел m 1, m 2, m 3. Тела 1 и 2 считать однородными дисками с радиусами r 1 и r 2. Решение Расставим внешние силы, действующие на систему. Внутренние силы учитывать не нужно, так как сумма их работ равна нулю. Запишем теорему об изменении кинетической энергии системы T 0 = 0 так как движение начинается из состояния покоя 15 Пример Пример
Решение Тело 1 совершает плоское движение Тело 2 вращается относительно неподвижной оси Тело 3 движется поступательно Выразим все скорости через v 3 и запишем суммарную кинетическую энергию Пример
Решение Вычислим работы всех сил Работа сил равна нулю, так как точка их приложения неподвижна Работа силы равна нулю, так как эта сила перпендикулярна к перемещению точки ее приложения C Работа сил равна нулю, так как эти силы приложены в мгновенном центре скоростей B катка 1 Тогда 17 Пример Пример
