Первый слайд презентации
Учебная дисциплина Схемотехника дискретных устройств Тема: Счётчики Московский Государственный Технический Университет имени Н.Э. Баумана 1830
Слайд 2: Счётчик
Счётчик – это узел вычислительных устройств, предназначенный для подсчета числа входных сигналов.
Слайд 3: Счётчик
По мере поступления входных сигналов счетчик последовательно перебирает свои состояния в определенном для данной схемы порядке. Например:
Слайд 4: Применение счётчиков
Счетчики широко применяются почти во всех цифровых устройствах автоматики и вычислительной техники. В ЭВМ счетчики используются: для подсчета шагов программы, для подсчета циклов сложения и вычитания при выполнении арифметических операций, для преобразования кодов, в делителях частоты и распределителях сигналов и т.д.
Слайд 5: Классификация счетчиков по основным признакам:
По системе счисления счетчики делятся на: двоичные, двоично-десятичные, десятичные, счетчики с основанием системы счисления неравным 2 и 10 ( пересчетные схемы).
Слайд 6: Классификация счетчиков по основным признакам:
По реализуемой операции счетчики подразделяются на: суммирующие, вычитающие и реверсивные. По схемной реализации счётчики подразделяются на асинхронные и синхронные.
Слайд 7: Основные параметры счетчиков :
модуль счета или коэффициент пересчета счетчика «К сч » характеризует число ( количество) устойчивых состояний, в которых может находиться n - разрядный счетчик, т. е. предельное число входных сигналов, которое может быть подсчитано счетчиком.
Слайд 8: Основные параметры счетчиков :
Длина списка используемых состояний К называется модулем пересчета или емкостью счетчика. Наиболее часто используются двоичные счетчики, у которых порядок смены состояний триггеров соответствует последовательности двоичных кодов. Применяются и другие виды кодирования, например одинарное, когда состояние счетчика определяется местоположением движущейся единицы.
Слайд 9: Основные параметры счетчиков :
Двоичный n - разрядный счетчик имеет 2 n различных состояний. Число разрядов двоичного счетчика можно определить из выражения : n log 2 K сч где К сч - коэффициент пересчета; n - ближайшее целое число, удовлетворяющее данному неравенству.
Слайд 10: Основные параметры счетчиков :
- Максимальная частота поступления входных сигналов f сч max - это частота, при которой счетчик еще сохраняет работоспособность. Она определяется, как правило, максимально допустимой частотой переключения триггера младшего разряда счетчика.
Слайд 11: Синтез счётчиков
Простейшим счетчиком является триггер со счетным входом, считающий сигнал по модулю 2, т.е. осуществляющий подсчет и хранение результата подсчета не более 2-х сигналов. Соединяя определенным образом несколько счетных триггеров, можно получить схему многоразрядного счетчика.
Слайд 12: Синтез счётчиков
Представление счётчика цепочкой счётных триггеров справедливо как для суммирующего, так и для вычитающего вариантов, поскольку закономерность по соотношению частот переключения разрядов сохраняется как при просмотре таблицы сверху, так и снизу.
Слайд 13: Синтез счётчиков
Различия при этом состоят в направлении переключения предыдущего разряда, вызывающего переключение следующего. При прямом счёте (суммирование) следующий разряд переключается при переходе предыдущего в направлении из 1 в 0, а при обратном счёте – при переключении из 0 в 1.
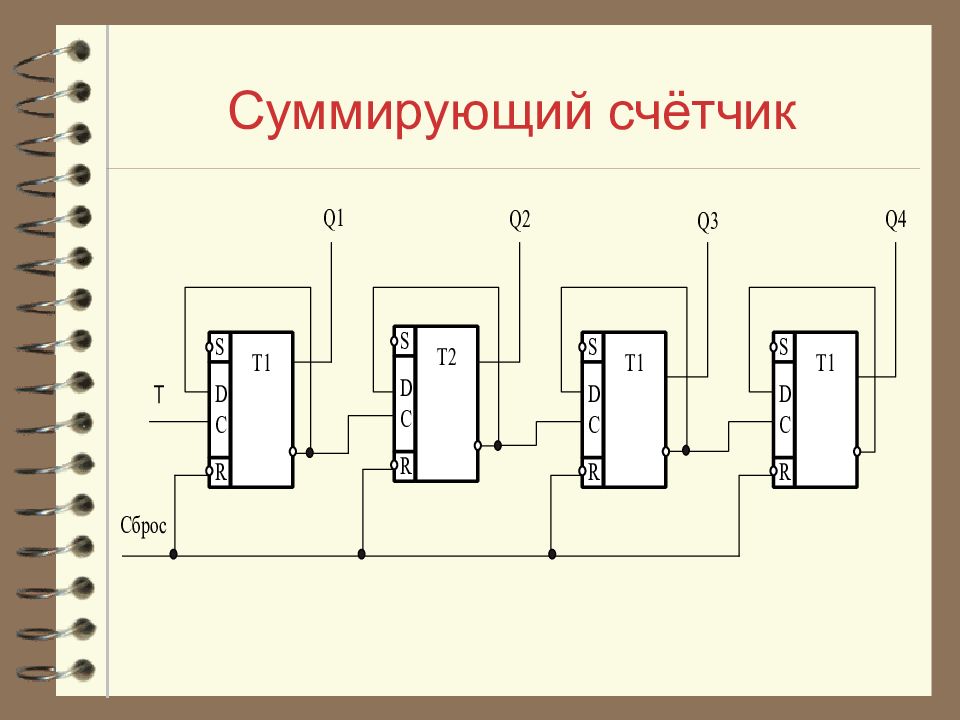
Слайд 14: Построение суммирующего счётчика
Суммирующий асинхронный счетчик на D - триггерах получается, если инверсный выход предыдущего триггера соединить со входом С последующего триггера. При использовании D - триггеров в качестве счетных, его инверсный выход соединяют со своим входом D. Счётный режим возможен только у триггеров динамического типа. Схема асинхронного 4-х разрядного суммирующего счетчика на D - триггерах приведена на следующем слайде.
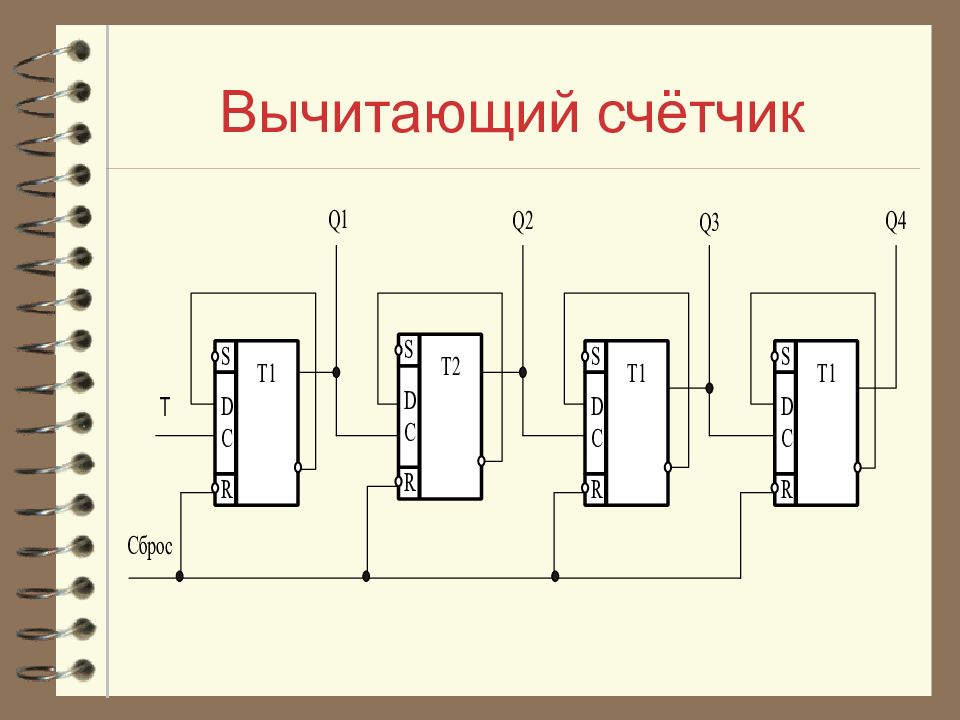
Слайд 16: Вычитающий счётчик
Для построения вычитающего счетчика на D - триггерах прямой выход предыдущего триггера соединяют со входом С последующего триггера.
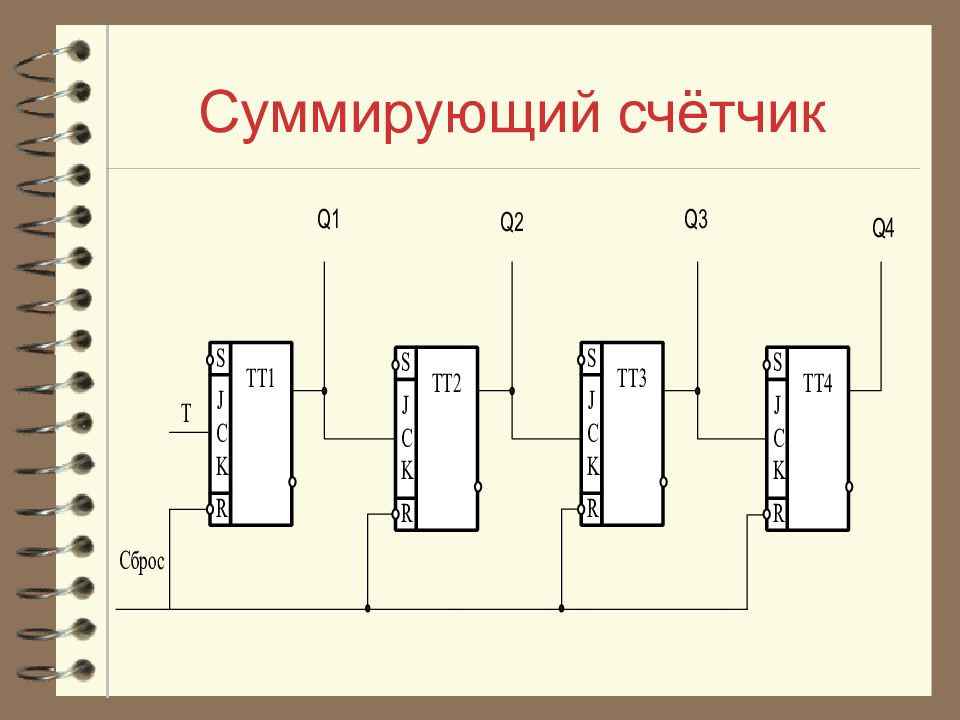
Слайд 18: Суммирующий счётчик
Для построения суммирующего асинхронного счетчика на J - K - триггерах необходимо соединить прямые выходы предыдущих триггеров со входом «С» последующих триггеров. J - K триггер должен находиться в счётном режиме, при котором J = K =1.
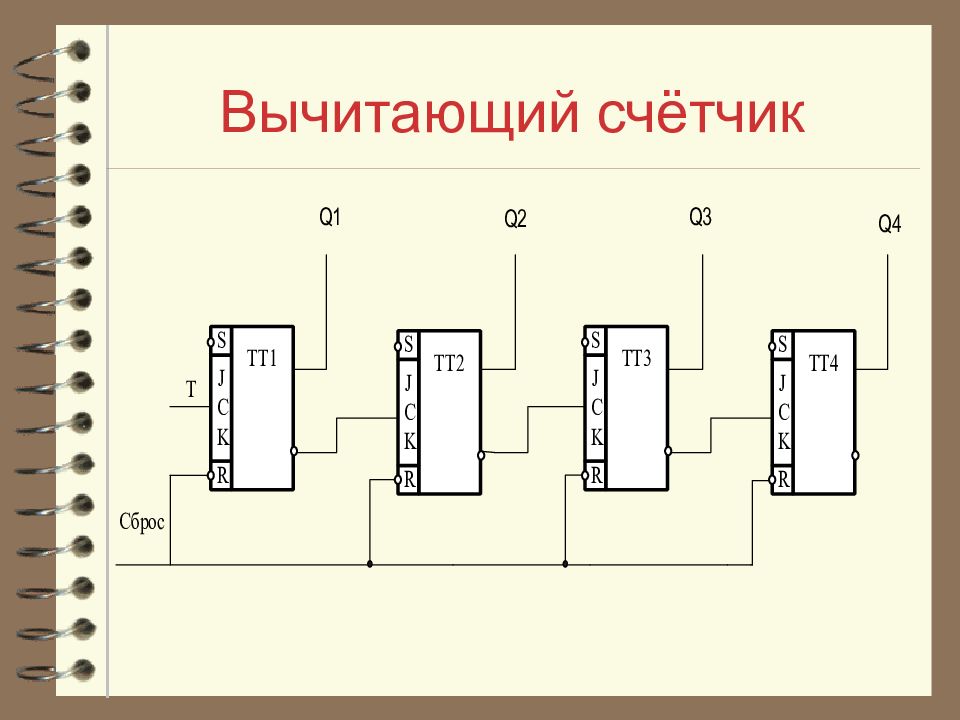
Слайд 20: Вычитающий счётчик
Вычитающий асинхронный счетчик на J - K - триггерах можно получить, если инверсный выход предыдущего триггера соединить со входом «С» последующего триггера. Схема такого счётчика представлена на след. слайде.
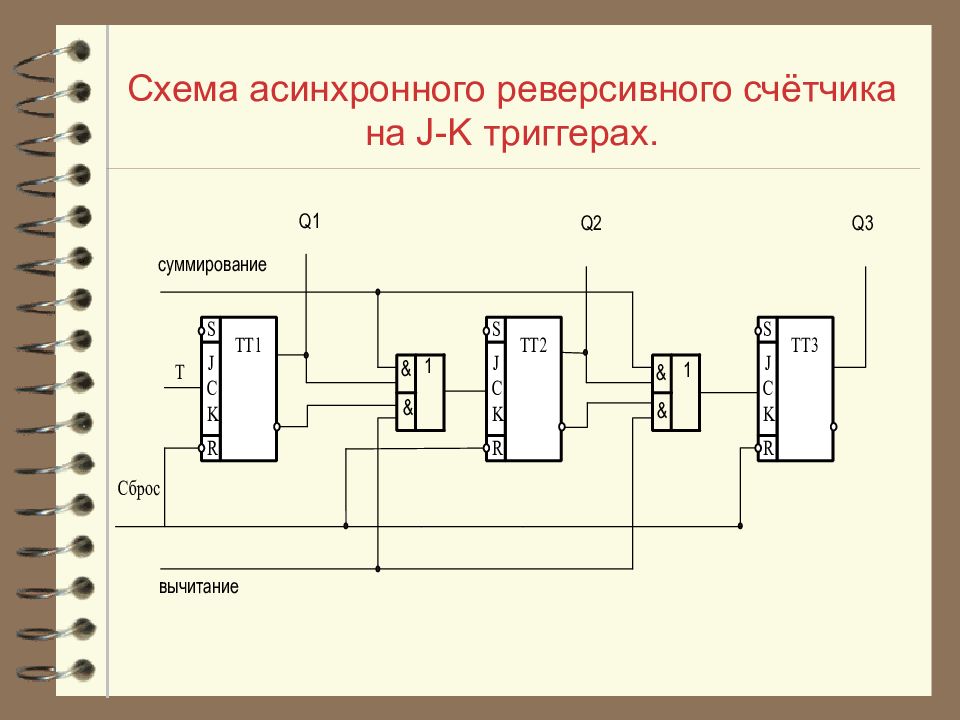
Слайд 22: Реверсивные счётчики
Реверсивные счетчики осуществляют подсчет сигналов как в прямом, так и в обратном направлении, т.е. они могут работать в режиме сложения и в режиме вычитания сигналов.
Слайд 23: Реверсивные счётчики
Для построения реверсивных счетчиков необходимо предусмотреть схемы, пропускающие сигналы на вход следующих триггеров либо с инверсного /при суммировании/, либо с прямого /при вычитании/ выходов предыдущего триггера.
Слайд 25: Счётчики с ограниченным модулем счёта
Рассмотренные выше счетчики имели коэффициент пересчета равный 2 n, где n - число разрядов счетчика. Однако на практике возникает необходимость в счетчиках, коэффициент пересчета которых отличен от 2 n. Очень часто, например, применяются счетчики с К сч = 3, 10 и т.д., т.е. счетчики, имеющие соответственно 3, 10 и т.д. устойчивых состояний.
Слайд 26: Счётчики с ограниченным модулем счёта
Принцип построения таких счетчиков заключается в исключении “ лишних” устойчивых состояний у счетчика К сч =2 n, т.е. в организации схем, запрещающих некоторые состояния.
Слайд 27: Счётчики с ограниченным модулем счёта
Принцип построения таких счетчиков заключается в исключении “ лишних” устойчивых состояний у счетчика К сч =2 n, т.е. в организации схем, запрещающих некоторые состояния. Число запрещенных состояний для любого счетчика можно определить из следующего выражения:
Слайд 28: Счётчики с ограниченным модулем счёта
Рассмотрим способ построения счетчика с естественным порядком счета, у которого уменьшение числа устойчивых состояний достигается за счет сбрасывания счетчика в нулевое состояние при записи в него заданного числа сигналов.
Слайд 29: Счётчики с ограниченным модулем счёта
В соответствии с этим способом к счетчику добавляется логическая схема, проверяющая условие: «код на счетчике изображает число равное К сч, и в зависимости от результата проверки направляет входной сигнал либо на шину "установка 0", либо на суммирование к записанному коду».
Слайд 30: Счётчики с ограниченным модулем счёта
Это условие можно проверить с помощью n -входовой схемы И, связанной с прямыми выходами тех триггеров, которые при записи в счетчике числа, равного К сч должны находиться в состоянии «1» и с инверсными выходами триггеров, которые в этом случае должны находиться в состоянии «0».
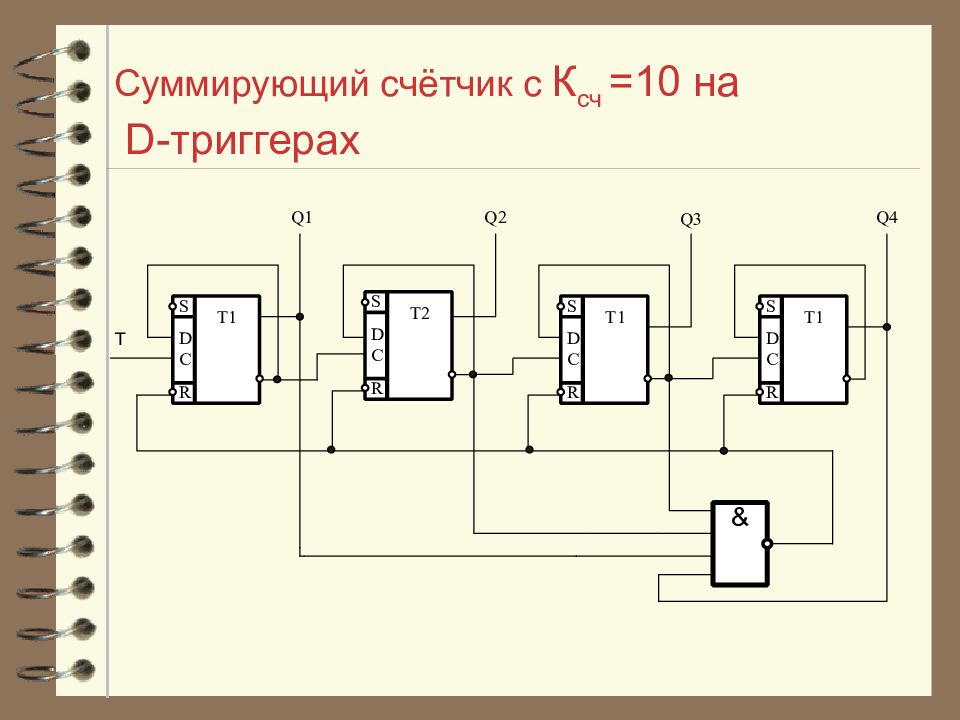
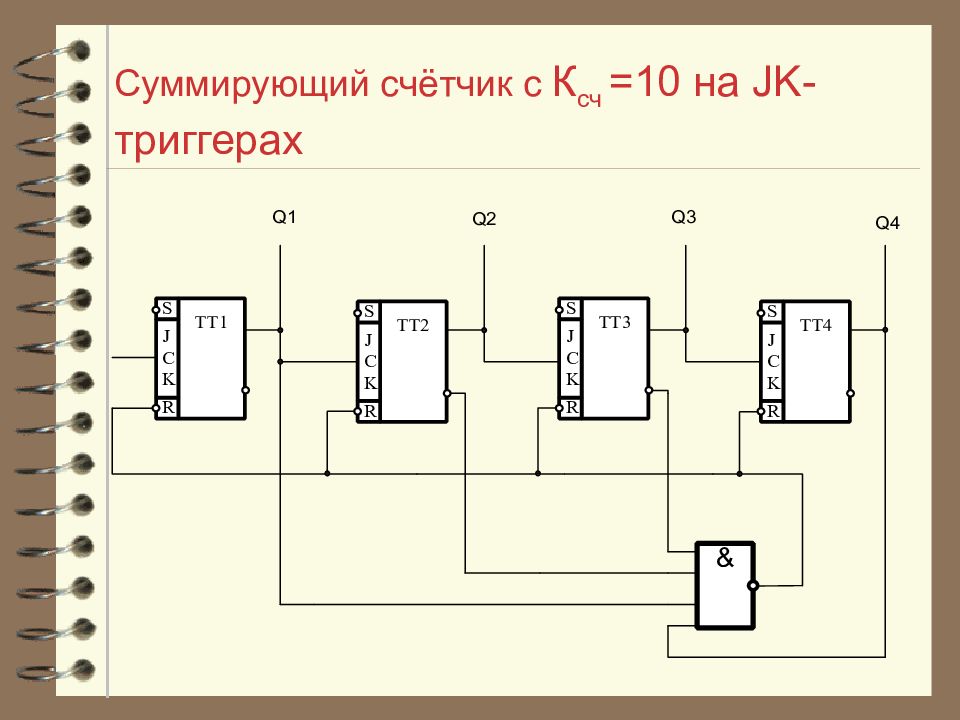
Слайд 31: Счётчики с ограниченным модулем счёта
Рассмотрим синтез схемы подобного счетчика на примере Ксч=10,т.е. счетчик должен иметь 10 состояний: от 0 до 9 в десятичной системе и от 0000 до 1001 в двоичной системе.
Слайд 32: Счётчики с ограниченным модулем счёта
Сначала определяется разрядность счетчика: Полученное значение n округляется до ближайшего целого числа, т.е. n =4. Затем определяется какие разряды счетчика будут находится в единичном состоянии при записи в счетчик Ксч.
Слайд 33: Счётчики с ограниченным модулем счёта
Прямые выходы этих разрядов заводятся на входы логической схемы ”И” и далее в цепь установки "0". Таким образом, при достижении счетчиком значения Ксч он автоматически возвращается в состояние 0000 и счет начинается сначала.
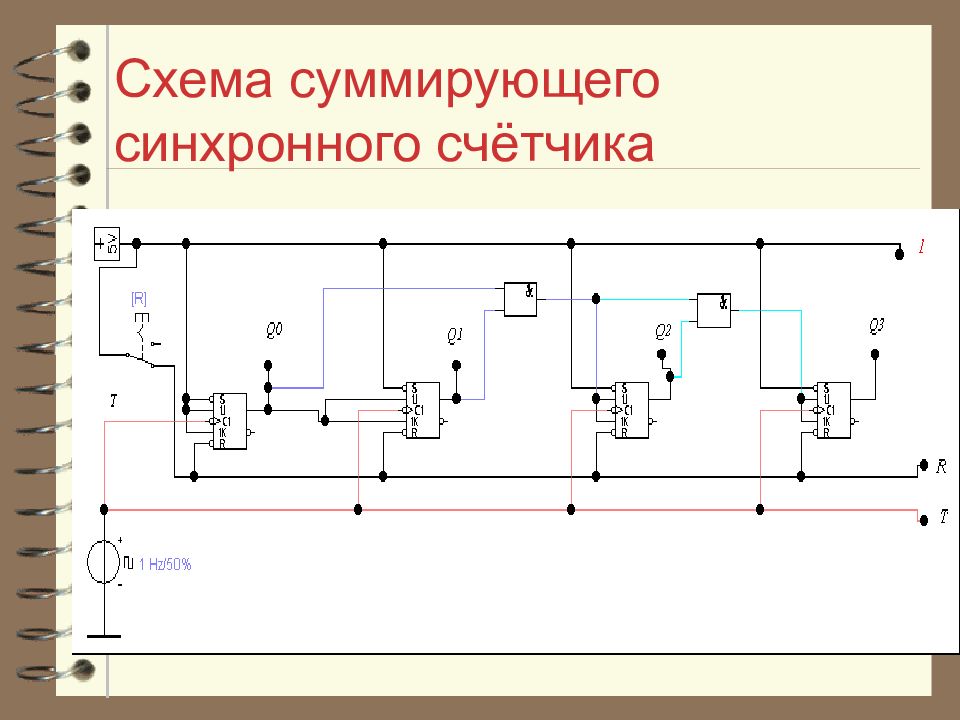
Слайд 36: Счётчики синхронного типа
Особенностью счётчиков синхронного типа является подача счётного импульса одновременно на все разряды счётчика. Управление правильностью переключения разрядов счётчика возлагается на логические элементы «И».
Слайд 37: Счётчики синхронного типа
Логический элемент «И» включает счётный режим на данном разряде счётчика подачей J=K=1, если младшие разряды по отношению к данному приняли состояние единиц. Это условие касается суммирующего синхронного счётчика.
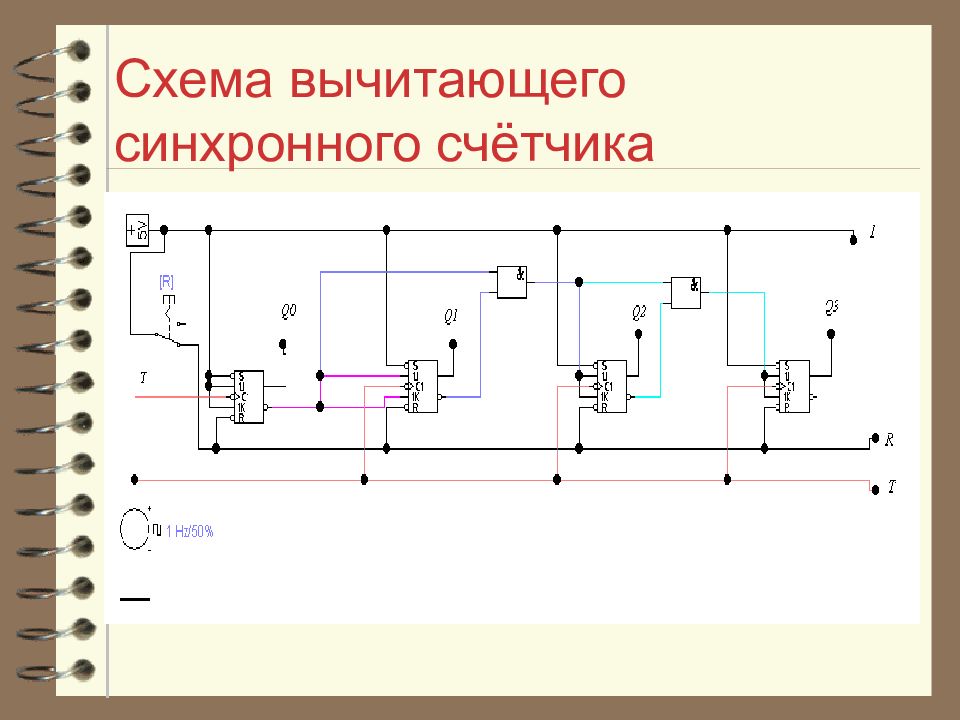
Слайд 38: Счётчики синхронного типа
В случае синхронного вычитающего счётчика переключение данного разряда должно быть разрешено, если все младшие разряды по отношению к данному приняли состояние «все нули».