Первый слайд презентации: УМОЗАКЛЮЧЕНИЕ
Д.ф.н. профессор кафедры социальной философии, РГСУ СКОРОДУМОВА ОЛЬГА БОРИСОВНА
Слайд 2: УМОЗАКЛЮЧЕНИЯ
Умозаключение есть форма мышления, в которой из одного или нескольких суждений на основании определенных правил получают новое суждение.
Слайд 3: УМОЗАКЛЮЧЕНИЯ
Умозаключение состоит из двух частей: те суждения, из которых мы исходим, на которые мы опираемся в умозаключении, — они называются его посылками; новое суждение, извлекаемое нами из посылок, называется выводом.
Слайд 4: ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Дедуктивными называют такие умозаключения, в которых выводное суждение следует из посылок с необходимостью, т.е. ЕСЛИ ПОСЫЛКИ ТАКОГО УМОЗАКЛЮЧЕНИЯ ИСТИННЫ, ТО ВЫВОД БУДЕТ ОБЯЗАТЕЛЬНО ИСТИННЫМ
Слайд 5: НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ
Такое название объясняется тем, что в этих умозаключениях всего одна посылка, представляющая собой простое суждение. Видоизменяя эту посылку, мы получаем новое суждение.
Слайд 6: НЕПОСРЕДСТВЕННЫЕ УМОЗАКЛЮЧЕНИЯ
Существует три разновидности непосредственных умозаключений: ПРЕВРАЩЕНИЕ. ОБРАЩЕНИЕ. ПРОТИВОПОСТАВЛЕНИЕ ПРЕДИКАТУ.
Слайд 7: ПРЕВРАЩЕНИЕ
ПРЕВРАЩЕНИЕ — вид непосредственного умозаключения, в котором заключение получается посредством изменения качества посылки.
Слайд 8: ПРЕВРАЩЕНИЕ
Общеутвердительные суждения А превращаются в общеотрицательные Е Все S есть Р. Ни одно S не есть не—Р. «Все металллы электропроводны» превращаются в суждение «Ни один металл не является неэлектропроводным».
Слайд 9: ПРЕВРАЩЕНИЕ
Общеотрицательные суждения Е превращаются в общеутвердительные А: Ни одно S не есть Р. Все S есть не — Р. « Ни один мошенник не является честным человеком» превращается в суждение «Все мошенники являются нечестными людьми».
Слайд 10: ПРЕВРАЩЕНИЕ
Частноутвердительные суждения I превращаются в частноотрицательные О: Некоторые S есть Р. Некоторые S не есть не— Р. Например, суждение «Некоторые люди благоразумны» превращается в суждение «Некоторые люди не есть неблагоразумны».
Слайд 11: ПРЕВРАЩЕНИЕ
Частноотрицательные суждения О превращаются в частноутвердительные I : Некоторые S есть не— Р. « Некоторые цветы не являются красивыми» превращается в суждение «Некоторые цветы являются некрасивыми».
Слайд 13: ОБРАЩЕНИЕ
Обращение — вид непосредственного умозаключения, в котором вывод получается путем постановки предиката посылки на место субъекта, а субъекта посылки — на место предиката. Общая схема обращения выглядит следующим образом: S есть Р. Р есть S. «Птицы есть позвоночные» путем обращения получаем вывод «Позвоночные есть птицы». «Все рыбы дышат жабрами» - «Дышащие жабрами есть рыбы»
Слайд 14: ОБРАЩЕНИЕ
В посылке перед субъектом стоит какой-то квантор: «все» или «некоторые». «Все дышащие жабрами» или только «некоторые дышащие жабрами» есть рыбы? Определяем на основе анализа отношения между субъектом и предикатом с помощью кругов Эйлера.
Слайд 15: ОБРАЩЕНИЕ
Отношение между субъектом и предикатом общеутвердительного суждения. Часть объема предиката, покрывается объемом субъекта. Обращение, при котором происходит изменение количества посылки, называется «обращением с ограничением». Некоторые дышащие жабрами рыбы.
Слайд 16: ОБРАЩЕНИЕ
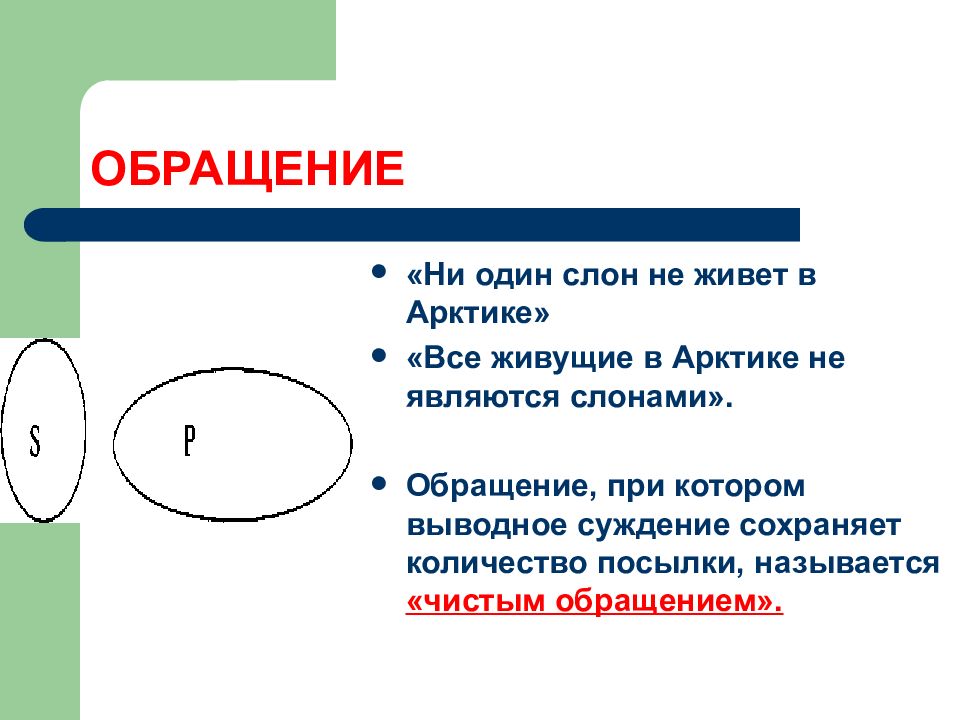
«Ни один слон не живет в Арктике» «Все живущие в Арктике не являются слонами». Обращение, при котором выводное суждение сохраняет количество посылки, называется «чистым обращением».
Слайд 17: ОБРАЩЕНИЕ
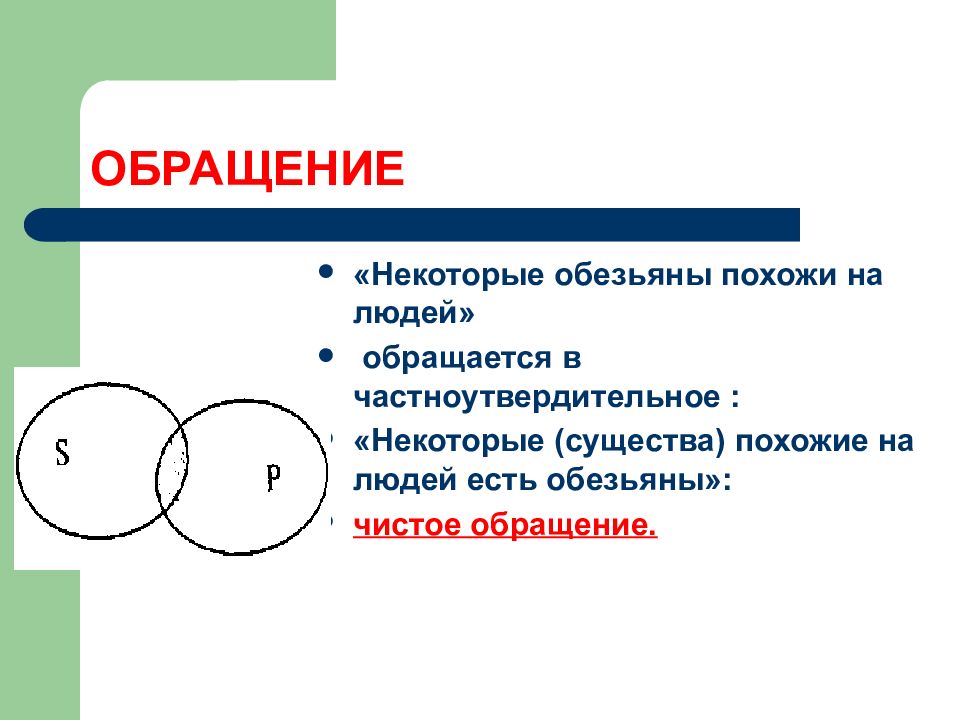
«Некоторые обезьяны похожи на людей» обращается в частноутвердительное : «Некоторые (существа) похожие на людей есть обезьяны»: чистое обращение.
Слайд 18: ОБРАЩЕНИЕ
ЧАСТНООТРИЦАТЕЛЬНЫЕ СУЖДЕНИЯ ТИПА О НЕОБРАТИМЫ, ИЗ НИХ НЕЛЬЗЯ СДЕЛАТЬ ВЫВОД ПУТЕМ ОБРАЩЕНИЯ. «Некоторые люди не являются богатыми». Нельзя сделать вывод «Все богатые не являются людьми», т.к. понятие «люди» в посылке не распределено, речь идет лишь о «некоторых людях».
Слайд 19: ОБРАЩЕНИЕ: итоги
А- I I - I E- A ЧАСТНООТРИЦАТЕЛЬНЫЕ СУЖДЕНИЯ О НЕ ОБРАЩАЮТСЯ Выделяющие суждения: А-А ( Все военнные и только военные имеют воинский билет)- (Все имеющие воинский билет военные). I – A (Некоторые юристы и только некоторые юристы являются судьями)-(Все судьи юристы).
Слайд 20: Противопоставление предикату
Противопоставление предикату — вид непосредственного умозаключения, в котором субъектом вывода является понятие, противоречащее предикату посылки, предикатом является субъект посылки, а связка изменяется на противоположную. Противопоставление предикату представляет собой соединение превращения с обращением, поэтому при его выполнении следует сначала произвести превращение посылки, а затем — обратить получившееся суждение:
Слайд 21: Противопоставление предикату
Все S есть Р. Все не— Р не есть S. Общеутвердительное суждение сначала превращаем в общеотрицательное «Все S не есть не—Р». Затем обращаем последнее суждение и получаем «Все не— Р не есть S». «Все студенты являются учащимися». Применяя превращение, получаем: «Ни один студент не является не—учащимся». Затем обращаем полученное суждение: «Все не—учащиеся не есть студенты»
Слайд 22: Противопоставление предикату
Ни один S не есть Р. Некоторые не—Р есть S. Общеотрицательное суждение сначала превращаем в общеутвердительное «Все S есть не — Р». Затем обращаем последнее суждение и получаем: «Некоторые не— Р есть S». Например, дана посылка «Ни один пингвин не умеет летать». Применяя превращение, получаем «Всякий пингвин есть не умеющий летать». Затем обращаем полученное суждение: «Некоторые не умеющие летать есть пингвины».
Слайд 23: Противопоставление предикату
Некоторые S не есть Р Некоторые не Р есть S Частноотрицательное суждение сначала превращается в частноутвердительное «Некоторые S есть не—Р». Затем обращаем последнее и получаем: « Некоторые не—Р есть S».
Слайд 24: Противопоставление предикату
Например, дана посылка: «Некоторые камни не являются драгоценными». Применяя превращение, получаем: «Некоторые камни являются недрагоценными». Затем обращаем полученное суждение: «Некоторые недрагоценные (вещи) являются камнями».
Слайд 25: Противопоставление предикату: итоги
А-Е E - I O-I Частноутвердительные суждения I путем противопоставления предикату не преобразуются. Из частноутвердительного суждения нельзя сделать вывод путем противопоставления предикату. Когда превращаем частноутвердительное суждение, оно дает частноотрицательное суждение, но последнее нельзя обратить.
Слайд 26: Простой категорический силлогизм
Дедуктивное умозаключение, состоящее из двух посылок и одного выводного суждения. Все животные смертны. Все динозавры — животные. ВСЕ ДИНОЗАВРЫ СМЕРТНЫ. Всего в силлогизме три простых суждения — две посылки и вывод.
Слайд 27: Простой категорический силлогизм
Понятия, из которых состоят посылки и вывод силлогизма, называются его терминами. В силлогизме всего три термина. Меньшим термином силлогизма называется субъект (ДИНОЗАВРЫ) выводного суждения. Он обозначается буквой «S» — как субъект в структуре простого суждения.
Слайд 28: Простой категорический силлогизм
Большим термином силлогизма называется предикат (СМЕРТНЫ) выводного суждения. Он обозначается буквой «Р» — как предикат в структуре простого суждения. Меньший и больший термины называются крайними терминами силлогизма. Меньшей называется посылка, в которую входит меньший термин, а большей - в которую входит больший термин.
Слайд 29: Простой категорический силлогизм
Средним термином силлогизма называется понятие, входящее в обе посылки, но отсутствующее в выводе. Он обозначается буквой «М». В нашем примере средним термином является понятие «животные».
Слайд 30: Простой категорический силлогизм
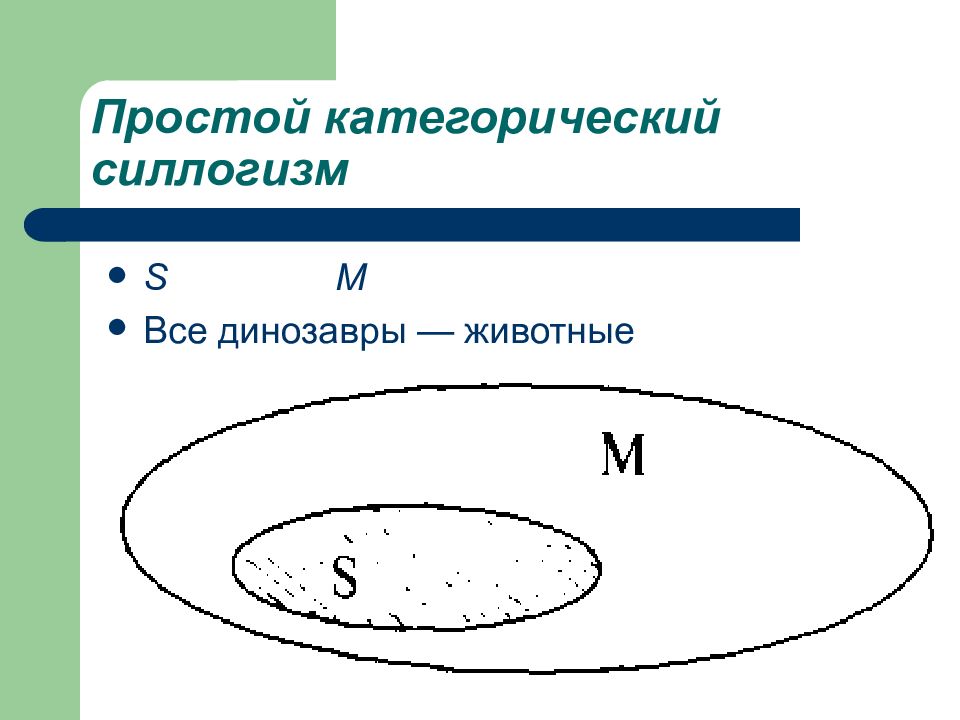
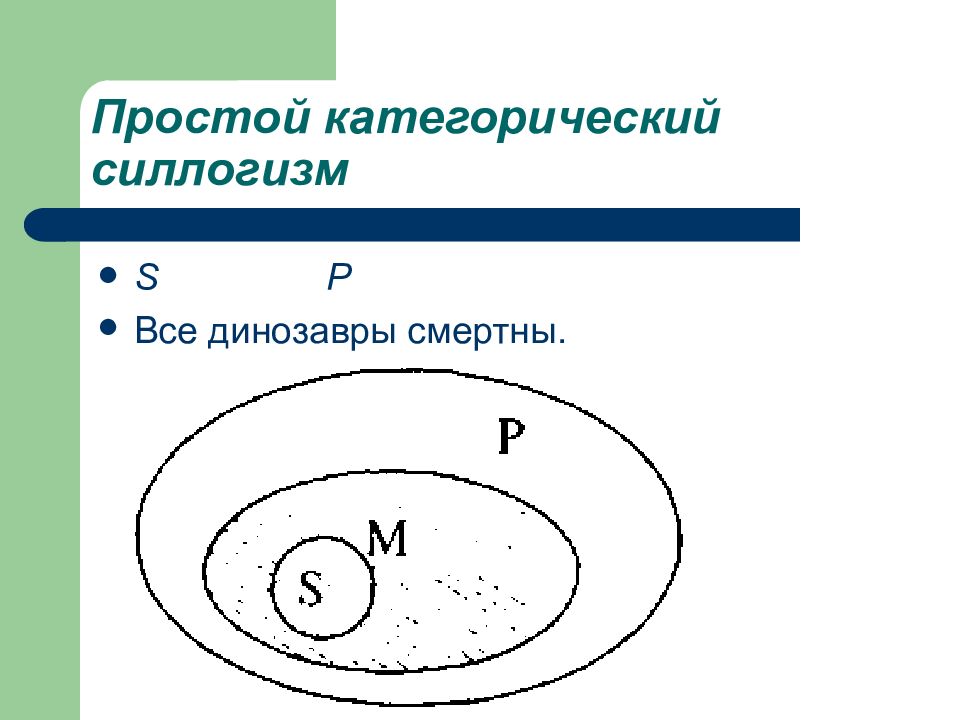
М Р Все животные смертны. S М Все динозавры — животные. S Р Все динозавры смертны.
Слайд 34: Простой категорический силлогизм
Общие правила силлогизма. Для того чтобы силлогизм был правильным, чтобы вывод из посылок вытекал с необходимостью, нужно при его построении соблюдать правила. Одни из них относятся к терминам силлогизма, другие — к его посылкам.
Слайд 35: Простой категорический силлогизм
ПРАВИЛА ТЕРМИНОВ. 1. В СИЛЛОГИЗМЕ ДОЛЖНО БЫТЬ ТОЛЬКО ТРИ ТЕРМИНА. Если появляется четвертый термин, то силлогизм разрушается: мы не можем найти среднего термина и установить отношение крайних терминов. Например: Все артисты самолюбивы. Олег Табаков талантлив.
Слайд 36: Простой категорический силлогизм
Ошибка учетверения терминов встречается довольно часто и обусловлена многозначностью слов нашего повседневного языка. Одно и то же слово в одной посылке может употребляться в одном смысле, а в другой посылке — в ином смысле, и выражать, таким образом, два разных понятия. Получается четыре термина.
Слайд 37: Простой категорический силлогизм
Ошибка учетверения терминов. Шуба греет. «Шуба» — русское слово. Некоторые русские слова греют.
Слайд 38: Простой категорический силлогизм
2. СРЕДНИЙ ТЕРМИН ДОЛЖЕН БЫТЬ РАСПРЕДЕЛЕН (ВЗЯТ В ПОЛНОМ ОБЪЕМЕ) ХОТЯ БЫ В ОДНОЙ ИЗ ПОСЫЛОК. Если большая посылка говорит лишь о части объема среднего термина и меньшая посылка говорит только о части его объема, то мы ничего не можем сказать о соотношении объемов крайних терминов. Арбуз круглый. Земля круглая.
Слайд 39: Простой категорический силлогизм
3. ЕСЛИ ТЕРМИН НЕ РАСПРЕДЕЛЕН В ПОСЫЛКЕ, ТО ОН НЕ МОЖЕТ БЫТЬ РАСПРЕДЕЛЕН И В ВЫВОДЕ. Все судьи справедливы. Прокуроры не есть судьи. ПРОКУРОРЫ НЕ СПРАВЕДЛИВЫ.
Слайд 40: Простой категорический силлогизм
Все судьи( M+) справедливы (P-). Прокуроры (S+) не есть судьи (M+). ПРОКУРОРЫ (S+) НЕ СПРАВЕДЛИВЫ (P+). Нет оснований вполне исключить прокуроров S из класса справедливых Р. Их объемы могут соотноситься трояким образом: Необходимого вывода сделать нельзя.
Слайд 41: Простой категорический силлогизм
Правила посылок. 4. ИЗ ДВУХ ОТРИЦАТЕЛЬНЫХ ПОСЫЛОК ВЫВОДА НЕ СЛЕДУЕТ. М Р Трапеции не есть ромбы. S М Квадраты не трапеции.
Слайд 42: Простой категорический силлогизм
5. Если одна из посылок — отрицательное суждение, то и вывод должен быть отрицательным. Все дельфины — млекопитающие. Это животное не является млекопитающим. Это животное не является дельфином.
Слайд 43: Простой категорический силлогизм
6.ИЗ ДВУХ ЧАСТНЫХ ПОСЫЛОК ВЫВОДА НЕ СЛЕДУЕТ. М Р Некоторые растения — лекарственные травы. S М Некоторые организмы — растения. 7.ЕСЛИ ОДНА ИЗ ПОСЫЛОК — ЧАСТНОЕ СУЖДЕНИЕ, ТО И ВЫВОД ДОЛЖЕН БЫТЬ ЧАСТНЫМ. Попытка при частной посылке сделать общий вывод приводит к нарушению либо правила 2, либо правила 3.
Слайд 44: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Первая фигура
Слайд 45: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Первая фигура Правила 1-й фигуры: 1. Большая посылка — общее суждение. 2. Меньшая посылка — утвердительное суждение.
Слайд 46: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Вторая фигура
Слайд 47: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Вторая фигура Правила 2-й фигуры: 1. Большая посылка — общее суждение. 2. Одна из посылок — отрицательное суждение.
Слайд 48: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Третья фигура
Слайд 49: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Третья фигура Правила 3-й фигуры: 1. Меньшая посылка — утвердительное суждение. 2. Заключение — частное суждение.
Слайд 50: Простой категорический силлогизм
ФИГУРЫ И МОДУСЫ СИЛЛОГИЗМА Четвертая фигура Выведение заключения из посылок по этой фигуре не характерно для естественного процесса рассуждения. На практике выводы в подобных случаях делаются обычно по 1-й фигуре:
Слайд 51: Простой категорический силлогизм
Например: Захват заложника (Р) — преступление против общественной безопасности (М) Преступление против общественной безопасности (М) — общественно опасное деяние, предусмотренное Особенной частью Уголовного кодекса (S) ___________________________________ Некоторые общественно опасные деяния, предусмотренные Особенной частью Уголовного кодекса (S), являются захватом заложника (Р) Такой ход рассуждения представляется в известной мере искусственным.
Слайд 52: Т аблица правильных модусов
1 ф. 2 ф. 3 ф. 4 ф. AAA ЕАЕ AA I AA I ЕАЕ АЕЕ I A I АЕЕ A I I E I O A II I A I E I О АОО ЕАО ЕАО ОАО E I О E I О
Слайд 53: Проверка силлогизмов
1. Найдите посылки и вывод данного силлогизма; запишите посылки одну под другой, а вывод отделите от них чертой. 2. Найдите меньший ( S ), больший (Р) и средний (М) термины силлогизма. 3. Проверьте, выполняет ли силлогизм общие правила терминов и посыпок. 4. Определите, какая посылка является большей, а какая — меньшей
Слайд 54: Проверка силлогизмов
5. Определить фигуру силлогизма. 6. Проверяете, выполняет ли силлогизм правила той фигуры, по которой он построен.
Слайд 55: Умозаключения из суждений с отношениями
Умозаключение, посылки и заключение которого являются суждениями с отношениями, называется умозаключением с отношениями. Петр — брат Ивана Иван — брат Сергея Петр — брат Сергея xRy
Слайд 56: СВОЙСТВА ОТНОШЕНИЙ
1) симметричность, 2) рефлексивность 3) транзитивность.
Слайд 57: СИММЕТРИЧНОСТЬ
1. Отношение называется симметричным (от греческого simmetria — «соразмерность»), если оно имеет место как между предметами х и у, так и между предметами у и х. Перестановка членов отношения не ведет к изменению вида отношения. Отношение симметричности символически записывается: xRy —> yRx.
Слайд 58: СИММЕТРИЧНОСТЬ
Отношения равенства, сходства, одновременности, различия и некоторые другие.
Слайд 59: РЕФЛЕКСИВНОСТЬ
2. Отношение называется рефлексивным (от латинского ге flexio — «отражение»), если каждый член отношения находится в таком же отношении к самому себе. Отношение рефлексивности записывается: xRy —> xRx ˄ yRy Отношения равенства и одновременности.
Слайд 60: ТРАНЗИТИВНОСТЬ
3. Отношение называется транзитивным (от латинского transitivus — «переход»), если оно имеет место между х и z тогда, когда оно имеет место между х и у и между у и z. Отношение транзитивности записывается: (xRy ˄ yRz ) -> xRz.
Слайд 61: ТРАНЗИТИВНОСТЬ
Отношения равенства, одновременности, отношения, «позднее», «находиться севернее (южнее, восточнее, западнее)», «быть ниже, выше» и т.п.
Слайд 62: ПОЛУЧЕНИЕ ДОСТОВЕРНЫХ ЗАКЛЮЧЕНИЙ ИЗ СУЖДЕНИЙ С ОТНОШЕНИЯМИ
Для получения достоверных заключений из суждений с отношениями необходимо опираться на правила, вытекающие из свойств отношений. Из свойства симметричности ( xRy —> yRx ) вытекает правило: если суждение xRy истинно, то суждение yRx тоже истинно.
Слайд 63: ПОЛУЧЕНИЕ ДОСТОВЕРНЫХ ЗАКЛЮЧЕНИЙ ИЗ СУЖДЕНИЙ С ОТНОШЕНИЯМИ
Из свойства рефлексивности ( xRy —> xRx ˄ yRy) вытекает правило: если суждение xRy истинно, то истинными будут суждения xRx и yRy.
Слайд 64: ПОЛУЧЕНИЕ ДОСТОВЕРНЫХ ЗАКЛЮЧЕНИЙ ИЗ СУЖДЕНИЙ С ОТНОШЕНИЯМИ
Из свойства транзитивности (xRy ˄ yRz —> xRz ) вытекает правило: если суждение xRy истинно и суждение yRz истинно, то суждение xRz также истинно.
Слайд 65: ПОЛУЧЕНИЕ ДОСТОВЕРНЫХ ЗАКЛЮЧЕНИЙ ИЗ СУЖДЕНИЙ С ОТНОШЕНИЯМИ
К. был на месте происшествия раньше Л. Л. был на месте происшествия раньше М. К. был на месте происшествия раньше М. Таким образом, истинность заключения из суждений с отношениями зависит от свойств отношений и регулируется данными правилами, « Сергеев знаком с Петровым» и «Петров знаком с Федоровым» не следует необходимого заключения «Сергеев знаком с Федоровым», так как «быть знакомым» не является транзитивным отношением.
Слайд 66: ЧИСТО УСЛОВНЫЕ УМОЗАКЛЮЧЕНИЯ
Первый член импликации называется основанием, а второй — следствием условного суждения. Чисто условным называется умозаключение, обе посылки которого являются условными суждениями: (р -> q)˄ (q -> г), р —> г Вывод в чисто условном умозаключении основывается на правиле: следствие следствия есть следствие основания.
Слайд 67: Условно-категорический силлогизм
УСЛОВНО-КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ есть умозаключение, в котором одна из посылок является условным суждением, а вторая посылка и вывод — простыми категорическими суждениями.
Слайд 68: Условно-категорический силлогизм
Данте: «... тот мерзок, кто ярится, если чужой он доблести свидетель». Если человек при виде чужой доблести ярится, то он мерзок. Данный человек при виде чужой доблести ярится. ____________________________ ДАННЫЙ ЧЕЛОВЕК МЕРЗОК.
Слайд 69: Условно-категорический силлогизм
Категорическая посылка — по отношению к условной посылке — может принимать один из 4-х видов: она может утверждать основание условной посылки; отрицать следствие; отрицать основание ; утверждать следствие.
Слайд 70: Условно-категорический силлогизм
Разновидности условно-категорического силлогизма, отличающиеся друг от друга видом категорической посылки, называются его модусами. Первый называется «утверждающим модусом» или modus ponens. От утверждения основания условной посылки переходим в выводе к утверждению ее следствия.
Слайд 71: modus ponens
Если у человека повышена температура, то он болен. У данного человека повышена температура. _______________________ ДАННЫЙ ЧЕЛОВЕК БОЛЕН.
Слайд 72: Условно-категорический силлогизм
Второй модус называется «отрицающим модусом» или modus tollens. От отрицания следствия условной посылки переходим в выводе к отрицанию ее основания. Два других модуса не имеют названий. Они считаются неправильными модусами, т.к. не дают необходимого вывода: вывод по этим двум модусам может быть верен, а может оказаться и ошибочным.
Слайд 73: modus tollens
Если у человека повышена температура, то он болен. Данный человек не болен. ______________________________ У ДАННОГО ЧЕЛОВЕКА НЕ ПОВЫШЕНА ТЕМПЕРАТУРА.
Слайд 74: УМОЗАКЛЮЧЕНИЕ ПО 3-МУ МОДУСУ:
Если у человека повышена температура, то он болен. У данного человека не повышена температура. _____________________________________ НЕЛЬЗЯ ! Данный человек не болен.
Слайд 75: УМОЗАКЛЮЧЕНИЕ ПО 4-МУ МОДУСУ:
Если у человека повышена температура, то он болен. Данный человек болен. ____________________________ НЕЛЬЗЯ ! У данного человека повышена температура
Слайд 76: Как установить, по какому модусу построено то или иное рассуждение?
1.Следует начинать с выделения посылок и вывода. Записываем сначала условную посылку, под ней — категорическую посылку, затем под чертой — выводное суждение. 2. Затем в условной посылке выделяем основание и следствие. 3. Утверждает ли категорическая посылка основание условной посылки или отрицает его? Утверждает ли она следствие условной посылки или отрицает его? 4. Определить модус.
Слайд 77: Разделительно-категорический силлогизм
Разделительно-категорический силлогизм есть умозаключение, в котором одна посылка является разделительным суждением, а вторая посылка и вывод — простыми категорическими суждениями. Я могу сходить на занятия или на дискотеку. Но я не пойду на занятия. ___________________________________ Следовательно, я пойду на дискотеку.
Слайд 78: modus ponendo - tollens
Первый модус называется утверждающе-отрицающим : в рассуждении по этому модусу от утверждения одной из альтернатив переходим в выводе к отрицанию другой альтернативы.
Слайд 79: modus tollendo - ponens
Второй модус называется отрицающе-утверждающим : в рассуждении по этому модусу от отрицания одной из альтернатив переходим в выводе к утверждению другой альтернативы.
Слайд 80: Разделительно-категорический силлогизм
Оба модуса считаются правильными. Но чтобы рассуждение, осуществляемое по тому или иному модусу, было корректным, обеспечивало необходимый вывод, нужно, чтобы разделительная посылка выполняла определенное требование.
Слайд 81: modus ponendo - tollens
ТРЕБОВАНИЕ К РАЗДЕЛИТЕЛЬНОЙ ПОСЫЛКЕ для модуса понендо-толленс: разделительная посылка должна быть строго разделительной, т.е. альтернативы должны исключать друг друга.
Слайд 82: modus tollendo - ponens
ТРЕБОВАНИЕ К РАЗДЕЛИТЕЛЬНОЙ ПОСЫЛКЕ для модуса толлендо-поненс : разделительная посылка должна быть исчерпывающей, т.е. в ней должны перечисляться все возможности, существующие в данном рассуждении.
Слайд 83: Как анализировать разделительно-категорический силлогизм:
1) выделяете альтернативы в разделительной посылке; 2) стараетесь понять, что представляет собой категорическая посылка по отношению к разделительной — утверждает она одну из альтернатив или отрицает ее? 3) в соответствии с этим определяете модус вашего силлогизма; 4) затем смотрите, выполняет ли разделительная посылка требование соответствующего модуса.
Слайд 84: Условно-разделительное умозаключение
Одна посылка условная, а другая разделительное суждение. Различают конструктивную (созидающую) и деструктивную (разрушающую) дилеммы, каждая из которых делится на простую и сложную.
Слайд 85: Условно-разделительное умозаключение
Простая конструктивная дилемма: Разделительная посылка утверждает основания условных посылок, вывод утверждает следствие этих посылок. Если студент спит на лекциях, то он не знает логики. Если студент спит на семинарах, то он не знает логики. Студент спит или на лекциях, или на семинарах. ______________________________________ Следовательно, студент не знает логики.
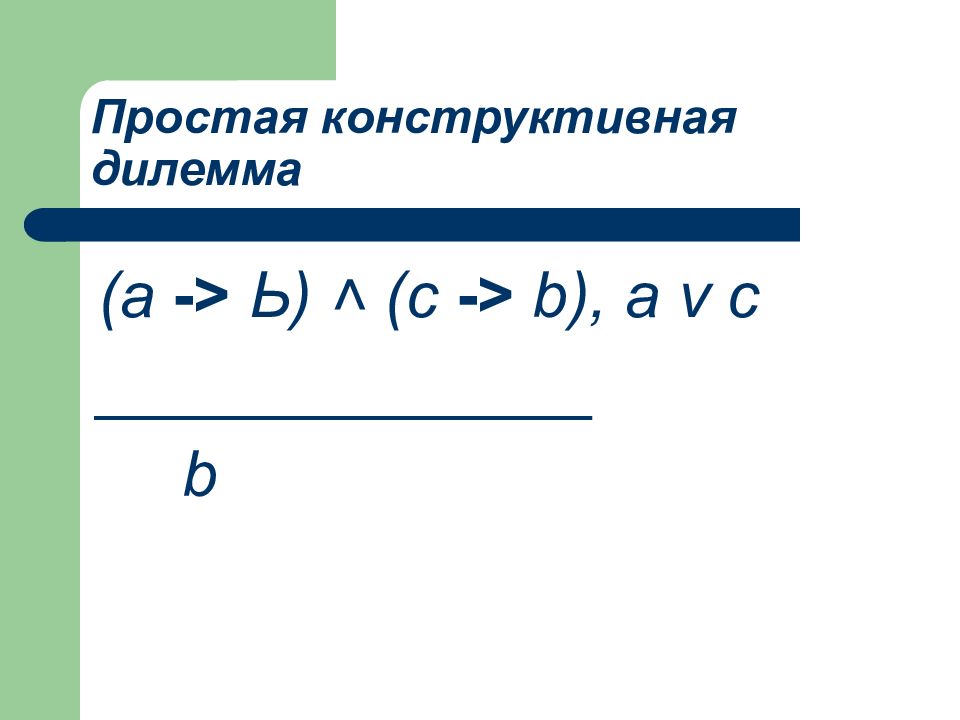
Слайд 86: Простая конструктивная дилемма
(а -> Ь) ˄ (с -> b ), a v с ______________ b
Слайд 87: Условно-разделительное умозаключение
Сложная конструктивная дилемма отличается тем, что условные суждения имеют разные следствия, поэтому, утверждая их основания в разделительной посылке, мы утверждаем оба следствия в заключении.
Слайд 88: Сложная конструктивная дилемма
Если пойдешь направо, коня потеряешь. Если пойдешь налево, голову потеряешь. Но нужно идти направо или налево. _________________________________ Следовательно, придется потерять коня или голову.
Слайд 89: Сложная конструктивная дилемма
(а -> b )˄ (с -> d ), a v с ____________________ b v d
Слайд 90: Простая деструктивная дилемма
Если студент нашел 500 долларов, то он устроит вечеринку с друзьями. Если студент нашел 500 долларов, то он пригласит свою девушку в театр. Но студент не устроил вечеринки и не ходил со своей девушкой в театр. _______________________________________ Следовательно, студент не нашел 500 долларов.
Слайд 91: Простая деструктивная дилемма
(а-> b ) ˄ (а->с), ┐ b v ┐ с ______________________ ┐ а
Слайд 92: Сложная деструктивная дилемма
Если бы я был богат, я купил бы себе дорогой автомобиль. Если бы я был министром, мне предоставили бы казенный автомобиль. Но у меня нет ни дорогого автомобиля, ни казенного автомобиля. ____________________________________ Следовательно, я не богат и я не министр.
Слайд 93: Сложная деструктивная дилемма
(а-> b ) ˄ ( c -> d ), ┐ b v ┐ d _____________________ ┐ a v ┐ c
Слайд 94: Сокращенный силлогизм. Энтимема
Земля планета, потому что она вращается вокруг Солнца. Земля вращается вокруг Солнца. Земля планета.
Слайд 95: Сокращенный силлогизм. Энтимема
Возможные варианты: 1. Все планеты вращаются вокруг Солнца. Земля вращается вокруг Солнца. Земля планета. 2. Некоторые тела, вращающиеся вокруг Солнца, есть планеты. Земля вращается вокруг Солнца. Земля планета.
Слайд 96: Сокращенный силлогизм. Энтимема
Эти силлогизмы можно проанализировать обычным образом. Первый силлогизм построен по 2-й фигуре, для которой требуется, чтобы одна из посылок была отрицательной. В этом силлогизме нет отрицательной посылки, поэтому вывод не следует с необходимостью.
Слайд 97: Сокращенный силлогизм. Энтимема
Второй силлогизм построен по 1-й фигуре. Здесь нарушено правило фигуры. От силлогизма 1-й фигуры требуется, чтобы большая посылка в нем была общим суждением, но истинным будет только частное суждение. Таким образом, данная нам энтимема неверна: вывод не вытекает из посылок.
Последний слайд презентации: УМОЗАКЛЮЧЕНИЕ: Логическая выводимость
РАЗВЕ ЗЕМЛЯ НЕ ПЛАНЕТА? Да, Земля планета и вывод здесь является истинным суждением. Но дело в том, что он не вытекает из данных посылок. Бывает часто, что выводное суждение представляется истинным, кажется, что и умозаключение должно быть правильным. Однако это далеко не так. Суждение может быть истинным, но его обоснование с помощью умозаключения может оказаться ошибочным.