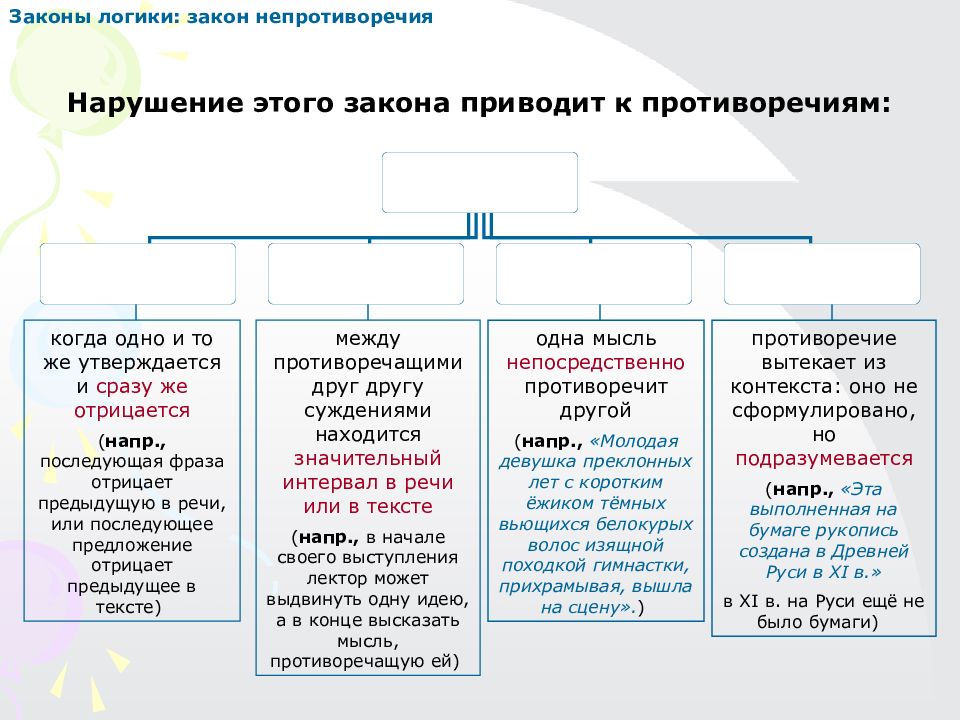
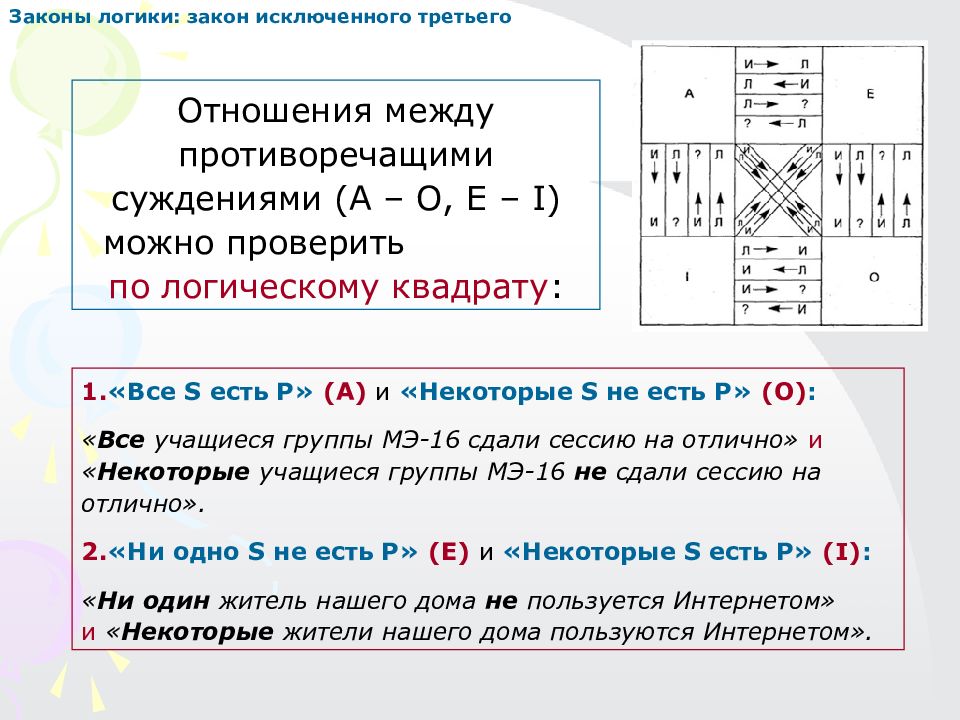
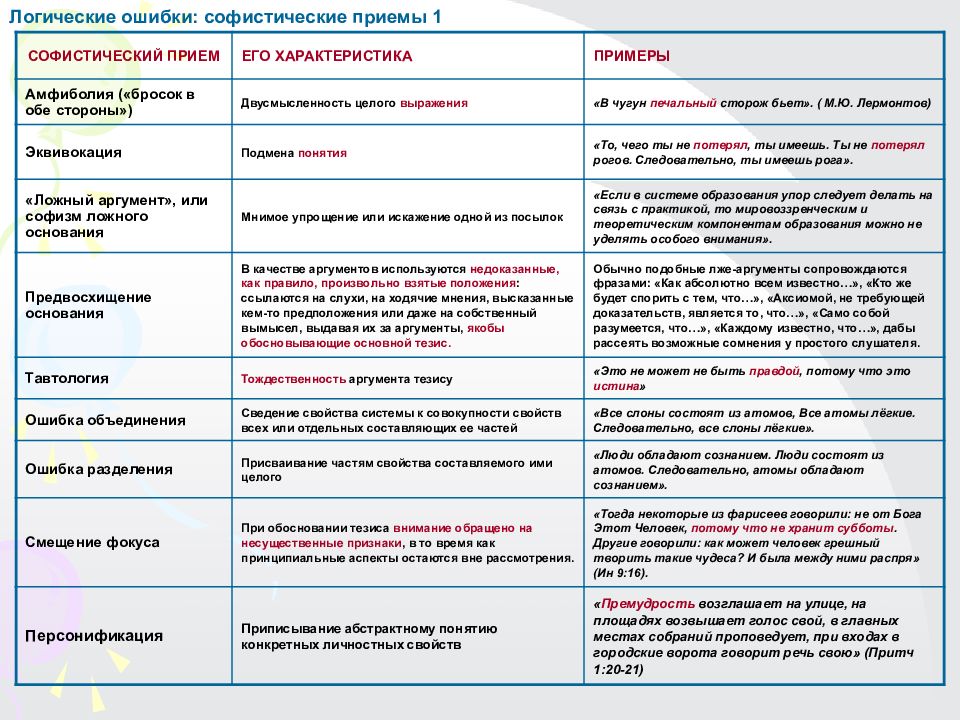
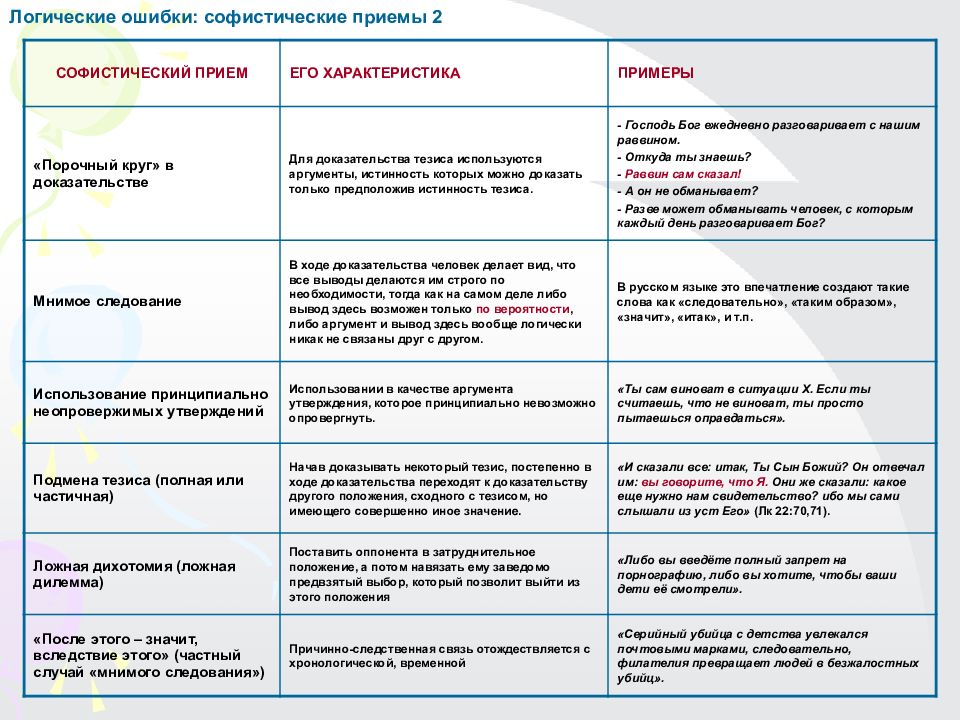
Первый слайд презентации: ЛОГИКА курс лекций для студентов ЦДО УрГЭУ
Преподаватель: к.ф.н., доцент Атманских Елена Алексеевна
Слайд 2
Для успешной сдачи зачета по логике необходимо прослушать курс лекций (до 12 часов), изучить все темы курса в соответствии с Программой (всё учебно-методическое обеспечение закреплено за каждой группой на Портале), а также самостоятельно выполнить на проверку ряд заданий, а именно 3 вида работ: Решение тестов самопроверки по всем темам (7 вопросов), попытки не ограничены. Зачет устанавливается от 50% за каждый правильный ответ. Тест по курсу (итоговый), состоящий из 25 вопросов, только 3 попытки. Положительный результат – от 50%. Выполнение одного варианта контрольной работы ( только по шифру! ), состоящей из четырёх практических заданий-упражнений. Обратите внимание: в контрольной работе процесс решения задачи необходимо показать, т.е. каждый шаг каждого выполняемого задания должен быть обоснован! Не допускается просто один ответ! Для автоматического зачета должны быть прослушаны лекции, выполнены все 3 вида работ ( без Самостоятельной работы-Практикума ), а итоговый тест должен быть решен не менее 75%.
Слайд 3
ЛОГИКА ( от греч. λόγος - «речь», «рассуждение», «мысль» ) — раздел философии, наука о формах и законах правильного мышления, занятого поисками истины Предмет и значение логики Значение логики: Развивает качество и культуру мышления любого человека, т.е. помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях. Т.о., логика является инструментом оперативного мышления человека. «Говорить путано умеет всякий, говорить ясно – немногие». (Г.Галилей) Является методологической основой всех наук, инструментом научного познания мира. Помогает связывать знания различных областей в единое целое – научную картину мира.
Слайд 4
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ с V в. до н.э.: Логика в Древнем Китае (конфуцианство, моизм): метод «исправления имён (понятий)» для упорядочения общества и правильного политико-административного управления. Конфуций : «Когда имена неправильны, суждения несоответственны. Когда суждения несоответственны, дела не исполняются». Индийская логика (буддизм и другие школы): определение методов достижения надежного знания для освобождения от страданий. Логика античности: Основателем логики в древнегреческой философии считается Аристотель. Его предшественниками были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же впервые систематизировал доступные знания о логике, обосновал формы и правила логического мышления. Цикл его сочинений «Органон» состоит из 6 работ, посвящённых логике: «Категории», «Об истолковании», «Топика», «Первая аналитика» и «Вторая аналитика», «Софистические опровержения». Логика Средневековья (схоласты, У.Оккам, Аль-Фараби): логика как инструмент обоснования религиозных представлений о мире. Логика Нового времени (Ф.Бэкон, Г.Лейбниц, Р.Декарт, И.Кант, Гегель и др.): основы индуктивной логики, одна из первых успешных попыток формализации и арифметизации логических операций. История логики
Слайд 5
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ с V в. до н.э.: Современная логика: Математическая (теоретическая логика, символическая логика) – раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики. Прикладная логика – направления формальных и неформальных логических исследований, связанных с конкретной сферой практического использования логического знания (компьютерная логика, логика науки, логика дискурса, юридическая логика и другие). Неформальная логика – новое направление современных логических исследований, занимающееся моделированием речевых актов (рассуждений): логическая структура повседневной речи, способы использования естественного языка, анализ высказываний как выявление ментального состояния человека. Металогика – раздел современной логики, исследует особенности построения формальных систем (логических теорий, логических исчислений). Она формулирует принципы и правила построения формальных систем, вводит особую терминологию и метасимволы, которые характеризуют металогический уровень современных логических исследований Составные части металогики – логическая семантика, логический синтаксис, логическая прагматика. История логики
Слайд 6
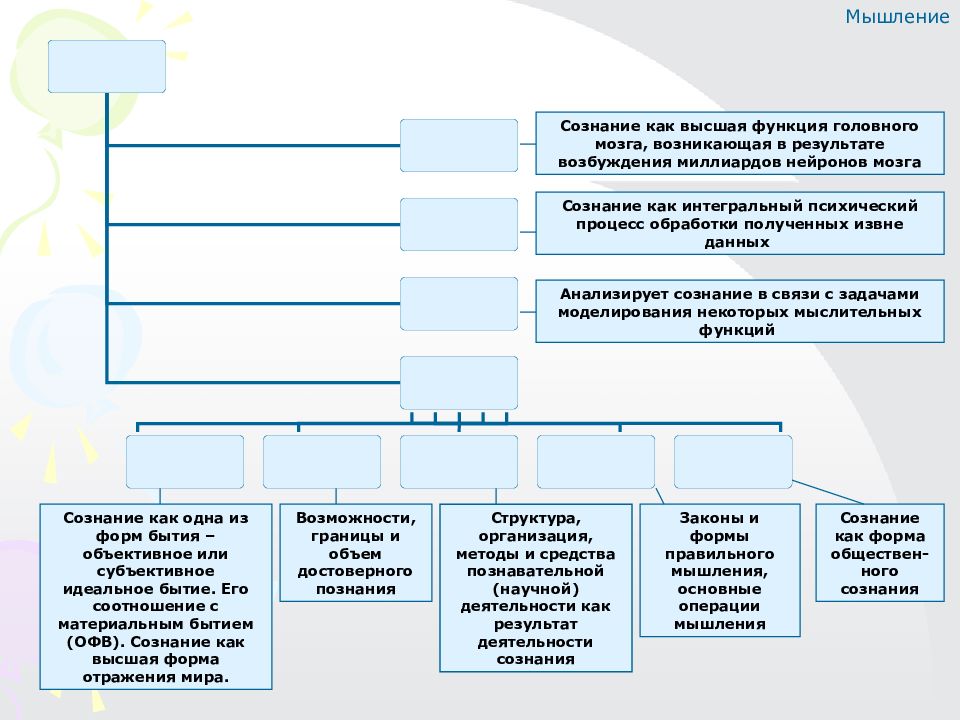
Сознание как высшая функция головного мозга, возникающая в результате возбуждения миллиардов нейронов мозга Сознание как интегральный психический процесс обработки полученных извне данных Анализирует сознание в связи с задачами моделирования некоторых мыслительных функций Законы и формы правильного мышления, основные операции мышления Структура, организация, методы и средства познавательной (научной) деятельности как результат деятельности сознания Возможности, границы и объем достоверного познания Сознание как одна из форм бытия – объективное или субъективное идеальное бытие. Его соотношение с материальным бытием (ОФВ). Сознание как высшая форма отражения мира. Сознание как форма обществен-ного сознания Мышление
Слайд 7
МЫШЛЕНИЕ — инструмент познания окружающего мира Познание есть активный процесс обработки информации, полученной в результате отражения объективного мира сознанием человека. Оно представляет собой единство чувственного и рационального. Мышление Формы чувственного познания (непосредственное отражение) : ощущение восприятие представление Чувственное познание дает нам знание об отдельных предметах, об их внешних свойствах. Формы абстрактного мышления (опосредованное отражение) : понятие суждение умозаключение Мышление позволяет постигнуть сущностные связи между объектами.
Слайд 8
ОСОБЕННОСТИ МЫШЛЕНИЯ: Интенциональность ― мышление направлено на некоторый объект (прежде всего) во внешнем мире, объективно или субъективно отражает его свойства. Идеальность (не материальность): мышление оперирует не реальными предметами и явлениями окружающего мира, а понятиями (идеями). Идеи – это продукты интеллектуальной деятельности. Обобщает и абстрагирует, т.е. выделяет самые характерные, «сущностнообразующие» признаки определенного класса предметов, отвлекаясь от их несущественных, единичных свойств. Продукт обобщения – знак (слово, символ,… язык вообще). Т.о., мышление опосредовано знаками. Знаками можно оперировать: передавать другим, сравнивать и т.д. Избирательность: способность выбирать определенные объекты, различные решения, условия, действия и т.п. Креативность: способность творить новое – то, чего пока нет в действительности, фантазировать. Диалогичность: соотнесённость сознаний разных субъектов, понимание. Активность: направлено на решение проблем, обновление знания, творчество. Логичность: предполагает рассуждение, т.е. цепочку выводов, вытекающих один из другого на основе логических правил, законов и операций мышления. Мышление
Слайд 9
ОПЕРАЦИИ МЫШЛЕНИЯ : Анализ — мысленное разделение предмета/явления на образующие его части. Синтез — мысленное соединение отдельных частей и признаков в единое целое. Сравнение — сопоставление предметов и явлений, при этом обнаруживаются их сходства и различия. Классификация — группировка предметов по признакам. Обобщение — объединение предметов по общим существенным признакам. Конкретизация — выделение частного из общего. Абстрагирование — выделение какой-либо стороны или аспекта явления, которые в действительности как самостоятельные не существуют. Систематизация — процедура объединения, т.е. сведения групп однородных по неким признакам единиц к определенному иерархиезированному единству на основе существующих между ними связей. Логика является инструментом оперативного мышления человека Мышление
Слайд 10
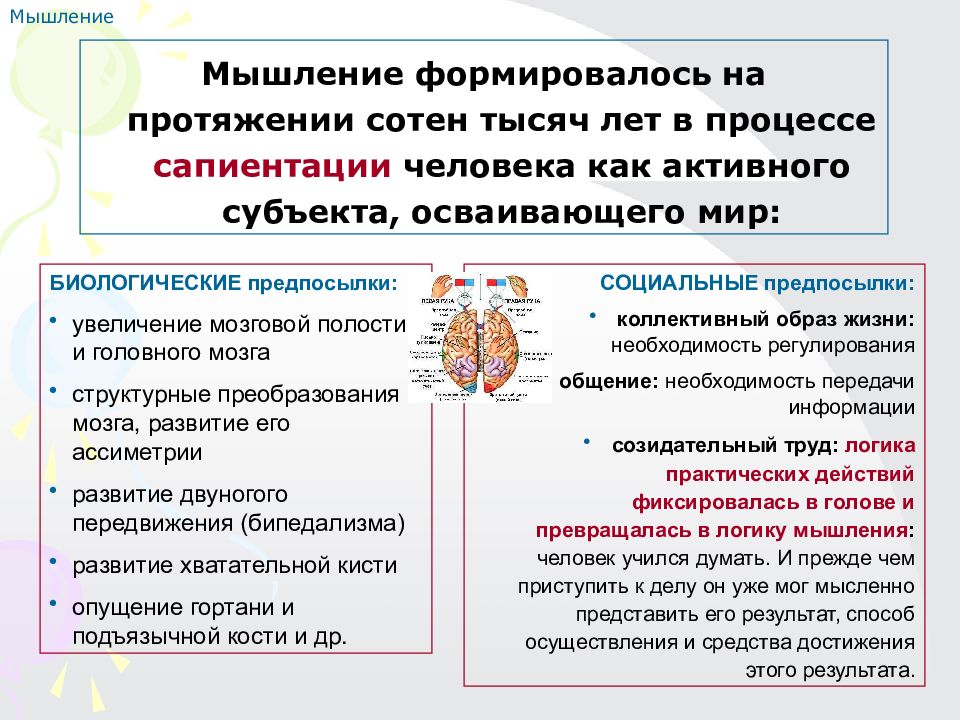
Мышление формировалось на протяжении сотен тысяч лет в процессе сапиентации человека как активного субъекта, осваивающего мир: Мышление БИОЛОГИЧЕСКИЕ предпосылки: увеличение мозговой полости и головного мозга структурные преобразования мозга, развитие его ассиметрии развитие двуногого передвижения (бипедализма) развитие хватательной кисти опущение гортани и подъязычной кости и др. СОЦИАЛЬНЫЕ предпосылки: коллективный образ жизни: необходимость регулирования общение: необходимость передачи информации созидательный труд: логика практических действий фиксировалась в голове и превращалась в логику мышления : человек учился думать. И прежде чем приступить к делу он уже мог мысленно представить его результат, способ осуществления и средства достижения этого результата.
Слайд 11
Система знаков и есть материализованная, предметная оболочка мысли, т.е. язык. Мышление и язык Мышление тесно связано с языком: Человек – единственное существо, способное оперировать предметами в их отсутствие. Для этого человек оперирует заместителями предметов – знаками. Знак – это отсутствие реальной вещи и одновременно ее присутствие в символической форме.
Слайд 12
Мышление и язык Знаком может быть не только буква или слово, но любой материальный заменитель другого предмета или явления: звуки, символы, цифры, индексы, товарные знаки, ноты, жесты, математические символы и т.п. Важнейшая характеристика знака – условное значение, то есть способность передавать представления о предметах так, чтобы разные люди одинаково понимали эти представления.
Слайд 13
ФУНКЦИИ ЯЗЫКА: коммуникативная — использование языка для общения конструктивная — использование языка для формирования и хранения информации конативная — передача информации когнитивная — формирование мышления индивида и общества эмоционально-экспрессивная — выражение чувств, эмоций волюнтативная — функция воздействия на человека метаязыковая — разъяснения средствами языка самого языка идеологическая — использование того или иного языка или типа письменности для выражения идеологических предпочтений номинативная (или назывная) — язык называет различные объекты денотативная, репрезентативная — ориентация на адресата аксиологическая — оценочная функция (хорошо/плохо); референтная — средство накопления человеческого опыта и др. Мышление и язык
Слайд 14
ОСОБЕННОСТИ ЯЗЫКА КАК СИСТЕМЫ ЗНАКОВ: Семантическая: каждый знак обладает смыслом, который требует понимания. Смысл – это информация о предмете, внутреннее содержание, значение чего-либо, постигаемое разумом. (напр., смысл понятия «птица» зафиксирован в наборе таких основных признаков как «теплокровная», «покрытая перьями», «крылатая», «летающая», «яйцекладущая», «имеющая клюв» и др.) Синтаксическая: знаковая система формируется на основе строгих правил и законов отношения между элементами языка (напр., правила грамматики: «Птиц а лета ют ».) Прагматическая: способность знака выражать отношение пользователя к предмету мысли – эмоциональные, психологические, эстетические, экономические и др. (напр., « красивая птица») Мышление и язык
Слайд 15
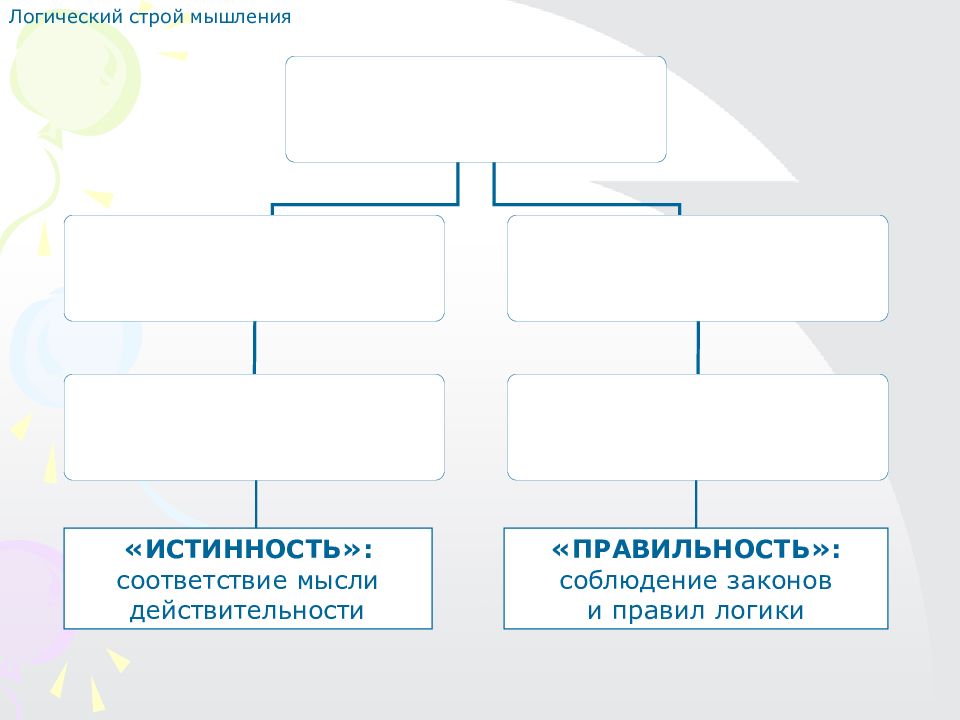
Логический строй мышления «ИСТИННОСТЬ»: соответствие мысли действительности «ПРАВИЛЬНОСТЬ»: соблюдение законов и правил логики
Слайд 16
Рассмотрим три совершенно различных по содержанию высказывания: « Все караси – это рыбы» – истинно по содержанию. «Все треугольники – это геометрические фигуры» – истинно по содержанию. «Все крокодилы поют песни» – ложно по содержанию. Несмотря на различное содержание, у этих трёх высказываний есть нечто общее – их правильная форма: «Все S суть P» S – субъект, т.е. понятие о предмете суждения Р – предикат, т.е. понятие о признаке предмета. Логический строй мышления
Слайд 17
Формальная структура мыслительной деятельности человека определяется отвлеченно от ее содержания. Её и изучает наука логика. Логика «не отвечает» за то, что мы мыслим, а только за то, как мы мыслим, поэтому она часто называется формальной логикой. Логический строй мышления
Слайд 18
Существует всего три формы мышления – понятие, суждение и умозаключение. Основные формы логического мышления
Слайд 19
ПОНЯТИЕ – форма мышления, в которой отражаются существенные признаки класса однородных предметов: Основные формы логического мышления: понятие они характерны для каждой единицы множества, раскрывают сущность этой единицы и всего множества в целом, в своей совокупности отграничивают данное множество от любого другого. Такие признаки именуются существенными, в отличие от других – несущественных. Например, есть множество разнообразных реальных деревьев, составляющий определенный класс (множество). А понятие «дерево» (как таковое) одно – в нем отражены одинаковые существенные признаки всех объектов этого класса: многолетнее растение с одним прямостоящим твёрдым стволом и отходящими от него ветвями, образующими крону.
Слайд 20
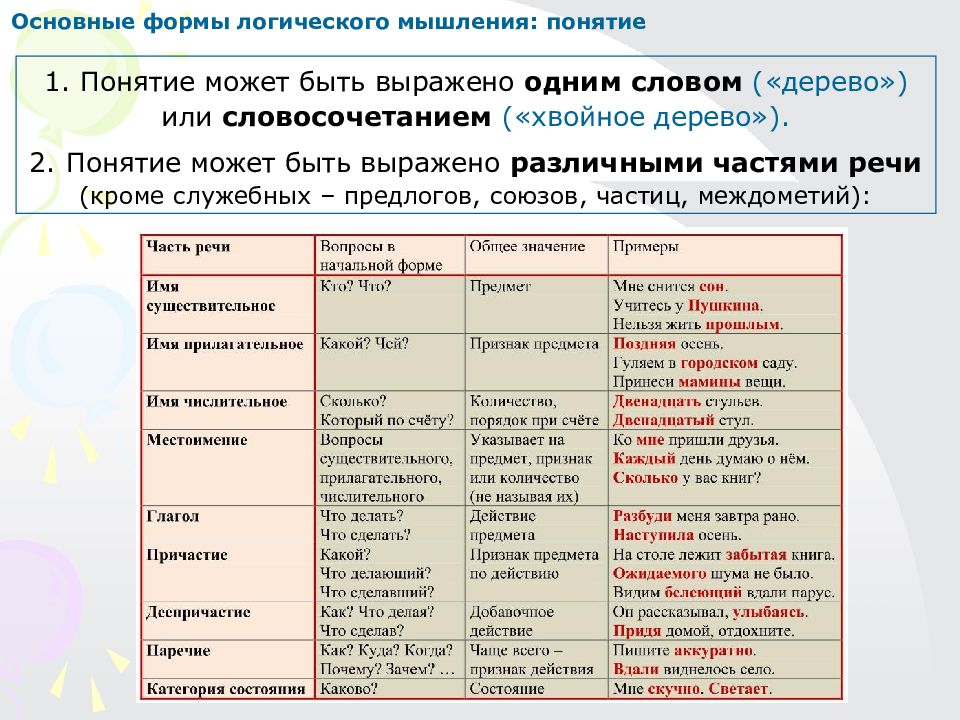
1. Понятие может быть выражено одним словом («дерево») или словосочетанием («хвойное дерево»). 2. Понятие может быть выражено различными частями речи (кроме служебных – предлогов, союзов, частиц, междометий): Основные формы логического мышления: понятие
Слайд 21
Что надо знать о понятиях? Существуют разные виды понятий: по объему и содержанию Существуют логические операции с понятиями: определения понятий ограничения и обобщения понятий деление понятий Существуют особые отношения между сравнимыми понятиями: совместимости (тождественность, пересечение, подчинение) и несовместимости (соподчинение, противоположность, противоречие) Понятие как форма мышления
Слайд 22
Каждое понятие имеет содержание и объем: Понятие как форма мышления: виды понятий Содержание понятия – качественная характеристика, т.е. совокупность существенных и общих признаков предмета, которая мыслится в данном понятии. Например, «лимон»: желтый, кислый, сочный, овальный плод с бугорчатой или ямчатой коркой, содержащей множество желёзок с эфирным маслом. Объем понятия – количество предметов или явлений, обладающих признаками, образующими содержание данного понятия. Например, «дикие животные»: все существующие дикие животные
Слайд 23
УПРАЖНЕНИЯ: Определить, содержание какого понятия здесь представлено: «холодный», «белый», «рассыпчатый», «пушистый», «искрящийся на солнце», «безвкусный»… Определить, содержание какого понятия здесь представлено: «прямоходящий», «разумный», «говорящий», «созидающий», «познающий», «нравственный»… Определить, объем какого понятия здесь представлен: «негроид», «европеоид», «монголоид», «австролоид», «американоид», «койсаноид»… Определить, объем какого понятия здесь представлен: «цветы», «деревья», «кустарники», «водоросли», «мхи», «папоротники», «хвощи»… Понятие как форма мышления: виды понятий
Слайд 24
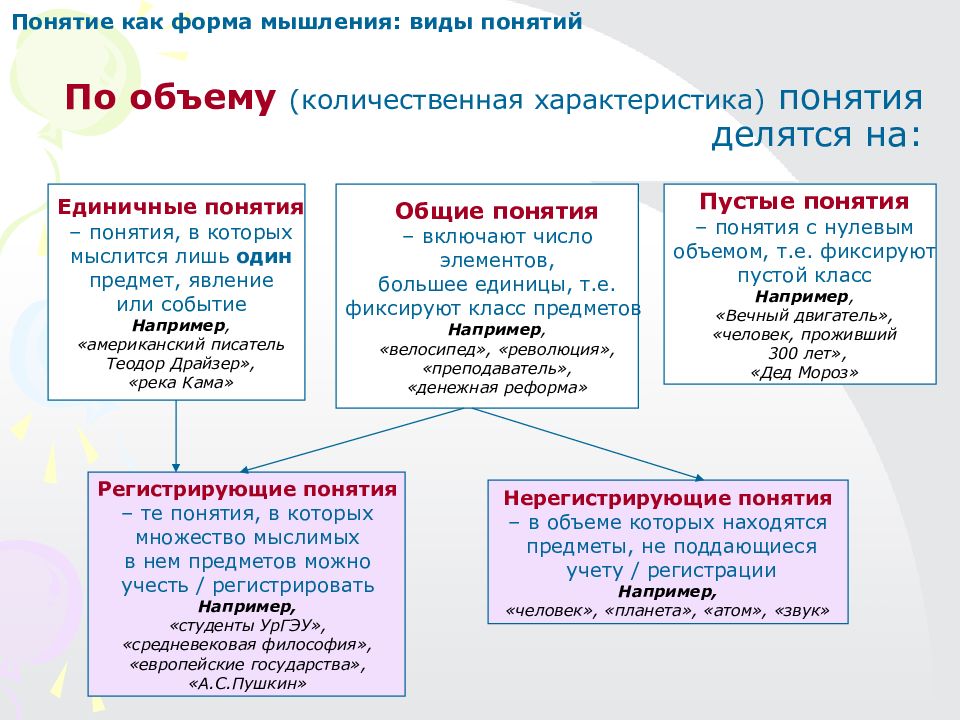
По объему (количественная характеристика) понятия делятся на: Единичные понятия – понятия, в которых мыслится лишь один предмет, явление или событие Например, «американский писатель Теодор Драйзер», «река Кама» Общие понятия – включают число элементов, большее единицы, т.е. фиксируют класс предметов Например, «велосипед», «революция», «преподаватель», «денежная реформа» Пустые понятия – понятия с нулевым объемом, т.е. фиксируют пустой класс Например, «Вечный двигатель», «человек, проживший 300 лет», «Дед Мороз» Регистрирующие понятия – те понятия, в которых множество мыслимых в нем предметов можно учесть / регистрировать Например, «студенты УрГЭУ», «средневековая философия», «европейские государства», «А.С.Пушкин» Нерегистрирующие понятия – в объеме которых находятся предметы, не поддающиеся учету / регистрации Например, «человек», «планета», «атом», «звук» Понятие как форма мышления: виды понятий
Слайд 25
По содержанию можно выделить следующие четыре пары понятий: Конкретные и абстрактные Относительные и безотносительные Положительные и отрицательные Собирательные и несобирательные Понятие как форма мышления: виды понятий
Слайд 26
КОНКРЕТНЫЕ ПОНЯТИЯ отражают целостный предмет или класс предметов как нечто самостоятельно существующее ( например: «школа», «опера», «Александр Македонский», «землетрясение», «студент», «романс», «дом», «поэма А. Блока «Двенадцать» и др.) ________________________________________________________________ АБСТРАКТНЫЕ ПОНЯТИЯ – в них мыслится не предмет, а какой-либо из признаков предмета, взятый сам по себе ( или состояния, или отношения между предметами, или действия, или идеальные объекты) ( например: «белизна», «справедливость», «истина», «любовь», «подобие», «тождество», «изменчивость») В действительности существуют белые одежды, справедливые действия, тождественные фигуры, но «белизна», «справедливость» и «тождество» как отдельные чувственно воспринимаемые вещи не существуют. Конкретные и абстрактные понятия: Понятие как форма мышления: виды понятий
Слайд 27
СООТНОСИТЕЛЬНЫЕ ПОНЯТИЯ: мыслятся только парами, т.е. существование одного из них предполагает существование другого например, «дети» - «родители», «ученик» - «учитель», «раб» - «господин», «начальник» - «подчиненный», «преступление» - «наказание», «истец» – «ответчик»… В языке эти понятия часто выражены антонимами (слова, противоположные по значению): например, «истина» - «ложь», «северный полюс магнита» - «южный полюс магнита», «левый» - «правый», «восход» - «закат», «друг» – «враг», «высоко» – «низко», «день» – «ночь»… ___________________________________________________ БЕЗОТНОСИТЕЛЬНЫЕ ПОНЯТИЯ: в них мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета, без своей противоположности например, «карандаш», «город», «овца», «наводнение» Относительные и безотносительные понятия: Понятие как форма мышления: виды понятий
Слайд 28
ПОЛОЖИТЕЛЬНЫЕ ПОНЯТИЯ фиксируют в предмете наличие того или иного признака ( например, «грамотный человек», «порядок», «отстающий ученик», «красивый поступок», «корыстная помощь») ________________________________________________________________________ ОТРИЦАТЕЛЬНЫЕ ПОНЯТИЯ означают, что указанное свойство отсутствует в предметах, или отрицают признаки положительных понятий ( например, « без грамотный человек», « бес порядок», « не отстающий ученик», « не красивый поступок», « бес корыстная помощь»). !В русском языке иногда частицы «не» или « без» («бес») сливаются со словом и слово без них не употребляется ( например, « не настье», « бес печность», « без упречность», « не нависть», « не ряха»). В русском языке нет понятий «настье», «печность », «упречность », «нависть», «ряха». Частица «не» здесь не выполняет функцию отрицания, а поэтому эти понятия являются положительными, так как они характеризуют наличие у предмета определенного качества (может быть, даже и плохого - «неряха», «беспечность» ). _________________________________________________________________________ В словах иностранного происхождения чаще всего используется отрицательная приставка «а» : « а ссиметрия», « а моральный» – отрицательные понятия, « а нонимный» – положительное понятие. Положительные и отрицательные понятия: Понятие как форма мышления: виды понятий
Слайд 29
СОБИРАТЕЛЬНЫЕ ПОНЯТИЯ: в них мыслятся признаки некоторой совокупности элементов, составляющих единое целое. Содержание собирательного понятия нельзя отнести к каждому отдельному элементу, входящему в его объем, оно относится ко всей совокупности элементов. Например, «полк», «стадо», «стая», «созвездие», «лес», «флот», «футбольная команда», «народ», «коллектив». «Футбольная команда» - это не просто совокупность футболистов, но коллектив объединенных общей деятельностью, общими интересами и целями игроков; включает в себя и признак «сыгранности», умения «вкладывать свои способности в общий результат»... Т.е. здесь предполагается «суммирующий», «системный» фактор. Собирательные понятия бывают общими («роща», «народ»…) и единичными («созвездие Большая Медведица», «население города Екатеринбурга»). _________________________________________________________________________ НЕСОБИРАТЕЛЬНЫЕ (разделительные) ПОНЯТИЯ: в них мыслятся признаки, относящиеся к каждому элементу класса. Например, несобирательные общие понятия – «дерево», «кража», «человек», «река», «игрушка», «растение»; несобирательные единичные понятия – «основатель Москвы Юрий Долгорукий», «первый космонавт Юрий Гагарин». Собирательные и несобирательные понятия: Понятие как форма мышления: виды понятий
Слайд 30
УПРАЖНЕНИЯ: дайте логическую характеристику понятий по объему (общее, единичное, пустое; регистрирующее или нерегистрирующее) и по содержанию (конкретное или абстрактное, относительное или безотносительное, положительное или отрицательное, собирательное или несобирательное) : «Книга»: по объему - …………………………………………………………………..; по содержанию - …………………………………………………………………………….; «Планета Марс»: по объему – ……………………………………………………; по содержанию – ……………………………………………………………………………..; «Красота»: по объему – ……………………………………………………………….; по содержанию – ……………………………………………………………………………..; «Невесёлый человек»: по объему – ………………………………………..; по содержанию – ……………………………………………………………………………..; «Студенческая группа»: по объему – …………………………………….; по содержанию – ……………………………………………………………………………….. Понятие как форма мышления: виды понятий
Слайд 31
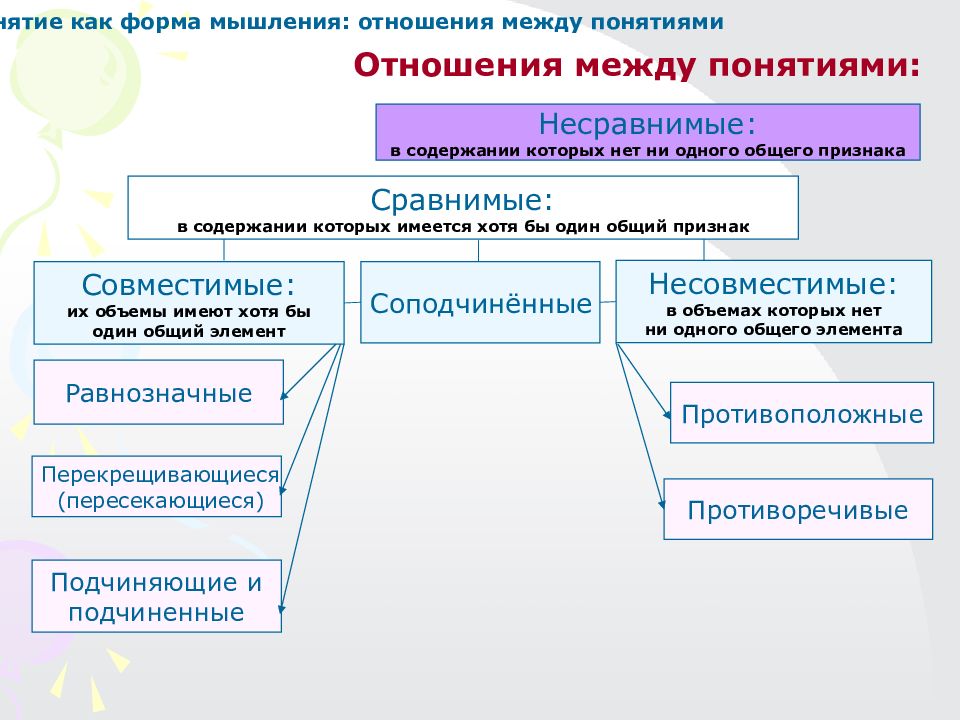
Отношения между понятиями: Сравнимые: в содержании которых имеется хотя бы один общий признак Несравнимые: в содержании которых нет ни одного общего признака Несовместимые: в объемах которых нет ни одного общего элемента Совместимые: их объемы имеют хотя бы один общий элемент Равнозначные Перекрещивающиеся (пересекающиеся) Соподчинённые Противоположные Подчиняющие и подчиненные Противоречивые Понятие как форма мышления: отношения между понятиями
Слайд 32
Леонард Эйлер (1707 – 1783) – швейцарский, немецкий и российский математик и механик Отношения между понятиями для наглядности схематично изображаются с помощью круговых схем – «кругов Эйлера». Используется в математике, логике и многих других науках Понятие как форма мышления: отношения между понятиями
Слайд 33
А – «Москва» В – «столица России» А – «кодекс» В – «свод законов» А В Понятие как форма мышления: отношения между совместимыми понятиями Отношения равнозначности (равнообъёмность): объемы равнозначных понятий полностью совпадают, а содержание различно. Совпадение объемов обусловлено тем, что оба понятия отражают одно и то же множество предметов и явлений. Однако это не свидетельствует о тождестве равнозначных понятий! Отражая одно и то же множество, равнозначащие понятия учитывают различные его стороны, различные существенные признаки.
Слайд 34
А В Понятие как форма мышления: отношения между совместимыми понятиями Отношения подчинения: объем подчиненного понятия полностью входит в объем подчиняющего, не исчерпывая его. Это обязательно родо-видовые отношения! А – цветок (род) В – чайная роза (вид) А – право (род) В – уголовное право (вид) От родо-видовых отношений следует отличать отношения структурные (части и целого). В подобных отношениях находятся, например, понятия «уголовный кодекс» (целое) и «статья уголовного кодекса» (часть), «лопата» (целое) и «черенок лопаты» (часть). Структурное отношение отличается от родо-видового тем, что часть не является видом по отношению к целому, нельзя, в частности, говорить, что черенок лопаты является разновидностью лопаты.
Слайд 35
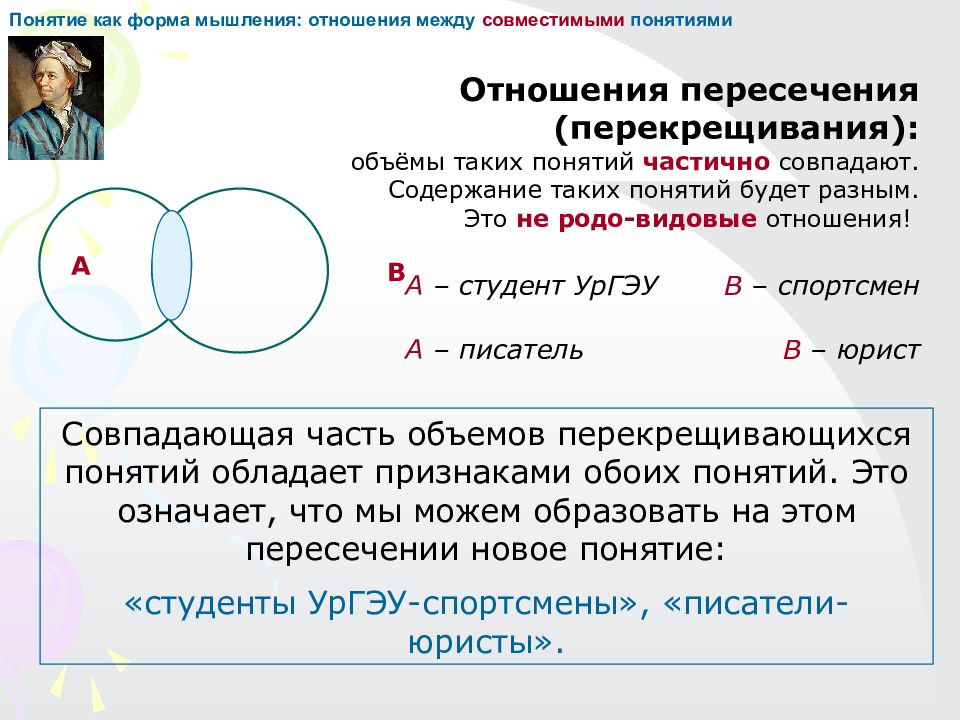
А В Понятие как форма мышления: отношения между совместимыми понятиями Отношения пересечения (перекрещивания): объёмы таких понятий частично совпадают. Содержание таких понятий будет разным. Это не родо-видовые отношения! А – студент УрГЭУ В – спортсмен А – писатель В – юрист Совпадающая часть объемов перекрещивающихся понятий обладает признаками обоих понятий. Это означает, что мы можем образовать на этом пересечении новое понятие: «студенты УрГЭУ-спортсмены», «писатели-юристы».
Слайд 36
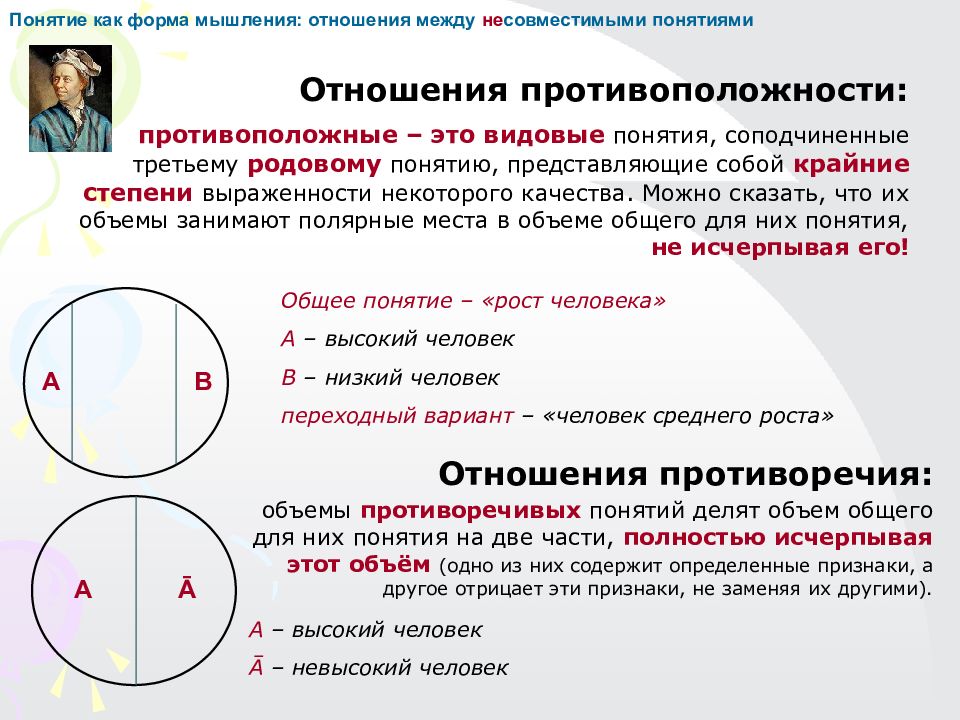
А В А Ā Понятие как форма мышления: отношения между не совместимыми понятиями Отношения противоположности: противоположные – это видовые понятия, соподчиненные третьему родовому понятию, представляющие собой крайние степени выраженности некоторого качества. Можно сказать, что их объемы занимают полярные места в объеме общего для них понятия, не исчерпывая его! Общее понятие – «рост человека» А – высокий человек В – низкий человек переходный вариант – «человек среднего роста» Отношения противоречия: объемы противоречивых понятий делят объем общего для них понятия на две части, полностью исчерпывая этот объём (одно из них содержит определенные признаки, а другое отрицает эти признаки, не заменяя их другими). А – высокий человек Ā – невысокий человек
Слайд 37
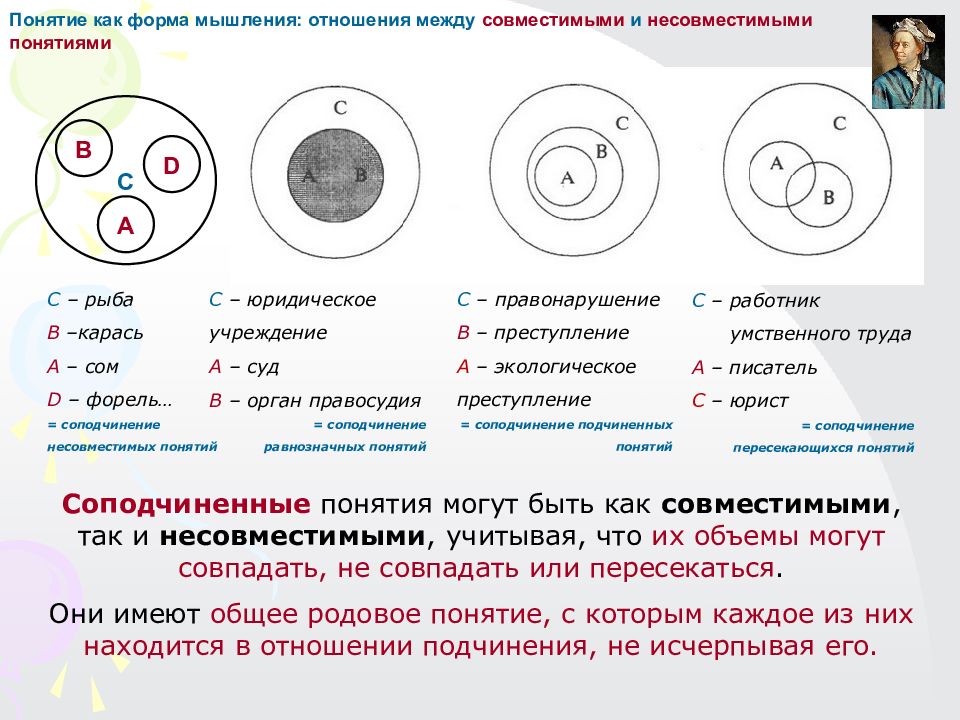
С В А D Соподчиненные понятия могут быть как совместимыми, так и несовместимыми, учитывая, что их объемы могут совпадать, не совпадать или пересекаться. Они имеют общее родовое понятие, с которым каждое из них находится в отношении подчинения, не исчерпывая его. С – рыба В –карась А – сом D – форель… = соподчинение несовместимых понятий Понятие как форма мышления: отношения между совместимыми и несовместимыми понятиями С – юридическое учреждение А – суд В – орган правосудия = соподчинение равнозначных поняти й С – правонарушение В – преступление А – экологическое преступление = соподчинение подчиненных понятий С – работник умственного труда А – писатель С – юрист = соподчинение пересекающихся понятий
Слайд 38
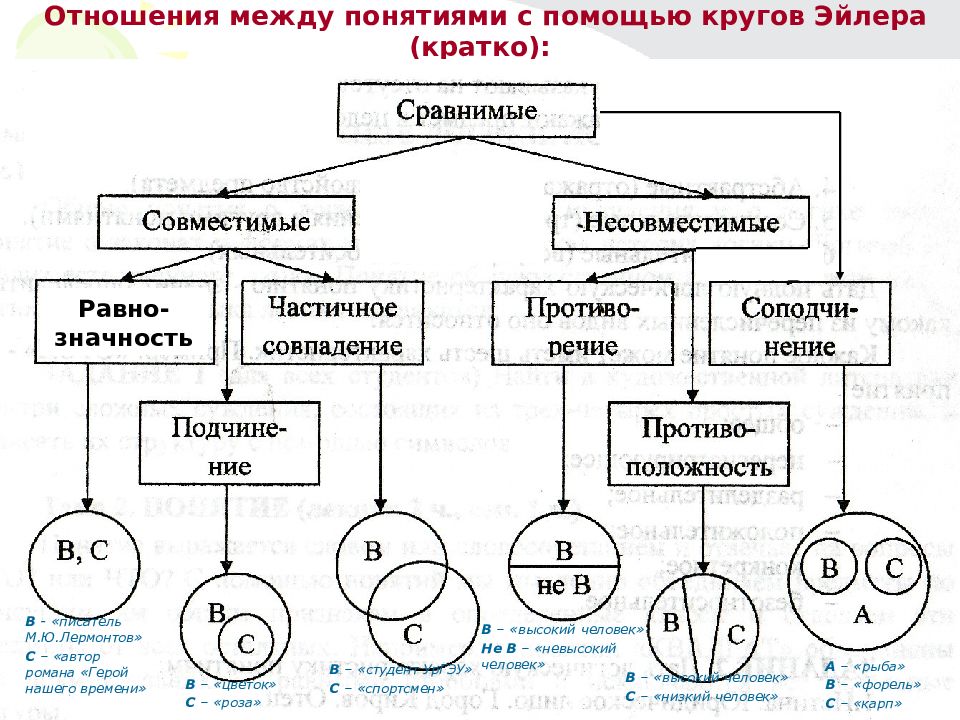
Отношения между понятиями с помощью кругов Эйлера (кратко): В - «писатель М.Ю.Лермонтов» С – «автор романа «Герой нашего времени» В – «студент УрГЭУ» С – «спортсмен» В – «цветок» С – «роза» А – «рыба» В – «форель» С – «карп» В – «высокий человек» С – «низкий человек» В – «высокий человек» Не В – «невысокий человек» Равно-значность
Слайд 39
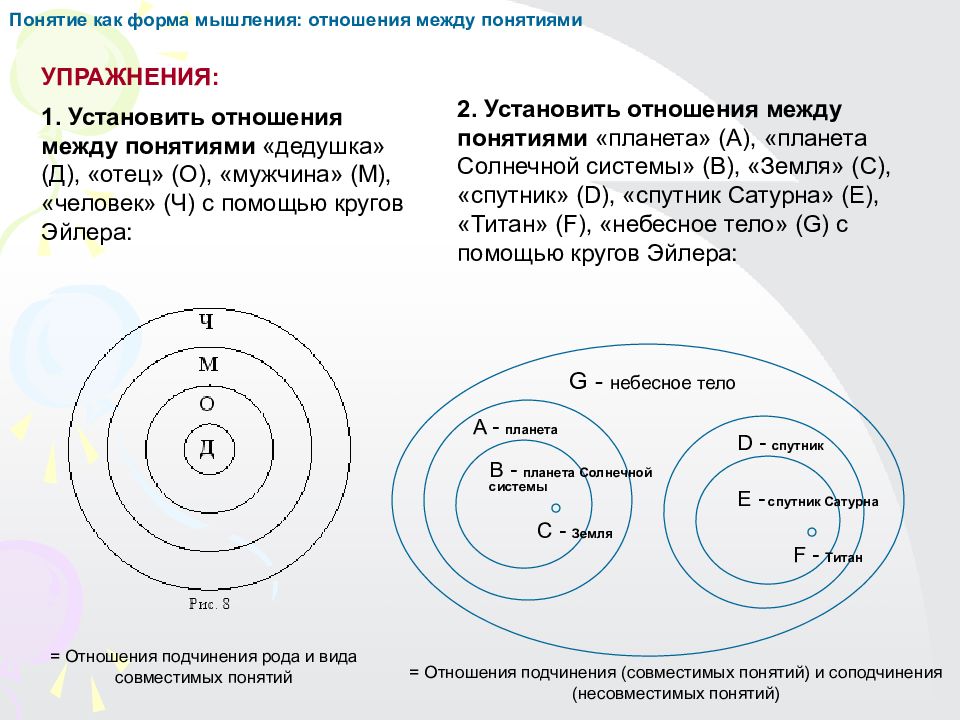
1. Установить отношения между понятиями «дедушка» (Д), «отец» (О), «мужчина» (М), «человек» (Ч) с помощью кругов Эйлера: УПРАЖНЕНИЯ: 2. Установить отношения между понятиями «планета» (A), «планета Солнечной системы» (B), «Земля» (C), «спутник» (D), «спутник Сатурна» (E), «Титан» (F), «небесное тело» (G) с помощью кругов Эйлера: G - небесное тело A - планета B - планета Солнечной системы C - Земля D - спутник E - спутник Сатурна F - Титан Понятие как форма мышления: отношения между понятиями = Отношения подчинения рода и вида совместимых понятий = Отношения подчинения (совместимых понятий) и соподчинения (несовместимых понятий)
Слайд 40
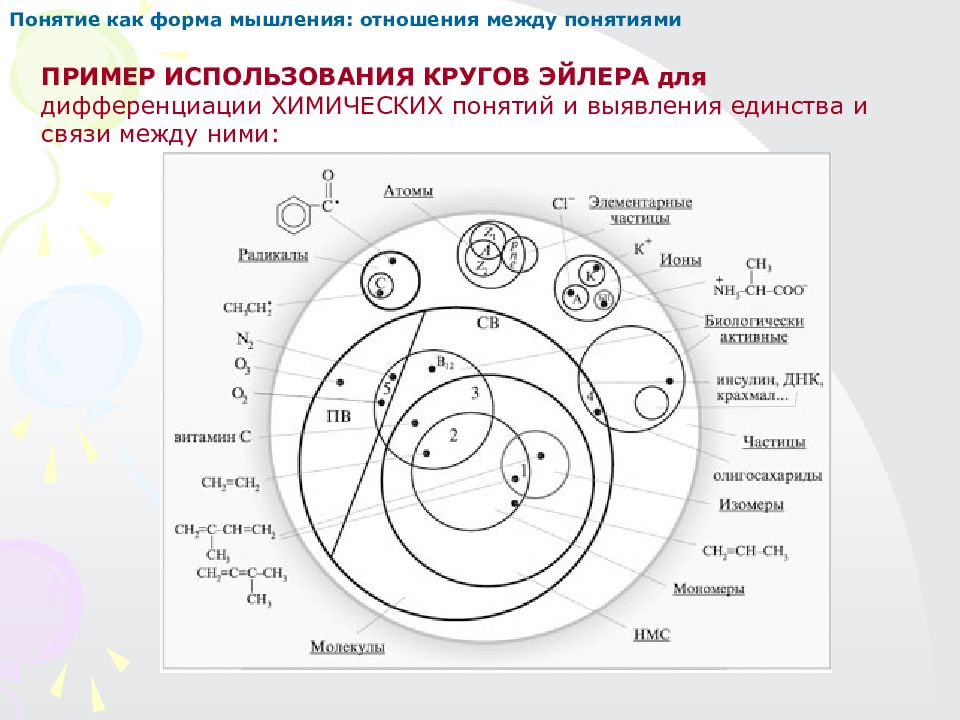
ПРИМЕР ИСПОЛЬЗОВАНИЯ КРУГОВ ЭЙЛЕРА для дифференциации ХИМИЧЕСКИХ понятий и выявления единства и связи между ними: Понятие как форма мышления: отношения между понятиями
Слайд 41
Понятие как форма мышления: логические операции с понятиями Логические операции с понятиями: ОГРАНИЧЕНИЕ – логическая операция перехода от понятия с б ó льшим объемом к понятию с меньшим объемом, от родового понятия к видовому путем прибавлении к содержанию понятия нового признака. Например: “поэт” → “великий поэт” → “великий английский поэт” → “великий английский поэт Джордж Гордон Байрон”. Пределом ограничения является единичное понятие (в данном примере это “великий английский поэт Джордж Гордон Байрон”). ____________________________________________________________ ОБОБЩЕНИЕ – логическая операция перехода от понятия с меньшим объемом к понятию с б ó льшим объемом, от видового понятия к родовому путем отбрасывания от первого его видообразующих признаков. Например: “Опера П. И. Чайковского “Евгений Онегин” → “опера П. И. Чайковского” → “опера русского композитора XIX в.” → “опера русского композитора” → “опера” → “произведение музыкального искусства” → “произведение искусства”. Пределом обобщения являются категории (философские, общенаучные и др.). Аав Аа А Схема ограничения и обобщения понятия: А – понятие, а, в – видообразующие признаки
Слайд 42
УПРАЖНЕНИЯ: Ограничить следующие понятия: «собственность» → «собственность в экономической системе» → «частная собственность» → «групповая частная собственность» → «акционерная групповая частная собственность» → «акционерная групповая частная собственность с уставным капиталом 10 млрд. рублей» → «акционерная групповая частная собственность с уставным капиталом 10 млрд. рублей фирмы «Заря» «дом» → «кирпичный дом» → «кирпичный многоквартирный дом» → «кирпичный многоквартирный десятиэтажный дом» → «кирпичный многоквартирный десятиэтажный дом № 11 по улице Ясной города Волгограда» Обобщить следующие понятия: «трагедия Шекспира «Ромео и Джульетта»» → «трагедия Шекспира» → «трагедия» → «драматическое произведение» → «род литературы» → «литература» → «искусство» → «духовная культура» «следователь военной прокуратуры капитан юстиции Иванов» → «следователь военной прокуратуры капитан юстиции» → «следователь военной прокуратуры» → «следователь прокуратуры» → «юрист» Понятие как форма мышления: логические операции с понятиями
Слайд 43
Существует закон обратного отношения между содержанием и объемом понятия: чем шире объем понятия, тем ý же его содержание; чем ý же объем понятия, тем шире его содержание. Например, Увеличивая содержание понятия «государство» путем прибавления нового признака – «современное», мы переходим к понятию «современное государство», имеющему меньший объем. Увеличивая объем понятия «учебник по теории государства и права», переходим к понятию «учебник», имеющему меньшее содержание. Обратите внимание, что закон обратного отношения применим к понятиям, находящимся друг к другу только в отношении «вида» и «рода» ! Понятие как форма мышления: логические операции с понятиями
Слайд 44
Понятие как форма мышления: логические операции с понятиями Классический (и наиболее распространенный) способ определения понятия заключается в том, что определяемое понятие подводится под ближайшее к нему родовое понятие, после чего следует указание на его существенные видовые отличия. Именно такие определения встречаются в учебниках, энциклопедиях, в научной и учебной практике. Определение понятия (дефиниция) – логическая операция, раскрывающая содержание понятия с указанием на его самые существенные признаки. Например, нам требуется дать определение понятию «квадрат». Следуя классическому способу, сначала подведём его под родовое понятие: «Квадрат – это геометрическая фигура », – а затем укажем его видовое отличие от других геометрических фигур, которое заключается в наличии равных сторон и прямых углов. Итак: «Квадрат – это геометрическая фигура, у которой все стороны равны и углы прямые».
Слайд 45
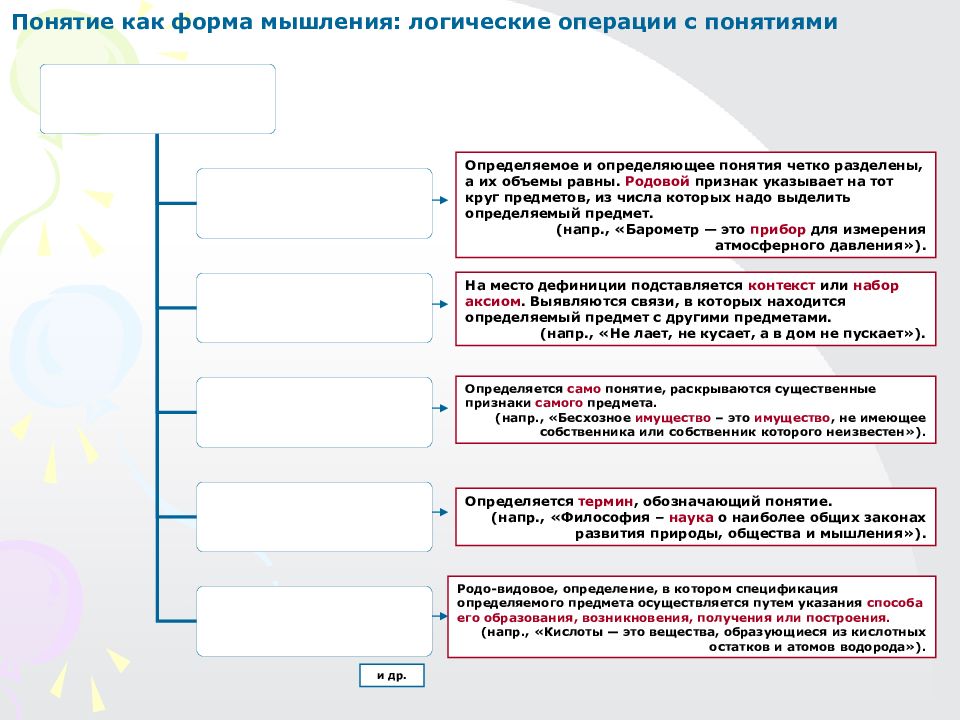
Понятие как форма мышления: логические операции с понятиями Определяемое и определяющее понятия четко разделены, а их объемы равны. Родовой признак указывает на тот круг предметов, из числа которых надо выделить определяемый предмет. (напр., «Барометр — это прибор для измерения атмосферного давления»). На место дефиниции подставляется контекст или набор аксиом. Выявляются связи, в которых находится определяемый предмет с другими предметами. (напр., «Не лает, не кусает, а в дом не пускает»). Определяется само понятие, раскрываются существенные признаки самого предмета. (напр., «Бесхозное имущество – это имущество, не имеющее собственника или собственник которого неизвестен»). Определяется термин, обозначающий понятие. (напр., «Философия – наука о наиболее общих законах развития природы, общества и мышления»). Родо-видовое, определение, в котором спецификация определяемого предмета осуществляется путем указания способа его образования, возникновения, получения или построения. (напр., «Кислоты — это вещества, образующиеся из кислотных остатков и атомов водорода»). и др.
Слайд 46
Правила определения понятий: 1. Определение должно быть соразмерным, т.е. объем определяемого понятия должен совпадать с объемом определяющего. Эта соразмерность легко проверяется через перестановку мест Dfd и Dfn. Например: «Наука о законах и формах правильного мышления есть логика». «Логика есть наука о законах и формах правильного мышления». Ошибки: а) слишком широкого определения, т.е. определяющее понятие имеет более широкий объем, чем определяемое: «Луна – спутник Земли». Кроме Луны имеются еще и искусственные спутники Земли. б) слишком узкого определения, т.е. определяющее понятие по своему объему ý же, чем определяемое: «Геометрия – это наука о треугольниках». Почему только о треугольниках? В) перекрещивания, т.е. слишком широкого и узкого определения одновременно: «Бочка – это сосуд для хранения жидкостей». узкое: в бочках хранят не только жидкости, но и рыбу, грибы, квашеную капусту, сыпучие вещества и др. широкое: бочка – не единственный сосуд для хранения всего этого. Понятие как форма мышления: логические операции с понятиями Б С
Слайд 47
Правила определения понятий: 2. Нельзя допускать круга в определении, т.е. когда определяющее само разъясняется через определяемое понятие. Нарушение этого правила ведет к логической ошибке – тавтологии. Ошибка: «Преступник – это человек, совершивший преступление». 3. Определение должно быть кратким, лаконичным: надо избегать многословия. Ошибка: Слишком многословное определение выходит за рамки своего назначения и может превратиться в простое описание. 4. Определение должно быть четким и ясным: надо избегать двусмысленных, сложных, расплывчатых и непонятных терминов, слов с переносным значением, образов, метафор, которые можно толковать по-разному. Ошибка: «Лев – это царь зверей». Слово «царь» используется в переносном значении, это метафора. Понятие как форма мышления: логические операции с понятиями
Слайд 48
Правила определения понятий: 5. Недопустимо давать определение через перечисление: всего не перечислишь, это с одной стороны. А с другой – в перечислении часто нет указания на существенные признаки: Ошибка: «Спорт – это футбол, хоккей, баскетбол». И не только. А все-таки, что же такое спорт? Вопрос так и остается открытым. 6. Определение не должно быть только отрицательным. Отрицательное определение указывает на признаки, которые не принадлежат предмету, но не указывает на признаки, принадлежащие предмету. Ошибки: «Кит – не рыба», «Сравнение – не доказательство». Понятие как форма мышления: логические операции с понятиями
Слайд 49
Приёмы, подменяющие определение понятий 1. Описание: перечисление существенных и несущественных внешних свойств предмета. При описании мы получаем чувственно-наглядный образ предмета. Недостаток описания – субъективный результат (разные люди по-разному опишут любой предмет). Например : «Апельсины имеют форму шара, они оранжевого цвета, состоят из горькой кожуры и кисло-сладкой мякоти, выделяют много сока, в мякоти встречаются косточки». «Человек – существо с двумя ногами, руками и головой». Понятие как форма мышления: логические операции с понятиями
Слайд 50
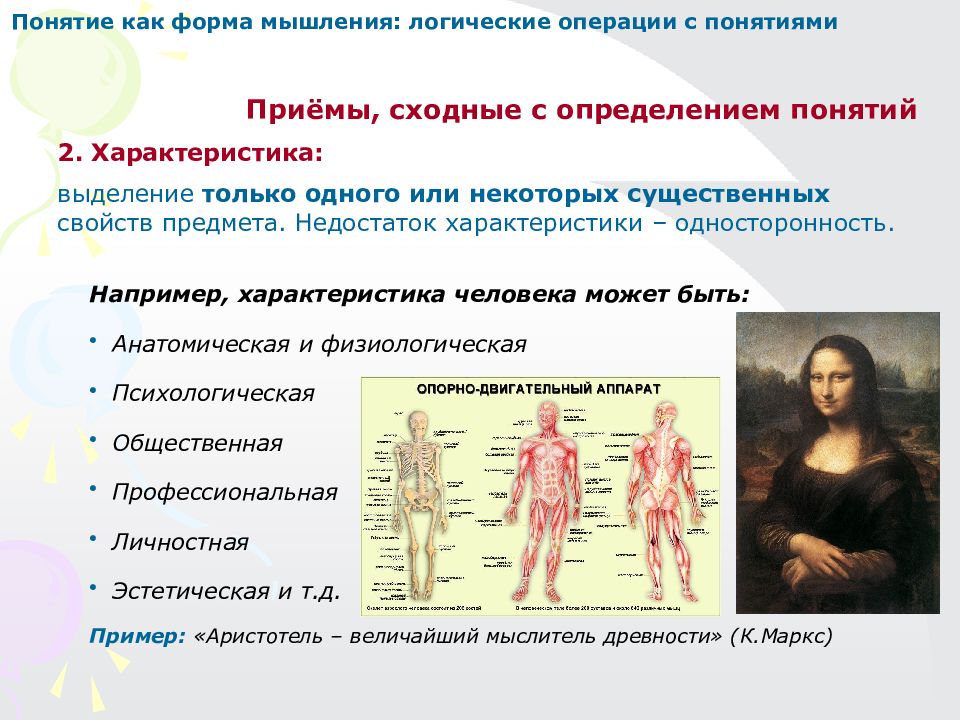
Приёмы, сходные с определением понятий 2. Характеристика: выделение только одного или некоторых существенных свойств предмета. Недостаток характеристики – односторонность. Например, характеристика человека может быть: Анатомическая и физиологическая Психологическая Общественная Профессиональная Личностная Эстетическая и т.д. Пример: «Аристотель – величайший мыслитель древности» (К.Маркс) Понятие как форма мышления: логические операции с понятиями
Слайд 51
Приёмы, сходные с определением понятий 3. Разъяснение посредством примера: приведение примера, иллюстрирующего понятие Например, если вас попросили объяснить, что такое «вежливость», но вы затрудняетесь дать ее определение, можно сказать: «Вежливость – это когда здороваются со знакомыми и благодарят за оказанную услугу». Понятие как форма мышления: логические операции с понятиями
Слайд 52
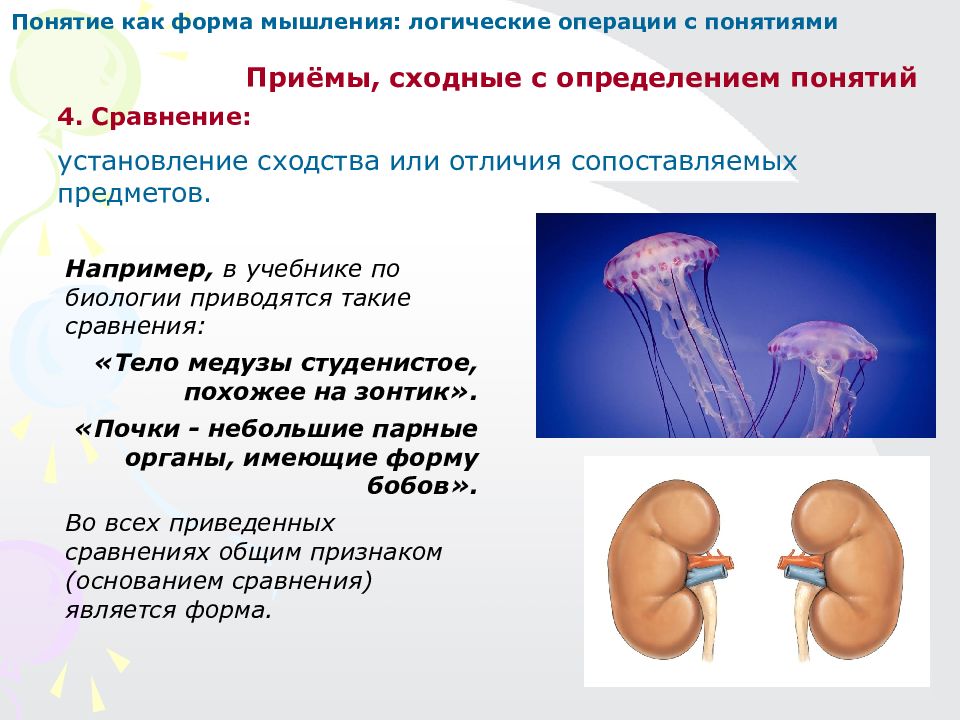
Приёмы, сходные с определением понятий 4. Сравнение: установление сходства или отличия сопоставляемых предметов. Например, в учебнике по биологии приводятся такие сравнения: «Тело медузы студенистое, похожее на зонтик». «Почки - небольшие парные органы, имеющие форму бобов». Во всех приведенных сравнениях общим признаком (основанием сравнения) является форма. Понятие как форма мышления: логические операции с понятиями
Слайд 53
Деление понятий – это логическая операция, посредством которой объем делимого родового понятия распределяется по объемам новых понятий, каждое из которых представляет вид исходного понятия. Чтобы проверить правильность логического деления, надо мысленно подставить такие выражения: «бывает», «есть», «делится на виды», «существует в виде»… В операции деления следует различать: делимое (родовое) понятие, объем которого следует раскрыть члены деления – виды, на которые делится родовое понятие основание деления, т.е. видообразующий признак, по которому ведется деление Понятие как форма мышления: логические операции с понятиями Пример: родовое понятие – «инертный газ» виды – Унуноктий, Гелий, Неон, Аргон, Криптон, Ксенон, Радон (перечислены все виды !) видообразующий признак – физические и химические свойства Унуноктий Гелий Неон Аргон Криптон Ксенон Радон
Слайд 54
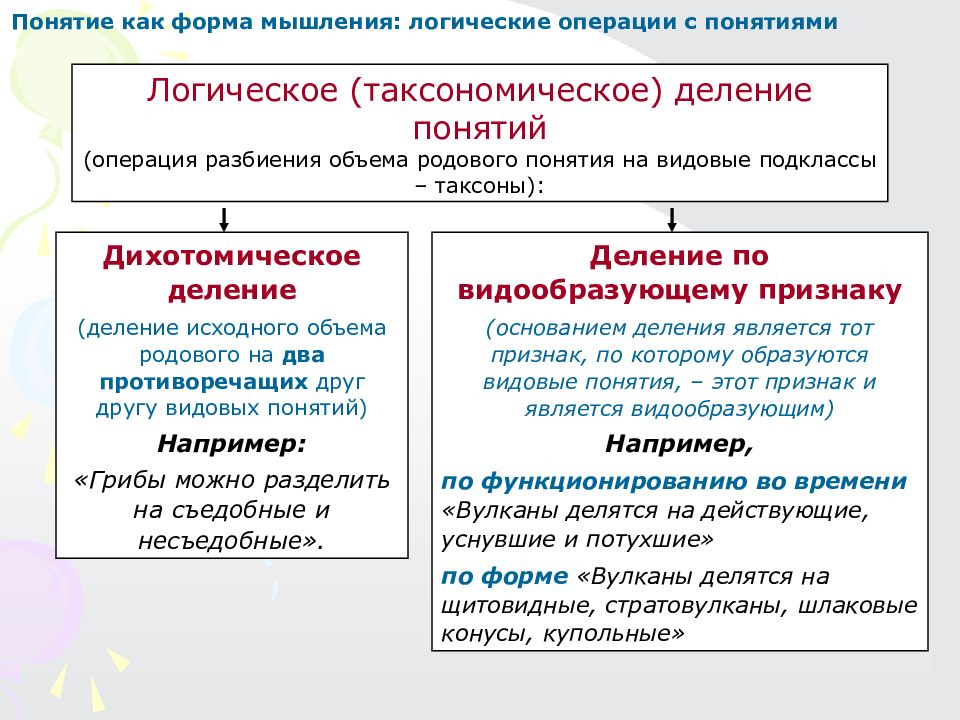
Понятие как форма мышления: логические операции с понятиями Логическое (таксономическое) деление понятий (операция разбиения объема родового понятия на видовые подклассы – таксоны): Деление по видообразующему признаку (основанием деления является тот признак, по которому образуются видовые понятия, – этот признак и является видообразующим) Например, по функционированию во времени «Вулканы делятся на действующие, уснувшие и потухшие» по форме «Вулканы делятся на щитовидные, стратовулканы, шлаковые конусы, купольные» Дихотомическое деление (деление исходного объема родового на два противоречащих друг другу видовых понятий) Например: «Грибы можно разделить на съедобные и несъедобные».
Слайд 55
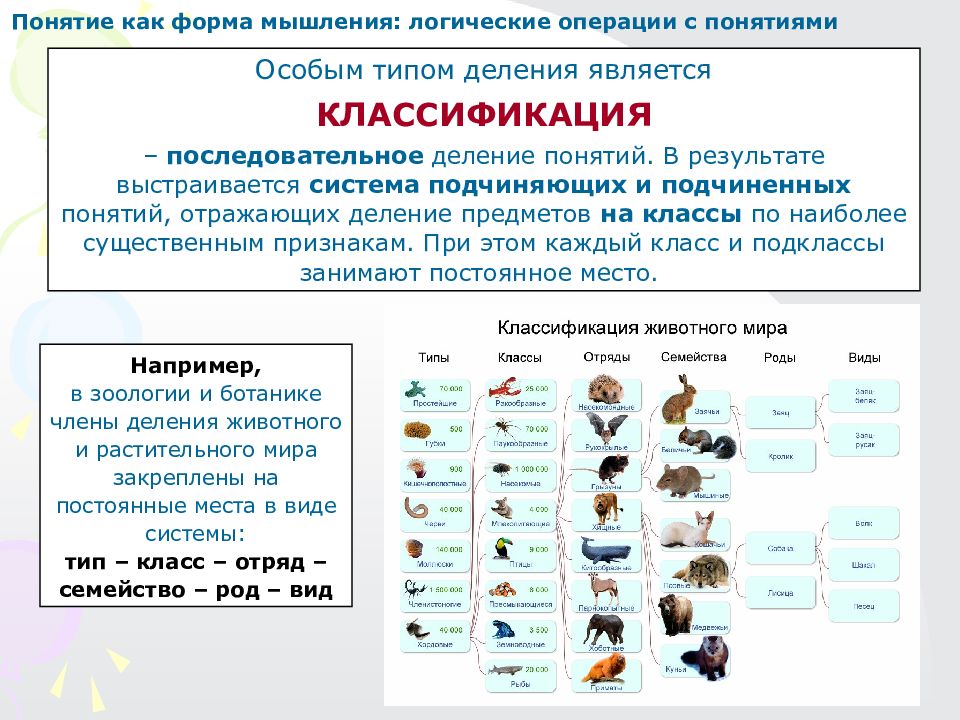
Понятие как форма мышления: логические операции с понятиями Особым типом деления является КЛАССИФИКАЦИЯ – последовательное деление понятий. В результате выстраивается система подчиняющих и подчиненных понятий, отражающих деление предметов на классы по наиболее существенным признакам. При этом каждый класс и подклассы занимают постоянное место. Например, в зоологии и ботанике члены деления животного и растительного мира закреплены на постоянные места в виде системы: тип – класс – отряд – семейство – род – вид
Слайд 56
Понятие как форма мышления: логические операции с понятиями Логическую операцию деления понятий следует отличать от аналитической процедуры мысленного расчленения предмета на части ( т.н. мереологическое деление )! Например, «Самолет состоит из частей : крыльев, фюзеляжа, мотора, управляющей системы, шасси». «Земной шар делится на Восточное и Западное полушария». «В книге можно выделить введение, заключение, основную часть и список литературы». «Дом состоит из комнат, коридора, крыши, крыльца».
Слайд 57
ПРАВИЛА ДЕЛЕНИЯ ПОНЯТИЙ: 1. Деление должно вестись только по одному основанию (признаку) В противном случае произойдет перекрещивание объемов понятий, выражающих члены деления. Правильное деление: «Высшие растения делятся на мхи, плауны, папоротники, голосеменные и цветковые растения». Неправильное деление: «Растения делятся на съедобные и несъедобные, однолетние и многолетние ». (Здесь не одно, а два основания деления) Понятие как форма мышления: логические операции с понятиями
Слайд 58
ПРАВИЛА ДЕЛЕНИЯ ПОНЯТИЙ: 2. Деление должно быть соразмерным, т. е. сумма объемов видовых понятий должна быть равна объему (делимого) родового понятия. Например: «Материки в современную геологическую эпоху делятся на Евразию, Африку, Австралию, Северную Америку, Южную Америку и Антарктиду». Нарушение этого правила ведет к ошибкам двух видов: а) Неполное деление, когда перечисляются не все виды данного родового понятия: «Арифметические действия делятся на сложение, вычитание, умножение, деление, возведение в степень». Не указано «извлечение корня» б) Деление с лишними членами: «Углы делятся на прямые, тупые, острые и накрест лежащие ». Здесь лишний член («накрест лежащие углы»). Понятие как форма мышления: логические операции с понятиями
Слайд 59
ПРАВИЛА ДЕЛЕНИЯ ПОНЯТИЙ: 3. Члены деления должны исключать друг друга, т. е. не иметь общих элементов, быть соподчиненными понятиями, объемы которых не пересекаются. Пример правильного деления: «Птицы делятся на килегрудые (летающие), бескилевые (бегающие) и плавающие». Пример ошибочного деления: «Птицы делятся на килегрудые (летающие), бескилевые (бегающие), плавающие и хищные ». Понятие как форма мышления: логические операции с понятиями Х Не-Х п л Здесь члены деления не исключают друг друга. Указанные объемы будут перекрещиваться: хищные птицы могут быть и летающими, и бегающими, и плавающими. б
Слайд 60
ПРАВИЛА ДЕЛЕНИЯ ПОНЯТИЙ: 4. Деление должно быть непрерывным. От рода следует сначала переходить к ближайшим видам, а от них к ближайшим подвидам. Например: « Предприятия торговли делятся на предприятия оптовой и розничной торговли » Если это правило нарушается, то происходит ошибка – скачок в делении: Пример: «Предприятия торговли делятся на предприятия оптовой, розничной торговли, специализированные магазины, универмаги, супермаркеты, универсамы, торговые комплексы и торговые дома ». Очевидно, что последние 6 видов входят в объем родового понятия «розничная торговля». Понятие как форма мышления: логические операции с понятиями
Слайд 61
Упражнения: Определите, в каких случаях имеет место логическое деление понятий, а в каком мереологическое : Животные делятся на позвоночных и беспозвоночных. Год делится на двенадцать месяцев. Дома делятся на одноэтажные и многоэтажные. Университет делится на факультеты. Евразия делится на Европу и Азию. Формами обучения в вузе являются дневная, вечерняя и заочная. Метр делится на сантиметры. Углы делятся на острые, тупые и прямые. Понятие как форма мышления: логические операции с понятиями
Слайд 62
Упражнения: 1. Разделить понятие «наука». Какие бывают науки в зависимости от предмета исследования? 2. Найти ошибку в делении понятий: « Республики бывают рабовладельческие, феодальные, президентские и парламентарные». « Животные делятся на хищников, травоядных, всеядных и млекопитающих». Понятие как форма мышления: логические операции с понятиями
Слайд 63
Суждение как форма мышления Суждение – это форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами Суждение выражается в форме повествовательного предложения. Например, «Каждая планета Солнечной системы вращается вокруг своей оси». «Все люди обладают способностью мышления». «Некоторые животные не являются хищниками». Ни вопросительное («Как пройти к оперному театру?»), ни побудительное («Передайте, пожалуйста, на билет!») предложения суждениями не являются, т.к. в них ничего не утверждается и не отрицается.
Слайд 64
Суждение как форма мышления 1. Вопрос в скрытой форме в повествовательном предложении: Например, «Следует установить признаки состава преступления». Здесь нет ни утверждения, ни отрицания, не отражается связь между понятиями. Поэтому данное предложение не является суждением. 2. В отдельных вопросительных и восклицательных предложениях в завуалированной форме может содержаться суждение: Например, обвиняемый говорит о соучастнике: «Откуда я знал, что он начнет отбирать вещи насильно?», имея в виду: «Я не знал, что он начнет отбирать вещи насильно». Или общественный защитник заявляет в суде: «Ну, какой он преступник!» в смысле: «Он не преступник». Поэтому, рассматривая любую грамматическую форму высказывания, необходимо устанавливать его логический смысл! Исключения:
Слайд 65
Суждение как форма мышления Что надо знать о суждениях? Любое суждение является истинным или ложным Суждение имеет определённую структуру: S (субъект), Р (предикат), связка (соединят S и Р): «(не) есть», «(не) является», «(не) суть », квантор (объем S ): «все», «некоторые», «ни один», «любой», «каждый» и т. п. Суждения бывают простые и сложные (сумма простых) Простые суждения различаются: по объему субъекта (единичные, частные, общие): «Это S », «Некоторые S », «Все S » по содержанию предиката ( атрибутивные (предикат представляет собой существенный признак субъекта), релятивные (предикат выражает собой какое-то отношение к субъекту), экзистенциальные (предикат указывает просто на существование или несуществование субъекта в действительности) ) по качеству связки (утвердительные, отрицательные): «есть», «не есть» В суждении между субъектом и предикатом по объему могут быть отношения эквивалентности, пересечения, подчинения, несовместимости В суждениях термины могут быть либо распределены (взяты в полном объёме), либо не распределены Простые суждения можно преобразовывать: превращать, обращать, противопоставлять предикату Существуют отношения между простыми суждениями по истинности, определяемые по логическому квадрату Сложные суждения бывают соединительными, разделительными (слабо и сильно), условными и эквивалентными
Слайд 66
Суждение как форма мышления Любое суждение является истинным или ложным. Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение «Все розы – это цветы» является истинным, а суждение «Все грибы – съедобные» – ложным.
Слайд 67
Суждение как форма мышления Суждение имеет определённую структуру, в которой можно выделить четыре части: 1. Субъект ( S ) – это то, о чём идёт речь в суждении. 2. Предикат ( Р ) – это то, что говорится о субъекте. 3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова «(не) есть», «(не) является», «(не) суть» и т. п. 4. Квантор – это указатель на объём субъекта. В роли квантора могут быть слова «все», «некоторые», «ни один», «любой», «каждый» и т. п. квантор субъект связка предикат Например : «Все собаки являются млекопитающими». («Все S есть Р»)
Слайд 68
Суждение как форма мышления Связка (т.е. утверждение или отрицание) может соответствовать или не соответствовать действительности, в зависимости от этого все суждение оказывается истинным или ложным : «С. совершил хулиганский поступок». «С. не совершал хулиганского поступка». Если в каком-то суждении отсутствует связка или квантор, то они всё равно подразумеваются : « Тигры – это хищники », – квантор отсутствует, но он подразумевается – это слово «все», а «–» заменяет связку «есть». Предмет и предикат могут выражаться различным количеством терминов: «Деяние, совершенное М., квалифицируется как убийство». Предметом суждения будет выражение «деяние, совершенное М.», предикатом – «квалифицируемо как убийство», связкой – утверждение «есть».
Слайд 69
Суждение как форма мышления Суждение может иметь различное словесное выражение. Одно и то же суждение может быть выражено разными предложениями: «Пионер – всем ребятам пример», «Пионер является примером для всех ребят», «Пионер ведёт себя так, чтобы быть образцом для всех ребят». Одно и то же суждение часто может быть выражено и личным, и безличным предложением: «Молния сожгла дерево». «Молнией сожгло дерево».
Слайд 70
Суждение как форма мышления В речи мы как правило используем суждения, которые не имеют четко выраженной логической формы. Чтобы работать с ними, им надо придать логическую форму, т. е. преобразовать суждение (не меняя его содержания!) так, чтобы в нём отчётливо были видны субъект, предикат, связка и квантор. При этом надо видеть, где находится отрицание – в связке или в предикате – и не нарушать данную структуру. Примеры: «В этом году весна началась раньше обычного». « Весна этого года ( S ) есть (связка) начавшаяся раньше обычного (Р)». («Это S есть Р») «Люди часто говорят и о несерьезном». « Все (квантор) люди (S) есть (связка) часто говорящие о несерьезном (Р)». («Все S есть Р») «Незаконная сделка является недействительной». « Всякая (квантор) незаконная сделка (S) является (связка) недействительной (Р)». («Все S есть Р») «Не всякий генерал от природы полный». « Некоторые (квантор) генералы ( S ) не являются (связка) полными от природы (Р)». («Некоторые S не есть Р») «В здоровом теле – здоровый дух». « Здоровый дух ( S ) есть (связка) в здоровом теле (Р)». («Все S есть Р») «Только здоровое тело ( S ) есть (связка) вместилище здорового духа (Р)»
Слайд 71
Суждение как форма мышления Суждения бывают простыми и сложными. СЛОЖНЫЕ: сумма простых суждений, Связанных между собой логическими союзами (связками): «и», «или», «если.., то», «если, и только если.., то» и др. Например: « Если 1) человек совершил преступление, то 2) он должен быть наказан». ПРОСТЫЕ: выражают связь двух понятий или выражены одним понятием, когда второе подразумевается, лишь мыслится. Например: «Сидоров имеет высшее юридическое образование». «Моросит (дождь)».
Слайд 72
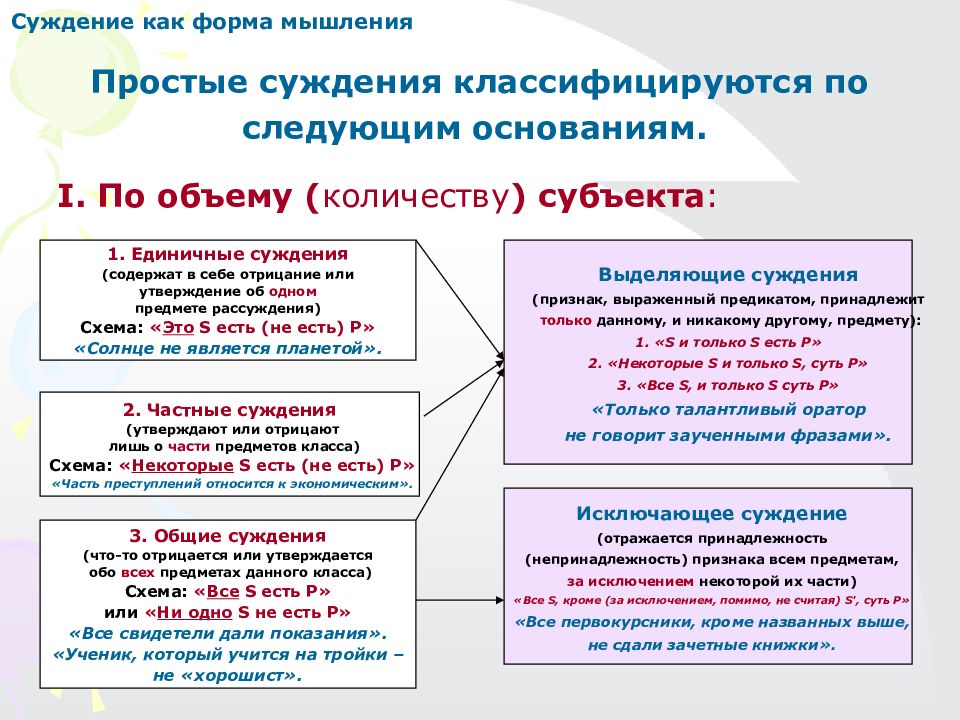
Суждение как форма мышления Простые суждения классифицируются по следующим основаниям. I. По объему ( количеству ) субъекта : 1. Единичные суждения (содержат в себе отрицание или утверждение об одном предмете рассуждения) Схема: « Это S есть (не есть) Р» «Солнце не является планетой». 2. Частные суждения (утверждают или отрицают лишь о части предметов класса) Схема: « Некоторые S есть (не есть) Р» «Часть преступлений относится к экономическим». 3. Общие суждения (что-то отрицается или утверждается обо всех предметах данного класса) Схема: « Все S есть Р» или « Ни одно S не есть Р» «Все свидетели дали показания». «Ученик, который учится на тройки – не «хорошист». Выделяющие суждения (признак, выраженный предикатом, принадлежит только данному, и никакому другому, предмету): «S и только S есть Р» 2. «Некоторые S и только S, суть Р» 3. «Все S, и только S суть Р» «Только талантливый оратор не говорит заученными фразами». Исключающее суждение (отражается принадлежность (непринадлежность) признака всем предметам, за исключением некоторой их части) «Все S, кроме (за исключением, помимо, не считая) S', суть Р» «Все первокурсники, кроме названных выше, не сдали зачетные книжки».
Слайд 73
Суждение как форма мышления УПРАЖНЕНИЯ: Определить вид простого суждения – единичное, частное или общее (выделяющее или исключающее): « Только Зимин является свидетелем происшествия». « Некоторые учащиеся ( и только учащиеся ) являются школьниками». « Все члены нашей группы, и только они, присутствуют на собрании». « Все ученики, за исключением Иванова, справились с заданием». «Заочное разбирательство уголовных дел в судах не допускается, кроме случаев, предусмотренных федеральными законами».
Слайд 74
I I. По качеству связки : Суждение как форма мышления Утвердительные: выражают принадлежность предмету некоторого признака. Например, «Лицо, виновное в совершении преступления, привлекается к уголовной ответственности». Отрицательные: выражают отсутствие у предмета некоторого признака с помощью отрицательной связки. Например, «Захватническая война не имеет законного основания». ! При этом следует различать отрицательное суждение и негативную форму выражения утвердительного суждения ( например, «Захватническая война незаконна », т.е. « является незаконной» ).
Слайд 75
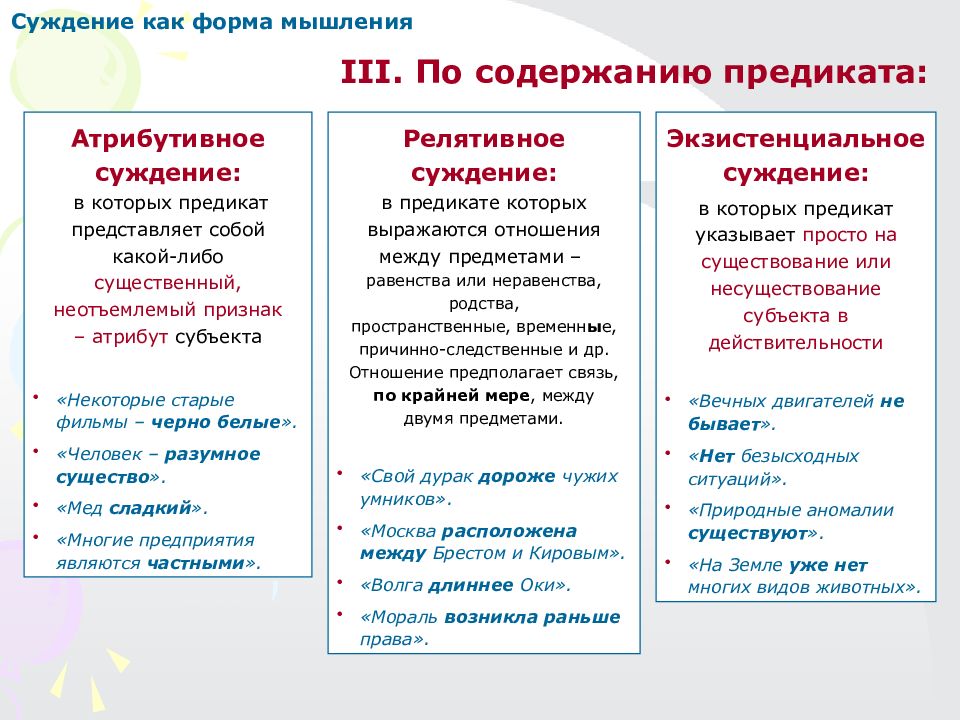
Суждение как форма мышления III. По содержанию предиката: Экзистенциальное суждение: в которых предикат указывает просто на существование или несуществование субъекта в действительности «Вечных двигателей не бывает ». « Нет безысходных ситуаций». «Природные аномалии существуют ». «На Земле уже нет многих видов животных». Релятивное суждение: в предикате которых выражаются отношения между предметами – равенства или неравенства, родства, пространственные, временн ы е, причинно-следственные и др. Отношение предполагает связь, по крайней мере, между двумя предметами. «Свой дурак дороже чужих умников». «Москва расположена между Брестом и Кировым». «Волга длиннее Оки». «Мораль возникла раньше права». Атрибутивное суждение: в которых предикат представляет собой какой-либо существенный, неотъемлемый признак – атрибут субъекта «Некоторые старые фильмы – черно белые ». «Человек – разумное существо ». «Мед сладкий ». «Многие предприятия являются частными ».
Слайд 76
Суждение как форма мышления В традиционной логике все указанные виды представляют простое категорическое суждение, в котором отношения между субъектом и предикатом выражаются определенно, без каких-либо условий и вариантов, в безоговорочной форме.
Слайд 77
Суждение как форма мышления Объединенная классификация простых категорических суждений: Общеутвердительные суждения «А» A ffirmo (я утверждаю, говорю да) Схема: «Все S есть Р» «Все студенты сдали экзамен». Общеотрицательные суждения «Е» N e go (я отрицаю, говорю нет ) Схема: «Все S не есть Р» «Ни один студент не сдал экзамен». Частноутвердительные суждения «I» Aff i rmo (я утверждаю, говорю да) Схема: «Некоторые S есть Р» «Некоторые студенты сдали экзамен». Частноотрицательные суждения «О» Neg o (я отрицаю, говорю нет ) Схема: «Некоторые S не есть Р» «Некоторые студенты не сдали экзамен».
Слайд 78
Суждение как форма мышления ! Обратите внимание ! Единичные суждения в объединённой классификации категорических суждений в самостоятельную группу не выделяются. По своей логической характеристике с точки зрения количества все единичные суждения относятся к общим суждениям, так как речь в них идёт обо всём объёме субъекта! Например: «Антарктида – это один из материков Земли». Проверка: « Вся Антарктида – это один из материков Земли».
Слайд 79
! Обратите внимание ! Грамматическая форма общих и частных суждений иногда совпадает. Например: «Грибы растут в лесах». Это частное суждение, так как грибы растут не только в лесах. Следовательно, не все, а некоторые грибы растут в лесах. Проверка: « Все грибы растут в лесах» или « Некоторые грибы растут в лесах»? Суждение как форма мышления: классификация суждений
Слайд 80
Суждение как форма мышления УПРАЖНЕНИЯ: Определить тип суждения – общеутвердительное, общеотрицательное, частноутвердительное и частноотрицательное : « Все школьники являются учащимися ». « Некоторые животные являются хищниками». « Все планеты не являются звёздами». « Ни одна планета не является звездой». « Некоторые грибы не являются съедобными». «Солнце – это небесное тело». «Москва основана в 1147 году». «Известный итальянский учёный эпохи Возрождения Галилео Галилей не является автором теории электромагнитного поля».
Слайд 81
Суждение как форма мышления: распределённость терминов В простых суждениях термины ( S и P ) могут быть либо распределены, т.е. взяты в полном объеме (обозначаются знаком «+»), либо не распределены, т.е. взяты в части объема (обозначаются знаком «–»).
Слайд 82
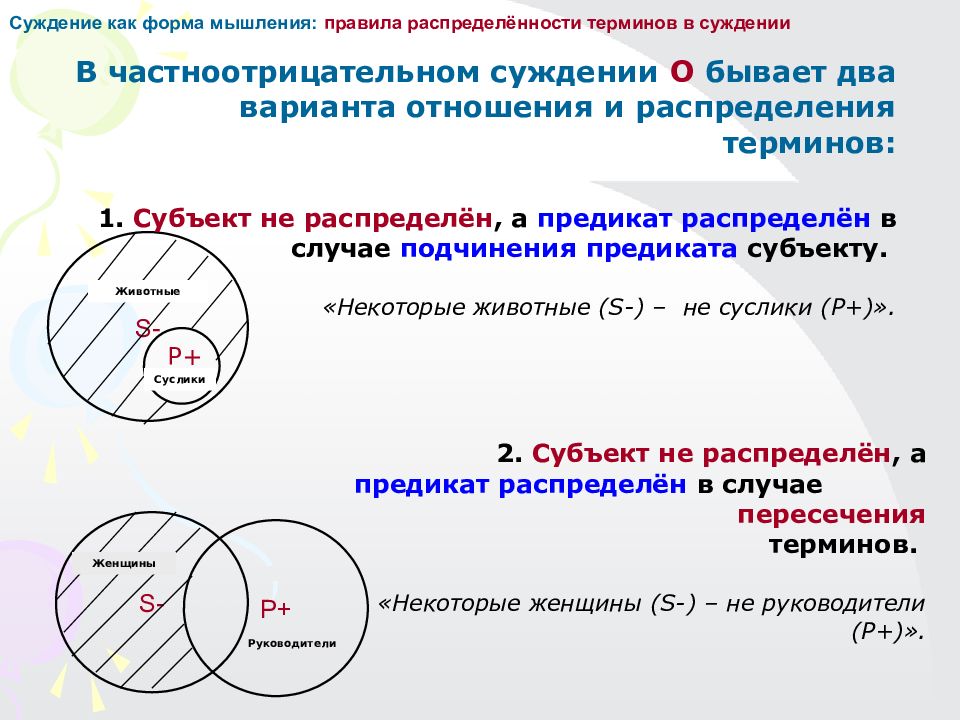
Суждение как форма мышления: правила распределённости терминов в суждении В общеутвердительном суждении А бывает два варианта отношения и распределения терминов: 1. Субъект находится в подчинении у предиката и распределен, а предикат не распределён и является подчиняющим понятием. «Все киты (S+) – млекопитающие (Р–)»: Речь здесь идет обо всех китах, значит субъект этого суждения распределен. Однако, здесь речь идет не обо всех млекопитающих, а только о части млекопитающих (именно – о тех, которые являются китами), следовательно, предикат данного суждения не распределен. S + S + P + 2. Субъект и предикат распределены в случае эквивалентности терминов. «Екатеринбург (S+) – столица Урала (Р+)». P - Киты Млекопитающие Екатеринбург Столица Урала
Слайд 83
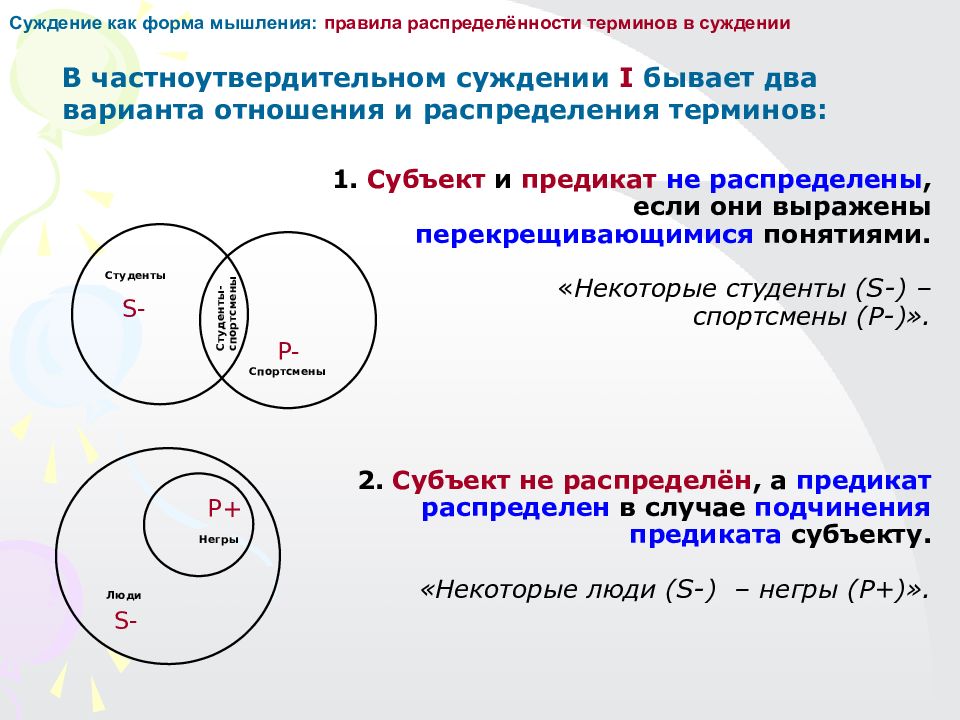
1. Субъект и предикат не распределены, если они выражены перекрещивающимися понятиями. « Некоторые студенты (S-) – спортсмены (Р-)». 2. Субъект не распределён, а предикат распределен в случае подчинения предиката субъекту. «Некоторые люди (S-) – негры (P+) ». Суждение как форма мышления: правила распределённости терминов в суждении В частноутвердительном суждении I бывает два варианта отношения и распределения терминов: Студенты Спортсмены Студенты-спортсмены Люди S - P + S - P - Негры
Слайд 84
S + P + Суждение как форма мышления: правила распределённости терминов в суждении В общеотрицательном суждении Е: оба термина всегда распределены, они полностью исключают друг друга, являются несовместимыми понятиями. «Ни один лось (S+) не является оленем (P+) ». И наоборот. Лоси Олени
Слайд 85
S - Суждение как форма мышления: правила распределённости терминов в суждении В частноотрицательном суждении О бывает два варианта отношения и распределения терминов: 1. Субъект не распределён, а предикат распределён в случае подчинения предиката субъекту. «Некоторые животные (S-) – не суслики (P+) ». 2. Субъект не распределён, а предикат распределён в случае пересечения терминов. «Некоторые женщины (S-) – не руководители (P+) ». S - Р+ Животные Суслики P + Женщины Руководители
Слайд 86
Суждение как форма мышления: отношения между субъектом и предикатом в суждении В таблице представлены все случаи отношений по объему и распределённости терминов в простых суждениях: S + Правило: субъект всегда распределён в общих суждениях и не распределён в частных; предикат всегда распределён в отрицательных суждениях, а в утвердительных он распределён тогда, когда объём предиката меньше или совпадает с объёмом субъекта.
Слайд 87
УПРАЖНЕНИЯ: определить характер соотношения объемов субъекта и предиката в следующих суждениях ( эквивалентность, пересечение, подчинение, несовместимость) : « Луна ( S ) является естественным спутником Земли (P) ». «Некоторые русские писатели ( S ) – это всемирно известные люди (P) ». «Все березы ( S ) – это деревья (P) ». «Все животные ( S ) не являются людьми (P) ». Суждение как форма мышления: отношения по объему
Слайд 88
Суждения можно преобразовывать, т. е. изменять их форму. Эта логическая операция позволяет уточнить логический смысл простых суждений, помогает более точно выражать различные оттенки наших высказываний. Преобразование суждений уже позволяет делать непосредственные умозаключения. Суждение как форма мышления: преобразование суждений
Слайд 89
ПРЕВРАЩЕНИЕ – в суждение вводится два отрицания: перед связкой ( положительная меняется на отрицательную или наоборот); перед предикатом (т.е. он меняется на противоречащий). При этом меняется качество суждения, но не его смысл! Общеутвердительное суждение превращается в общеотрицательное (А → Е): «Это не хорошо» → «Это не есть хорошо» Схема: «Все S суть Р» → «Ни одно S не суть не-Р» Общеотрицательное суждение превращается в общеутвердительное (Е → А): «Ни одна кошка не является собакой» → «Всякая кошка является не собакой» Схема: «Ни один S не есть Р» → «Все S есть не-Р» Частноутвердительное суждение превращается в частноотрицательное ( I → О): «Некоторые дни на прошлой неделе были холодными» → «Некоторые дни на прошлой неделе не были не холодными» Схема: «Некоторые S суть Р» → «Некоторые S не суть не-Р» Частноотрицательное суждение превращается в частноутвердительное (О → I): «Некоторые адвокаты не суть спортсмены» → «Некоторые адвокаты суть не спортсмены» Схема: «Некоторые S не суть Р» → «Некоторые S суть не-Р» Суждение как форма мышления: преобразование суждений Примеры и схемы превращения:
Слайд 90
Значение ПРЕВРАЩЕНИЯ в практике мышления: Путем превращения можно уточнить мысль: «Звёзды находятся в движении» и «Звёзды не не подвижны». Путем превращения можно придать новый оттенок мысли, резко усилив ее смысловое содержание: «Я могу быть честным» и «Я не могу не быть честным». В юридических дискуссиях, спорах и т.д. подобный прием встречается нередко, когда мы используем выражения типа: «не есть не...», «не является не...» и др. Суждение как форма мышления: преобразование суждений
Слайд 91
ОБРАЩЕНИЕ – субъект и предикат меняются местами. При этом количество суждения может изменяться, а качество не меняется. Поскольку при обращении изменяется предмет мысли, постольку изменяется и смысл суждения, т. е. мы имеем уже новое суждение! Суждение как форма мышления: преобразование суждений
Слайд 92
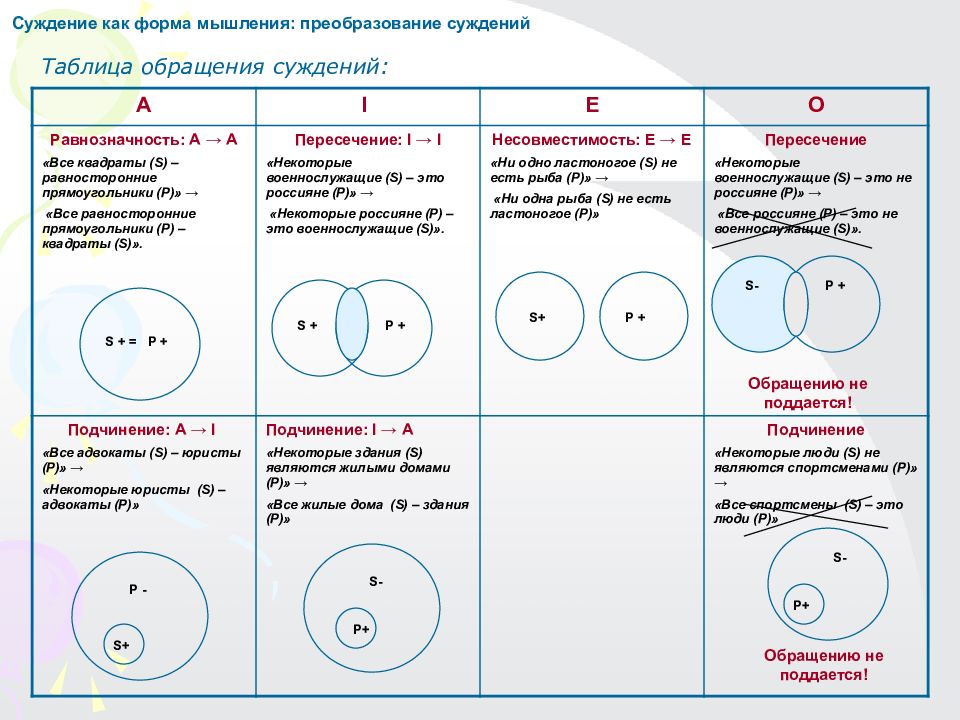
Суждение как форма мышления: преобразование суждений Таблица обращения суждений: A I Е О Равнозначность: А → А «Все квадраты ( S ) – равносторонние прямоугольники (Р)» → «Все равносторонние прямоугольники (Р) – квадраты ( S )». Пересечение: I → I «Некоторые военнослужащие ( S ) – это россияне (Р)» → «Некоторые россияне (Р) – это военнослужащие ( S )». Несовместимость: Е → Е «Ни одно ластоногое (S ) не есть рыба (Р)» → «Ни одна рыба ( S ) не есть ластоногое (Р)» Пересечение «Некоторые военнослужащие ( S ) – это не россияне (Р)» → «Все россияне (Р) – это не военнослужащие ( S )». Подчинение: А → I «Все адвокаты ( S ) – юристы (Р)» → «Некоторые юристы (S ) – адвокаты (Р)» Подчинение: I → А «Некоторые здания ( S ) являются жилыми домами (Р)» → «Все жилые дома (S ) – здания (Р)» Подчинение «Некоторые люди ( S ) не являются спортсменами (Р)» → «Все спортсмены (S ) – это люди (Р)» S + = Р + Р - S + S + Р + S - Р+ S + Р + S - Р + Обращению не поддается! Р+ S - Обращению не поддается!
Слайд 93
Значение ОБРАЩЕНИЯ в практике мышления: Полнее раскрываются взаимоотношения между субъектом и предикатом суждения, а следовательно, связи и отношения между предметами мысли, отражаемыми в суждении: «Всякое суждение есть предложение, но не всякое предложение есть суждение». Обращение может принимать и не столь развернутую, полную форму. Примером сокращенного обращения может служить пословица: «Не все то золото, что блестит». Очевидно, это результат обращения суждения: «Не всё блестящее есть золото». С помощью обращения проверяется правильность определений. Если после перестановки определяемого и определяющего смысл определения не меняется, значит, оно правильное. В юридической практике иногда требуется более точно выявить соотношения между теми или иными понятиями. Например: «Всякий закон есть нормативный правовой акт», но «Не всякий нормативный правовой акт есть закон» (есть еще указы, инструкции, правила и т. п.). Суждение как форма мышления: преобразование суждений
Слайд 94
ПРОТИВОПОСТАВЛЕНИЕ ПРЕДИКАТУ – сначала суждение поддается превращению, а потом обращению: субъектом становится понятие, противоречащее предикату, а предикатом – субъект исходного суждения. Меняется качество суждения. А → Е → Е : «Все адвокаты – юристы» «Ни один адвокат не является не юристом» «Ни один не юрист не является адвокатом» Схема: А: «Все S суть Р» Е: «Ни одно S не суть не Р» Е: «Все не Р не суть S » Е → А → I : «Ни одна кошка не является собакой» «Всякая кошка является не собакой» «Некоторые не собаки есть кошки» Схема: Е: «Ни один S не есть Р» А: «Все S есть не Р» I : «Некоторые не Р есть S » I: Частноутвердительное суждение не противопоставляется предикату, поскольку оно превращается в суждение частноотрицательное О, а суждение О не обращается. О → I → I : «Некоторые адвокаты не суть спортсмены» «Некоторые адвокаты суть не спортсмены» «Некоторые не спортсмены есть адвокаты» Схема: О: «Некоторые S не суть Р» I : «Некоторые S суть не-Р» I : «Некоторые не Р есть S » Примеры и схемы противопоставления предикату: Суждение как форма мышления: преобразование суждений
Слайд 95
Значение ПРОТИВОПОСТАВЛЕНИЯ ПРЕДИКАТУ в практике мышления : мы уточняем наши знания, высказываем нечто новое, что не было в явной форме выражено в исходном суждении: Например, А: «Акционерная компания обладает статусом юридического лица», Е: «Акционерная компания не может не обладать статусом юридического лица», Е: «Не обладающая статусом юридического лица компания не есть акционерная компания». Суждение как форма мышления: преобразование суждений
Слайд 96
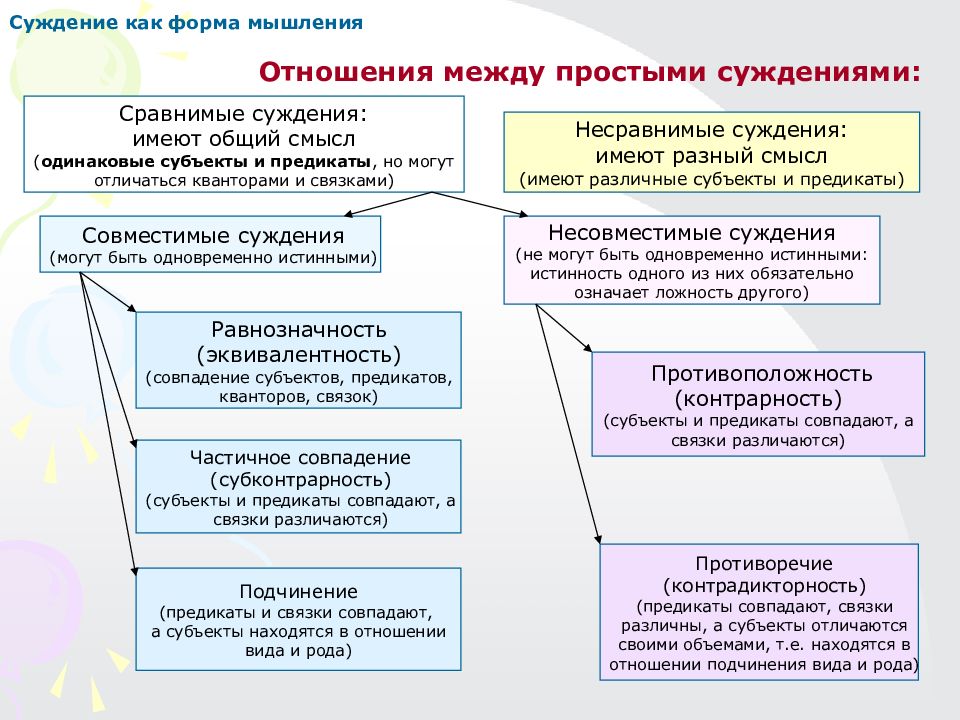
Суждение как форма мышления Отношения между простыми суждениями: Сравнимые суждения: имеют общий смысл ( одинаковые субъекты и предикаты, но могут отличаться кванторами и связками) Несравнимые суждения: имеют разный смысл (имеют различные субъекты и предикаты) Несовместимые суждения (не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого) Совместимые суждения (могут быть одновременно истинными) Равнозначность (эквивалентность) (совпадение субъектов, предикатов, кванторов, связок) Частичное совпадение (субконтрарность) (субъекты и предикаты совпадают, а связки различаются) Противоположность (контрарность) (субъекты и предикаты совпадают, а связки различаются) Противоречие (контрадикторность) (предикаты совпадают, связки различны, а субъекты отличаются своими объемами, т.е. находятся в отношении подчинения вида и рода) Подчинение (предикаты и связки совпадают, а субъекты находятся в отношении вида и рода)
Слайд 97
Суждение как форма мышления: несравнимые суждения НЕСРАВНИМЫЕ СУЖДЕНИЯ. РАЗЪЯСНЕНИЯ С ПРИМЕРАМИ: Несравнимые простые суждения имеют разные субъекты и предикаты: Например: 1. «Закон суров» и «Небо ясное». 2. «Все грибы съедобные» и «Некоторые пироги съедобные». 3. «Все школьники изучают математику». и «Некоторые спортсмены – это олимпийские чемпионы». Истинность и ложность таких суждений не зависит друг от друга!
Слайд 98
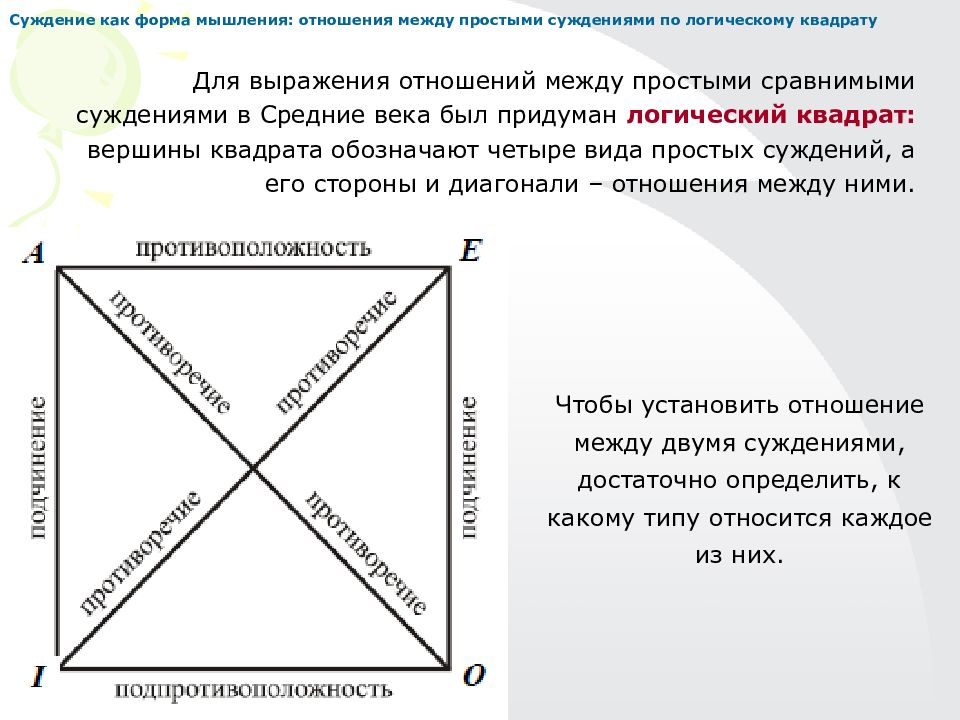
Суждение как форма мышления: отношения между простыми суждениями по логическому квадрату Для выражения отношений между простыми сравнимыми суждениями в Средние века был придуман логический квадрат: вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому типу относится каждое из них.
Слайд 99
Суждение как форма мышления: совместимые суждения СРАВНИМЫЕ СОВМЕСТИМЫЕ СУЖДЕНИЯ. РАЗЪЯСНЕНИЯ С ПРИМЕРАМИ: Эквивалентность (равнозначность) есть полная совместимость: суждения имеют одинаковые субъекты и предикаты, однотипную (утвердительную или отрицательную) связку, одну и ту же количественную характеристику, но отличаются словесной формой. Например: «Водитель автомобиля совершил аварию». «Причина аварии заключается в действиях водителя автомобиля». Для эквивалентных суждений характерна следующая зависимость: одновременно являются либо истинными, либо ложными!
Слайд 100
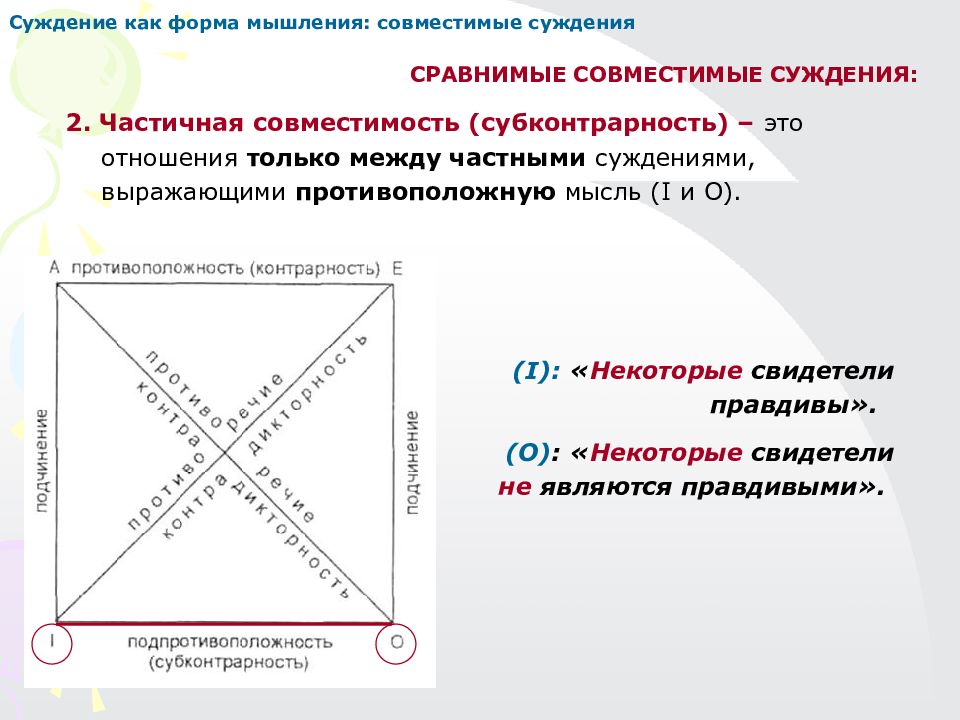
Суждение как форма мышления: совместимые суждения СРАВНИМЫЕ СОВМЕСТИМЫЕ СУЖДЕНИЯ: 2. Частичная совместимость (субконтрарность) – это отношения только между частными суждениями, выражающими противоположную мысль (I и О). ( I ): « Некоторые свидетели правдивы». (О) : « Некоторые свидетели не являются правдивыми».
Слайд 101
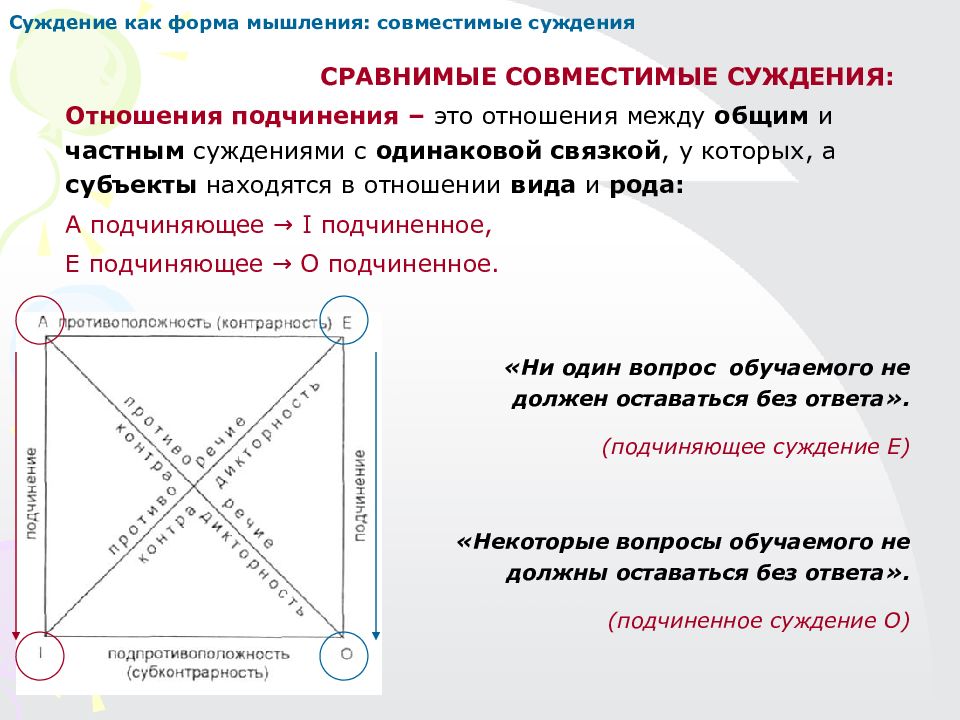
Суждение как форма мышления: совместимые суждения СРАВНИМЫЕ СОВМЕСТИМЫЕ СУЖДЕНИЯ: Отношения подчинения – это отношения между общим и частным суждениями с одинаковой связкой, у которых, а субъекты находятся в отношении вида и рода: А подчиняющее → I подчиненное, Е подчиняющее → О подчиненное. «Ни один вопрос обучаемого не должен оставаться без ответа». (подчиняющее суждение Е) «Некоторые вопросы обучаемого не должны оставаться без ответа». (подчиненное суждение О)
Слайд 102
Суждение как форма мышления : несовместимые суждения СРАВНИМЫЕ НЕСОВМЕСТИМЫЕ СУЖДЕНИЯ: Противоположность (контрарность) характерна для простых суждений, у которых субъекты и предикаты совпадают, а связки различаются. Контрарными могут быть только общие суждения: (А и Е). «Все адвокаты юристы». (А) «Ни один адвокат не является юристом». (Е)
Слайд 103
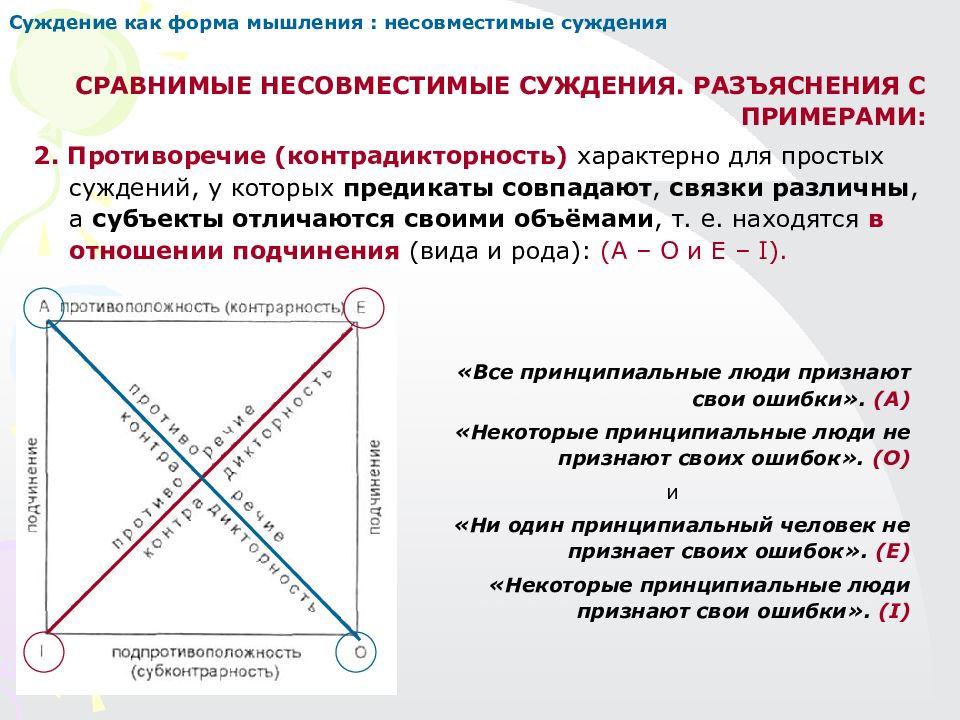
Суждение как форма мышления : несовместимые суждения СРАВНИМЫЕ НЕСОВМЕСТИМЫЕ СУЖДЕНИЯ. РАЗЪЯСНЕНИЯ С ПРИМЕРАМИ: 2. Противоречие (контрадикторность) характерно для простых суждений, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода): (А – О и Е – I). «Все принципиальные люди признают свои ошибки». (А) «Некоторые принципиальные люди не признают своих ошибок». (О) и «Ни один принципиальный человек не признает своих ошибок». (Е) «Некоторые принципиальные люди признают свои ошибки». ( I )
Слайд 104
С помощью логического квадрата можно установить истинность и ложность в отношениях между суждениями. Это есть умозаключения по логическому квадрату. Суждение как форма мышления: умозаключения по логическому квадрату противоположность подпротивоположность подчинение подчинение Противоположные суждения не могут быть одновременно истинными: «Все выпускники умеют быстро читать» (А) – истина. «Ни один выпускник не умеет быстро читать» (Е) – ложь. Но могут быть одновременно ложными: «Все грибы являются съедобными» (А) «Все грибы не являются съедобными» (Е) 1. Отношения противоположности (контрарности) А – Е:
Слайд 105
2. Отношения подчинения А (Е) – I (О): Из истинности общих суждений следует истинность частных, но не наоборот! «Все птицы имеют крылья» (А) и «Некоторые птицы имеют крылья» ( I ) – оба истинны Но из того, что «Некоторые дни недели являются нерабочими» (I), вовсе не следует, что «Все дни недели являются нерабочими» (А) противоположность подпротивоположность подчинение подчинение Из ложности частных суждений следует ложность общих. Но не наоборот! Если ложью является утверждение I : «Некоторые люди могут обходиться без воды и пищи», то тем более ложным будет высказывание А: «Все люди могут обходиться без воды и пищи». Но из ложности общего суждения А «Все грибы съедобны», вовсе не следует ложность частного суждения I «Некоторые грибы съедобны». Суждение как форма мышления: умозаключения по логическому квадрату
Слайд 106
3. Отношения подпротивоположности (частичной совместимости) I – O : Суждения могут быть частично истинны. Но из истинности одного из них нельзя сделать однозначный вывод об истинности другого суждения: « Некоторые люди боятся собак » (I) и « Некоторые люди не боятся собак » (О) - ? Но эти суждения не могут быть одновременно ложными. Е сли ложно I : «Некоторые учащиеся отказываются изучать логику», значит, истинно О: «Некоторые учащиеся не отказываются изучать логику». 4. Отношения противоречия А – O, Е – I : Противоречащие суждения не могут быть одновременно истинными и одновременно ложными. Если истинно: «Некоторые птицы не летают», значит, ложно «Все птицы летают» и наоборот. Если ложно: «Ни один человек не боится смерти», значит, истинно: «Некоторые люди боятся смерти». противоположность подпротивоположность подчинение подчинение Суждение как форма мышления: умозаключения по логическому квадрату
Слайд 107
Если А – истинно, то E - ложно I - истинно O - ложно Если А – ложно, то E - неопределённо I - неопределённо O - истинно Если I – истинно, то A - неопределённо E – ложно O - неопределённо Если I – ложно, то A - ложно E – истинно O – истинно Если Е – истинно, то А - ложно I - ложно O - истинно Если Е – ложно, то А - неопределённо I - истинно O - неопределённо Если О – истинно, то Е - неопределённо А – ложно I – неопределённо Если О – ложно, то Е - ложно А – истинно I – истинно Таблица обоснованных выводов из каждого из четырех видов простых категорических суждений: Суждение как форма мышления: умозаключения по логическому квадрату
Слайд 108
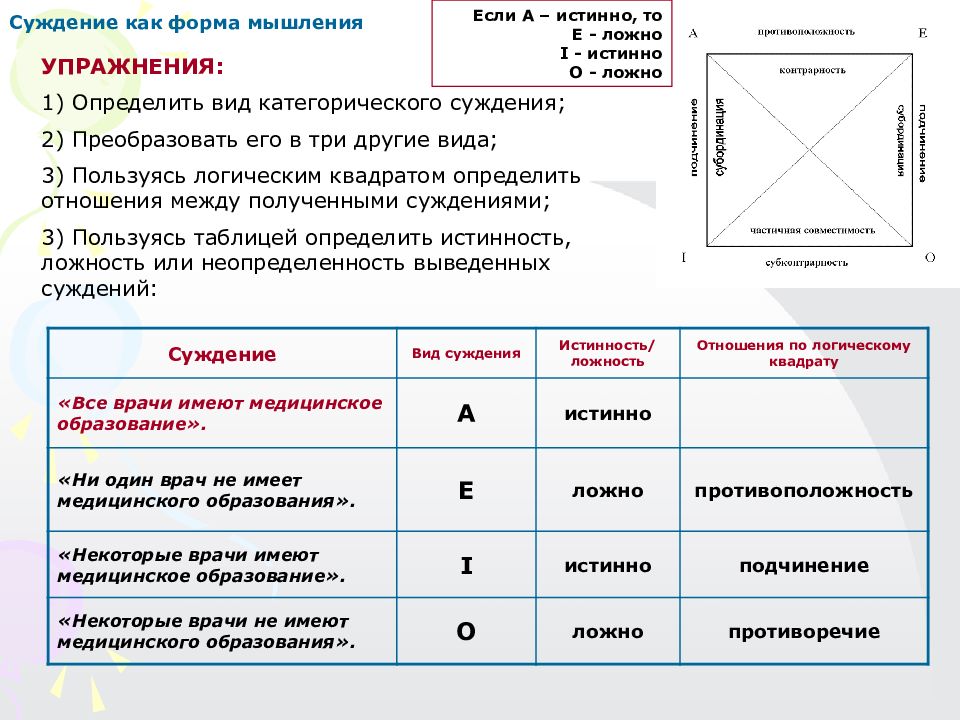
Суждение как форма мышления УПРАЖНЕНИЯ: 1) Определить вид категорического суждения; 2) Преобразовать его в три другие вида; 3) Пользуясь логическим квадратом определить отношения между полученными суждениями; 3) Пользуясь таблицей определить истинность, ложность или неопределенность выведенных суждений: Суждение Вид суждения Истинность/ ложность Отношения по логическому квадрату «Все врачи имеют медицинское образование». А истинно «Ни один врач не имеет медицинского образования». Е ложно противоположность «Некоторые врачи имеют медицинское образование». I истинно подчинение «Некоторые врачи не имеют медицинского образования». О ложно противоречие Если А – истинно, то E - ложно I - истинно O - ложно
Слайд 110
I. Соединительные (конъюнктивные) суждения: два или несколько простых суждений, связанных «и», «а», «но», «также», «однако», «да», точка (.), запятая (,), двоеточие (:), точка с запятой (;), дефис (-). В символической записи: р ^ q ^ г ^... ^ n ПРИМЕР: «Сверкнула молния (1), загремел гром (2), и пошёл дождь (3)». (р ^ q ^ г ) Суждение как форма мышления: сложные суждения
Слайд 111
II. Разделительные (дизъюнктивные) суждения: два или несколько простых суждений, связанных «или», «либо». Нестрогая (слабая) дизъюнкция — члены дизъюнкции не исключают друг друга, а связки «или», «либо» употребляются в соединительно-разделительном значении («и то, и другое вместе»). В символической записи: p v q v r v... v n ПРИМЕР: «Договор купли-продажи может быть заключен в устной или письменной форме». ---------------------------------------------------------------------------------------- 2. Строгая (сильная) дизъюнкция — члены дизъюнкции исключают друг друга, а связки «или», «либо» употребляются в разделительном значении («что-то одно из двух»). В символической записи: p v q v r v... v n ПРИМЕР: «Деяние может быть умышленным или неосторожным». Члены строгой дизъюнкции альтернативны, т.е. не могут быть одновременно истинными. Если деяние совершено умышленно, то его нельзя считать неосторожным, и, наоборот, – деяние, совершенное по неосторожности, не может быть отнесено к умышленным. Суждение как форма мышления: сложные суждения
Слайд 112
III. Условные (импликативные) суждения: образуются из двух или нескольких простых суждений с помощью «если…, то», «постольку…, поскольку», «тогда…, когда», «следовательно», «значит», «так, как…», «потому, что…» и т.п. Они устанавливают причинно-следственную связь. В символической записи: р→q ПРИМЕР: « Если вещество является металлом (1), то оно электропроводно (2) ». В данном случае эти два суждения связаны таким образом, что из первого вытекает второе ( если вещество – металл, то оно обязательно электропроводно ), однако из второго не вытекает первое ( если вещество электропроводно, то это вовсе не означает, что оно является металлом ). Первая часть импликации называется основанием, а вторая – следствием. Из основания вытекает следствие, но из следствия не вытекает основание. Если же существует смысловая независимость основания и следствия, то нет и импликации ( « Если в огороде бузина, то в Киеве дядько» ) ! Суждение как форма мышления: сложные суждения
Слайд 113
IV. Суждения двойной импликации (эквивалентности): образуются из двух или нескольких простых суждений, связанных двойной (прямой и обратной) зависимостью, выражаемой логической связкой «если и только если..., то...», «тогда и только тогда …, когда». В символической записи: р↔q р ≡ q ПРИМЕР: « Если (и только если) число является чётным (1), то оно делится без остатка на «два» (2) ». В данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т. к. две её части являются равнозначными суждениями. Это можно проверить, переставив суждения местами. Суждение как форма мышления: сложные суждения
Слайд 114
V. Отрицательное суждение: сложное суждение, образуемое логическими союзами «неправда, что р », «ложно, что р », «неверно, что р », где р – простое суждение. Смысл отрицания состоит в следующем: если какое-то суждение (р) - истинно, то его отрицание (¬p) будет ложным. В символической записи: ¬р ПРИМЕР: р: «Человек совершил преступление». ¬р: «Человек не совершил преступление». или « Неверно, что человек совершил преступление». Суждение как форма мышления: сложные суждения
Слайд 115
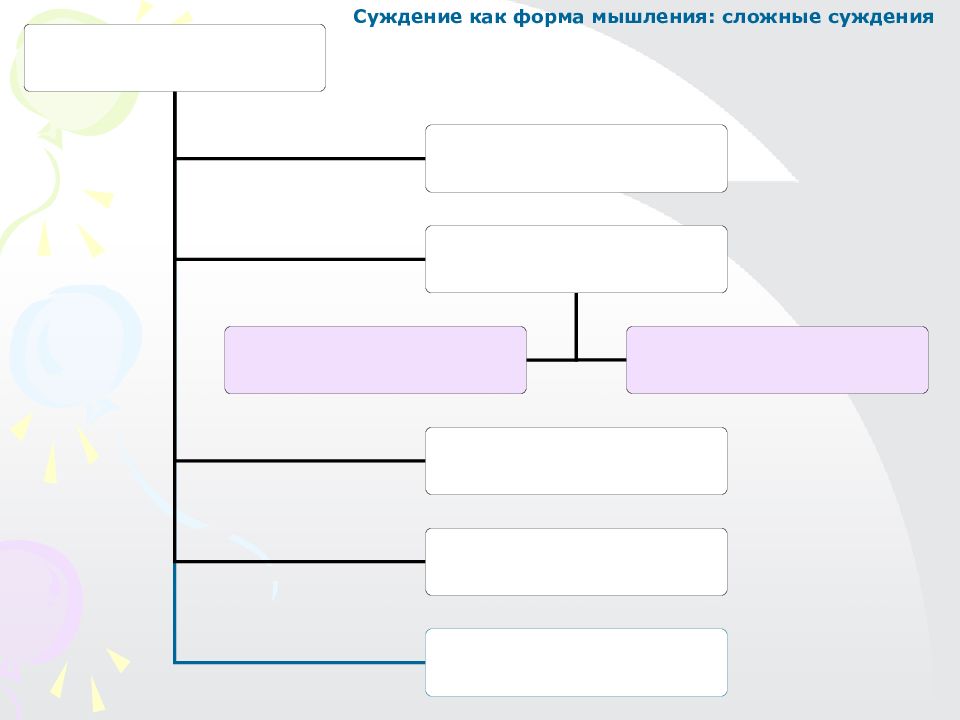
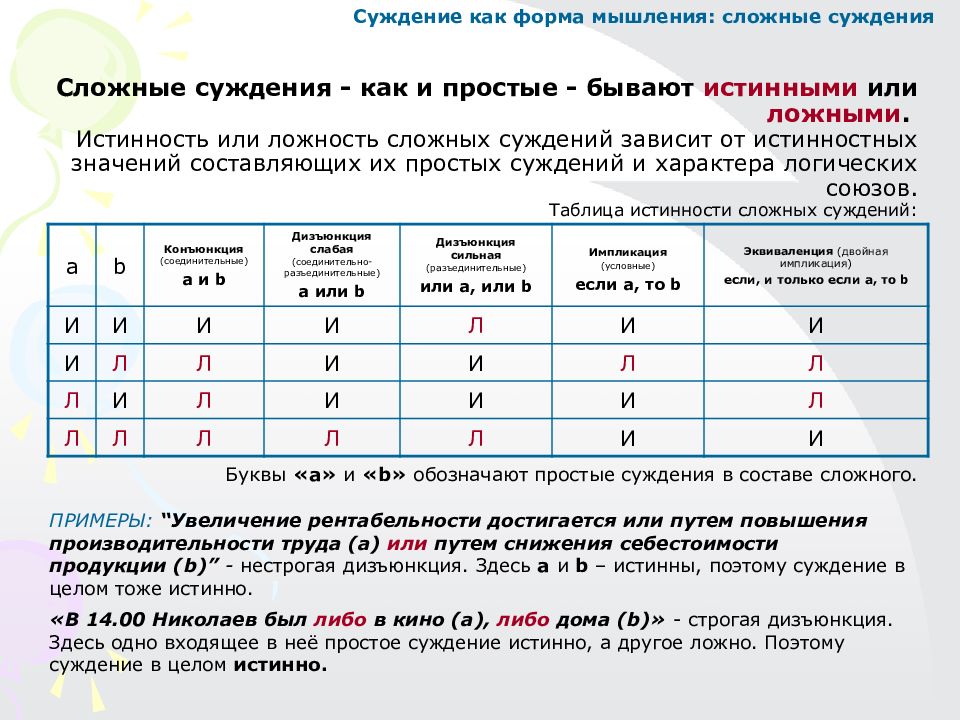
Сложные суждения - как и простые - бывают истинными или ложными. Истинность или ложность сложных суждений зависит от истинностных значений составляющих их простых суждений и характера логических союзов. Таблица истинности сложных суждений: Буквы «а» и « b » обозначают простые суждения в составе сложного. a b Конъюнкция (соединительные) a и b Дизъюнкция слабая (соединительно- разъединительные) a или b Дизъюнкция сильная (разъединительные) или a, или b Импликация (условные) если a, то b Эквиваленция (двойная импликация) если, и только если a, то b И И И И Л И И И Л Л И И Л Л Л И Л И И И Л Л Л Л Л Л И И ПРИМЕРЫ: “Увеличение рентабельности достигается или путем повышения производительности труда (а) или путем снижения себестоимости продукции (b)” - нестрогая дизъюнкция. Здесь a и b – истинны, поэтому суждение в целом тоже истинно. «В 14.00 Николаев был либо в кино (а), либо дома (b)» - строгая дизъюнкция. Здесь одно входящее в неё простое суждение истинно, а другое ложно. Поэтому суждение в целом истинно. Суждение как форма мышления: сложные суждения
Слайд 116
УПРАЖНЕНИЯ: 1. найдите простые суждения, составляющие сложное суждение; 2. определите логические связки и тип сложного суждения ( конъюнкция, дизъюнкция (сильная или слабая), импликация, эквиваленция ); 3. определите истинность или ложность суждений: «Мудрец стыдится своих недостатков, но не стыдится исправлять их». (Конфуций) «Леса на территории нашей страны бывают лиственными или хвойными или смешанными». «Данное животное есть волк или медведь». « Если рак - рыба, то белый медведь не хищник» → « Если бы рак был рыбой, то белый медведь не был бы хищником». « Если работник хорошо работает, то у него хорошая зарплата» При ложности основания и следствия: «Если работник работает плохо, то у него плохая зарплата» (« Если бы работник хорошо работал, то у него была бы хорошая зарплата»). «Треугольники имеют равные углы тогда и только тогда, когда и стороны их равны». Суждение как форма мышления: сложные суждения
Слайд 117
Умозаключение УМОЗАКЛЮЧЕНИЕ – третья форма абстрактного мышления. Его логическая сущность состоит в движении мысли от анализа имеющегося знания к синтезу нового знания, т.е. в выведении нового знания из суждений, истинность которых установлена. На стадии умозаключения о вещах можно рассуждать, не обращаясь к ним самим. Достаточно иметь о них несколько верных высказываний. В этом состоит сущность теоретического мышления.
Слайд 118
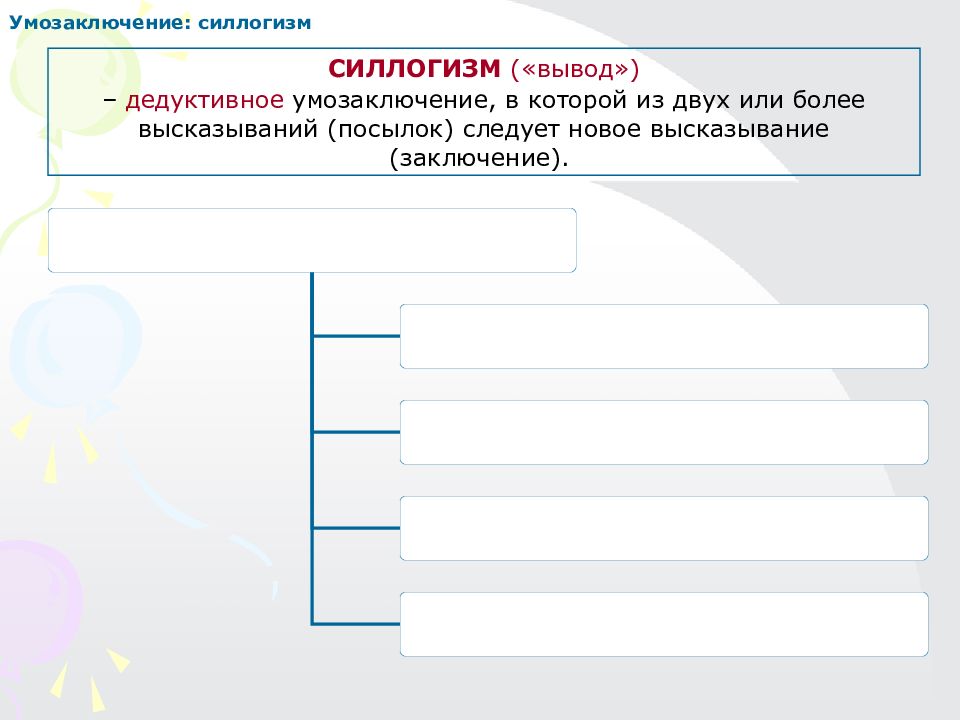
Умозаключение Что надо знать об умозаключениях? Умозаключения бывают непосредственные (из одной посылки) и опосредованные (из нескольких посылок) Непосредственные умозаключения можно 1)превращать, 2)обращать, 3)противопоставлять предикату и 4)выводить «по логическому квадрату» Опосредованные суждения бывают индуктивные, дедуктивные и по аналогии Силлогизм как форма дедуктивного умозаключения бывает простой категорический, разделительный, условно- категорический, эквивалентно-категорический и др. Простой категорический силлогизм имеет 4 фигуры и 19 правильных модусов Существуют общие правила простого категорического силлогизма (3 правила терминов и 4 правила посылок) и специальные правила фигур (по 2 для каждой фигуры) Простой силлогизм имеет сокращенные формы: энтимема, эпихейрема, сорит
Слайд 119
Умозаключение I. ПОСЫЛКИ – исходные суждения, из которых делается вывод. Их может быть одна и более. 1. Посылки должны быть истинными суждениями. Если хотя бы одна из посылок ложна, то и вывод ложен: Все птицы – это млекопитающие животные. Все воробьи – это птицы. Все воробьи – это млекопитающие животные. Здесь ложность первой посылки приводит к ложному выводу, несмотря на то, что вторая посылка является истинной. 2. Посылки должны быть связаны между собой. Если посылки между собой не связаны, то вывод из них сделать невозможно: Все планеты – это небесные тела. Все сосны являются деревьями. ??? II. ЗАКЛЮЧЕНИЕ (вывод) – полученное новое суждение (знание) с помощью логических правил. Структура умозаключения:
Слайд 120
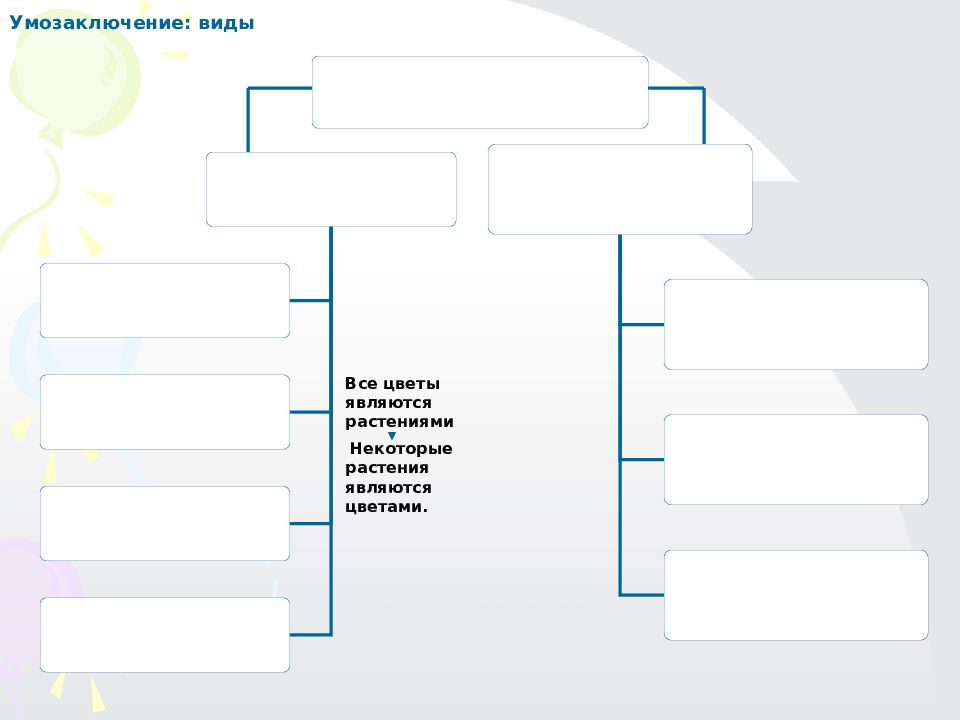
Умозаключение: виды Все цветы являются растениями Некоторые растения являются цветами.
Слайд 121
Умозаключение: опосредованные умозаключения ИНДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ (индукция) – процесс логического вывода на основе перехода от частного положения к общему. Выводами индукции являются общие суждения обо всех объектах какого-либо класса. Полная индукция: Неполная индукция: Общее заключение обо всех элементах множества делается на основании рассмотрения каждого из них. Дает достоверное знание, т.е. она гарантирует истинность заключения при истинности посылок. Схема полной индукции: S’ есть Р S’’ есть Р ... Sn есть Р S’, S’’… Sn исчерпывают множество S Все S есть Р Пример: Старший сын в семье Ивановых, Петя, ходит в школу. Средний сын в семье Ивановых, Кирилл, ходит в школу. Их младшая сестра Катя ходит в школу. Петя, Кирилл и Катя – все дети в семье Ивановых. Следовательно, все дети семьи Ивановых посещают школу. Выводом является общее суждение о множестве предметов, получаемое на основании знания только некоторых предметов, принадлежащих данному множеству. Схема неполной индукции: S’ есть Р S’’ есть Р ... Sn есть Р S’, S’’… Sn часть множества S Вероятно, все S есть Р
Слайд 122
НЕПОЛНАЯ ИНДУКЦИЯ относится 1) к бесконечным, открытым множествам, а также 2) к конечным, но практически не перечислимым в силу большого числа их элементов. Именно с такими множествами обычно имеет дело наука. Неполная индукция даёт вероятное знание. Посылки здесь лишь подтверждают заключение и подводят к некоторому предположению. !Но при этом из истинных посылок может получиться ложное заключение: Пример 1. Известная история с цветом лебедей. Дело в том, что до XVII века в Европе, Азии и Америке встречались только белые лебеди. На основе этих наблюдений было сформировано индуктивное обобщение: «Все лебеди белые». Однако в 1606 году в открытой в то время Австралии были обнаружены черные лебеди, т.е. контрпример, опровергающий истинность данного индуктивного вывода. Пример 2. До некоторых пор наблюдаемые факты приводили к обобщению: «Все тела при нагревании расширяются». Оказалось, однако, что вода при нагревании от 0 до 4 ° С, наоборот, сжимается. Исключения составили также чугун и висмут. Умозаключение: опосредованные умозаключения
Слайд 123
УМОЗАКЛЮЧЕНИЕ ПО АНАЛОГИИ (аналогия) – это умозаключение, в котором на основе сходства предметов в одних признаках делается вывод об их сходстве и в других признаках. Аналогия представляет собой переход к знанию той же степени общности, то есть от единичных суждений к единичным, от частных - к частным, от общих - к общим. Пример: Планета Земля расположена в Солнечной системе, на ней есть атмосфера, вода и жизнь. Планета Марс расположена в Солнечной системе, на ней есть атмосфера и вода. Вероятно, на Марсе есть жизнь. Умозаключение: опосредованные умозаключения Заключения аналогии не являются достоверно истинными при истинности посылок, а только вероятно истинными. Оно не может служить доказательством, оно всегда требует дополнительной проверки. Эту способность необходимо учитывать в любой деятельности. Но степень вероятности этих умозаключения может быть значительно повышена, если для сравнения берутся возможно более существенные признаки предметов, в возможно большем их количестве, при возможно более глубоком изучении существующих между ними взаимосвязей.
Слайд 124
ДЕДУКТИВНОЕ УМОЗАКЛЮЧЕНИЕ (дедукция) – это умозаключения, в которых из общего правила делается вывод для частного случая Например: Все звёзды излучают энергию. Солнце – это звезда. Солнце излучает энергию. Мог бы из двух данных посылок вытекать иной вывод, кроме того, который из них вытекает? Не мог! Вытекающий вывод – единственно возможный в этом случае. Э З С В дедукции рассуждение идёт от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы всегда истинны, необходимы. Умозаключение: опосредованные умозаключения
Слайд 125
Умозаключение: силлогизм СИЛЛОГИЗМ («вывод») – дедуктивное умозаключение, в которой из двух или более высказываний (посылок) следует новое высказывание (заключение).
Слайд 126
Умозаключение Простой категорический силлогизм – это вид силлогизма, в котором заключение и обе посылки являются простыми категорическими суждениями. Структура категорического силлогизма: Б ó льший термин – Р – это предикат заключения Меньший термин – S – субъект заключения Средний термин – M – понятие, которое входит в обе посылки и не входит в заключение Бóльшая посылка – посылка, содержащая б ó льший термин Р Меньшая посылка – посылка, содержащая меньший термин S Заключение обычно помещается после слов «значит», «следовательно» или перед словами «потому что», «ибо», «так как», «ведь». Например: Все граждане РФ (М) имеют право на образование (Р). Иванов ( S ) – гражданин РФ (М). Следовательно, Иванов ( S ) имеет право на образование (Р). Умозаключение: простой категорический силлогизм
Слайд 127
Умозаключение Фигуры простого категорического силлогизма Простой категорический силлогизм имеет свои разновидности, которые называются фигурами силлогизма. Они различаются по положению среднего термина (М) в посылках. Умозаключение: простой категорический силлогизм Чтобы определить фигуру ПКС, надо: Проверить, где находится бóльшая посылка. Если она расположена на втором месте, то ее нужно передвинуть на первое место, а меньшую посылку на второе: Некоторые лошади ( S ) – зебры (М) Все зебры (М) – полосатые (Р) Некоторые лошади ( S ) – полосатые (Р) Все зебры (М) – полосатые (Р) Некоторые лошади ( S ) – зебры (М) Некоторые лошади ( S ) – полосатые (Р) 2. В посылках соединить термины от любого крайнего, через средние (М) к другому крайнему: М Р S M __________ S Р
Слайд 128
Умозаключение Простой категорический силлогизм имеет четыре фигуры: Все газы (М) – это химические элементы (Р). Гелий (S) – это газ (М). __________________ Гелий (S) – это химический элемент (Р) Первая фигура: средний термин занимает место субъекта в большей посылке и место предиката в меньшей посылке: Вторая фигура: средний термин занимает место предиката в обеих посылках: Все рыбы ( Р ) дышат жабрами ( М ). Все киты (S) не дышат жабрами (М). ___________________ Все киты (S) не рыбы (Р) М Р S Р М S Третья фигура: средний термин занимает место субъекта в обеих посылках: Все тигры (М) – это млекопитающие (Р). Все тигры (М) – это хищники (S). ___________________ Некоторые хищники (S) – это млекопитающие (Р). S Р М Четвёртая фигура: средний термин занимает место предиката в большей и место субъекта в меньшей посылке: Все квадраты (Р) – это прямоугольники (М). Все прямоугольники (М) – это не треугольники (S). _________________ Все треугольники (S) – это не квадраты (Р). М Р S Умозаключение: простой категорический силлогизм
Слайд 129
Умозаключение Назначение третьей фигуры – доказательство исключений из общего правила и необоснованности тех или иных обобщений. Назначение четвёртой фигуры – обоснование умозаключений в тех случаях, когда «связь идей» обратна «связи вещей» (например, обоснование целесообразности). Назначение второй фигуры – отвержение ложного подчинения, в том числе обоснование неправомерности подведения данного случая под данное правило. Назначение первой фигуры – обоснование подчинения, в том числе правомерности подведения данного случая под данное правило. Фигуры силлогизма Назначение фигур S P M P S M S P P M S M S P M P M S S P P M M S Умозаключение: простой категорический силлогизм
Слайд 130
Умозаключение Модусы категорического силлогизма: это разновидности силлогизма, отличающиеся друг от друга количественной и качественной характеристиками входящих в них посылок и заключения ( обозначаются тремя заглавными буквами тех суждений, из которых построено силлогизм ). В четырех фигурах силлогизма максимальное число комбинаций равно 64. Однако правильных модусов всего 19 : Умозаключение: простой категорический силлогизм Фигуры Фигура 1 Фигура 2 Фигура 3 Фигура 4 Модусы AAA – Barbara EAE – Cesare AAI – Darapti AAI – Bramantip EAE – Cellarent AEE – Camestres IAI – Disamis AEE – Camenes AII - Darii EIO - Festino AII - Datisi IAI - Dimaris EIO – Ferioque AOO – Baroko EAO – Felapton EAO – Fesapo OAO – B о kardo EIO – Fresison EIO – Ferison
Слайд 131
Умозаключение Модусы первой фигуры F E R IO : E: Ни одно М не есть Р I: Некоторые S есть М O: Некоторые S не есть Р P - смертные P - полосатость M - зебры S - лошади M - растения M - люди S - Сократ M - деревья S - берёза P – способность летать S – формы жизни P – способность говорить Умозаключение: простой категорический силлогизм B A RB A R A : А: Все М есть Р А: Все S есть М А: Все S есть Р C E L A R E NT : E: Ни одно М не есть Р A: Все S есть М E: Ни одно S не есть Р D A R II : А: Все М есть Р I: Некоторые S есть М I: Некоторые S есть Р Все зебры (+) – полосатые (-) Некоторые лошади (-) – зебры (+) Некоторые лошади (-) – полосатые (-) Все люди (+) смертны (-) Сократ (+) – человек (-) Сократ (+) смертен (-) Ни одно дерево (+) не летает (+) Все берёзы (+) – деревья (-) Ни одна берёза (+) не летает (+) Ни одно растение (+) не говорит (+) Некоторые формы жизни (-) – растения (+) Некоторые формы жизни (-) не говорят (-)
Слайд 132
Умозаключение Модусы второй фигуры C E S A R E : Е: Ни одно Р не есть М А: Все S есть М Е: Ни одно S не есть Р C A M E STR E S : A: Все Р есть М E: Ни одно S не есть М E: Ни одно S не есть Р B A R O K O : А: Все Р есть М О: Некоторые S не есть М О: Некоторые S не есть Р P - рыба M - китайцы M - греки P - греки S - поэты M - рыба M - птица S - галка S - галка P - щука P - афиняне S - поэты Умозаключение: простой категорический силлогизм Ни одна рыба (+) не есть птица (+) Все галки (+) – птицы (-) Ни одна галка (+) не есть рыба (+) Ни один грек (+) не является китайцем (+) Некоторые поэты (-) – китайцы (-) Некоторые поэты (-) не являются греками (+) Все щуки (+) – рыбы (-) Ни одна галка (+) не есть рыба (+) Ни одна галка (+) не есть щука (+) F E ST I N O : Е: Ни одно Р не есть М I : Некоторые S есть М O : Некоторые S не есть Р Все афиняне (+) – греки (-) Некоторые поэты (-) не являются греками (+) Некоторые поэты (-) – не афиняне (+)
Слайд 133
Модусы третьей фигуры: D A R A PT I F E L A PT O N D I S A M I S B O C A RD O D A T I S I F E R I S O N Умозаключение S – живущие в воде P - млекопитающие P - греки S - люди M - киты M - поэты P - птицы S - белые M - гуси P - камни S - цветы M - розы P - поэты S - люди M - греки P - слоны S - белые M - гуси Умозаключение: простой категорический силлогизм А: Все М есть Р А: Все М есть S _____ I : Некоторые S есть Р Все киты (+) есть млекопитающие (-) Все киты (+) живут в воде (-) Некоторые живущие в воде (-) – млекопитающие (-) I : Некоторые М есть Р А: Все М есть S I : Некоторые S есть Р Некоторые поэты (-) – греки (-) Все поэты (+) – люди (-) Некоторые люди (-) – греки (-) А: Все М есть Р I: Некоторые М есть S I : Некоторые S есть Р Все гуси (+) – птицы (-) Некоторые гуси (-) – белые (-) Некоторые белые (-) – птицы (-) Е: Все М (+) не есть Р (+) А: Все М (+) есть S (-) О: Некоторые S (-) не есть Р (+) Е: Все М (+) не есть Р (+) I : Некоторые М (-) есть S (-) О: Некоторые S (-) не есть Р (+) О: Некоторые М (-) не есть Р (+) А: Все М (+) есть S (-) О: Некоторые S (-) не есть Р (+)
Слайд 134
Умозаключение Модусы четвёртой фигуры BR A M A NT I P C A M E N E S D I M A R I S F E S A P O FR E S I S O N S - смертные M - люди P - греки S - цветы M - розы P - алые S - медведи M - люди P - греки S - крылатые M - птицы P - осы S - поэты M - греки P - турки Умозаключение: простой категорический силлогизм А: Все Р (+) есть М (-) А: Все М (+) есть S (-) I : Некоторые S (-) есть Р (-) I : Некоторые Р (-) есть М (-) А: Все М (+) есть S (-) I : Некоторые S (-) есть Р (-) А: Все Р (+) есть М (-) Е: Все М (+) не есть S (+) Е: Все S (+) не есть Р (+) Е: Все Р (+) не есть М (+) А: Все М (+) есть S (-) О: Некоторые S (-) не есть Р (+) Е: Все Р (+) не есть М (+) I : Некоторые М (-) есть S (-) О: Некоторые S (-) не есть Р (-)
Слайд 135
Умозаключение Общие правила категорического силлогизма Из истинных посылок всегда можно получить истинное заключение. Его истинность обусловлена правилами силлогизма. Три из них относятся к терминам, четыре – к посылкам. Правила терминов: Правило трёх терминов: в силлогизме должно быть три термина – не больше и не меньше. Примеры нарушения этого правила: а) Наличие четырех терминов, а значит – невозможность вывода: Все люди (1) красноречивы (2). Иванов (3) – предприниматель (4). ? б) «Учетверение терминов» – ошибочное отождествление среднего термина в обеих посылках ( разные понятия принимаются за одно ) : Движение (М) вечно (Р). Хождение в институт (S) – движение (M). Хождение в институт (S) вечно (P). Здесь «движение» трактуется в разном смысле – философском и обыденном. Умозаключение: простой категорический силлогизм
Слайд 136
Умозаключение Правила терминов: Правило среднего термина: средний термин должен быть распределён хотя бы в одной из посылок. Для этого он должен быть или субъектом общего суждения, или предикатом отрицательного суждения. Если же средний термин взят не в полном объеме в обеих посылках, то выполнить роль связующего звена он не сможет, и получить точный вывод будет невозможно: А Все натуралисты (Р+) наблюдательны (М-). А Иванов ( S+ ) наблюдателен (М-). А Иванов (S+) – натуралист (Р-). Посылки, и вывод у нас – общеутвердительные суждения типа А. В общеутвердительных суждениях предикат всегда не распределен (кроме случаев равнозначности терминов). В данном случает средний термин М дважды выполняет функции предиката. Таким образом, он не распределен, и, следовательно, однозначного вывода о том, что Иванов натуралист, мы сделать не можем. Умозаключение: простой категорический силлогизм
Слайд 137
Умозаключение Правила терминов: Правило крайних терминов: термин, не распределённый в посылке, не может быть распределен в заключении. Если термин в посылке не распределен, то, следовательно, речь идет о части элементов класса, но если в заключении термин распределен, то, следовательно, вывод переносится на весь класс – происходит «незаконное расширение термина»: А Все металлы (М+) электропроводны (Р-). А Все металлы ( М+) имеют вес ( S -). А Все имеющие вес (S+) электропроводны (Р-). Мы видим, что субъект меньшей посылки выполняет функцию предиката, и, следовательно, в общеутвердительном суждении он не распределен. Но в заключении термин «имеющий вес» выполняет функцию субъекта, и в общеутвердительном суждении он распределен. Следовательно, на основании имеющихся посылок делать вывод о том, что «все имеющие вес электропроводны», неверно. Умозаключение: простой категорический силлогизм
Слайд 138
Умозаключение Общие правила категорического силлогизма Правила посылок: 1. Из двух отрицательных суждений нельзя сделать никакого заключения. Хотя бы одна из них должна быть утвердительным суждением. Бухгалтеры не менеджеры Продавцы не бухгалтеры ? 2. Из двух частных посылок определенного вывода сделать нельзя. Хотя бы одна из посылок должна быть общим суждением. Некоторые учащиеся – студенты Некоторые студенты – спортсмены ? 3. Если одна из посылок отрицательна, то и вывод будет отрицательным. Все коммерческие организации извлекают прибыль Эта организация не извлекает прибыль Эта организация не является коммерческой 4. Если одна из посылок частная, то и заключение должно быть частным. Все коммерческие организации извлекают прибыль Некоторые организации являются коммерческими Некоторые организации извлекают прибыль Умозаключение: простой категорический силлогизм
Слайд 139
Умозаключение Умозаключение: простой категорический силлогизм СПЕЦИАЛЬНЫЕ ПРАВИЛА ФИГУР Правила первой фигуры: 1. Меньшая посылка должна быть утвердительной ( A, I ); 2. Большая посылка должна быть общей (А, Е). Правила второй фигуры: 1. Одна из посылок должна быть отрицательной (Е, 0); 2. Большая посылка должна быть общей (А, Е). Правила третьей фигуры: 1. Меньшая посылка должна быть утвердительной (А, I); 2. Заключение должно быть частным (I, О). Правила четвертой фигуры: 1. Если большая посылка утвердительная (А, I), то меньшая посылка должна быть общей (А, Е); 2. Если одна из посылок отрицательная(Е, О), то большая посылка должна быть общей (А, Е).
Слайд 140
Умозаключение Простой категорический силлогизм можно сократить. Тогда у нас получится простой сокращённый силлогизм, который называется энтимема. Умозаключение: сокращенные формы силлогизма
Слайд 141
Умозаключение 1. ЭНТИМЕМА – это простой сокращенный силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что из любого силлогизма можно вывести три энтимемы. Например: Все металлы электропроводны. Железо – это металл. Железо электропроводно. Из данного силлогизма следуют три энтимемы: 1. « Железо электропроводно, так как оно является металлом». - пропущена б ó льшая посылка 2. « Железо электропроводно, потому что все металлы электропроводны». - пропущена меньшая посылка 3. « Все металлы электропроводны, а железо – это металл». - пропущен вывод Умозаключение: сокращенные формы силлогизма
Слайд 142
Умозаключение ЭПИХЕЙРЕМА – это сложносокращенный силлогизм, посылками которого являются энтимемы. Содержит лишь общеутвердительные высказывания. Все А суть С, так как А суть В Все D суть А, так как D суть Е Все D суть С Пример: Ложь (А) заслуживает презрения (С), т.к. она (А) безнравственна (В). ( 1-я энтимема) Лесть ( D ) есть ложь (А), т.к. она (D) есть умышленное извращение истины (Е). ( 2-я энтимема) Лесть (D) заслуживает презрения (С). Данная эпихейрема состоит из двух энтимем с пропущенными б ó льшими посылками : «Всё безнравственное заслуживает презрения». «Умышленное извращение истины есть ложь». Умозаключение: сокращенные формы силлогизма
Слайд 143
Умозаключение СЛОЖНЫЙ СИЛЛОГИЗМ: силлогизм, котором одна или обе посылки являются сложными суждениями. Умозаключение: сложные силлогизмы
Слайд 144
Умозаключение: сложные силлогизмы Сложный силлогизм, в котором в котором хотя бы одна из посылок есть суждение разделительное, называется разделительным. Разделительно-категорический силлогизм, в котором первая посылка представляет собой строго разделительное суждение с перечислением всех членов деления, а вторая посылка – простое категорическое суждение Чисто разделительный силлогизм, обе посылки и вывод которого являются строго разделительными суждениями: Четырехугольники (S ) суть равносторонние (Р) или они неравносторонние (Р1). Равносторонние четырехугольники (Р) есть квадраты (Р2) или ромбы (Р3) Четырехугольники (S ) есть неравносторонние (Р1), или квадраты (Р2), или ромбы (Р3). Схема: S есть Р или S есть Р1 Р есть Р2 или Р3 S есть Р1 или Р2 или Р3 Утверждающе-отрицающий модус: первая посылка представляет собой строгую дизъюнкцию нескольких вариантов, вторая утверждает один из них, а вывод отрицает все остальные ( таким образом, рассуждение движется от утверждения к отрицанию ): Суждение может быть либо утвердительным (А), либо отрицательным (В). Это суждение утвердительное (А). Это суждение не является отрицательным (не-В). Схема: ((А v В) ^А) → ¬ В 2. Отрицающе-утверждающий модус: первая посылка представляет собой строгую дизъюнкцию нескольких вариантов чего-либо, вторая отрицает все данные варианты, кроме одного, а вывод утверждает один оставшийся вариант ( таким образом, рассуждение движется от отрицания к утверждению ): Люди бывают европеоидами (А), или монголоидами (В), или негроидами (С). Этот человек не монголоид и не негроид_______________________ Этот человек является европеоидом. Схема: ((А v В v С) ¬В ^ С) → А
Слайд 145
Умозаключение: сложные силлогизмы Сложные силлогизмы, которые содержат в себе условные (импликативные) суждения называются условными. Условно-категорический силлогизм, в котором б ó льшая посылка является суждением условным, а меньшая – категорическим Утверждающий модус: первая посылка представляет собой импликацию основания и следствия; вторая посылка является утверждением основания; а в выводе утверждается следствие: Если вещество (А) – металл (В), то оно электропроводно (С ). Данное вещество – это металл ( D )._________ Данное вещество (С) электропроводно (D). Схема: Если А есть B, то С есть D A есть В_______________ C есть D 2. Отрицающий модус: первая посылка представляет собой импликацию основания и следствия; вторая посылка является отрицанием следствия; а в выводе отрицается основание: Если иск (А) предъявлен недееспособным лицом (В), то суд (С) оставляет иск без рассмотрения ( D ). Суд (С) не оставил иск без рассмотрения (не- D )).__ Неверно, что иск (А) предъявлен недееспособным лицом (В). Схема: Если A есть B, то C есть D C не есть D__________ А не есть В Чисто условный силлогизм, обе посылки которого являются условными суждениями: Если через проводник пропустить ток (а), то он нагреется ( b ) Если проводник нагреется ( b ), то он расширится ( c ) __________________ Если через проводник пропустить ток (a), то проводник расширится (с). Схема: a → b b → c a → с
Слайд 146
Умозаключение: сложные условно-разделительные силлогизмы Силлогизмы, в которых вывод делается из трех и более посылок, где две и более посылок – условные высказывания, а одна посылка является разделительным суждением, называются условно-разделительными. В зависимости от числа условных высказываний (альтернатив), различают: дилеммы ( два условных высказывания) трилеммы ( три условных высказывания) n-леммы ( n условных высказываний) При выводе заключения лемматического силлогизма утверждается необходимость выбора только одной альтернативы.
Слайд 147
Умозаключение: условно-разделительные силлогизмы Основания различны, а следствие в условных суждениях одно и то же. Поскольку в разделительной посылке простой конструктивной дилеммы утверждаются основания условных суждений, то в заключении утверждается их общее следствие. Схема: А → В, С → В, А v С. Сл-но, В Пример: Если у больного болит зуб (А), то рекомендуется принять обезболивающее (В). Если болит голова (С), то тоже рекомендуется принять обезболивающее (В). В данном случае болит либо зуб (А), либо голова (С). Больному рекомендуется обезболивающее (В). Следствия условных суждений различны. Поскольку в разделительной посылке сложной конструктивной дилеммы утверждаются основания условных суждений, то в заключении утверждаются их следствия. Схема: А → В, С → D, А v С. Сл-но, В v D Пример: Если я лягу вовремя спать (А), то не подготовлюсь к экзамену (В). Если же я буду заниматься ночью (С), то приду на экзамен с головной болью (D). Но мне остается только или ложиться спать (А) или заниматься ночью (С). Сл-но, я приду на экзамен не подготовленным (В ) или с головной болью (D). Основания условных суждений одни и те же, а следствия различны. Поскольку в разделительной посылке простой деструктивной дилеммы отрицаются следствия общего основания, то в заключении отрицается основание. Схема: А → В, А → С, ¬ В v ¬С. Сл-но, ¬А Пример: Если человек болен тифом (А), то на 4 день болезни у него будет температура (В) и появится сыпь (С). У больного нет высокой температуры (¬В), либо нет сыпи (¬С). Значит, человек не болен тифом (¬А). Основания условных суждений различны. Поскольку разделительная посылка сложной деструктивной дилеммы отрицает оба следствия условных суждений, то заключение является отрицанием обоих оснований. Схема: А → В, С → D, ¬В v ¬D. Сл-но, ¬А v ¬С Пример: Если студент знает материал (А), то сможет привести доказательства (В). Если студент понимает (С), то сможет решить задачу ( D ). Студент либо не может привести доказательства (¬В), либо не может решить задачу (¬D). Значит, он либо не знает (¬А ), либо не понимает материал (¬С). Как основания, так и следствия условных суждений различны. При этом разделительная посылка является дизъюнкцией утверждения основания одного из условных суждений и отрицания следствия другого из условных суждений, а заключение – дизъюнкция утверждения основания и следствия этих разных условных суждений. Схема: А → В, С → D, А v ¬D. В v ¬С Пример: Если данный человек работает (А), то он получает зарплату (В). Если данный человек учится (С), то получает стипендию ( D ). Данный человек или работает (А), или не получает стипендию (¬D). Сл-но, данный человек или получает зарплату (В), или не учится (¬С).
Слайд 148
Умозаключение: полисиллогизм ПОЛИСИЛЛОГИЗМ представляет собой несколько соединенных между собой последовательной связью простых силлогизмов. При этом вывод, следствие одного из простых силлогизмов становится посылкой для последующего. Таким образом, получается своеобразная «цепь» силлогизмов.
Слайд 149
Умозаключение: полисиллогизм ПОЛИСИЛЛОГИЗМЫ Прогрессивный полисиллогизм: его заключение становится б ó льшей посылкой следующего силлогизма. Мышление выстраивается в плавно развивающуюся последовательную линию, возможную, когда предикат заключения, выходя из первой посылки, остается неизменным в процессе всего рассуждения: Все позвоночные имеют красную кровь. Все млекопитающие суть позвоночные. Все млекопитающие имеют красную кровь. Все млекопитающие имеют красную кровь. Все хищные суть млекопитающие. Все хищные имеют красную кровь. Все хищные имеют красную кровь. Тигры суть хищные животные. Тигры имеют красную кровь. Регрессивный полисиллогизм: его заключение становится меньшей посылкой за счет смены предиката, происходящей, когда субъект первого силлогизма, выходя из второй посылки, в процессе всего рассуждения остается неизменным, в то время как, предикат заключения вводится лишь в последней посылке: Позвоночные суть животные. Тигры суть позвоночные. Тигры суть животные. Животные суть организмы. Тигры суть животные. Тигры суть организмы. Организмы стареют. Тигры суть организмы. Тигры стареют.
Слайд 150
Умозаключение Умозаключение: сокращенные формы силлогизма Прогрессивный и регрессивный полисиллогизмы в мышлении чаще всего применяются в сокращенной форме – в виде соритов.
Слайд 151
Умозаключение Умозаключение: сокращенные формы силлогизма Существует два вида соритов: прогрессивный и регрессивный получается из прогрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и больших посылок последующих. Начинается с посылки, содержащей предикат заключения, и заканчивается посылкой, содержащей субъект заключения. Пример: Все продукты, содержащие витамины (А), полезны (В). Фрукты (С) - продукты, содержащие витамины (А). Бананы (D) фрукты (С). Бананы (D) полезны(В). Схема прогрессивного сорита: Все А суть В Все С суть А Все D суть С Все D суть В получается из регрессивного полисиллогизма путем выбрасывания заключений просиллогизмов и меньших посылок эписиллогизмов. В просиллогизме меняем местами посылки. Начинается с посылки, содержащей субъект заключения, и кончается посылкой, содержащей предикат заключения. Пример: Все розы (А) - цветы (В). Все цветы (В) - растения (С). Все растения (С) дышат (D). Все розы (А) дышат (D). Схема регрессивного сорита: Все А суть В Все В суть С Все С суть D Все А суть D
Слайд 152
Законы логики ЗАКОНЫ ЛОГИКИ (или логические законы) – это общее название множества законов, образующих основу логически правильного мышления. Цель законов логики — сформулировать основания правил и рекомендаций, следуя которым можно достичь истины. Поэтому законы мышления не являются законами в том смысле, в котором указанный термин используется для описаний явлений природы. Законы логики представляют собой законы правильного мышления человека о мире, а не законы самого мира.
Слайд 153
Законы логики: закон тождества I. ЗАКОН ТОЖДЕСТВА был сформулирован Аристотелем в трактате «Метафизика» следующим образом: «…Иметь не одно значение – значит не иметь ни одного значения; если же у слов нет (определённых) значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности – и с самим собой; ибо невозможно ничего мыслить, если не мыслить (каждый раз) что-нибудь одно». Любая мысль обязательно должна быть тождественна самой себе. Это означает, что нельзя отождествлять различные мысли, как нельзя и различать мысли, совпадающие по своему содержанию. Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность, уклоняться от темы и т. п. Символическая запись этого закона: А = А (А суть А)
Слайд 154
Законы логики: закон тождества При нарушении закона тождества возможны следующие логические ошибки: Амфиболия («бросок в обе стороны»): это двусмысленность целого выражения, которое может иметь более одного толкования. В речи амфиболию можно преодолеть с помощью интонации, пауз, логического ударения, а на письме – тире. Например: «Казнить нельзя помиловать». «Продавцы преследовали воровку с утюгом» 2. Эквивокация («ровноголосие»): использование одного и того же слова в разных значениях в одном рассуждении (напр., при употреблении омонимов – слов, схожих в звуковом отношении, но различных по значению: «коса», «наряд», «горн»… ) Например: «Ученики прослушали объяснение учителя». 3. Логомахия («спор о словах»): когда в процессе общения участники коммуникации по-разному понимают термины, что ведет к конфликту между собеседниками. Например: Иногда в ходе судебных заседаний или на предварительном следствии вкладывается различное содержание в понятия «взятка» и «подарок», чтобы в выводах изменить необходимым образом суть поступка конкретного человека.
Слайд 155
Законы логики: закон тождества ® С помощью нарушения закона тождества можно создать какой-нибудь комический эффект. Например, Николай Васильевич Гоголь в поэме «Мёртвые души», описывая помещика Ноздрёва, говорит, что тот был « историческим человеком », потому что где бы он ни появлялся, с ним обязательно случалась какая-нибудь « история ». ® С помощью нарушения этого закона создаются и многие анекдоты. Например: – Я сломал руку в двух местах. – Больше не попадай в эти места.
Слайд 156
Законы логики: закон непротиворечия II. ЗАКОН НЕПРОТИВОРЕЧИЯ: запрещает одновременную истинность двух несовместимых (противоречащих и противоположных) суждений, одно из которых нечто утверждает, а другое то же самое отрицает об одном и том же предмете, в одно и то же время и в одном и том же отношении. ¬ ( а Λ ¬ а ): неверно, что А и не-А. Например: Противоречие есть: «Все люди говорят на своем родном языке» (А) и «Некоторые люди не говорят на своем родном языке» (О) (по логическому квадрату: Если А – истинно, то O - ложно) Проверяем по логическому квадрату: Если А истинно, то E, О – ложно. Если I истинно, то Е – ложно. Если Е истинно, то А, I – ложно. Если О истинно, то А – ложно.
Слайд 157
Законы логики: закон непротиворечия Другой вариант: « Эта бумага белая » и « Эта бумага черная ». Могут быть одновременно ложными, т.к. эта бумага может быть серой, красной, синей … Здесь дело в том, что предикатами являются не противоречащие понятия (то же слово с частицей «не»), а противоположные. То же самое: «Эта вода горячая» и «Эта вода холодная» («Эта вода тёплая») «Эта речка глубокая» и «Эта речка мелкая» («Эта речка средней глубины» или «Эта речка где-то глубокая, а где-то мелкая».) Однако закон непротиворечия допускает одновременную ложность двух противоположных суждений! По логическому квадрату: если А (Е) – ложно, то E (А) – неопределённо, т.е. допускается его ложность. «Все грибы являются съедобными» (А) и «Все грибы не являются съедобными» (Е). Истинным же является третье суждение: «Некоторые грибы являются съедобными, а некоторые не являются».
Слайд 158
Законы логики: закон непротиворечия когда одно и то же утверждается и сразу же отрицается ( напр., последующая фраза отрицает предыдущую в речи, или последующее предложение отрицает предыдущее в тексте ) между противоречащими друг другу суждениями находится значительный интервал в речи или в тексте ( напр., в начале своего выступления лектор может выдвинуть одну идею, а в конце высказать мысль, противоречащую ей) одна мысль непосредственно противоречит другой ( напр., «Молодая девушка преклонных лет с коротким ёжиком тёмных вьющихся белокурых волос изящной походкой гимнастки, прихрамывая, вышла на сцену». ) противоречие вытекает из контекста: оно не сформулировано, но подразумевается ( напр., «Эта выполненная на бумаге рукопись создана в Древней Руси в XI в.» в XI в. на Руси ещё не было бумаги) Нарушение этого закона приводит к противоречиям:
Слайд 159
Законы логики: закон противоречия Например, высказывание А.П.Чехова: «В детстве у меня не было детства», – кажется противоречивым, т. к. оно вроде бы подразумевает одновременную истинность двух суждений, одно из которых отрицает другое: «У меня было детство», «У меня не было детства». Но здесь термин «детство» употребляется в различных значениях: детство как определённый возраст; детство как состояние души, пора счастья и безмятежности. Поэтому никакого противоречия здесь нет, т.е. закон противоречия не нарушен! МНИМЫЕ ПРОТИВОРЕЧИЯ Мнимое противоречие можно использовать как художественный приём: Названия известных литературных произведений: «Живой труп» (Л. Н. Толстой), «Мещанин во дворянстве» (Ж. Мольер), «Барышня-крестьянка» (А. С. Пушкин), «Горячий снег» (Ю. В. Бондарев) и др. Заголовки газетной или журнальной статьи: «Знакомые незнакомцы», «Древняя новизна», «Необходимая случайность» и т. п.
Слайд 160
Одновременную ложность двух суждений без нарушения закона противоречия мы часто используем в повседневной жизни, когда, характеризуя кого-то или что-то, строим стереотипные обороты типа: «Они не молодые, но и не старые», «Это не полезно, но и не вредно», «Он не богат, однако и не беден», «Данная вещь стоит не дорого, но и не дёшево», «Этот поступок не является плохим, но в то же время его нельзя назвать хорошим». Законы логики: закон противоречия
Слайд 161
Необходимо различать формально-логические и диалектические противоречия. Формально-логические противоречия – это противоречия путаного, непоследовательного, неправильного рассуждения, затрудняющие познание окружающей действительности. Диалектические противоречия – наличие в объекте противоположных, взаимоисключающих сторон, свойств, моментов, тенденций, которые, в то же время, предполагают друг друга и в составе данного объекта существуют лишь во взаимной связи, в единстве. Это источник и движущая сила развития как объективного мира, так и самого человеческого мышления. Законы логики: закон непротиворечия
Слайд 162
Законы логики: закон исключенного третьего III. ЗАКОН ИСКЛЮЧЕННОГО ТРЕТЬЕГО: из двух противоречащих суждений одно истинно, другое ложно, а третьего не дано. Противоречащими называются такие два суждения, в одном из которых о предмете нечто утверждается, а в другом то же самое о том же самом предмете отрицается (в одно и то же время и в одном и том же отношении). Соблюдение данного закона означает невозможность отвечать на один и тот же вопрос в одно и то же время и в одном и том же смысле «да» и «нет», а также невозможность поисков некоего среднего ответа между ними. ( A v ¬ A : A или не-A )
Слайд 163
Законы логики: закон исключенного третьего «Все S есть Р» (А) и «Некоторые S не есть Р» (О) : « Все учащиеся группы МЭ-16 сдали сессию на отлично» и « Некоторые учащиеся группы МЭ-16 не сдали сессию на отлично». «Ни одно S не есть Р» (Е) и «Некоторые S есть Р» ( I ) : « Ни один житель нашего дома не пользуется Интернетом» и « Некоторые жители нашего дома пользуются Интернетом». Отношения между противоречащими суждениями (А – О, Е – I) можно проверить по логическому квадрату :
Слайд 164
Законы логики: закон исключенного третьего !!! Закон исключенного третьего может быть применим к противоположным по логическому квадрату суждениям (А - Е) в случаях, когда противоположность, выражаемая общим высказыванием, является альтернативной, т. е. отрицанием другой: «Все S есть Р» (А) и «Ни одно S не есть Р» (Е) : Если истинно, что «Все науки имеют свой предмет исследования», то ложно, что «Ни одна наука не имеет своего предмета исследования». (и наоборот)
Слайд 165
Законы логики: закон исключенного третьего Чтобы увидеть, используется ли в каком-то высказывании закон исключенного третьего, надо мысленно представить себе альтернативу (строгую дизъюнкцию) с помощью разделительного союза «или» : (A v ¬ A: A или не-A) «Сократ смертен или Сократ бессмертен». Здесь ясно, что закон исключенного третьего отсекает все иные варианты, при которых Сократ и не смертен и не бессмертен.
Слайд 166
Законы логики: закон достаточного основания IV. ЗАКОН ДОСТАТОЧНОГО ОСНОВАНИЯ был сформулирован немецким ученым (философом, логиком, математиком) – Готфридом Вильгельмом Лейбницем: «Если нет никакого основания, почему произошло именно так, а не по-другому, значит, это не может казаться истиной или справедливым утверждением». Например, если прокурор вынес обвинительный приговор подсудимому, он должен предоставить все необходимые доказательства, то есть обосновать обвинение. Если у него нет аргументов, как бы он ни хотел обвинить человека, ничего не получится. Проще: Любая мысль должна быть обоснована или аргументирована вескими доказательствами. Если есть b, то есть и его основание а.
Слайд 167
Законы логики: закон достаточного основания Примеры нарушения этого закона: «Этот человек не болеет, у него ведь нет кашля». «Гражданин Иванов не мог совершить преступление, ведь он прекрасный работник, заботливый отец и хороший семьянин». «Студент покраснел, — следовательно, он виноват». «Эта комната светлая, так как в ней три окна». «Категорически отвергаю, будто я мелкий хулиган, так как я человек с высшим образованием» «Перчатку потеряешь — к несчастью. Зеркало разбить — к беде».
Слайд 168
Законы логики: закон достаточного основания На законе достаточного основания базируется важный юридический принцип презумпции невиновности, который предписывает считать человека невиновным, даже если он даёт показания против себя, до тех пор, пока его вина не будет достоверно доказана какими-либо фактами. Закон достаточного основания, требуя от любого рассуждения доказательной силы, предостерегает нас от поспешных выводов, голословных утверждений, дешёвых сенсаций, слухов, сплетен и небылиц. Запрещая принимать что-либо только на веру, этот закон выступает надёжной преградой для любого интеллектуального мошенничества. Не случайно он является одним из главных принципов науки.
Слайд 169
Когда логические законы нарушается непроизвольно, по незнанию, тогда возникает паралогизмы – логические ошибки, которые можно характеризовать как ненамеренную потерю или подмену предмета мысли. Логические ошибки: паралогизмы Это может быть результатом низкой культуры ума, неумением правильно пользоваться имеющимися знаниями, отсутствием навыков системного мышления и т.д., а также неумения контролировать свои эмоции в ходе рассуждения или доказательства (дискуссии, спора и т.д.)
Слайд 170
Но иногда эти законы нарушаются преднамеренно (например, с идеологическими или узко практицистскими задачами), чтобы запутать собеседника и доказать ему заведомо какую-нибудь ложную мысль. Тогда появляются не просто ошибки, а софизмы – внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов. Логические ошибки: софизмы СОФИСТИКА (от греч. σοφία – мастерство, знание, мудрость) – философское течение, существовавшее в Древней Греции с сер. V до 1-й пол. IV в. до н.э. и абсолютизировавшее относительность знаний. Так, Протагор, самый знаменитый софист древности, учил, что человек есть «мера всех вещей», и следовательно, нет объективной истины. Софисты выработали такие приемы «мнимого» доказательства, с помощью которых брались доказывать любые нелепости, даже противоположные мысли и побеждать в споре любой ценой
Слайд 171
Логические ошибки: софистические приемы 1 СОФИСТИЧЕСКИЙ ПРИЕМ ЕГО ХАРАКТЕРИСТИКА ПРИМЕРЫ Амфиболия («бросок в обе стороны») Двусмысленность целого выражения «В чугун печальный сторож бьет». ( М.Ю. Лермонтов) Эквивокация Подмена понятия «То, чего ты не потерял, ты имеешь. Ты не потерял рогов. Следовательно, ты имеешь рога». «Ложный аргумент», или софизм ложного основания Мнимое упрощение или искажение одной из посылок «Если в системе образования упор следует делать на связь с практикой, то мировоззренческим и теоретическим компонентам образования можно не уделять особого внимания». Предвосхищение основания В качестве аргументов используются недоказанные, как правило, произвольно взятые положения : ссылаются на слухи, на ходячие мнения, высказанные кем-то предположения или даже на собственный вымысел, выдавая их за аргументы, якобы обосновывающие основной тезис. Обычно подобные лже-аргументы сопровождаются фразами: «Как абсолютно всем известно…», «Кто же будет спорить с тем, что…», «Аксиомой, не требующей доказательств, является то, что…», «Само собой разумеется, что…», «Каждому известно, что…», дабы рассеять возможные сомнения у простого слушателя. Тавтология Тождественность аргумента тезису «Это не может не быть правдой, потому что это истина » Ошибка объединения Сведение свойства системы к совокупности свойств всех или отдельных составляющих ее частей «Все слоны состоят из атомов, Все атомы лёгкие. Следовательно, все слоны лёгкие». Ошибка разделения Присваивание частям свойства составляемого ими целого «Люди обладают сознанием. Люди состоят из атомов. Следовательно, атомы обладают сознанием». Смещение фокуса При обосновании тезиса внимание обращено на несущественные признаки, в то время как принципиальные аспекты остаются вне рассмотрения. «Тогда некоторые из фарисеев говорили: не от Бога Этот Человек, потому что не хранит субботы. Другие говорили: как может человек грешный творить такие чудеса? И была между ними распря» (Ин 9:16). Персонификация Приписывание абстрактному понятию конкретных личностных свойств « Премудрость возглашает на улице, на площадях возвышает голос свой, в главных местах собраний проповедует, при входах в городские ворота говорит речь свою» (Притч 1:20-21)
Слайд 172
Логические ошибки: софистические приемы 2 СОФИСТИЧЕСКИЙ ПРИЕМ ЕГО ХАРАКТЕРИСТИКА ПРИМЕРЫ «Порочный круг» в доказательстве Для доказательства тезиса используются аргументы, истинность которых можно доказать только предположив истинность тезиса. - Господь Бог ежедневно разговаривает с нашим раввином. - Откуда ты знаешь? - Раввин сам сказал! - А он не обманывает? - Разве может обманывать человек, с которым каждый день разговаривает Бог? Мнимое следование В ходе доказательства человек делает вид, что все выводы делаются им строго по необходимости, тогда как на самом деле либо вывод здесь возможен только по вероятности, либо аргумент и вывод здесь вообще логически никак не связаны друг с другом. В русском языке это впечатление создают такие слова как «следовательно», «таким образом», «значит», «итак», и т.п. Использование принципиально неопровержимых утверждений Использовании в качестве аргумента утверждения, которое принципиально невозможно опровергнуть. «Ты сам виноват в ситуации Х. Если ты считаешь, что не виноват, ты просто пытаешься оправдаться». Подмена тезиса (полная или частичная) Начав доказывать некоторый тезис, постепенно в ходе доказательства переходят к доказательству другого положения, сходного с тезисом, но имеющего совершенно иное значение. «И сказали все: итак, Ты Сын Божий? Он отвечал им: вы говорите, что Я. Они же сказали: какое еще нужно нам свидетельство? ибо мы сами слышали из уст Его» (Лк 22:70,71). Ложная дихотомия (ложная дилемма) Поставить оппонента в затруднительное положение, а потом навязать ему заведомо предвзятый выбор, который позволит выйти из этого положения «Либо вы введёте полный запрет на порнографию, либо вы хотите, чтобы ваши дети её смотрели». «После этого – значит, вследствие этого» (частный случай «мнимого следования») Причинно-следственная связь отождествляется с хронологической, временной «Серийный убийца с детства увлекался почтовыми марками, следовательно, филателия превращает людей в безжалостных убийц».
Слайд 173
Логические ошибки: софистические приемы 3 СОФИСТИЧЕСКИЙ ПРИЕМ ЕГО ХАРАКТЕРИСТИКА ПРИМЕРЫ Обобщение Мысленный переход от отдельных фактов или событий к их отождествлению «Политик обманул нас, говоря о расходах. Следовательно, все политики – жулики». Ложная альтернатива Предполагает допущение, что существуют только две взаимоисключающие возможности, в то время как возможностей либо больше двух, либо они не являются взаимоисключающими. Например, в теледебатах оппоненты занимают диаметрально противоположные позиции, каждая из которых хороша по-своему. Это заставляет зрителей предполагать, что истинна только одна из них. «Не следует» Заключение не вытекает из посылок «А. прекрасный юрист, значит, он может быть президентом». Поспешное или чрезмерное обобщение Индуктивное обобщение не опирается на достаточно показательную выборку примеров (фактов ) Из перечисления 5–6 депутатов Думы, которые выступают с публичными неэтичными заявлениями, вовсе не вытекает мысль, что все депутаты — невоспитанные люди. Составной вопрос Вопрос составлен таким образом, что предполагает определенный вывод вне зависимости от того, ответите ли Вы «да» или «нет». В состав основного вопроса включен другой, ответ на который предполагается уже полученным. «Значит Вы уже больше не принимаете участия в деятельности преступных вооруженных формирований и террористических организаций?» Подмена признака Уместность аналогии всегда ограничена как тем признаком, по которому она проводится, так и степенью подобия по этому признаку. Шекспировский Гамлет, уподобляя облака различным животным, имел в виду их очертания, а не действительные признаки животных. Противоречия в основаниях Для доказательства тезиса используются аргументы, противоречащие друг другу. «В детстве у меня не было детства».
Слайд 174
Логические ошибки: неправомерные риторические приемы апелляция к личности оппонента, а не к его доводам переход на личности: «Вы глупы и некрасивы, поэтому ваш тезис неверен». поиск обстоятельств, якобы заставляющих оппонента выдвигать данный тезис: «Вы говорите так, потому что хотите произвести впечатление на публику, поэтому ваш тезис неверен». указание на то, что оппонент сам поступает вопреки своим доводам: «Вы сами курите, поэтому ваши доводы о вреде курения неверны». нахождение легко критикуемого единомышленника: «Гитлер тоже был вегетарианцем!». апелляция к большинству: «Все вокруг считают так, следовательно, это верно». апелляция к авторитету: «Это мнение принадлежит авторитету, разве вы его не уважаете?». Используется и в обратную сторону: «Это мнение высказывал Гитлер, Вы что, согласны с Гитлером?» апелляция к традиции: «Так считается с древнейших времен, потому это верно». апелляция к милосердию: «Если вы не согласитесь с моим мнением, то разрушите мне всю жизнь». апелляция к незнанию; отсутствие доказательств чего-то, считается доказательством обратного: «Привидения существуют, так как никто не доказал, что их нет». «аргумент к тошноте», повторение тезиса (возможно, разными людьми) до тех пор, пока противная сторона не потеряет интерес к его оспариванию. апелляция к страху, аргумент с позиции силы: «Вас могут наказать, если вы не согласитесь с моим мнением». выдача желаемого за действительное: «Я хочу, чтобы так было, значит, так и есть». «соломенное чучело»: «Теория эволюции смешна, это абсурд, что рыба эволюционирует в птицу.»
Слайд 175
Люди постоянно общаются друг с другом, обмениваются мыслями, сведениями, идеями, знаниями, информацией и т. д. Коммуникация по определению диалогична, т.е. предполагает, как минимум, двух участников. Процесс диалогического общения является одной из важнейших сфер, где используется логика. Диалог (греч. Διάλογος – «разговор двух») – обмен высказываниями между двумя и более людьми, совместный процесс мыслительной деятельности Логические основы аргументации
Слайд 176
Логические основы аргументации: диалог, дискуссия, спор Мирный обмен мнениями, предполагает сходные взгляды ее участников на обсуждаемый предмет, и, как правило, доброжелательное или терпимое отношение её участников друг к другу Обсуждение проблемы для нахождения путей ее решения или установления консенсуса, а также утверждения истины Противостояние разнообразных мнений, точек зрения, где каждый стремится к победе только своей позиции
Слайд 177
Логические основы аргументации: виды и правила вопроса В ходе диалога мы обычно задаем вопросы и отвечаем на них. Вопрос – это логическая форма, в которой выражено требование уточнить или дать новую информацию на основе уже имеющейся и которая направлена на получение ответа в виде некоторого суждения. Словесно вопрос принимает форму вопросительного предложения (кроме риторических - «Какой же он студент?»; побудительных – «Может быть уступите место пожилому человеку?» и некоторых др. )
Слайд 178
То, что известно; некоторая исходная информация (выраженная, как правило, каким-нибудь суждением) То, что требует выяснения Например: « Когда была создана теория электромагнитного поля?» Логические основы аргументации: виды и правила вопроса
Слайд 179
Направлены на получение нового знания. Это вопросы, на которые пока нет ответов. Например: «Как возникла Вселенная?» Имеют своей целью передачу уже имеющихся знаний (информации). Например: «Какова температура плавления свинца?» Логические основы аргументации: виды и правила вопроса
Слайд 180
включают в себя вопросительные слова «кто», «что», «где», «когда», «почему», «как» и т. п., указывающие направление поиска ответов и, соответственно, категорию объектов, свойств или явлений, в которой следует искать нужные ответы. Например: «Кто создал периодическую систему химических элементов?» В этих вопросах ответ как бы уже заложен в виде готового суждения, которое надо лишь подтвердить или отвергнуть. Например: « Полезно ли изучение математики ?» Логические основы аргументации: виды и правила вопроса
Слайд 181
Другие критерии классификации вопросов: и др. Логические основы аргументации: виды и правила вопроса
Слайд 182
Пример скрытого вопроса: они выражаются лишь своими предпосылками, а требование устранить неизвестное восстанавливается после осмысления предпосылок вопроса. Например, прочитав текст: «Все больше рядовых граждан заполняют налоговые декларации », мы не обнаружим здесь явно сформулированных вопросов. Однако при осмыслении прочитанного может возникнуть желание спросить: «Что такое налоговая декларация?», «Зачем ее необходимо заполнять?», «Как правильно ее заполнять?» Текст, таким образом, содержит скрытые вопросы. Логические основы аргументации: виды и правила вопроса
Слайд 183
Базисная часть вопроса должна быть истинным суждением. В этом случае вопрос считается логически корректным. Если же основная часть вопроса представляет собой ложное суждение, то вопрос следует признать логически некорректным. Подобные вопросы не требуют ответа и подлежат отвержению. Логически корректный вопрос: «Когда было предпринято первое кругосветное путешествие?» (его основная часть выражена истинным суждением : «В истории человечества имело место первое кругосветное путешествие». ) Логически некорректный вопрос: «В каком году знаменитый английский учёный Исаак Ньютон закончил работу над общей теорией относительности?» (его основная часть представлена ложным суждением : «Автором общей теории относительности является знаменитый английский учёный Исаак Ньютон». ) Логические основы аргументации: виды и правила вопроса
Слайд 184
Если спрашивающий знает о ложности базиса вопроса и задает вопрос с целью провокации, запутывая своего оппонента, то такой вопрос называют провокационным, а его постановка есть софистический прием. (Посредством провокационных вопросов иногда ставят в затруднительное положение логически не подготовленных людей). Так, в ходе дискуссии о гуманизации уголовных наказаний противникам отмены смертной казни задавался вопрос: «Вы лично сейчас, здесь готовы привести в исполнение смертный приговор?». Вопрос является провокационным. Его предпосылка: «Если человек не исключает смертной казни в качестве высшей меры наказания, то он должен быть готов привести такой приговор в исполнение в любое время, в любом месте». Эта предпосылка является ложной. Логические основы аргументации: виды и правила вопроса
Слайд 185
Правила постановки простых и сложных вопросов: 1. Корректность: вопросы должны быть правильно поставленными, корректными. Провокационные и неопределенные вопросы недопустимы. 2. Предусмотрение альтернативности ответа («да» или «нет») на уточняющие вопросы: например, «Признает ли Петров себя виновным в предъявленном ему обвинении?» Ответы: «Да, признает» или «Нет, не признает». 3. Краткость и ясность формулировки вопроса: длинные, запутанные, нечеткие вопросы затрудняют их понимание и ответ на них. 4. Простота вопроса: если вопрос сложный, то его лучше разбить на несколько простых. Например, «Были ли братья Иван и Константин Аксаковы издателями газеты «День»?» Этот сложный вопрос следует разбить на два простых, так как ответы будут различными – «да», «нет» (ибо Иван Аксаков был издателем газеты «День», а Константин - нет, он был только автором многочисленных статей в ней). 5. В сложных разделительных вопросах необходимо перечислять все альтернативы: например, «К какому виду электростанций относится данная электростанция: теплоэлектростанция (ее разновидность - атомная электростанция), гидроэлектростанция, солнечная или геотермальная?» Здесь нет пятой альтернативы - ветровая электростанция. 6. Необходимость отличать обычный вопрос от риторического: например, «Кто из вас не любит А. С. Пушкина?» Риторические вопросы являются суждениями, так как в них содержится утверждение или отрицание, обычные же вопросы суждениями не являются. 7. В вопросе не следует употреблять слова с двойным и более значениями. Логические основы аргументации: виды и правила вопроса
Слайд 186
Логические основы аргументации: ответ Ответ - это суждение, дающее информацию, которая запрашивается в вопросе.
Слайд 187
По области поиска ответы делятся на прямые и косвенные: а) прямые – берутся непосредственно из области поиска ответа, при формулировке их не прибегают к дополнительным сведениям и рассуждениям: Например, «Когда состоялись ХХII Олимпийские игры?» – «ХХII Олимпийские игры состоялись в 1980 году». «Является ли кит рыбой?» – «Нет, кит не является рыбой». б) косвенные – ответы, получаемые из более широкой области, нежели область поиска ответа: Например, «Когда состоялись XXII Олимпийские игры?» – «ХХII Олимпийские игры состоялись за два года до ХII Чемпионата мира по футболу». Логические основы аргументации: ответ
Слайд 188
По грамматической форме ответы могут быть краткими и развёрнутыми: а) краткие – односложные утвердительные или отрицательные ответы "да" или "нет". Краткие ответы дают на простые вопросы: "Ты будешь ужинать?" – "Да". б) развёрнутые – ответы, в которых повторяются все элементы вопроса: "Был ли Р. Декарт философом и математиком?" – "Да, Р. Декарт был философом и математиком". Логические основы аргументации: ответ
Слайд 189
По объёму представленной в ответе информации ответы делятся на полные и неполные: а) полный – ответ, включающий информацию по всем элементам сложного вопроса: "Кем, когда и в связи с чем было написано стихотворение "На смерть поэта"?" – "Стихотворение "На смерть поэта" было написано М.Ю. Лермонтовым в 1837 г. в связи с трагической гибелью А.С. Пушкина". б) неполный – ответ, включающий информацию по отдельным (не всем) элементам вопроса: "Кем, когда и в связи с чем было написано стихотворение "На смерть поэта"?" – "Стихотворение "На смерть поэта" написано М.Ю. Лермонтовым в связи с трагической гибелью А.С. Пушкина". Ответ не указывает времени написания стихотворения. Логические основы аргументации: ответ
Слайд 190
По содержанию и структуре соответствия поставленному вопросу: а) релевантный (ответ по существу): ответ, согласующийся с предпосылкой вопроса. Релевантные ответы устраняют познавательную неопределенность частично или полностью. По этому признаку их делят на слабые и сильные : Вопрос: «Кто является автором работы «Человеческое, слишком человеческое»?» сильный ответ: «Фридрих Ницше»; слабый ответ: «Какой-то немецкий философ». б) нерелевантный (ответ не по существу): не согласуется с предпосылкой вопроса, т.е. является ответом не на заданный вопрос. Такой ответ не устраняет познавательную неопределённость, вызвавшую вопрос. Вопрос: «В каком городе родился А.С. Пушкин?» Нерелевантный ответ: «Пушкин родился в дворянской семье». Логические основы аргументации: ответ
Слайд 191
Требования, которые предъявляются логикой к ответам: - ответ не должен быть нерелевантным (давать другую, не относящуюся к запрашиваемой в вопросе, информацию); - ответ должен быть истинным (правильно отражать действительность); - ответ не должен быть тавтологичным (повторять предпосылку вопроса или общеизвестную информацию); - ответ должен быть исчерпывающим, информационно полным. Логические основы аргументации: ответ
Слайд 192
Логические основы аргументации: виды Аргументация – процедура обоснования утверждений в процессе диалога Логическая аргументация представляет собой особую форму интеллектуальной коммуникации, содержанием которой является поиск способов теоретического обоснования правоты отстаиваемой позиции. Особенность логической аргументации – ее доказательность и убедительность.
Слайд 193
Логические основы аргументации: доказательство ДОКАЗАТЕЛЬСТВО – разновидность аргументации, направленная на подтверждение истинности тезиса логическими доводами Структура логического доказательства: В косвенном доказательстве используются антитезис и другие виды суждений, альтернативные тезису. Тезис — утверждение, истинность которого надо доказать Тезис не должен содержать внутреннего противоречия или двусмысленности Тезис не должен быть метафизическим или абстрактно-всеобщим по своему содержанию Аргументы (основания) — это те истинные суждения, которыми пользуются при доказательстве тезиса Аргументами могут быть: теоретические и эмпирические обобщения (законы науки, теоремы, аксиомы, определения понятий, нормы права и т.п.), а также утверждения о фактах, истинность которых установлена. Аргументы должны быть обоснованы Аргументы не должны противоречить друг другу Аргументы должны быть независимы от тезиса В качестве аргумента при обосновании теоретического положения не может выступать единичный эмпирический факт Эмпирические факты как основания доказательства должны быть воспроизводимы Демонстрация (форма доказательства) — способ логической связи аргументов с тезисом Демонстрация должна быть логически правильной Требования к логическому доказательству:
Слайд 194
Пример. Если бы Теплов совершил убийство, то он был бы на месте преступления в ту ночь, когда оно было совершено. Но в ту ночь Теплов не был на месте преступления, что подтверждено свидетельскими показаниями. Следовательно, он не совершал данного убийства. Пример. Мы предполагаем, что какой-то поступок был совершен либо Майоровым, либо Корнеевым, либо Гладких. Но на основании имеющихся аргументов вынуждены признать, что ни Майоров, ни Корнеев не совершали этого поступка. Исключая соответствующие альтернативы дизъюнкции, получаем заключение: «Поступок совершил Гладких». Логические основы аргументации: доказательство
Слайд 195
ОШИБКИ В ДОКАЗАТЕЛЬСТВЕ: I. Ошибки в отношении аргументов: 1. Содержательная ошибка – попытка обосновать тезис с помощью ложных или произвольных аргументов: несуществующих фактов, событий, слухов и т.п. Аргументы должны быть истинны, проверены, не противоречить друг другу. Часто употребление ложных, недоказанных или непроверенных аргументов сопровождается оборотами: "как известно", "давно установлено", "совершенно очевидно", "никто не станет отрицать" и т.п. Слушателю или читателю как бы оставляется одно: упрекать себя за незнание того, что давно и всем известно. 2. Круг в доказательстве (порочный круг) – справедливость доказываемого положения обосновывается посредством этого же положения, высказанного, возможно, в несколько иной форме. Один из героев Мольера глубокомысленно пояснял, что опиум усыпляет, поскольку обладает снотворным действием, а его снотворная сила проявляется в том, что он усыпляет. 3. Приписывание утверждений – приписывание одной стороной другой утверждений, которые на самом деле другая сторона не делала, но которые, якобы, вытекают из её предыдущих утверждений. 4. Использование принципиально неопровержимых утверждений – использование в качестве аргумента утверждения, которое принципиально невозможно опровергнуть. Логические основы аргументации: доказательство
Слайд 196
ОШИБКИ В ДОКАЗАТЕЛЬСТВЕ: II. Ошибки в отношении тезиса: 1. Тезис нечетко сформулирован. Например, в тезисе «Законы нужно уважать» неясно, о каких законах идет речь: о законах природы, общества или юридических законах. 2. Сужение тезиса Например, тезис «Иванов хорошо знаком с русской литературой» можно сузить до высказывания «Иванов хорошо знаком с современной русской литературой». 3. Расширение тезиса ("Кто доказывает много, тот ничего не доказывает" – старая латинская пословица). Например, когда одна партия возражает против каких-то конкретных реформ, например, по приватизации собственности, то их оппоненты расширяют выдвигаемый тезис и обвиняют своих противников в отказе от реформ вообще. 4. Полная подмена тезиса: умышленное или неумышленное изменение смысла доказываемого тезиса. В результате доказательство относится к одному утверждению, а кажется, что оно относится к другому. Тезис должен оставаться неизменным на протяжении всего хода доказательства или опровержения. Например, на суде адвокат может убедительно доказать, что доводы обвинения не являются обоснованными и поэтому его подзащитный не может считаться виновным. Некоторые люди из этого обычно заключают, что раз виновность не доказана, то подсудимый вообще невиновен. Логические основы аргументации: доказательство
Слайд 197
ОШИБКИ В ДОКАЗАТЕЛЬСТВЕ: III. Ошибки в отношении логической связи («потерянная логическая связь» ) 1. Если хотя бы одна из посылок доказательства неверна, оно теряет силу: С помощью ложной посылки «Только птицы летают» можно вывести ложное заключение, скажем, что майские жуки, поскольку они не птицы, не летают. 2. Умозаключение не опирается на логический закон Неправильным является, например, рассуждение: «Если страна развитая, она имеет многопартийную политическую систему; в Англии многопартийная политическая система; значит, Англия – развитая страна». Заключение является верным, но оно не следует из принятых посылок. Нельзя рассуждать по схеме: "если есть первое, то есть и второе; есть второе; значит, есть первое". Эта схема не представляет собой закона логики и не обеспечивает истинности следствия при истинных посылках. 3. Мнимая логическая связь: Логическая уловка, при которой мнимая, желаемая логическая связь выдаётся за истинную. 4. «После» не значит «вследствие» (или «После этого — значит по причине этого»): логическая уловка, при которой причинно-следственная связь отождествляется с хронологической, временной: «Серийный убийца с детства увлекался почтовыми марками, следовательно, филателия превращает людей в безжалостных убийц». Логические основы аргументации: доказательство
Слайд 198
ОПРОВЕРЖЕНИЕ – логическая операция установления ложности или необоснованности ранее выдвинутого тезиса. Может пониматься и процесс разрушения структуры доказательства и как конечный его результат. Опровержение должно показать, что: неправильно построено само доказательство (аргументы или демонстрация) выдвинутый тезис ложен или не доказан Логические основы аргументации: опровержение
Слайд 199
Структура опровержения: Тезис опровержения – это суждение, которое требуется опровергнуть Аргументы (основания) опровержения – это суждения, с помощью которых опровергается тезис Демонстрация (форма опровержения) – это способ логической связи аргументов и тезиса опровержения Логические основы аргументации: опровержение
Слайд 200
СПОСОБЫ ОПРОВЕРЖЕНИЯ: I. Опровержение тезиса (прямое): Опровержение фактами – самый верный и успешный способ опровержения. В качестве фактов должны быть приведены действительные события, явления, статистические данные, которые противоречат тезису, т. е. опровергаемому суждению. Например, чтобы опровергнуть тезис «На Венере возможна органическая жизнь», достаточно привести такие данные: температура на поверхности Венеры 470-480° С, а давление - 95-97 атмосфер. Эти данные свидетельствуют о том, что жизнь на Венере невозможна. Вполне достаточно показать одного альбиноса, чтобы дать опровержение того, что "альбиносы не существуют". Логические основы аргументации: опровержение
Слайд 201
СПОСОБЫ ОПРОВЕРЖЕНИЯ: I. Опровержение тезиса (косвенное): 1. Опровержение через ложность (или противоречивость) следствий, вытекающих из тезиса: доказывается, что из данного тезиса вытекают следствия, противоречащие истине. Этот прием называется «сведение к абсурду». Поступают так: опровергаемый тезис временно признается истинным, но затем из него выводятся такие следствия, которые противоречат истине. Пример: Из высказывания «Треугольник - это окружность» вытекает как то, что треугольник имеет углы (так как быть треугольником значит иметь три угла), так и то, что у него нет углов (поскольку он окружность); следовательно, верным является не исходное высказывание, а его отрицание «Треугольник не является окружностью». Логические основы аргументации: опровержение
Слайд 202
СПОСОБЫ ОПРОВЕРЖЕНИЯ: I. Опровержение тезиса (косвенное): 2. Опровержение тезиса через доказательство антитезиса: по отношению к опровергаемому тезису (суждению а ) выдвигается противоречащее ему суждение (т. е. не-а ), и суждение не-а (антитезис) доказывается. Если антитезис истинен, то тезис ложен, и третьего не дано по закону исключенного третьего. Например, надо опровергнуть широко распространенный тезис: «Все собаки лают» (суждение А, общеутвердительное). Для суждения А противоречащим будет суждение О - частноотрицательное: «Некоторые собаки не лают». Для доказательства последнего достаточно привести несколько примеров или хотя бы один пример: «Собаки у пигмеев никогда не лают». Итак, доказано суждение О. В силу закона исключенного третьего, если О - истинно, то А - ложно. Следовательно, тезис опровергнут. Логические основы аргументации: опровержение
Слайд 203
СПОСОБЫ ОПРОВЕРЖЕНИЯ: II. Критика аргументов: Подвергаются критике аргументы, которые были выдвинуты оппонентом в обоснование его тезиса. Доказывается ложность или несостоятельность этих аргументов. Ложность аргументов не означает ложности тезиса: тезис может оставаться истинным. Иногда бывает, что тезис истинен, но человек не может подобрать для его доказательства истинные аргументы. Например, случается так, что человек не виновен, но не имеет достаточных аргументов для доказательства этого. На этом строится презумпция невиновности – один из основополагающих принципов уголовного судопроизводства. Основной принцип презумпции невиновности гласит: «Обвиняемый не виновен, пока не доказано обратное». Логические основы аргументации: опровержение
Слайд 204
СПОСОБЫ ОПРОВЕРЖЕНИЯ: III. Критика демонстрации: Этот способ опровержения состоит в том, что показываются ошибки в форме доказательства, т.е. отсутствие логической связи между аргументами и тезисом. Наиболее распространенной ошибкой является та, что истинность опровергаемого тезиса не вытекает, не следует из аргументов, приведенных в подтверждение тезиса. Доказательство может быть неправильно построенным, если нарушено какое-либо правило дедуктивного умозаключения или сделано «поспешное обобщение» или неправильное умозаключение. Но обнаружив ошибки в ходе демонстрации, мы опровергаем ее ход, но не опровергаем сам тезис. Задача же доказательства истинности тезиса лежит на том, кто его выдвинул. Логические основы аргументации: опровержение
Слайд 205
Парадокс (от греч. – «неожиданный, странный»), или логический тупик – это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям. Логические основы аргументации: парадокс Пример – антиномии И.Канта: Мир конечен – мир бесконечен. Каждая сложная субстанция состоит из простых частей – не существует ничего простого. В мире существует свобода – в мире не существует свободы, но существует только свободная (спонтанная) причинность. Существует безусловно необходимая первопричина мира (Бог) – не существует никакой абсолютно необходимой сущности, ни в мире, ни вне мира, как его первопричины. Антиномии возникают не вследствие субъективной ошибки, но связаны с диалектичностью процесса познания. Пример - апория Зенона Элейского «Ахиллес и черепаха»: Мы вполне можем увидеть, как быстроногий Ахиллес догоняет и перегоняет медленно ползущую впереди него черепаху; однако мысленный анализ приводит нас к необычному заключению, что Ахиллес никогда не сможет догнать черепаху, хотя он и движется в 10 раз быстрее нее. Когда он преодолеет расстояние до черепахи, то она за это же время (ведь она тоже движется) пройдет в 10 раз меньше (так как движется в 10 раз медленнее), а именно 1/10 часть того пути, который прошел Ахиллес, и на эту 1/10 часть будет всегда впереди него. Это противоречия между видимым и мыслимым. АНТИНОМИЯ: противоречие в законе, т.е. рассуждение, образуемое двумя высказываниями, каждое из которых приводит к взаимоисключающим выводам, которые нельзя отнести ни к истинным, ни к ложным. АПОРИЯ: вымышленная, логически верная ситуация, которая не может существовать в реальности
Слайд 206
Гипотеза как форма развития знания В процессе познавательной деятельности человек стремится к достижению объективной истин. Но истина не дается в готовом виде. На пути к ней человек строит различного рода догадки, допущения, предположения, объясняющие причины или сущность исследуемого явления. Гипотеза (от греч. hypothesis - основание, предположение) – форма развития человеческих знаний, представляющая собой обоснованное предположение, объясняющее свойства и причины исследуемых явлений. Термин «гипотеза» употребляется в двояком значении: Во-первых, как само предположение, объясняющее исследуемое явление (гипотеза в узком смысле). Во-вторых, как прием мышления в целом, включающий в себя выдвижение предположения, его развитие и доказательство.
Слайд 207
Гипотеза как форма развития знания Гипотеза - универсальная форма развития научных знаний и научного логического мышления. Это значит, что новое (развивающееся) знание всегда возникает первоначально в форме гипотезы, которая объясняет уже открытые явления и предсказывает новые. Так, идея об атомистическом строении мира, которая зародилась в умах Левкиппа и Демокрита за две с лишним тысячи лет до открытия химической атомистики (в XIX в.) была гипотезой. И лишь после длительной ее проверки, подтверждения экспериментами и новых открытий эта гипотеза превратилась в научную теорию.
Слайд 208
Гипотеза как форма развития знания Логическая структура гипотезы: Основание гипотезы – исходные данные (совокупность фактов или обоснованных утверждений, на которых основывается предположение); Форма гипотезы – совокупность умозаключений, которые являются результатом обработки исходных данных и ведут от основания гипотезы к основному предположению; Предположение (гипотеза в узком смысле слова) – логические выводы из фактов и утверждений, выражающих содержание гипотезы; Процедура проверки гипотезы, превращающая предположение в достоверное знание или опровергающая его. Гипотеза – система суждений, понятий и умозаключений разных видов.
Слайд 209
Гипотеза как форма развития знания Этапы построения гипотезы: 1. Предпосылки к построению гипотезы появляются тогда, когда возникает потребность объяснить ряд новых фактов, которые не укладываются в рамки известных ранее научных теорий или других объяснений. 2. Осуществляется синтез фактов и формулируется гипотеза, то есть предположения, которые объясняют данные факты. Причем гипотеза может выдвигаться не одна, а несколько, которые объясняют одно и то же явление по-разному. В этом случае гипотезы называются конкурирующими. При их дальнейшей проверке может оказаться, что все гипотезы, кроме одной, будут опровергнуты. 3. Осуществляется выведение из данной гипотезы всех вытекающих из нее следствий. Всякая хорошо организованная гипотеза должна допускать свою принципиальную проверку на истинность. Основной способ подтверждения и опровержения гипотез заключается в выведение следствий и их верификация (установление истинности) или фальсификация (опровержение). 4. Эмпирическая проверка. 5. Научная теория в отличие от гипотезы представляет собой уже не вероятное, а достоверное знание.
Слайд 210
Гипотеза как форма развития знания Основные черты научной теории: Научная теория - это знание об определенном предмете или строго определенной, органически связанной группе явлений. Объединение знания в теорию определяется ее предметом. Теорию в качестве важнейшего ее признака характеризует объяснение известной совокупности фактов, а не простое их описание, вскрытие закономерностей их функционирования и развития. Теория должна обладать прогностической силой, предсказывать течение процессов. В развитой теории все ее главные положения должны быть объединены общим началом, основанием. Наконец, все входящие в содержание теории положения должны быть обоснованы. НАУЧНАЯ ТЕОРИЯ – это система знаний (концептуальная конструкция), описывающая и объясняющая определенную совокупность явлений, дающая обоснование всех выдвинутых положений и сводящая открытые в данной области законы к единому основанию
Слайд 211
Гипотеза как форма развития знания Структура научной теории: философские основания научной теории – система философских идей и принципов, социокультурных и ценностных факторов, посредством которых обосновываются представления научной картины мира, идеалы и нормы науки и которые служат одним из условий включения научных знаний в культуру соответствующей исторической эпохи; методологические основания теории – категориальный аппарат (фундаментальные понятия), принципы, законы, уравнения, аксиомы и т.п.; логические основания теории (совокупность определенных правил и способов доказательства); категориальный аппарат теории, с помощью которого выражается и излагается ее основное содержание; идеи, в которых органически слиты отражение объективной реальности и постановка практических задач перед людьми.
Последний слайд презентации: ЛОГИКА курс лекций для студентов ЦДО УрГЭУ
Гипотеза как форма развития знания Основные функции научной теории: 1. Синтетическая функция - объединение отдельных достоверных знаний в единую, целостную систему. 2. Объяснительная функция - выявление причинных и иных зависимостей, многообразия связей данного явления, его существенных характеристик, законов его происхождения и развития, и т.п. 3. Методологическая функция - на базе теории формулируются многообразные методы, способы и приемы исследовательской деятельности. 4. Предсказательная - функция предвидения. На основании теоретических представлений о "наличном" состоянии известных явлений делаются выводы о существовании неизвестных ранее фактов, объектов или их свойств, связей между явлениями и т.д. Предсказание о будущем состоянии явлений (в отличие от тех, которые существуют, но пока не выявлены) называют научным предвидением. 5. Практическая функция. Конечное предназначение любой теории - быть воплощенной в практику, быть "руководством к действию" по изменению реальной действительности. Поэтому вполне справедливо утверждение о том, что нет ничего практичнее, чем хорошая теория.