Вихревая линия, вихревая поверхность, вихревая трубка, вихревой жгут, вихрь Интенсивность или напряжение вихря Циркуляция скорости Теорема Стокса, следствие из теоремы Стокса Теоремы Гельмгольца Теорема Био-Савара Вихревые схемы крыла Метод дискретных вихрей 1 Лекция 9 Фролов В.А. Лекции по аэродинамике, 2020
2 Вихревая линия, вихревая поверхность, Определение 1. Вихревой линией называют линию, в каждый момент времени вектор угловой скорости направлен по касательной к ней. (09.1) Рисунок 09.1 – Вихревая линия Определение 2. Если через каждую точку некоторой линии L, не являющейся вихревой линией, провести вихревые линии, то их совокупность образует вихревую поверхность. Рисунок 09.2 – Вихревая поверхность за крылом Фролов В.А. Лекции по аэродинамике, 2020
3 Дифференциальное уравнение вихревой линии Фролов В.А. Лекции по аэродинамике, 2020 Условие коллинеарности двух векторов (09.2) (09.3) (09.4) Другое условие коллинеарности двух векторов
4 Вихревая трубка, вихревой жгут, вихрь, интенсивность вихря Определение 3. Если линия L является замкнутым контуром, то вихревая поверхность превращается в вихревую трубку. Определение 4. Вихревая трубка вместе с заключённым в ней вращающимся воздухом образует вихревой жгут, который обычно для краткости называют вихрем. Определение 5. Интенсивностью или напряжением вихря J называют удвоенный поток вектора угловой скорости через поперечное сечение вихря S (09.5) Определение 6. Циркуляцией скорости Г по замкнутому контуру L называют криволинейный интеграл вида (09.6) Рисунок 9.3 – Определение циркуляции Фролов В.А. Лекции по аэродинамике, 2020
5 Теорема Стокса Теорема Стокса : циркуляция скорости по замкнутому контуру L равна суммарной интенсивности вихрей, пересекающих произвольную поверхность S, опирающийся на этот контур Рисунок 9.4 – Вихри, пересекающие поверхность S, опирающуюся на контур L ( 09. 7 ) Для одного вихря ( 09. 8 ) Фролов В.А. Лекции по аэродинамике, 2020
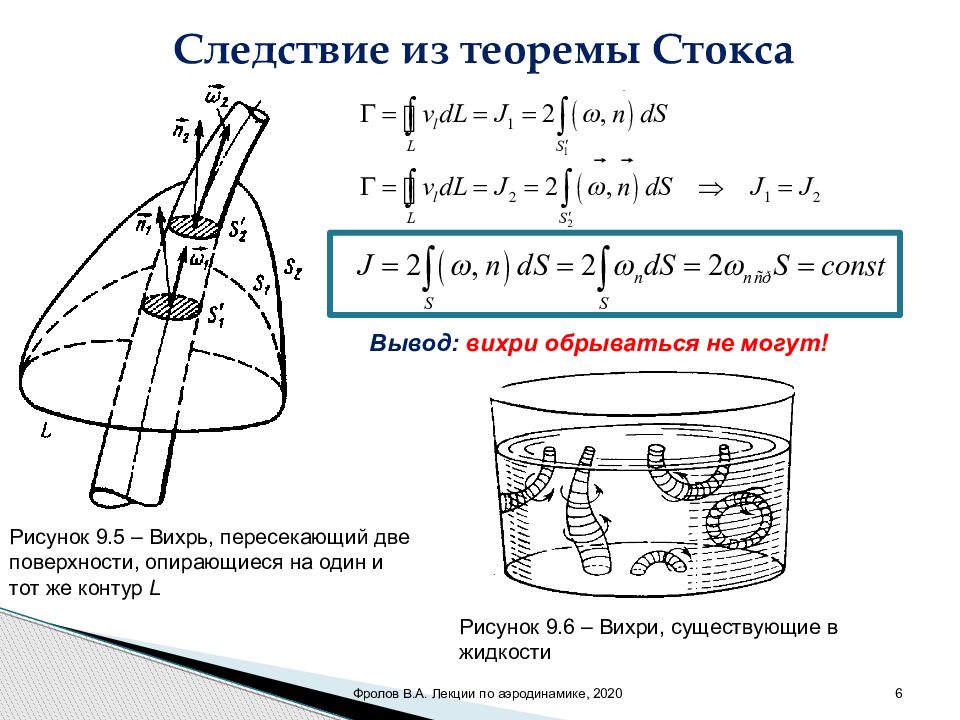
6 Следствие из теоремы Стокса Рисунок 9.5 – Вихрь, пересекающий две поверхности, опирающиеся на один и тот же контур L Вывод : вихри обрываться не могут! Рисунок 9.6 – Вихри, существующие в жидкости Фролов В.А. Лекции по аэродинамике, 2020
7 Теоремы Гельмгольца Теорема 1. В непрерывных течениях идеального газа вихревая трубка с течением времени не разрушается и всегда остаётся вихревой трубкой. Теорема 2. В непрерывных течениях идеального газа напряжение вихревого жгута с течением времени не изменяется. Фролов В.А. Лекции по аэродинамике, 2020
8 Теорема Био-Савара Рисунок 9.7 – Скорость, индуцированная прямолинейным отрезком вихря ( 9. 9 ) бесконечный вихрь полубесконечный вихрь Фролов В.А. Лекции по аэродинамике, 2020
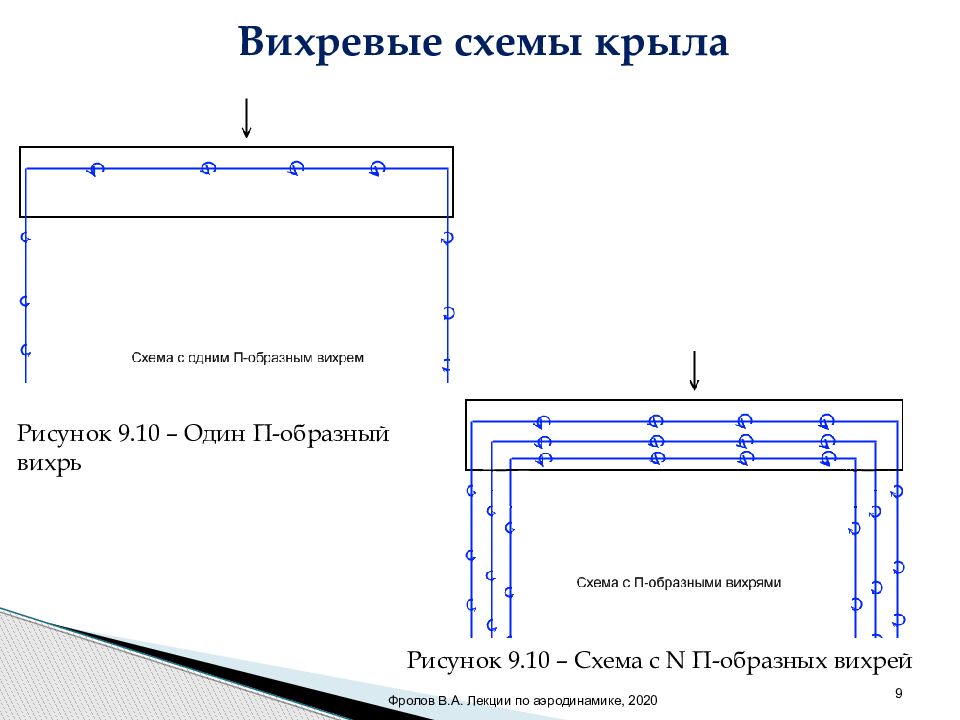
9 Вихревые схемы крыла Фролов В.А. Лекции по аэродинамике, 2020 Рисунок 9.10 – Один П-образный вихрь Рисунок 9.10 – Схема с N П-образны х вихрей
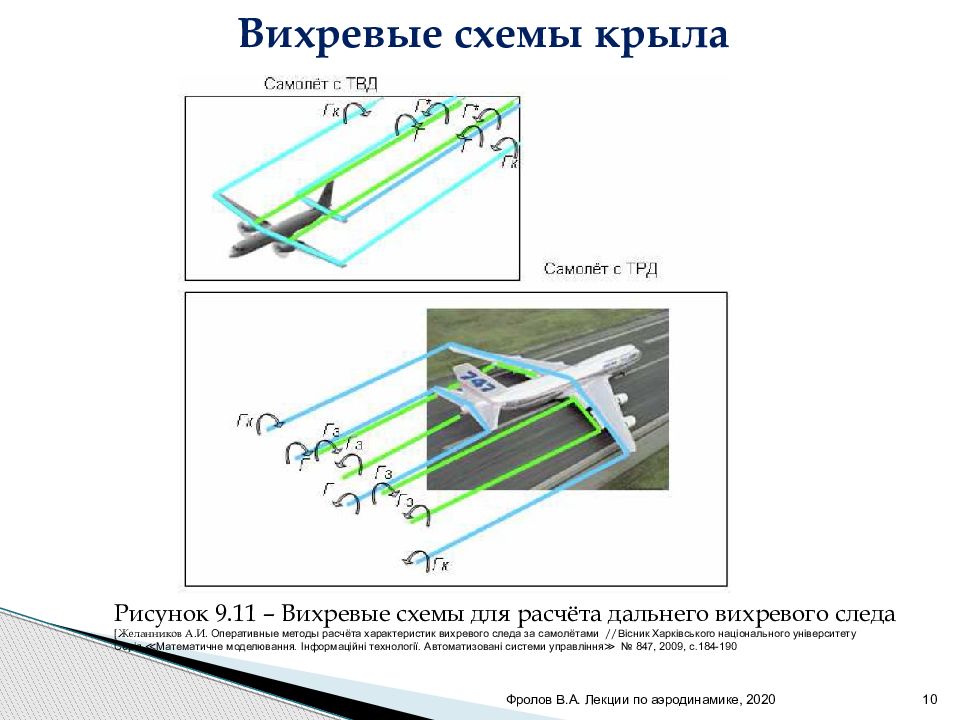
Фролов В.А. Лекции по аэродинамике, 2020 10 Рисунок 9.1 1 – Вихревые схемы для расчёта дальнего вихревого следа [ Желанников А.И. Оперативные методы расчёта характеристик вихревого следа за самолётами // Вісник Харківського національного університету Серія ≪Математичне моделювання. Інформаційні технології. Автоматизовані системи управління≫ № 847, 2009, с.184-190 Вихревые схемы крыла
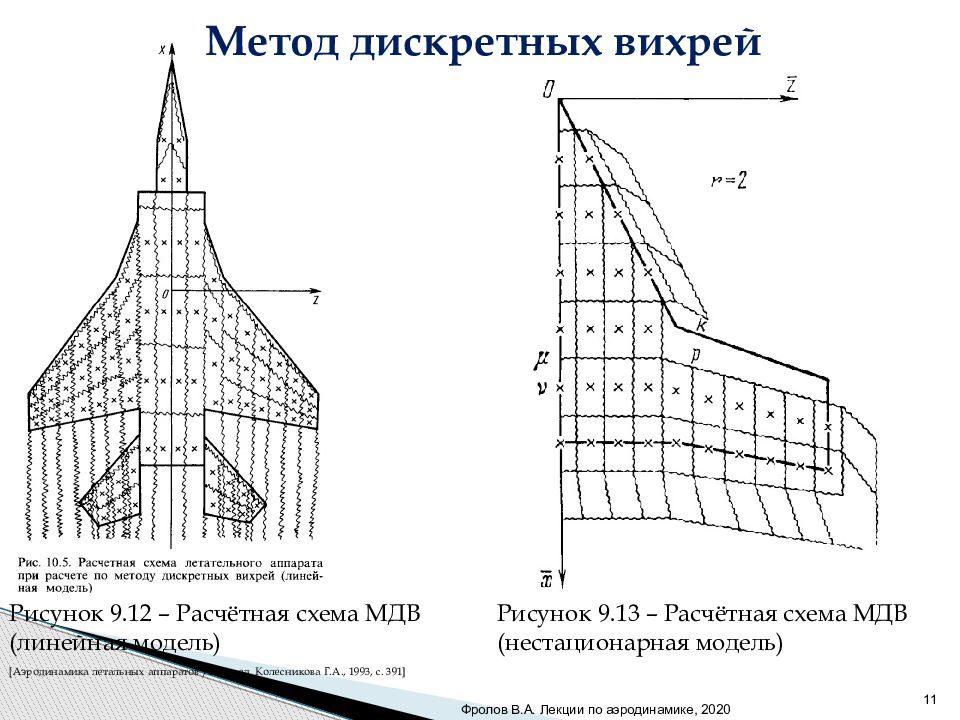
11 [ Аэродинамика летальных аппаратов / Под ред. Колесникова Г.А., 1993, с. 391 ] Фролов В.А. Лекции по аэродинамике, 2020 Рисунок 9.12 – Расчётная схема МДВ (линейная модель) Рисунок 9.13 – Расчётная схема МДВ (нестационарная модель) Метод дискретных вихрей
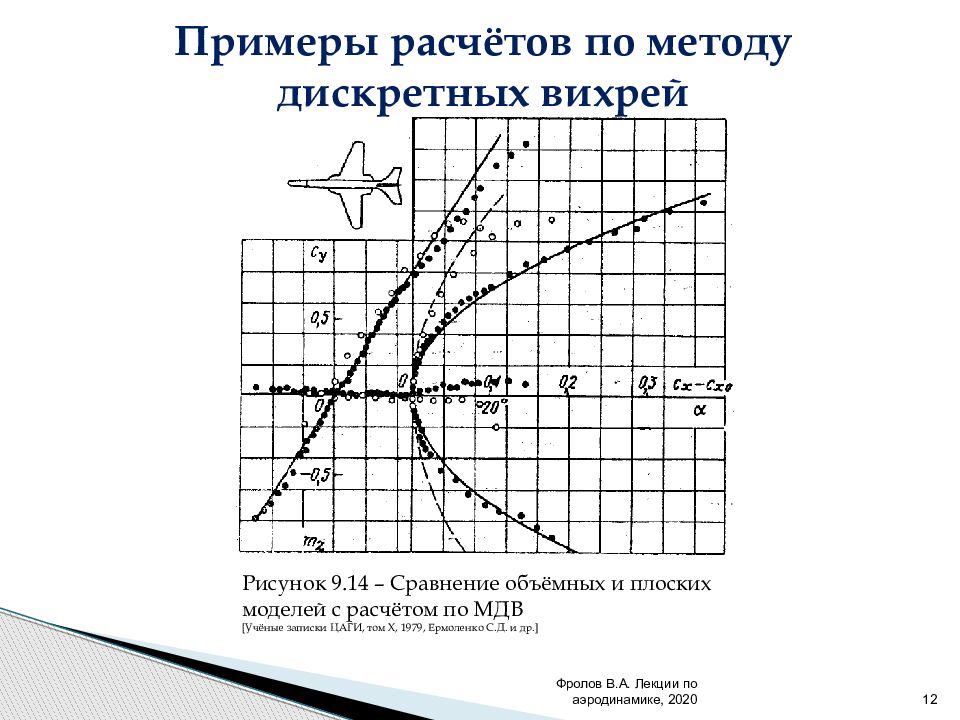
Фролов В.А. Лекции по аэродинамике, 2020 12 Рисунок 9.14 – Сравнение объёмных и плоских моделей с расчётом по МДВ [ Учёные записки ЦАГИ, том X, 1979, Ермоленко С.Д. и др. ] Примеры расчётов по методу дискретных вихрей
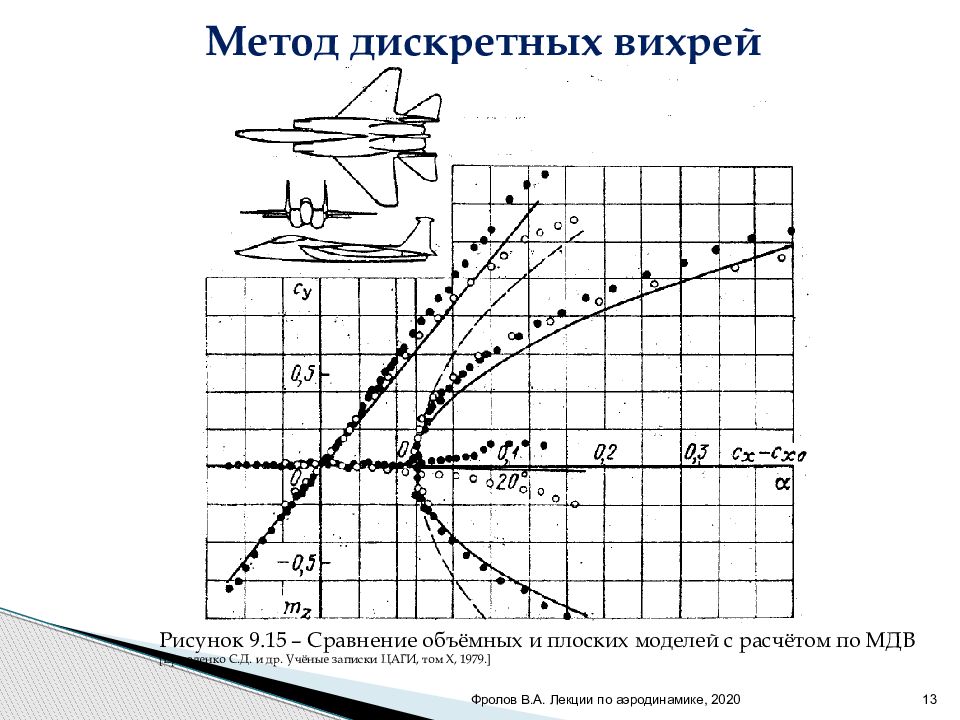
Фролов В.А. Лекции по аэродинамике, 2020 13 Метод дискретных вихрей Рисунок 9.15 – Сравнение объёмных и плоских моделей с расчётом по МДВ [ Ермоленко С.Д. и др. Учёные записки ЦАГИ, том X, 1979.]
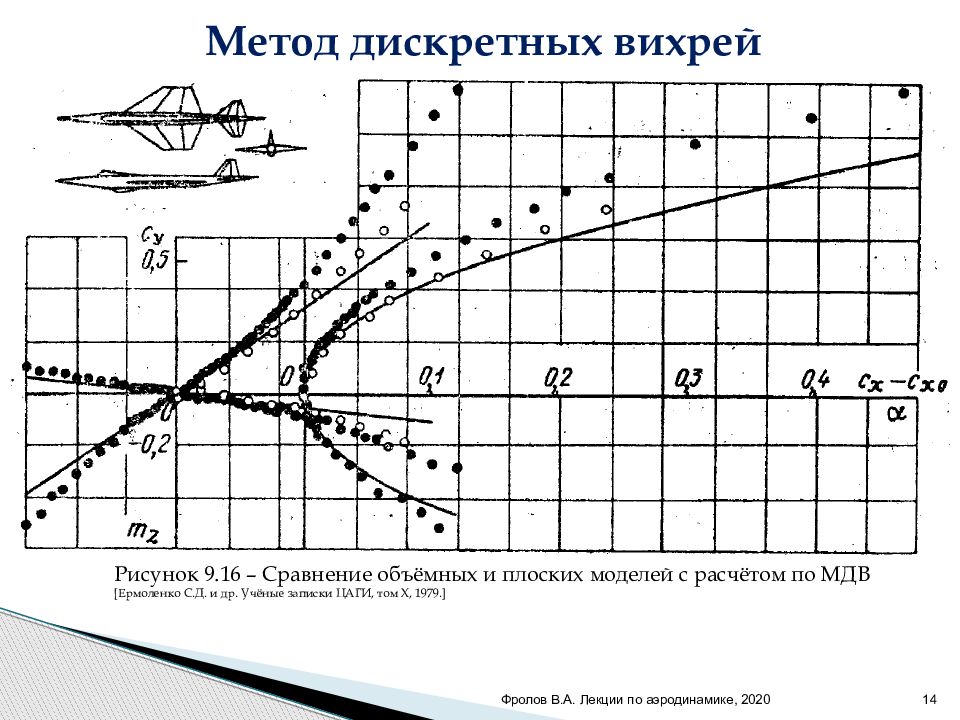
Фролов В.А. Лекции по аэродинамике, 2020 14 Метод дискретных вихрей Рисунок 9.16 – Сравнение объёмных и плоских моделей с расчётом по МДВ [ Ермоленко С.Д. и др. Учёные записки ЦАГИ, том X, 1979.]
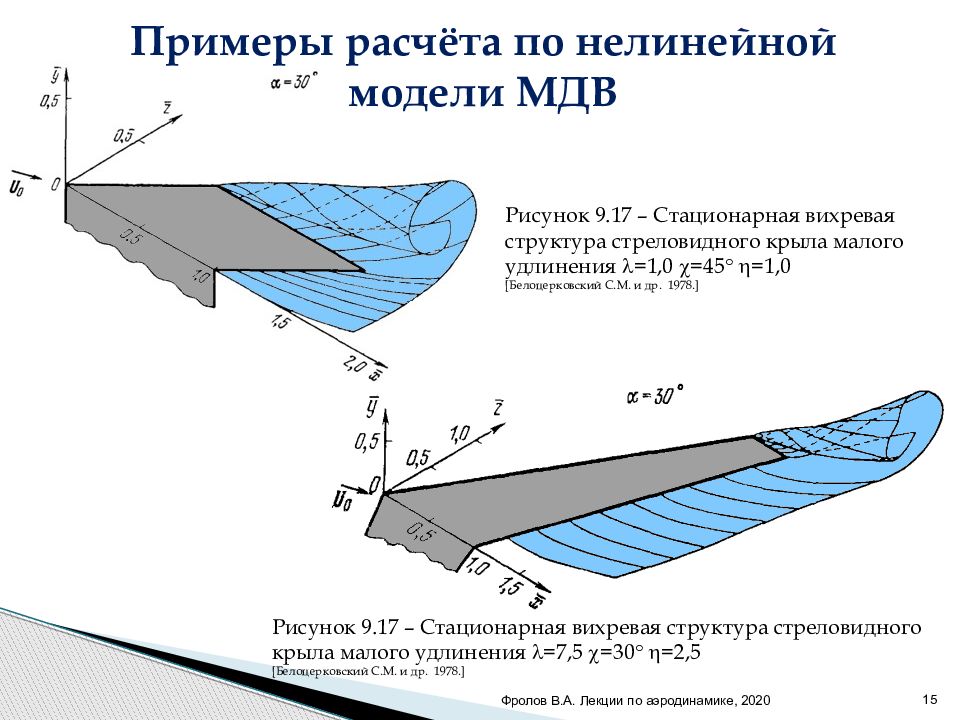
Фролов В.А. Лекции по аэродинамике, 2020 15 Рисунок 9.17 – Стационарная вихревая структура стреловидного крыла малого удлинения =7,5 =30 =2,5 [ Белоцерковский С.М. и др. 197 8.] Рисунок 9.17 – Стационарная вихревая структура стреловидного крыла малого удлинения =1,0 =45 =1,0 [ Белоцерковский С.М. и др. 197 8.] Примеры расчёта по нелинейной модели МДВ
