Затухающие механические и электромагнитные колебания.
Затухающие колебания. Затухающие механические колебания. Формулировка модели и постановка задачи. 1. Период колебаний не меняется (или почти не меняется), так как он не зависит от массы маятника, а, следовательно, от количества высыпавшегося песка. 2. Амплитуда колебаний уменьшается с течением времени. Колебания, амплитуда которых уменьшается с течением времени, называются затухающими колебаниями.
Затухающие колебания. Затухающие механические колебания. Формулировка модели и постановка задачи. Второй закон Ньютона: Проекция силы трения на OX : Проекция квазиупругой силы на OX : Проекция скорости на OX : Проекция ускорения на OX :
Затухающие колебания. Затухающие механические колебания. Формулировка модели и постановка задачи. Уравнение движения можно переписать в виде: Разделим уравнение на m : Введем следующие обозначения : 0 – собственная частота незатухающих колебаний без учета трения.
Затухающие колебания. Затухающие механические колебания. Постановка задачи. Теперь можно переписать уравнение движения в виде: (1) Мы получили дифференциальное уравнение затухающих колебаний. С точки зрения математики это уравнение с постоянными коэффициентами. Приступим к его решению.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. (1) В уравнение (1) подставим функцию и получим характе-ристическое уравнение: - характеристическое уравнение.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. Корни этого характеристического уравнения: Как известно, общим решением дифференциального уравнения второго порядка с постоянными коэффициентами является функция: Подкоренные выражения в формулах, определяющих корни характеристического уравнения, в зависимости от значений параметров и могут быть как положительными, так и отрицательными. Это приводит к тому, что существует два класса решений.
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. 1. Если 0, то подкоренное выражение будет отрицательным, а корни характеристического уравнения – комплексными. Обозначим тогда Решение уравнения в этом случае будет иметь вид: Или в действительной форме: Здесь A и 0 – произвольные постоянные имеющие смысл амплитуды и начальной фазы колебаний,
Затухающие колебания. Решение дифференциального уравнения затухающих колебаний. 2. Если > 0, то подкоренные выражения в формулах, определяющих корни характеристического уравнения будут положительными, а корни характеристического уравнения 1 и 2 – действительными.
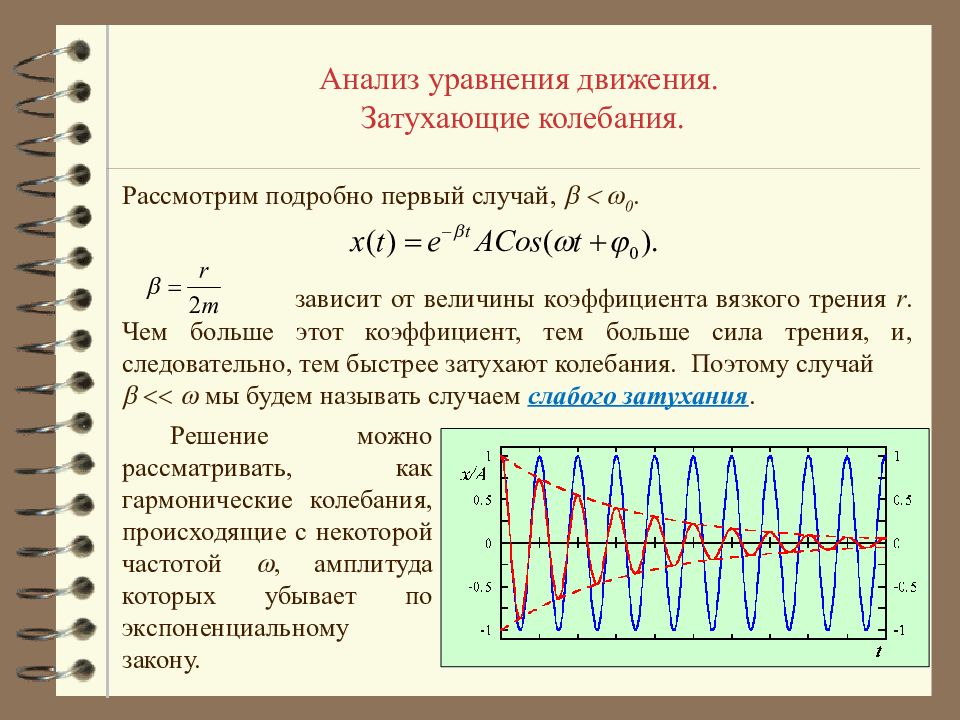
Анализ уравнения движения. Затухающие колебания. Рассмотрим подробно первый случай, 0. зависит от величины коэффициента вязкого трения r. Чем больше этот коэффициент, тем больше сила трения, и, следовательно, тем быстрее затухают колебания. Поэтому случай мы будем называть случаем слабого затухания. Решение можно рассматривать, как гармонические колебания, происходящие с некоторой частотой , амплитуда которых убывает по экспоненциальному закону.
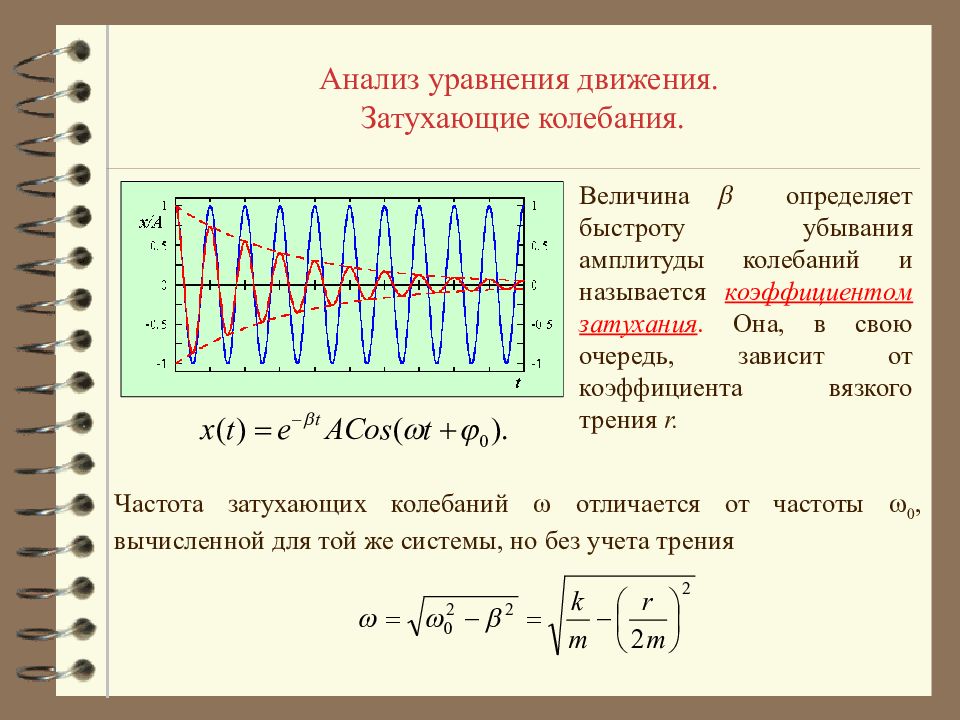
Анализ уравнения движения. Затухающие колебания. Величина определяет быстроту убывания амплитуды колебаний и называется коэффициентом затухания. Она, в свою очередь, зависит от коэффициента вязкого трения r. Частота затухающих колебаний отличается от частоты 0, вычисленной для той же системы, но без учета трения
Для случая слабого затухания, когда 0, различие частот и периодов несущественно и часто при решении практических задач в случае слабого затухания период и частоту колебаний определяют по формулам для свободных (незатухающих) колебаний. Период затухающих колебаний: Анализ уравнения движения. Затухающие колебания.
Величины, характеризующие процесс затухания колебаний. Для описания процесса убывания колебаний вводятся специальные величины, характеризующие этот процесс. Величина, называемая декрементом затухания показывает, во сколько раз уменьшается амплитуда колебаний за один период Т : Величина равна натуральному логарифму отношения амплитуд колебаний, измеренных через один полный период и называется логарифмическим декрементом затухания.
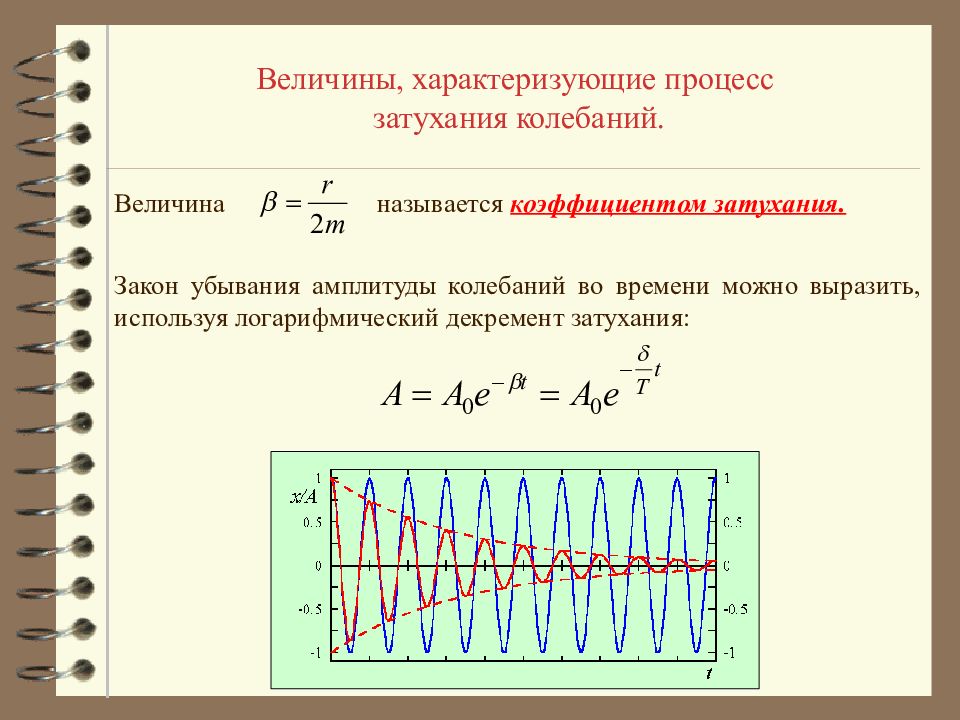
Величины, характеризующие процесс затухания колебаний. Величина Закон убывания амплитуды колебаний во времени можно выразить, используя логарифмический декремент затухания: называется коэффициентом затухания.
Величины, характеризующие процесс затухания колебаний. Время , за которое амплитуда колебаний уменьшается в e раз называют временем релаксации колебаний. Время релаксации колебаний можно выразить через другие параметры: Согласно закону убывания амплитуды колебаний через время после начала колебаний их амплитуда составит
Величины, характеризующие процесс затухания колебаний. Определим число колебаний N e, которое совершит система за время, равное времени релаксации. За один период число колебаний составит За время число колебаний системы составит С другой стороны, Следовательно,
Величины, характеризующие процесс затухания колебаний. Величина Q, пропорциональная числу колебаний системы, совершаемых за время, когда амплитуда колебаний уменьшается е раз, называется добротностью колебательной системы. Q = N e, Таким образом, чем выше добротность колебательной системы, тем большее число колебаний она сможет совершить за то время, пока амплитуда колебаний уменьшится в e раз. Высокодобротные колебательные системы обладают малым затуханием, и наоборот, низкодобротные характеризуются высоким затуханием.
Анализ решения уравнения движения. Апериодический процесс. Рассмотрим случай, когда > 0. В этом случае подкоренные выражения в формулах, определяющих корни характеристического уравнения будут положительными, а корни характеристического уравнения 1 и 2 – действительными. следовательно, 1 и 2 отрицательны и оба слагаемых в решении представляют собой монотонно убывающие функции. > 0, и В этом случае колебательный процесс не возникнет, а движение тела будет апериодическим (то есть непериодическим). Тело, выведенное из положения равновесия, вернется в это положение и остановится.
Анализ решения уравнения движения. Апериодический процесс. Как мы видим, условием возникновения апериодического процесса является > 0, то есть Это возможно, если коэффициент вязкого трения Если же в системе возникнут затухающие колебания.
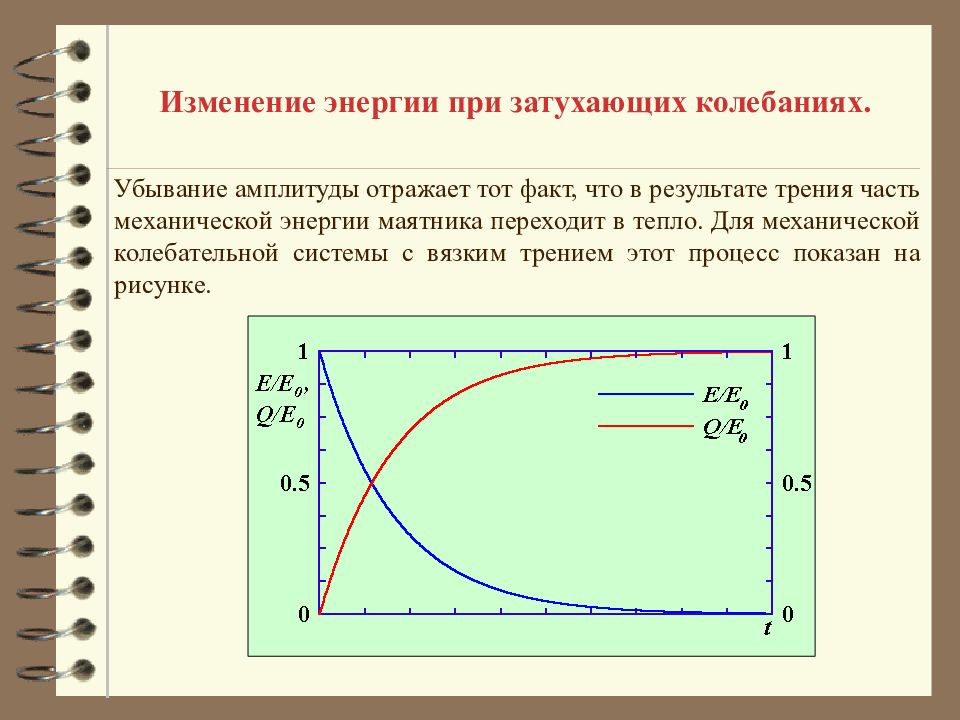
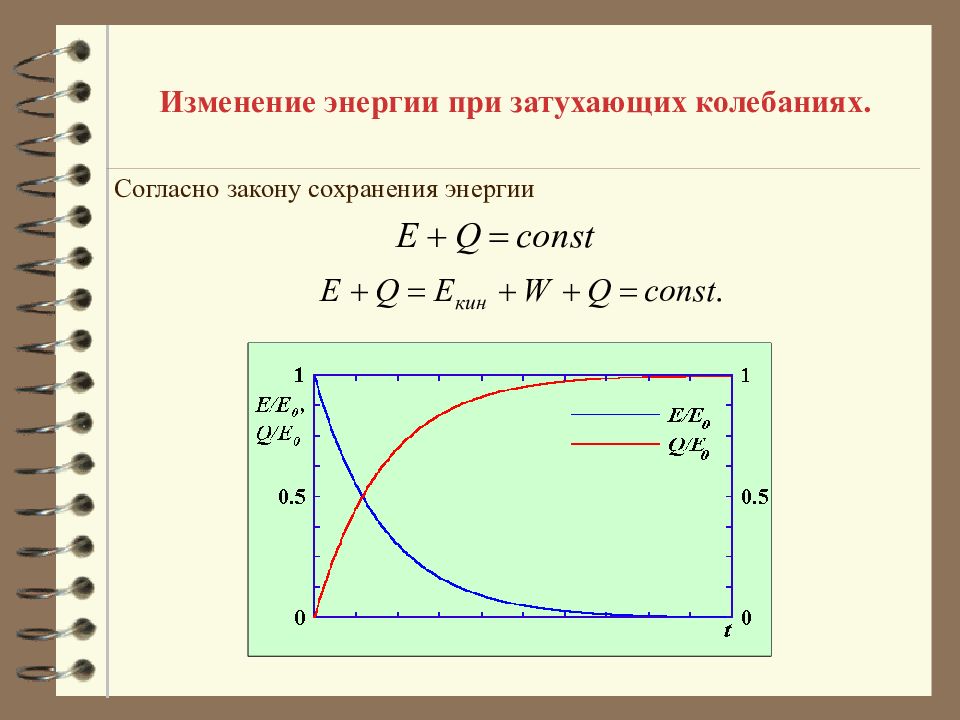
Изменение энергии при затухающих колебаниях. Убывание амплитуды отражает тот факт, что в результате трения часть механической энергии маятника переходит в тепло. Для механической колебательной системы с вязким трением этот процесс показан на рисунке.
Изменение энергии при затухающих колебаниях. Согласно закону сохранения энергии
