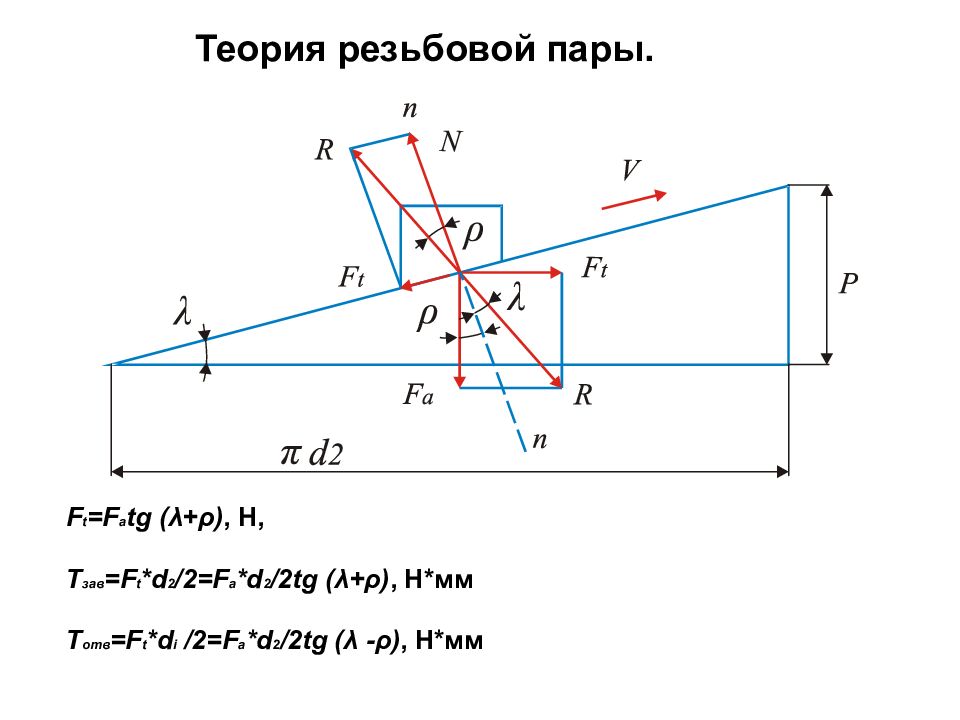
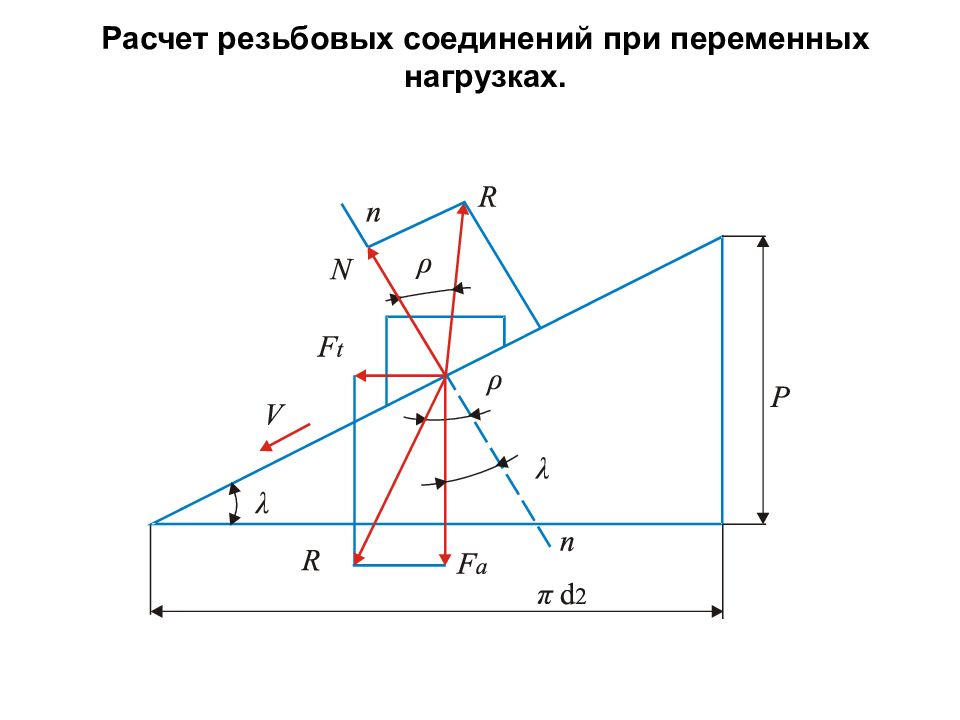
Теория резьбовой пары. F t = F a tg (λ+ρ), H, T зав = F t * d 2 /2= F a * d 2 /2 tg (λ+ρ), Н*мм T отв = F t * d i /2= F a * d 2 /2 tg (λ -ρ), H *мм
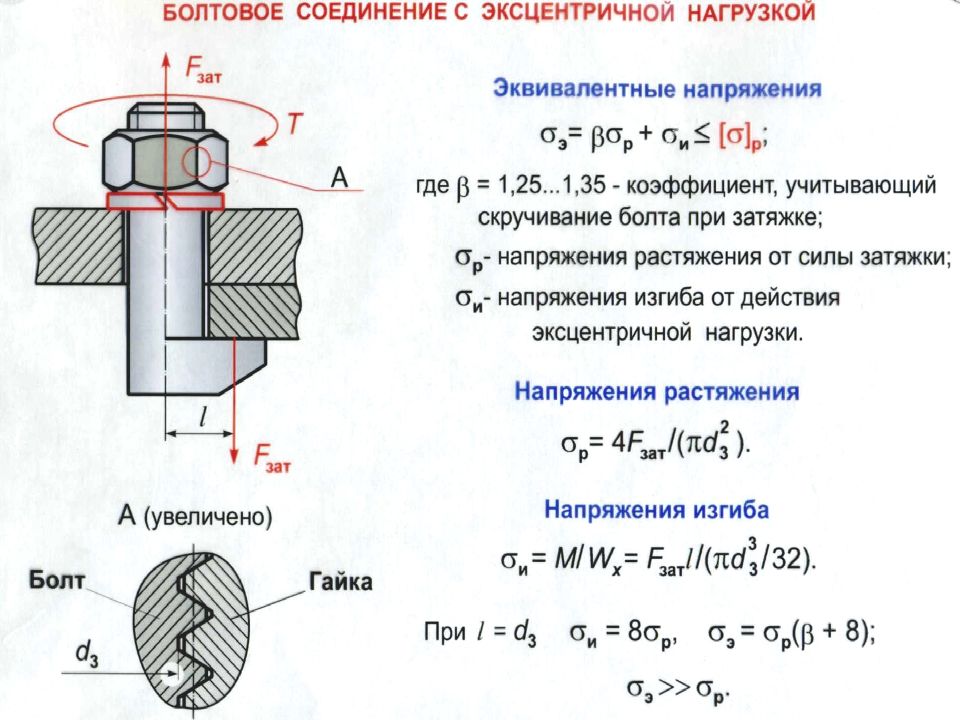
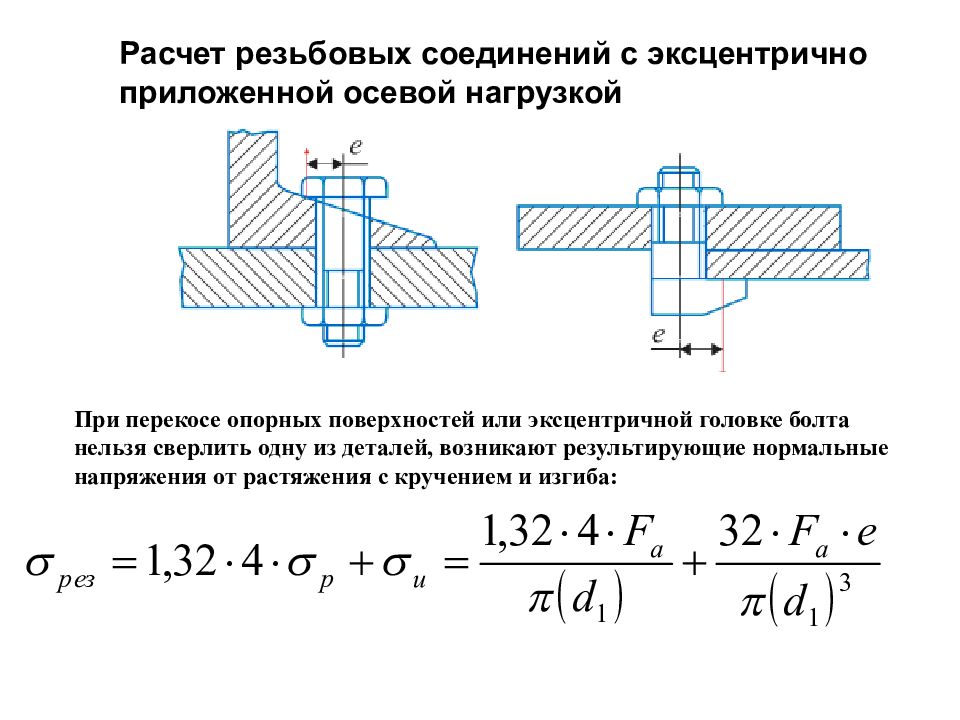
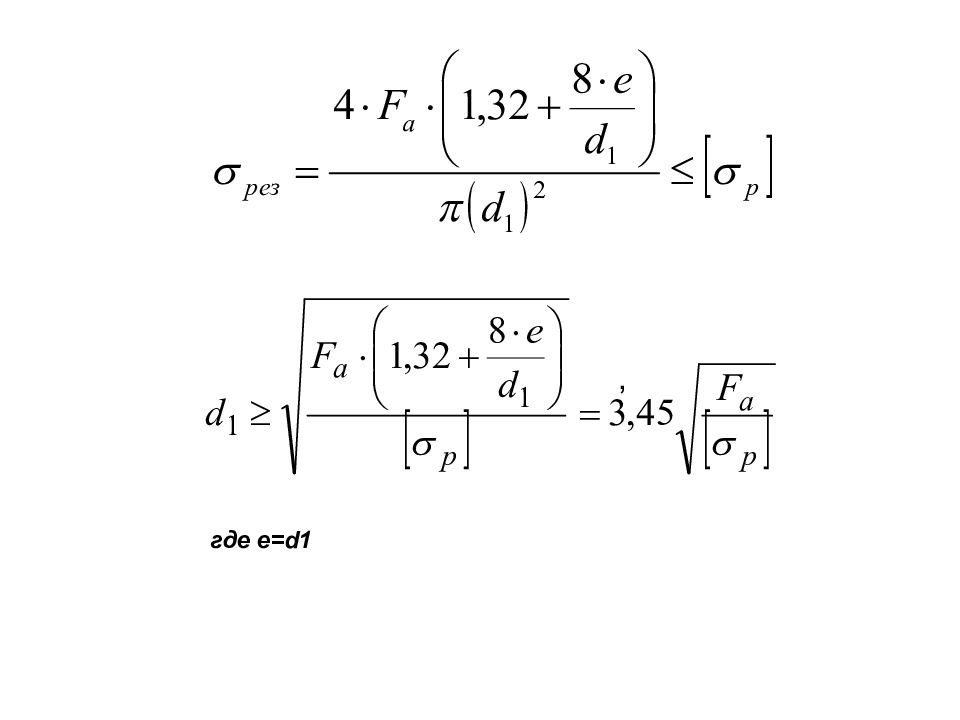
Расчет резьбовых соединений с эксцентрично приложенной осевой нагрузкой При перекосе опорных поверхностей или эксцентричной головке болта нельзя сверлить одну из деталей, возникают результирующие нормальные напряжения от растяжения с кручением и изгиба:
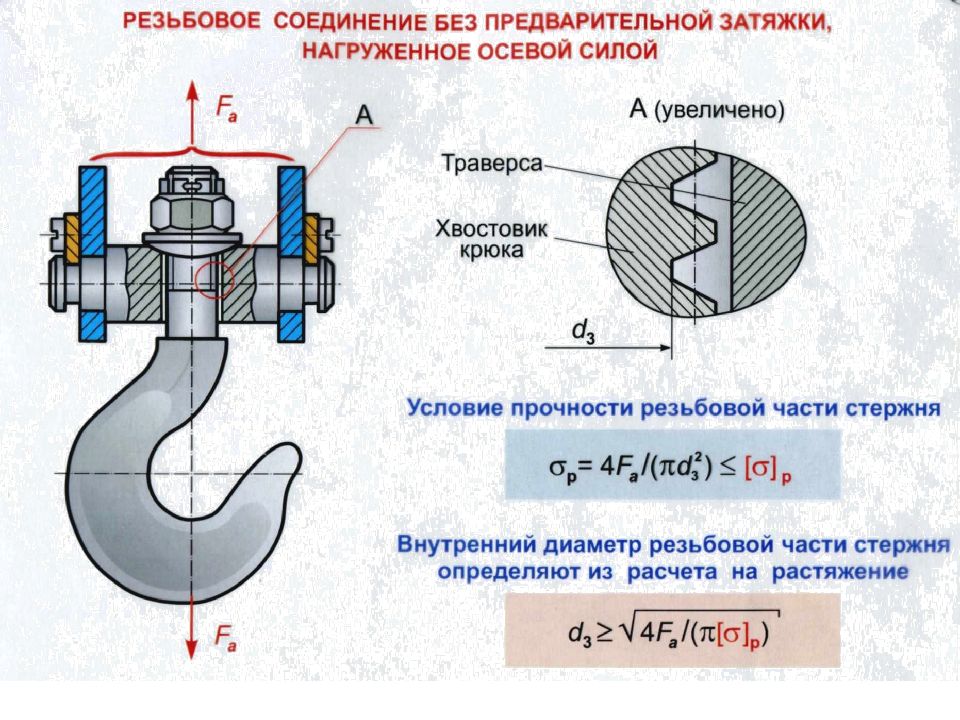
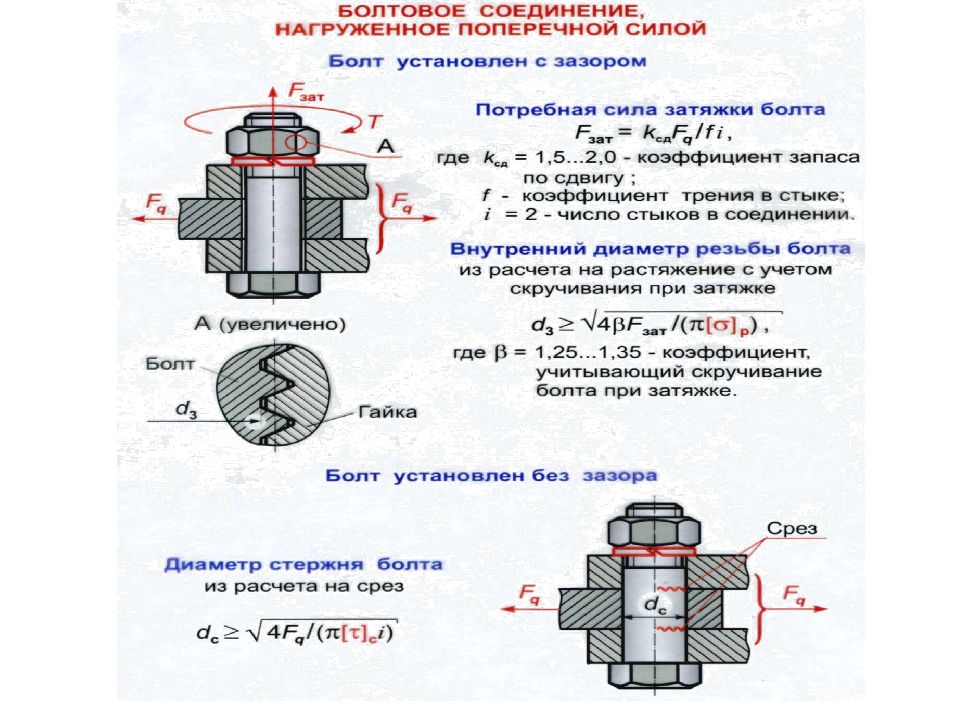
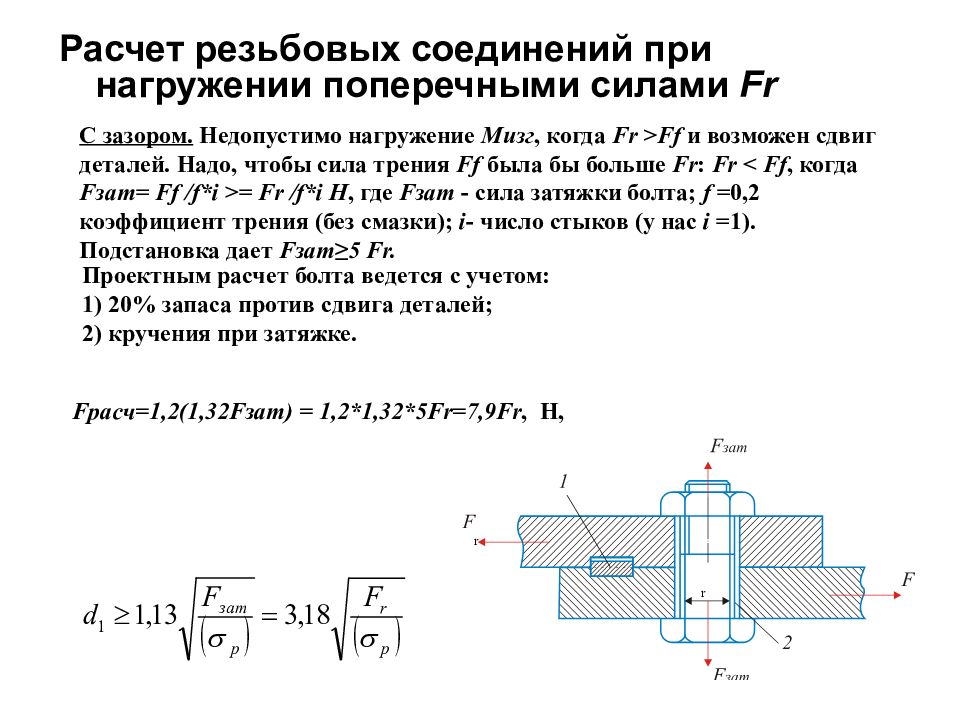
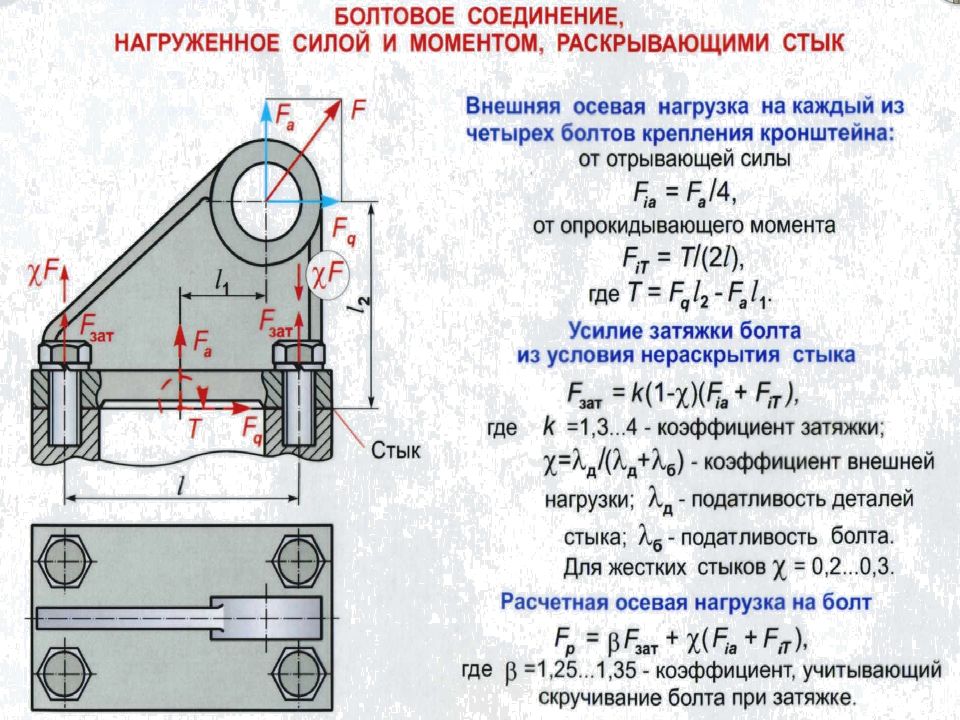
Расчет резьбовых соединений при нагружении поперечными силами Fr С зазором. Недопустимо нагружение Мизг, когда Fr > Ff и возможен сдвиг деталей. Надо, чтобы сила трения Ff была бы больше Fr : Fr < Ff, когда F зат = Ff / f * i >= Fr / f * i H, где F зат - сила затяжки болта; f =0,2 коэффициент трения (без смазки); i - число стыков (у нас i =1). Подстановка дает F зат ≥ 5 Fr. Проектным расчет болта ведется с учетом: 1) 20% запаса против сдвига деталей; 2) кручения при затяжке. Fpac ч=1,2(1,32 F зат) = 1,2*1,32*5 Fr =7,9 Fr, Н, r r
Без зазора. При монтаже под развертку с небольшим натягом стержень болта диаметром d работает на срез от поперечной силы Fr. Условие прочности на срез Fr <=π d ^2/4[τ p ], H,
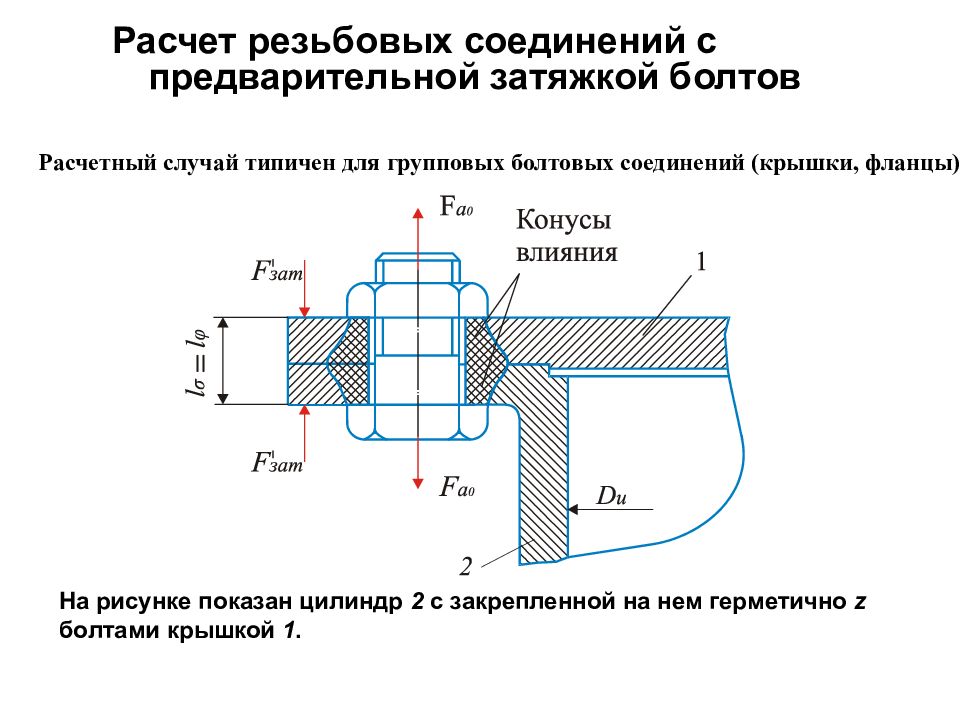
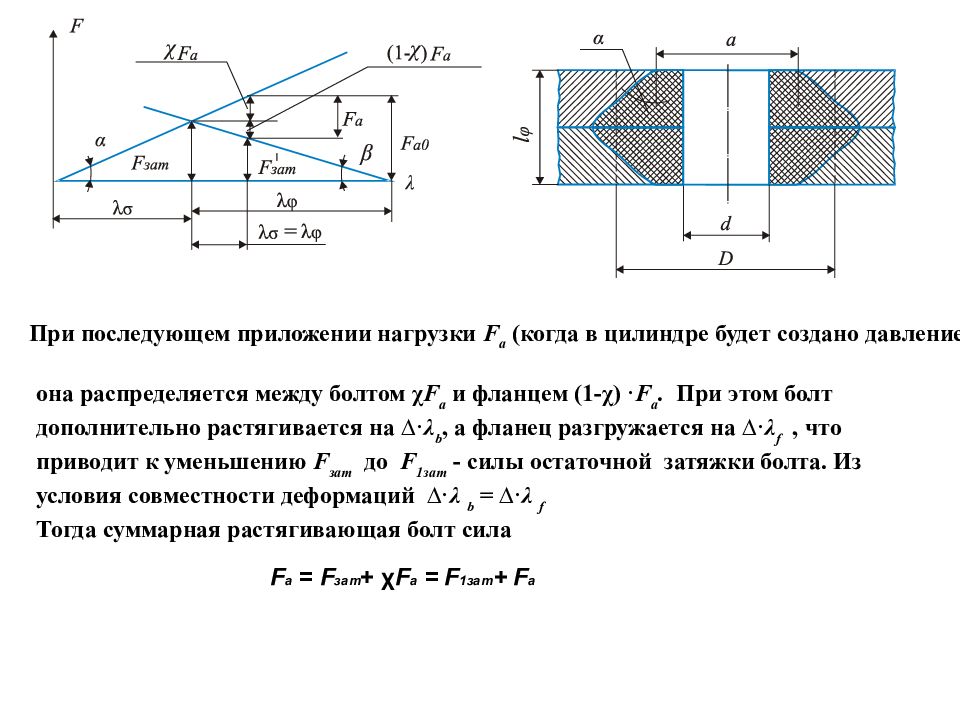
Расчет резьбовых соединений с предварительной затяжкой болтов Расчетный случай типичен для групповых болтовых соединений (крышки, фланцы). На рисунке показан цилиндр 2 с закрепленной на нем герметично z болтами крышкой 1.
При последующем приложении нагрузки F а (когда в цилиндре будет создано давление Р ) она распределяется между болтом χ F а и фланцем (1-χ) · F а. При этом болт дополнительно растягивается на ∆· λ b, а фланец разгружается на ∆· λ f, что приводит к уменьшению F зат до F 1зат - силы остаточной затяжки болта. Из условия совместности деформаций ∆· λ b = ∆· λ f Тогда суммарная растягивающая болт сила F a = F зат + χ F а = F 1зат + F а
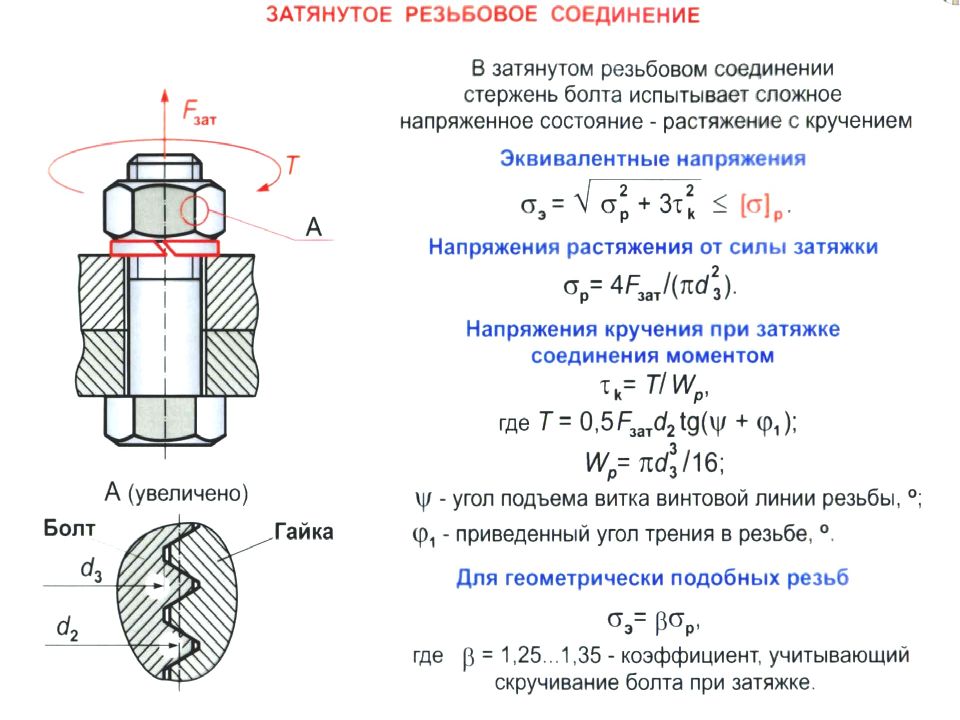
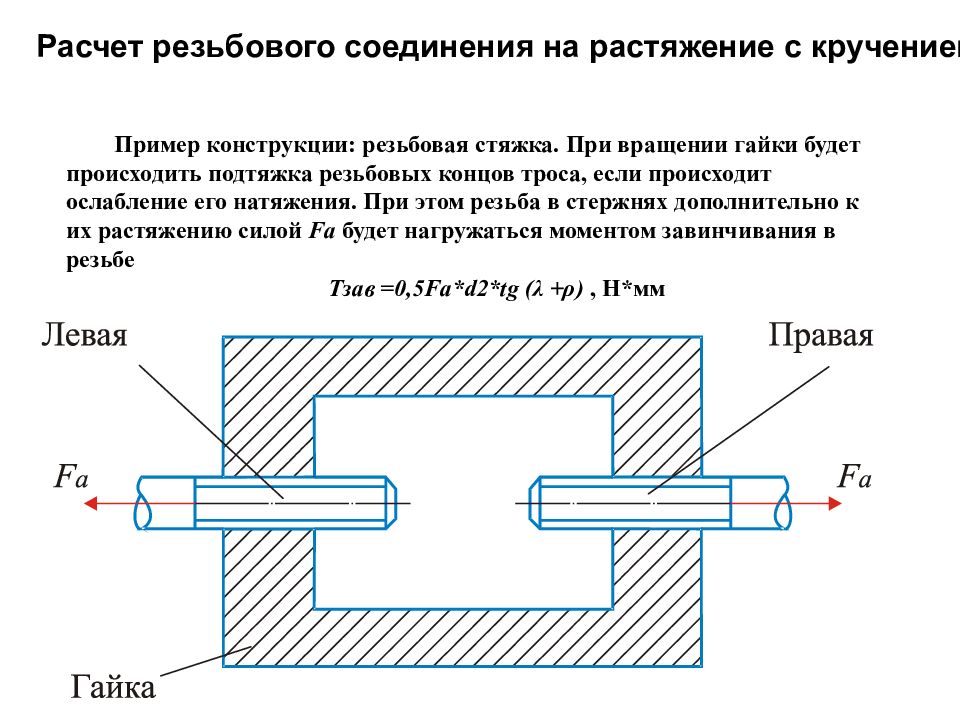
Расчет резьбового соединения на растяжение с кручением Пример конструкции: резьбовая стяжка. При вращении гайки будет происходить подтяжка резьбовых концов троса, если происходит ослабление его натяжения. При этом резьба в стержнях дополнительно к их растяжению силой Fa будет нагружаться моментом завинчивания в резьбе Тзав =0,5 Fa * d 2* tg (λ +ρ), Н*мм
Нормальные σ и касательные τ напряжения в резьбе: Выражая Fa через σ, d 2= l,12 d 1 и tg (λ+ρ)=0,23 при характерных значениях углов λ и ρ, получим τ =0,5 σ Н/мм, Значит, расчет на растяжение от Fa и кручение от Тзав можно заменить расчетом только на растяжение, приняв Fa =1,32 Fa (так как σ= Fa ). где (σр) оценивается так же, как и при чисто осевом нагружении резьбы. При этом коэффициент перед возрос с 1,13 до 1,3. ,
где e = d 1 ,
Расчет резьбовых соединений при переменных нагрузках.
Повышение выносливости резьбовых соединений при переменных нагрузках. а) уменьшением, σ а при σ m ах = const ; б) уменьшением, концентрации напряжений К σ; в) улучшением, распределения нагрузки между витками резьбы (гайка растяжения)
Общая нагрузка на z болтов крышки где Р - давление внутри цилиндра с диаметром D c. Нагрузка на один болт До приложения нагрузки F a для геометричности стыка нужно создать предварительную затяжку болта F зат. Она растягивает болт и сжимает фланец l b = l f длина болта и фланца E b и E f - модули упругости материалов болта и фланца S b и S f - площади поперечного сечения болта с диаметром d 1 и пустотелого цилиндра с диаметрами D и d С b и C f - коэффициенты жесткости болта и фланца
- коэффициент основной нагрузки, где С b = tan (α) и C f = tan (β). Величину χ, получаем из равенства ∆· λ b = ∆· λ f или Заметим, что постановка упругих прокладок между цилиндром 2 и крышкой 1 уменьшит С f, что увеличит нагрузку на болт χ F а из-за роста при этом χ. При оценке неизвестной площади S f в расчете C f во время определения величины воспользуемся методом профессора И.И. Бобарыкова. Он в 1911 г. предложил считать, что сжатие фланца ограничивается объемом, создаваемым конусами влияния, наружный диаметр меньших оснований которых а равен диаметру опорной поверхности гайки и образующие которых наклонены к плоскости, перпендикулярной стыку, под углом α. При этом tan α=1/2.
Для упрощения расчетов проф. Бобарыков предложил считать равной площади поперечного сечения равновеликого по объему конусам влияния пустотелого цилиндра где d — диаметр отверстия во фланце под болт Произведя оценку χ, перейдем к расчету суммарной нагрузки на болт F а по формуле. Входящее в формулу усилие предварительной затяжки выразим в виде условия невозможности раскрытия стыка F з am = k · [(1-χ) · Fa ] где k = 1,5…5- коэффициент запаса против раскрытия стыка разгрузкой фланца (1-χ)· Fa.
Величина k зависит от условий нагружения и является справочным параметром, всегда большим единицы и поэтому не допускающим раскрытия стыка за счет недопустимого (выше F з am ) повышения рабочего усилия Fa. Подставляя F з am получим F a = F з am + χ F а = k = β· F a При некоторых средних значениях k = 3 и χ=0,3 (без прокладок) =2,4. Расчетная нагрузка принимается с учетом кручения при затяжке F з am : F р. Тогда где [ σ р ] оценивается так же, как для первого расчетного случая. Все рассмотренные расчетные случаи приводятся к виду где А = 1,13 ( Fa ) -1,3 ( Fa + Тз am ) -1,6( Fr )(без зазора) – 2( F з am ) – 3,18( Fr ) ( c зазором) - 3.45 ( Fr +Ми ).
