2.3.Основные пилотажно-навигационные параметры полета летательного аппарата ЛЕКЦИЯ № 4 ТЕМА 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ОБЪЕКТА УПРАВЛЕНИЯ Пилотажно-навигационная информация содержит: параметры движения центра масс объекта (прямоугольные координаты X g, L g, H ; воздушную, путевую или земную скорости, углы пути и наклона траектории ); параметры, которые определяют движение относительно центра масс: углы тангажа, крена, рыскания ; углы атаки и скольжения ; угловые скорости крена, рыскания и тангажа и их производные; 3) параметры перехода от одной системы координат к другой: углы Эйлера, направляющие косинусы или уравнения Пуассона, кватернионы или дифференциальные уравнения Родрига-Гамильтона и Келли-Клейна ;
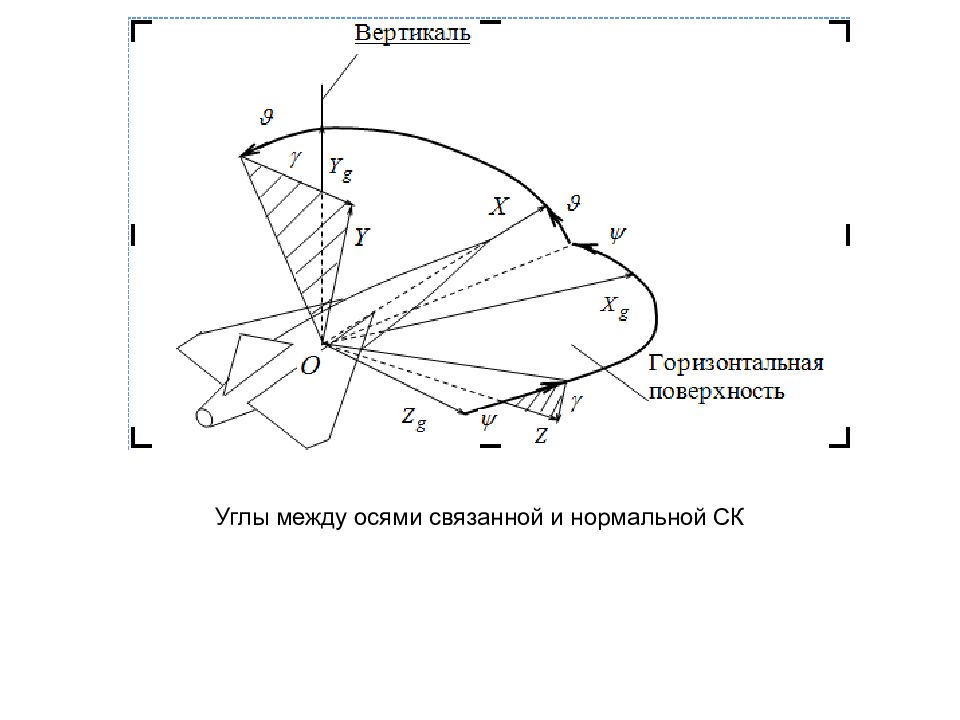
4) параметры окружающей среды: - температура внешнего воздуха Т н ; - атмосферное давление р н и - плотность ρ ; 5) параметры, которые определяют движение ЛА относительно других объектов. Для анализа динамики полета самолета важное значение имеют кинематические параметры: воздушная, земная и путевая скорости, а также скорость ветра. Воздушная скорость или с корость ЛА (или просто скорость) − скорость начала СвСК относительно среды, не возмущенной ЛА. Земная скорость − скорость начала СвСК относительно которой-нибудь из земных систем координат или поверхности Земли. Путевой скоростью называется проекция земной скорости на горизонтальную плоскость НЗСК. Скорость ветра − скорость возмущенного потока воздуха относительно Земли. Если воздух неподвижен, скорость ЛА совпадает с земной. Углы рыскания, тангажа и крена определяют положение СвСК OXYZ относительно НСК - рис., эти углы называются углами Эйлера Угол рыскания самолета измеряется в границах от 0 к ±180°; угол тангажа – от -90° к +90°, а угол крена – от -180° к +180°.
Углы между осями связанной и нормальной СК
Угол рыскания - угол между направлением оси нормальной системы координат и направлением горизонтальной проекции продольной оси самолета. Угол рыскания положительный, когда ось совмещается с проекцией продольной оси на горизонтальную плоскость поворотом вокруг оси против часовой стрелки, если смотреть с конца этой оси, а иначе: выбранное или заданное направление полета находится правее продольной оси ЛА. Углом тангажа называется угол между продольной осью и горизонтальной плоскостью нормальной системы координат. Угол тангажа положительный, когда продольная ось находится выше горизонтальной плоскости. Углом крена называется угол между поперечной осью связанной системы координат и осью нормальной системы координат, смещенной в положение, при котором угол рыскания равен нулю. Угол крена положителен, когда ось или правое полукрыло находятся ниже горизонтальной плоскости. Переход от ориентации НСК к ориентации СвСК осуществляется последовательными поворотами: на угол вокруг оси, на угол вокруг оси, на угол вокруг оси.
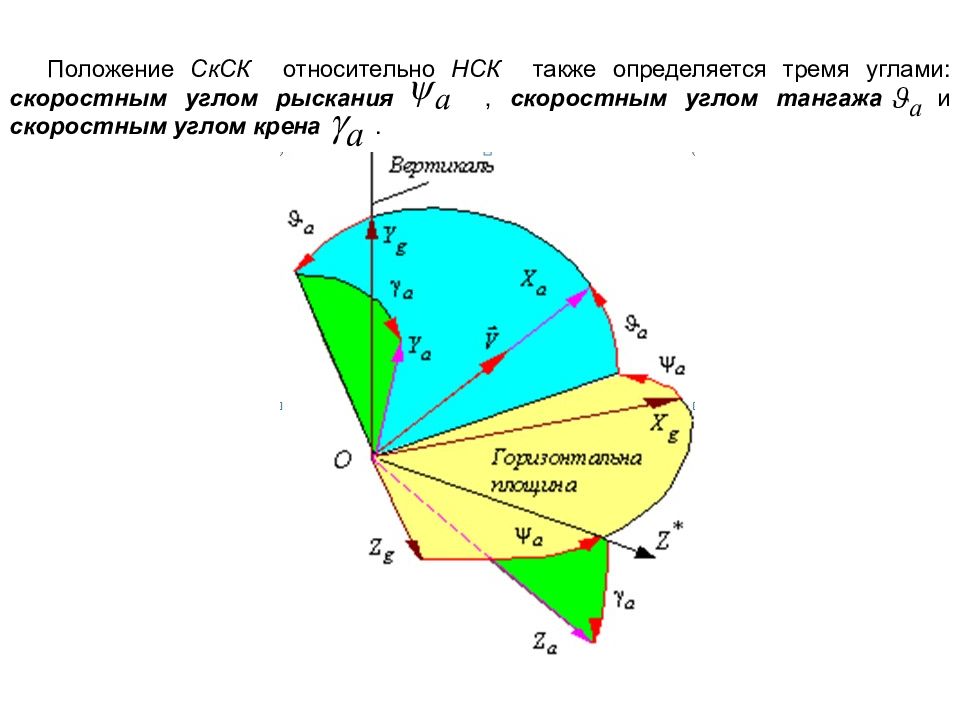
Положение СкСК относительно НСК также определяется тремя углами: скоростным углом рыскания, скоростным углом тангажа и скоростным углом крена.
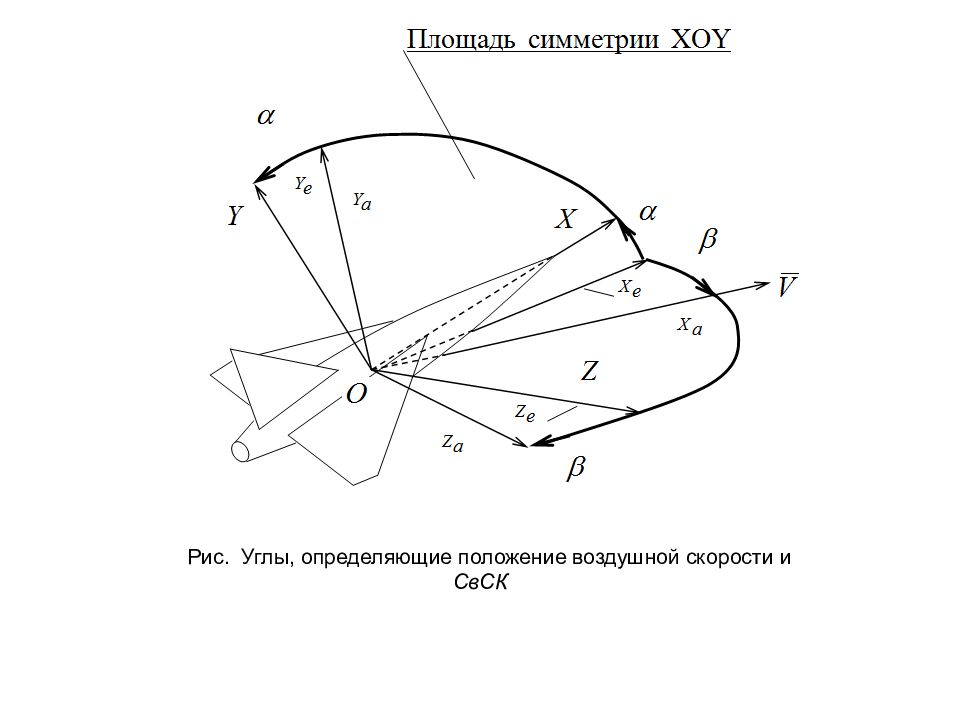
Определение этих углов аналогично углам для системы координат OXYZ. Положение самолета относительно воздушного потока, что влияет на величину аэродинамических сил, задается двумя аэродинамическими углами и, определяющих относительное положение СвСК и СкСК – рис.. Угол атаки - угол между продольной осью OX и проекцией скорости ЛА на плоскость OXY связанной системы координат (плоскость симметрии ЛА). Угол атаки следует считать положительным, если проекция скорости ЛА на нормальную ось отрицательная или продольная ось находится над вектором скорости. Угол скольжения - угол между вектором скорости ЛА и плоскостью OXY связанной системы координат (плоскостью симметрии ЛА). Угол скольжения следует считать положительным, если проекция скорости ЛА на поперечную ось положительная или самолет скользит на правое полукрыло.
Рис. Углы, определяющие положение воздушной скорости и СвСК
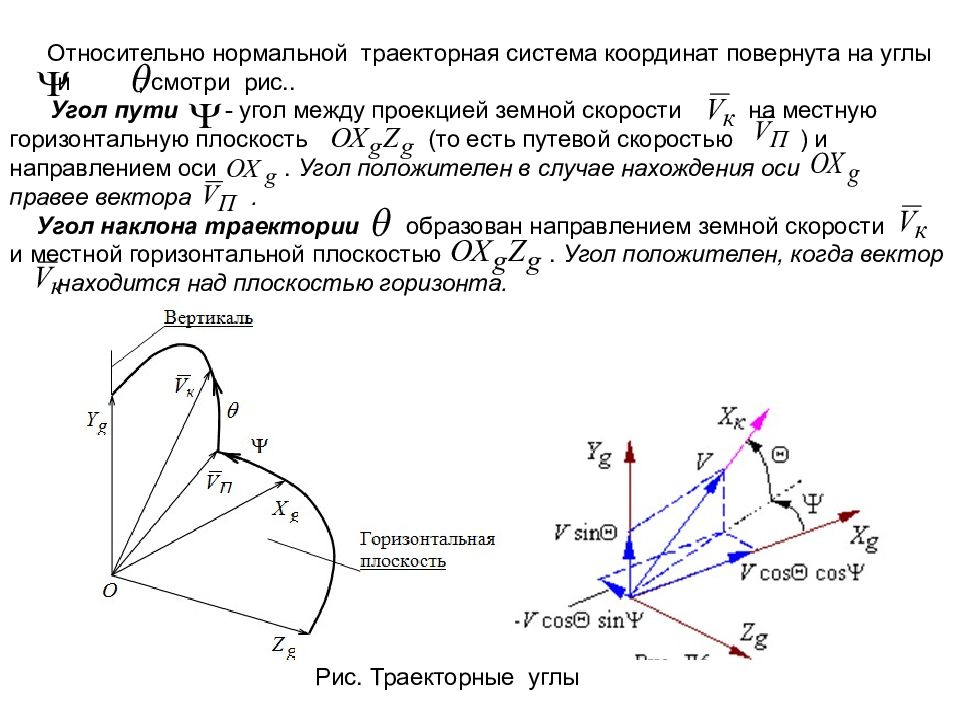
Относительно нормальной траекторная система координат повернута на углы и, смотри рис.. Угол пути - угол между проекцией земной скорости на местную горизонтальную плоскость (то есть путевой скоростью ) и направлением оси. Угол положителен в случае нахождения оси правее вектора. Угол наклона траектории образован направлением земной скорости и местной горизонтальной плоскостью. Угол положителен, когда вектор находится над плоскостью горизонта. Рис. Траекторные углы
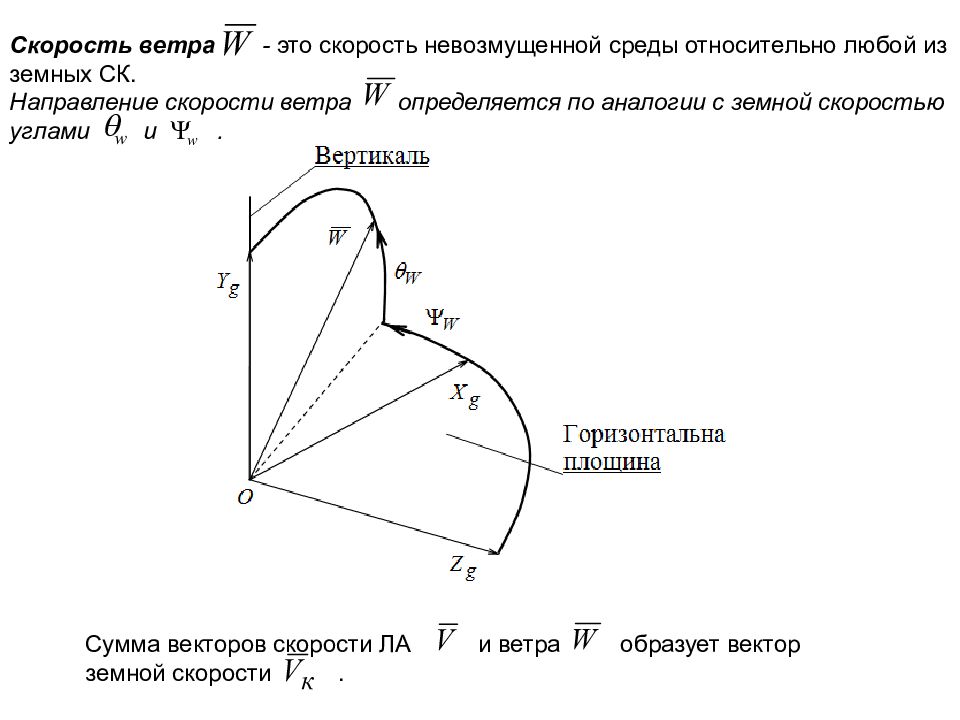
Скорость ветра - это скорость невозмущенной среды относительно любой из земных СК. Направление скорости ветра определяется по аналогии с земной скоростью углами и. Сумма векторов скорости ЛА и ветра образует вектор земной скорости.
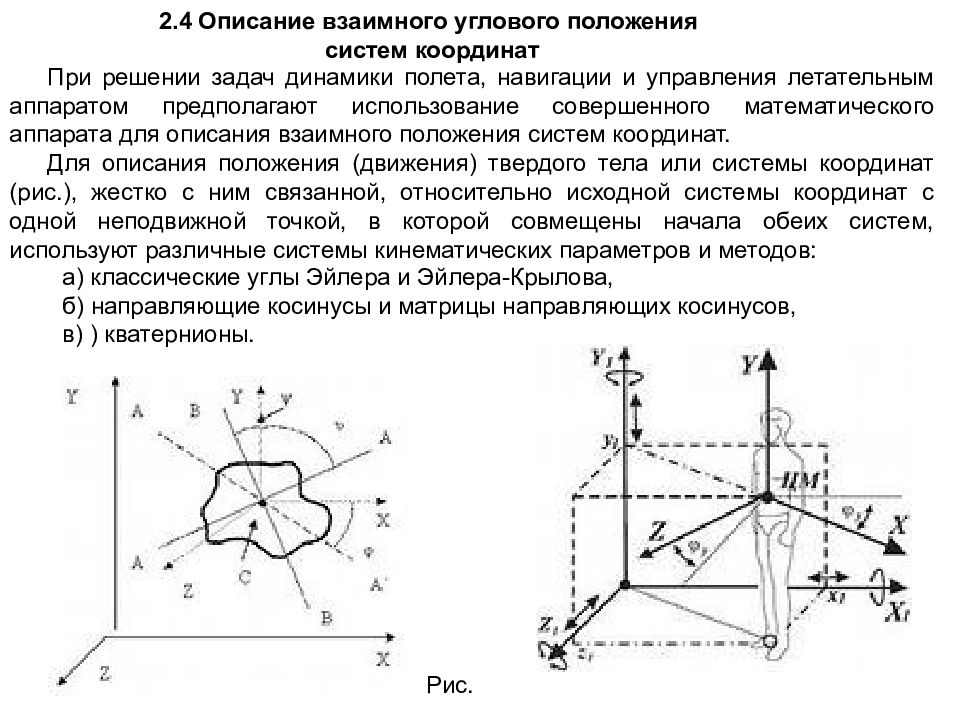
2.4 Описание взаимного углового положения систем координат При решении задач динамики полета, навигации и управления летательным аппаратом предполагают использование совершенного математического аппарата для описания взаимного положения систем координат. Для описания положения (движения) твердого тела или системы координат (рис.), жестко с ним связанной, относительно исходной системы координат с одной неподвижной точкой, в которой совмещены начала обеих систем, используют различные системы кинематических параметров и методов: а) классические углы Эйлера и Эйлера-Крылова, б) направляющие косинусы и матрицы направляющих косинусов, в) ) кватернионы. Рис.
Часто при описании ЛА как объекта управления возникает необходимость в переходе от одной системы координат к другой. Две прямоугольные правые системы координат можно совместить путем вращения. За положительное принимается вращение по часовой стрелке для наблюдателя, смотрящего в положительном направлении соответствующей оси. Относительное угловое положение двух систем координат определяется девятью направляющими косинусами, т.е. косинусами девяти углов между их соответствующими осями. (2.9) Направляющие косинусы вектора – это косинусы углов, которые он образует с осями используемой системы координат. Если вектор задан своими проекциями в системе,то Направляющие косинусы и матрицы направляющих косинусов
Направляющие косинусы являются основой одного из методов описания взаимного положения ортогональных систем координат – использование матриц направляющих косинусов (таблиц косинусов). Матрица направляющих косинусов представляет собой таблицу размерности 3 х3, элементы которой – косинусы углов между осями исходной и подвижной систем координат. В общем случае матрицу направляющих косинусов можно представить в виде (2.11) ( ) – косинусы углов между осями исходной и подвижной систем координат. Если известны углы Эйлера (Эйлера –Крылова), определяющие взаимное положение двух систем координат, то можно сформировать матрицу направляющих косинусов, описывающую переход от исходной к подвижной системе. Направляющие косинусы вектора (2.9) полностью определяют его направление, но не содержат никакой информации о его длине. (2.10) Отсюда
Каждый элемент ( ) матрицы направляющих косинусов (2.11) представляет собой скалярное произведение ортов соответствующих осей исходной (например, НЗСК ) и подвижной (например, СвСК ) систем координат, т.е. (2.12) и т.д. Для удобства пользования матрицами направляющих косинусов могут быть введены обозначения осей исходной-начальной и подвижной-конечной систем координат (2.13) Матрицу в дальнейшем будем называть матрицей перехода, здесь и далее верхний индекс матрицы перехода соответствует исходной( начало ), а нижний – системе координат, к которой осуществляется переход( конец ). Матрица перехода является ортогональной.
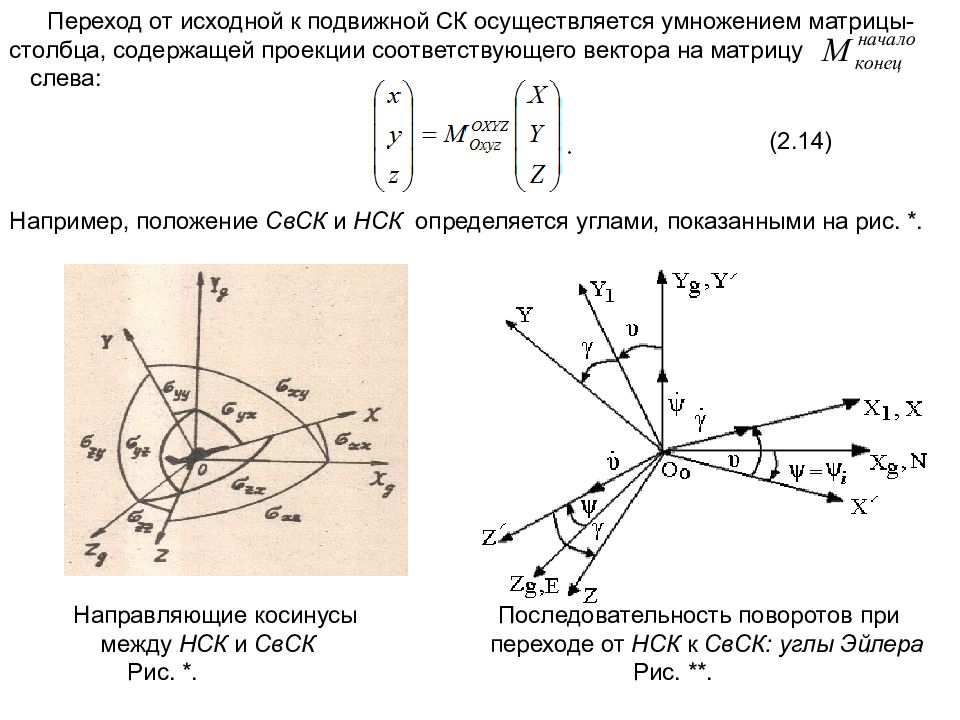
Переход от исходной к подвижной СК осуществляется умножением матрицы-столбца, содержащей проекции соответствующего вектора на матрицу слева: (2.14) Например, положение СвСК и НСК определяется углами, показанными на рис. *. Направляющие косинусы Последовательность поворотов при между НСК и СвСК переходе от НСК к СвСК : углы Эйлера Рис. *. Рис. **.
В большинстве случаев для определения относительного углового положения двух систем координат пользуются углами Эйлера – рис.**( в динамике ЛА эти углы называются углами тангажа, крена и рыскания ), связь которых с направляющими косинусами показана в табл. 2.1. Таблица 2.1.
В таблице 2.1(приведены два варианта) элементы равны соответствующим направляющим косинусам углов (рис. *), так.
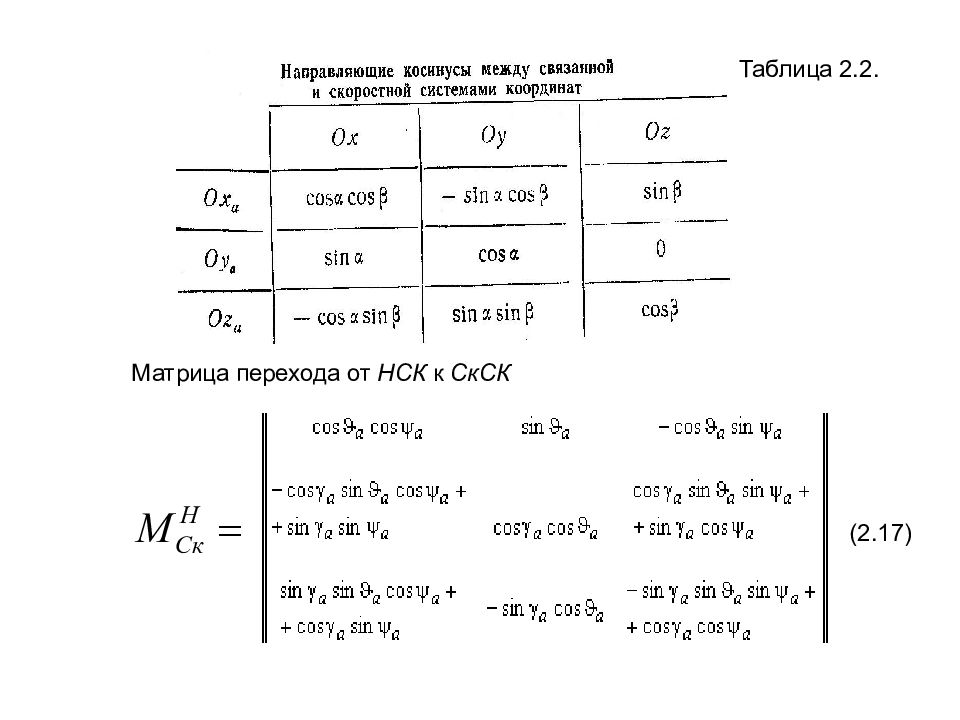
Переход к любой системе координат может быть представлен как результат последовательного поворота вокруг координатных осей. Так для перехода от НСК к СвСК общепринятой является следующая последовательность поворотов (рис. **): на угол рыскания вокруг оси ; на угол тангажа вокруг нового положения оси ; на угол крена вокруг оси. Здесь же показаны векторы соответствующих угловых скоростей. Матрица перехода от СвСК к НСК может быть представлена в следующем виде: (2.15) Обратный переход осуществляется с помощью транспонированной матрицы перехода = ( ). Матрица перехода от СвСК к Ск СК имеет вид (2.16) или в табличной форме – табл. 2.2.
Таблица 2.2. Матрица перехода от НСК к СкСК (2.17)
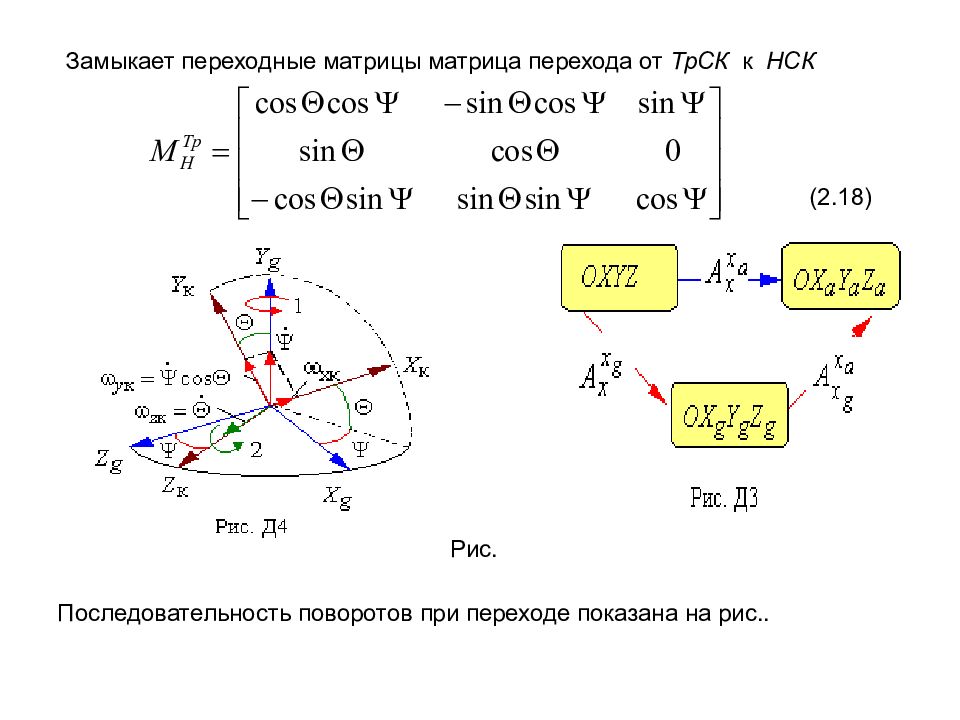
Замыкает переходные матрицы матрица перехода от ТрСК к НСК (2.18) Рис. Последовательность поворотов при переходе показана на рис..
Введение матрицы перехода описывает все возможные переходы от одной из перечисленных в п. 2.2.1. СК к другой. Так переход от ТрСК к СкСК осуществляется с помощью матрицы (2.19) На практических занятиях и при выполнении домашних заданий будут рассмотрены различные переходы между такими СК, как нормальная, связанная, скоростная и траекторная. Рассмотренные системы, параметры и элементы дают возможность составлять уравнение динамики полета ЛА в избранных системах координат и анализировать его устойчивость и управляемость.
