Синус, косинус, тангенс и котангенс.
На практике синусы и косинусы применяются во всех инженерных специальностях, особенно в строительных. Их используют моряки и летчики в расчетах курса движения. Не обходятся без синусов и косинусов геодезисты, и даже путешественники. В географии применяют для измерения расстояний между объектами, а также в спутниковых навигационных системах.
Детская школа Гауди в Барселоне
Ресторан в Лос- Манантиалесе в Аргентине
М ост в Сингапуре
Немного из истории… 1. Древние вавилоняне и египтяне изучали тригонометрию как часть астрономии ; разделили окружность на 360 2. Древние индийцы: ввели названия «синус», «косинус», составили таблицы синусов, косинусов 3. IX-XV вв – Средний и Ближний восток: составляли таблицы котангенса, тангенса, косеканса; ввели понятие единичной окружности
Немного из истории… 4. Насир ад-Дин Мухаммад ат-Туси (1201-1274) выделил раздел тригонометрии из астрономии. 5. Лев Герсонид (1288-1344) – открыл теорему синусов. 6. XVII-XIX вв : применение тригонометрии в механике, физике, технике, как часть математического анализа ( Виетт, Бернулли) – тригонометрические символы, графики – синусоиды. 7. Л.Эйлер: придал тригонометрии современный вид.
Тригонометрия раздел математики, изучающий соотношение сторон и углов в треугольнике («три» - три, « гониа » - угол, « метриа » - измеряю)
Единицы измерения углов Градусы Радианы
Градусная мера угла 1 – цена одного деления окружности, разделенной на 360 частей =1
Углом в 1 0 (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную 1/360 части окружности. Вся окружность состоит из 360 «кусочков» круговых дуг, или угол, описываемый окружностью, равен 360 0. На рисунке изображен угол β, равный 50 0 то есть этот угол опирается на круговую дугу размером 50/360 длины окружности.
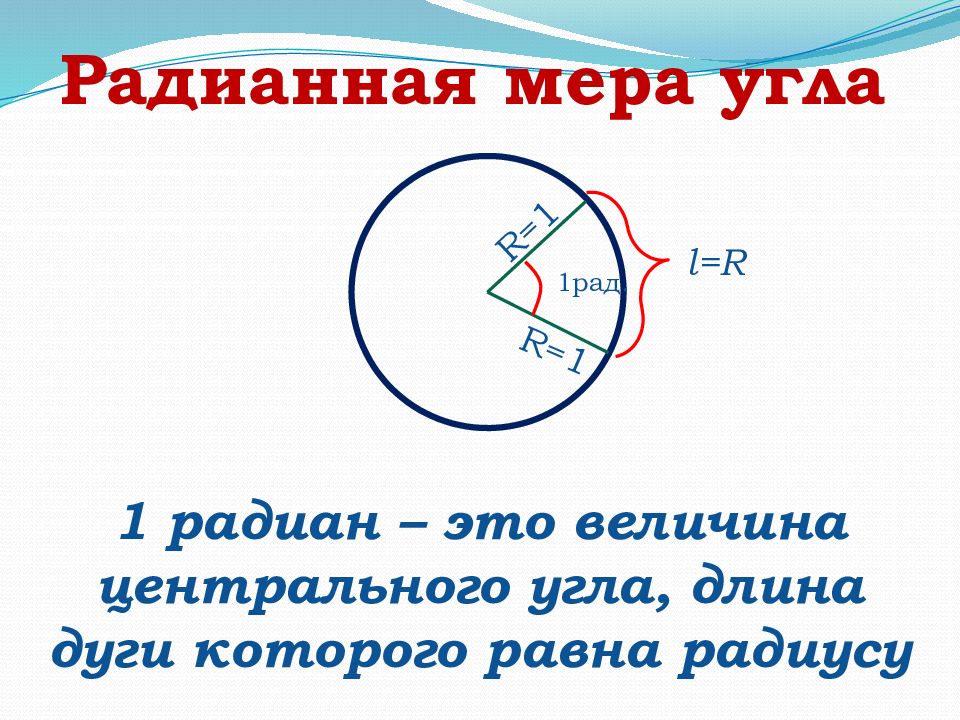
Радианная мера угла 1 радиан – это величина центрального угла, длина дуги которого равна радиусу 1рад. R =1 R =1 l=R
Единицы измерения углов Градусы Радианы радиан =180
радиан =180 Перевод из градусной меры в радианную :
Пример: 1. 2. 3.
Пример: 4. 5. 6.
Пример: 1. 2. 3.
Пример: 4. 5. 6.
радиан =180 Перевод из радианной меры в градусную:
Пример: 1. 2. 3.
Пример: 1. 2. 3.
№1: Переведите в радианную меру углы: 1) 45 2) 15 3) 72 4) 100 5) 200 6) 360 7) 215 8) 150 9) 330
№2: Переведите в градусную меру углы: 1) 2) 3) 4) 5) 6)
Перевод из градусной меры в радианную: Перевод из радианной меры в градусную:
Самостоятельная работа 1. Переведите в радианную меру углы: 1) 60 2) 145 3) 240 I вариант II вариант 1) 32 0 2) 105 3) 40 2. Переведите в градусную меру углы: 1) 2) 1) 2)
Ответы 1. 1) 2) 3) I вариант II вариант 1) 2) 3) 2. 1) 72 2) 480 1) 405 2) 150
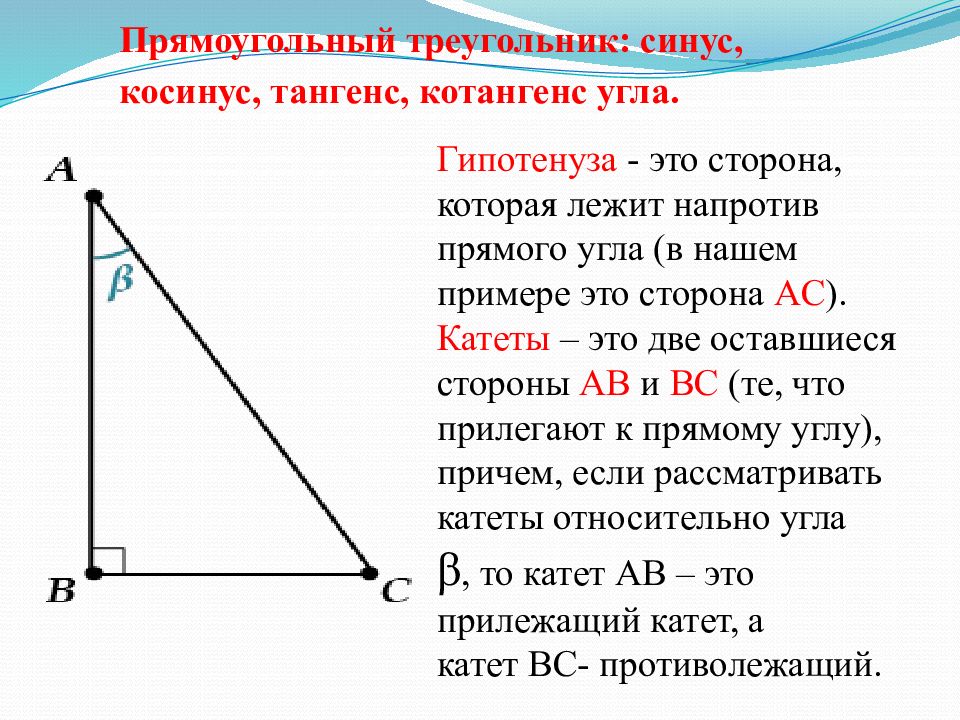
Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла. Гипотенуза - это сторона, которая лежит напротив прямого угла (в нашем примере это сторона AC ). Катеты – это две оставшиеся стороны AB и BC (те, что прилегают к прямому углу), причем, если рассматривать катеты относительно угла β, то катет AB – это прилежащий катет, а катет BC- противолежащий.
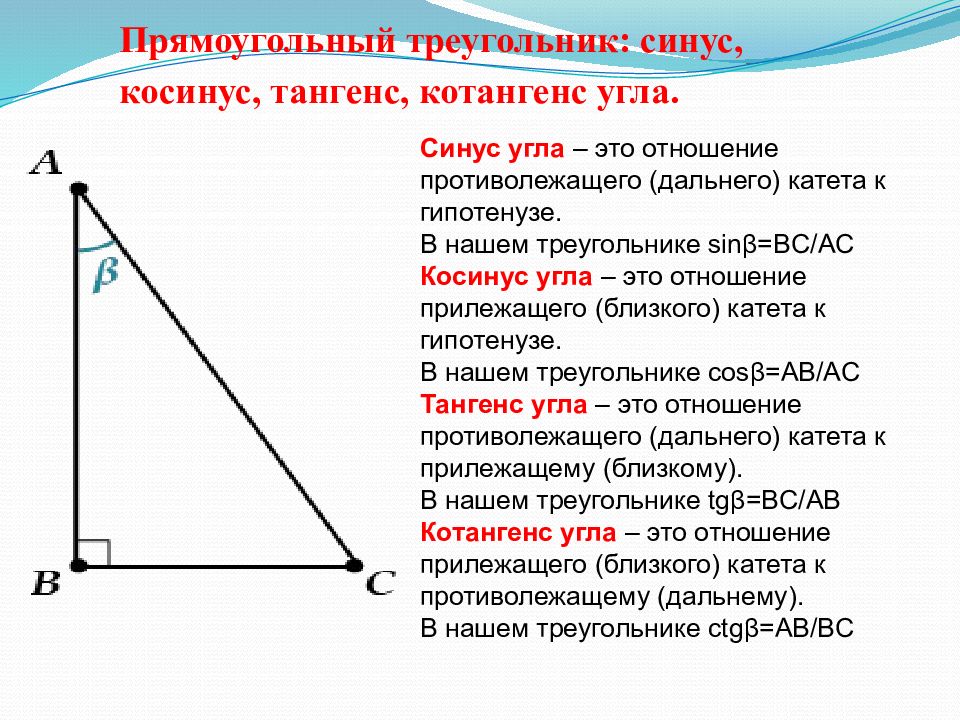
Прямоугольный треугольник: синус, косинус, тангенс, котангенс угла. Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе. В нашем треугольнике sin β=BC/AC Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе. В нашем треугольнике cos β=AB/AC Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому). В нашем треугольнике tg β=BC/AB Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему). В нашем треугольнике ctg β=AB/BC
Синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле). Рассмотрим, к примеру, косинус угла β. По определению, из треугольника ABC : cos β=AB/AC=4/6=2/3, но ведь мы можем вычислить косинус угла β и из треугольника AHI: cosβ=AH/AI=6/9=2/3 . Видите, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
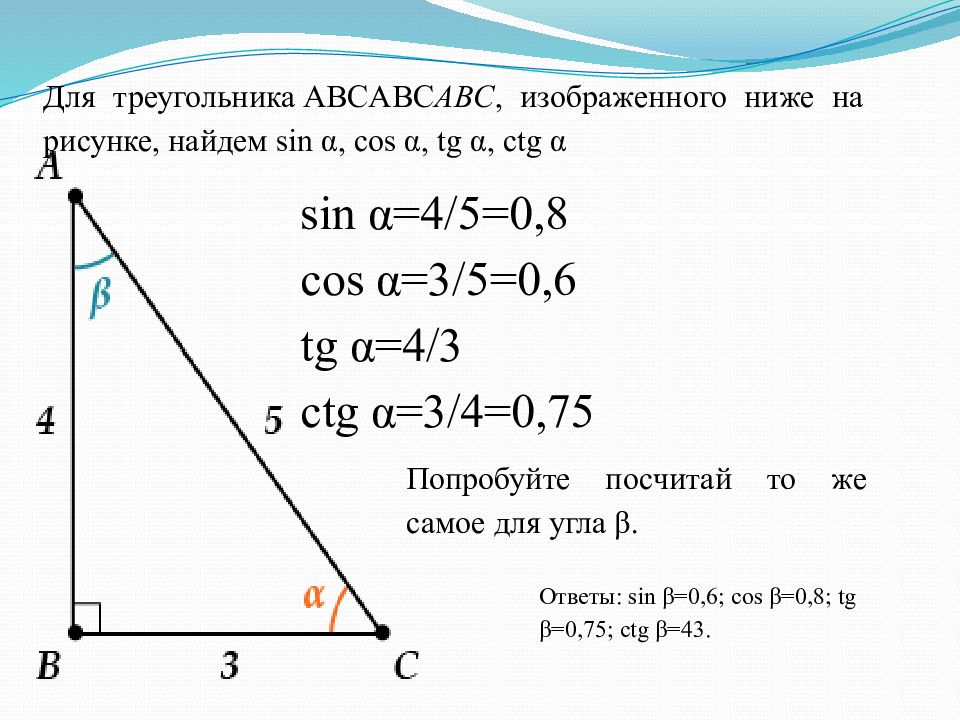
Для треугольника ABCABC ABC, изображенного ниже на рисунке, найдем sin α, cos α, tg α, ctg α sin α =4/5=0,8 cos α =3/5=0,6 tg α =4/3 ctg α=3/4=0,75 Попробуйте посчитай то же самое для угла β. Ответы: sin β=0,6; cos β=0,8; tg β=0,75; ctg β=43.
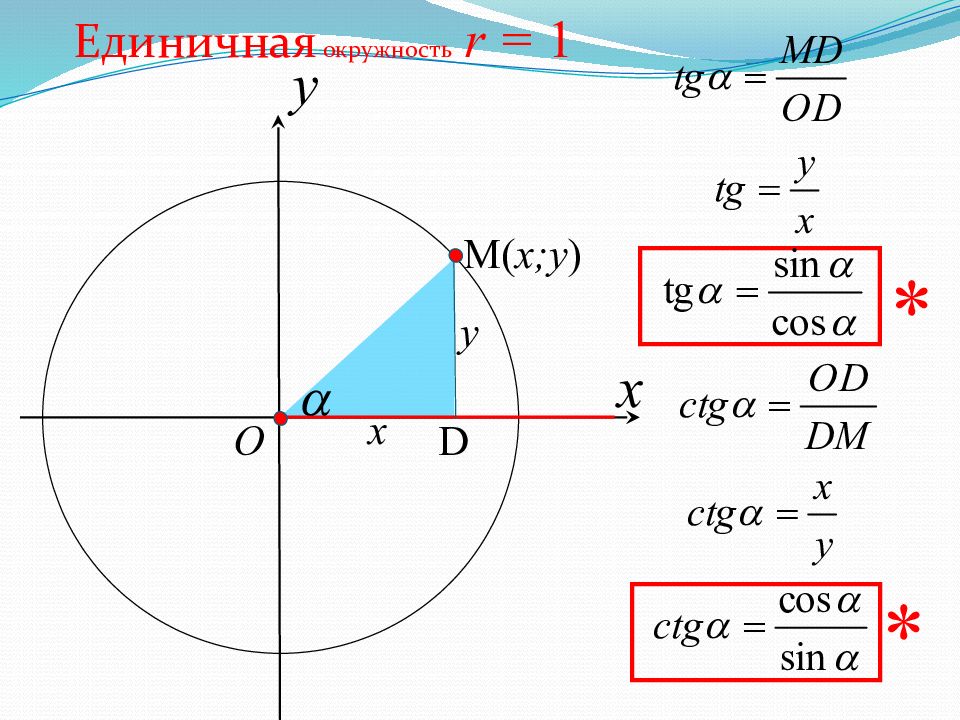
Окружность с радиусом, равным 1называется единичной. Данная окружность построена в декартовой системе координат. Радиус окружности равен единице, при этом центр окружности лежит в начале координат, начальное положение радиуса-вектора зафиксировано вдоль положительного направления оси x (в нашем примере, это радиус AB). Единичная окружность r = 1
x y O Положительное направление поворота: против часовой стрелки. Отрицательное направление поворота: по часовой стрелке. + –
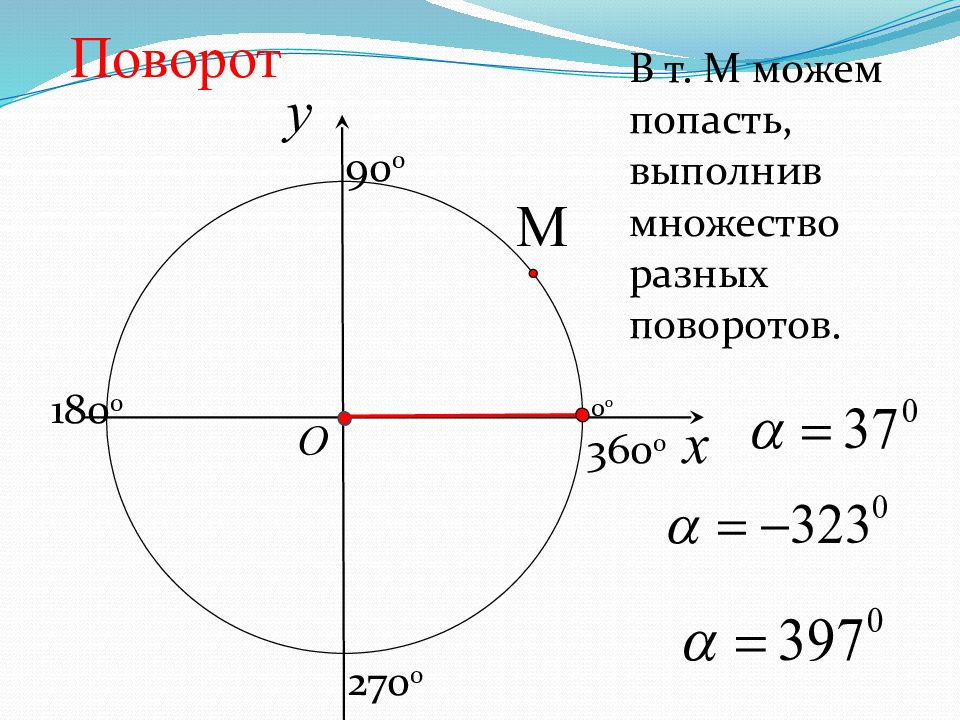
x y O Поворот M В т. М можем попасть, выполнив множество разных поворотов. 90 0 180 0 270 0 360 0 0 0
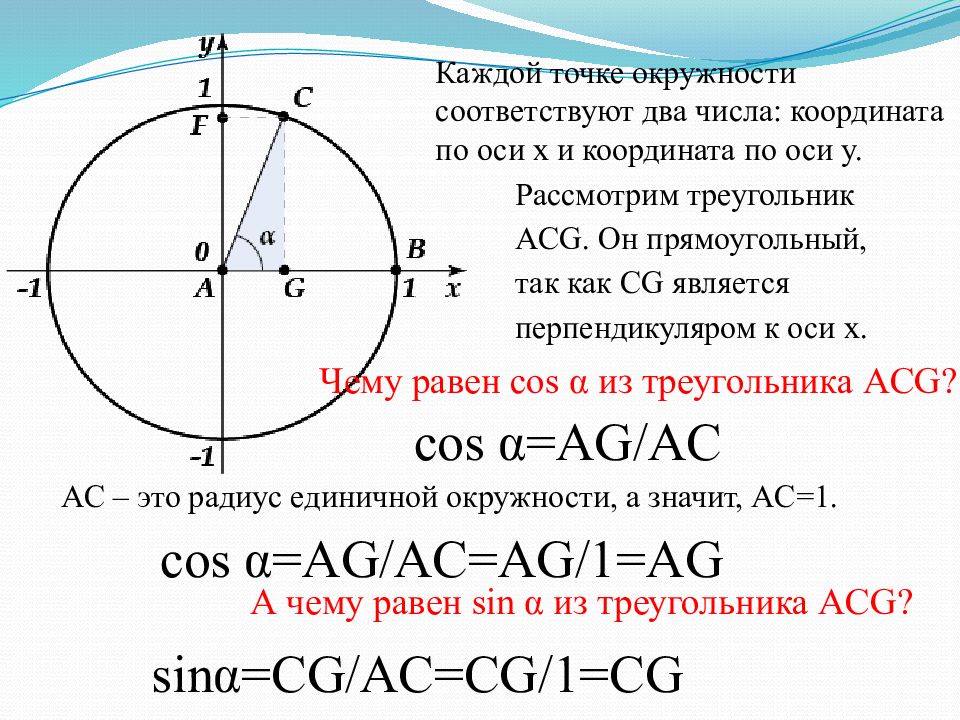
Каждой точке окружности соответствуют два числа: координата по оси x и координата по оси y. Рассмотрим треугольник ACG. Он прямоугольный, так как CG является перпендикуляром к оси x. Чему равен cos α из треугольника ACG? cos α=AG/AC AC – это радиус единичной окружности, а значит, AC=1. cos α =AG/AC=AG/1=AG А чему равен sin α из треугольника ACG? sin α=CG/AC=CG/1=CG
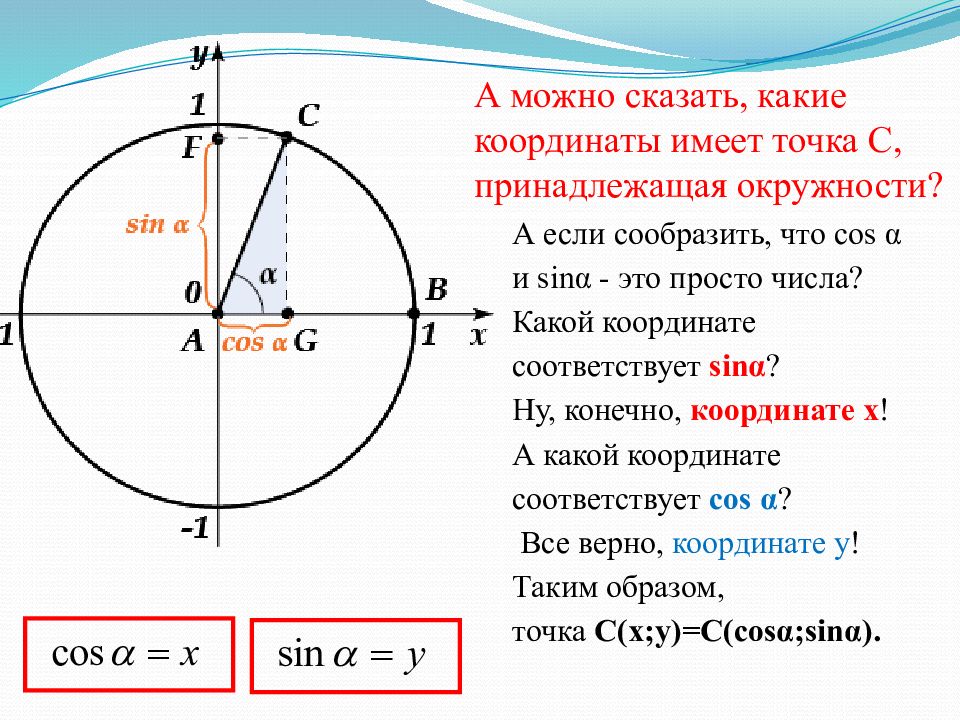
А можно сказать, какие координаты имеет точка C, принадлежащая окружности? А если сообразить, что cos α и sin α - это просто числа? Какой координате соответствует sin α ? Ну, конечно, координате x ! А какой координате соответствует cos α ? Все верно, координате y ! Таким образом, точка C( x;y )=C( cos α;sinα).
x Единичная окружность r = 1 y O x y D * * M ( x;y )
C инусом угла называется ордината y точки М, а косинусом угла – абсцисса x точки М. x = a cos y ; = a sin
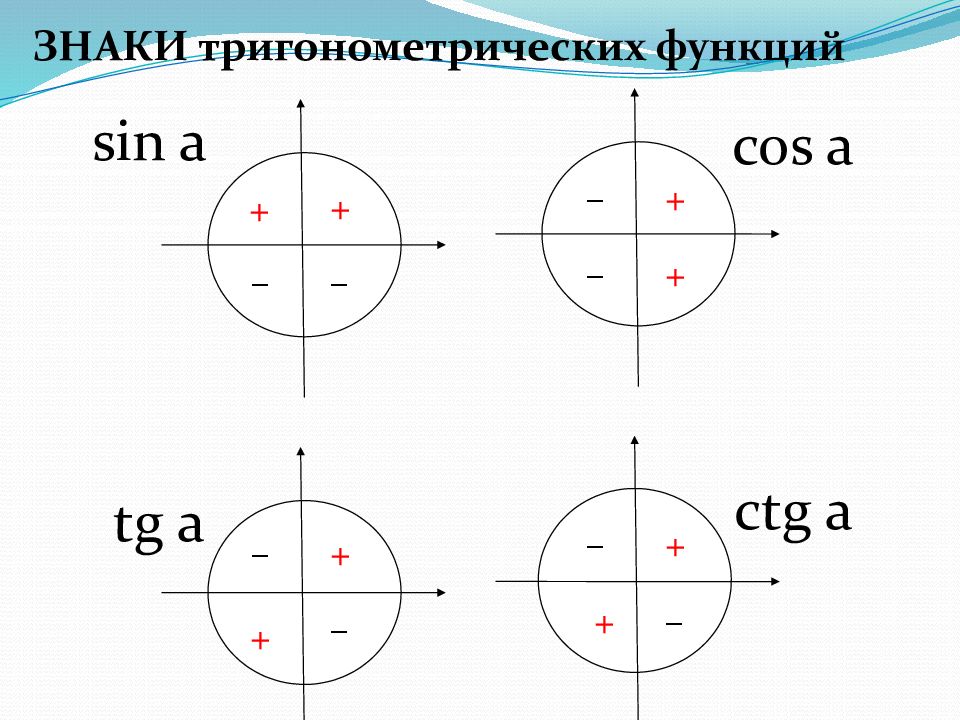
– + + + + + + + + – – – – – – – ЗНАКИ тригонометрических функций sin a cos a tg a ctg a
Домашнее задание Выучить формулы перевода из градусной меры угла в радианную и обратно. Выучить определения sin, cos, tg, ctg 3 ) Переведите в радианную меру углы: 75 , 15, 130, 220, 340 4 ) Переведите в градусную меру углы: ,,,,
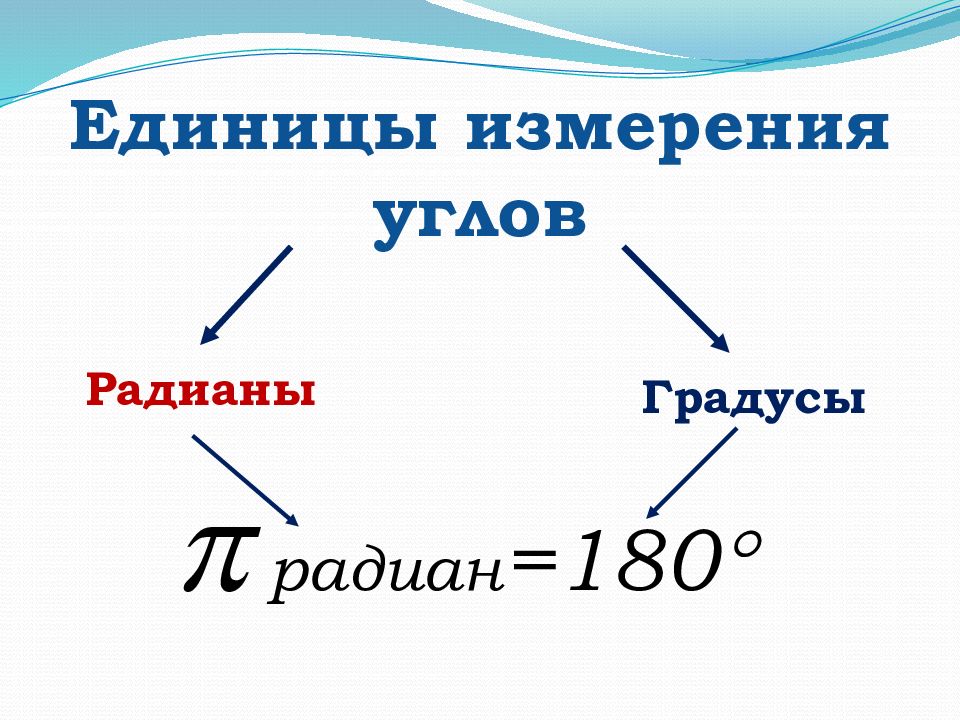
Ответьте на вопросы: 1) Что означает «тригонометрия»? 2) Разделом какой науки являлась тригонометрия в начале развития? 3)Какие единицы измерения углов Вы знаете? 4 ) Чему равно радиан ? 5) Как перевести из градусной меры в радианную и обратно? 6) Было ли интересно на уроке?
