1 Навигация. Пилотажно-навигационное оборудование Ясенок Андрей Васильевич
2 Список литературы В.Я. Мамаев, А.Н. Синяков, К.К. Петров, Д.А. Горбунов. Воздушная навигация и элементы самолетовождения. СПБ. 2002. К.М. Антонович. Использование спутниковых радионавигационных систем в геодезии. М. 2005. Ю.А. Соловьев Системы спутниковой навигации. - М. 2000. Андреев В.Д. Теория инерциальной навигации. М. 1966.
3 Самолетовождение Самолетовождение – выполнение полета по заданным пространственно-временным траекториям в фактических географических и метеорологических условиях. Самолетовождение включает в себя навигацию и пилотирование (управление) летательным аппаратом на всех этапах полета. Самолетовождение обеспечивается экипажем, пилотажно-навигационным оборудованием и наземными техническими средствами службы движения.
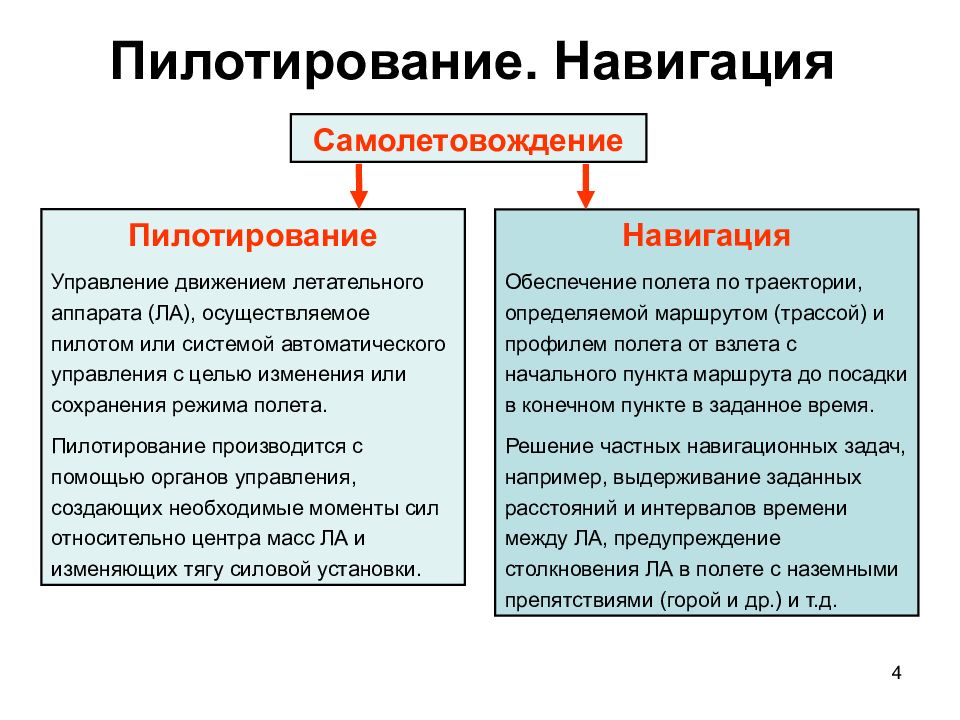
4 Пилотирование. Навигация Самолетовождение Пилотирование Управление движением летательного аппарата (ЛА), осуществляемое пилотом или системой автоматического управления с целью изменения или сохранения режима полета. Пилотирование производится с помощью органов управления, создающих необходимые моменты сил относительно центра масс ЛА и изменяющих тягу силовой установки. Навигация Обеспечение полета по траектории, определяемой маршрутом (трассой) и профилем полета от взлета с начального пункта маршрута до посадки в конечном пункте в заданное время. Решение частных навигационных задач, например, выдерживание заданных расстояний и интервалов времени между ЛА, предупреждение столкновения ЛА в полете с наземными препятствиями (горой и др.) и т.д.
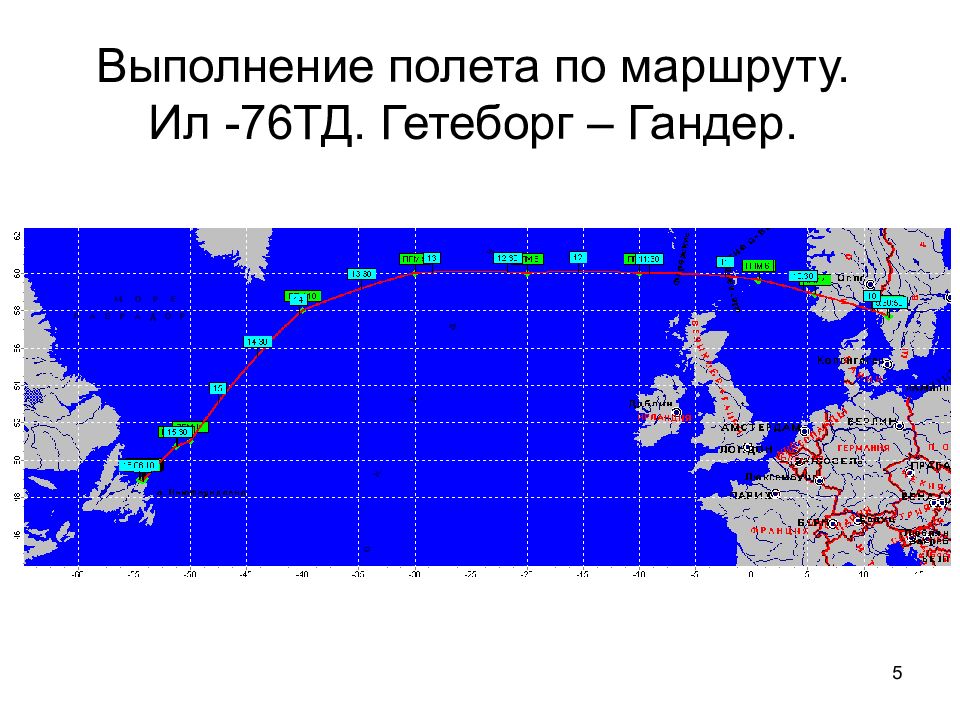
5 Выполнение полета по маршруту. Ил -76ТД. Гетеборг – Гандер.
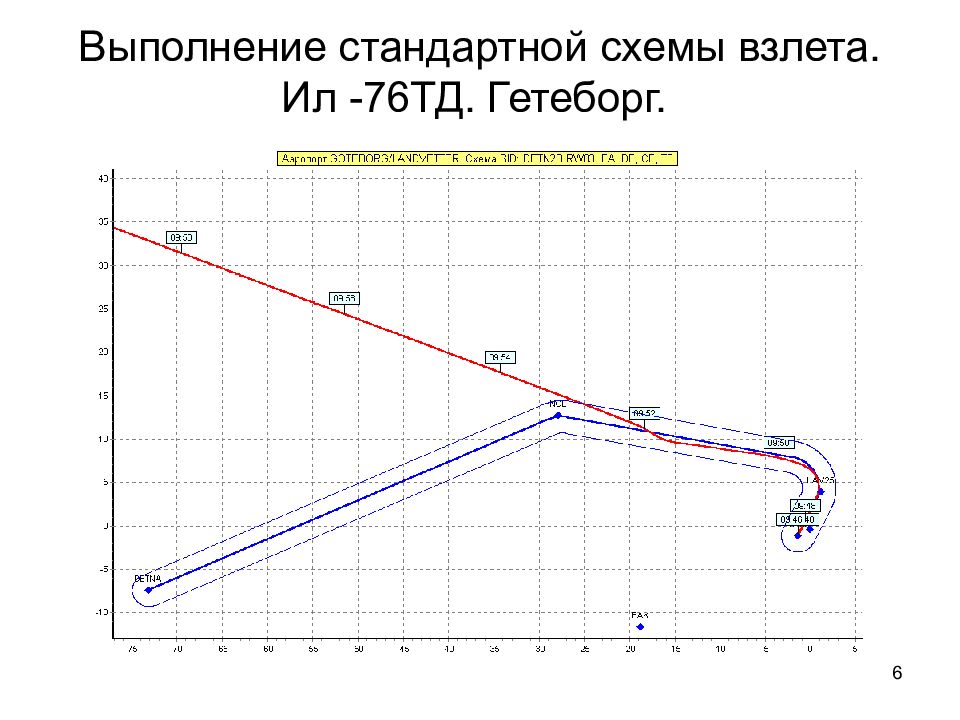
6 Выполнение стандартной схемы взлета. Ил -76ТД. Гетеборг.
7 Навигационные элементы (параметры) При выполнении полета по заданной траектории (или маршруту) навигация сводится в основном к получению и контролю информации о текущих навигационных элементах движения центра масс ЛА относительно системы координат, привязанной к земной поверхности. Основные навигационные элементы: время; текущие координаты ЛА в выбранной системе координат; высота и вертикальная скорость: угловые параметры (курс, крен, тангаж и т.д.); скорость (путевая, воздушная).
8 Системы координат
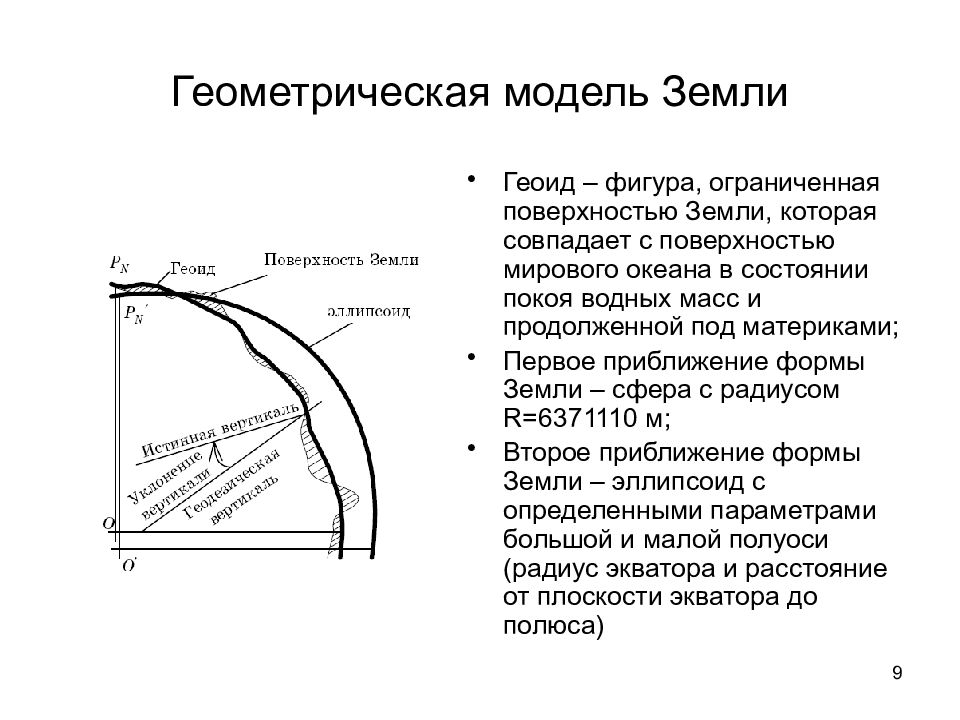
9 Геометрическая модель Земли Геоид – фигура, ограниченная поверхностью Земли, которая совпадает с поверхностью мирового океана в состоянии покоя водных масс и продолженной под материками; Первое приближение формы Земли – сфера с радиусом R =6371110 м; Второе приближение формы Земли – эллипсоид с определенными параметрами большой и малой полуоси (радиус экватора и расстояние от плоскости экватора до полюса)
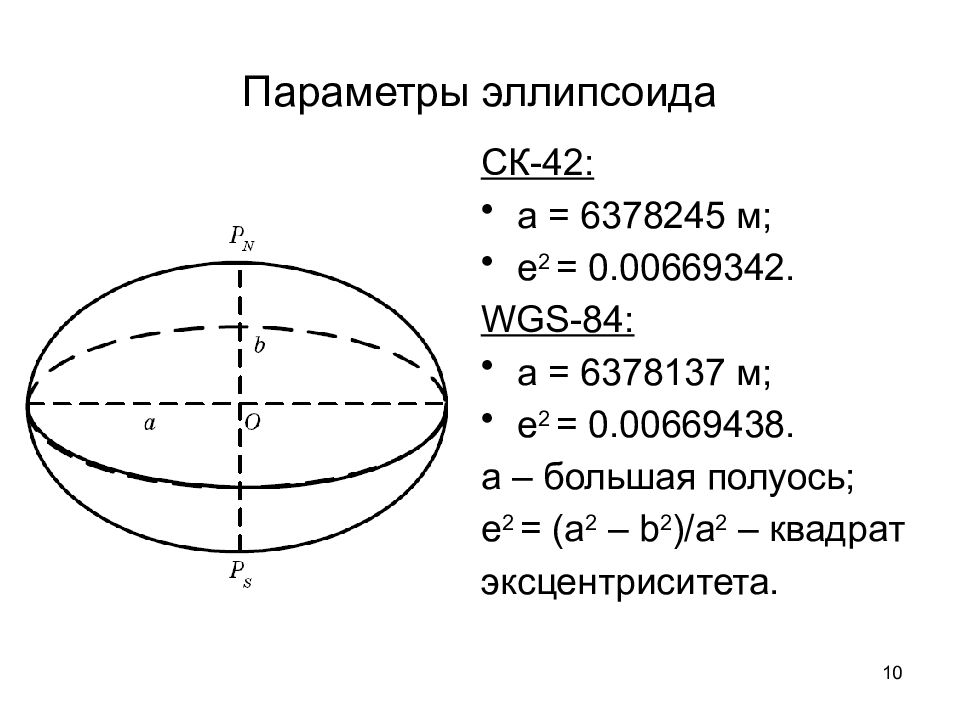
10 Параметры эллипсоида СК-42: a = 6378245 м; e 2 = 0.00669342. WGS - 8 4: a = 6378137 м; e 2 = 0.006 6943 8. а – большая полуось; e 2 = ( a 2 – b 2 )/a 2 – квадрат эксцентриситета.
11 Глобальные системы координат
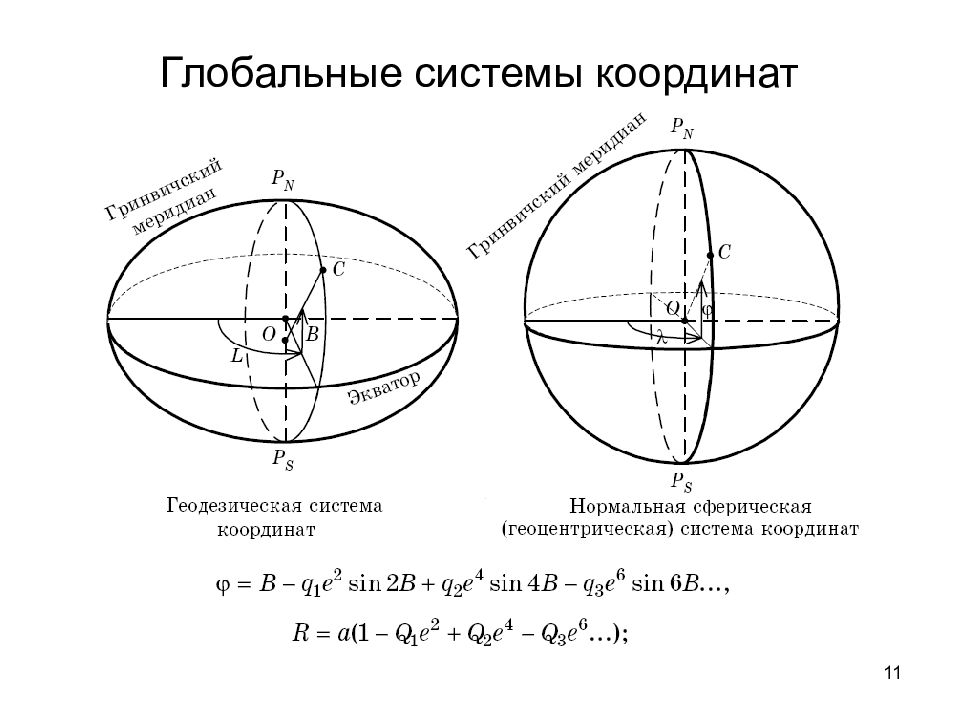
12 Параметры глобальных систем координат Экватор – окружность, плоскость которой перпендикулярна оси вращения Земли и включает центр системы координат. Меридиан – окружность, плоскость которой проходит через ось вращения Земли. Параллель – окружность, плоскость которой перпендикулярна оси вращения (параллельна экватору). Экватор на Земле один, а меридианов и параллелей бесконечное множество – через любую точку можно провести свой меридиан или параллель. Один из меридианов (Гринвичский) выбран в качестве начального. Широта (φ) – угол между плоскостью экватора и направлением из центра сферы в данную точку. Широта изменяется от 90° южной широты до 90° северной широты. На экваторе широта равна нулю, а на географических полюсах ±90°. Долгота (λ) – угол между плоскостями начального меридиана и меридиана данной точки. Долгота изменяется от 180° западной долготы до 180° восточной.
13 Единицы измерений координат Единицами измерения широты и долготы являются угловые градусы, минуты, секунды и их десятичные доли (десятые, сотые и т.д.). За рубежом используются следующие буквенные обозначения: N (north) – север, S (south) – юг, E (east) – восток, W (west) – запад. Значения широты и долготы в аэронавигационных документах могут быть записаны в следующем виде: 37° 23′ 12′′ с.ш. = N37° 23.2′ = +37.38667° 134° 45′ 45′′ з.д. = W134° 45.75′ = -134.7625°
14 Примерная длина меридиана и экватора : S = 2πR з ≈ 2 х 3,14 1 59 х 6371 ≈ 40030 км Примерная длина дуги меридиана (экватора) в 1° или в 1’: 1° дуги = S/360° = 40 030 км/360° = 111,2 км 1’ дуги = 111,2 км/60’ = 1,852 км Примерная длина потому, что меридиан является не окружностью, а эллипсом и длина дуги различается на разных широтах. Длина дуги параллели зависит от широты ( φ ) и определяется формулой L пар = L экв х cos φ, где L экв – длина дуги экватора с заданной разностью долготы. Для одной и той же разности долготы длина дуги параллели с приближением к полюсам уменьшается ( функция косинуса убывает с увеличением угла ). Связь угловых и линейных единиц измерений координат
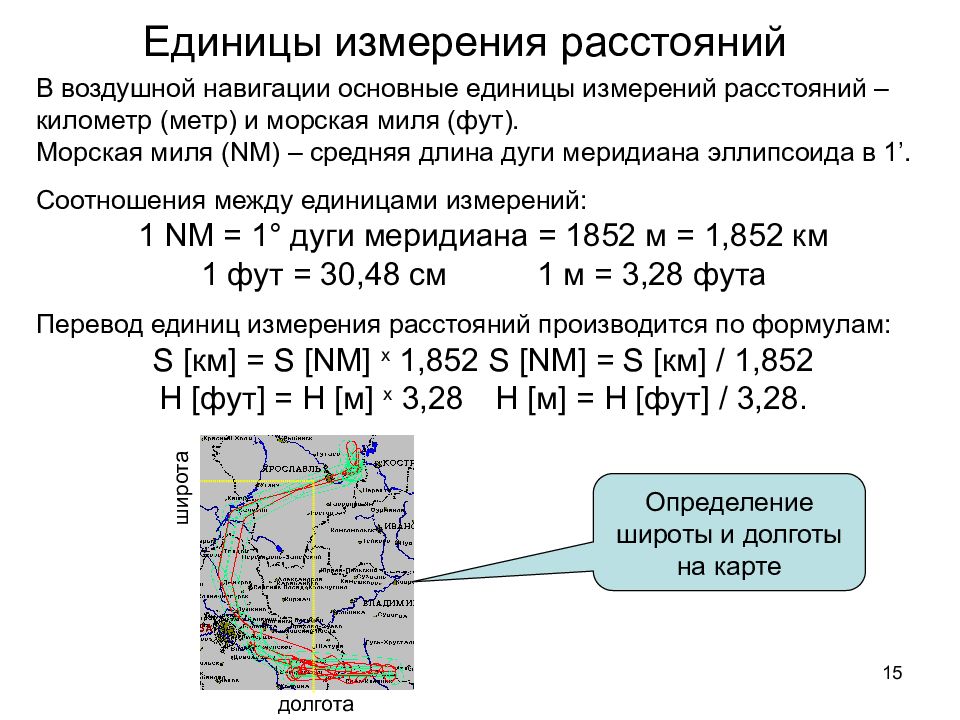
15 Единицы измерения расстояний В воздушной навигации основные единицы измерений расстояний –километр (метр) и морская миля (фут). Морская миля (NM) – средняя длина дуги меридиана эллипсоида в 1’. Соотношения между единицами измерений: 1 N М = 1° дуги меридиана = 1852 м = 1,852 км 1 фут = 30,48 см 1 м = 3,28 фута Перевод единиц измерения расстояний производится по формулам: S [ км ] = S [N М ] x 1,852 S [N М ] = S [ км ] / 1,852 H [ фут ] = Н [ м ] x 3,28 H [ м ] = H [ фут ] / 3,28. Определение широты и долготы на карте долгота широта
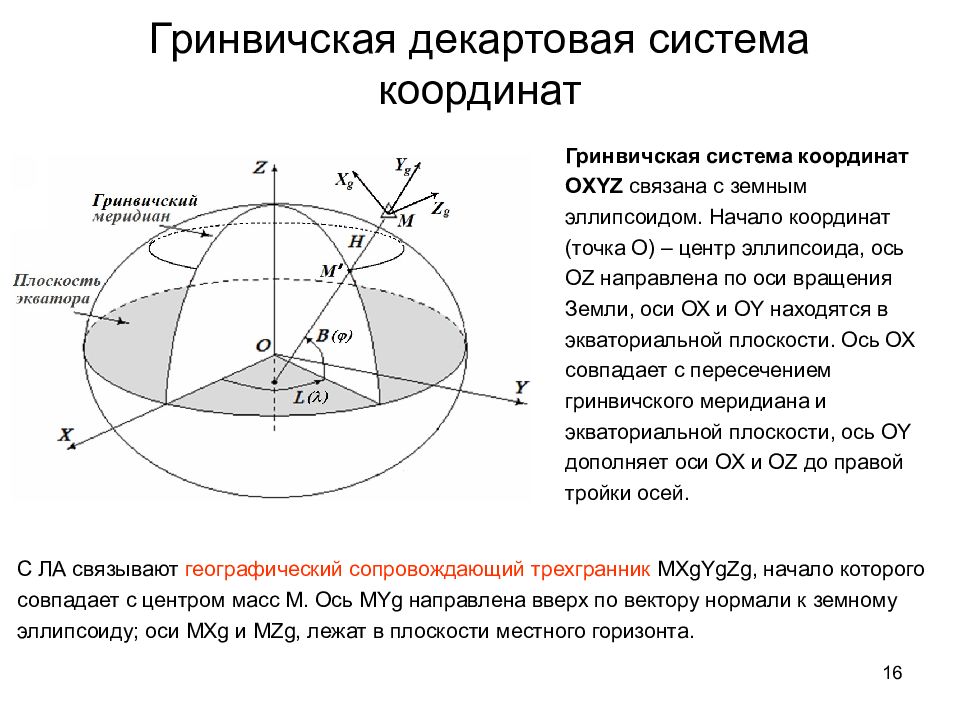
16 С ЛА связывают географический сопровождающий трехгранник MXgYgZg, начало которого совпадает с центром масс М. Ось MYg направлена вверх по вектору нормали к земному эллипсоиду; оси MXg и MZg, лежат в плоскости местного горизонта. Гринвичская декартовая система координат Гринвичская система координат О XYZ связана с земным эллипсоидом. Начало координат (точка О) – центр эллипсоида, ось OZ направлена по оси вращения Земли, оси ОХ и OY находятся в экваториальной плоскости. Ось ОХ совпадает с пересечением гринвичского меридиана и экваториальной плоскости, ось OY дополняет оси ОХ и OZ до правой тройки осей.
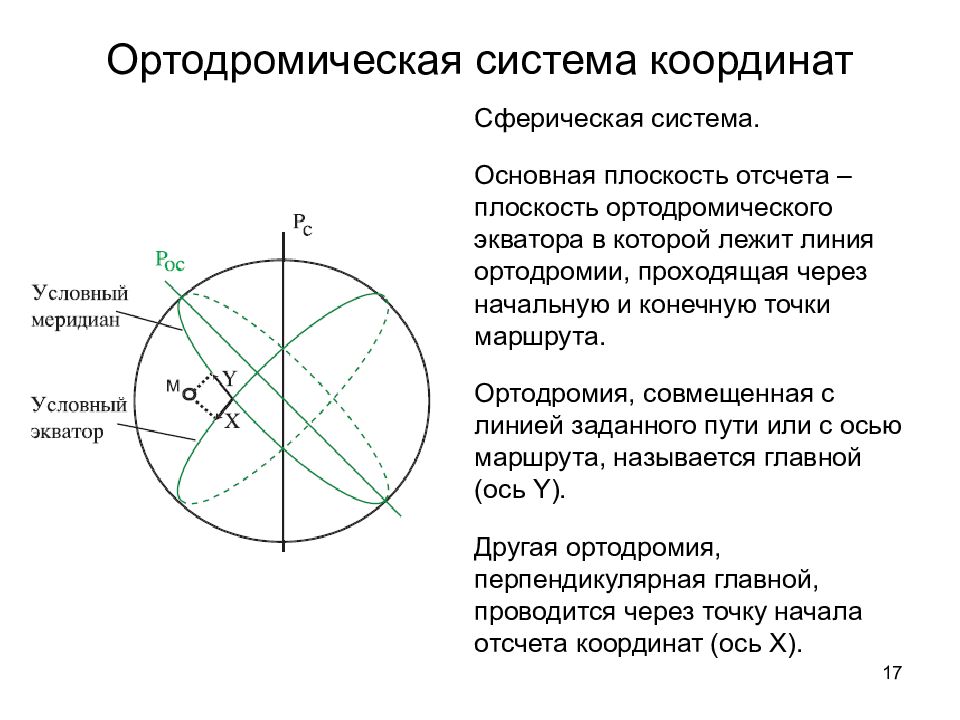
17 Ортодромическая система координат Сферическая система. Основная плоскость отсчета – плоскость ортодромического экватора в которой лежит линия ортодромии, проходящая через начальную и конечную точки маршрута. Ортодромия, совмещенная с линией заданного пути или с осью маршрута, называется главной (ось Y). Другая ортодромия, перпендикулярная главной, проводится через точку начала отсчета координат (ось X).
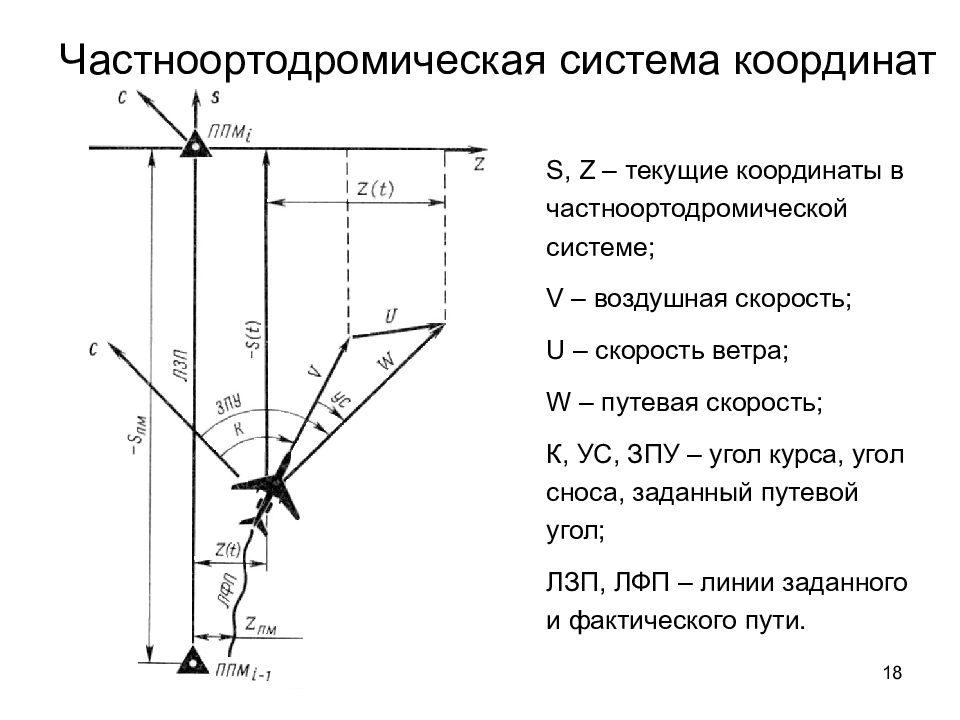
18 Частноортодромическая система координат S, Z – текущие координаты в частноортодромической системе; V – воздушная скорость; U – скорость ветра; W – путевая скорость; К, УС, ЗПУ – угол курса, угол сноса, заданный путевой угол; ЛЗП, ЛФП – линии заданного и фактического пути.
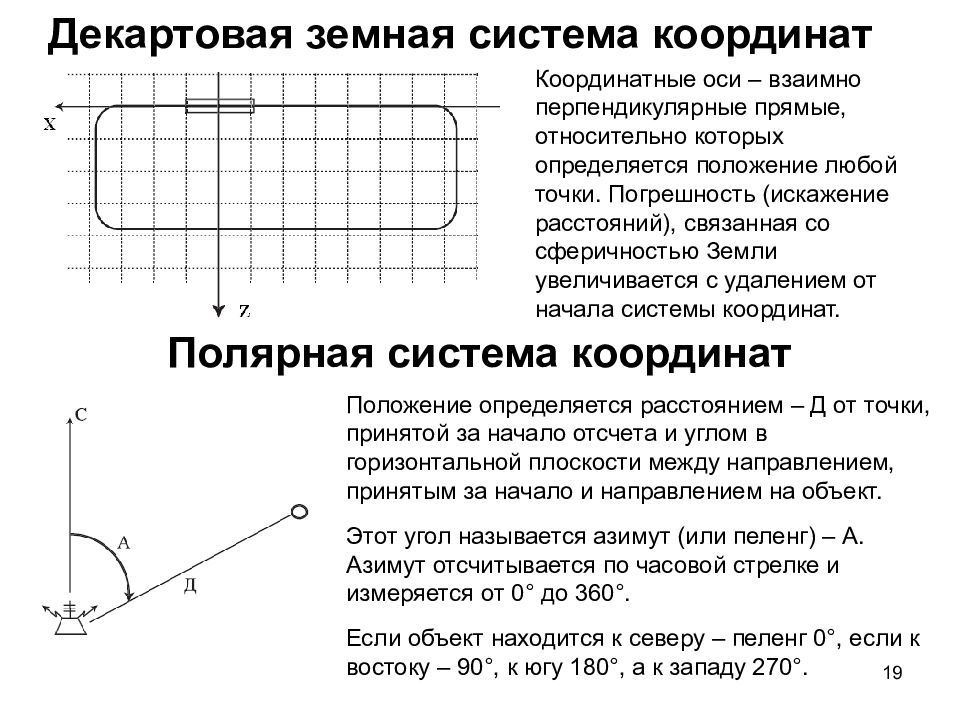
19 Декартовая земная система координат Координатные оси – взаимно перпендикулярные прямые, относительно которых определяется положение любой точки. Погрешность (искажение расстояний), связанная со сферичностью Земли увеличивается с удалением от начала системы координат. Полярная система координат Положение определяется расстоянием – Д от точки, принятой за начало отсчета и углом в горизонтальной плоскости между направлением, принятым за начало и направлением на объект. Этот угол называется азимут (или пеленг) – А. Азимут отсчитывается по часовой стрелке и измеряется от 0° до 360°. Если объект находится к северу – пеленг 0°, если к востоку – 90°, к югу 180°, а к западу 270°.
20 Пересчет геодезических координат в декартовую систему координат Исходные данные для преобразования: координаты самолета B, L, H ; координаты Bo, Lo, H o начала декартовой топоцентрической системы; азимут (направление) A o оси X. 1. Координаты B, L, H и Bo, Lo, H o преобразуются в прямоугольные геоцентрические координаты. X = (N + H) × cos(B) × cos(L), Y = (N + H) × cos(B) × sin(L), Z = [(1 – e 2 ) × N + H ] × sin ( B ), где N – радиус кривизны первого вертикала; a, e 2 – большая полуось и квадрат эксцентриситета эллипсоида. 2. Вычисляются проекции геоцентрических координат относительно начала топоцентрической системы. dX = X – Xo, dY = Y – Yo, dZ = Z – Zo. 3. Прямоугольные топоцентрические координаты. X тц = dX×[-sin(Lo)sin(Ao) – sin(Bo)cos(Lo)cos(Ao)] + dY×[cos(Lo)sin(Ao) – sin(Bo)sin(Lo)cos(Ao)] + dZ×[cos(Bo)cos(Ao) ], Y тц = dX×[cos(Bo)cos(Lo) ] + dY×[cos(Bo)cos(Lo)] + dZ×[sin(Bo)], Z тц = dX×[-sin(Lo)cos(Ao) + sin(Bo)cos(Lo)sin(Ao)] + dY×[cos(Lo)cos(Ao) + sin(Bo)sin(Lo)sin(Ao)] - dZ×[cos(Bo)sin(Ao) ].
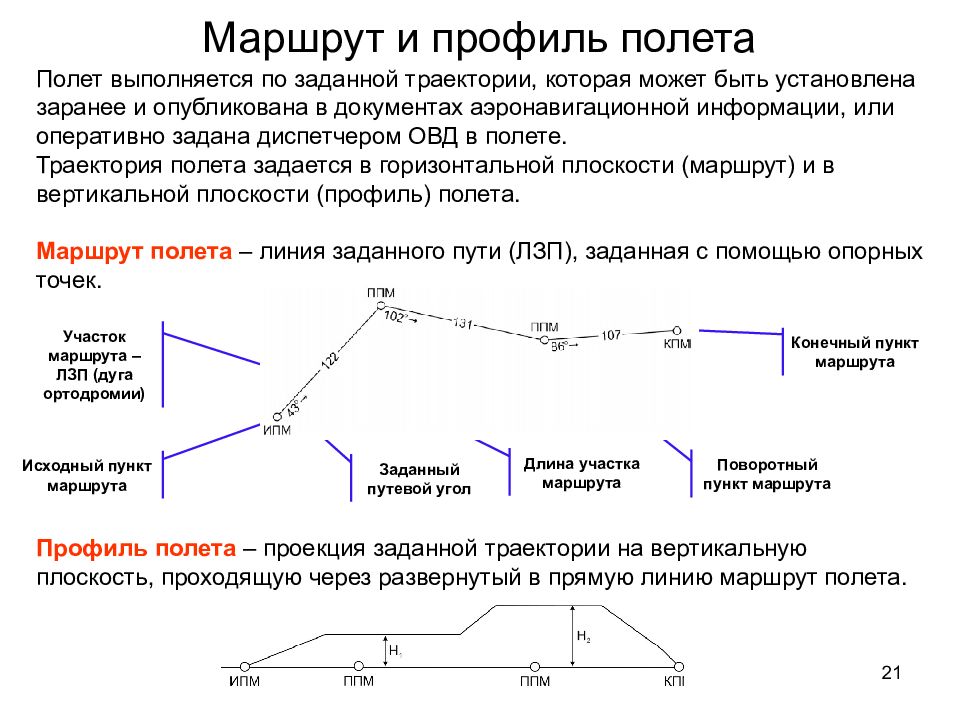
21 Маршрут и профиль полета Полет выполняется по заданной траектории, которая может быть установлена заранее и опубликована в документах аэронавигационной информации, или оперативно задана диспетчером ОВД в полете. Траектория полета задается в горизонтальной плоскости (маршрут) и в вертикальной плоскости (профиль) полета. Маршрут полета – линия заданного пути (ЛЗП), заданная с помощью опорных точек. Исходный пункт маршрута Конечный пункт маршрута Поворотный пункт маршрута Заданный путевой угол Длина участка маршрута Участок маршрута – ЛЗП (дуга ортодромии) Профиль полета – проекция заданной траектории на вертикальную плоскость, проходящую через развернутый в прямую линию маршрут полета.
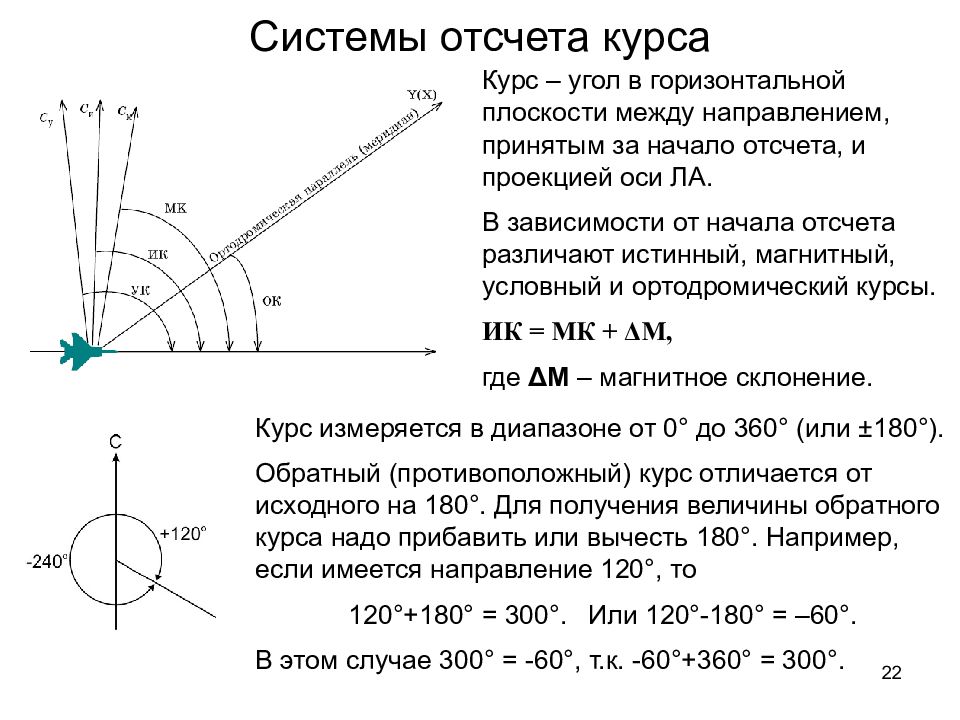
22 Системы отсчета курса Курс – угол в горизонтальной плоскости между направлением, принятым за начало отсчета, и проекцией оси ЛА. В зависимости от начала отсчета различают истинный, магнитный, условный и ортодромический курсы. ИК = МК + Δ М, где Δ М – магнитное склонение. Курс измеряется в диапазоне от 0° до 360° (или ± 18 0°). Обратный (противоположный) курс отличается от исходного на 180°. Для получения величины обратного курса надо прибавить или вычесть 180°. Например, если имеется направление 120°, то 120°+180° = 300°. Или 120°-180° = –60°. В этом случае 300° = -60°, т.к. -60°+360° = 300°.
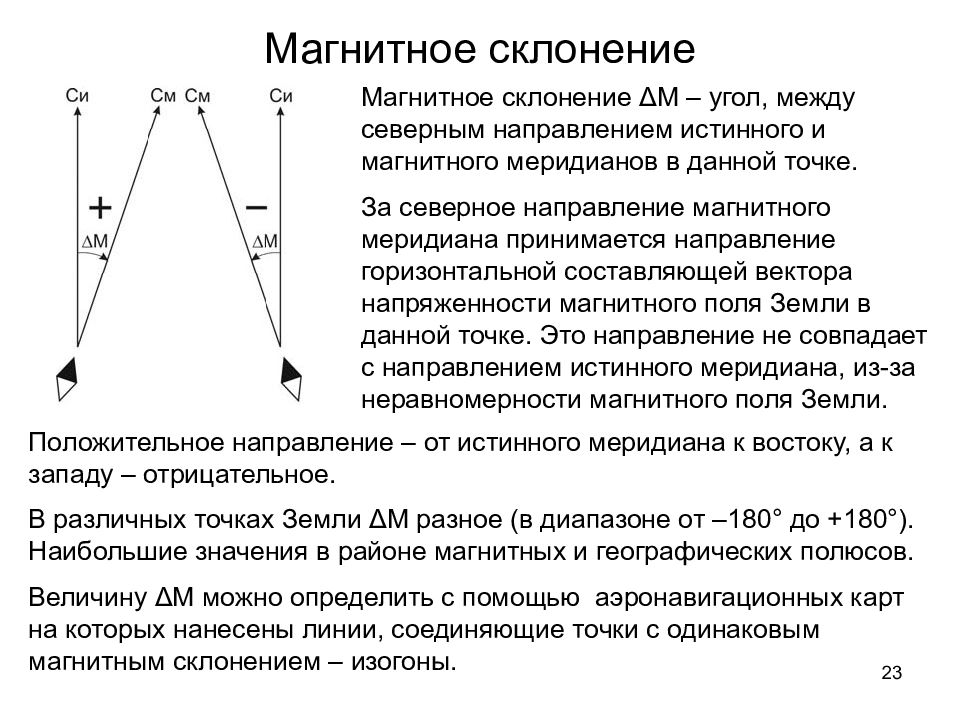
23 Магнитное склонение Магнитное склонение ΔМ – угол, между северным направлением истинного и магнитного меридианов в данной точке. За северное направление магнитного меридиана принимается направление горизонтальной составляющей вектора напряженности магнитного поля Земли в данной точке. Это направление не совпадает с направлением истинного меридиана, из-за неравномерности магнитного поля Земли. Положительное направление – от истинного меридиана к востоку, а к западу – отрицательное. В различных точках Земли ΔМ разное (в диапазоне от –180° до +180°). Наибольшие значения в районе магнитных и географических полюсов. Величину ΔМ можно определить с помощью аэронавигационных карт на которых нанесены линии, соединяющие точки с одинаковым магнитным склонением – изогоны.
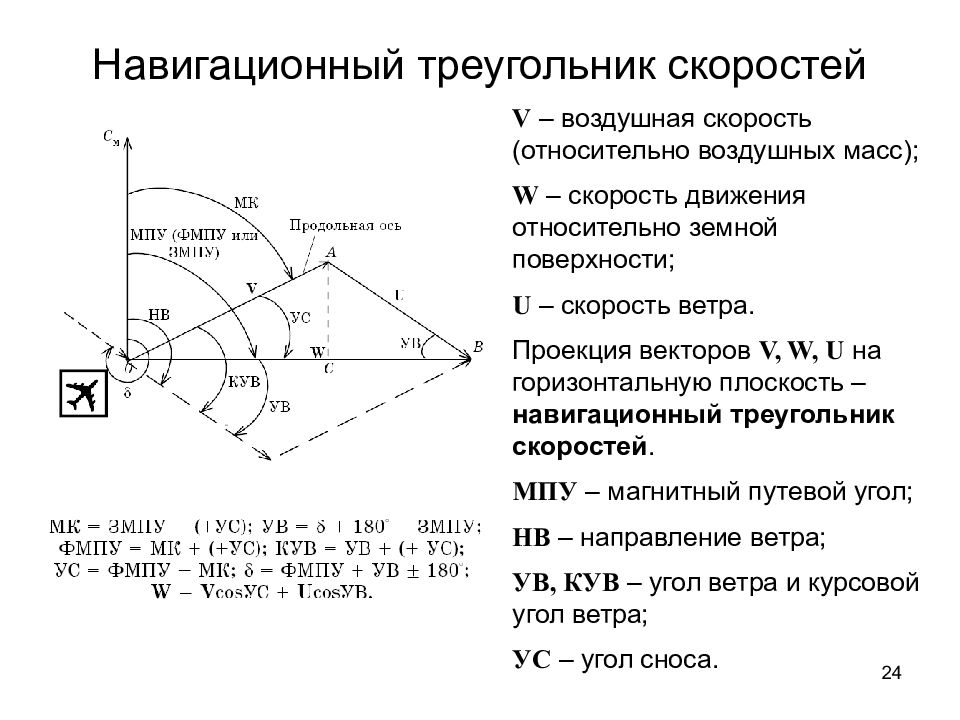
24 Навигационный треугольник скоростей V – воздушная скорость (относительно воздушных масс); W – скорость движения относительно земной поверхности; U – скорость ветра. Проекция векторов V, W, U на горизонтальную плоскость – навигационный треугольник скоростей. МПУ – магнитный путевой угол; НВ – направление ветра; УВ, КУВ – угол ветра и курсовой угол ветра; УС – угол сноса.
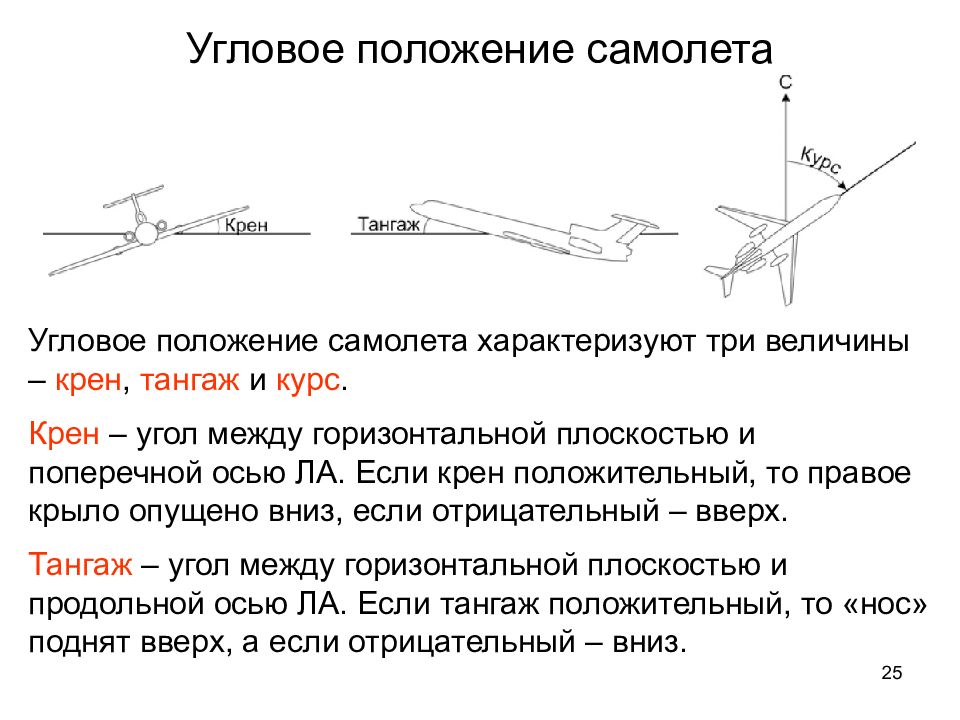
25 Угловое положение самолета Угловое положение самолета характеризуют три величины – крен, тангаж и курс. Крен – угол между горизонтальной плоскостью и поперечной осью ЛА. Если крен положительный, то правое крыло опущено вниз, если отрицательный – вверх. Тангаж – угол между горизонтальной плоскостью и продольной осью ЛА. Если тангаж положительный, то «нос» поднят вверх, а если отрицательный – вниз.
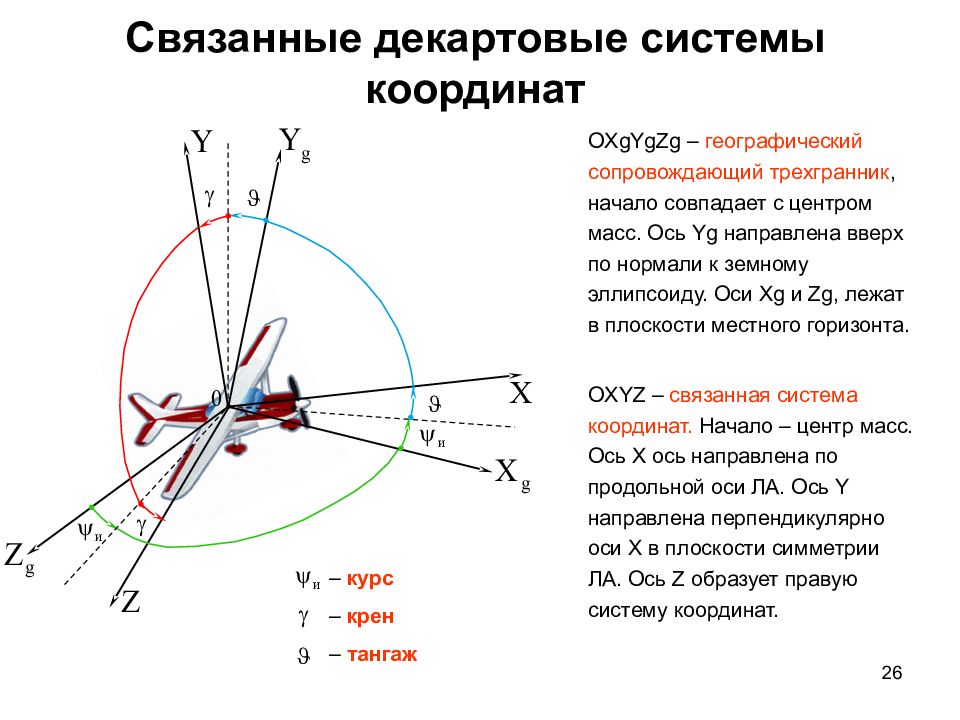
26 ОXgYgZg – географический сопровождающий трехгранник, начало совпадает с центром масс. Ось Yg направлена вверх по нормали к земному эллипсоиду. Оси Xg и Zg, лежат в плоскости местного горизонта. ОXYZ – c вязанная система координат. Начало – центр масс. Ось Х ось направлена по продольной оси ЛА. Ось Y направлена перпендикулярно оси X в плоскости симметрии ЛА. Ось Z образует правую систему координат. Связанные декартовые системы координат – курс – крен – тангаж
