Первый слайд презентации: 26.03.2020 Тема урока: Шар и сфера, сечения шара. Касательная плоскость к сфере
Слайд 2: Окружность и круг (Основные определения)
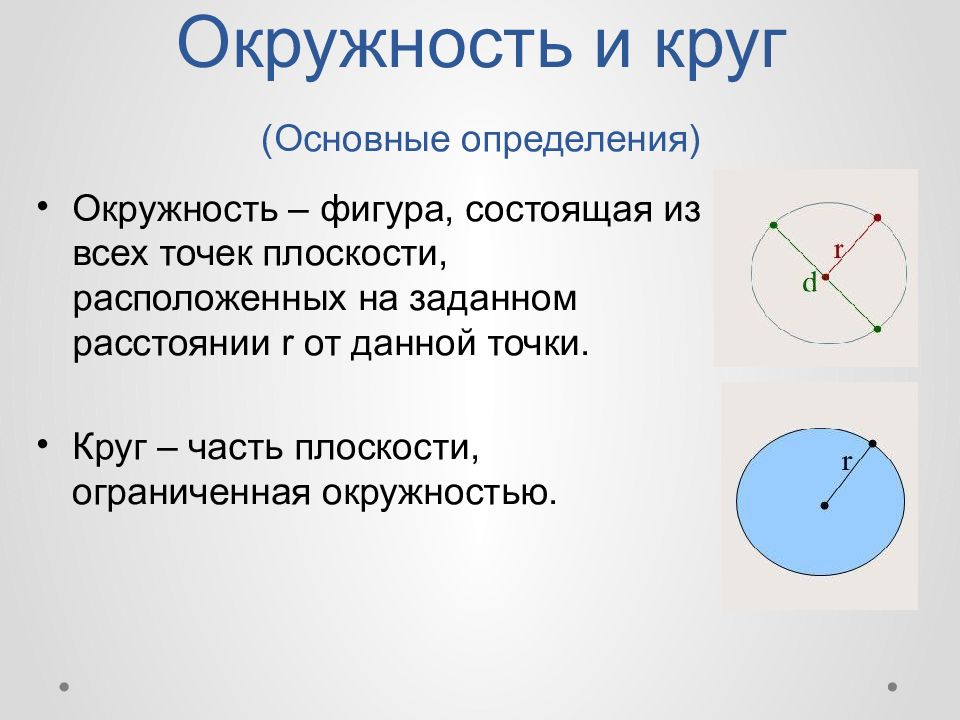
Окружность – фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии r от данной точки. Круг – часть плоскости, ограниченная окружностью.
Слайд 3: Сфера
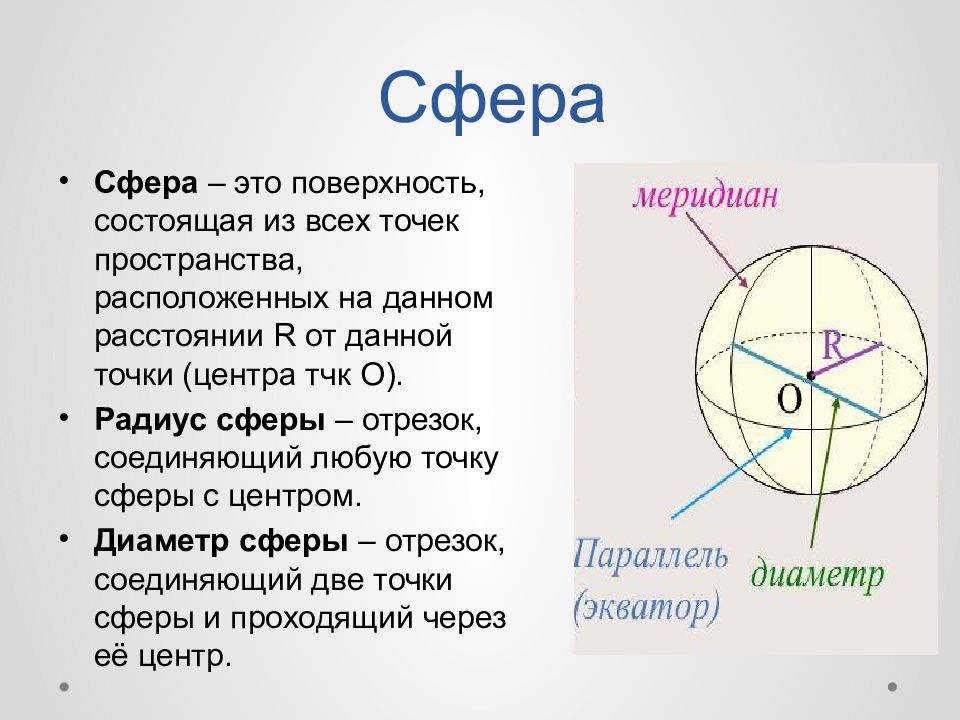
Сфера – это поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки (центра тчк O). Радиус сферы – отрезок, соединяющий любую точку сферы с центром. Диаметр сферы – отрезок, соединяющий две точки сферы и проходящий через её центр.
Слайд 5: Шар
Шар – это тело, ограниченное сферой. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
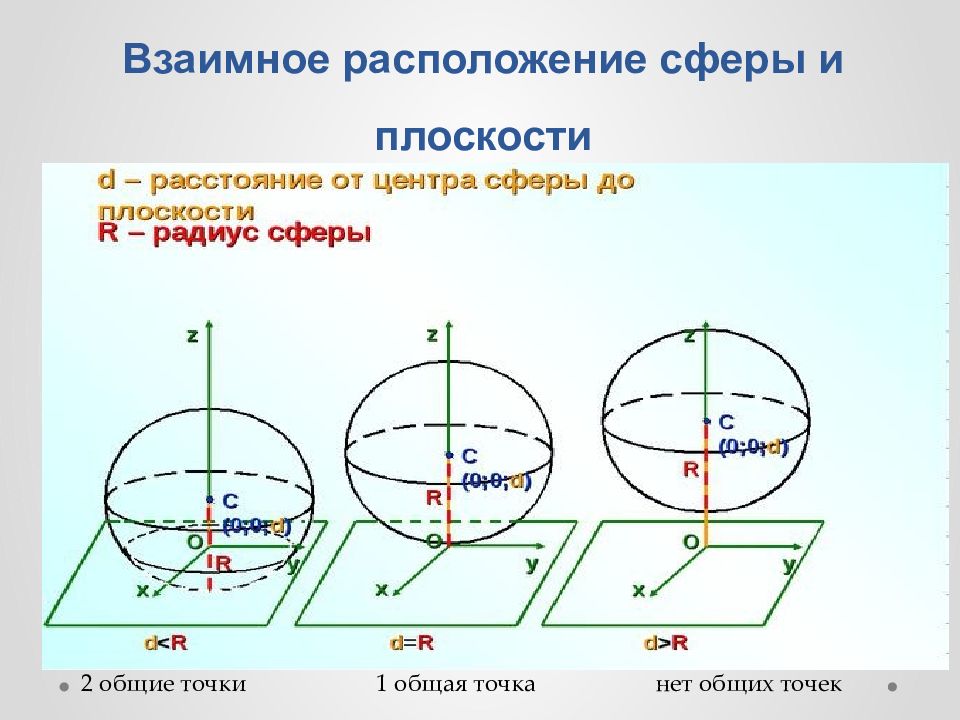
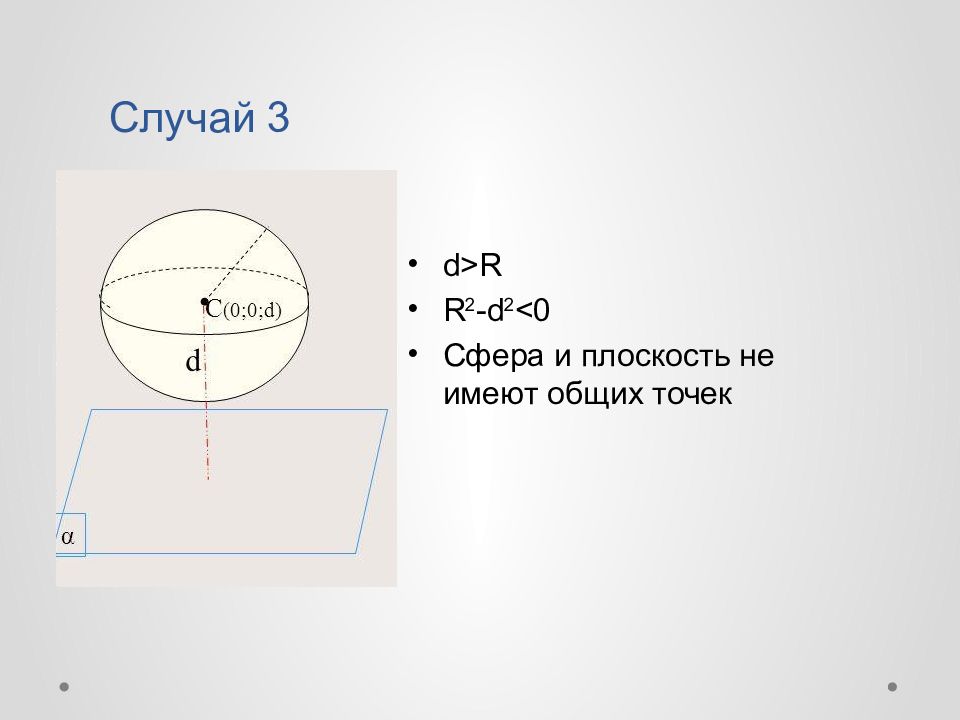
Слайд 9: Взаимное расположение сферы и плоскости
2 общие точки 1 общая точка н ет общих точек
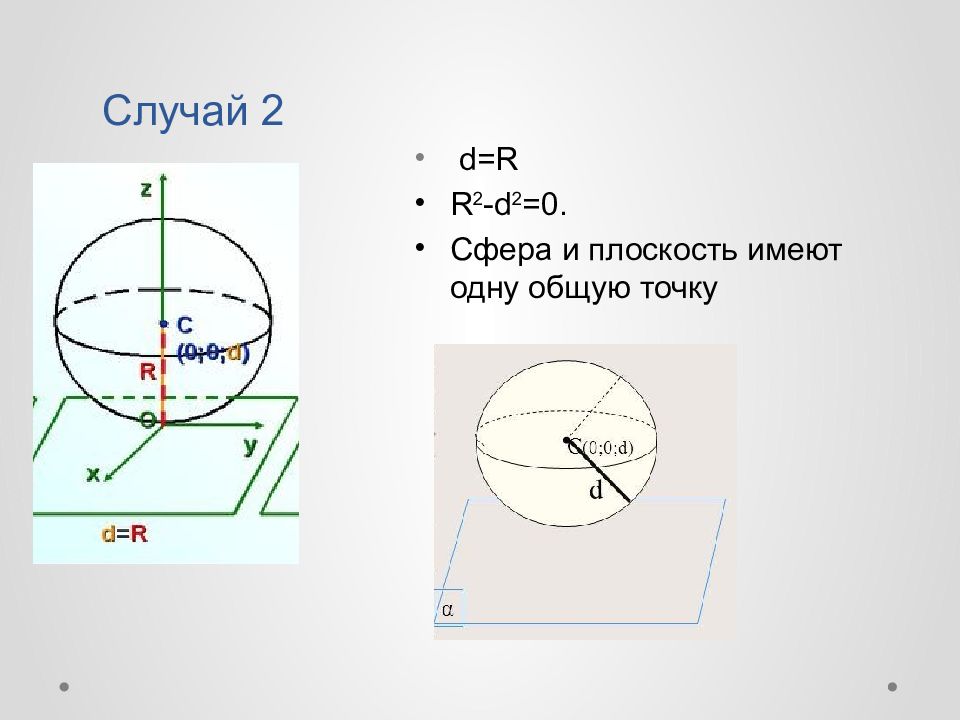
Слайд 10: Случай 1
D<R. R 2 – D2<0. C ечение сферы плоскостью есть окружность радиуса r. r= √R 2 -d 2 Сечение шара плоскостью есть круг. Плоскость, проходящая через диаметр шара, называется диаметральной. Круг, полученный в результате сечения, называется большим кругом.
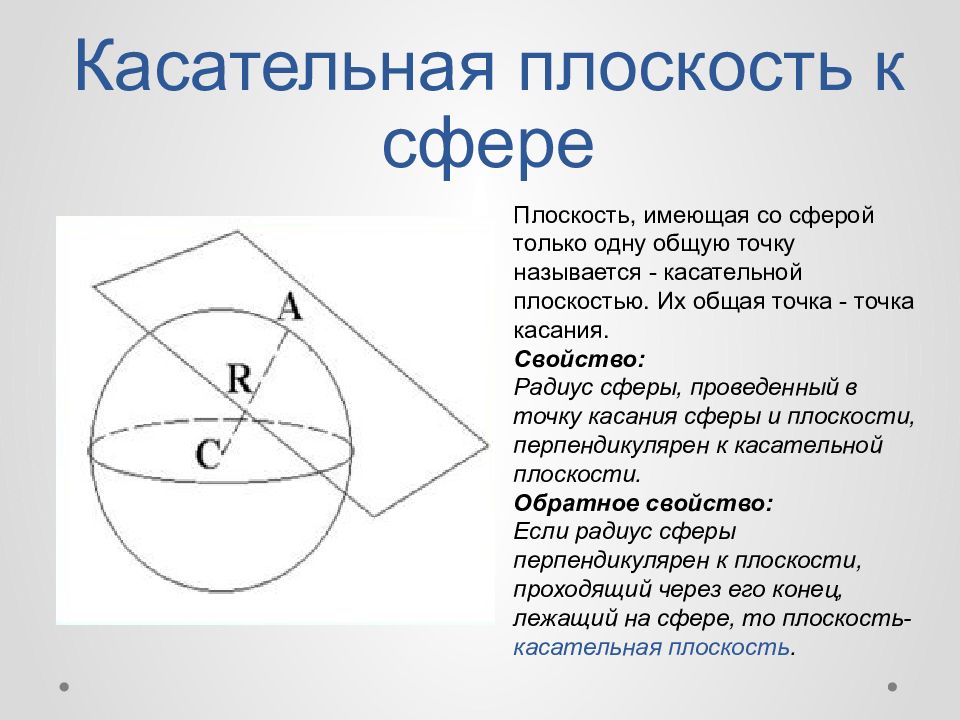
Слайд 13: Касательная плоскость к сфере
Плоскость, имеющая со сферой только одну общую точку называется - касательной плоскостью. Их общая точка - точка касания. Свойство: Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости. Обратное свойство: Если радиус сферы перпендикулярен к плоскости, проходящий через его конец, лежащий на сфере, то плоскость- касательная плоскость.
Слайд 17: Самостоятельная работа
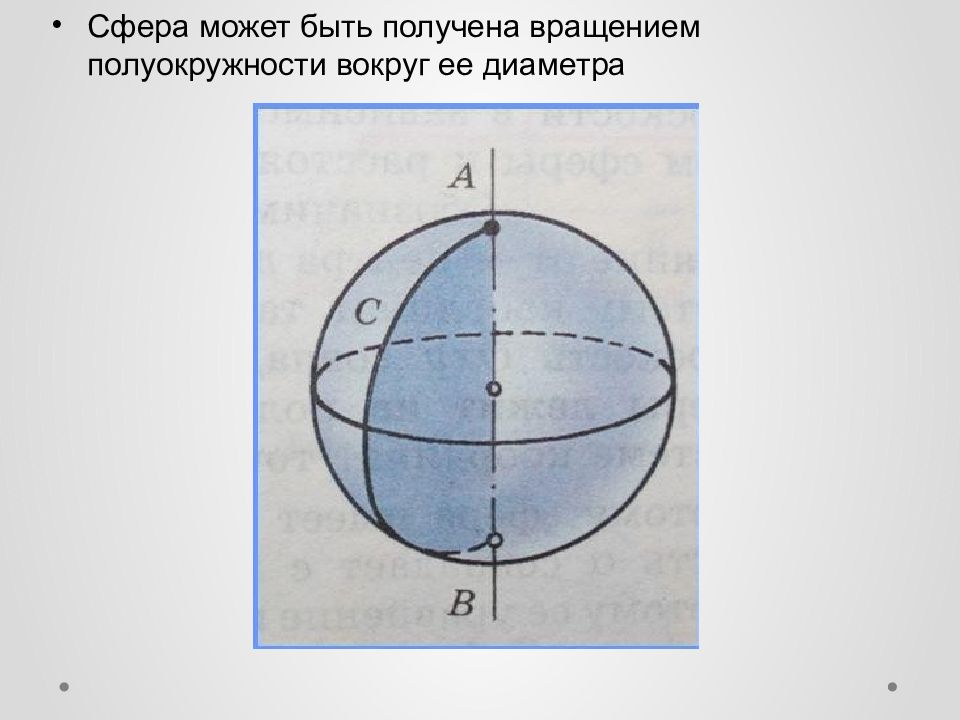
Ответьте на вопросы или вставьте пропущенное слово (слова ): 1. Как называется тело, ограниченное сферой? 2. Вращением какой геометрической фигуры может быть получена сфера? 3. Как называется отрезок, соединяющий две точки сферы и проходящий через её центр? 4. Какая геометрическая фигура получается в сечении шара плоскостью? 5. Как называется сечение сферы плоскостью, проходящей через её центр? 6. Сколько общих точек имеют сфера и плоскость, если расстояние от центра сферы до плоскости равно радиусу сферы? 7. Радиус сферы, проведённый в точку касания сферы и прямой, _______________ к этой прямой. 8. Чем меньше радиус сечения шара плоскостью, тем _________ расстояние от центра шара до секущей плоскости. 9. Если в шаре проведены два больших круга, то их общий отрезок является _____________ шара. 10. Если каждая грань многогранника является касательной плоскостью к сфере, то такой многогранник называется _____.
Последний слайд презентации: 26.03.2020 Тема урока: Шар и сфера, сечения шара. Касательная плоскость к сфере: Продолжение
11. В пирамиду можно вписать сферу (шар) тогда и только тогда, если ________________________________________. 12. Центр шара, описанного около прямой призмы, лежит __________________, проведённой через центр окружности, описанной около основания. Выберите верный вариант(ы) ответа: 13.Если на сфере лежат все вершины многогранника, то она называется … а) описанной около многогранника; б) вписанной в многогранник; в) касательной к многограннику. 14. Шар можно описать около … а) любого конуса; б) любой четырёхугольной призмы; в) любой правильной призмы; г) пирамиды, боковые рёбра которой равны; д) любой треугольной пирамиды; е) наклонной призмы. 15. В прямую призму, в основание которой вписана окружность, можно вписать сферу, если … а) высота призмы равна диаметру вписанной окружности; б) центр сферы лежит на высоте призмы; в) высота призмы равна радиусу вписанной окружности.