Первый слайд презентации
Арксинус и арккосинус. Учитель математики Абакарова Раисат Алибековна МКОУ «Уркарахская многопрофильная гимназия им. А. Абубакара" Дахадаевского района Республика Дагестан Тема урока
Слайд 2
Цели и задачи урока: Сформировать знания обучающихся о понятиях: арксинус и арккосинус числа. Научить вычислять их значения по таблице. Развивать мышление, память, вычислительные навыки, навыки самоконтроля и взаимоконтроля. Воспитывать ответственность, самостоятельность, трудолюбие. Совершенствовать навыки устного счета
Слайд 3
1. Кофункция тангенса – это…? . 2. От чего зависит значение функции? 3. Мера измерения угла? 4. Какой функции недостает: синус, косинус, котангенс? 5. Значение тригонометрических функций повторяется через? косинус От аргумента градус, радиан тангенс период Блиц-опрос
Слайд 4
6. y = со s x – тригонометрическая… . 7. Как называется график функции y = sin x ? 8. (0;?) – Что это? 9. Он не только в земле, но и в математике. 10. Предложение, требующее доказательства? функция c инусоида ордината аксиома корень
Слайд 5
. 11. Отношение противолежащего катета к гипотенузе - это 12. y = sin x - нечетная функция, y = со s x - 13. Функции синус, косинус, тангенс и котангенс изучаются в разделе математики, который называется… синус четная тригонометрия
Слайд 6: Решение задач
Устный счет: 19+200= :(-3)= -13= +6= : (-0,2)= 219 -73 -86 -80 400
Слайд 7: Решение задач
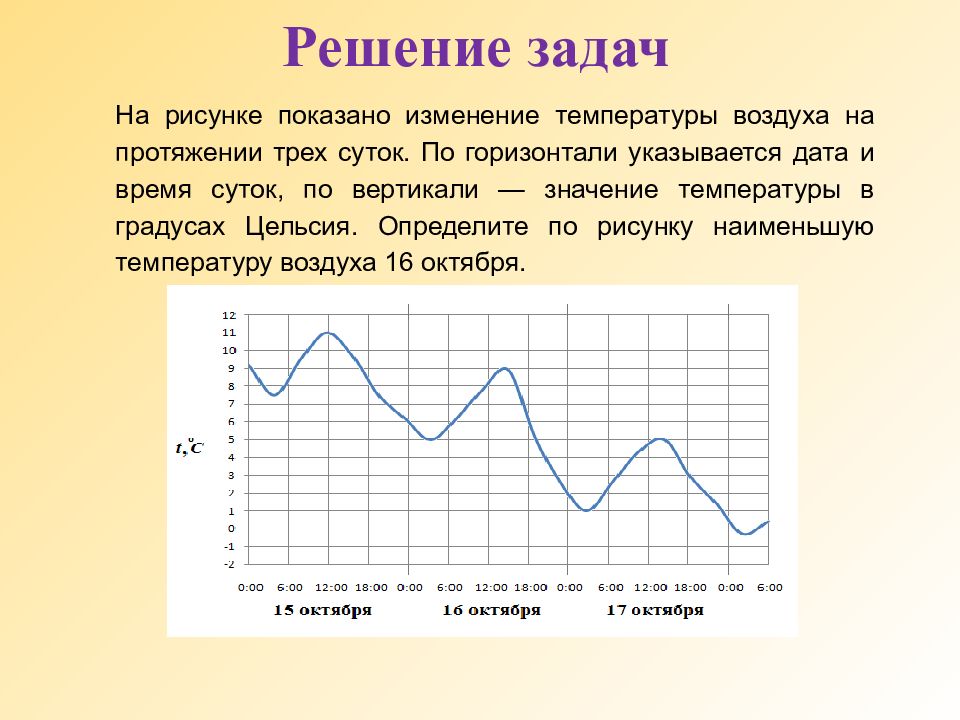
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 16 октября.
Слайд 8: Решение задач
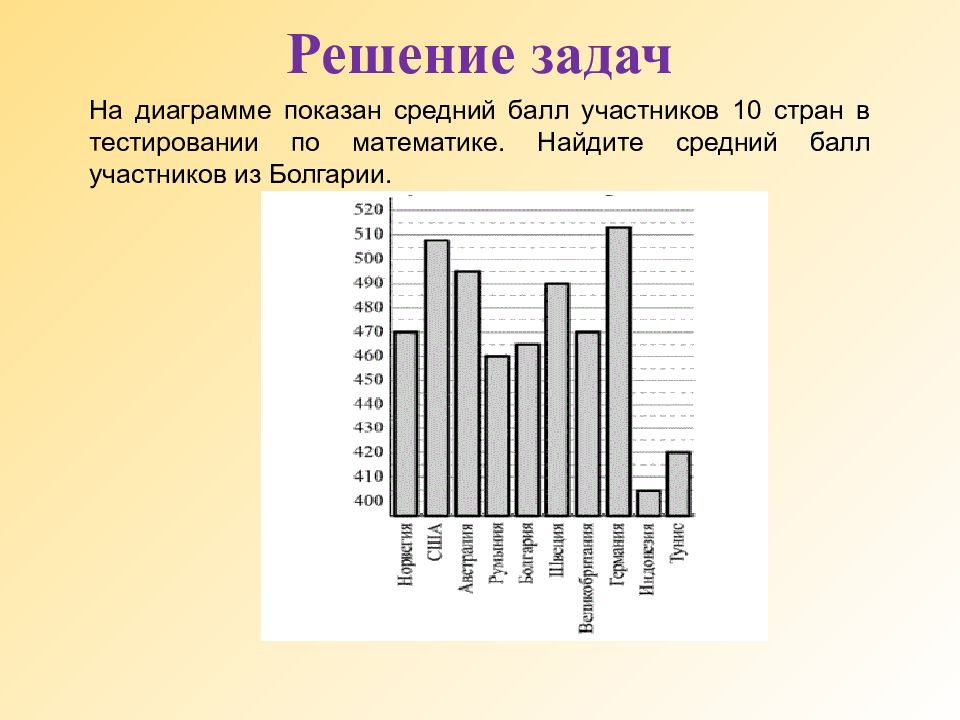
На диаграмме показан средний балл участников 10 стран в тестировании по математике. Найдите средний балл участников из Болгарии.
Слайд 9: Решение задач
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (9;8), (4;8)
Слайд 11
градусы 0 30 45 60 90 180 270 360 радианы 0 Таблица перевода градусов в радианы
Слайд 12
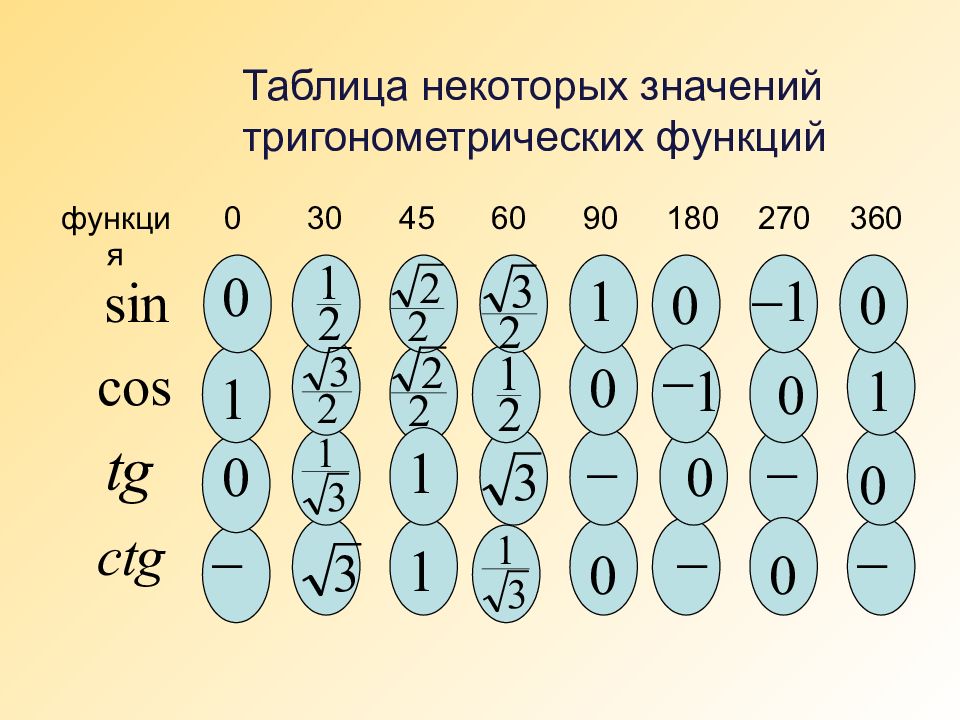
функция 0 30 45 60 90 180 270 360 Таблица некоторых значений тригонометрических функций
Слайд 13
Тригонометрические функции – это математические функции, зависящие от угла. Определяют тригонометрические функции обычно как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. К тригонометрическим функциям относятся функции: y = sin x; y = cos x; y = tg x; y = ctg x; y = sec x; y = cosec x.
Слайд 14
Обра́тные тригонометри́ческие фу́нкции — математические функции, являющиеся обратными к тригонометрическим функциям.
Слайд 15
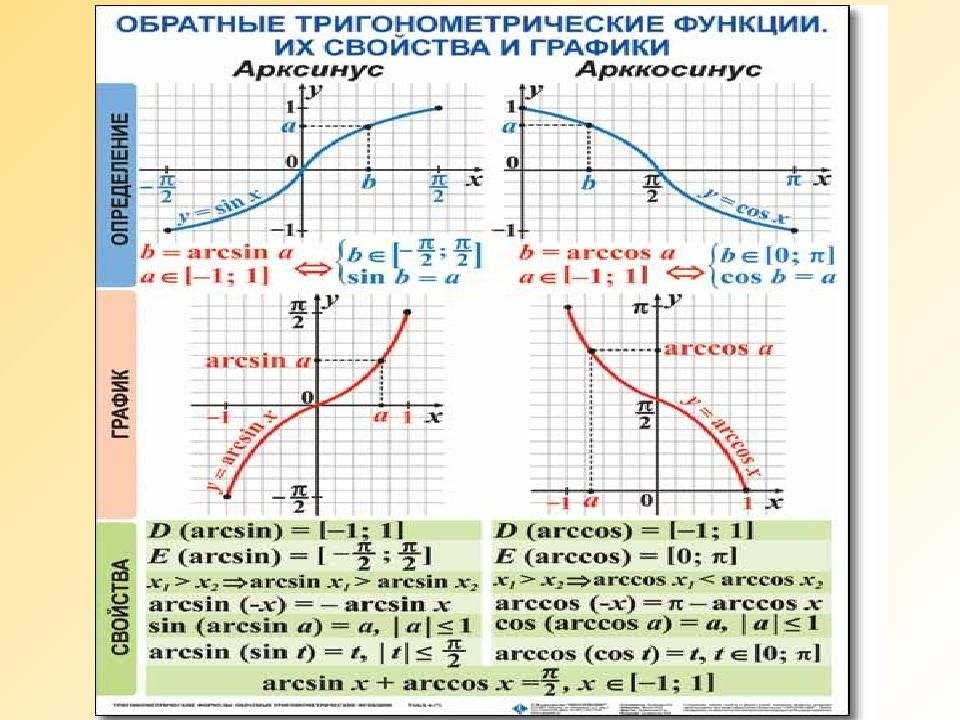
Обратные тригонометрические функции у= arcsinx график у= arccosx график у= arctgx график у= arcctgx график
Слайд 16: Сведения из истории
Современные обозначения arcsin и arctg появляются в 1772г.в работах венского математика Щерфера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее уже рассматривал Д. Б ернулли, который употреблял иную символику.
Слайд 17: Сведения из истории
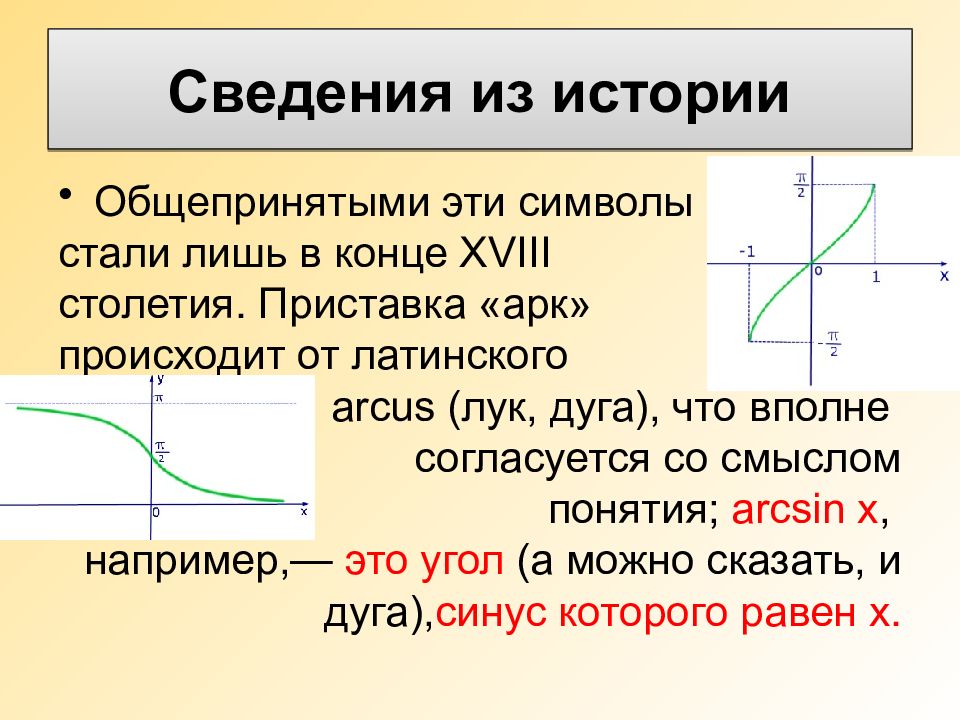
Общепринятыми эти символы стали лишь в конце XVIII столетия. Приставка « арк » происходит от латинского arcus (лук, дуга), что вполне согласуется со смыслом понятия ; arcsin х, например,— это угол ( а можно сказать, и дуга), синус которого равен х.
Слайд 18
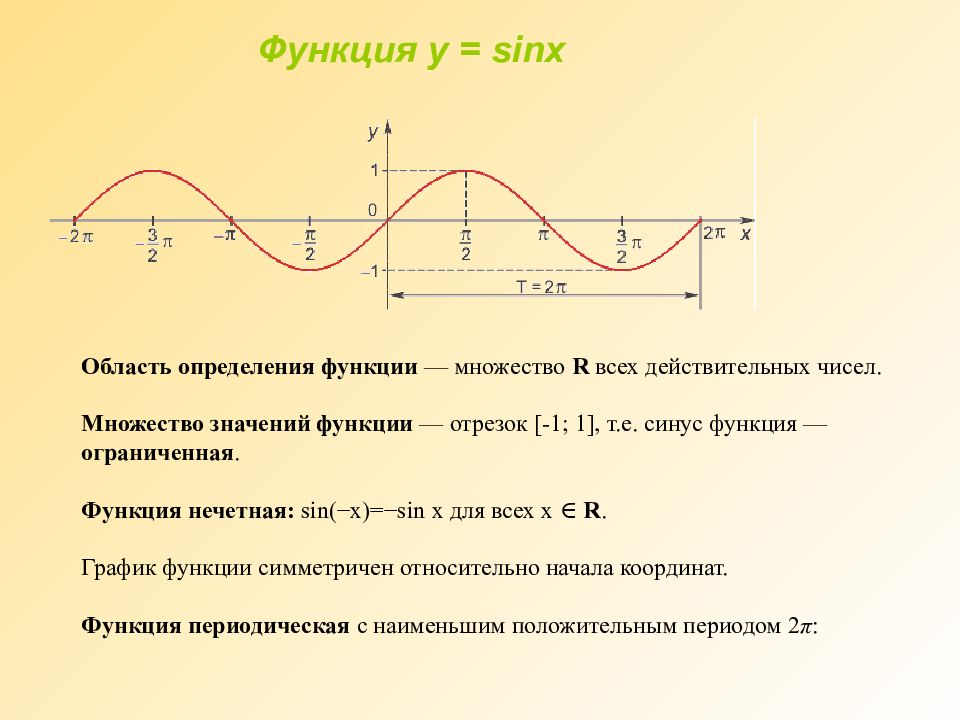
Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная. Функция нечетная: sin(−x)=−sin x для всех х ∈ R. График функции симметричен относительно начала координат. Функция периодическая с наименьшим положительным периодом 2 π : Функция у = sinx
Слайд 19: Функция у = sin x
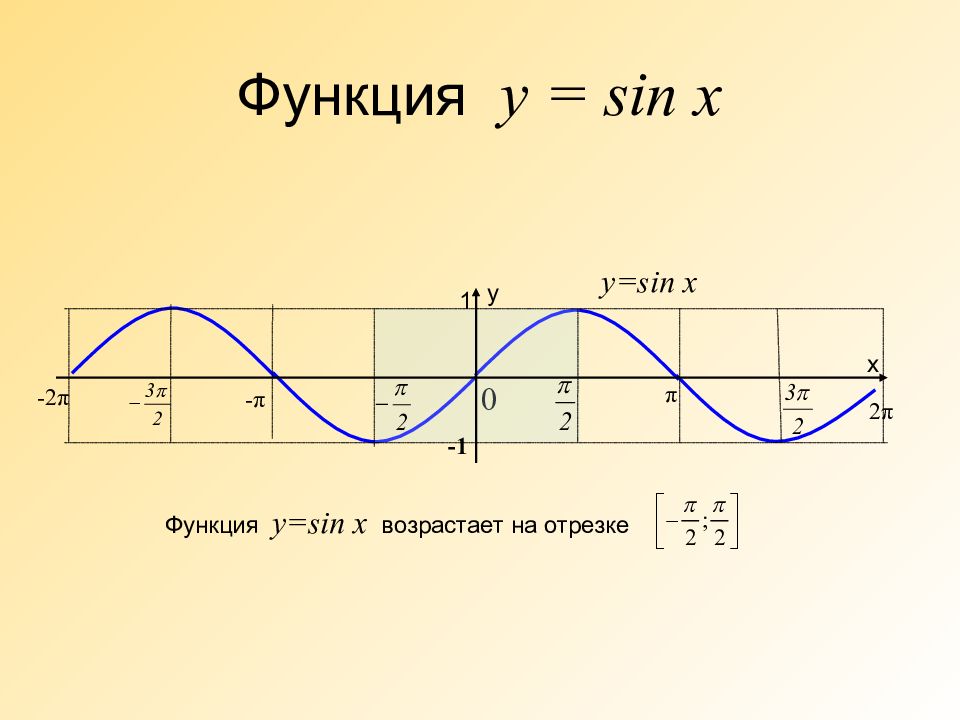
0 y=sin x Функция y=sin x возрастает на отрезке 1 -1 π 2 π - π -2 π х у
Слайд 20: Арксинус
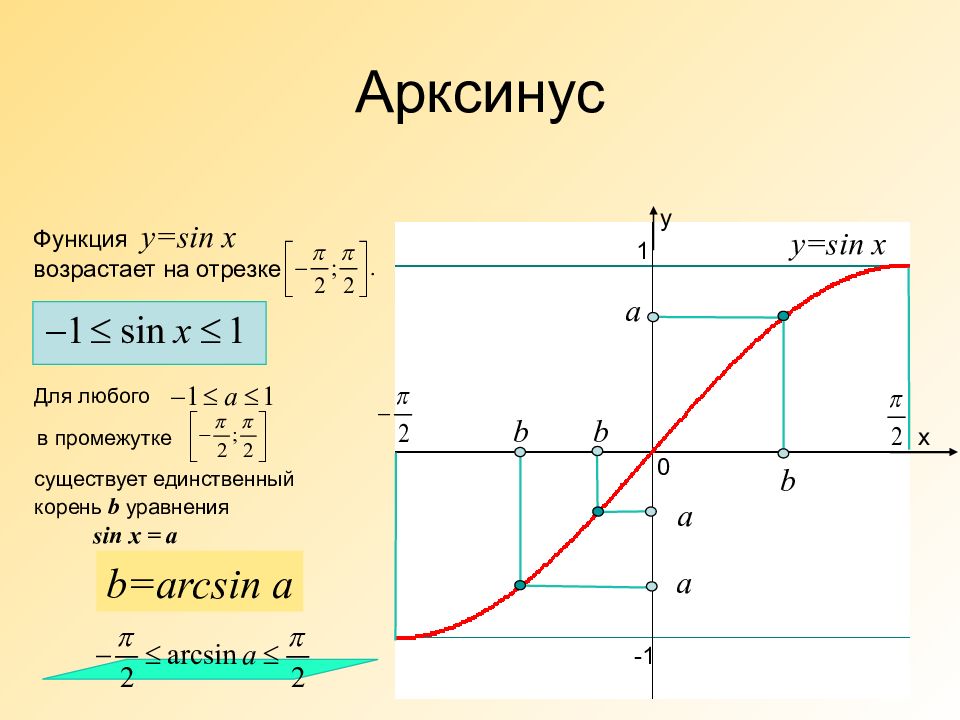
х у 0 1 -1 Арксинус а b y=sin x Функция y=sin x возрастает на отрезке Для любого в промежутке существует единственный корень b уравнения sin x = a b=arcsin a а b а b
Слайд 21: Арксинус
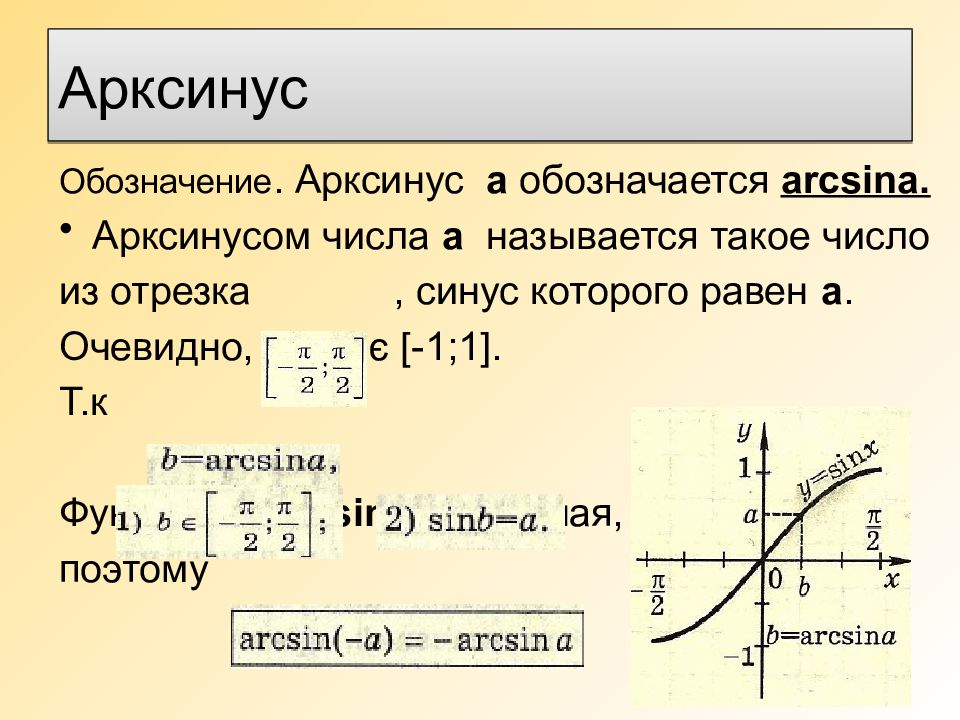
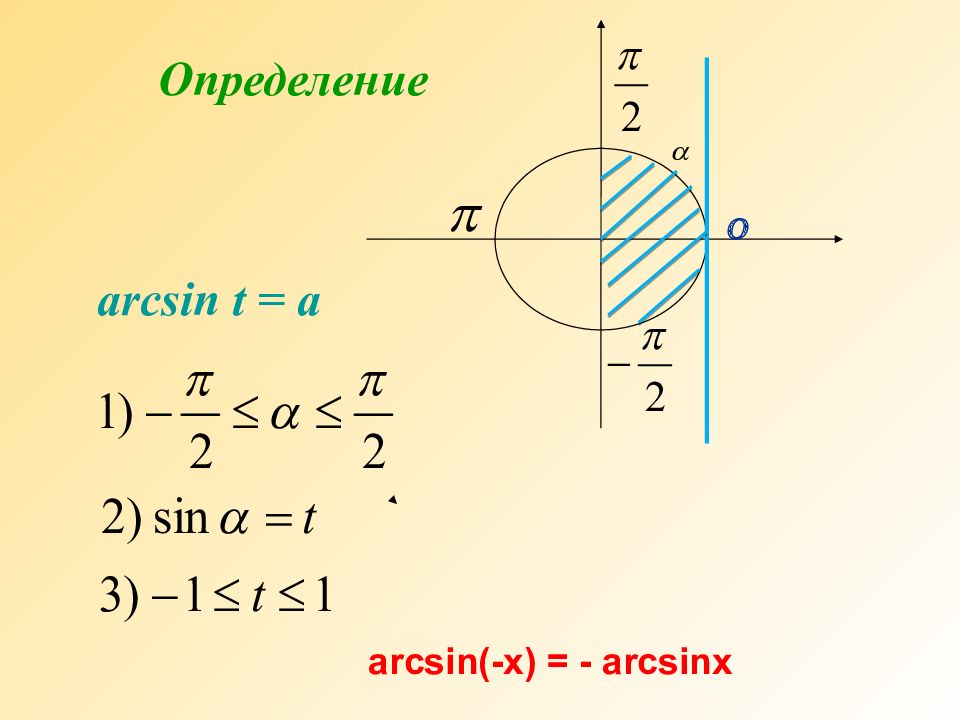
Обозначение. Арксинус а обозначается arcsina. Арксинусом числа а называется такое число из отрезка, синус которого равен а. Очевидно, что а є [-1;1 ]. Т.к Функция y= arcsin x - нечетная, поэтому
Слайд 23
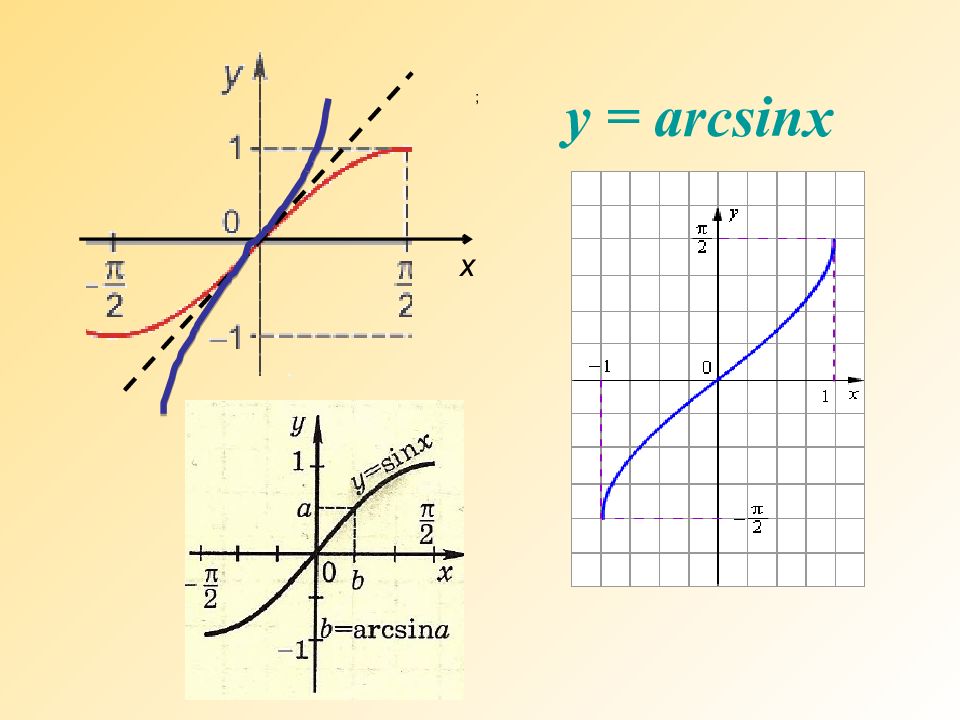
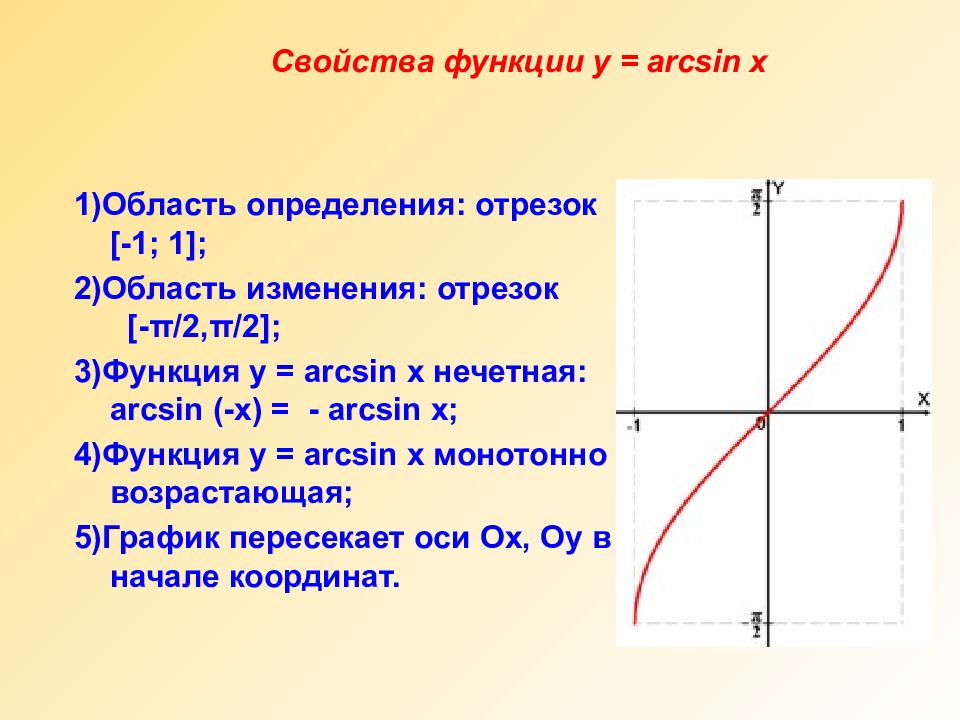
Свойства функции y = arcsin x 1)Область определения: отрезок [-1; 1]; 2)Область изменения: отрезок [- π /2, π /2]; 3)Функция y = arcsin x нечетная: arcsin (-x) = - arcsin x; 4)Функция y = arcsin x монотонно возрастающая; 5)График пересекает оси Ох, Оу в начале координат.
Слайд 26
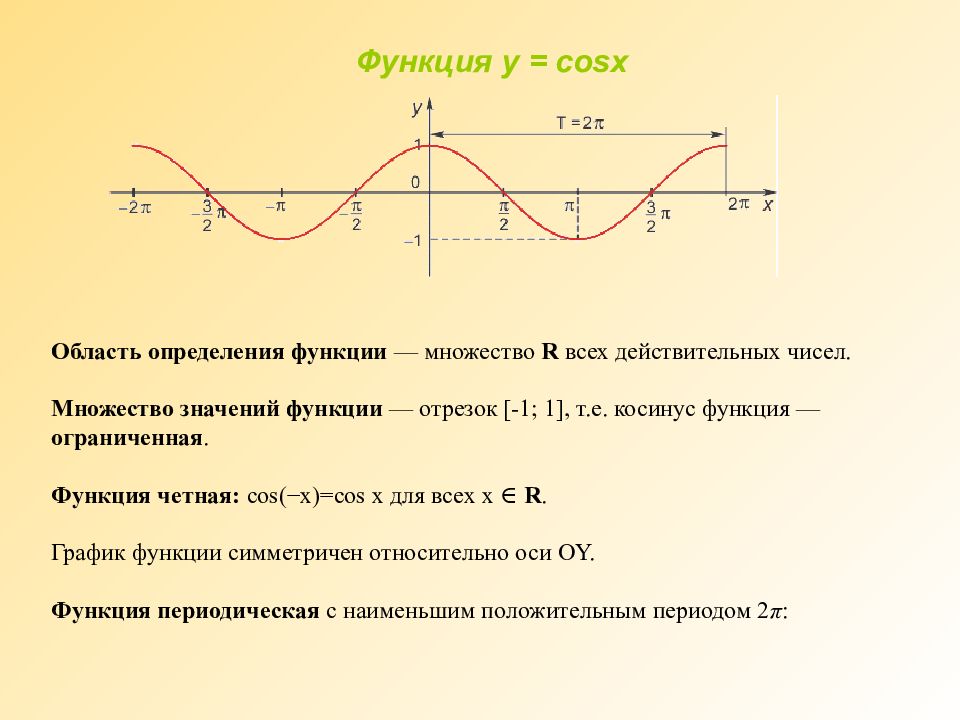
Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная. Функция четная: cos(−x)=cos x для всех х ∈ R. График функции симметричен относительно оси OY. Функция периодическая с наименьшим положительным периодом 2 π : Функция у = cosx
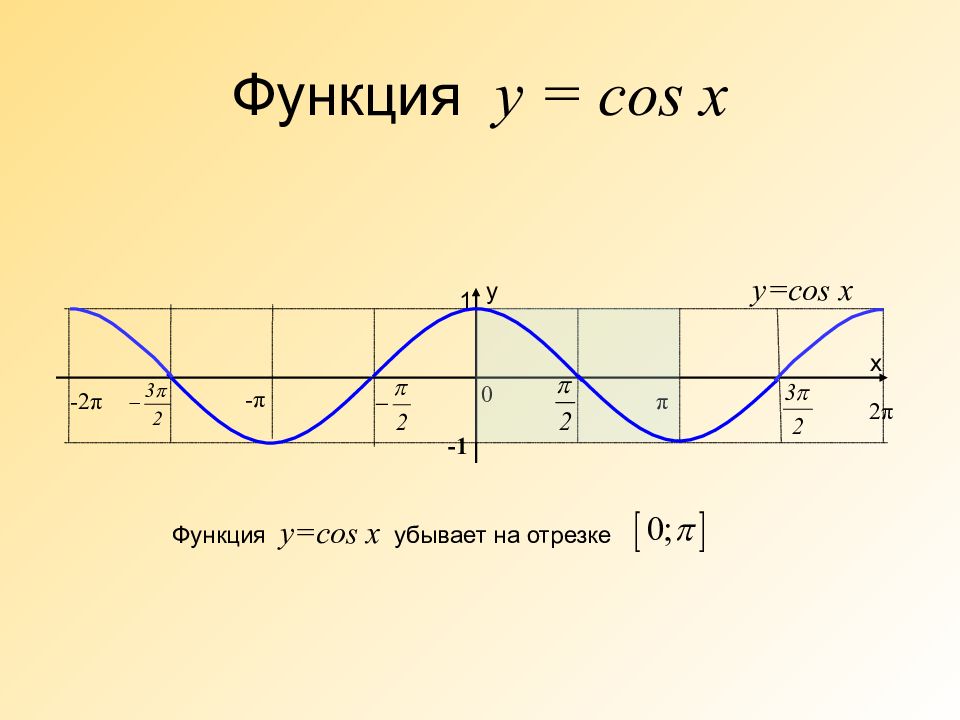
Слайд 27: Функция у = cos x
-1 π 2 π 0 - π -2 π y=cos x Функция y=cos x убывает на отрезке 1 х у
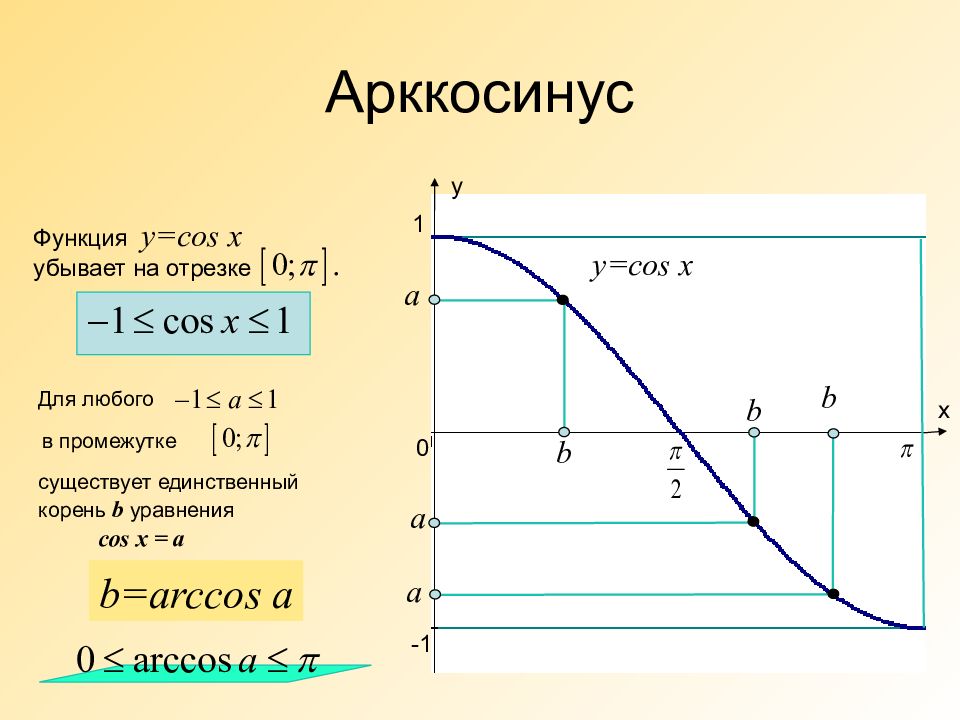
Слайд 28: Арккосинус
х у 0 1 -1 Арккосинус а b y=cos x Функция y=cos x убывает на отрезке Для любого в промежутке существует единственный корень b уравнения cos x = a b=arccos a а b а b
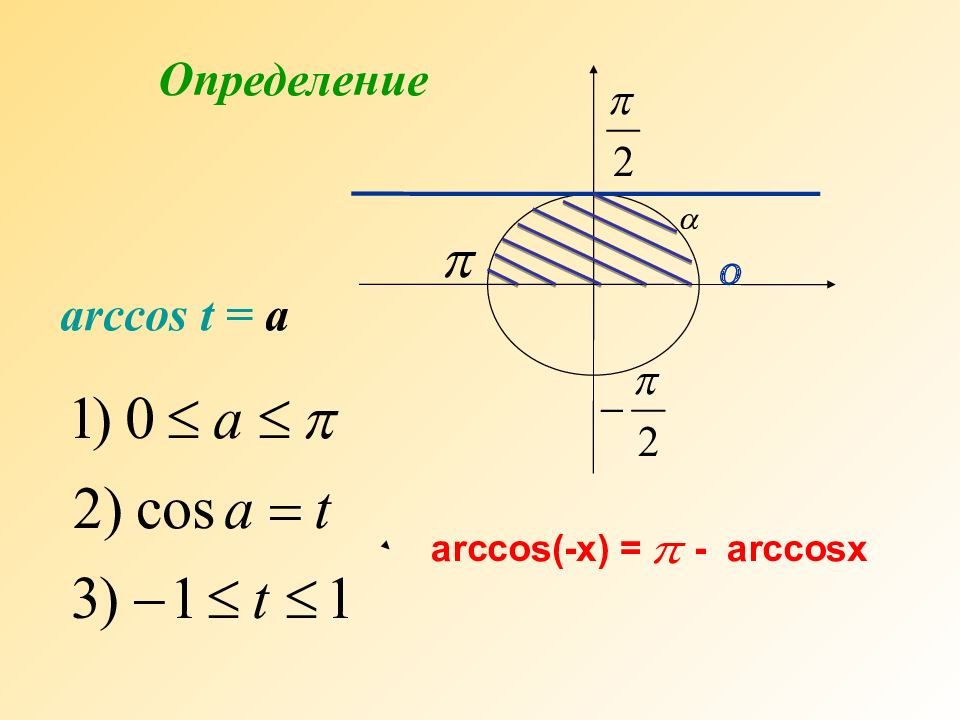
Слайд 29: Арккосинус
Обозначение : Арккосинус а обозначается arccosa. Арккосинусом числа а называется такое число из отрезка, косинус которого равен а. Очевидно, что а є [-1; 1] Т.к. Функция y= arccosx - четная, поэтому
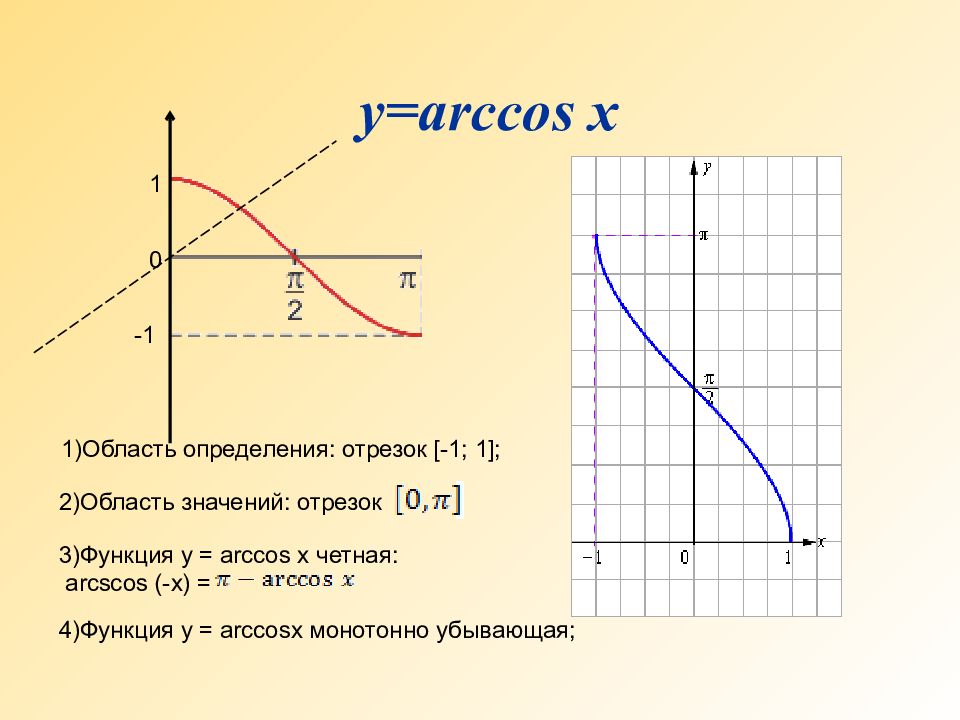
Слайд 30
у= arccos x 1 -1 0 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у = arcс os x четная: arcs cos (-x) = 4)Функция у = arcс os x монотонно убывающая;
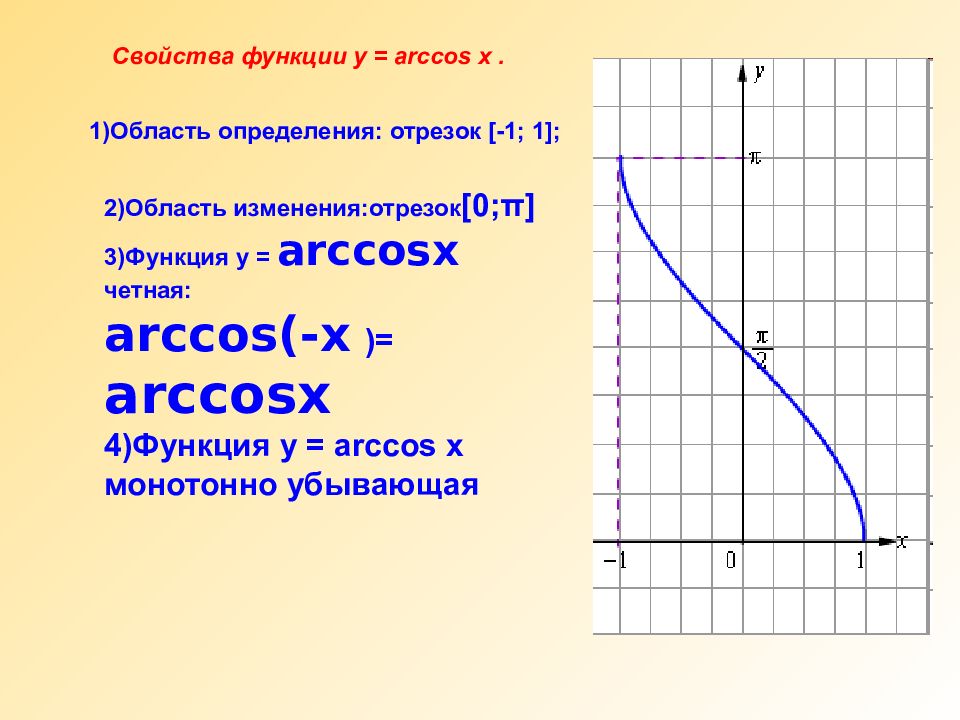
Слайд 31
2)Область изменения:отрезок [ 0; π ] 3)Функция y = arccosx четная: arccos(-x )= arccosx 4)Функция y = arc cos x монотонно убывающая Свойства функции y = arc cos x. 1)Область определения: отрезок [-1; 1];
Слайд 35
Работаем устно Имеет ли смысл выражение? Может ли arcsint и arccost принимать значение равное
Слайд 38
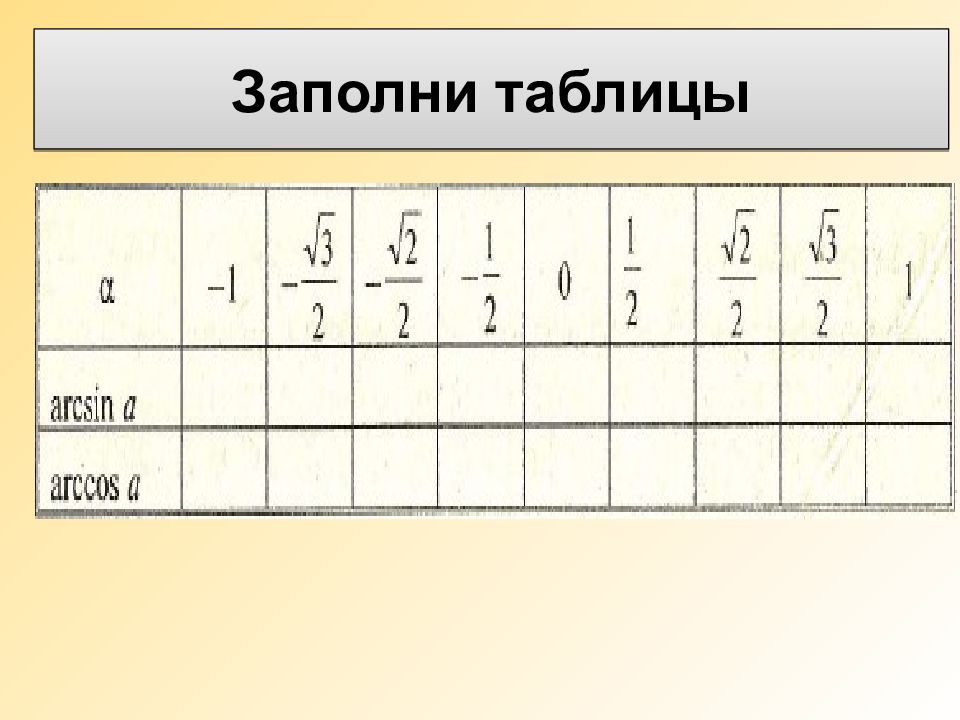
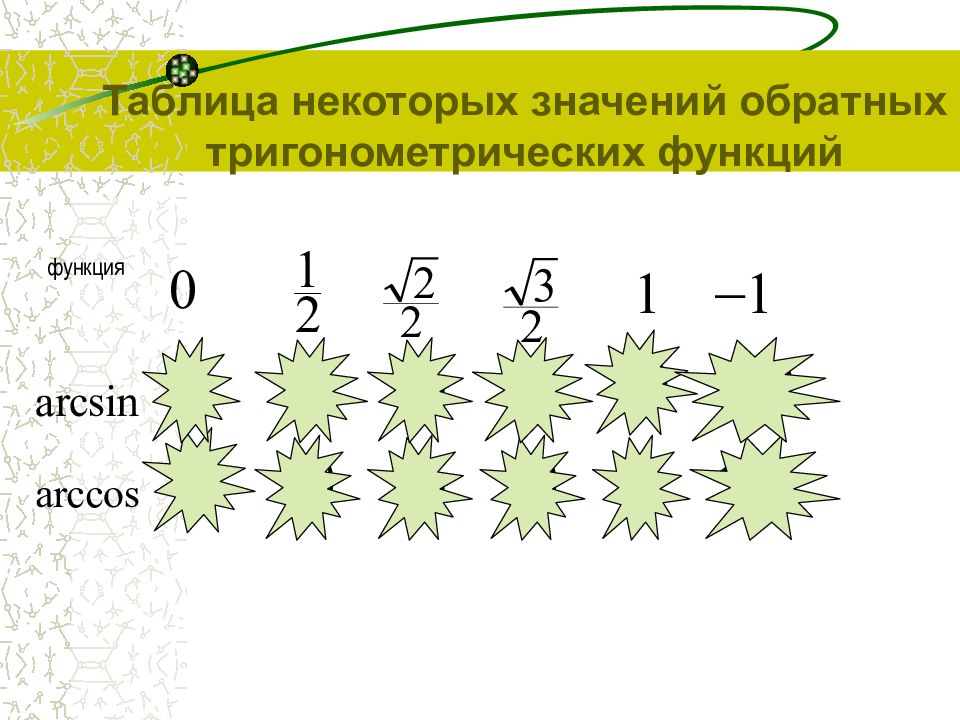
Таблица некоторых значений обратных тригонометрических функций функция 0 30 45 60 90 270 90 60 45 30 0 180