Слайд 2
Все сложные тригонометрические неравенства решаются с помощью тех же алгоритмов, что и тригонометрические уравнения, но в самом конце приходится решать простейшие тригонометрические неравенства. Все простейшие тригонометрические неравенства решаются одним и тем же способом: 1. Выделяем на единичной окружности дугу, координаты точек которой удовлетворяют нашему неравенству. 2. Определяем начальную точку движения по этой дуге, исходя из того, что мы «умеем» двигаться только в положительном направлении, то есть против часовой стрелки (от меньшего числа к большему) 3. Двигаясь по выделенной дуге в положительном направлении, определяем конечную точку движения. 4. После того, как мы определили начальную и конечную точку движения по дуге, записываем решение неравенства и ответ.
Слайд 3
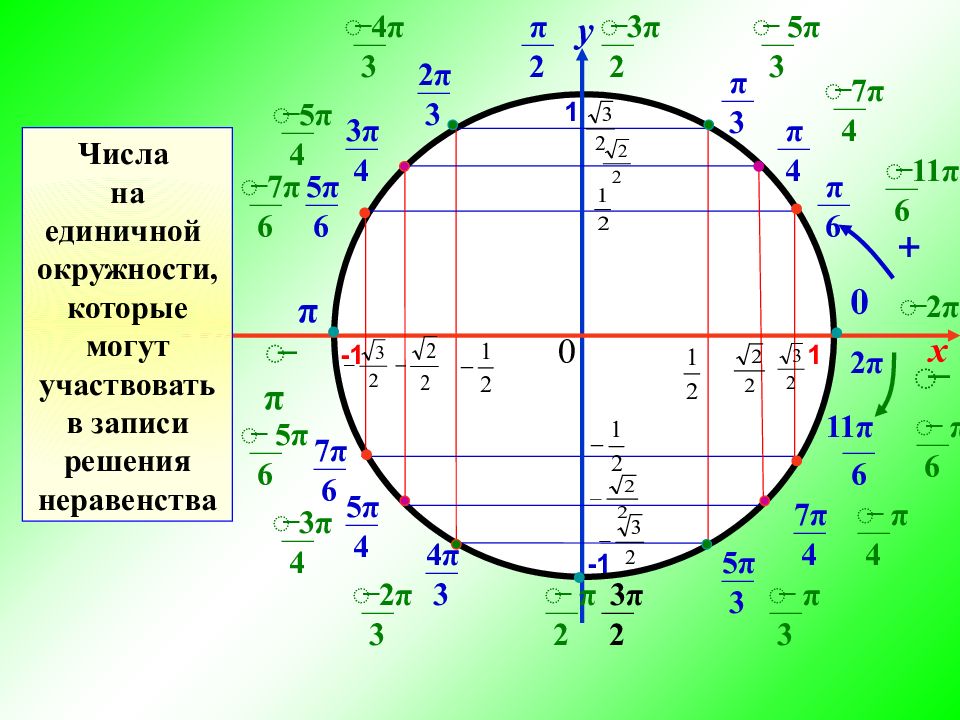
x y 1 -1 1 -1 — π 6 — π 4 — π 3 — π 2 — 2 π 3 — 3 π 4 — 5 π 6 π 0 — 5 π 4 — 7 π 6 — 4 π 3 — 3 π 2 — 7 π 4 — 5 π 3 — 11 π 6 — ̶ 3 π 2 — ̶ 5 π 3 — ̶ 7 π 4 — ̶ 11 π 6 ̶ 2 π — ̶ π 6 — ̶ π 4 — ̶ π 3 — ̶ π 2 — ̶ 2 π 3 — ̶ 3 π 4 — ̶ 5 π 6 ̶ π — ̶ 7 π 6 — ̶ 5 π 4 — ̶ 4 π 3 2 π ̶ + Числа на единичной окружности,которые могут участвовать в записи решения неравенства
Слайд 4
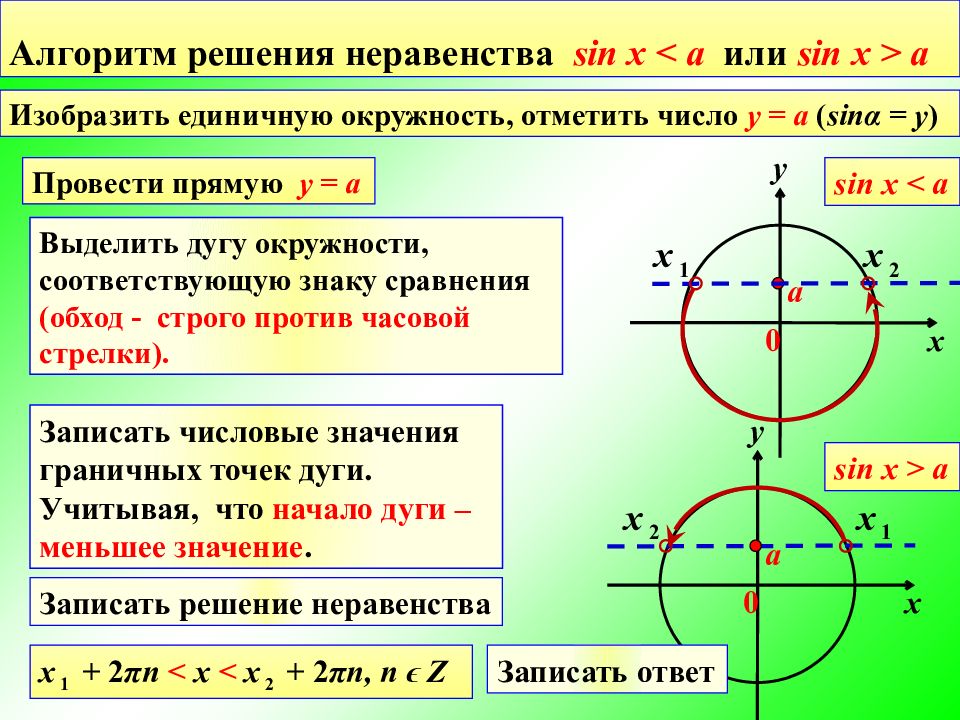
Алгоритм решения неравенства sin x < a или sin x > a Изобразить единичную окружность, отметить число у = a ( sin α = y ) y х 0 a Провести прямую у = a y х 0 sin x < a sin x > a a Выделить дугу окружности, соответствующую знаку сравнения (обход - строго против часовой стрелки). Записать числовые значения граничных точек дуги. Учитывая, что начало дуги – меньшее значение. х 2 х 1 х 1 х 2 Записать решение неравенства х 1 + 2 π n < x < х 2 + 2 π n, n ϵ Z Записать ответ
Слайд 5
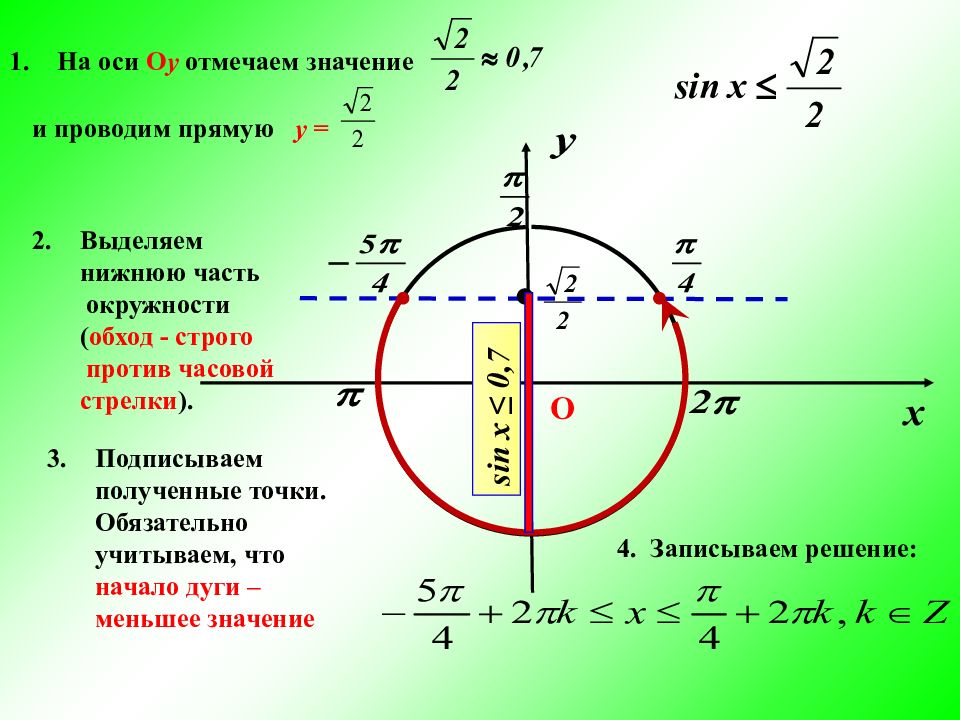
На оси О у отмечаем значение Выделяем нижнюю часть окружности ( обход - строго против часовой стрелки ). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение 4. Записываем решение: О и проводим прямую у = sin x ≤ 0,7
Слайд 7
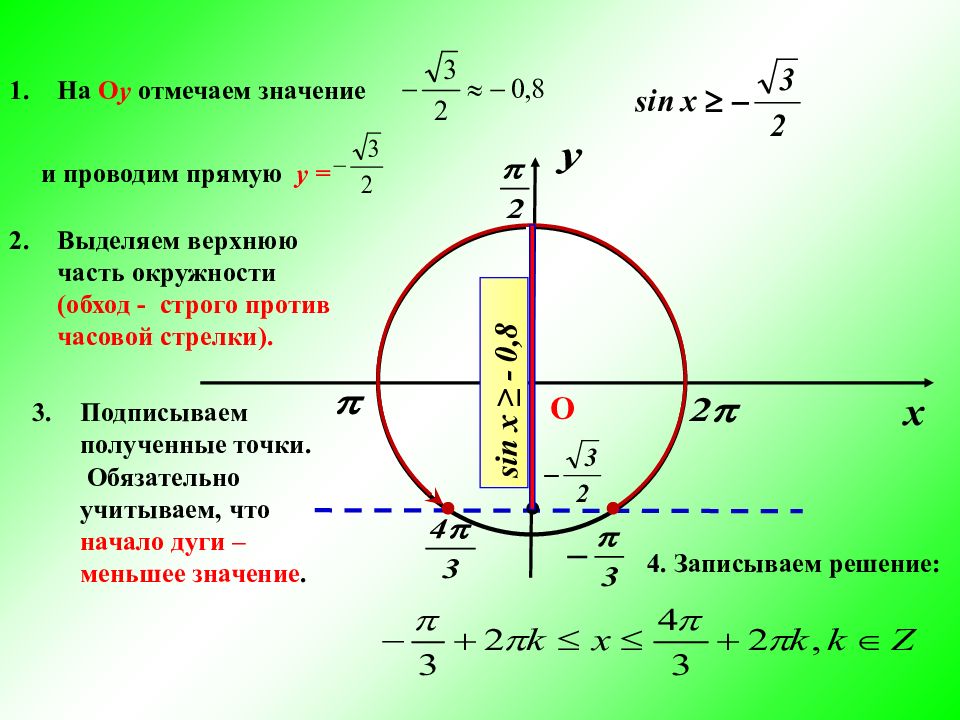
На О у отмечаем значение и проводим прямую у = Выделяем верхнюю часть окружности (обход - строго против часовой стрелки). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Записываем решение: О sin x ≥ - 0,8
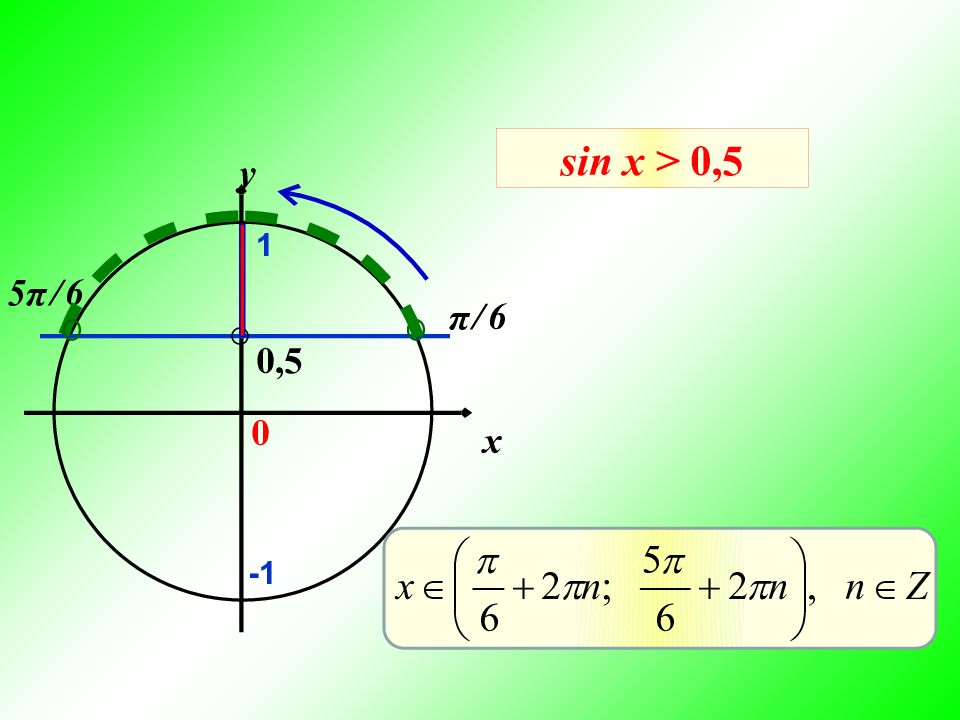
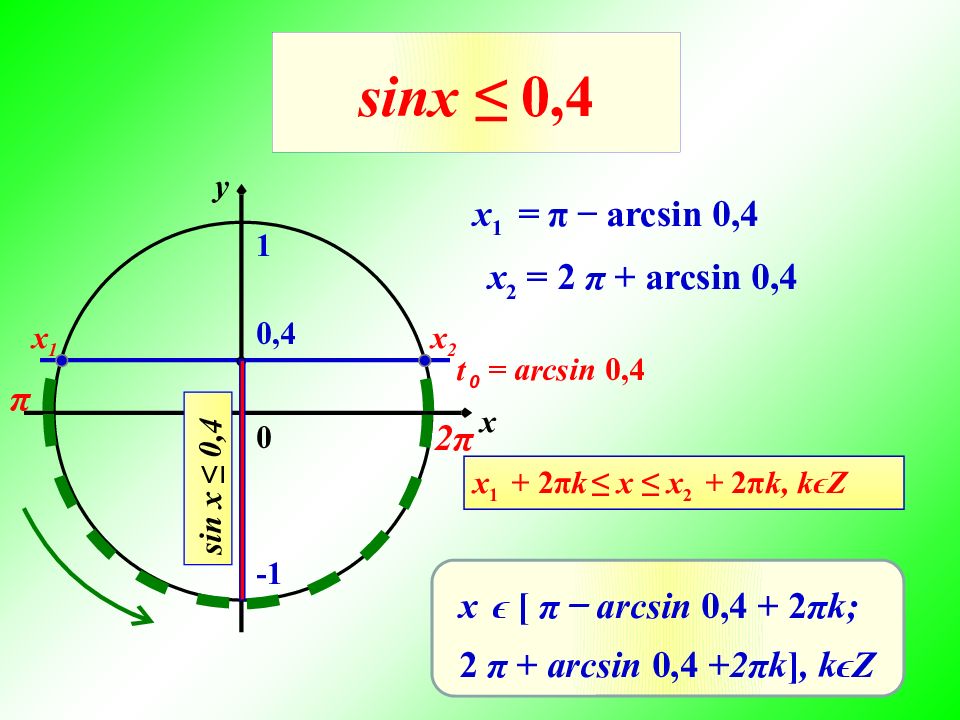
Слайд 9: sinx ≤ 0,4
0 x y x 1 = π ̶ arcsin 0,4 0,4 x 2 x 1 -1 1 x 2 = 2 π + arcsin 0,4 x ϵ [ π ̶ arcsin 0,4 + 2 π k; 2 π + arcsin 0,4 +2 π k ], k ϵ Z t 0 = arcsin 0,4 π 2 π sin x ≤ 0,4 x 1 + 2 π k ≤ x ≤ x 2 + 2 π k, k ϵ Z
Слайд 10
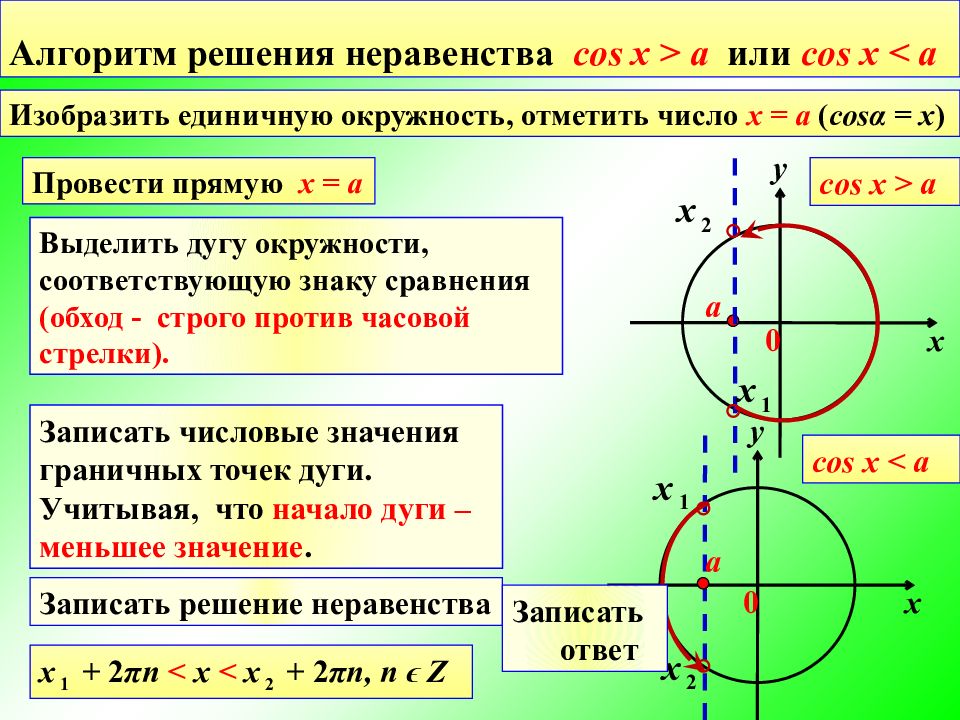
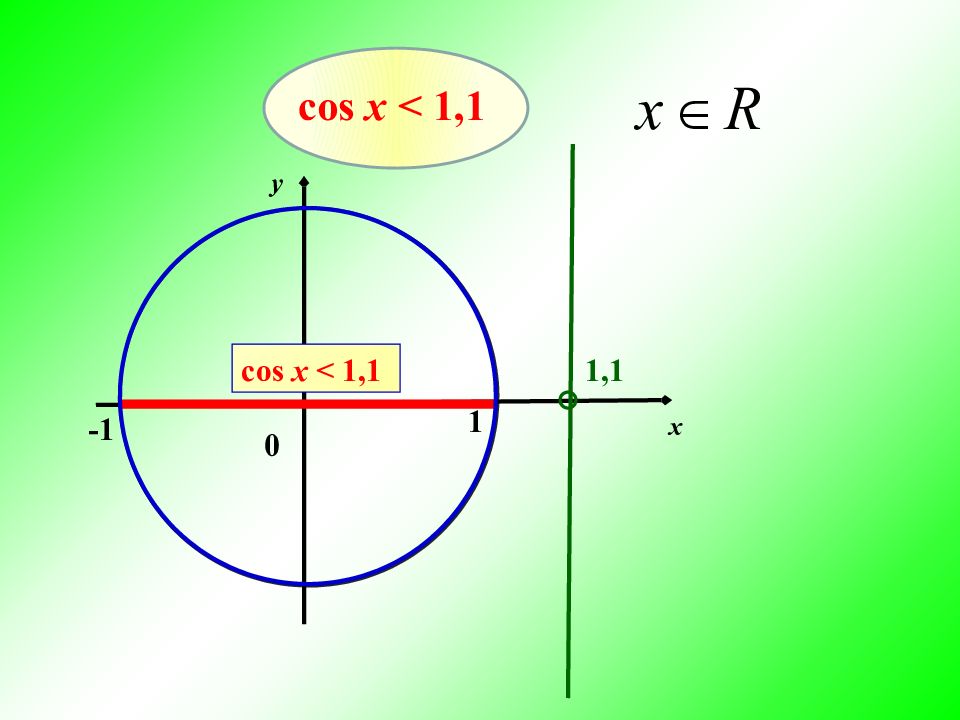
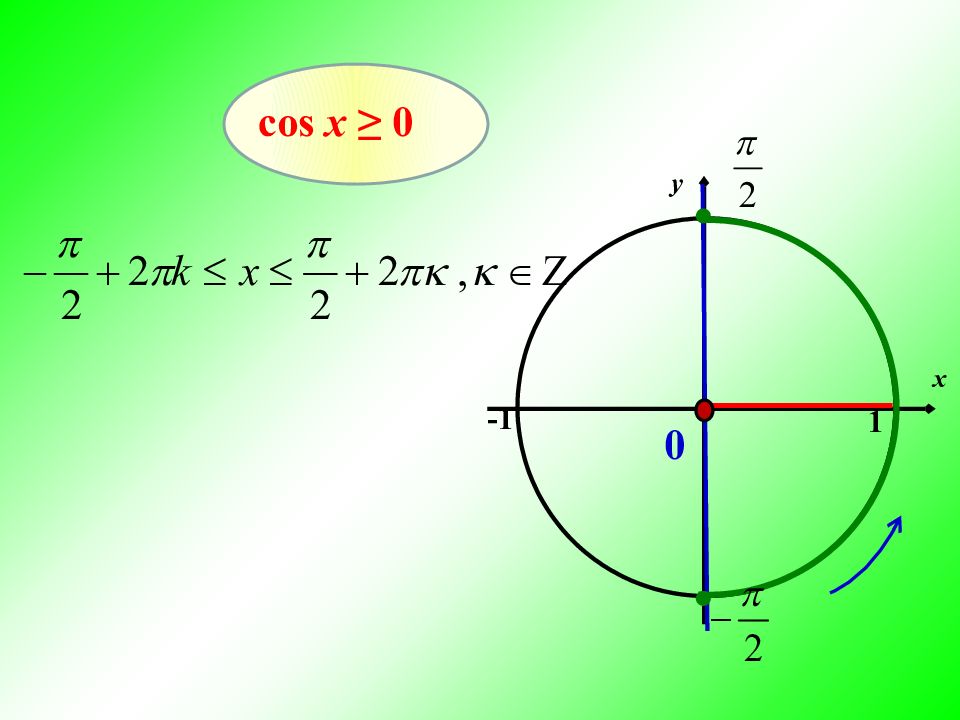
Алгоритм решения неравенства cos x > a или cos x < a Изобразить единичную окружность, отметить число x = a ( cos α = x ) y х 0 a Провести прямую x = a y х 0 cos x > a cos x < a a Выделить дугу окружности, соответствующую знаку сравнения (обход - строго против часовой стрелки). Записать числовые значения граничных точек дуги. Учитывая, что начало дуги – меньшее значение. х 2 х 1 х 1 х 2 Записать решение неравенства х 1 + 2 π n < x < х 2 + 2 π n, n ϵ Z Записать ответ
Слайд 11
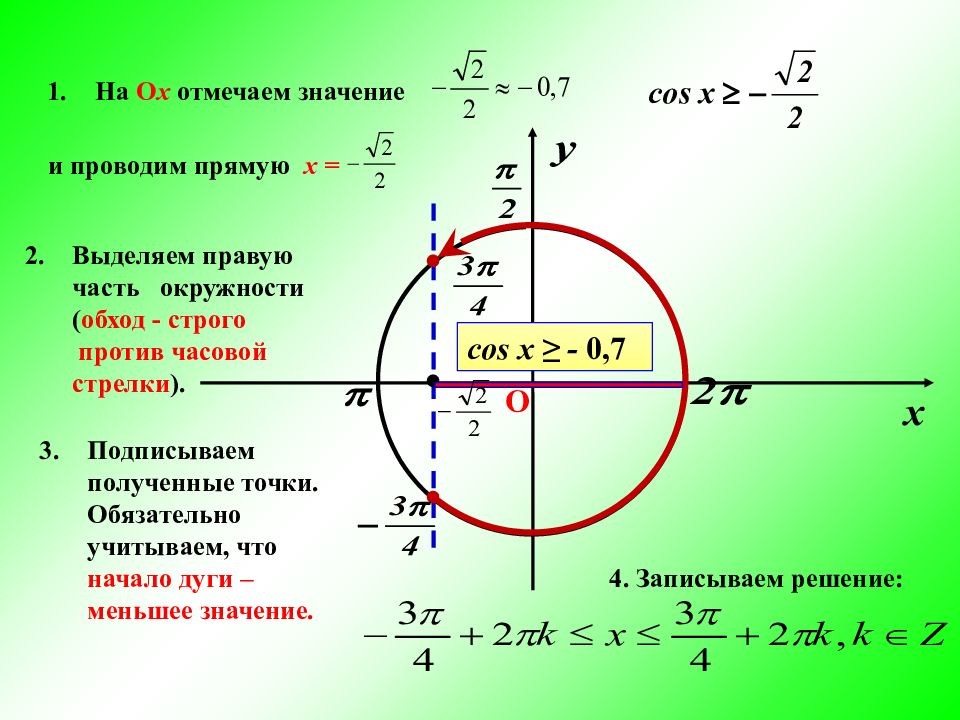
На О х отмечаем значение и проводим прямую х = Выделяем правую часть окружности ( обход - строго против часовой стрелки ). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Записываем решение: О cos x ≥ - 0,7
Слайд 12
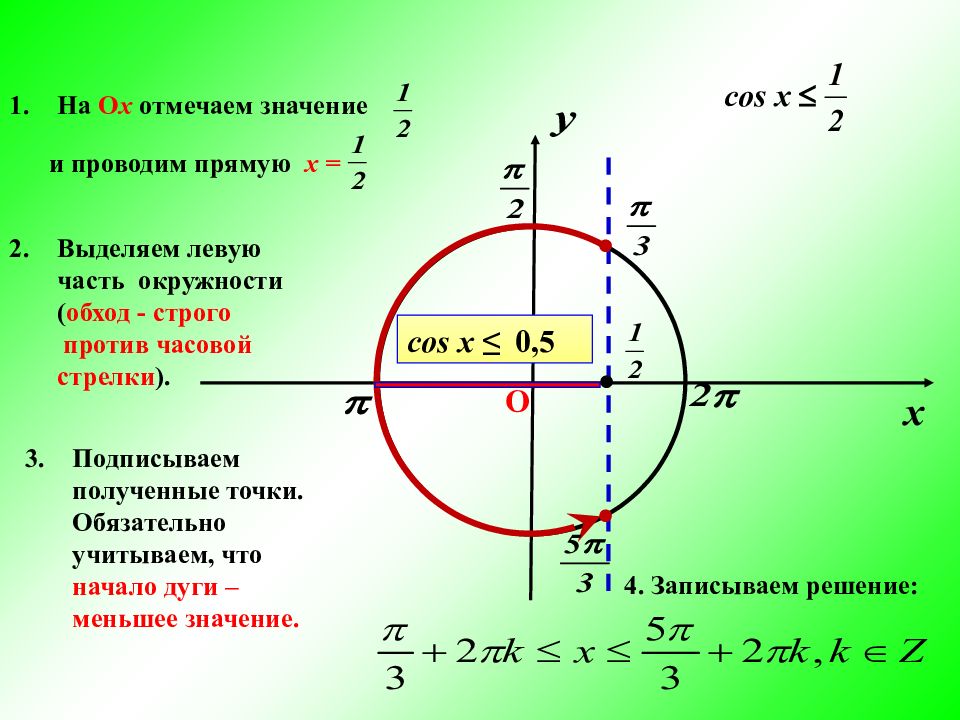
На О x отмечаем значение и проводим прямую х = Выделяем левую часть окружности ( обход - строго против часовой стрелки ). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение. 4. Записываем решение: О cos x ≤ 0,5
Слайд 15
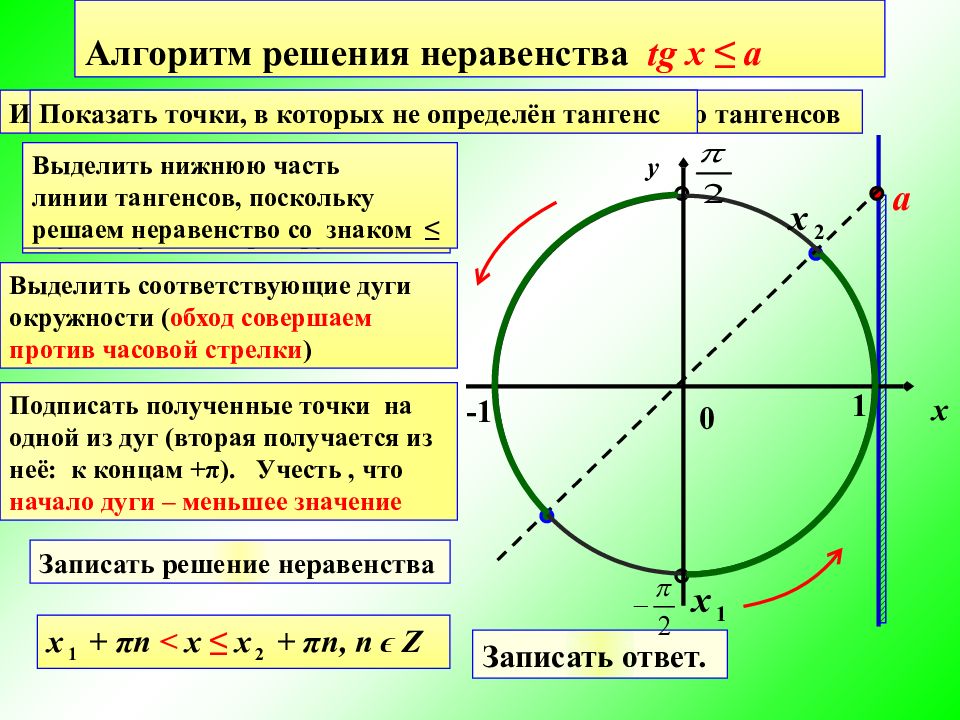
а -1 x y 1 0 Алгоритм решения неравенства tg x ≤ a Изобразить единичную окружность и провести линию тангенсов Показать точки, в которых не определён тангенс На линии тангенсов отметить число a и провести луч через эту точку и центр окружности Выделить нижнюю часть линии тангенсов, поскольку решаем неравенство со знаком ≤ Выделить соответствующие дуги окружности ( обход совершаем против часовой стрелки ) Подписать полученные точки на одной из дуг (вторая получается из неё: к концам + π ). Учесть, что начало дуги – меньшее значение х 1 х 2 Записать решение неравенства х 1 + π n < x ≤ х 2 + π n, n ϵ Z Записать ответ.
Слайд 17
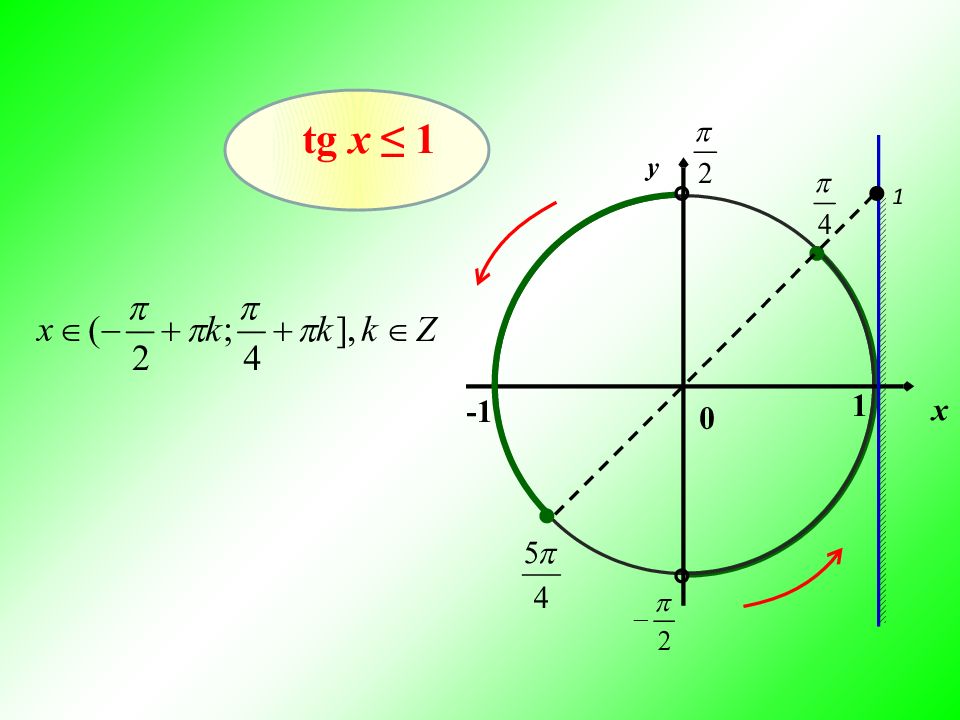
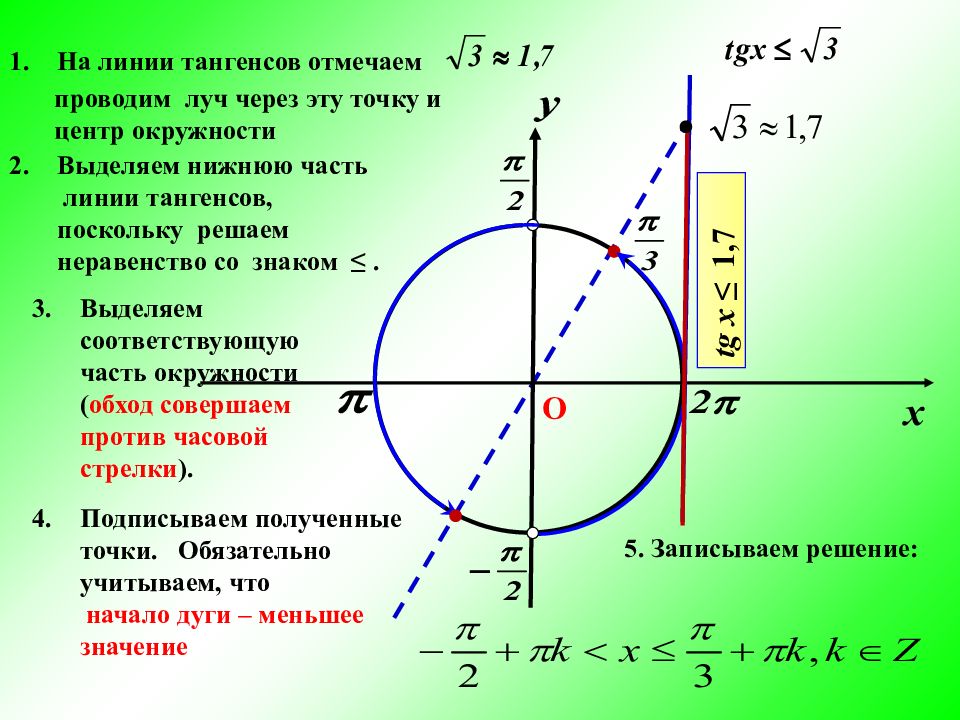
5. Записываем решение: На линии тангенсов отмечаем Выделяем нижнюю часть линии тангенсов, поскольку решаем неравенство со знаком ≤. Выделяем соответствующую часть окружности ( обход совершаем против часовой стрелки ). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение проводим луч через эту точку и центр окружности О tg x ≤ 1,7
Последний слайд презентации: Решение простейших тригонометрических неравенств
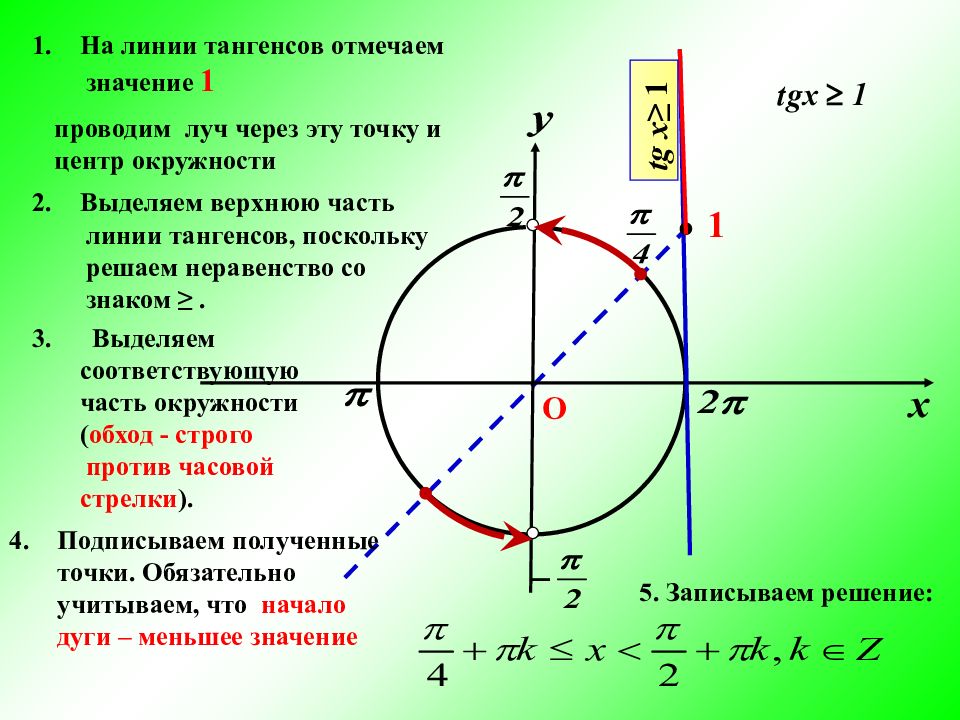
5. Записываем решение: На линии тангенсов отмечаем значение 1 Выделяем верхнюю часть линии тангенсов, поскольку решаем неравенство со знаком ≥. 3. Выделяем соответствующую часть окружности ( обход - строго против часовой стрелки ). Подписываем полученные точки. Обязательно учитываем, что начало дуги – меньшее значение 1 проводим луч через эту точку и центр окружности О tg x≥ 1