Функция y = cos x её свойства и график
Цель : Изучить функцию y = cos x Задачи: 1. Изучить свойства функции у = cos x. 2. Уметь применять свойства функции у = cos x и читать график. 3. Формировать практические навыки построения графика функции у = cos x на основе изученного теоретического материала. 4. Закрепить понятия с помощью выполнения заданий.
Функция y = cos x определена на всей числовой прямой, и множеством её значений является отрезок [−1;1]. Следовательно, график этой функции расположен в полосе между прямыми y= −1 и y=1. Так как функция y = cos x периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn, n∈Z, график будет таким же.
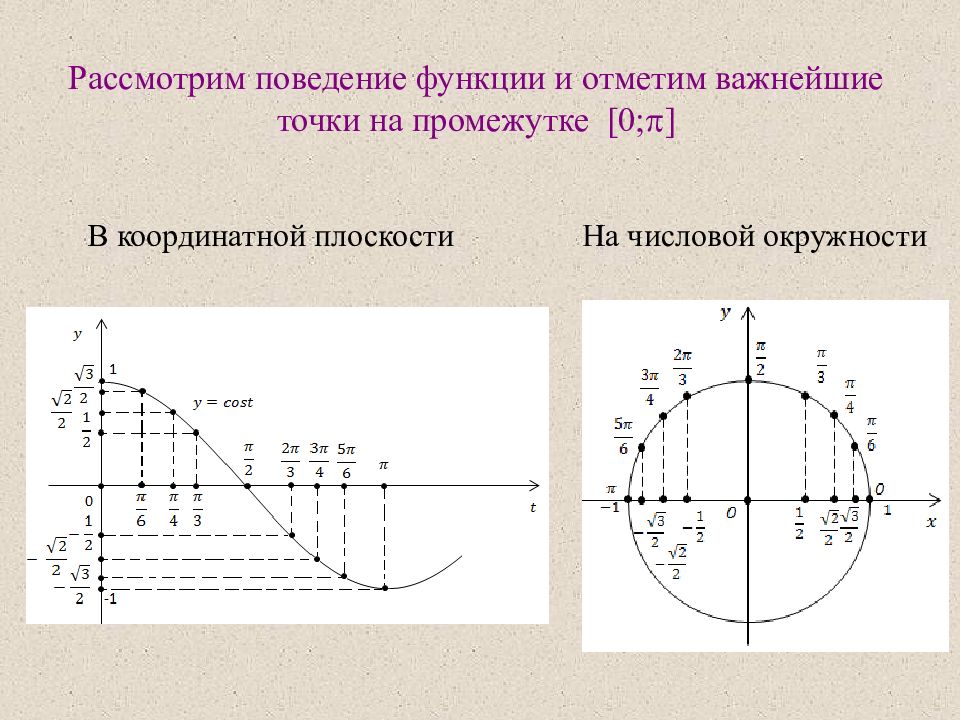
Рассмотрим поведение функции и отметим важнейшие точки на промежутке [0; ] В координатной плоскости На числовой окружности
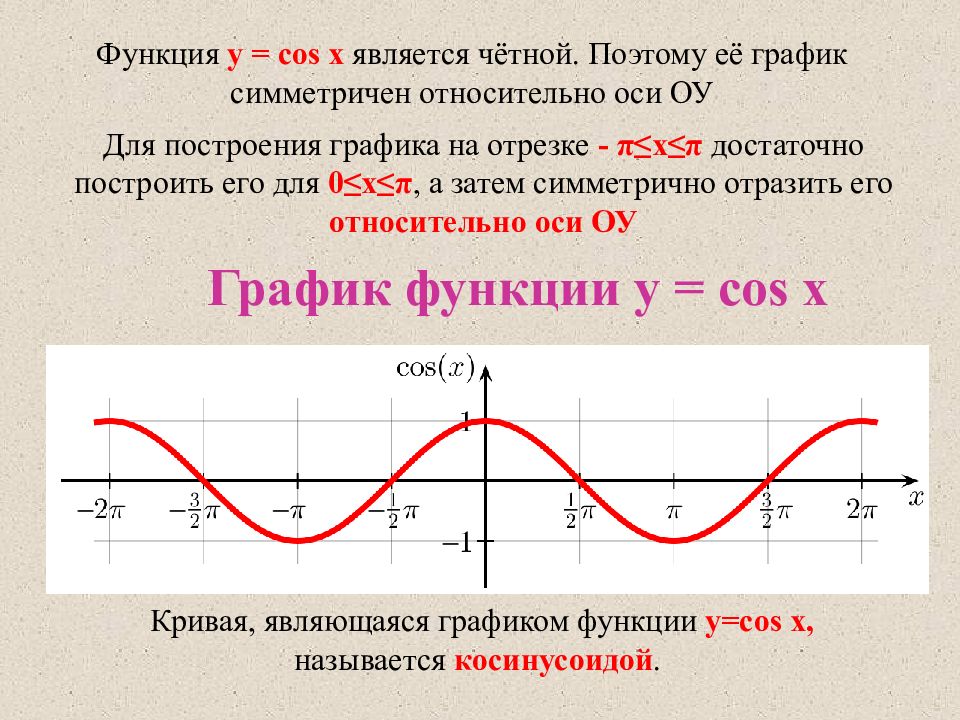
Функция y = cos x является чётной. Поэтому её график симметричен относительно оси ОУ Для построения графика на отрезке - π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси ОУ График функции y = cos x Кривая, являющаяся графиком функции y= cos x, называется косинусоидой.
Свойства функции y = cos x 1. Область определения — множество R всех действительных чисел. D(y) = (-∞ ; + ∞ ) 2. Множество значений Е(у) = [−1;1] 3. Функция периодическая с периодом T= 2π. 4. Функция чётная cos(-x) = cos x (график симметричен относительно оси ОУ ). 5. Функция ограничена и сверху, и снизу. 6. Функция y= cos x принимает: - значение, равное 0, при x=π /2+ πn,n∈Z; - наибольшее значение, равное 1, при x=2πn,n∈Z ; - наименьшее значение, равное −1, при x=π+2πn,n∈Z;
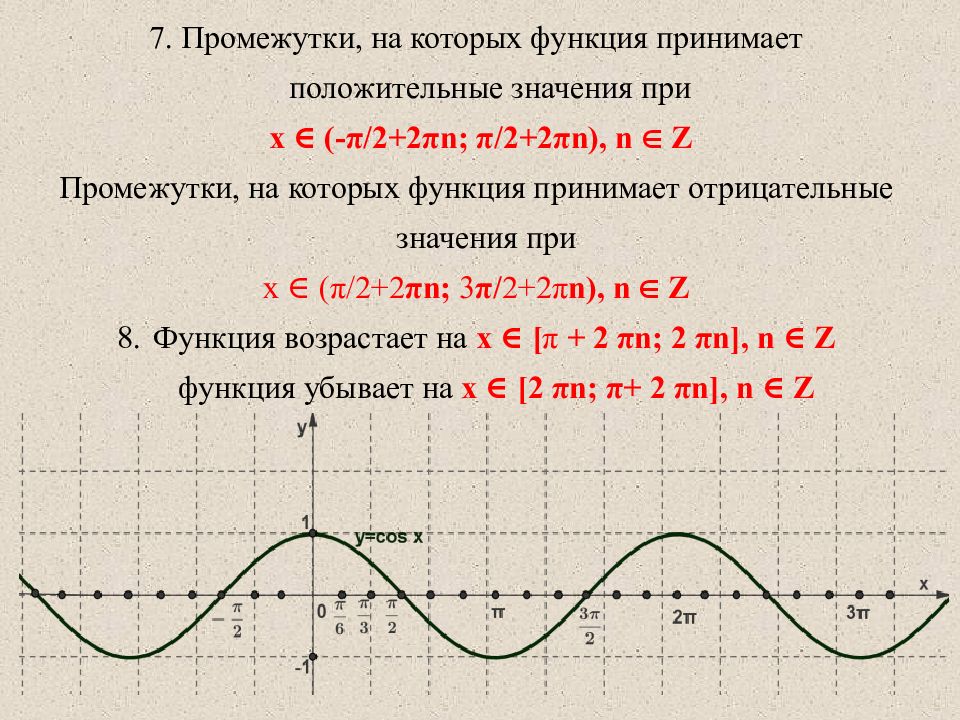
7. Промежутки, на которых функция принимает положительные значения при x ∈ ( -π/2+2π n; π/2+2π n), n ∈ Z Промежутки, на которых функция принимает отрицательные значения при x ∈ ( π /2+2 π n; 3 π / 2+2 π n), n ∈ Z Функция возрастает на x ∈ [ π + 2 π n; 2 π n ], n ∈ Z функция убывает на x ∈ [ 2 π n ; π + 2 π n ], n ∈ Z
Решение задач Задача №1 Найти пределы изменения функции y = cos t на данном отрезке [ /6; /2] Функция монотонно убывает на указанном промежутке, значит, наибольшее значение принимает на левом конце отрезка у( /6)=3/2, а наименьшее значение принимает на его правом конце у(/2) = 0 Решение
Задача №2 Найти наибольшее и наименьшее значение функции y = cos t на данном отрезке [ / 3 ; 7 / 6 ] На данном промежутке функция немонотонна. Решение Наибольшее значение принимает на левом конце отрезка у( /3)=1/2, а наименьшее значение у() = -1
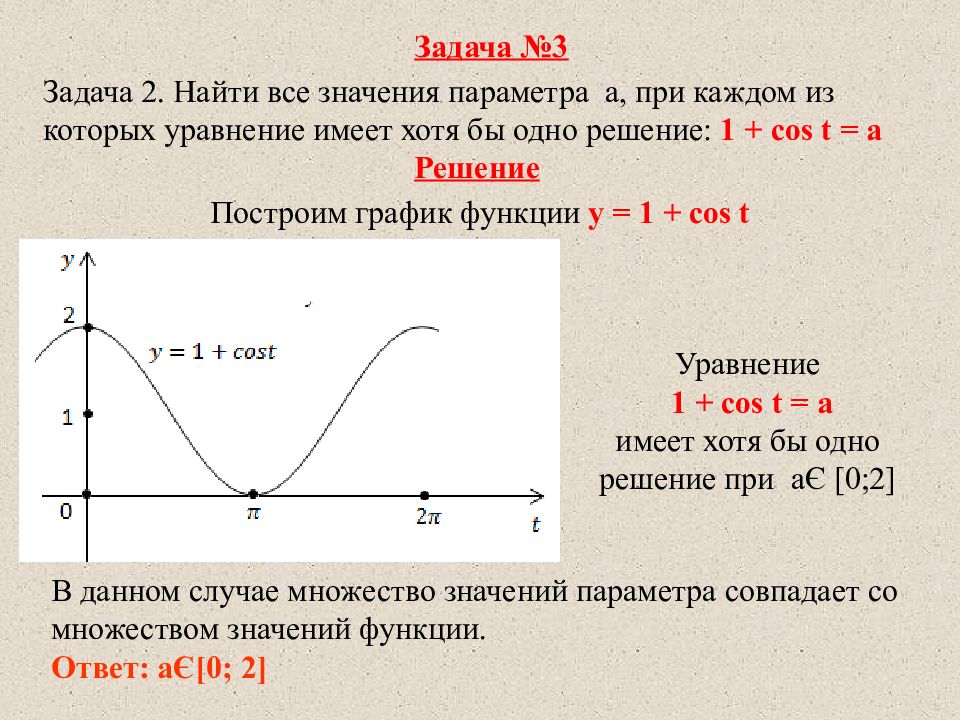
Задача 2. Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы одно решение: 1 + cos t = a Задача №3 Решение Построим график функции y = 1 + cos t Уравнение 1 + cos t = a имеет хотя бы одно решение при a Є [0;2] В данном случае множество значений параметра совпадает со множеством значений функции. Ответ: а Є [0; 2]
Задача №4 Решить уравнение Построим в одних координатных осях графики функций Решение Графики имеют только одну общую точку А(0; 1) Ответ: х=0
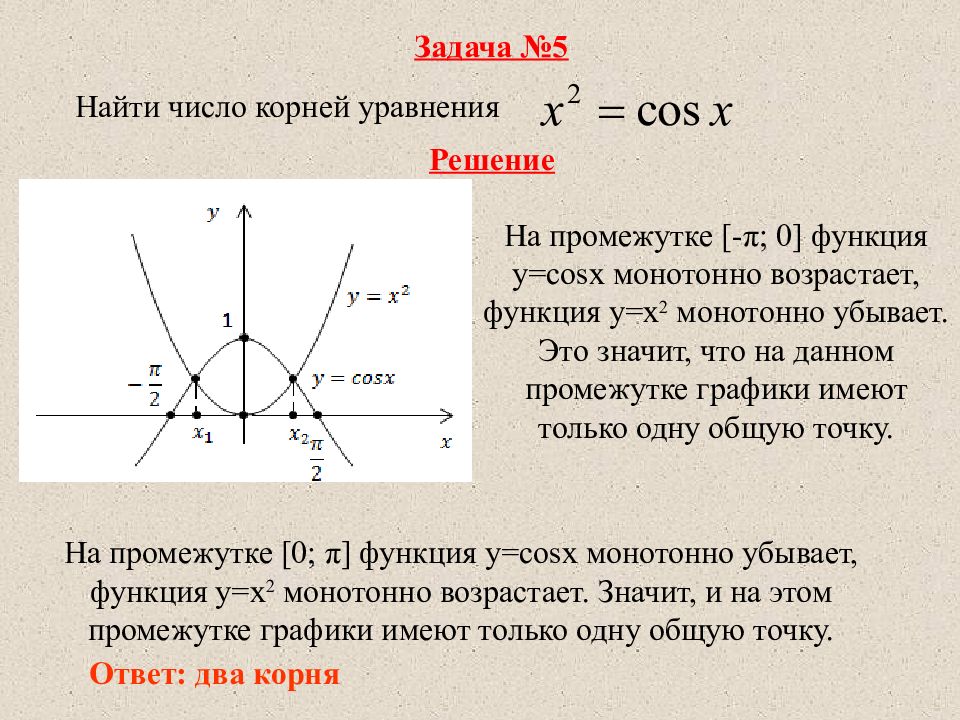
Задача №5 Найти число корней уравнения Решение На промежутке [- π ; 0] функция у= cosx монотонно возрастает, функция у=х 2 монотонно убывает. Это значит, что на данном промежутке графики имеют только одну общую точку. На промежутке [ 0; π ] функция у= cosx монотонно убывает, функция у=х 2 монотонно возрастает. Значит, и на этом промежутке графики имеют только одну общую точку. Ответ: два корня
Построить график функции y=cos3x Задача №5 Косинус – четная функция, строим график на участке [0; π /3], затем симметрично отображаем относительно оси y и получаем график на промежутке [- π /3; π /3] длина которого равна периоду. График сжимается к оси Оу в 3 раза. Решение
Задания для самостоятельного решения 1) Постройте графики функций 1) у = cos x + 1; 2) у = cos x – 1; 3) у = cos (x + π /2) 4) у = cos (x – π /3) 2 ) Найти наибольшее и наименьшее значение функции y= cos (x) на отрезке [0; 4π/3]
3) Определить область значений функции y=−8cosx+3. 4) Определить чётность или нечётность функции: f(x)=x5⋅cos6x. 5) Определить, возрастает или убывает функция y=cosx на отрезке: [−4π;−3π]. 6) Найти наибольшее и наименьшее значения функции: y=cos 4 2x−sin 4 2x+4. 7) Определить наименьшее и наибольшее значения функции y=cosx на полуинтервале (−4π / 3;−π / 3].
Заключение. Мы рассмотрели график функции y = cos x, изучили особенности ее поведения, использовали их и свойства функции при решении задач, в том числе и задач с параметром
