Первый слайд презентации: Центр тяжести
При определении центра тяжести полезны несколько теорем. 1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости. 2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси. 3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
Слайд 3: Существуют два способа определения центра тяжести тела: аналитический и экспериментальный
где S – площадь всей пластины sk - площадь её части xk, yk - координаты центра тяжести частей пластины Точка С в данном случае носит название центра тяжести площади
1. Симметрия. Если тело имеет центр симметрии, то центр тяжести находится в центре симметрии. Если тело имеет плоскость симметрии. Например, плоскость ХОУ, то центр тяжести лежит в этой плоскости. 2. Разбиение. Для тел, состоящих из простых по форме тел, используется способ разбиения. Тело разбивается на части, центр тяжести которых находится методом симметрии. Центр тяжести всего тела определяется по формулам центра тяжести объема (площади).
Слайд 5: Экспериментальный способ
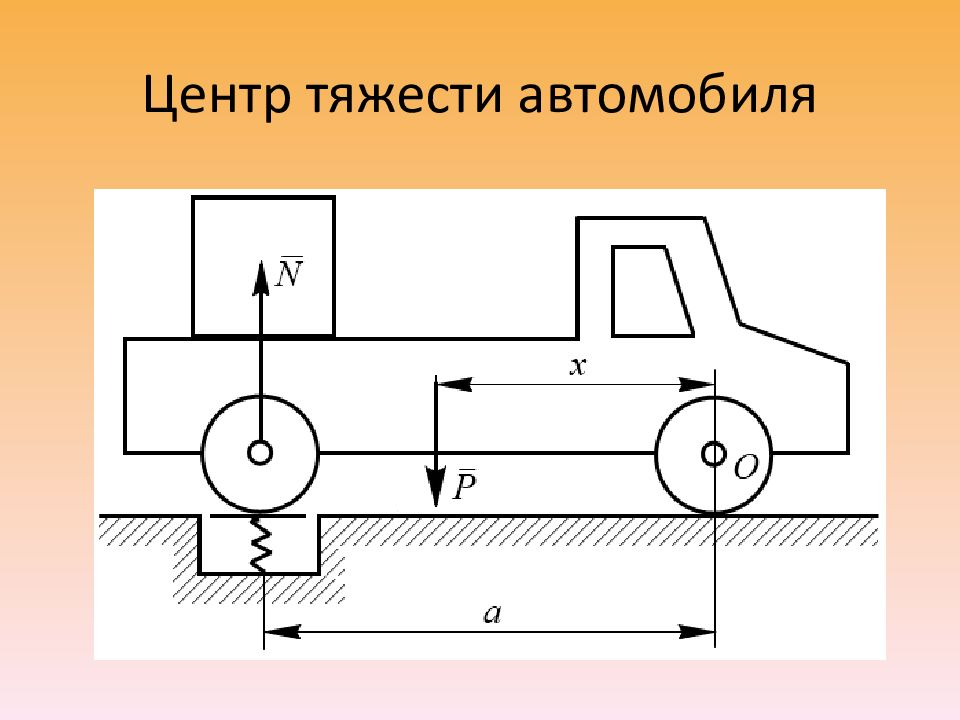
Центры тяжести неоднородных тел сложной конфигурации можно определять экспериментально: методом подвешивания и взвешивания. Первый способ состоит в том, что тело подвешивается на тросе за различные точки. Направление троса на котором подвешено тело, будет давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела. Метод взвешивания состоит в том, что сначала определяется вес тела, например автомобиля. Затем на весах определяется давление заднего моста автомобиля на опору. Составив уравнение равновесия относительно какой- либо точки, например оси передних колес, можно вычислить расстояние от этой оси до центра тяжести автомобиля
Слайд 7: Методические указания к решению задач по определению положения центров тяжести однородных тел
При решении задач на определение центра тяжести однородных тел сложной формы следует придерживаться следующего порядка: 1. Выбрать метод, который наиболее применим к данной задаче (метод разбиения или метод дополнения ). 2. Разбить сложное тело на простые элементы, для которых центры тяжести известны. 3. Выбрать оси координат. При этом необходимо помнить, что: если тело имеет плоскость симметрии, то его центр тяжести лежит в этой плоскости; если тело имеет ось симметрии, то его центр тяжести лежит на этой оси; если тело имеет центр симметрии, то его центр тяжести совпадает с центром симметрии. 4. Определить координаты центров тяжести отдельных простых тел относительно выбранных осей. 5. Используя формулы, соответствующие выбранному методу, определить искомые координаты центра тяжести заданного тела.
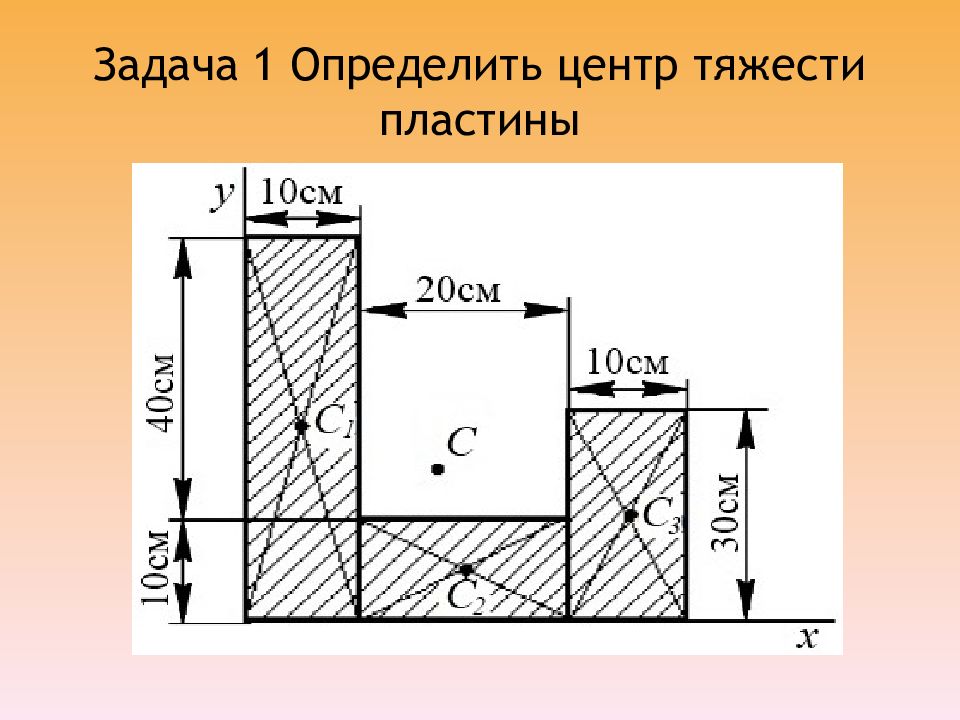
Слайд 11: Решение
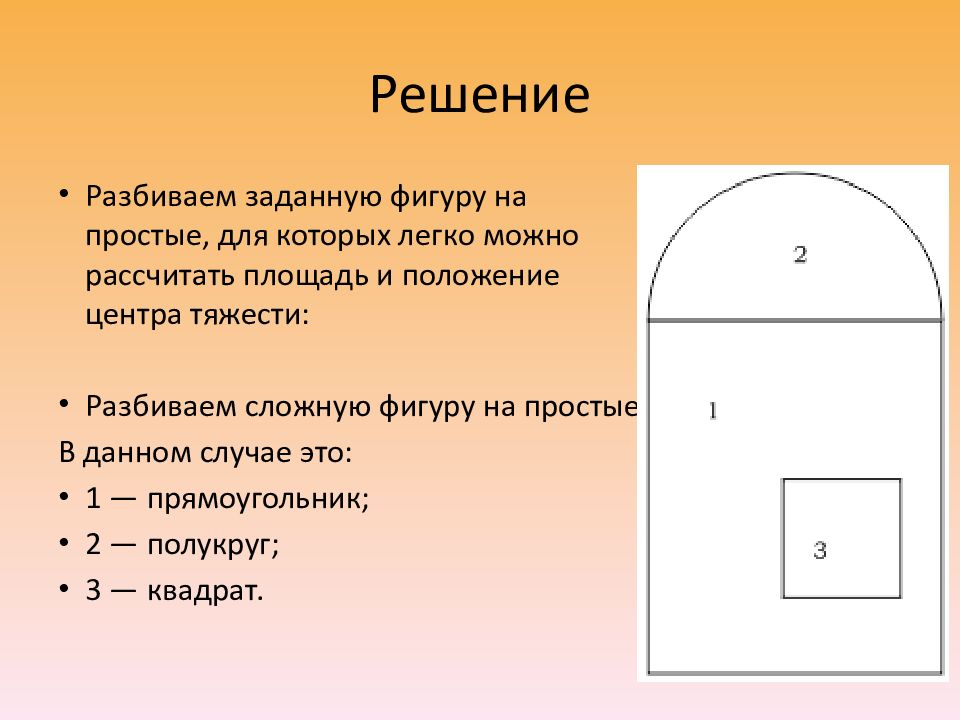
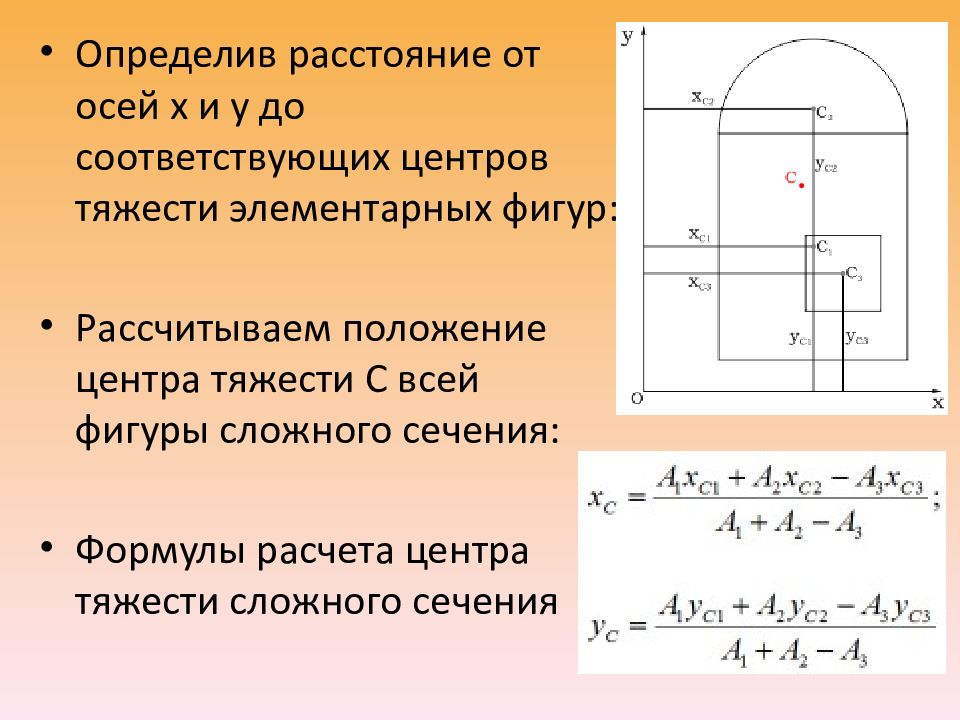
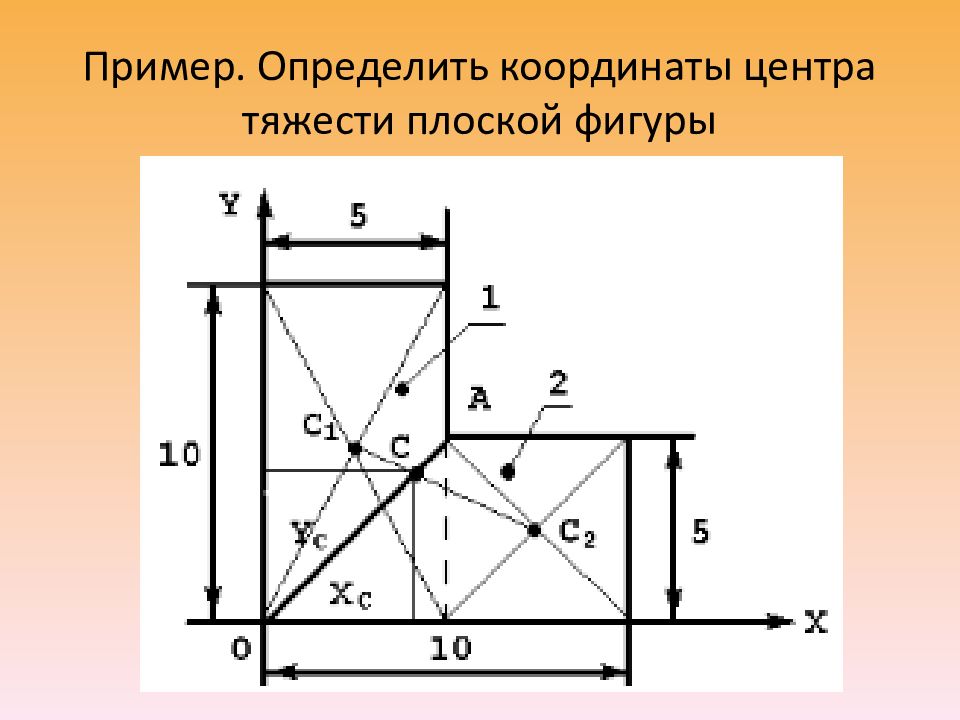
Разбиваем заданную фигуру на простые, для которых легко можно рассчитать площадь и положение центра тяжести: Разбиваем сложную фигуру на простые В данном случае это: 1 — прямоугольник; 2 — полукруг; 3 — квадрат.
Слайд 12
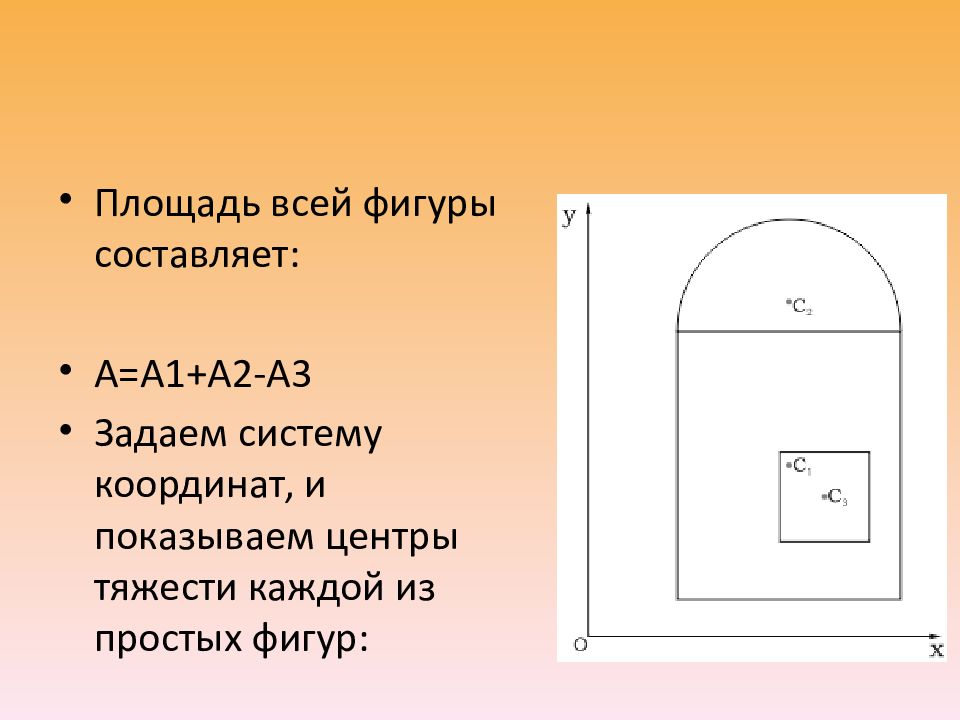
Площадь всей фигуры составляет: A=A1+A2-A3 Задаем систему координат, и показываем центры тяжести каждой из простых фигур:
Слайд 13
Определив расстояние от осей x и y до соответствующих центров тяжести элементарных фигур: Рассчитываем положение центра тяжести C всей фигуры сложного сечения: Формулы расчета центра тяжести сложного сечения
Слайд 14: Задача 3
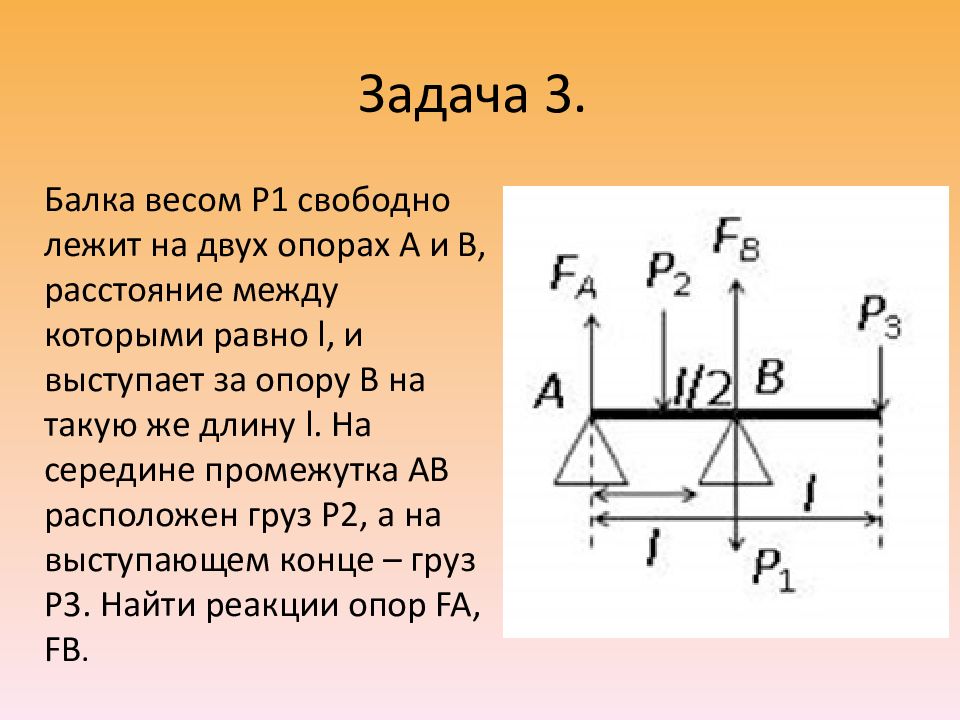
Балка весом P1 свободно лежит на двух опорах A и B, расстояние между которыми равно l, и выступает за опору B на такую же длину l. На середине промежутка AB расположен груз P2, а на выступающем конце – груз P3. Найти реакции опор FA, FB.
Слайд 15: Решение
Уравнение равновесия сил FA + FB - P1 - P2 - P3 = 0. 2. Уравнение равновесия моментов относительно точки B FAl - P2l/2 + P3l = 0
Слайд 16: 3. Определим реакции опор:
FA = P2/2 - P3; FB = P1 + P2/2 + 2P3. Ответ: FA = P2/2 - P3; FB = P1 + P2/2 + 2P3.
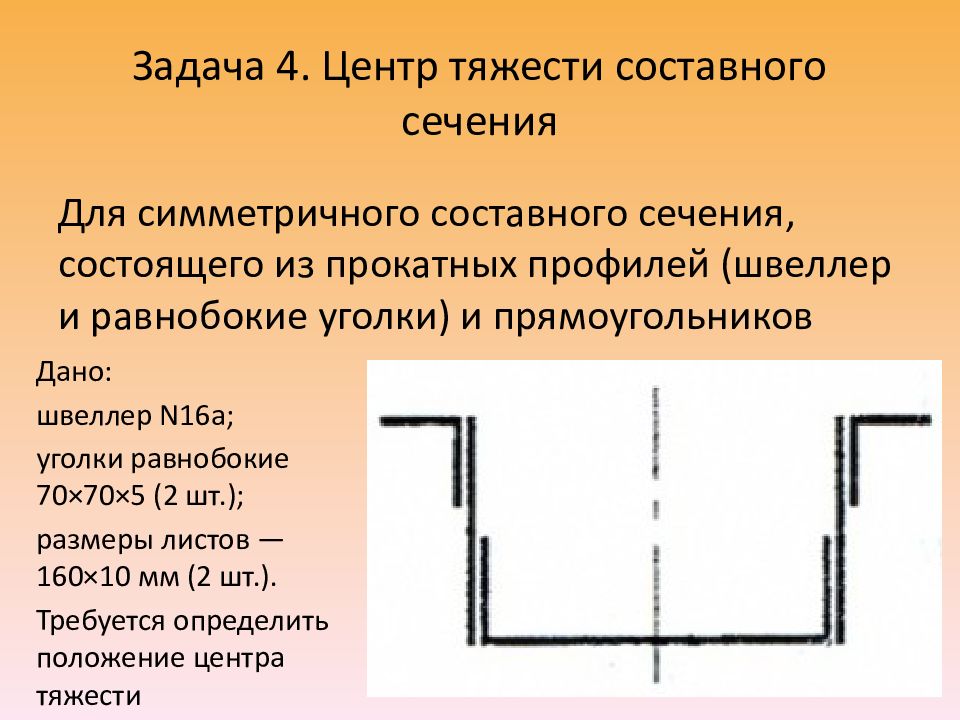
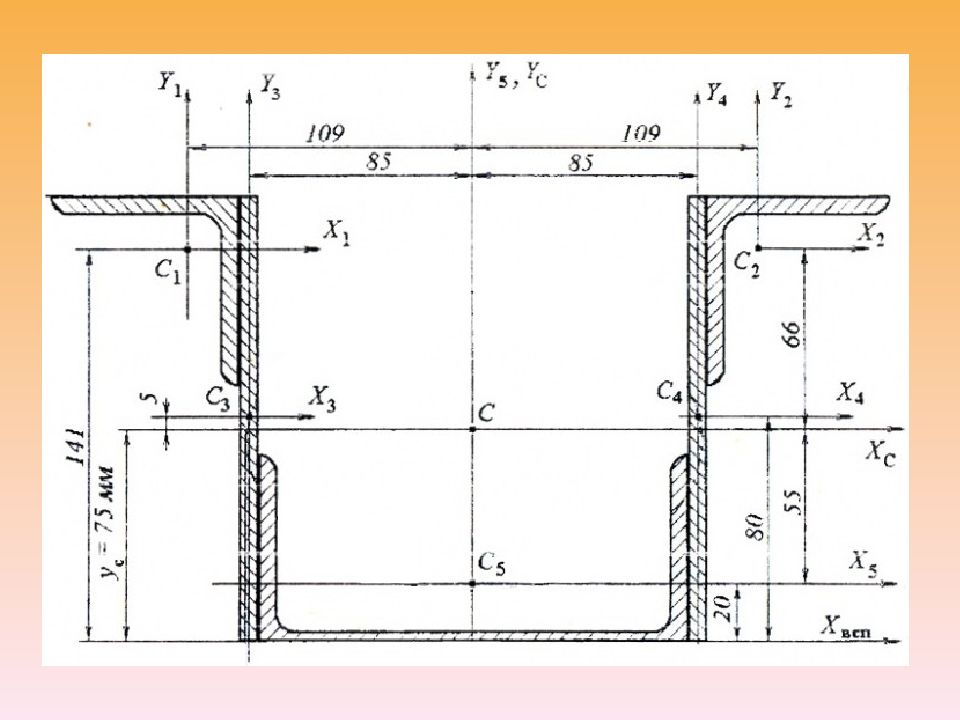
Слайд 17: Задача 4. Центр тяжести составного сечения
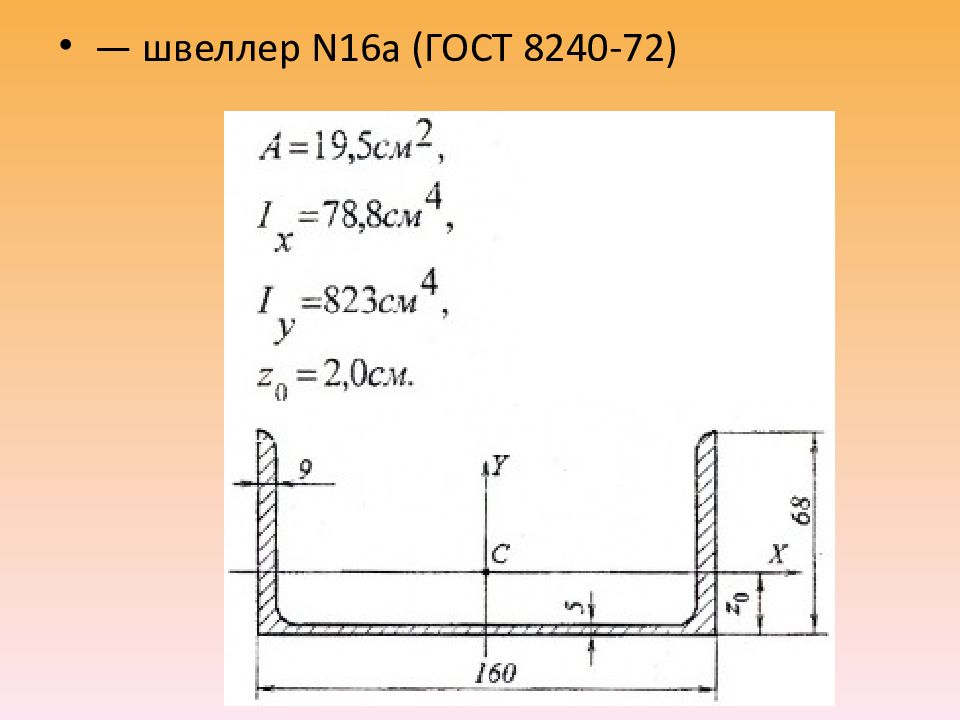
Для симметричного составного сечения, состоящего из прокатных профилей (швеллер и равнобокие уголки) и прямоугольников Дано: швеллер N16а; уголки равнобокие 70×70×5 (2 шт.); размеры листов — 160×10 мм (2 шт.). Требуется определить положение центра тяжести
Слайд 18: Решение
Находим геометрические характеристики фигур, составляющих заданное сечение: — уголки равнобокие 70×70×5 (ГОСТ 8509-72)
Слайд 20
— прямоугольник 160×10 мм Вычерчиваем составное сечение в масштабе 1:2, отмечаем центры тяжести отдельных фигур Ci и проводим их центральные оси Xi, Yi.
Слайд 21
Положение центра тяжести и главных осей Одной из главных центральных осей является ось симметрии YC. Выбрав вспомогательную ось Xвсп и определив по чертежу координаты центров тяжести отдельных фигур yi относительно этой оси, находим положение главной центральной оси XC по формуле:
Слайд 24
Тогда формула для определения координаты Х c примет вид: где А 1 = 5×10 = 50 см 2 — площадь первой фигуры, А 2 =5×5=25 см 2 площадь второй фигуры, Х 1 =2,5 см — координата центра тяжести первой фигуры, Х 2 = 7,5 см — координата центра тяжести второй фигуры. Отсюда cм. Аналогично можем найти и координату У c, однако это не имеет смысла, так как центр тяжести всей фигуры должен лежать на оси симметрии, которой является линия ОА, поэтому и координата У c также равна 4,17 см.
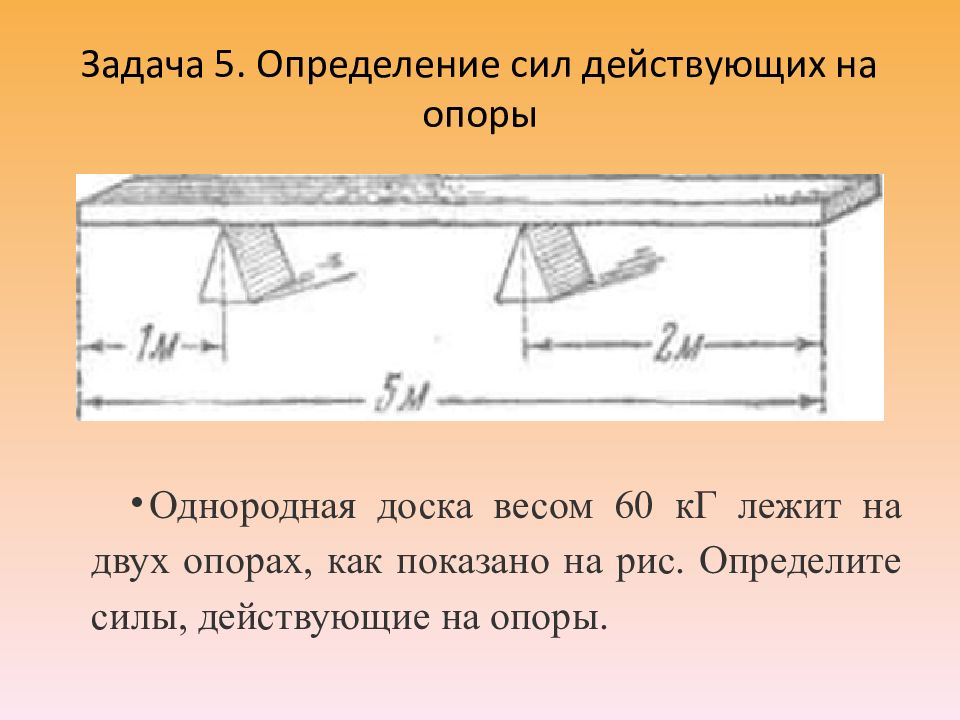
Слайд 25: Задача 5. Определение сил действующих на опоры
Однородная доска весом 60 кГ лежит на двух опорах, как показано на рис. Определите силы, действующие на опоры.
Слайд 26: Алгоритм
1) Зная массу доски, найти ее вес ( F = m (кг) * g (Н/м) 2) Зная вес, найти вес 1 м доски 3) Найти вес доски на каждом из участков 4) Привести распределенную нагрузку к сосредоточенной, приложенной к середине каждого участка (F1, F2 и F3) 5) Написать уравнение суммы моментов относительно опоры А 6) Из уравнения найти реакцию опоры R(B) 7) Написать уравнение суммы моментов относительно опоры B 6) Из уравнения найти реакцию опоры R(A) 7) Произвести проверку: сумма всех нагрузок = 0
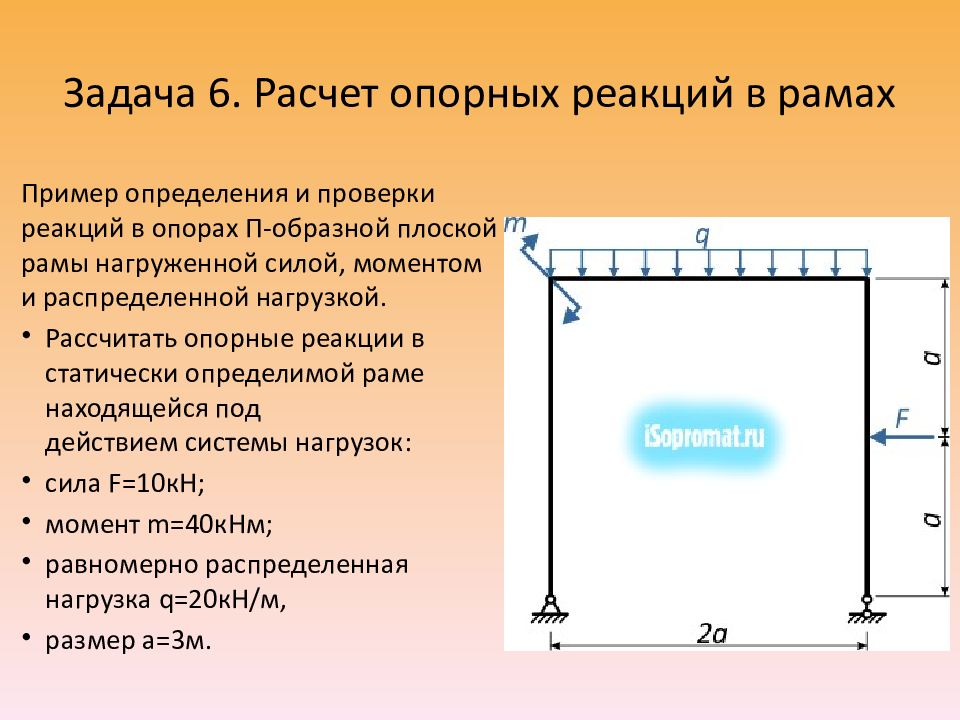
Слайд 27: Задача 6. Расчет опорных реакций в рамах
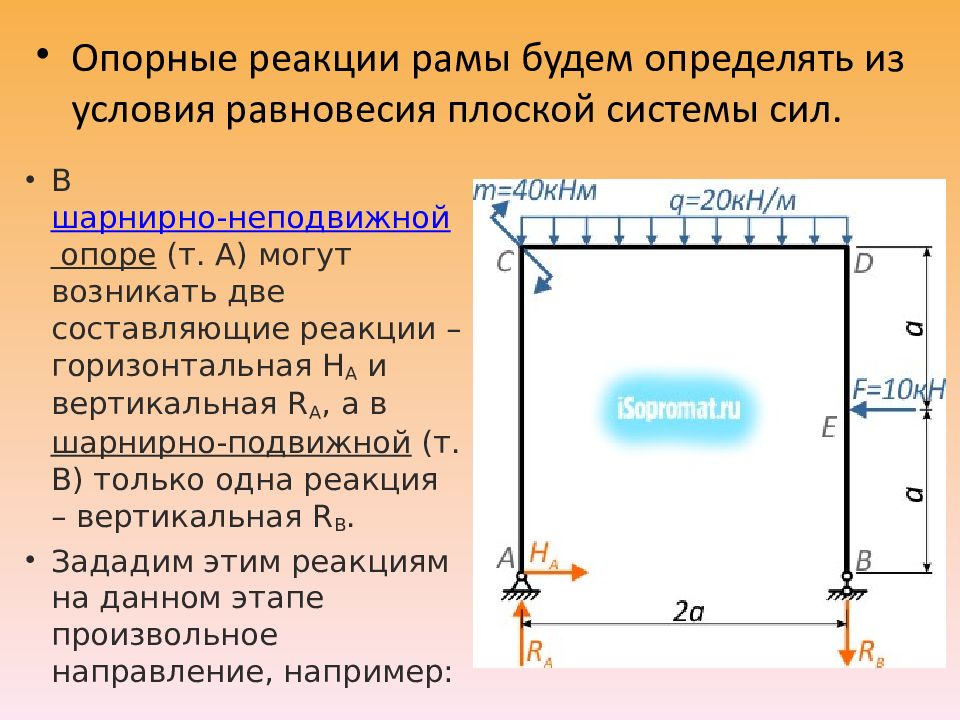
Пример определения и проверки реакций в опорах П-образной плоской рамы нагруженной силой, моментом и распределенной нагрузкой. Рассчитать опорные реакции в статически определимой раме находящейся под действием системы нагрузок: сила F=10кН; момент m=40кНм; равномерно распределенная нагрузка q=20кН/м, размер a=3м.
Слайд 28: Решение
Расчет реакций Перед началом решения задачи перенесем на расчетную схему числовые данные нагрузок и обозначим характерные точки (сечения) рамы буквами A, B, C, D и E.
Слайд 29
Опорные реакции рамы будем определять из условия равновесия плоской системы сил. В шарнирно-неподвижной опоре (т. A) могут возникать две составляющие реакции – горизонтальная H A и вертикальная R A, а в шарнирно-подвижной (т. B) только одна реакция – вертикальная R B. Зададим этим реакциям на данном этапе произвольное направление, например:
Слайд 30
Для нахождения трех неизвестных усилий нам потребуется три уравнения статики : два уравнения суммы моментов относительно опорных точек и сумма проекций всех сил на горизонтальную ось X, которые должны равняться нулю. Запишем их:
Слайд 31
Из каждого уравнения выражаем и находим соответствующую величину опорной реакции:
Слайд 32
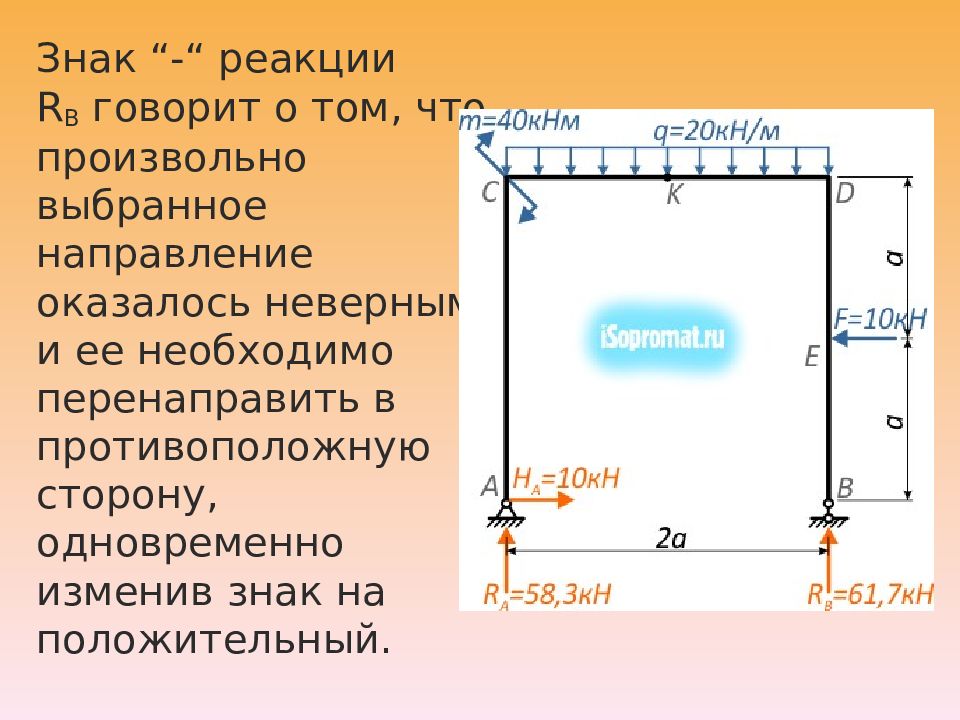
Знак “-“ реакции R B говорит о том, что произвольно выбранное направление оказалось неверным, и ее необходимо перенаправить в противоположную сторону, одновременно изменив знак на положительный.
Последний слайд презентации: Центр тяжести
В задачах подобного рода после расчета реакций в опорах настоятельно рекомендуется выполнять проверку полученных значений, так как даже небольшая ошибка, в дальнейших расчетах может привести к неправильному результату. Проверка реакций Арифметическую проверку реакций выполним, записав сумму моментов относительно, например, середины ригеля CD (точки K):