Слайд 2: Лозунг ДП
Действуем максимально лениво! Не пересчитываем то, что когда-то уже посчитали. ДП – решение сложных задач через более простые 2
Слайд 3: Схема. Всегда в голове
База Переход Общая задача = по структуре маленьким Что есть ответ? 3
Слайд 4: Для сильно опережающих
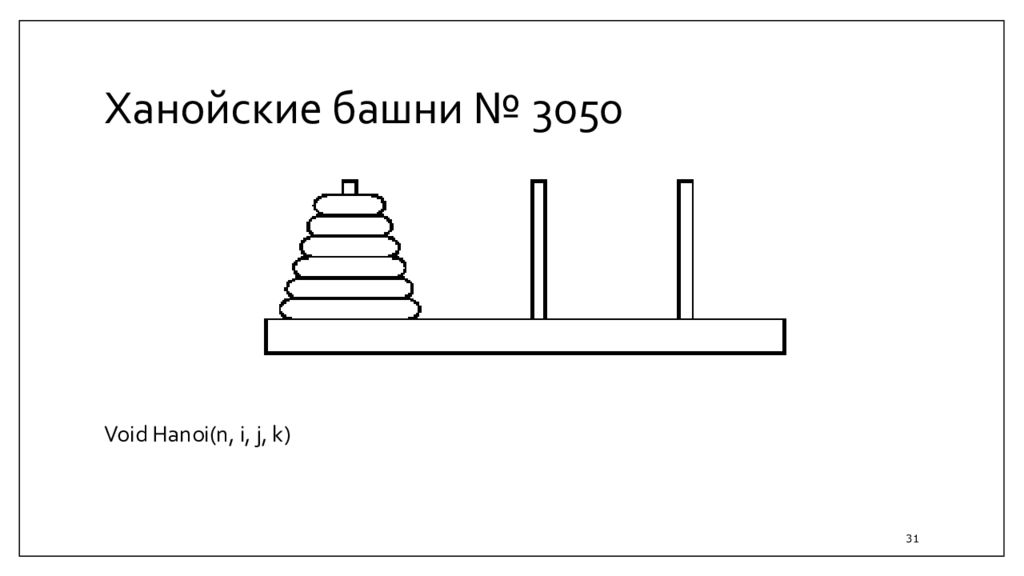
Спиралька № 1470 Ханойские башни №3050 Рюкзак с выводом № 3090 Таблица №1150 4
Слайд 5: Снова Числа Фибоначчи №201
Можно и в массив, главное – не пересчитывайте заново с первого Можно тремя переменными Как поменять два числа? Какие способы вы знаете? Помните как мы вычисляли среднее по величине из трёх? Какое число вмещается в тип int ? 49ое вместится? 5
Слайд 8: Камни. 1119
Дано N золотых слитков массой m 1, …, m N. Ими наполняют рюкзак, который выдерживает вес не более M. Какую наибольшую массу золота можно унести в таком рюкзаке? 8
Слайд 9: Решение
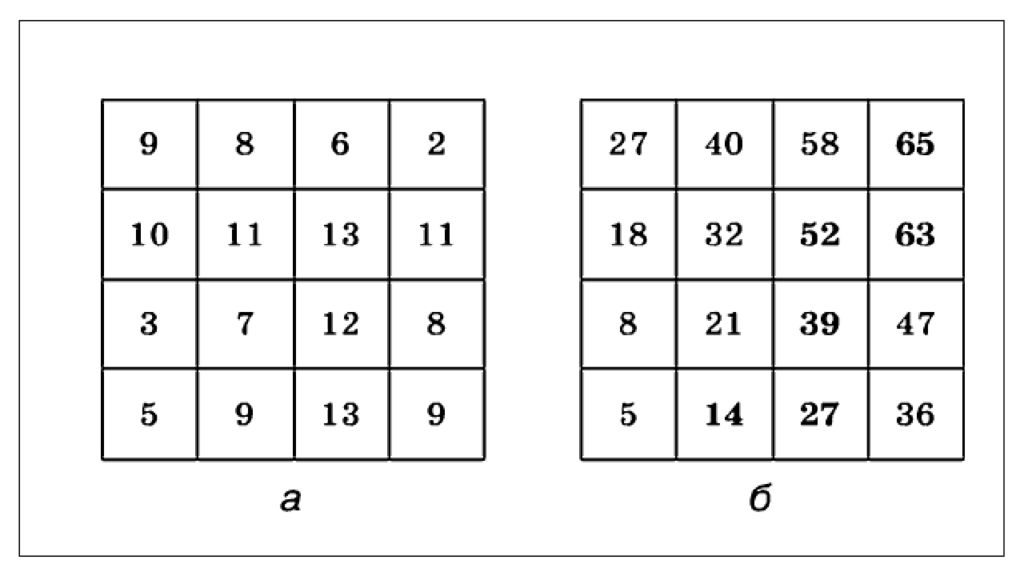
Сформируем матрицу A, в которой номер строки – номер камня, номер столбца – набранный вес В нулевой столбец запишем нули Max и сортировки – в <algorithm> vector из vector -ов Кто найдет опечатку в таблице? 9
Слайд 10: Камни. 1119
Дано N золотых слитков массой m 1, …, m N. Ими наполняют рюкзак, который выдерживает вес не более M. Какую наибольшую массу золота можно унести в таком рюкзаке? 10
Слайд 11: Камни. 1119
Дано N золотых слитков массой m 1, …, m N. Ими наполняют рюкзак, который выдерживает вес не более M. Какую наибольшую массу золота можно унести в таком рюкзаке? 11
Слайд 12: Где опечатка?
Аккуратно с выходом за границы массива Не забудьте: if ((j-p[i]) >=0) { сравниваем A[i,j], else {A[i,j] = из строки выше }} cout<<endl; 12
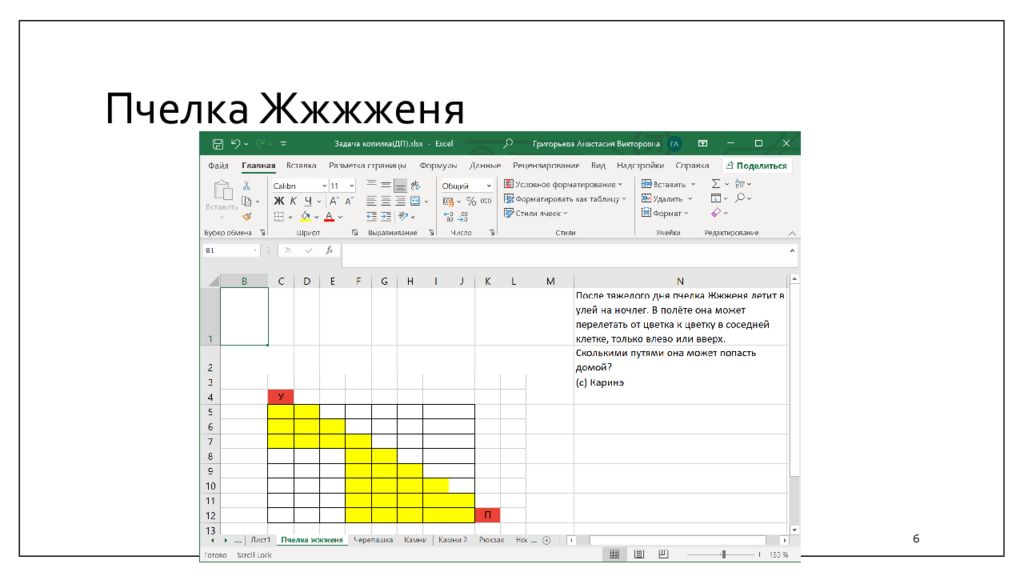
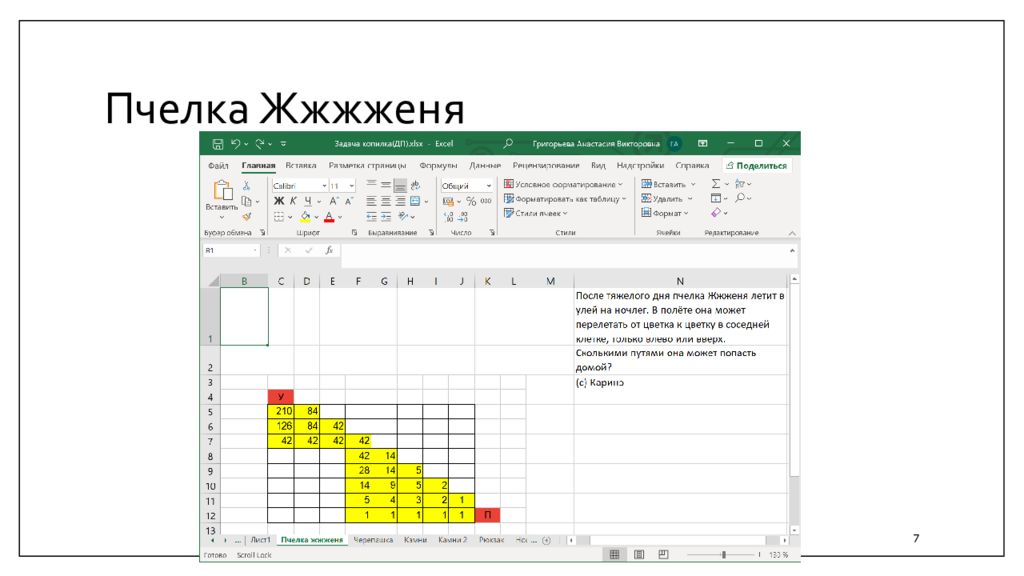
Слайд 14: Решение задачи «Черепашка ». П.П
Полный перебор вариантов – универсальный способ решения. Но рассмотрим его потенциальные возможности Пусть дана таблица 4х4. Любой путь состоит из трёх перемещений вверх и трех перемещений вправо, т.е. длина пути равна шести. Другими словами, дано 6 шагов, из них 3 выбираются для перемещений вверх, оставшиеся 3 – для перемещений вправо определяются однозначно. Т.о. количество способов выбора трех перемещений из шести При нахождении суммы (стоимости) пути потребуется 5 операци сложения, всего 100 операций. Оценим время решения задачи для компьютера с миллионным быстродействием (см. презентация предыдущих занятий о сложности алгоритмов и быстродействии на примере задачи о тупоугольном треугольнике)
Слайд 15: Длительность вычислений
Слайд 17: Код (на паскале)
Слайд 20: Сдать можно как задачу №2965
Т ам даже не требуется вывести путь И идет черепашка в другом направлении http:// informatics.mccme.ru/mod/statements/view3.php?id=656&chapterid=2965#1 С восстановлением пути №619
Слайд 25: Решение
Для каждого члена исходной последовательности вычислить максимальную длину возрастающей подпоследовательности, оканчиающейся этим элементов. Например: 2 5 3 4 6 1 1 2 1 1 1 1 0 0 0 0 0 0 А это номер элемента, предшествующего нашему. Для восстановления ответа в будущем Будем вычислять характеристики всех членов последовательности от первого до N -ого по порядку и заносить полученные результаты в массив. Пусть известны характеристики для всех членов последовательности с 1-ого до ( i-1)- го и нужно узнать ее для i - ого. Тогда какой-то из элементов от 1-ого до ( i-1 )-ого будет предпоследним. Очевидно, что предпоследний может быть любой элемент, меньший i - ого. А наилучшая характеристика у нашего i - ого элемента получится, если взять предыдущий элемент с максимальной характеристикой. Решение
Слайд 29: Рюкзак № 3089
Вектор из пар: vector<pair< int, int >> K(n+1) K[ i ].first K[ i ].second В остальном вспоминаем задачу Камни. 29 Рюкзак с восст.ответа № 30 90