1. Понятие о статически неопределимых системах Статически неопределимой называется система, внутренние усилия которой нельзя определить лишь из уравнений статики. Статически неопределимые системы (СНС) отличаются от статически определимых рядом свойств: − они надежнее; − выдерживают б ó льшую нагрузку; − у них деформации меньше; − изменение температуры, смещение опор, неточность изготовления элементов вызывают дополнительные внутренние усилия; − внутренние усилия зависят от физических и геометрических характеристик элементов; − у них есть «лишние» связи.
Число лишних связей называется степенью статической неопределимости. Степень статической неопределимости n простой системы определяется из дискового аналога по формуле Степень статической неопределимости фермы определяется по формуле
Расчет статически неопределимой системы начинается с превращения ее в статически определимую. Для этого необходимо исключить лишние связи и заменить их реакции неизвестными силами. Полученная система называется основной системой (ОС). 2. Выбор основной системы Например, у этой балки, названной заданной системой (ЗС), степень статической неопределимости n=1 : Если исключить лишнюю связь (правую опору) и обозначить неизвестную реакцию через X, получим ее ОС :
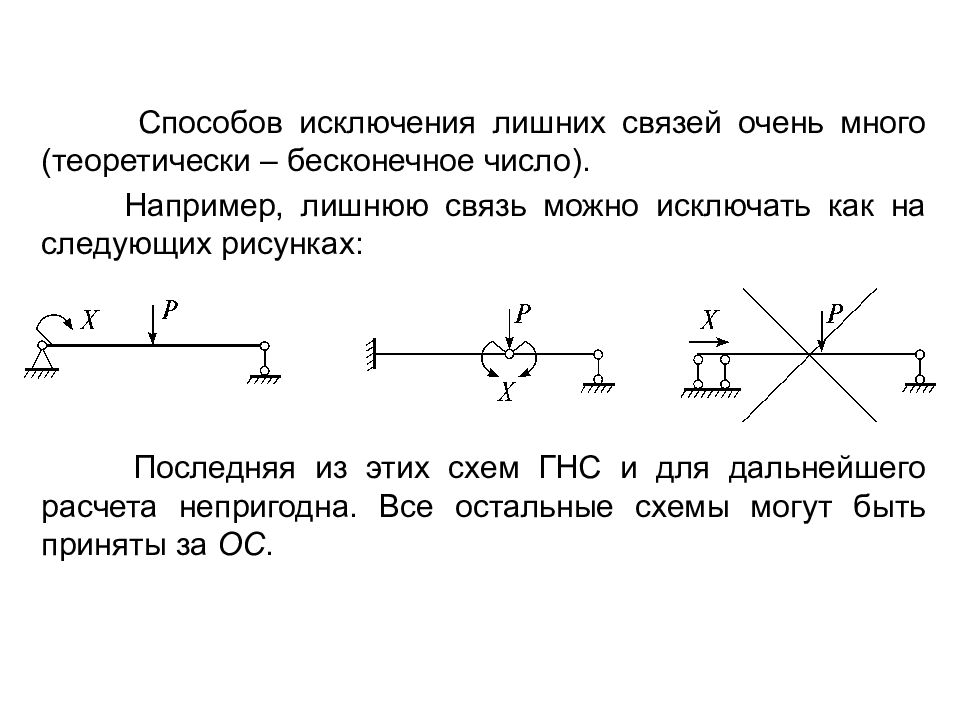
Способов исключения лишних связей очень много (теоретически – бесконечное число). Например, лишнюю связь можно исключать как на следующих рисунках: Последняя из этих схем ГНС и для дальнейшего расчета непригодна. Все остальные схемы могут быть приняты за ОС.
В расчетах линейно-упругих систем используется гипотеза о том, что внешняя нагрузка в элементах заданной системы распределяется единственным образом. Следовательно, результаты расчетов по различным ОС должны быть одинаковыми. Однако объем вычислений в разных ОС может быть разным. Поэтому из многих вариантов ОС нужно выбирать наиболее оптимальную. В нашем примере первый вариант ОС предпочтительнее остальных, т.к. в ней эпюры строятся легче.
Основная система должна быть: простой для расчета ; обязательно геометрически неизменяемой; учитывать характерные особенности сооружения и действующей нагрузки.
В этом методе за основные неизвестные принимаются силы (внутренние усилия). Поэтому его называют методом сил. Рассмотрим предыдущую балку и потребуем, чтобы ЗС и ее ОС были эквивалентными. Для этого перемещение в направлении исключенной связи в ОС должно равняться нулю. Запишем его как =0. Это условие эквивалентности часто называется условием совместности деформаций. По принципу суперпозиции, перемещение равно сумме перемещения X от воздействия X и перемещения P от заданной нагрузки P : = X + P =0.
Когда сила X неизвестна, определить X нельзя. Поэтому рассмотрим единичное состояние (ЕС) основной системы, где действует только единичная сила P =1 : В линейно-упругой системе выполняется условие X = X. Тогда получим X+ P =0. − каноническое уравнение метода сил Из него определяется неизвестная сила: X= – P / . Перемещение от еди-ничной силы называется податливостью.
Если в системе имеется n лишних связей, то нужно исключить все эти связи и выбрать ОС с n неизвестными X 1, X 2, , X n. Тогда из условий эквивалентности ЗС и ее ОС можно составить n уравнений совместности деформаций. При рассмотрении n единичных состояний основной системы эти уравнения приводятся к системе линейных уравнений: − система канонических уравнений метода сил
Здесь − главные коэффициенты – боковые коэффициенты, iP − грузовые коэффициенты. Введем матричные обозначения: матрица податливости Тогда система канонических уравнений примет вид X + P = 0. Из нее определяется X= – –1 P, где –1 − обратная матрица податливости. вектор неизвестных вектор нагрузки нуль- вектор
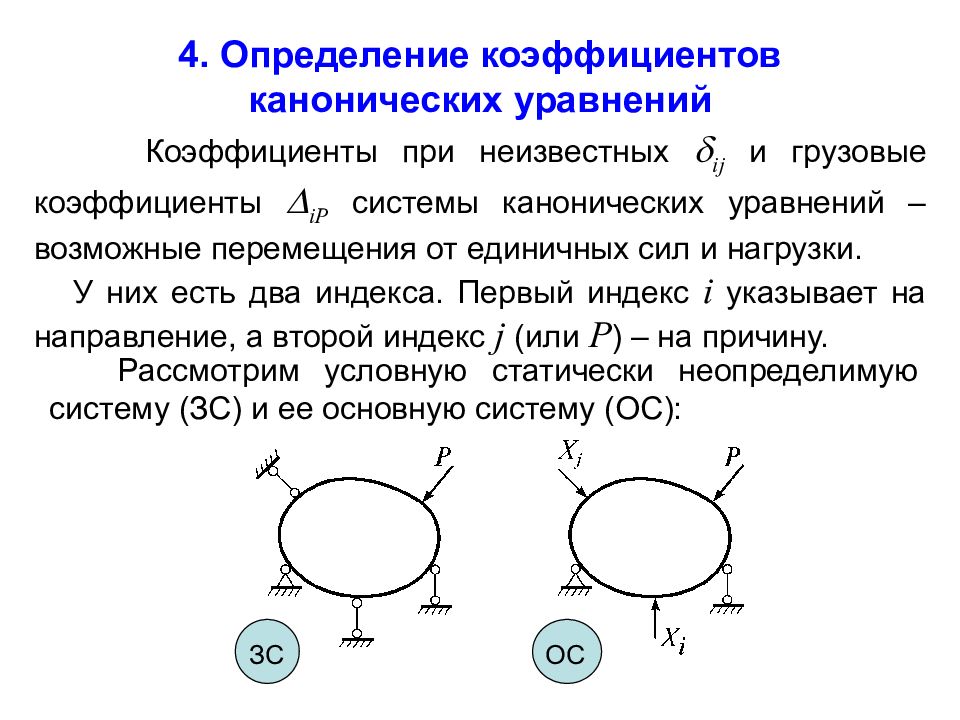
Коэффициенты при неизвестных ij и грузовые коэффициенты iP системы канонических уравнений – возможные перемещения от единичных сил и нагрузки. У них есть два индекса. Первый индекс i указывает на направление, а второй индекс j (или P ) – на причину. Рассмотрим условную статически неопределимую систему (ЗС) и ее основную систему (ОС): ЗС ОС
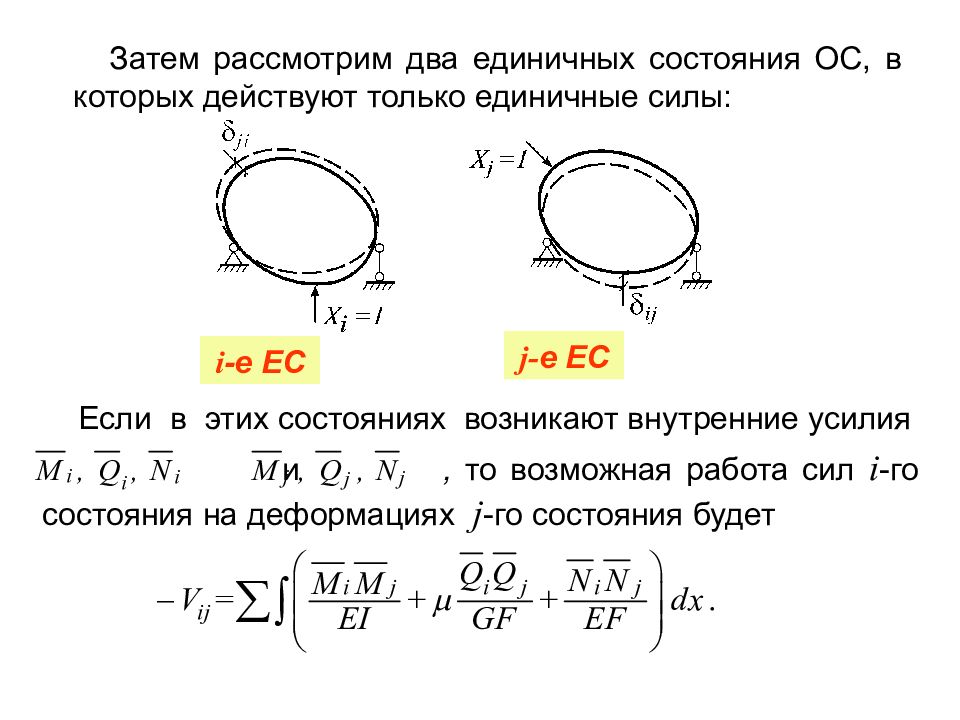
Затем рассмотрим два единичных состояния ОС, в которых действуют только единичные силы: i -е ЕС j - е ЕС Если в этих состояниях возникают внутренние усилия и , то возможная работа сил i -го состояния на деформациях j -го состояния будет
С другой стороны, возможная работа внешних сил i -го состояния на перемещениях j - го состояния равна W ij =1 ij = ij. По принципу возможных перемещений W ij =–V ij. Из их равенства получаем − формула вычисления коэффициентов при неизвестных
Теорема Максвелла. Перемещение в i -ом направлении от единичной силы в j -ом направлении равна перемещению в j- ом направлении от единичной силы в i -ом направлении, т.е. ij = ji. Доказательство. Возможную работу сил i -го единичного состояния на перемещениях j -го состояния мы уже определили: W ij = ij. А возможная работа сил j -ого состояния на перемещениях i -го состояния равна (см. рис.): W ji =1 ji = ji. По теореме Бетти W ij =W ji. Следовательно, ij = ji. Эта теорема позволяет уменьшать объем вычислений при вычислении боковых коэффициентов системы канонических уравнений.
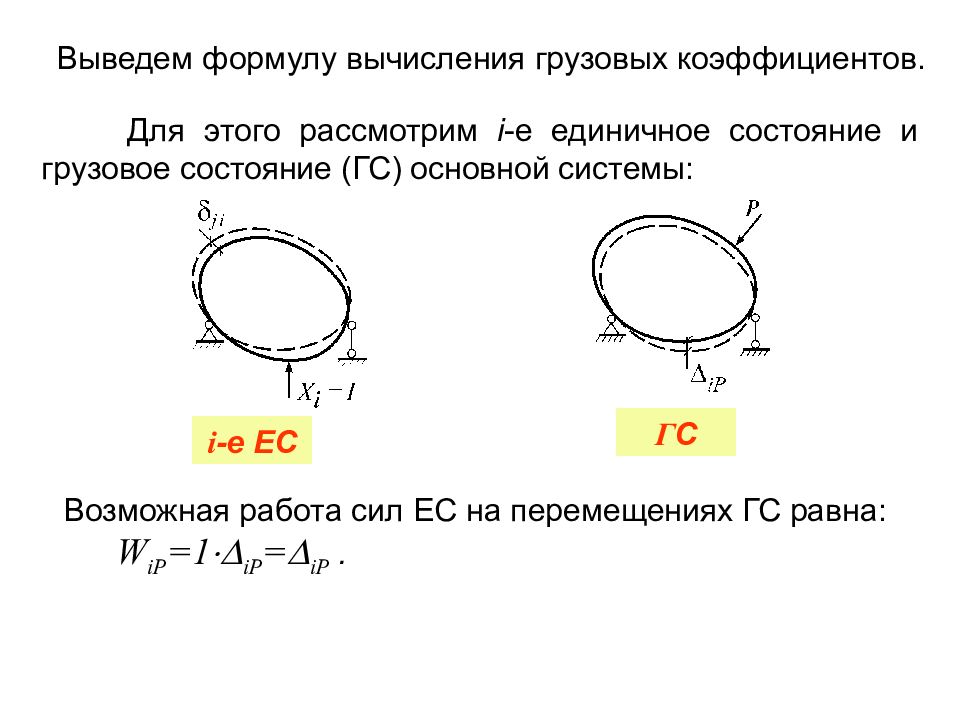
Выведем формулу вычисления грузовых коэффициентов. Возможная работа сил ЕС на перемещениях ГС равна: W iP =1 iP = iP. i -е ЕС Для этого рассмотрим i -е единичное состояние и грузовое состояние (ГС) основной системы: Г С
По принципу возможных перемещений W iP =–V iP. Отсюда − формула вычисления грузовых коэффициентов Возможная работа внутренних сил i - го единичного состояния на деформациях грузового состояния равна:
В рамах и балках перемещения определяются в основном изгибными деформациями. Поэтому коэффициенты канонических уравнений можно вычислять по сокращенным формулам: Здесь знак использован для сокращения записи формулы вычисления интеграла Мора и означает условное «произведение» двух эпюр.
5. Проверка правильности коэффициентов При вычислении коэффициентов канонических уравнений метода сил возможны ошибки. Поэтому их надо проверять. Рассмотрим два способа проверки. Универсальная проверка используется для одновременной проверки всех коэффициентов системы канонических уравнений: если сумма всех коэффициентов системы канонических уравнений равна произведению суммарной единичной эпюры на себя, т.е. то все коэффициенты системы канонических уравнений вычислены верно. Здесь − суммарная единичная эпюра
Постолбцовая проверка используется для проверки грузовых коэффициентов: если сумма всех грузовых коэффициентов равна произведению суммарной единичной эпюры на грузовую эпюру, т.е. то грузовые коэффициенты вычислены верно. После этих проверок можно решать систему канонических уравнений метода сил и определять неизвестные X 1, X 2, …, X n.
6. Определение внутренних усилий Внутренние усилия заданной СНС можно найти двумя способами: 1) подставляя найденные величины X 1, X 2, …, X n в основную систему и определяя ее усилия M, Q, N в СОС; 2) используя единичные эпюры в единичных состояниях и грузовые эпюры M P, Q P, N P в грузовом состоянии. С учетом закона Гука и принципа суперпозиции получаются формулы:
При расчете рам и балок обычно используется только первая из этих формул. Тогда эпюра Q строится по эпюре M с использованием теоремы Журавского, а эпюра N строится по эпюре Q способом вырезания узлов, т.е.:
7. Алгоритм метода сил Расчет рам методом сил состоит из следующих этапов: 1. Определение степени статической неопределимости. 2. Выбор основной системы. 3. Запись канонических уравнений. 4. Рассмотрение единичных и грузового состояний. 5. Построение единичных и грузовой эпюр. 6. Определение коэффициентов канонических уравнений. 7. Решение системы канонических уравнений. 8. Построение эпюр M, Q, N. 9. Проверка правильности расчета. Такая проверка состоит из двух частей: статическая проверка − проверка выполнения условий равновесия; кинематическая проверка – проверка выполнения всех условий или одного условия
8. Определение перемещений СНС Перемещения СНС по этой формуле можно искать в трех вариантах : 1) используются эпюры и M в заданной СНС; однако построение этих эпюр связано с решением двух трудоёмких задач раскрытия статической неопределимости; 2−3) одна из этих эпюр строится в статически определимой основной системе; в этом случае используются формулы или где M 0 и M P – единичная и грузовая эпюры в любой основной системе метода сил. Перемещения статически неопределимых систем можно вычислять по формуле Мора. В системах с преобладанием изгибных деформаций (например, в рамах и балках) она имеет вид:
