Преподаватель: Солодухин Андрей Геннадьевич
1. Эйлеров цикл и эйлеров граф: определения 2. Гамильтоновы графы 3. Алгоритмы поиска эйлеровых циклов
ПОВТОРЕНИЕ: МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ Маршрутом в графе называется последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной Маршрут в котором все ребра различны, называется цепью Цепь называется простой, если и все вершины в ней различны Путь – это … ориентированная цепь, в которой дуги имеют одинаковое направление
Две вершины и называются связными, если существует маршрут с концами и. Граф называется связным, если для любой пары различных вершин существует соединяющий их маршрут. Длиной маршрута называют число ребер в нем, причем каждое ребро считается столько раз, сколько раз оно считается в маршруте. Орграф называется односторонне связным, если для любых двух различных вершин х i и x j существует, по крайней мере, один путь из х i в х j или из x j в х i или оба одновременно. Орграф называют слабо связным, если для любых двух различных вершин графа существует, по крайней мере, один маршрут (неориентированный двойник пути), соединяющий их.
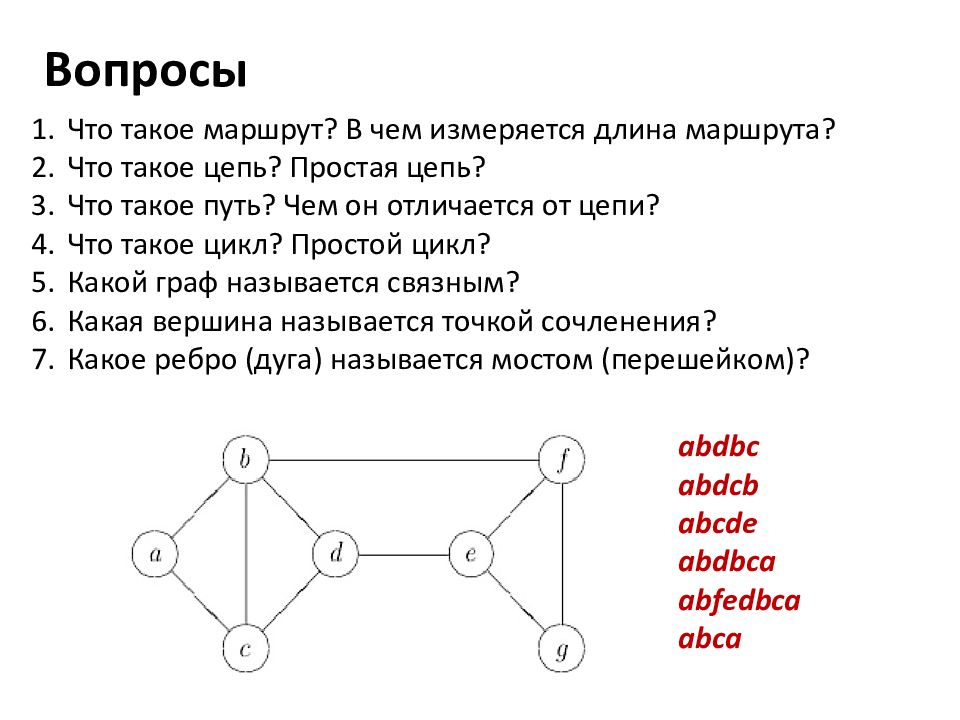
Что такое маршрут? В чем измеряется длина маршрута? Что такое цепь? Простая цепь? Что такое путь? Чем он отличается от цепи? Что такое цикл? Простой цикл? Какой граф называется связным? Какая вершина называется точкой сочленения? Какое ребро (дуга) называется мостом (перешейком)? Вопросы abdbc abdcb abcde abdbca abfedbca abca
ОПРЕДЕЛЕНИЯ Эйлеровым путем графа называется путь, содержащий все ребра графа ровно один раз Эйлеровым циклом называется цикл, содержащий все рѐбра графа и притом по одному разу. Граф, обладающий эйлеровым циклом, называется эйлеровым графом. Задача китайского почтальона Почтальон должен разнести почту по вверенному ему району, для чего он проходит по всем без исключения улицам района и возвращается в исходную точку (на почту). Требуется найти кратчайший маршрут почтальона.
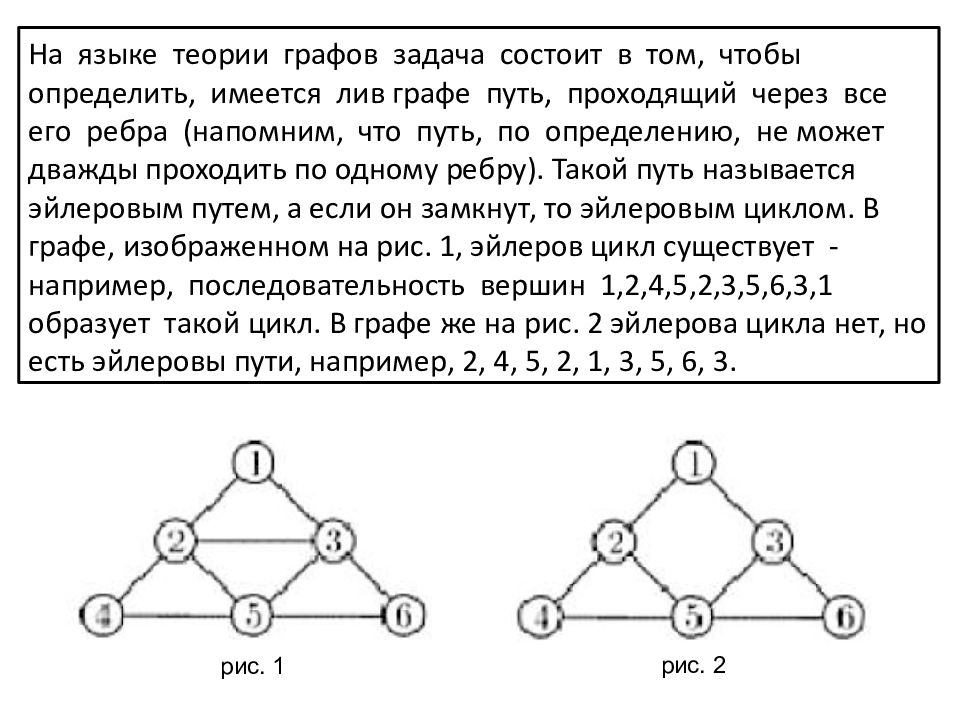
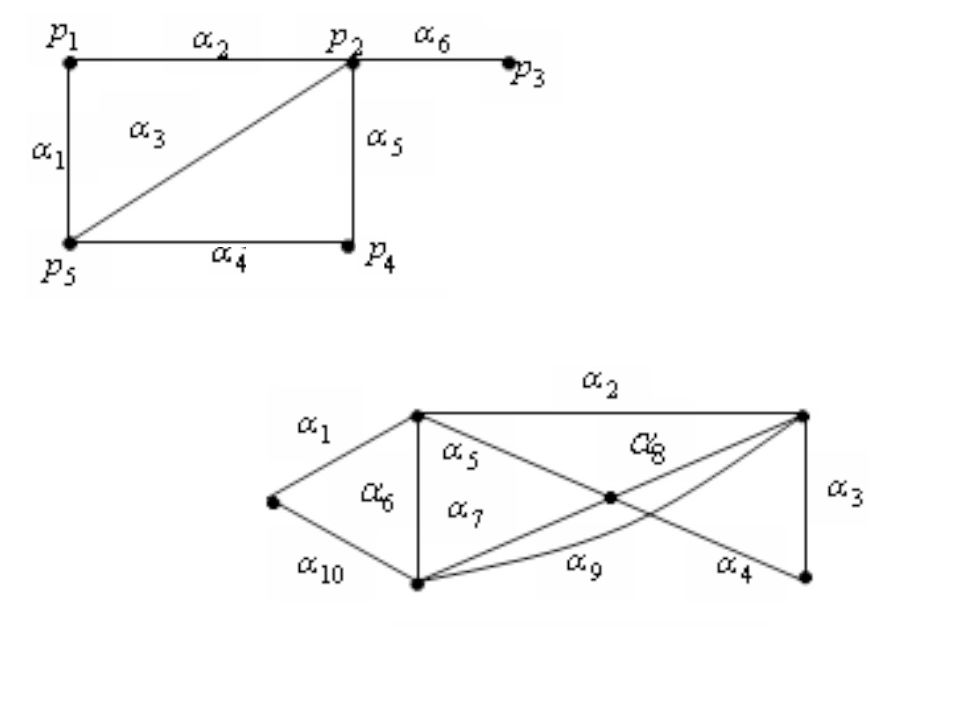
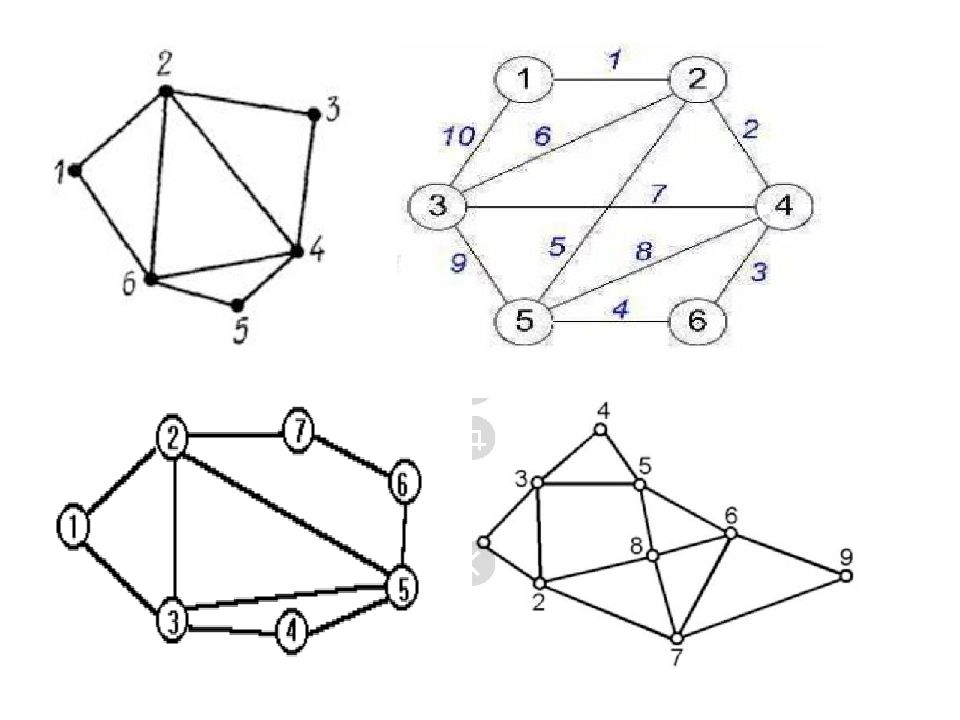
На языке теории графов задача состоит в том, чтобы определить, имеется лив графе путь, проходящий через все его ребра (напомним, что путь, по определению, не может дважды проходить по одному ребру). Такой путь называется эйлеровым путем, а если он замкнут, то эйлеровым циклом. В графе, изображенном на рис. 1, эйлеров цикл существует -например, последовательность вершин 1,2,4,5,2,3,5,6,3,1 образует такой цикл. В графе же на рис. 2 эйлерова цикла нет, но есть эйлеровы пути, например, 2, 4, 5, 2, 1, 3, 5, 6, 3. рис. 1 рис. 2
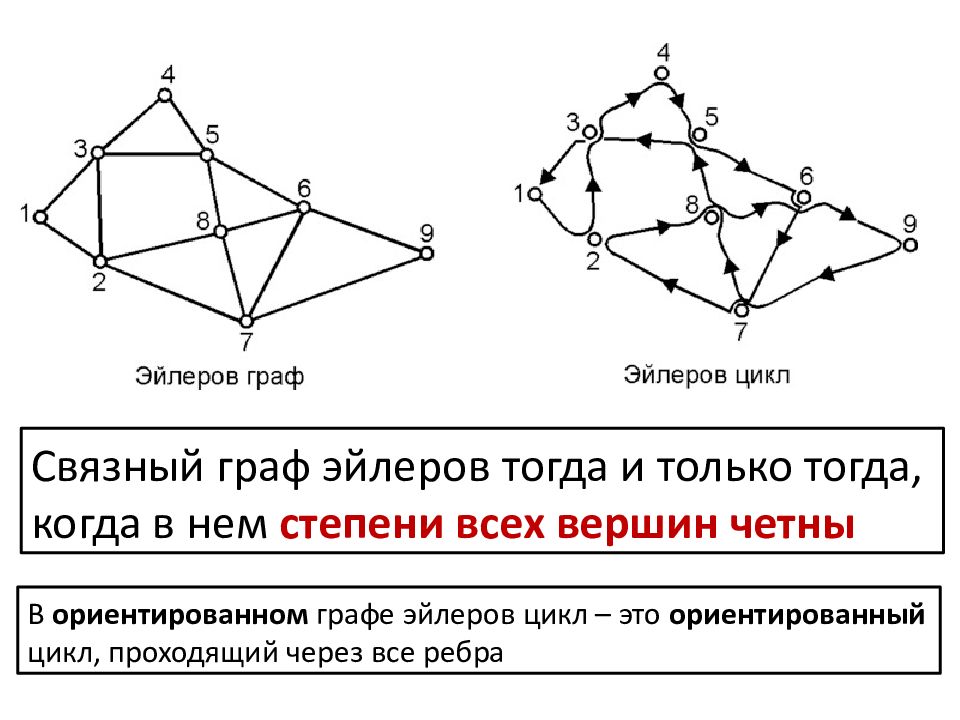
Связный граф эйлеров тогда и только тогда, когда в нем степени всех вершин четны В ориентированном графе эйлеров цикл – это ориентированный цикл, проходящий через все ребра
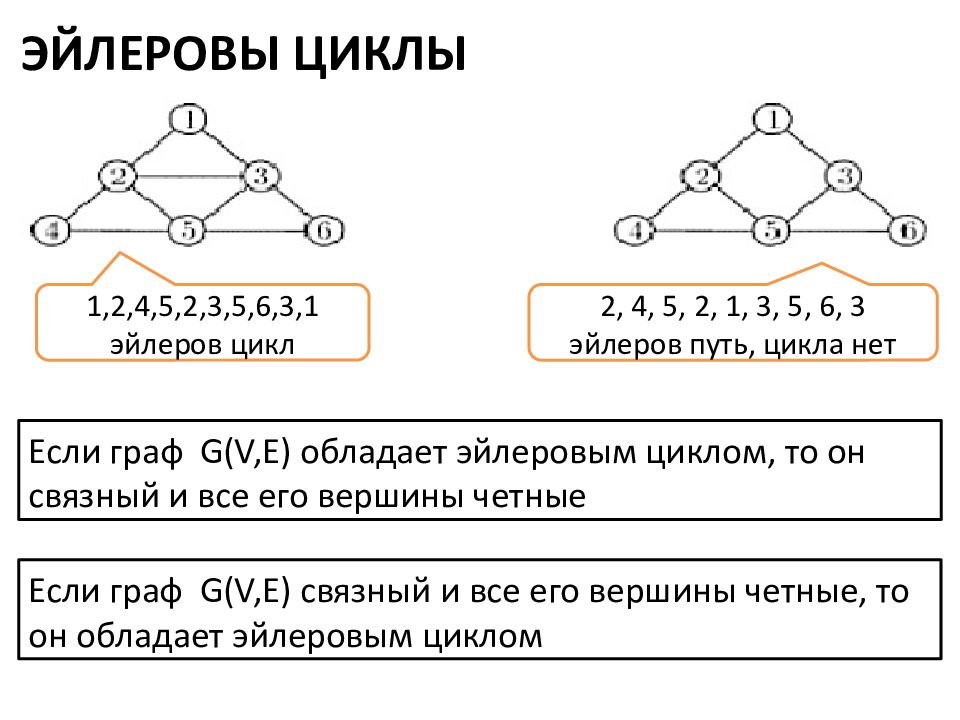
ЭЙЛЕРОВЫ ЦИКЛЫ 1,2,4,5,2,3,5,6,3,1 эйлеров цикл 2, 4, 5, 2, 1, 3, 5, 6, 3 эйлеров путь, цикла нет Если граф G(V,E) обладает эйлеровым циклом, то он связный и все его вершины четные Если граф G(V,E) связный и все его вершины четные, то он обладает эйлеровым циклом
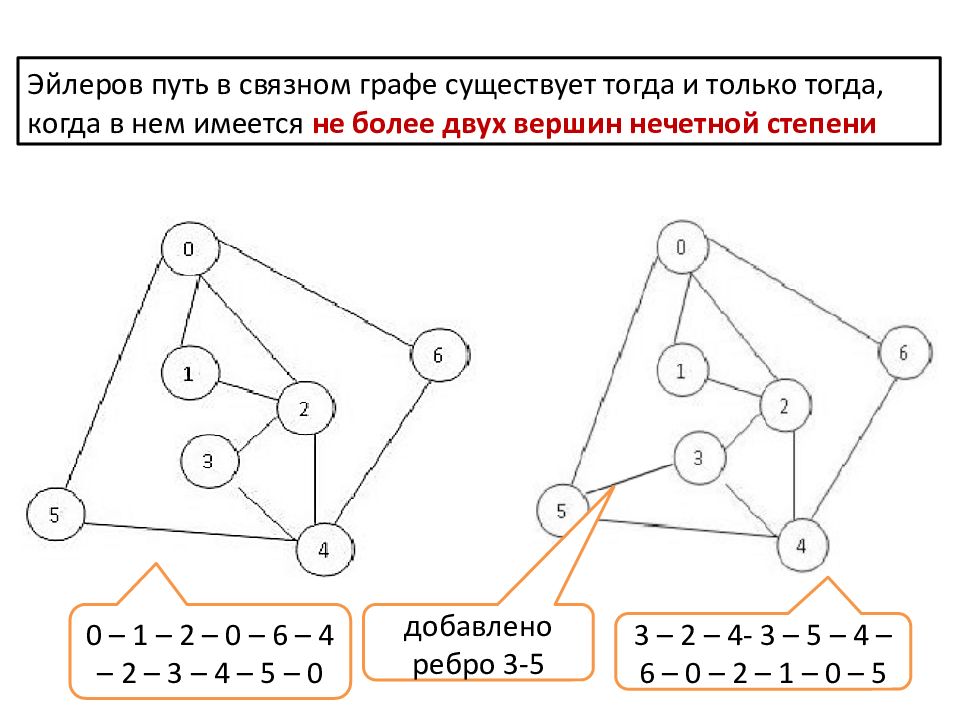
Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более двух вершин нечетной степени добавлено ребро 3-5 3 – 2 – 4- 3 – 5 – 4 – 6 – 0 – 2 – 1 – 0 – 5 0 – 1 – 2 – 0 – 6 – 4 – 2 – 3 – 4 – 5 – 0
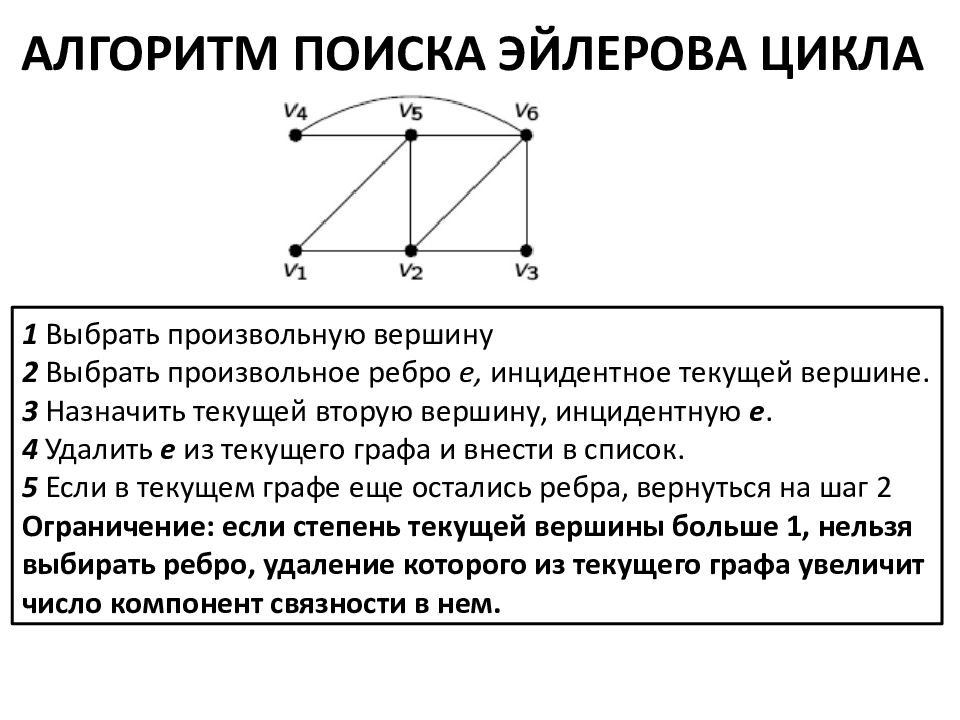
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 Ограничение: если степень текущей вершины больше 1, нельзя выбирать ребро, удаление которого из текущего графа увеличит число компонент связности в нем.
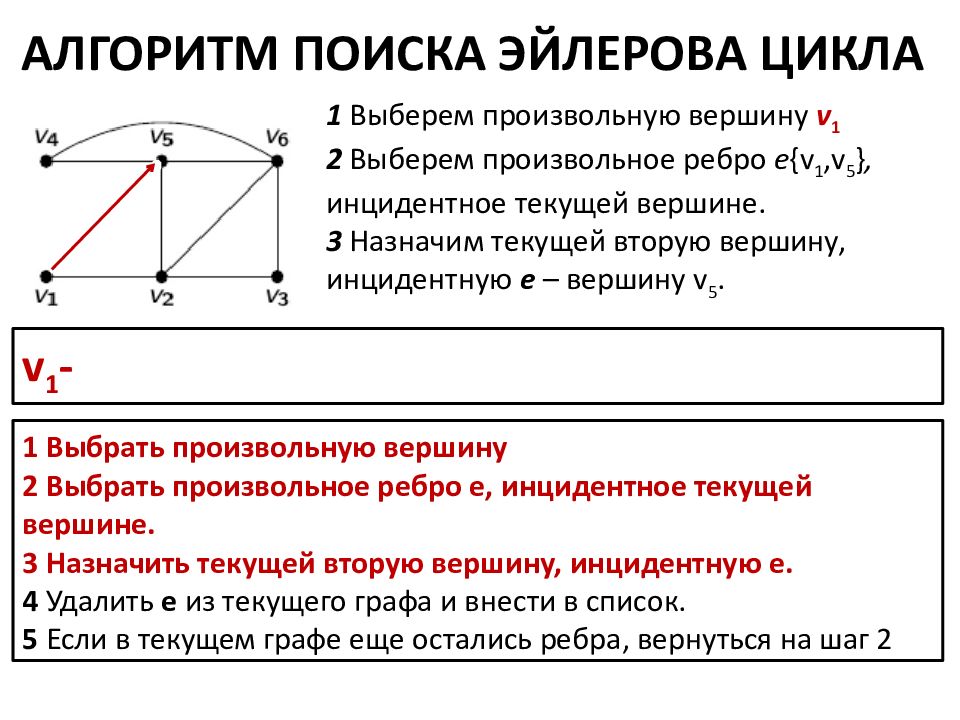
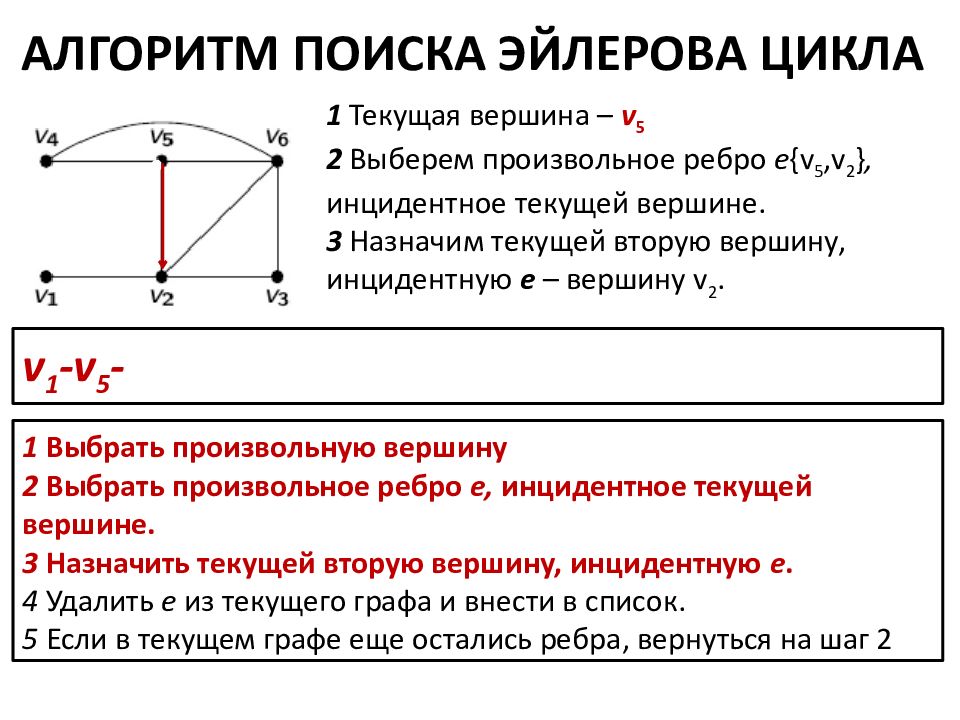
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 1 Выберем произвольную вершину v 1 2 Выберем произвольное ребро е {v 1,v 5 }, инцидентное текущей вершине. 3 Назначим текущей вторую вершину, инцидентную e – вершину v 5. v 1 -
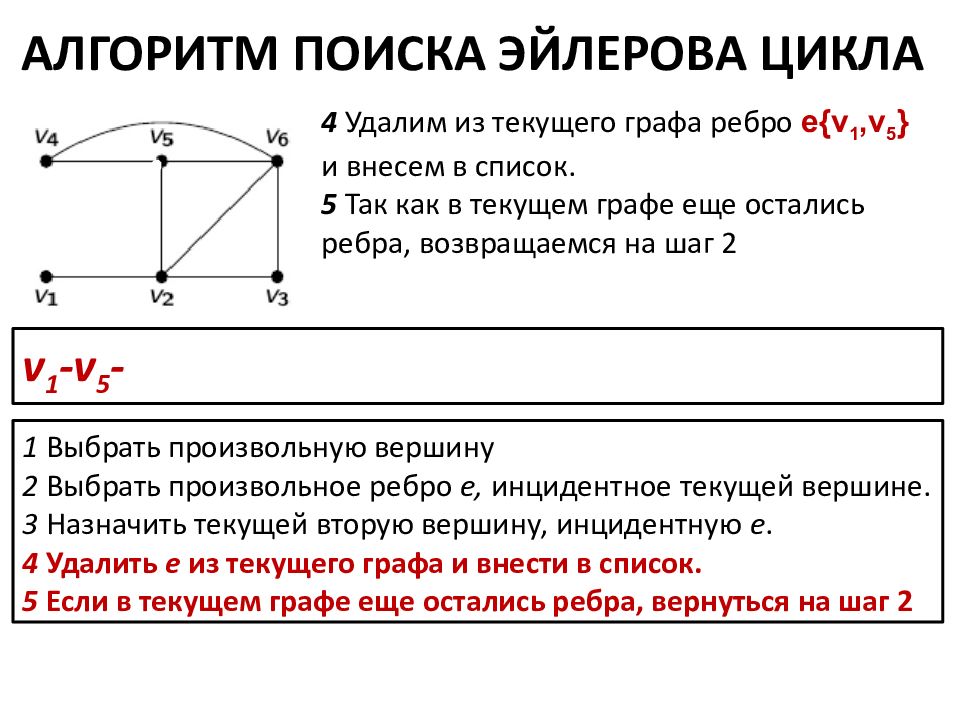
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 4 Удалим из текущего графа ребро е {v 1,v 5 } и внесем в список. 5 Так как в текущем графе еще остались ребра, возвращаемся на шаг 2 v 1 -v 5 -
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 v 1 -v 5 - 1 Текущая вершина – v 5 2 Выберем произвольное ребро е {v 5,v 2 }, инцидентное текущей вершине. 3 Назначим текущей вторую вершину, инцидентную e – вершину v 2.
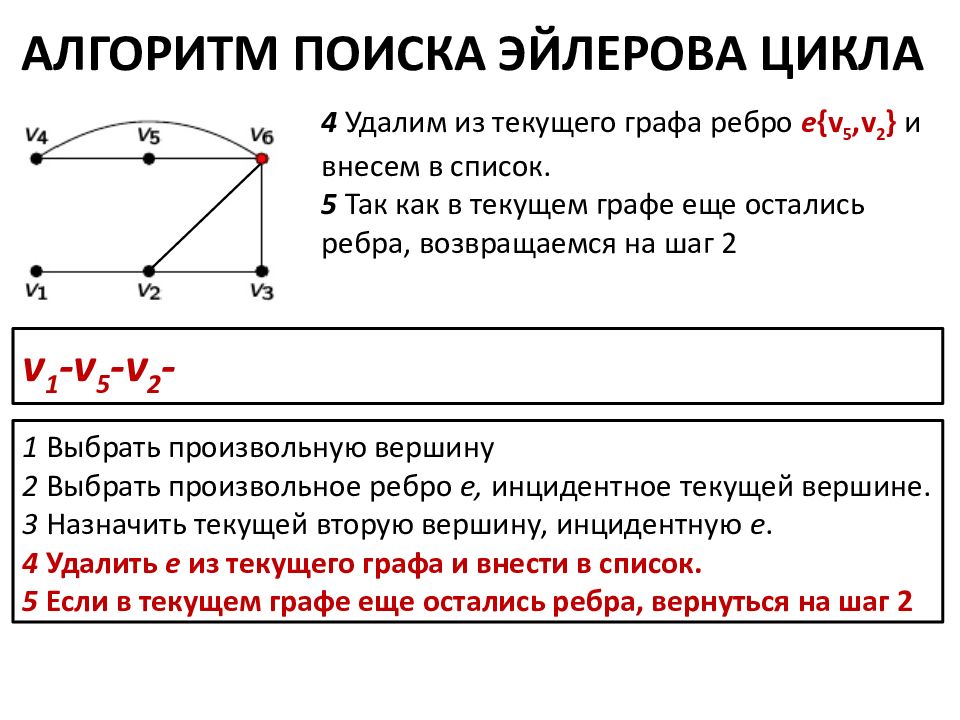
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 4 Удалим из текущего графа ребро е {v 5,v 2 } и внесем в список. 5 Так как в текущем графе еще остались ребра, возвращаемся на шаг 2 v 1 -v 5 - v 2 -
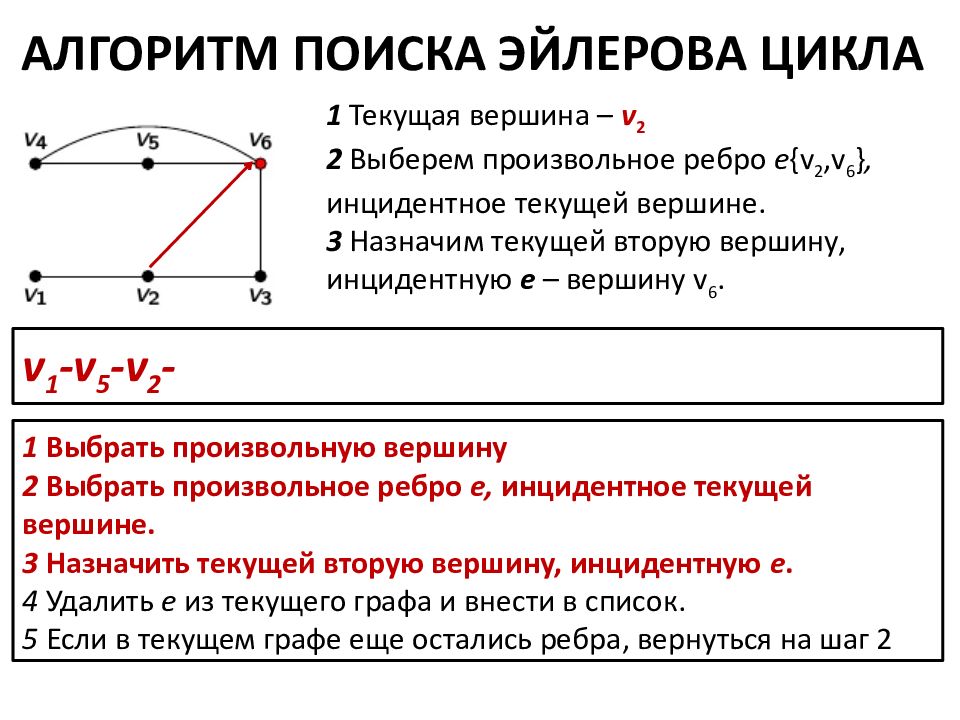
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 v 1 -v 5 -v 2 - 1 Текущая вершина – v 2 2 Выберем произвольное ребро е {v 2,v 6 }, инцидентное текущей вершине. 3 Назначим текущей вторую вершину, инцидентную e – вершину v 6.
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 4 Удалим из текущего графа ребро е {v 2,v 6 } и внесем в список. 5 Так как в текущем графе еще остались ребра, возвращаемся на шаг 2 v 1 -v 5 - v 2 -v 6 -
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 v 1 -v 5 -v 2 -v 6 - 1 Текущая вершина – v 6 2 Выберем ребро е {v 6,v 4 }, инцидентное текущей вершине. РЕБРО {v 6,v 3 } ВЫБИРАТЬ НЕЛЬЗЯ ! 3 Назначим текущей вторую вершину, инцидентную e – вершину v 4.
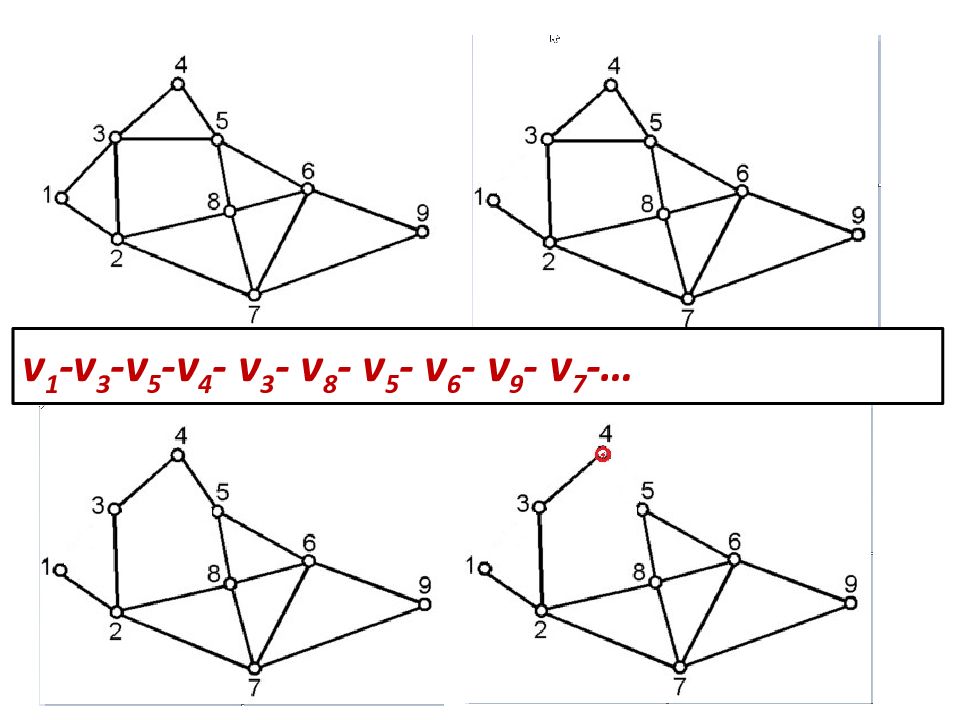
АЛГОРИТМ ПОИСКА ЭЙЛЕРОВА ЦИКЛА 1 Выбрать произвольную вершину 2 Выбрать произвольное ребро е, инцидентное текущей вершине. 3 Назначить текущей вторую вершину, инцидентную e. 4 Удалить e из текущего графа и внести в список. 5 Если в текущем графе еще остались ребра, вернуться на шаг 2 4 Удалим из текущего графа ребро е {v 6,v 4 } и внесем в список. 5 Так как в текущем графе еще остались ребра, возвращаемся на шаг 2 ... И ТАК ДАЛЕЕ v 1 -v 5 - v 2 -v 6 - v 4 - v 5 - v 6 - v 3 - v 2 - v 1
v 1 -v 3 - v 5 -v 4 - v 3 - v 8 - v 5 - v 6 - v 9 - v 7 -…
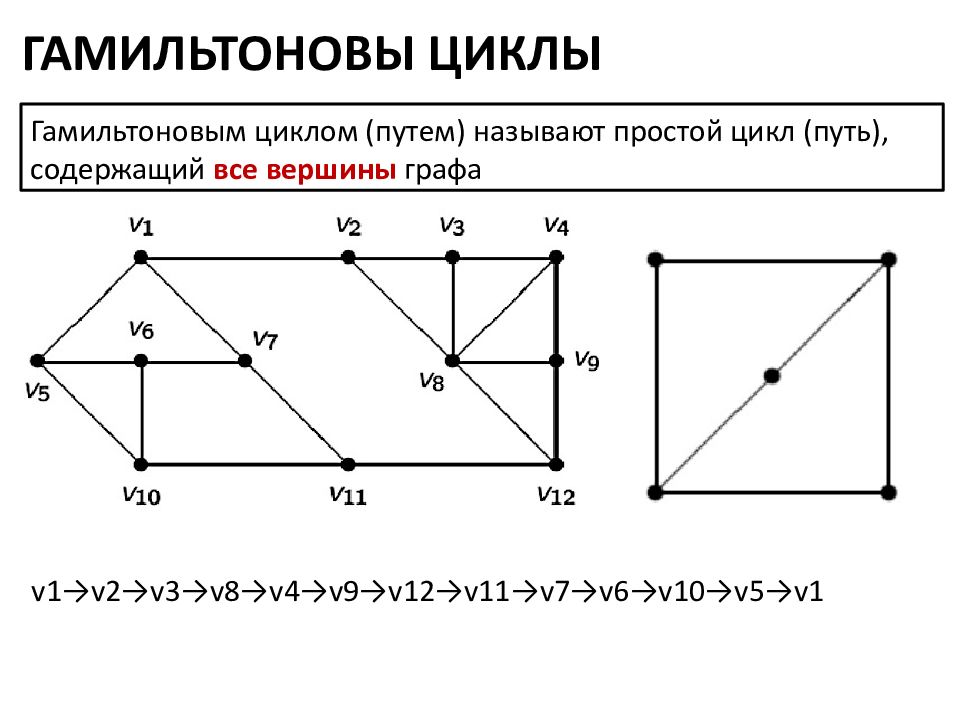
ГАМИЛЬТОНОВЫ ЦИКЛЫ Гамильтоновым циклом (путем) называют простой цикл (путь), содержащий все вершины графа v1→v2→v3→v8→v4→v9→v12→v11→v7→v6→v10→v5→v1
Задача коммивояжера разрешима тогда и только тогда, когда граф этой задачи гамильтонов. Задача коммивояжера : Дан список городов, соединенных дорогами, длины которых известны. Коммивояжер должен объехать все города, побывав в каждом по одному разу, и вернуться в свой город. Требуется найти кратчайший маршрут коммивояжера. Имеется чертеж печатной платы, в которой необходимо просверлить отверстия для последующей пайки деталей. Для станка с программным управлением требуется найти кратчайший маршрут движения головки со сверлом, чтобы общая длина передвижений головки была наименьшей
СРАВНЕНИЕ ЗАДАЧ ОБ ЭЙЛЕРОВЫХ И ГАМИЛЬТОНОВЫХ ЦИКЛАХ Для решения вопроса о существовании эйлерова цикла в графе достаточно выяснить, все ли его вершины четные. Критерий же существования гамильтонова цикла на произвольном графе до сих пор не найден. Для гамильтоновых циклов (и путей) неизвестно никаких просто проверяемых необходимых и достаточных условий их существования, а все известные алгоритмы требуют для некоторых графов перебора большого числа вариантов. Такие задачи называют задачами переборного типа или неподдающимися задачами.
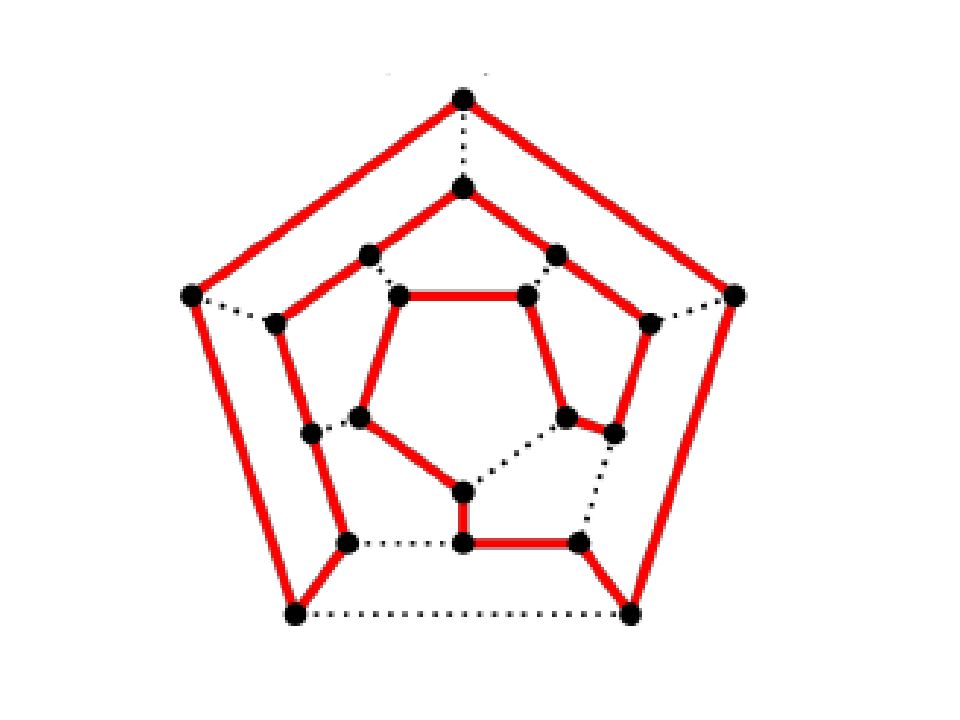
Есть несколько достаточных условий существования гамильтоновых циклов в графе: 1. Всякий полный граф является гамильтоновым, так как он содержит простой цикл, которому принадлежат все вершины данного графа. 2. Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие рѐбра, то он также является гамильтоновым. 3. Если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы. Теорема Дирака. Если в графе G(V,E) c n вершинами (n ≥ 3) выполняется условие d(v) ≥ n/2 для любого v V, то граф G является гамильтоновым.
Контрольные вопросы: Дайте определение эйлерова графа. Сформулируйте алгоритм построения эйлерова цикла. Какой граф называют гамильтоновым ? Существует ли эйлеров граф, обладающий висячей вершиной ? Чем отличается эйлеров путь от гамильтонова?
Программирование, компьютеры и сети https ://progr-system.ru /
