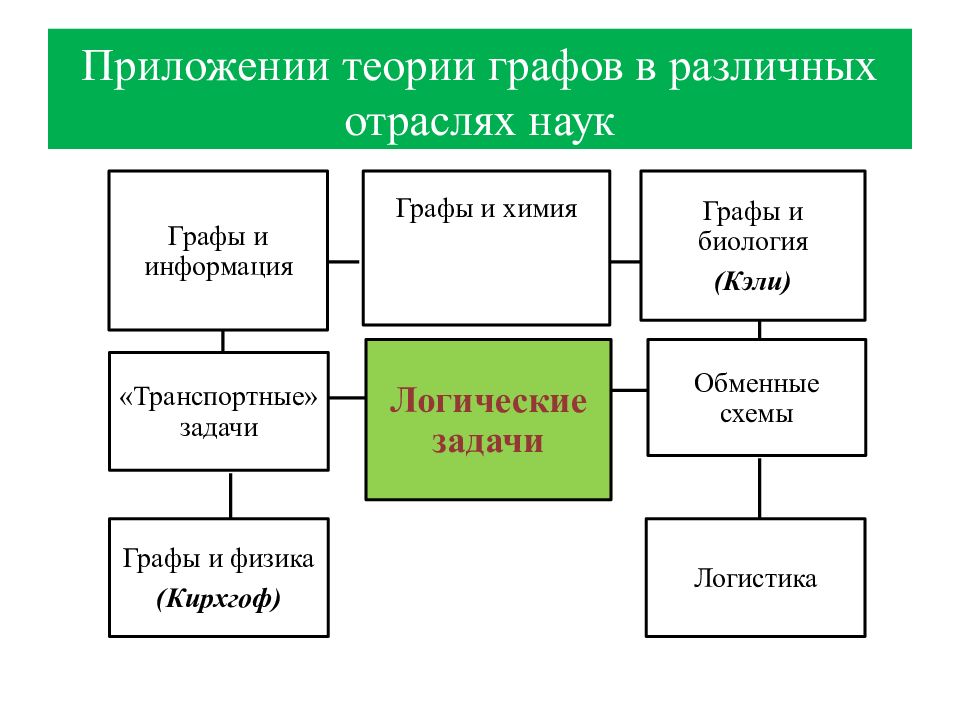
Первый слайд презентации: Теория графов
Слайд 3: Цель:
изучить теоретический материал по теме «Теория графов» и возможность его применения Задачи: рассмотреть основные определения; сформулировать и доказать основные теоремы, в т.ч. лемму «о рукопожатиях», теоремы Кёнига, Оре, Холла
Слайд 4: План лекции
Введение в теорию графов 1) основные определения; 2) виды графов; II. Основные леммы и теоремы; III. Применение «Теории графов» к решению задач
Слайд 5: Определение
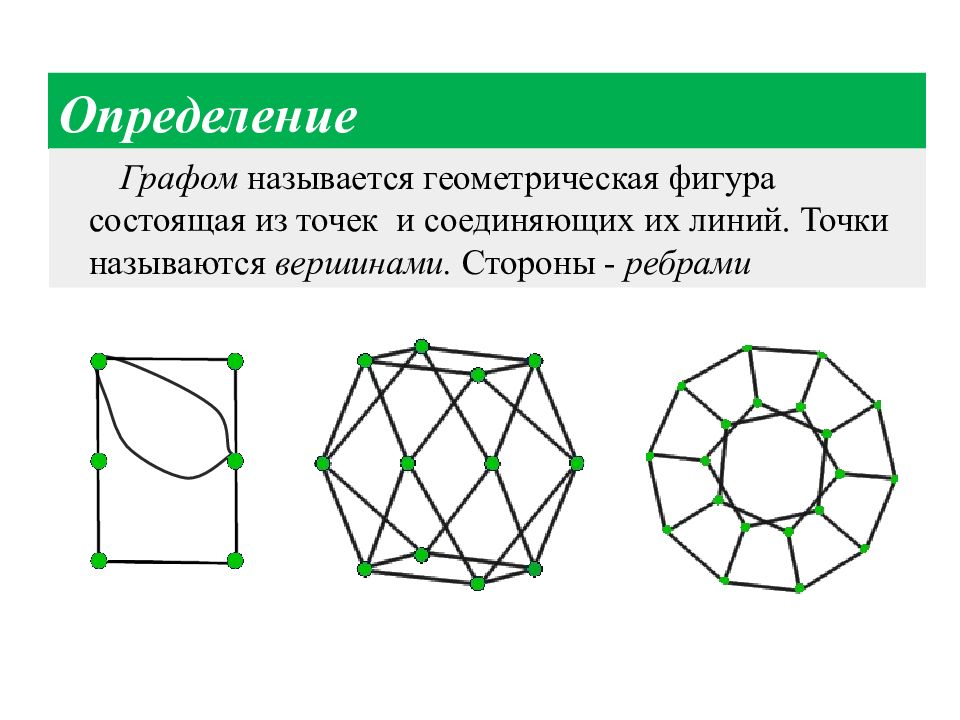
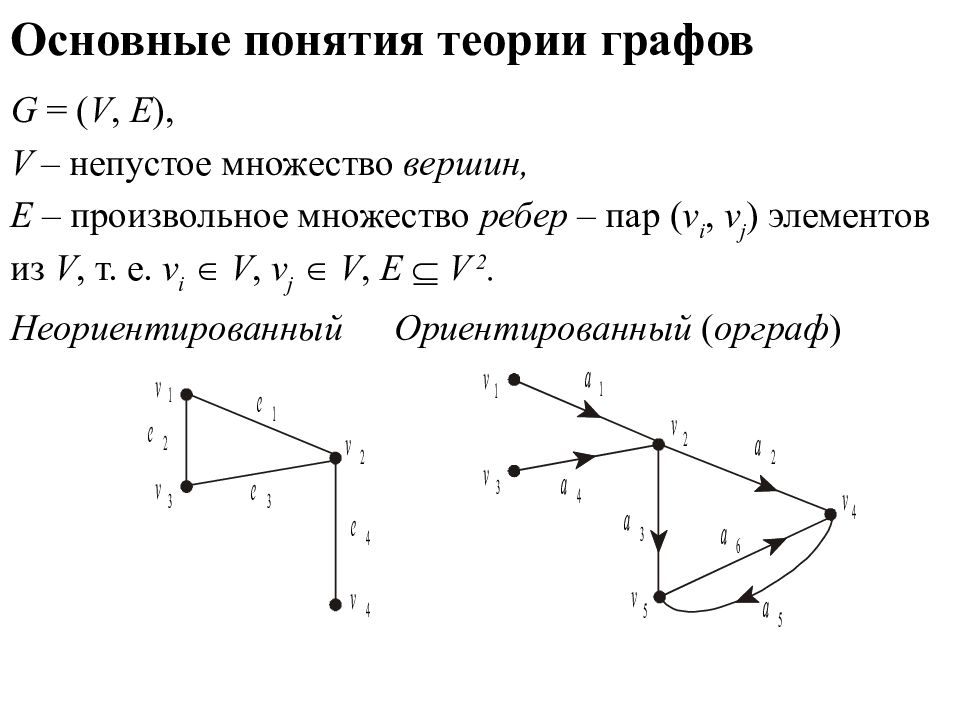
Графом называется геометрическая фигура состоящая из точек и соединяющих их линий. Точки называются вершинами. Стороны - ребрами
Слайд 6
два ребра называются смежными, если они имеют общую вершину; ребра называется петлей если его концы совпадают; два ребра называют кратными если они соединяют одну и ту же пару вершин; Определения A B C D E m p s t r q Пример: Смежные ребра: D С и CA, CD и DB, DB и BA, BA и AC Изолированная вершина: E Кратные ребра: m и p Петля: q вершина называется изолированной, если она не является концом ни для одного ребра
Слайд 7
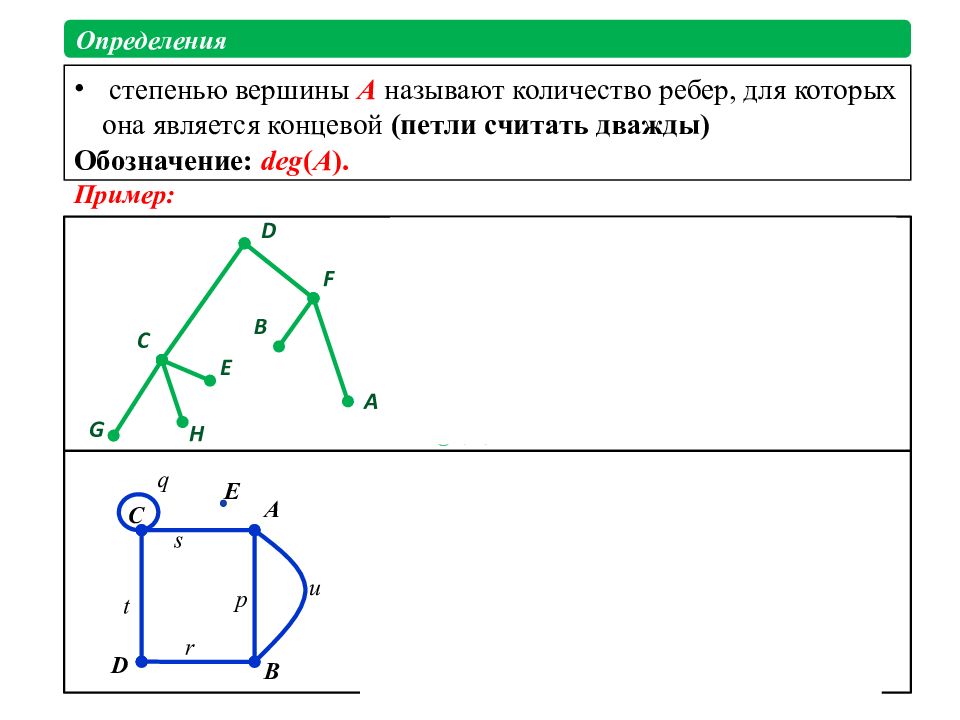
степенью вершины A называют количество ребер, для которых она является концевой (петли считать дважды) Обозначение: deg ( A ). G H E C D F A B A B C D E u p s t r q deg(E) = 0 deg(C) = 2 E – изолированная вершина deg(G) = 1 deg(H) = 1 deg(E) = 1 deg(B) = 1 deg(A) = 1 deg(C) = 4 deg (D) = 2 G, H, E, B, A - висячие вершины Определения Пример:
Слайд 8: Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер Доказательство: Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней всех вершин мы учтем это ребро дважды; Если ребро является петлей, то при подсчете суммы степеней всех вершин мы также учтем это ребро дважды; В любом графе число вершин нечетной степени четно Следствие степенью вершины называют количество ребер, для которых она является концевой (петли считать дважды) |=> (по определению степени вершины) ч.т.д
Слайд 9
В любом графе число вершин нечетной степени четно Следствие Доказательство: Т.к. каждое ребро инцидентно двум вершинам, в сумму степеней вершин графа каждое ребро вносит двойку. Таким образом, мы приходим к утверждению, которое установлено Эйлером и является исторически первой теоремой теории графов.
Слайд 10: Пример:
Может ли в государстве, в котором из каждого города выходит 3 дороги быть ровно 100 дорог Ответ: не может Решение : Города – вершины графа ( k, k є N ). Степень кратности каждой вершины 3 => Дороги – ребра графа ( p = 100 ) По Лемме 3 k = 2p. Если р = 100, то k = Но k є N => p ≠ 100
Слайд 11: Виды графов
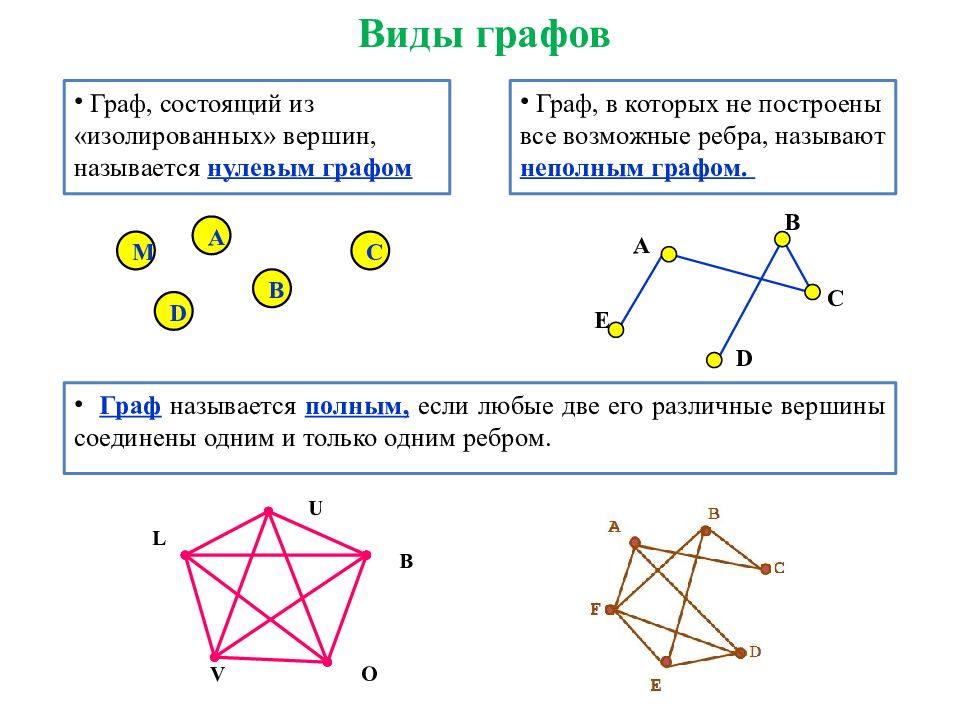
Граф, состоящий из «изолированных» вершин, называется нулевым графом Граф называется полным, если любые две его различные вершины соединены одним и только одним ребром. Граф, в которых не построены все возможные ребра, называют неполным графом. M A D B C A B C D E L U B O V
Слайд 12: Виды графов
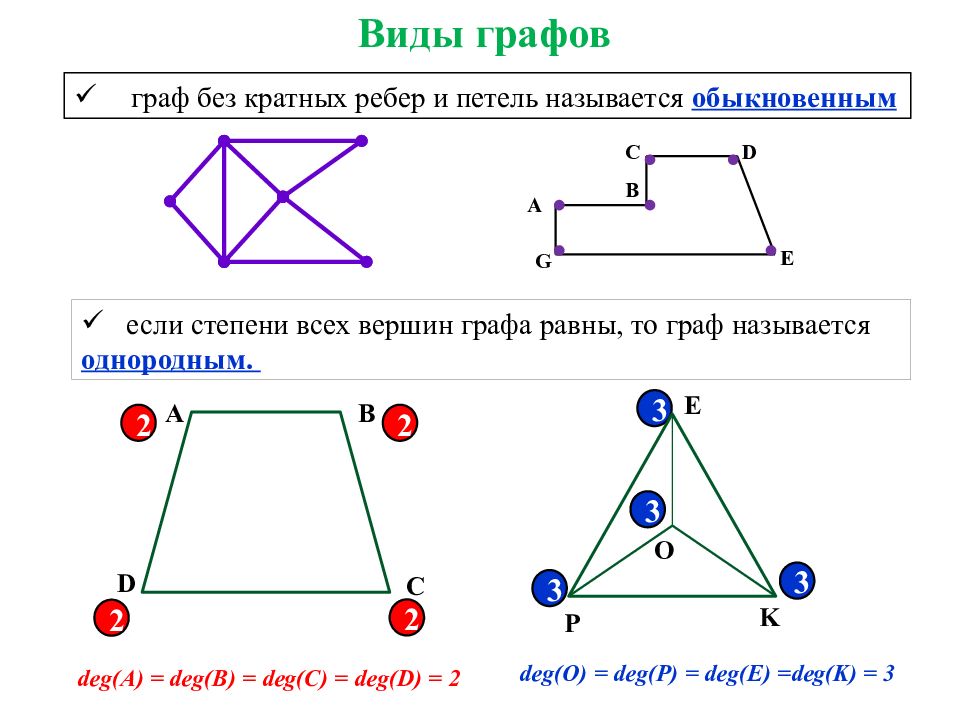
граф без кратных ребер и петель называется обыкновенным если степени всех вершин графа равны, то граф называется однородным. 2 2 2 2 3 3 3 3 А B C D E K O P deg(A) = deg(B) = deg(C) = deg(D) = 2 deg(O) = deg(P) = deg(E) =deg(K) = 3 A B C D E G Виды графов
Слайд 13: Виды графов
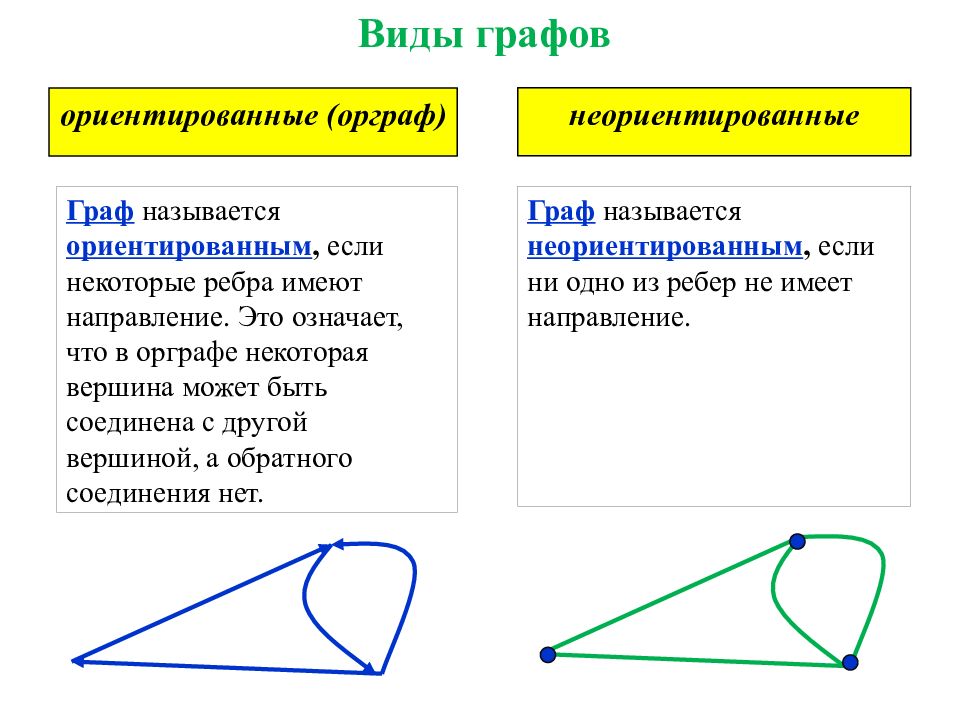
ориентированные (орграф) Виды графов неориентированные Граф называется ориентированным, если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Граф называется неориентированным, если ни одно из ребер не имеет направление.
Слайд 14
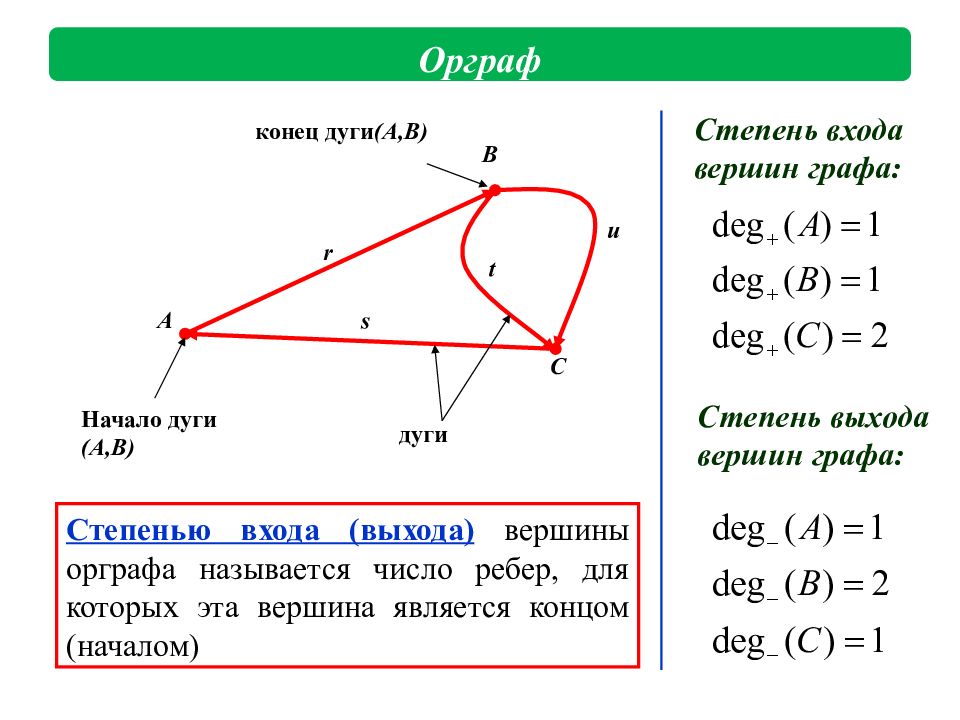
A B C u t s r дуги Начало дуги ( A,B) конец дуги ( A,B) Степенью входа (выхода) вершины орграфа называется число ребер, для которых эта вершина является концом (началом) Степень входа вершин графа: Орграф Степень выхода вершин графа:
Слайд 15: Связный граф
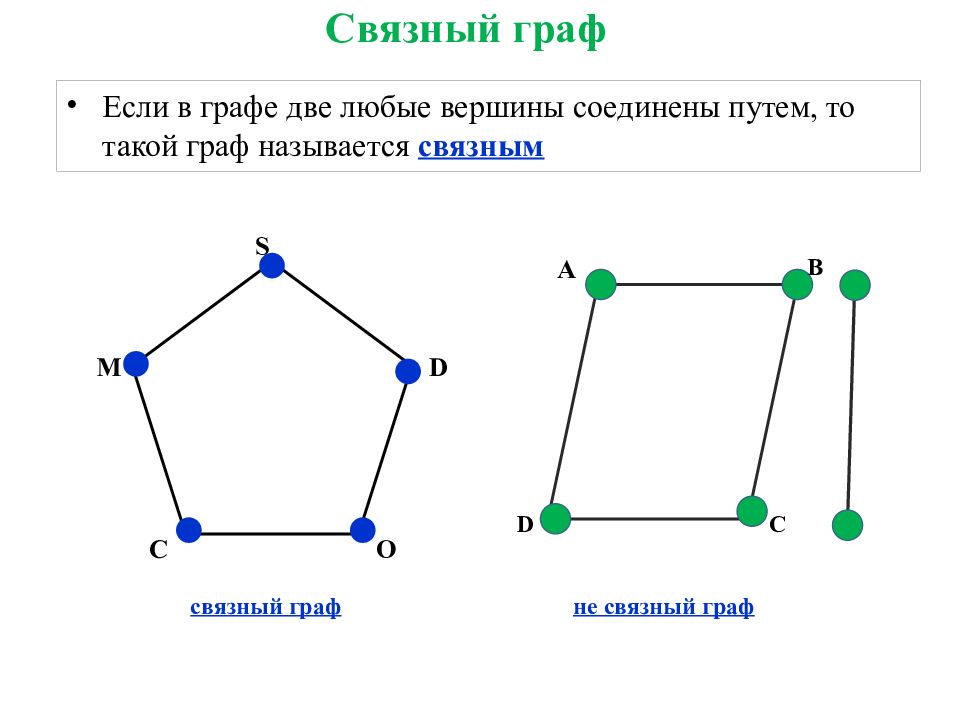
Если в графе две любые вершины соединены путем, то такой граф называется связным M S D O C A B C D связный граф не связный граф
Слайд 16
Компонента связности - множество вершин такое, что из любой вершины этого множества есть путь в любую другую вершину этого множества, но ни из какой вершины этого множества нельзя попасть в некоторую вершину вне этого множества. Очевидно, что сумма количеств вершин компонент связности равна количеству вершин графа. Определения Максимальный связный подграф графа называется компонентной связности Пример: граф с 10 компонентами
Слайд 17: Пример:
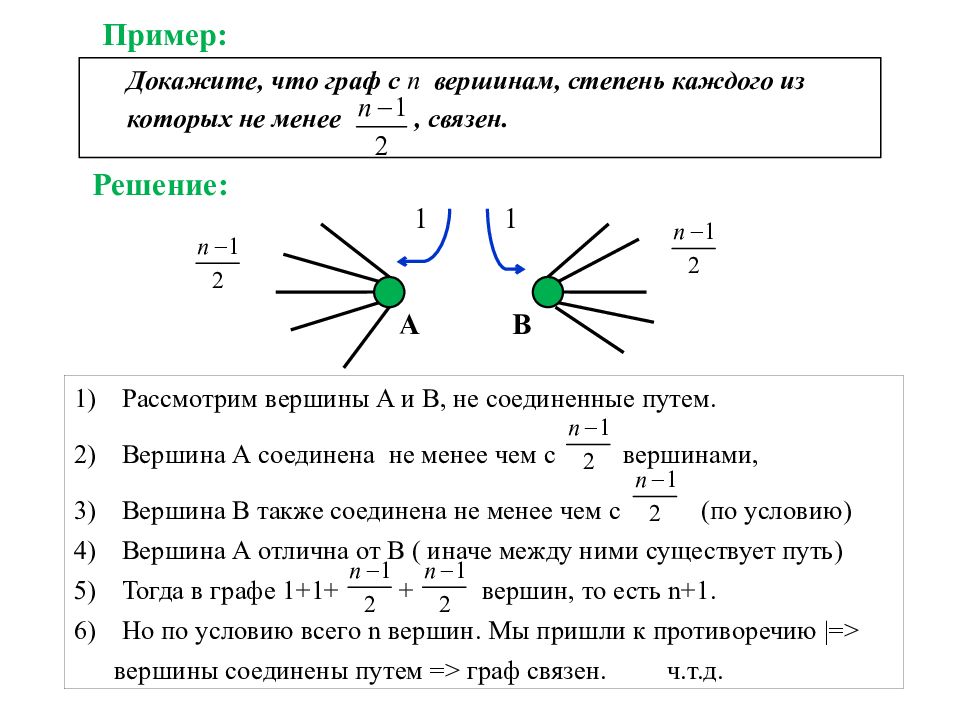
Докажите, что граф с n вершинам, степень каждого из которых не менее, связен. Рассмотрим вершины A и B, не соединенные путем. Вершина А соединена не менее чем с вершинами, Вершина B также соединена не менее чем с (по условию) Вершина А отлична от В ( иначе между ними существует путь) Тогда в графе 1+1+ + вершин, то есть n+1. Но по условию всего n вершин. Мы пришли к противоречию | = > вершины соединены путем = > граф связен. ч.т.д. Решение : Пример: 1 1 A B
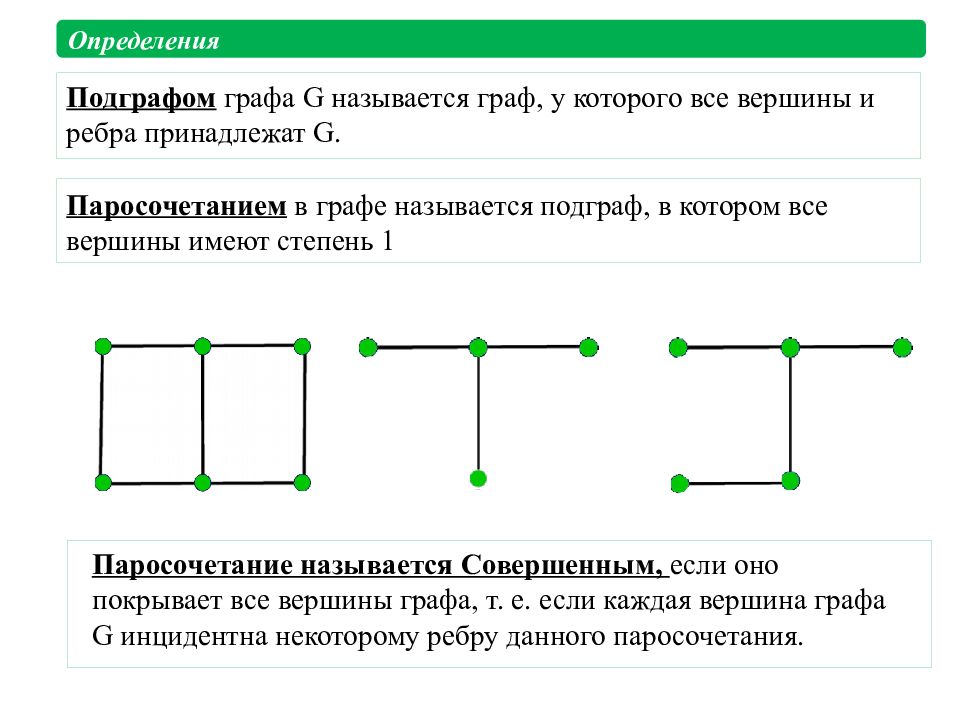
Слайд 19: Паросочетанием в графе называется подграф, в котором все вершины имеют степень 1
Подграфом графа G называется граф, у которого все вершины и ребра принадлежат G. Определения Паросочетание называется Совершенным, если оно покрывает все вершины графа, т. е. если каждая вершина графа G инцидентна некоторому ребру данного паросочетания.
Слайд 20: Свойства паросочетаний
чаще всего паросочетания воспринимаются для двудольных графов паросочетание в графе называются максимальным, если в графе нет паросочетаний с большим числом ребер вершина графа называется насыщенной в паросочетании, если в этом паросочетании существует ребро с концом в этой вершине и свободной в паросочетании если в нем нет такого ребра
Слайд 21
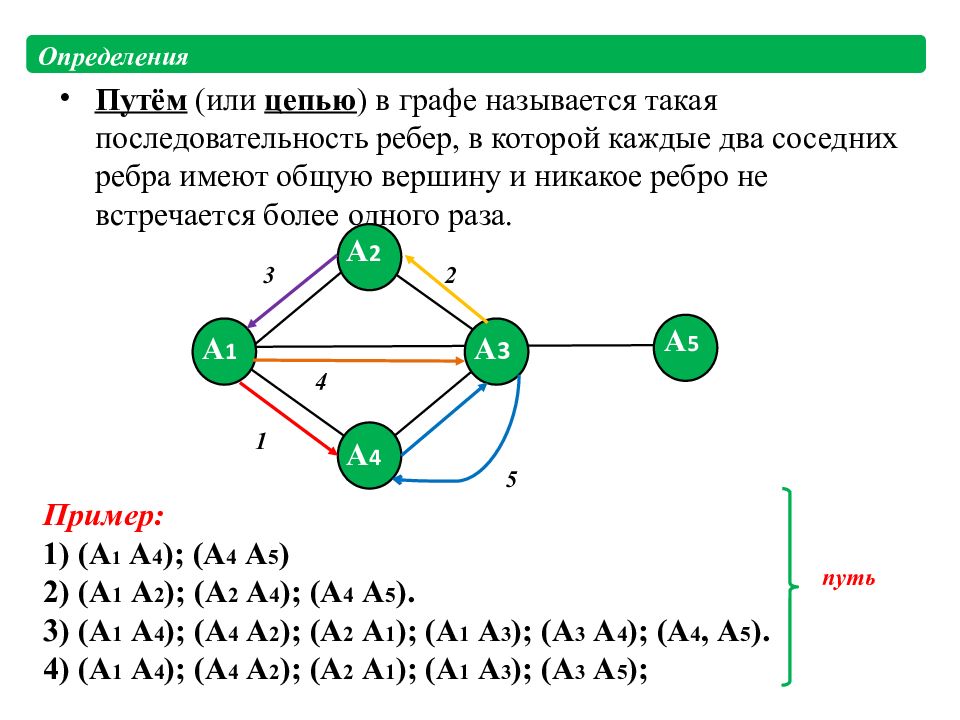
Путём (или цепью ) в графе называется такая последовательность ребер, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза. A 1 A 2 A 3 A 4 A 5 Пример: 1) (А 1 А 4 ); (А 4 А 5 ) 2) (А 1 А 2 ); (А 2 А 4 ); (А 4 А 5 ). 3) (А 1 А 4 ); (А 4 А 2 ); (А 2 А 1 ); (А 1 А 3 ); (А 3 А 4 ); (А 4, А 5 ). 4) (А 1 А 4 ); (А 4 А 2 ); (А 2 А 1 ); (А 1 А 3 ); (А 3 А 5 ); путь Определения 1 2 3 4 5
Слайд 22
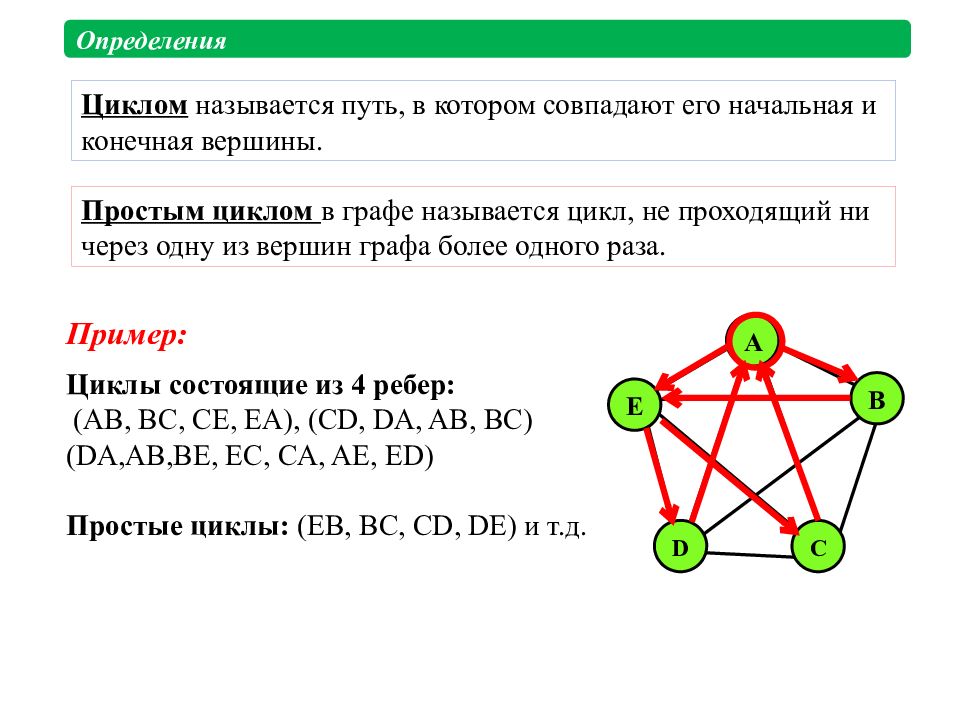
Циклом называется путь, в котором совпадают его начальная и конечная вершины. Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза. Определения Пример: A B C D E Циклы состоящие из 4 ребер: ( AB, BC, CE, EA), (CD, DA, AB, BC) ( DA,AB,BE, EC, CA, AE, ED) Простые циклы: (EB, BC, CD, DE) и т.д.
Слайд 23: Двудольный граф
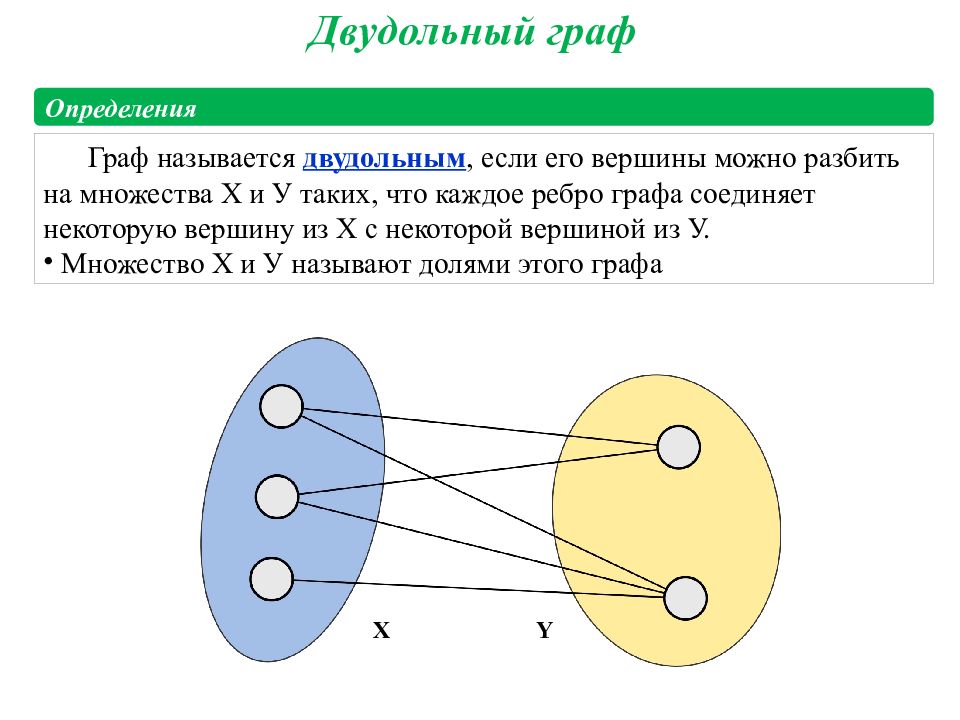
Граф называется двудольным, если его вершины можно разбить на множества Х и У таких, что каждое ребро графа соединяет некоторую вершину из Х с некоторой вершиной из У. Множество Х и У называют долями этого графа Определения Х Y
Слайд 24: Теорема Кенига
Граф является двудольным тогда и только тогда, когда он содержит более одной вершины и все его циклы имеют четную длину
Слайд 27: Задача о назначениях
Дан двудольный граф, требуется построить максимальное паросочетание Задача о деревенских свадьбах Назначение на должность: имеются вакантные должности и претенденты на них, о каждом претенденте известно какие должности он может занять, требуется заполнить максимум вакансий Выбор представителей: в парламенте есть несколько комиссий, член парламенты может заседать в нескольких комиссиях; нужно выбрать председателя каждой комиссии Пример:
Слайд 28: Задача о деревенских свадьбах
В деревне живут несколько девушек и несколько юношей. Некоторые юноши знакомы с некоторым девушками. Требуется поженить максимально возможное число пар при условии, что женить можно только знакомые пары Пример:
Слайд 29: Теорема Холла о свадьбах
Доказательство: Необходимость: Совершенное паросочетание Р в графе G можно рассмотреть как функцию, отображающую каждую вершину из Х в смежную ей вершину Y. По определению совершенного паросочетания эта функция является биекций, откуда |X|=|Y|. Более того, P отображает каждое подмножество M X в некоторое подмножество Y M содержащие |M| элементов, являющихся смежными к вершинам из М вершин. Но тогда Y M O(M) и | М | = | Y M | |O(M)| ч.т.д X 1 X 2 X 3 X 4 X 5 X 6 Y 5 Y 4 Y 3 Y 2 Y 1 Дан двудольный граф с долями X и Y. Совершенное паросочетание существует тогда и только тогда когда | Х | = |Y| и |O(M)| ≥ |M| для всякого M X
Слайд 30: Достаточность
Пусть G – двудольный граф, для которого |X| = |Y| = n и выполнено условие (1). Докажем что в G существует паросочетание P, содержащие n ребер. Проведем индукцией по n. В случае n = 1 ( база). Единственная вершина из Х и единственная вершина из Y должны быть соединены ребром, чтобы условие (1) выполнялось. Но тогда можно взять Р = G. Перейдем к шагу индукции: предположим, что для двудольных графов с меньшим чем n числом вершин в каждой доле утверждения теоремы верно. Возможно два случая
Слайд 31: Эйлеровы графы
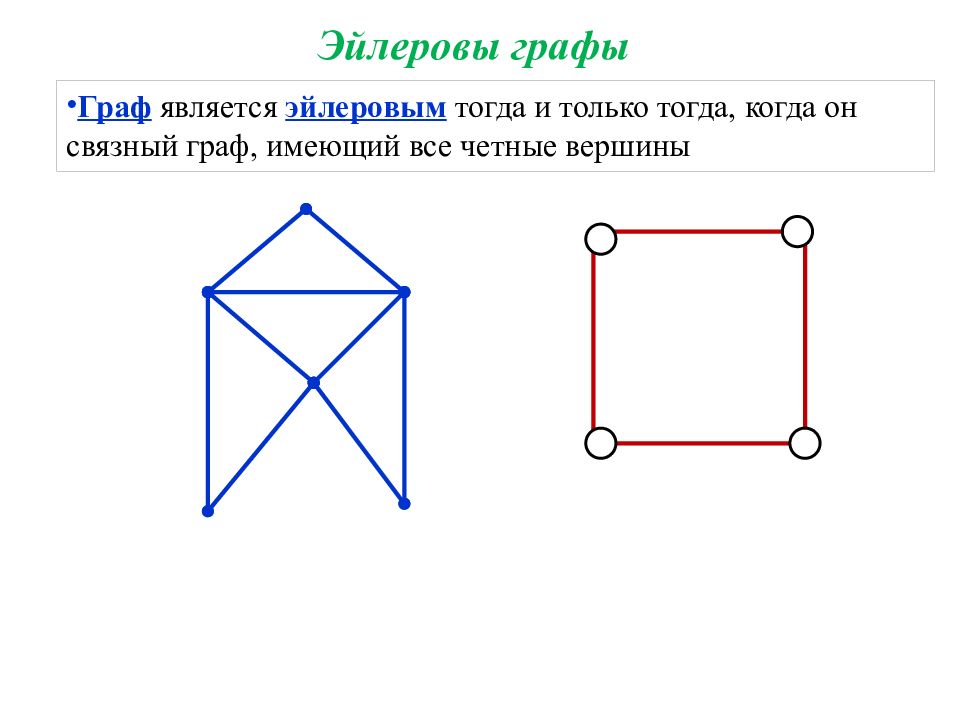
Граф является эйлеровым тогда и только тогда, когда он связный граф, имеющий все четные вершины
Слайд 32
Эйлеровым путем в графе называется путь, содержащий все ребра графа. Определения Эйлеровым циклом или эйлеровой цепью называется цикл, содержащий все ребра графа и притом по одному разу. Если граф G(V,E) обладает эйлеровым циклом, то он связный и все его вершины четные. Теорема №1 Теорема №2 (Эйлер) Граф без изолированных вершин является эейлоровым, тогда и только тогда, когда он связен и степени всех вершин его четны
Слайд 33: Гамильтоновы графы
Гамильтонов путем (циклом) графа называется путь ( цикл) проходящий через каждую вершину только один раз Граф, содержащий гамильтонов цикл, называется гамильтоновым Пример: гамильтонов путь : (C, D, A, B, M) ; (B, A, D, C, F) A B C D M F
Слайд 34
Предположим что существует граф G, который удовлетворяет условию теоремы, но не является гамильтоновым графом. Будем добавлять к нему новые ребра до тех пор, пока не получим максимальный негамильтонов граф G 1 Пусть u, v несмежные вершины в полученном графе G1. Если добавить ребро uv, появится гамильтонов цикл. Тогда путь ( u, v ) – гамильтонов. Для вершин u,v выполняется неравенство: deg u + deg v ≥ n По принципу Дирихле всегда найдутся две смежные вершины t 1 и t 2 на пути ( u, v ) т.е. u…t 1 t 2..v, такие что существует ребро ut 2 и ребро ut 1 |S|+|T| = deg u + deg v ≥ n, но |S|+|T| < n, тогда |S T| = |S|+|T| Теорема (Оре) Доказательство: Пусть дан обыкновенный связный граф, содержащий n > 2 вершин, такой что сумма степеней любых двух несмежных вершин не меньше, чем n. Тогда граф гамильтонов.
Слайд 35: Планарные ( плоские ) графы
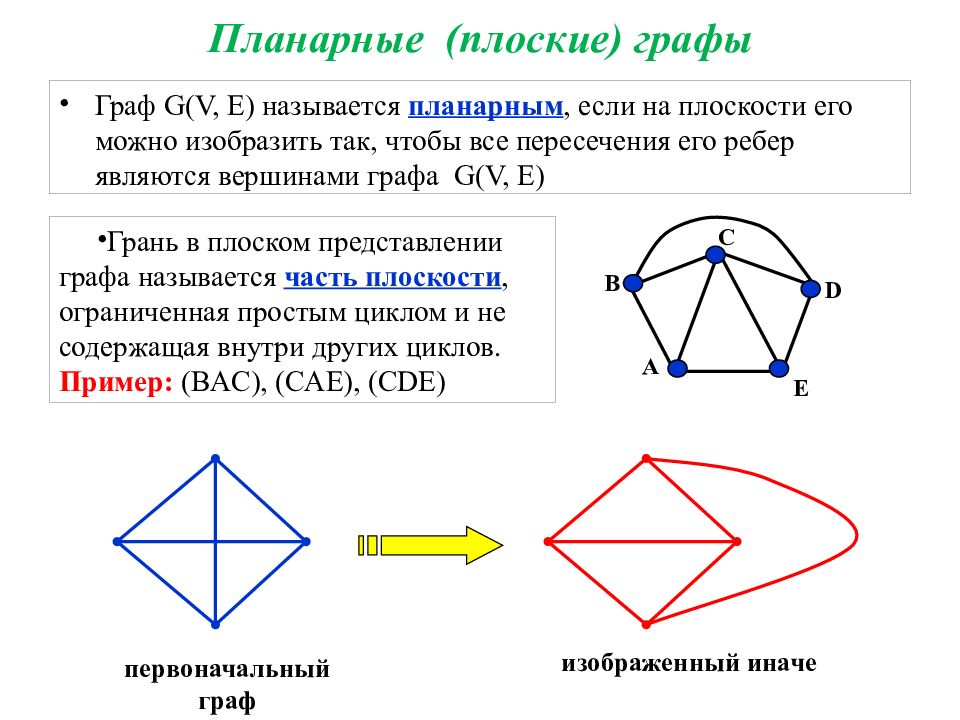
Граф G(V, E) называется планарным, если на плоскости его можно изобразить так, чтобы все пересечения его ребер являются вершинами графа G(V, E) первоначальный граф изображенный иначе Грань в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов. Пример: ( BAC), (CAE), (CDE) A B C D E
Слайд 36
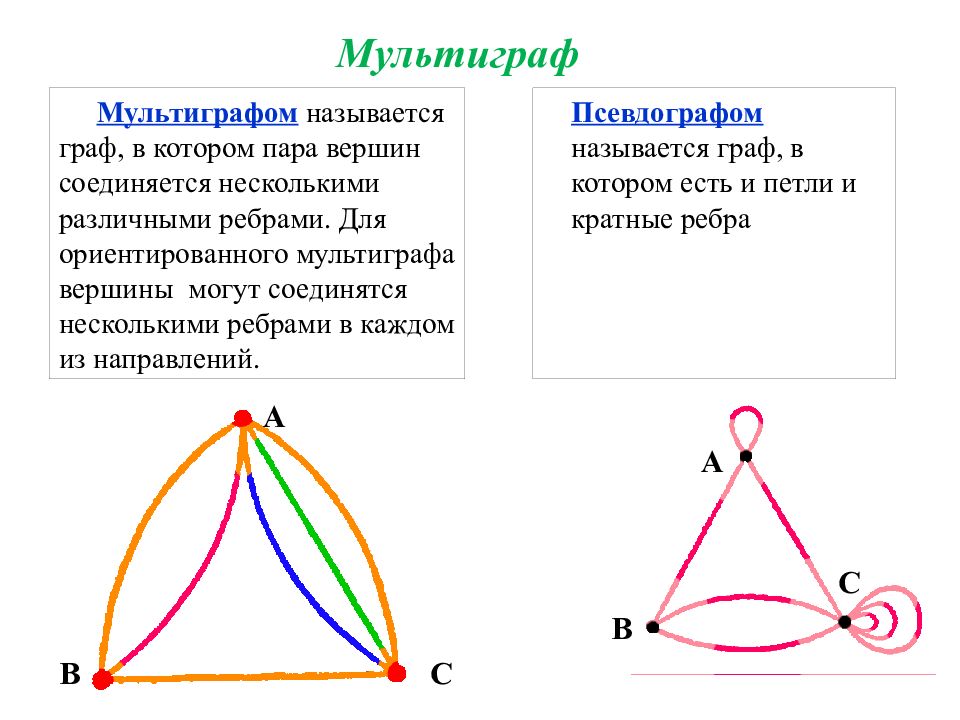
Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами. Для ориентированного мультиграфа вершины могут соединятся несколькими ребрами в каждом из направлений. Мультиграф A B C Псевдографом называется граф, в котором есть и петли и кратные ребра A C B
Слайд 37: Пример:
Каждый из 102 учеников одной школы знаком не менее, чем с 68 другими. Докажите, что среди них найдутся четверо, имеющие одинаковое число знакомых 1) пусть верно обратное. 2) тогда для каждого числа от 68 до 101 имеется не более трех человек, имеющих такое же число знакомых. 3) имеется ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 3 ∙ 4. Это означает что для каждого числа от 68 до 101 есть ровно три человека, имеющие такое число знакомых 4) Но тогда количество людей, имеющих нечетное количество знакомых нечетно. ( Л ) | => верно обратное, т.е. среди учеников найдутся четверо, имеющие одинаковое число знакомых Решение: Пример:
Слайд 38
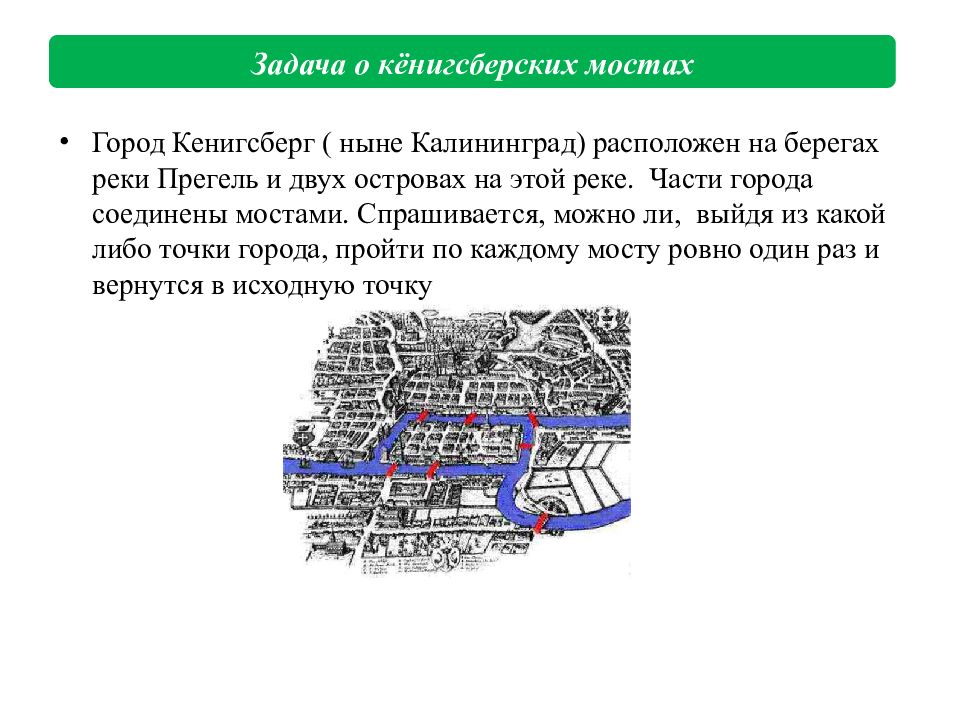
Город Кенигсберг ( ныне Калининград) расположен на берегах реки Прегель и двух островах на этой реке. Части города соединены мостами. Спрашивается, можно ли, выйдя из какой либо точки города, пройти по каждому мосту ровно один раз и вернутся в исходную точку Задача о кёнигсберских мостах
Слайд 39: Решение:
Объекты – части города Связи - мосты Можно ли обойти данный граф пройдя по каждому ребру ровно один раз и вернуться и вернувшись в исходную вершину, то есть существует ли последовательность ребер графа со следующими свойствами: любые два соседних ребра имеют общую вершину; последнее ребро имеет общую вершину с первым; каждое ребро графа встречается в последовательности ровно один раз
Слайд 40
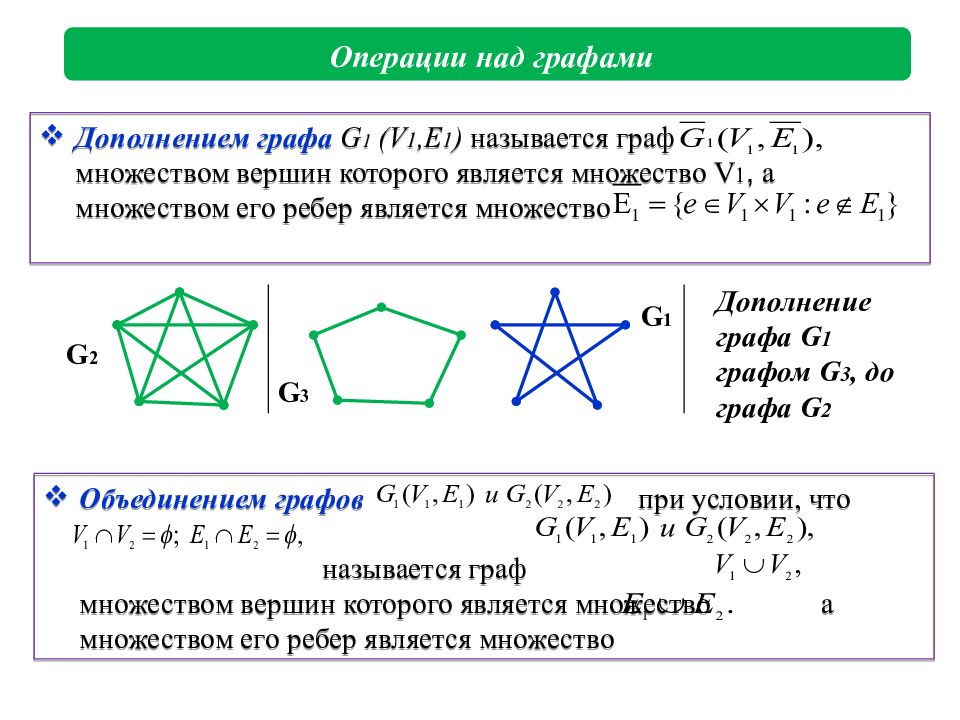
Дополнением графа G 1 (V 1,E 1 ) называется граф множеством вершин которого является множество V 1, а множеством его ребер является множество Операции над графами G 2 G 1 G 3 Дополнение графа G 1 графом G 3, до графа G 2 Объединением графов при условии, что называется граф множеством вершин которого является множество а множеством его ребер является множество
Слайд 41
Операции над графами Пересечением графов называется граф множеством вершин которого является множество а множеством его ребер – множество Суммой по модулю два графа при условии, что называется граф множеством вершин которого является множество а множеством его ребер – множество Другими словами, этот граф не имеет изолированных вершин и состоит только из ребер, присутствующих либо в первом графе, либо во втором, но не в обоих графах одновременно.
Слайд 42
Аналитический способ задания графов Граф G(V,E) задан, если задано множество элементов V и отображение Е множества V в V. Отображение Е может быть как однозначным, так и многозначным. В общем случае на V и E никаких ограничений не накладывается. Пусть дано множество { }, которое имеет мощность. Вместо { } иногда пишут { }, { }. Для того чтобы задать отображение Е на V или, что то же самое, отображение V в V, необходимо каждому элементу поставить в соответствие Е. Это подмножество обозначают через поэтому Другой формой аналитического способа задания является задание графа как совокупности множества элементов V и подмножества упорядоченных пар Подмножество множества пар декартова произведения эквивалентно бинарному отношению R, заданному на множестве V. Поэтому множество V и бинарное отношение R на множестве V также определяет некоторый граф G. Способы задания графов
Последний слайд презентации: Теория графов
Геометрический способ Множество элементов V графа G изображают кружками, это множество вершин. Каждую вершину соединяют линиями с теми вершинами, для которых выполняется условие. Множество линий, которое соответствует множеству упорядоченных пар, есть множество ребер графа. Матричный способ Квадратная матрица элементами которой являются нули и единицы, а также некоторое число m, называется матрицей смежности графа G(V,E) тогда и только тогда когда ее элементы образуются по следующему правилу: элемент стоящий на пересечении столбца, равен единице, если имеется ребро, идущие из вершины в вершину, и равен нулю в противном случае. Элемент равен единице, если при вершине имеется петля, и равен нулю в противном случае. Элемент равен некоторому числу m, где m – число ребер графа, идущее из вершины в вершину. Пусть - вершины, а - ребра некоторого ориентированного графа G(V,E). Матрица размером ( m x n), где называется матрицей инцидентности для ориентированного графа.