Слайд 2: Минимальный остов
Алгоритмы Борувки – Краскала, Ярника – Прима – Дейкстры.
Слайд 3: Минимальный остов
Остовом называется ацикличный связный подграф данного графа, содержащий все его вершины. Пусть G=(V,E,c) связный взвешенный неориенти-рованный граф. Под весом с( H ) произвольного ненулевого подграфа H будем понимать сумму весов всех ребер подграфа H. Ацикличный остовный подграф (содержащий все вершины графа G ) будем называть остовным лесом графа G. Остов T называется минимальным, если для любого остова T’ выполняется неравенство c(T) c(T’).
Слайд 4: Минимальный остов
Этот раздел посвящен решению следую-щей задачи: в данном связном графе найти минимальный остов ( задача о минимальном остове ).
Слайд 5
Предположим, что F остовный лес связного взвешенного графа G. Будем говорить, что F продолжаем до мини-мального остова, если существует такой минимальный остов T, что F T. Минимальный остов
Слайд 6: Минимальный остов
Справедлива следующая лемма. Пусть остовный лес F продолжаем до минимального остова и H одна из компонент связности леса F. Если с ребро минимального веса из Ext(H) (т.е. внешнее по отношению к H : один его конец лежит в H, в другой – нет), то остовный лес F + c продолжаем до минимального остова.
Слайд 7: Минимальный остов
Эта лемма позволяет сконструировать два алгоритма построения минимального остова во взвешенном ( n,m ) - графе G. Пусть F 0 – тривиальный остовный лес (т.е. остовный лес без ребер). Ясно, что F 0 можно продолжить до минимального остова. Оба алгоритма строят последовательность F 0, F 1, …, F n -1, состоящую из остовных лесов, причем F i = F i -1 + e i где e i – ребро из Ext ( F i-1 ). Указанную после-довательность называют растущим лесом.
Слайд 8: Минимальный остов
Последовательность строится таким образом, чтобы для каждого i ( i [ 1, n-1 ] ) остовный лес можно было бы продолжить до минимального остова. Ясно, что тогда F n-1 является минимальным остовом. При переходе от F i-1 к F i ( т.е. при выборе ребра e i ) возможны две стратегии.
Слайд 9: Минимальный остов
Стратегия 1. В качестве e i выбираем ребро минимального веса среди всех ребер, внешних к остовному лесу F i-1. Пусть H – одна из двух компонент связности, леса F i-1, содержащая концевую вершину ребра e i. Если F i-1 продолжаем до минималь-ного остова, то в силу леммы лес F i = F i-1 + e i обладает тем же свойством.
Слайд 10: Минимальный остов
Стратегия 2. Здесь предполагается, что каждый остовный лес F i ( i 1 ) имеет только од-ну неодноэлементную компоненту связности H i. Удобно считать, что H 0 состоит из не-которой заранее выбранной вершины графа G. Таким образом речь идет о построении последовательности H 0, H 1, …, H n -1, состоящей из поддеревьев графа G, причем H i = H i -1 + e i, причем e i Ext ( F i-1 ). Указанную последователь-ность называют растущим деревом.
Слайд 11: Минимальный остов
Стратегия 1 реализуется алгоритмом Борувки – Краскала, стратегия 2 – алгоритмом Ярника – Прима – Дейкстры.
Слайд 13: Отакар Борувка (10 мая 1899 22 июля 1995)
Чешский математик, про - фессор университета Брно. Идея алгоритма построе-ния минимального остова была изложена в его рабо-те в 1926 году. Однако, работа была практически забыта.
Слайд 14: Джозеф Краскал (29 января 1928 ― 19 сентября 2010 )
Американский математик. Учился в Чикагском и в Принстонском университетах. В 1954 году получил степень PhD. Одним их его научных руководителей был Алберт Таккер (помните теорему Куна-Таккера о необходимых усло-виях экстремума в задаче ма-тематического программирова-ния?). Член американской ассоциации статистики, ведущий ученый Bell Labs. Алгоритм построения минималь-ного остова был опубликован в 1956 году.
Сортируем ребра графа по возрастанию весов. Тривиальный лес объявить растущим. Проходим ребра в "отсортированном" порядке. Для каждого ребра выполняем: если вершины, соединяемые данным ребром лежат в разных деревьях растущего леса, то объединяем эти деревья в одно, а ребро добавляем к строящемуся остову. если вершины, соединяемые данным ребром лежат в одном дереве растущего леса, то исключаем ребро из рассмотрения. Если есть еще нерассмотренные ребра и не все деревья объединены в одно, то переходим к шагу 3, иначе выход.
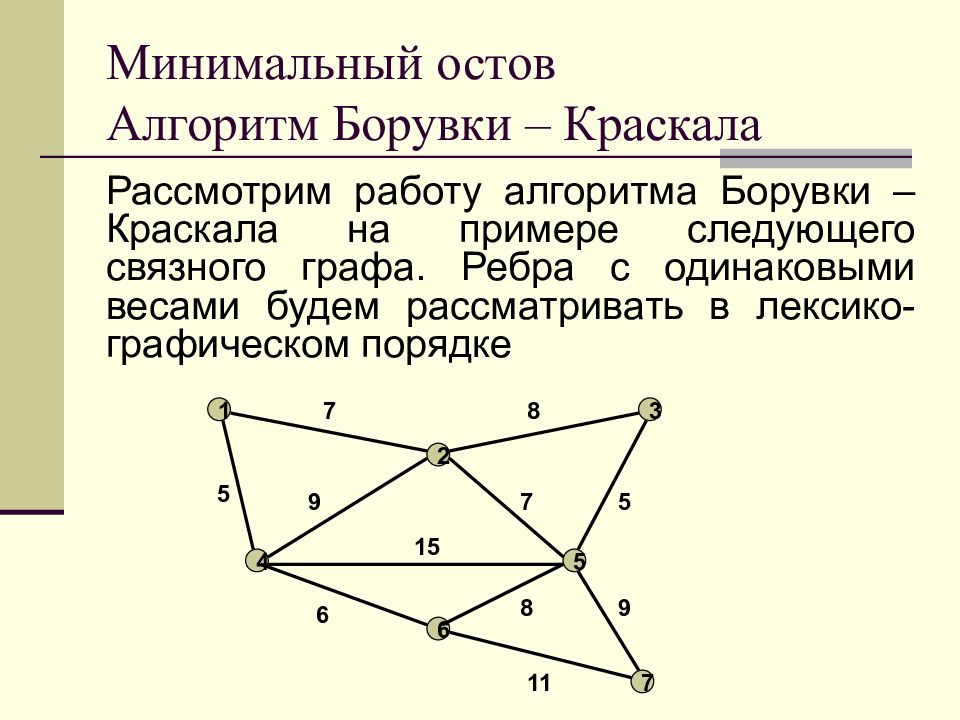
Слайд 16: Минимальный остов Алгоритм Борувки – Краскала
Рассмотрим работу алгоритма Борувки – Краскала на примере следующего связного графа. Ребра с одинаковыми весами будем рассматривать в лексико-графическом порядке 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9 Минимальный остов Алгоритм Борувки – Краскала
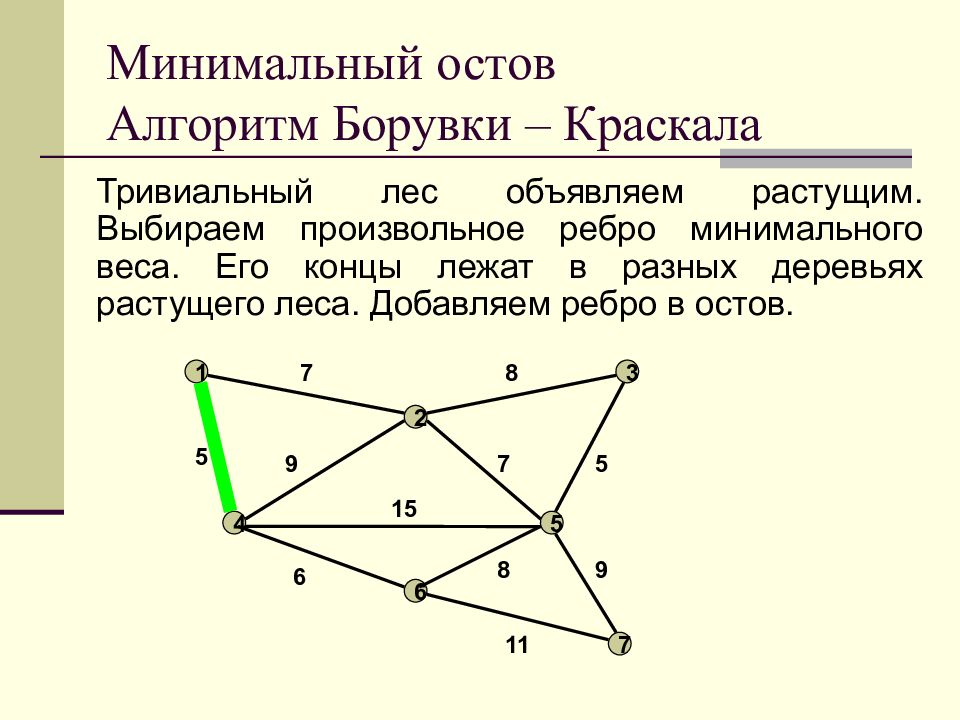
Слайд 17: Минимальный остов Алгоритм Борувки – Краскала
Тривиальный лес объявляем растущим. Выбираем произвольное ребро минимального веса. Его концы лежат в разных деревьях растущего леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
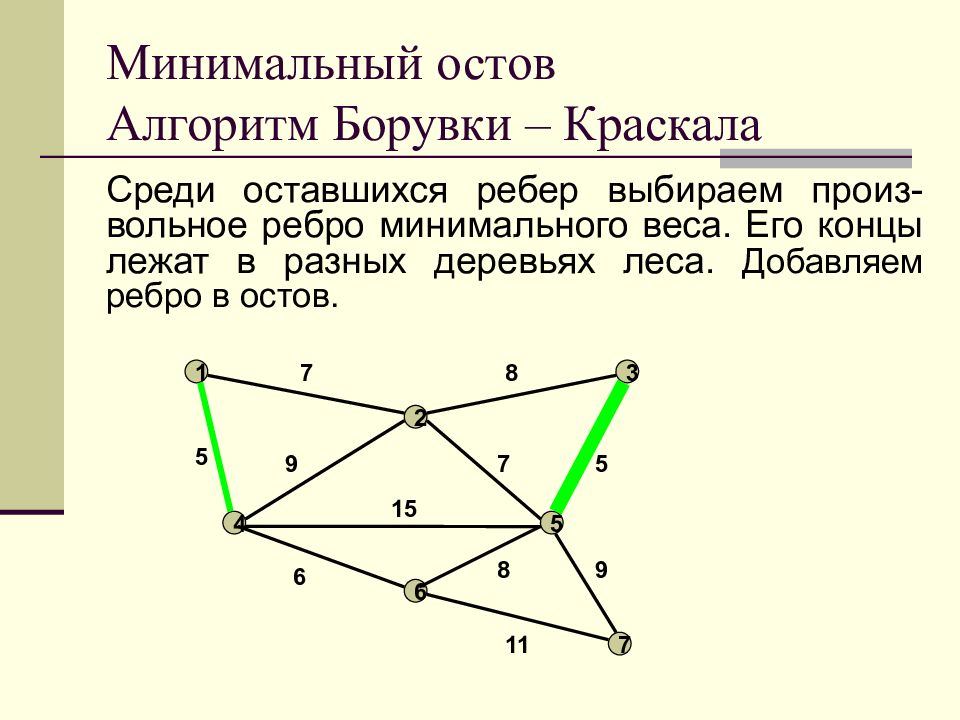
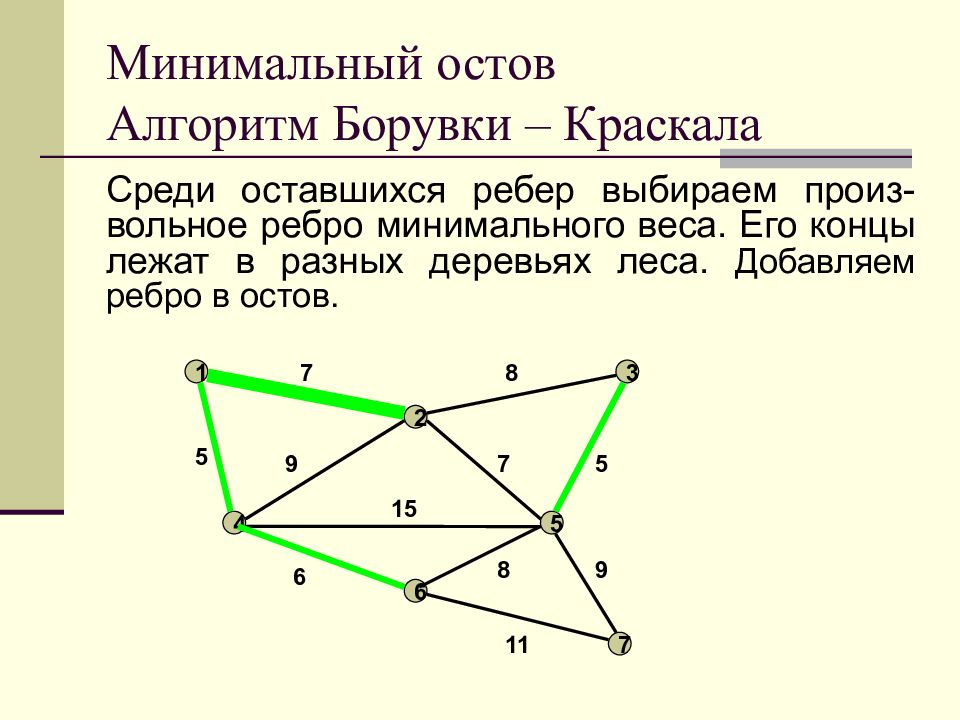
Слайд 18: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в разных деревьях леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
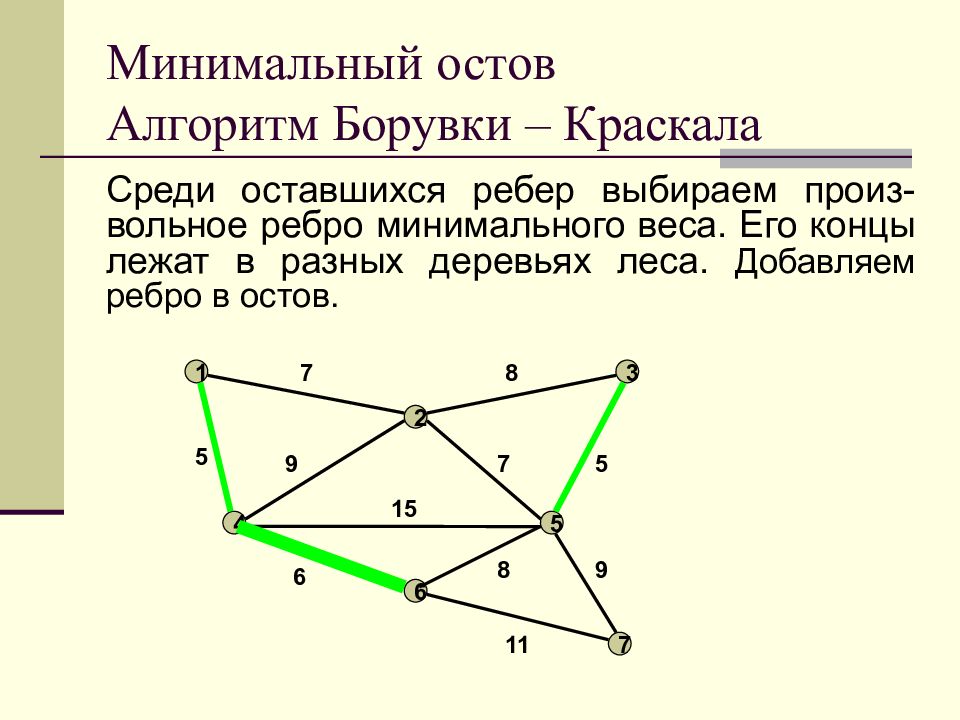
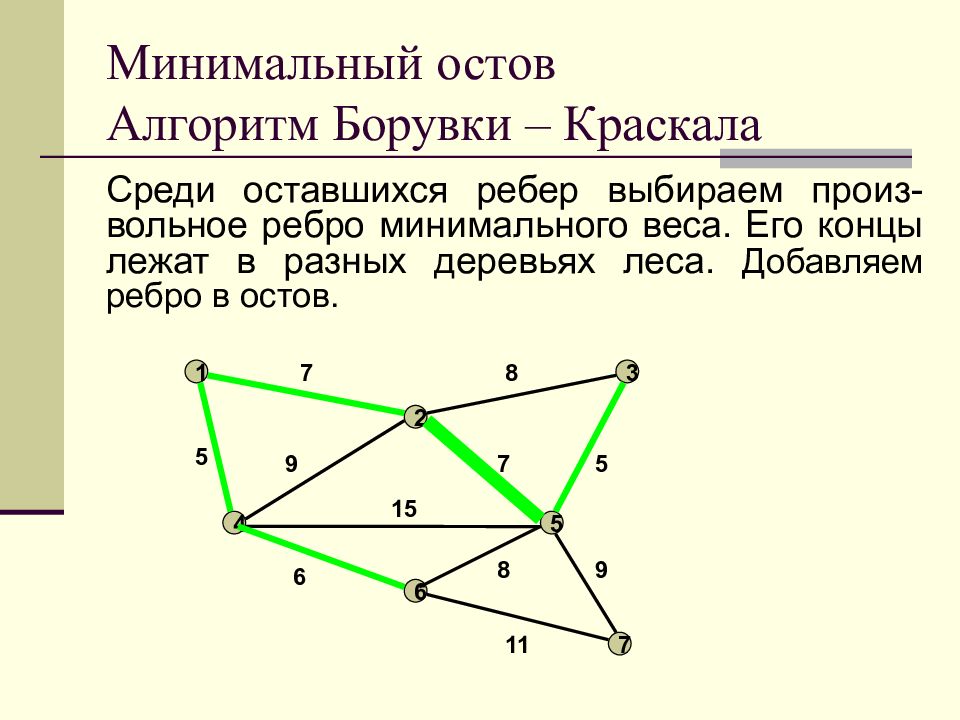
Слайд 19: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в разных деревьях леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 20: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в разных деревьях леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 21: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в разных деревьях леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
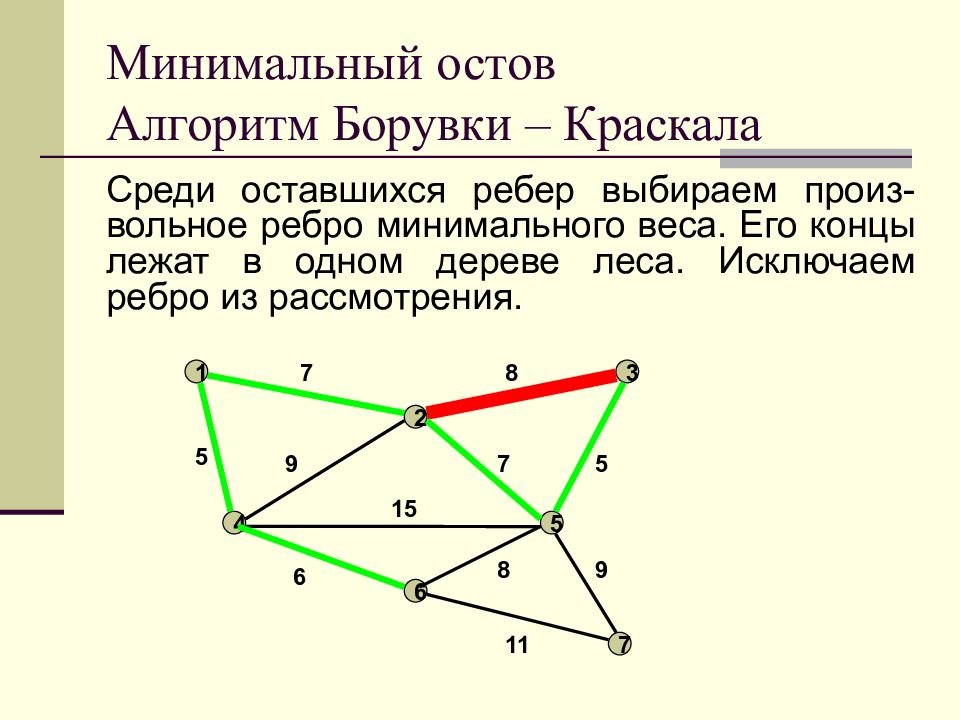
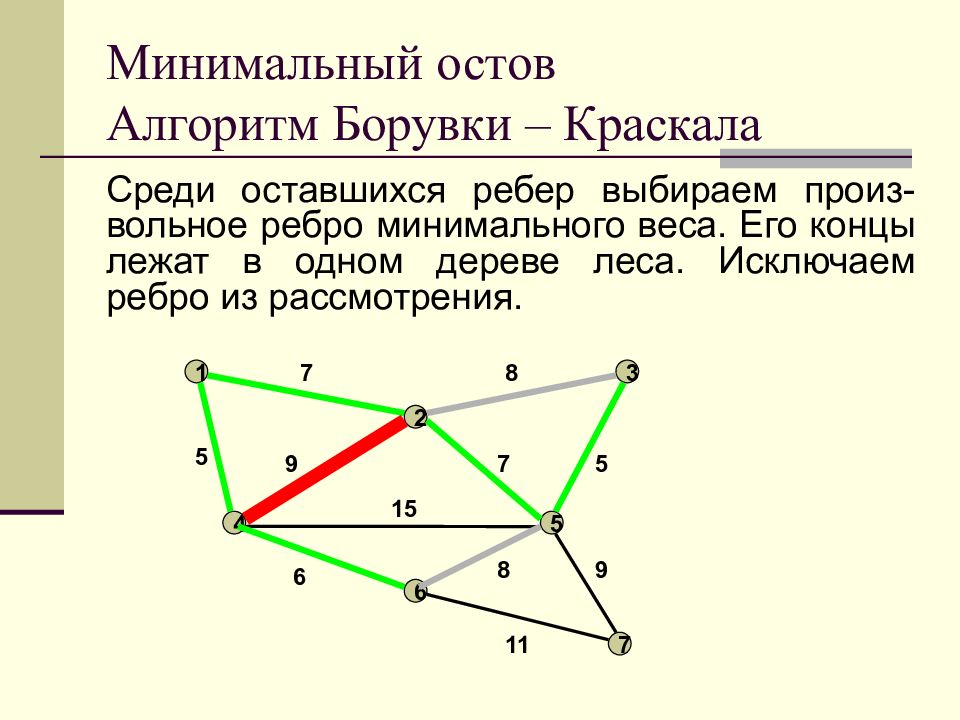
Слайд 22: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в одном дереве леса. Исключаем ребро из рассмотрения. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
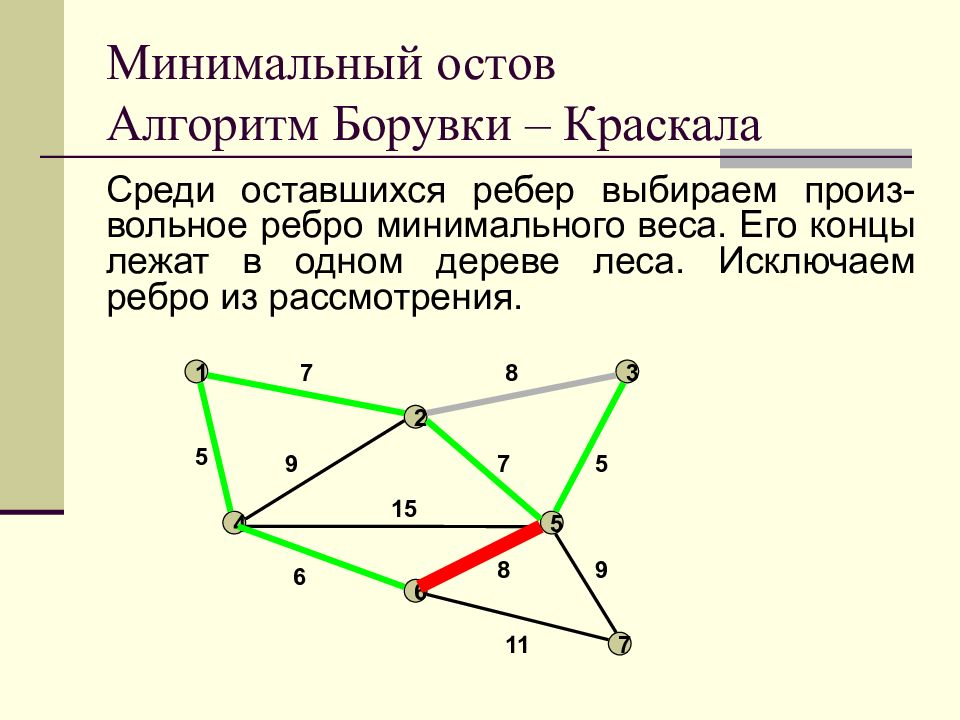
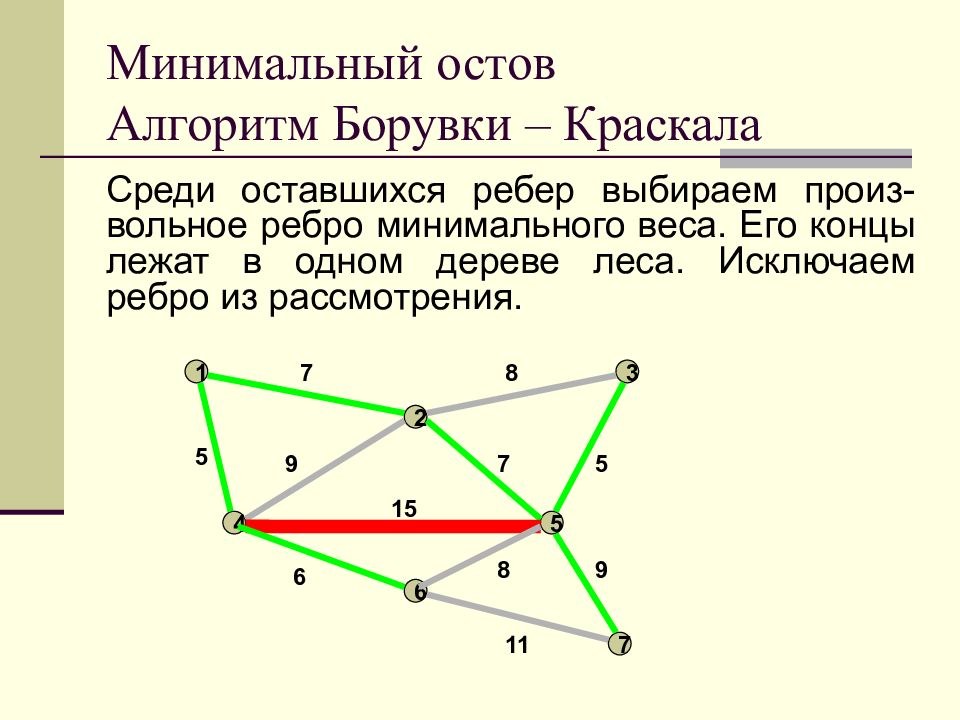
Слайд 23: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в одном дереве леса. Исключаем ребро из рассмотрения. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 24: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в одном дереве леса. Исключаем ребро из рассмотрения. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
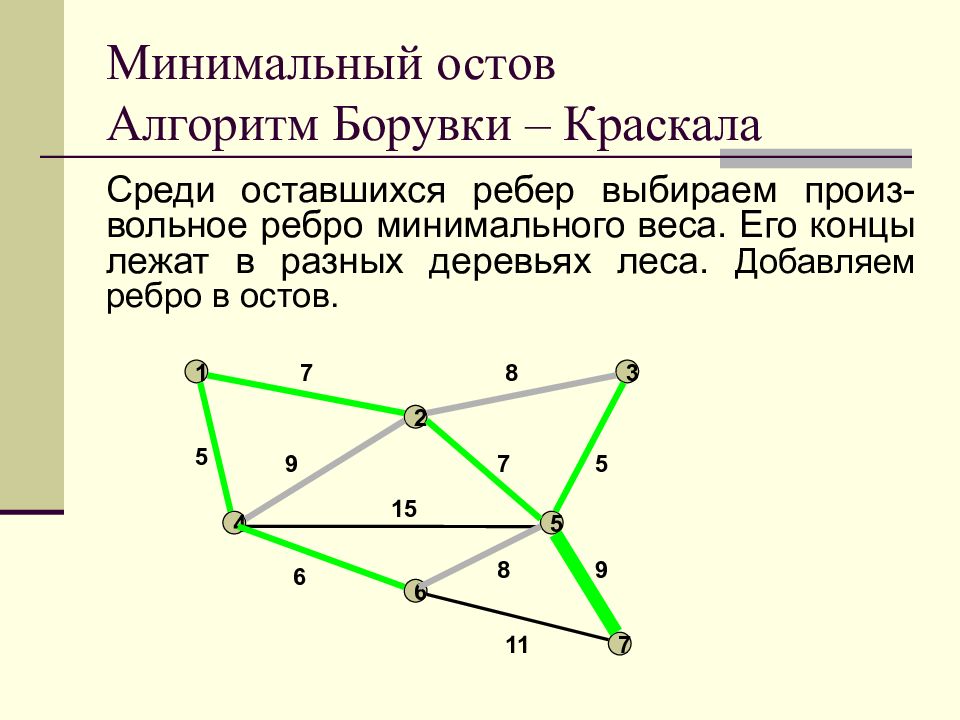
Слайд 25: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в разных деревьях леса. Добавляем ребро в остов. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
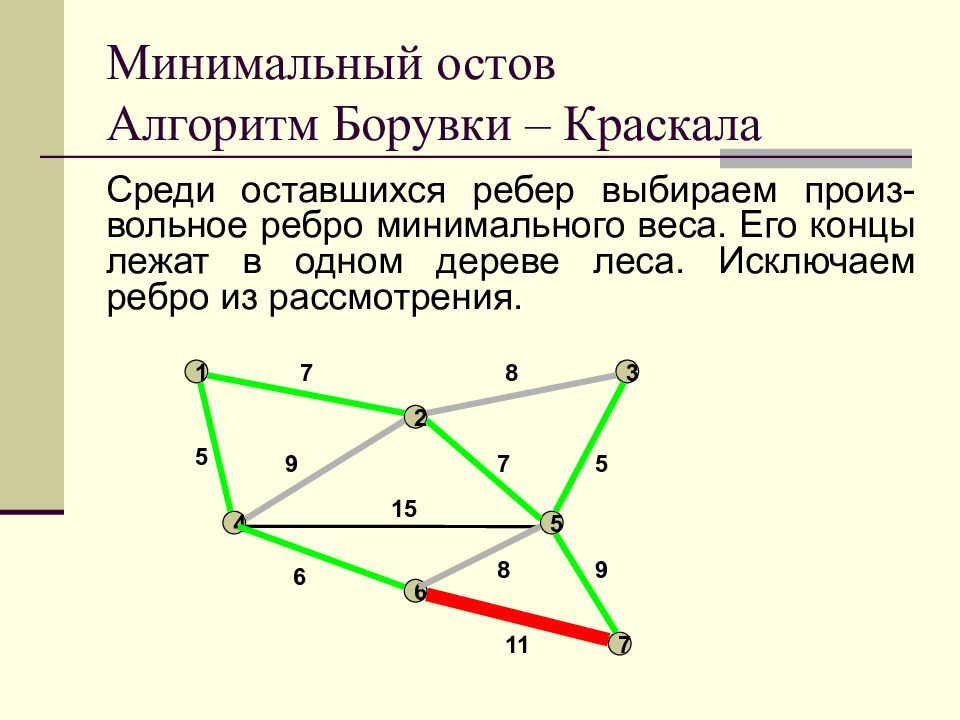
Слайд 26: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в одном дереве леса. Исключаем ребро из рассмотрения. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 27: Минимальный остов Алгоритм Борувки – Краскала
Среди оставшихся ребер выбираем произ-вольное ребро минимального веса. Его концы лежат в одном дереве леса. Исключаем ребро из рассмотрения. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
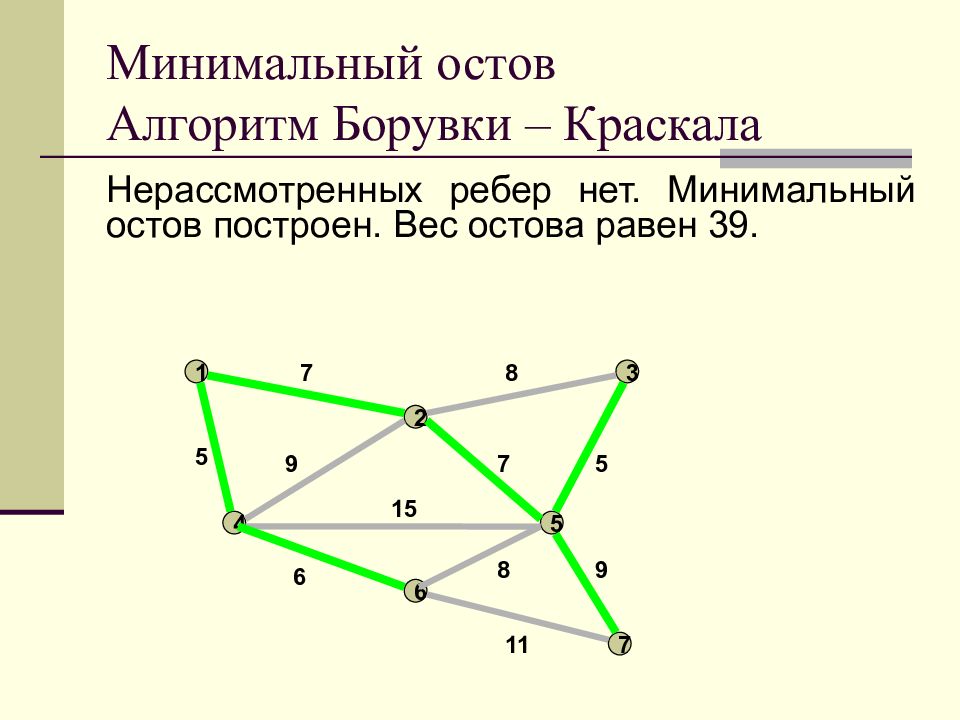
Слайд 28: Минимальный остов Алгоритм Борувки – Краскала
Нерассмотренных ребер нет. Минимальный остов построен. Вес остова равен 39. Минимальный остов Алгоритм Борувки – Краскала 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 30
Войтех Ярник (22 декабря 1897 – 22 сентября 1970) Чешский математик. Ос-новные работы посвящены теории чисел и матема-тическому анализу. В 1930 году разработал алгоритм построения ми-нимального остова.
Слайд 31
Роберт Прим (род. в 1921 в Техасе, США) Американский математик. Получил степень PhD в Принстонском универси-тете в 1949. Позже рабо-тал вместе с Джозефом Красаклом в Bell Labs. Предложил алгоритм по-строения минимального остова в 1957 году.
Слайд 32
Эдсгер Дейкстра (11 мая 1930 – 6 августа 2002) Голландский математик – специалист в области компьютерных наук. В 1972 году стал лауреатом премии Тьюринга за существенный вклад в развитие языков програм - мирования. Разработал алгоритм построения минимального остова в 1959 году.
Слайд 33: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Выбирается произвольная вершина – она будет корнем остовного дерева. Измеряется расстояние от нее до всех внешних по отношению к растущему дереву вершин (расстояние от внешней вершины до ближайшей к ней вершины дерева) До тех пор пока в дерево не добавлены все вершины делать: Найти вершину, расстояние от дерева до которой минимально. Добавить ее к дереву. Пересчитать расстояния от вершин до дерева следующим образом: если расстояние до какой- либо вершины из новой вершины меньше текущего расстояния от дерева, то старое расстояние от дерева заменить новым.
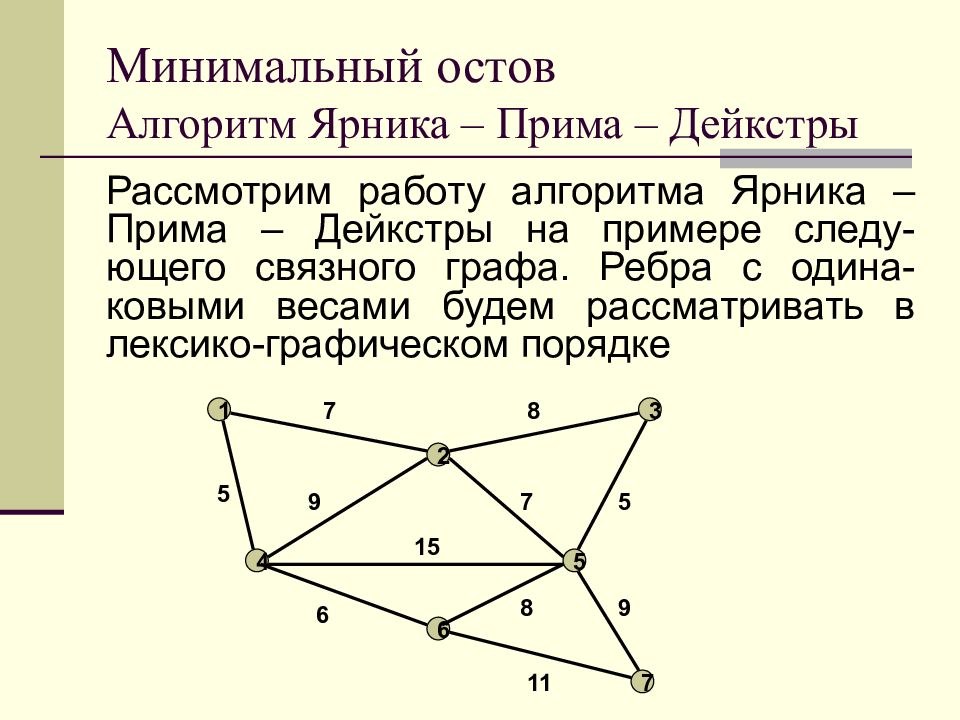
Слайд 34: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Рассмотрим работу алгоритма Ярника – Прима – Дейкстры на примере следу-ющего связного графа. Ребра с одина-ковыми весами будем рассматривать в лексико-графическом порядке 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9 Минимальный остов Алгоритм Ярника – Прима – Дейкстры
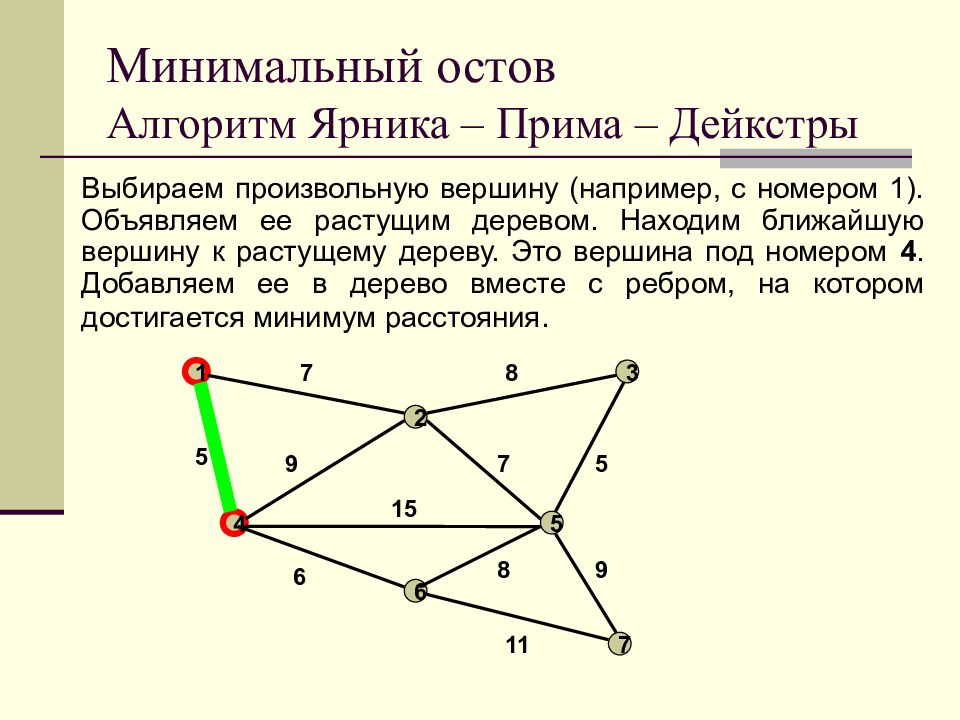
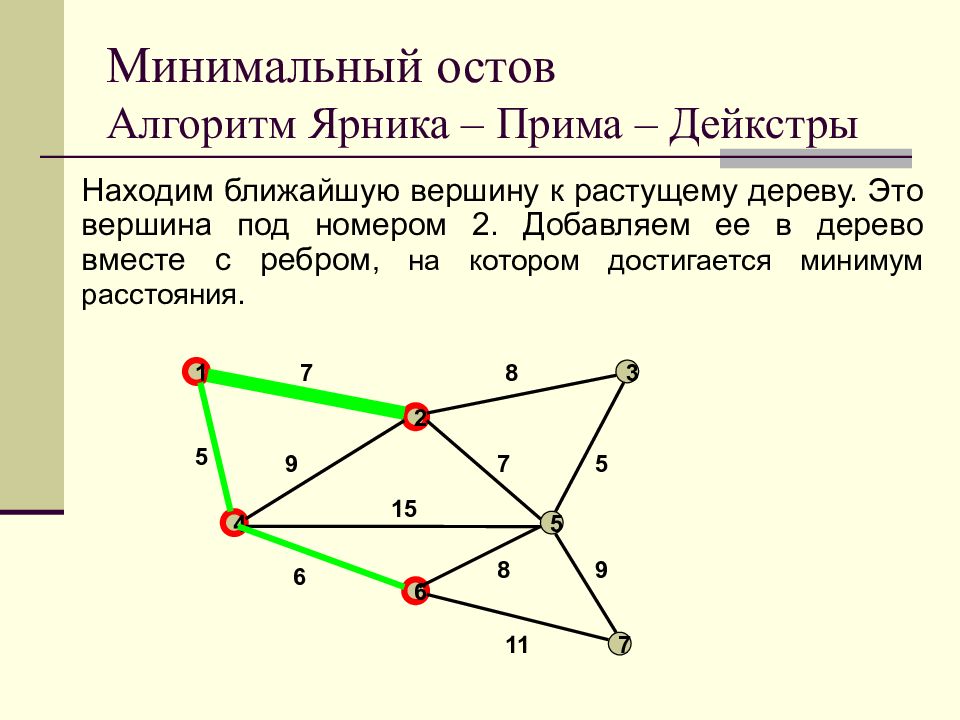
Слайд 35: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Выбираем произвольную вершину (например, с номером 1). Объявляем ее растущим деревом. Находим ближайшую вершину к растущему дереву. Это вершина под номером 4. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
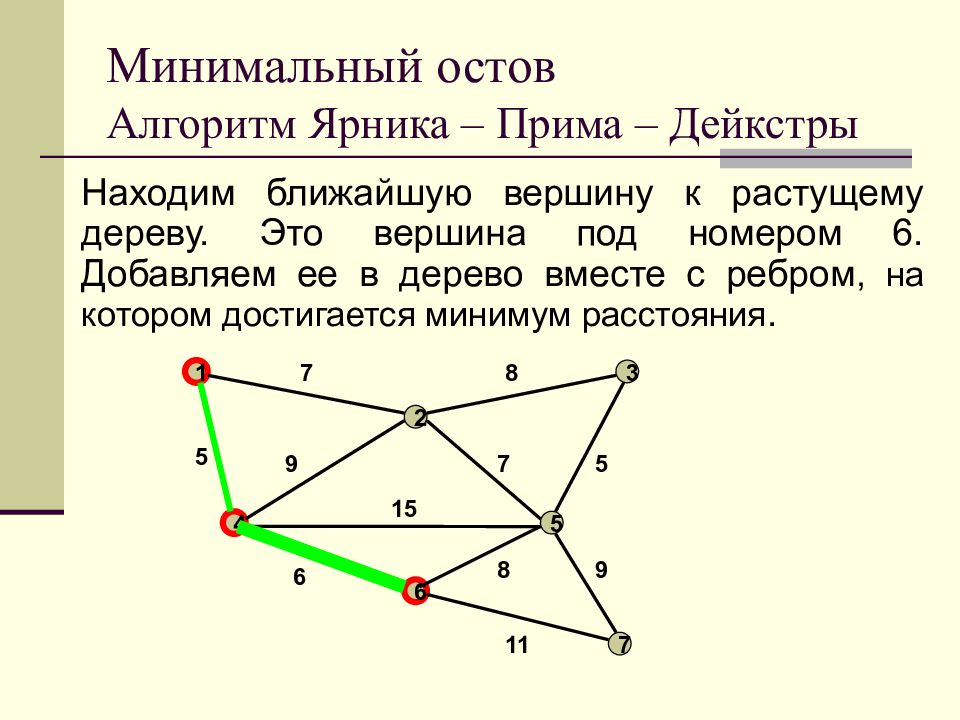
Слайд 36: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Находим ближайшую вершину к растущему дереву. Это вершина под номером 6. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 37: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Находим ближайшую вершину к растущему дереву. Это вершина под номером 2. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
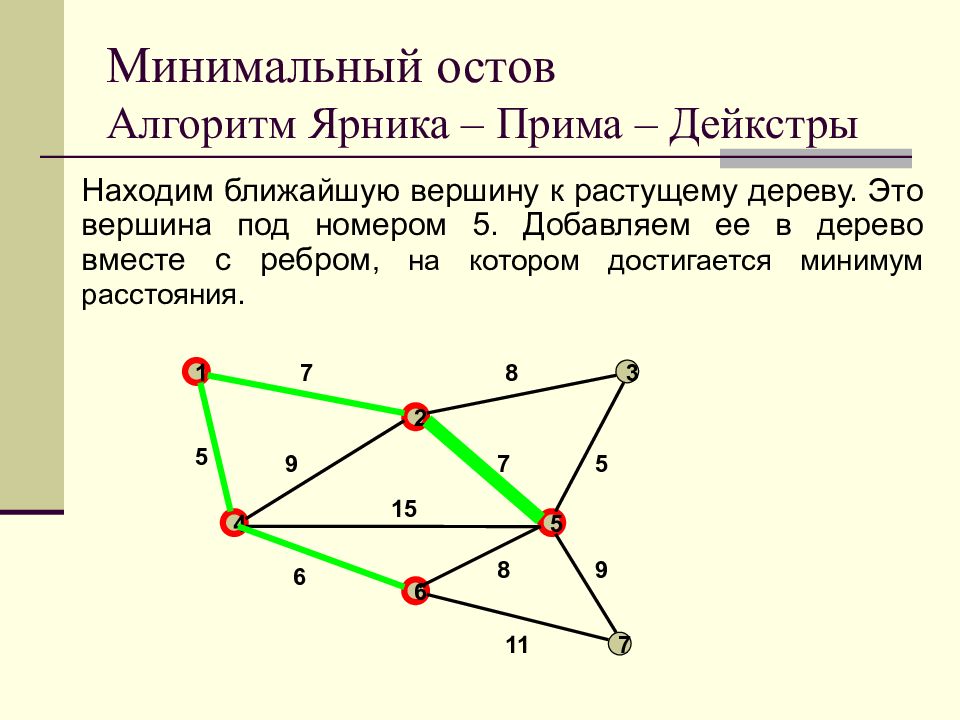
Слайд 38: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Находим ближайшую вершину к растущему дереву. Это вершина под номером 5. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
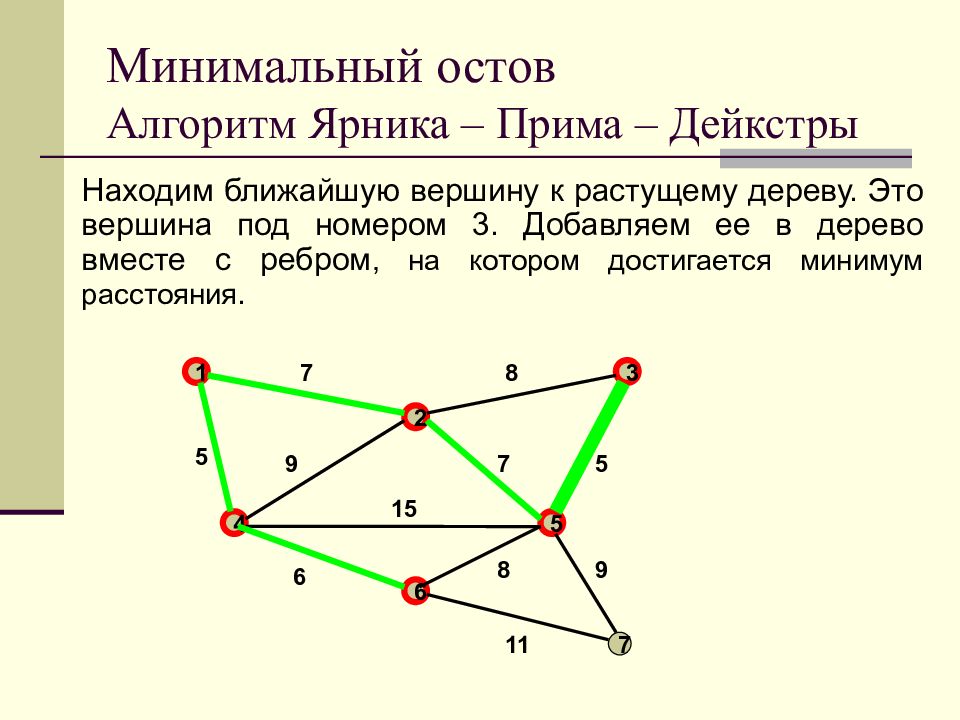
Слайд 39: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Находим ближайшую вершину к растущему дереву. Это вершина под номером 3. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
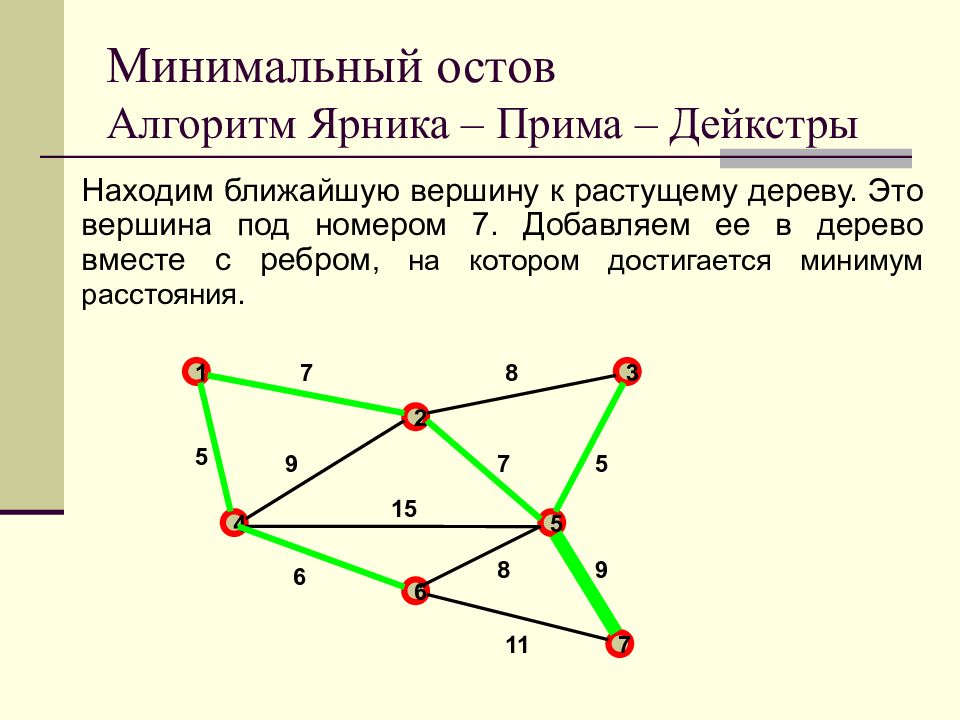
Слайд 40: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Находим ближайшую вершину к растущему дереву. Это вершина под номером 7. Добавляем ее в дерево вместе с ребром, на котором достигается минимум расстояния. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
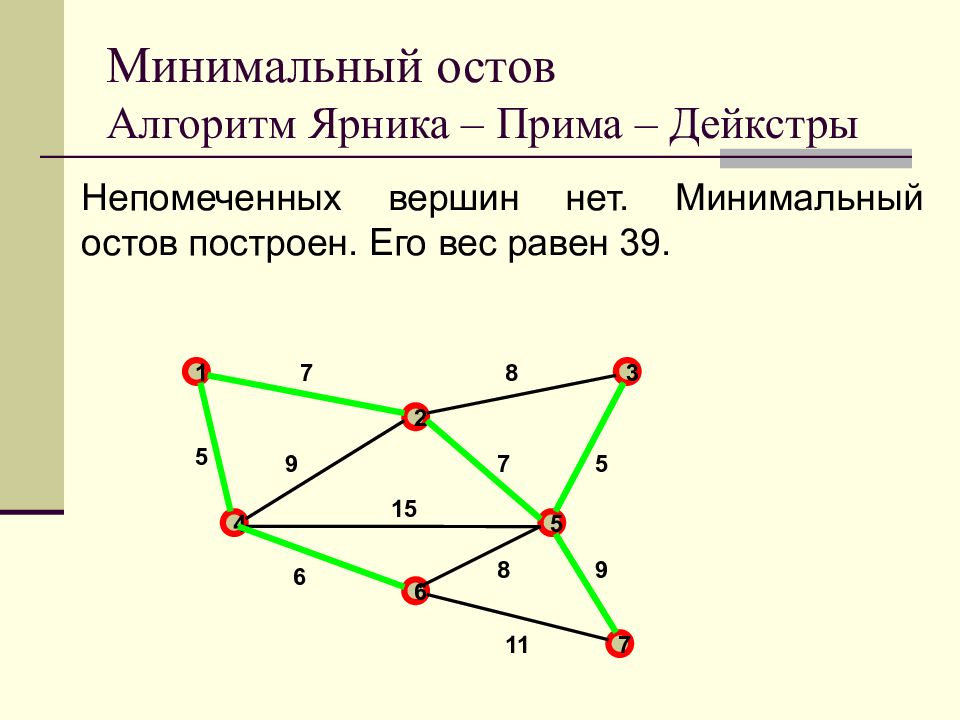
Слайд 41: Минимальный остов Алгоритм Ярника – Прима – Дейкстры
Непомеченных вершин нет. Минимальный остов построен. Его вес равен 39. Минимальный остов Алгоритм Ярника – Прима – Дейкстры 1 2 3 4 5 6 7 7 8 9 7 5 5 15 6 11 8 9
Слайд 42: Минимальный остов
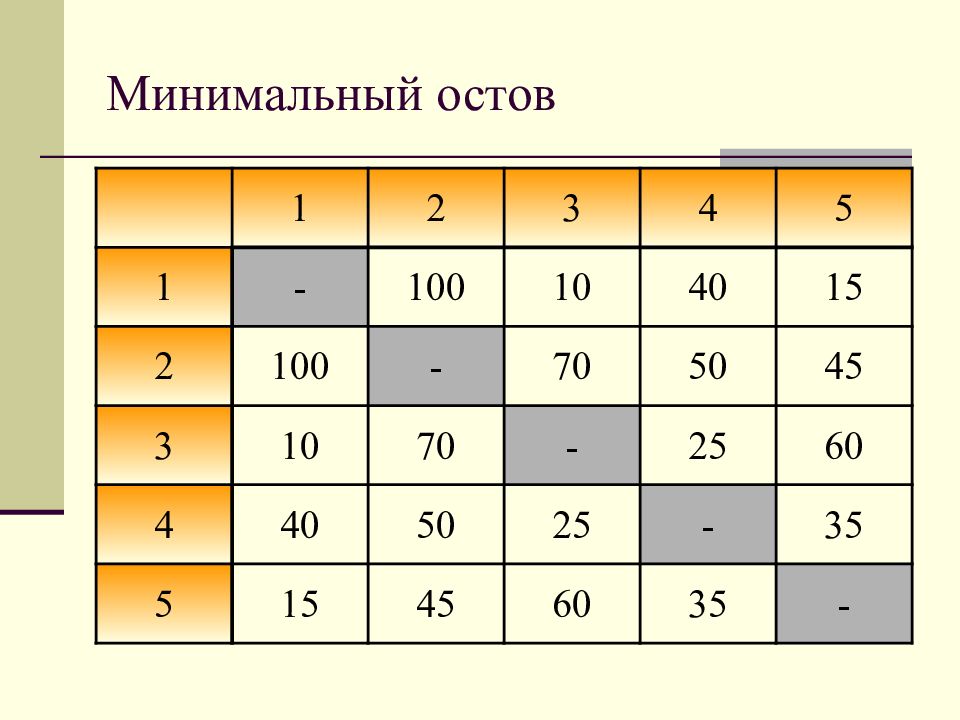
Рассмотрим следующую задачу. Минимальный остов Телефонная компания арендовала место, обозна-ченное узлом 1 для основного центра связи, и опре-делила расположение дополнительных центров (узлы 2,3, …5). Необходимо проложить кабель так, чтобы каждый дополнительный центр связи был связан с основным либо непосредственно, либо через другие дополнительные центры. В целях экономии компания стремиться израсходовать кабеля как можно меньше. Расстояния между центрами даны в таблице.
Слайд 43: Минимальный остов
1 2 3 4 5 1 - 100 10 40 15 2 100 - 70 50 45 3 10 70 - 25 60 4 40 50 25 - 35 5 15 45 60 35 -
Слайд 45: Пути в сетях
Взвешенный орграф G=(V,E,c) называется сетью. Пусть P — некоторый ( v,w ) – путь: Положим Величину с ( P ) назовем длиной пути P.
Слайд 46: Пути в сетях
Наименьшую из длин ( v,w ) – путей назовем расстоянием от v до w, … … а тот ( v,w ) – путь, длина которого равна расстоянию от v до w, будем называть кратчайшим (v,w)– путем. Ясно, что расстояние от v до w может отличаться от рассто - яния от w до v. ! !
Слайд 47: Пути в сетях
Задача о кратчайшем пути между фикси-рованными вершинами формулируется сле-дующим образом: В заданной сети G с двумя выделен-ными вершинами s и t найти кратчай-ший ( s,t )–путь.
Слайд 48: Пути в сетях
В этой задаче предполагается отсутствие циклов отрицательной длины (иначе задача окажется некорректной).
Слайд 50
Лестер Рэндольф Форд младший (род. 23 сентября 1927) Американский математик. В 1956 году предложил алгоритм построения кратчайшего пути в сетях.
Слайд 51
Ричард Беллман (26 августа 1920 – 19 марта 1984) Американский математик — специалист по прикладной математике. Окончил Бруклин-ский колледж в 1941 году ( B.A. ), универси-тет Висконсин–Мэдисон ( M.A. ). Работал в подразделении теоретической физики лаборатории в Лос–Аламос, где в 1946 году получил степень PhD. Награжден почетной медалью IEEE ( Institute of Electrical and Electronics Engineers ) за вклад в развитие теории принятия решений, теории управления и, в особенности, за создание и развития теории динамического програм-мирования. Был действительным членом Американской академии наук и искусств (с 1975 года), и Национальной инженерной академии США (с 1977 года). Предложил алгоритм построения кратчай-шего пути в сетях в 1958 году.
Слайд 52: Пути в сетях Алгоритм Форда – Беллмана
Для описания алгоритма будем использовать следующие обозначения: D [ v ] – массив, в котором будет «накапли-ваться» расстояние от выделенной верши-ны s до всех остальных вершин графа; ПРЕДШ [ v ] – массив, в котором на месте v будет храниться номер вершины – предшест-венницы вершины v в кратчайшем ( s,v ) – маршруте.
Слайд 53: Пути в сетях Алгоритм Форда – Беллмана
Для всех вершин v из V положить D [ v ]:=c( s,v ), Если c ( s,v ) < ПРЕДШ [ v ]:= s иначе ПРЕДШ [ v ]:= 0; Следующую операцию повторить n - 2 раза: для всех вершин v из V \ { s } D [ v ]:=min{ D [ v ],D[ w ]+ c [ w,v ] | w из V } ПРЕДШ [ v ]:=w* ( та вершина, которая обеспечила минимум D [ v ]). После выполнения этого алгоритма массив D содержит длины кратчайших ( s,v ) – путей, а по массиву ПРЕДШ [ v ] можно восстановить сам путь.
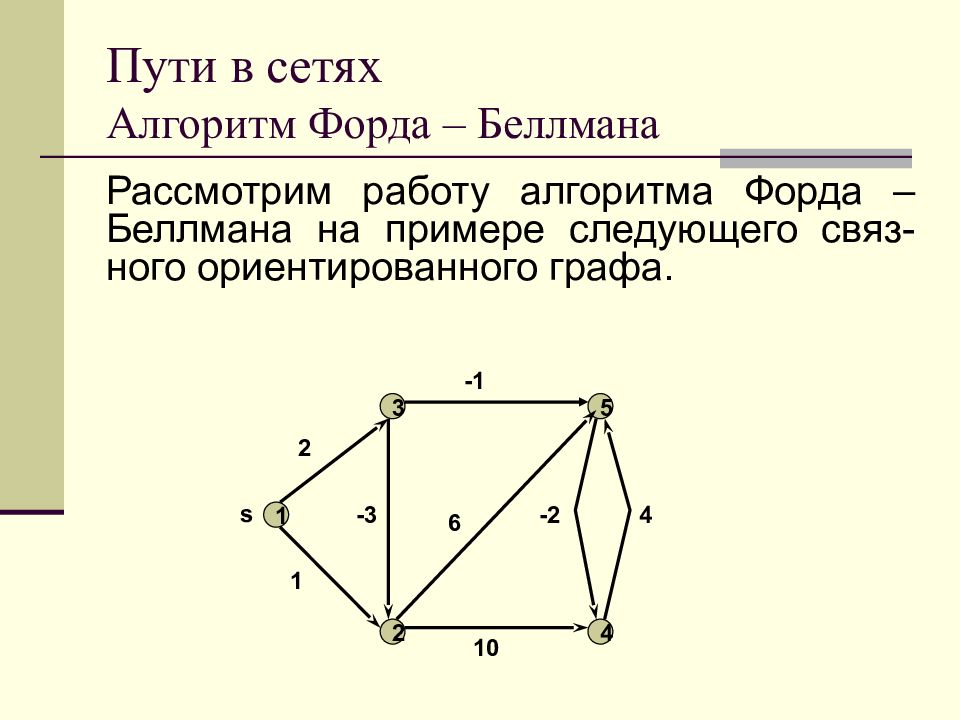
Слайд 54: Пути в сетях Алгоритм Форда – Беллмана
Рассмотрим работу алгоритма Форда – Беллмана на примере следующего связ - ного ориентированного графа. Пути в сетях Алгоритм Форда – Беллмана 1 2 3 4 5 s 1 2 -3 -1 6 10 -2 4
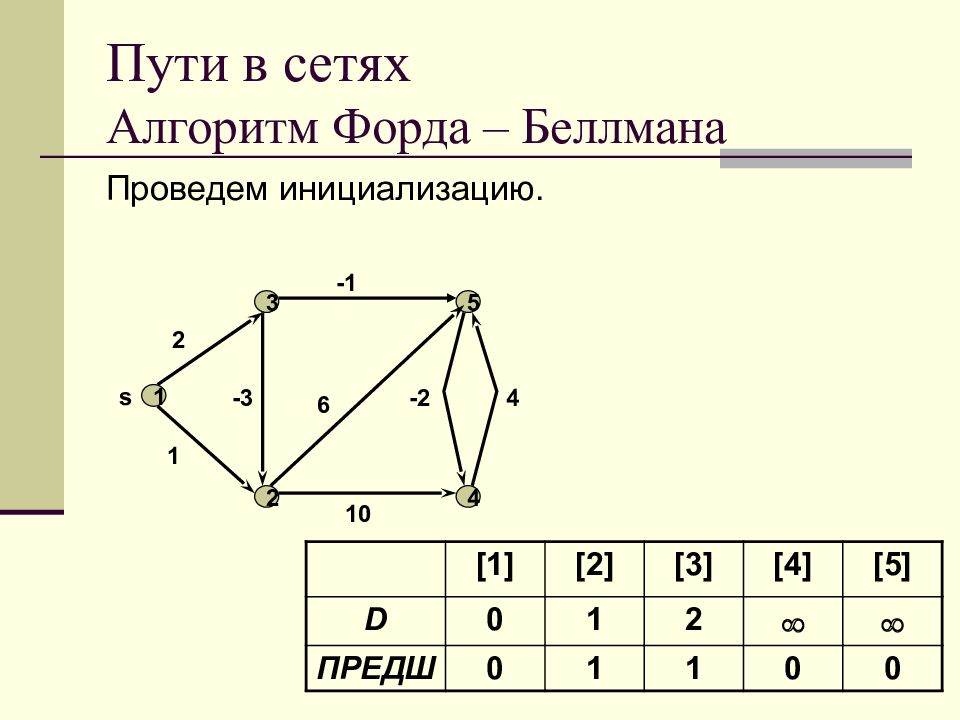
Слайд 55: Пути в сетях Алгоритм Форда – Беллмана
Проведем инициализацию. [1] [2] [3] [4] [5] D 0 1 2 ПРЕДШ 0 1 1 0 0 1 2 3 4 5 s 1 2 -3 -1 6 10 -2 4
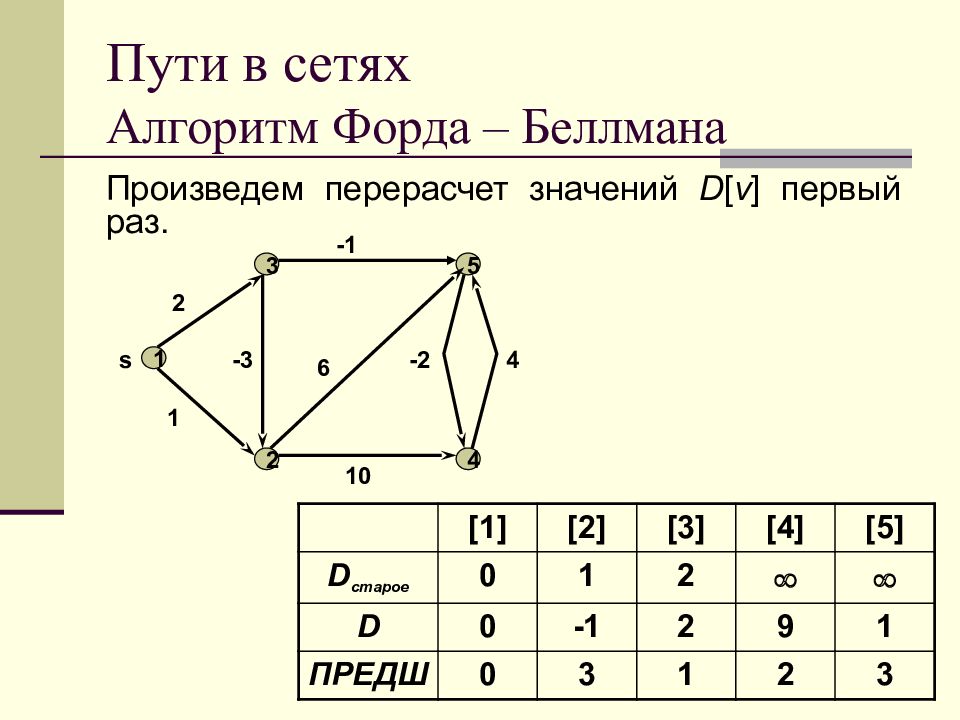
Слайд 56: Пути в сетях Алгоритм Форда – Беллмана
Произведем перерасчет значений D [ v ] первый раз. 1 2 3 4 5 s 1 2 -3 -1 6 10 -2 4 [1] [2] [3] [4] [5] D старое 0 1 2 D 0 - 1 2 9 1 ПРЕДШ 0 3 1 2 3
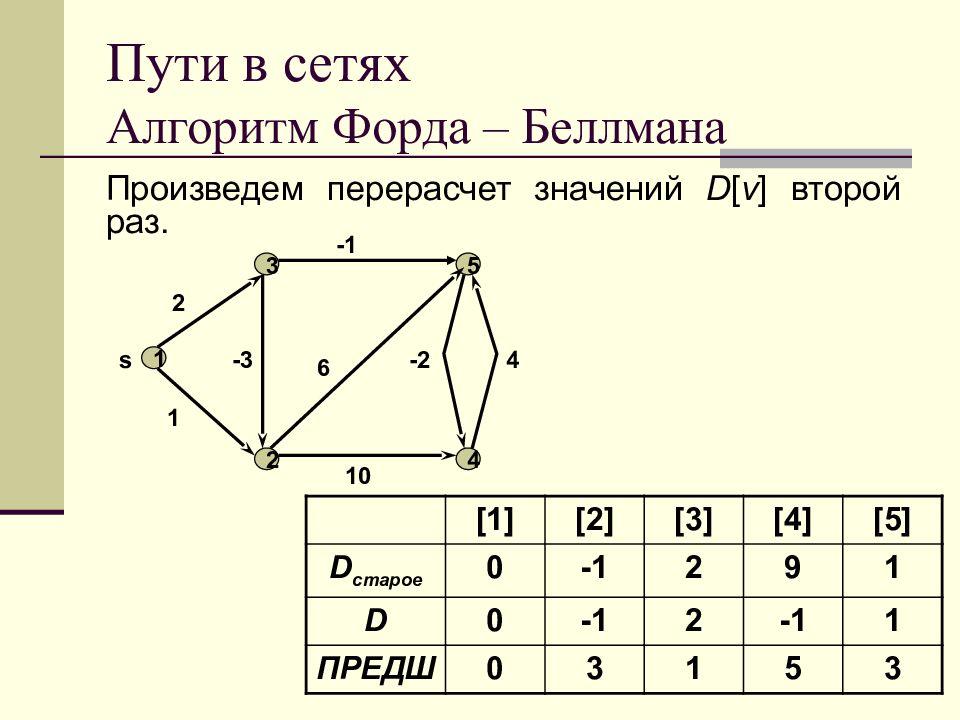
Слайд 57: Пути в сетях Алгоритм Форда – Беллмана
Произведем перерасчет значений D [ v ] второй раз. 1 2 3 4 5 s 1 2 -3 -1 6 10 -2 4 [1] [2] [3] [4] [5] D старое 0 - 1 2 9 1 D 0 - 1 2 -1 1 ПРЕДШ 0 3 1 5 3
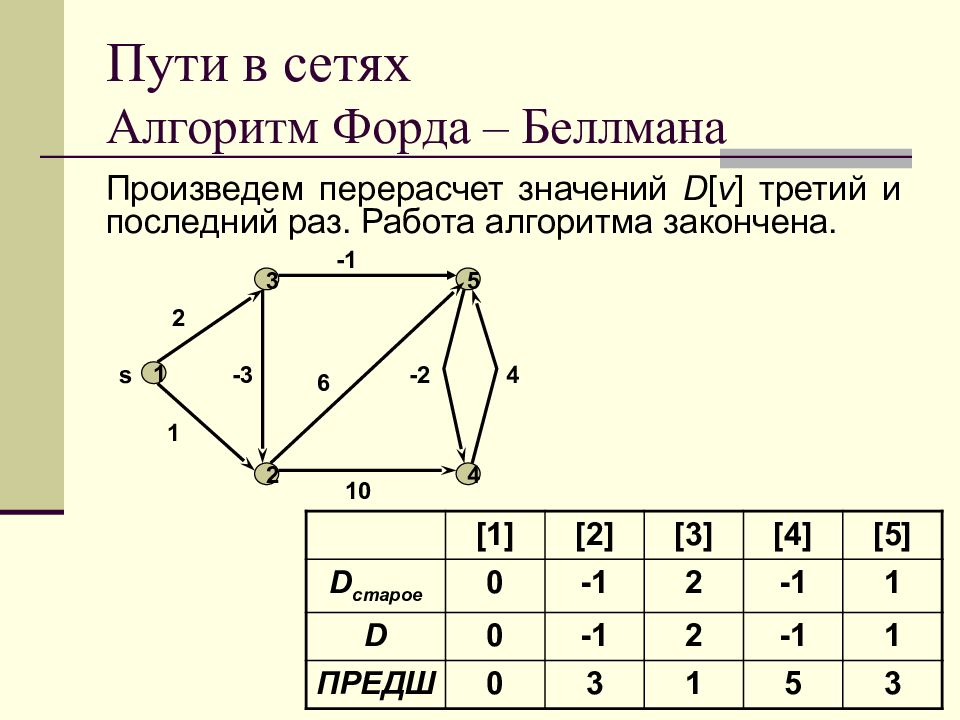
Слайд 58: Пути в сетях Алгоритм Форда – Беллмана
Произведем перерасчет значений D [ v ] третий и последний раз. Работа алгоритма закончена. 1 2 3 4 5 s 1 2 -3 -1 6 10 -2 4 [1] [2] [3] [4] [5] D старое 0 - 1 2 -1 1 D 0 - 1 2 -1 1 ПРЕДШ 0 3 1 5 3
Слайд 60: Пути в сетях Алгоритм Дейкстры
Для описания алгоритма будем использовать следующие обозначения: D [ v ] – метки вершин, в которых будет «накапливаться» расстояние от выделенной вершины s до вершины v графа; ПРЕДШ [ v ] – массив, в котором на месте v будет храниться номер вершины – предшест-венницы вершины v в кратчайшем ( s,v ) – маршруте; F – множество еще не просмотренных вершин.
Слайд 61: Пути в сетях Алгоритм Дейкстры
D [ s ]:=0; ПРЕДШ [ s ]:=0; F := V \{ s } для всех v из F положим D [ v ]:= c [ s,v ] ; ПРЕДШ [ v ]:=s; n-1 раз делать выбрать w F : D [ w ] = min{ D [ u ] | u F }; F := F \{ w }; для всех v F делать если ( D [ w ]+ c [ w,v ]< D [ v ]), то D [ v ]:= D [ w ]+ c [ w,v ]; ПРЕДШ [ v ]:= w. инициализация
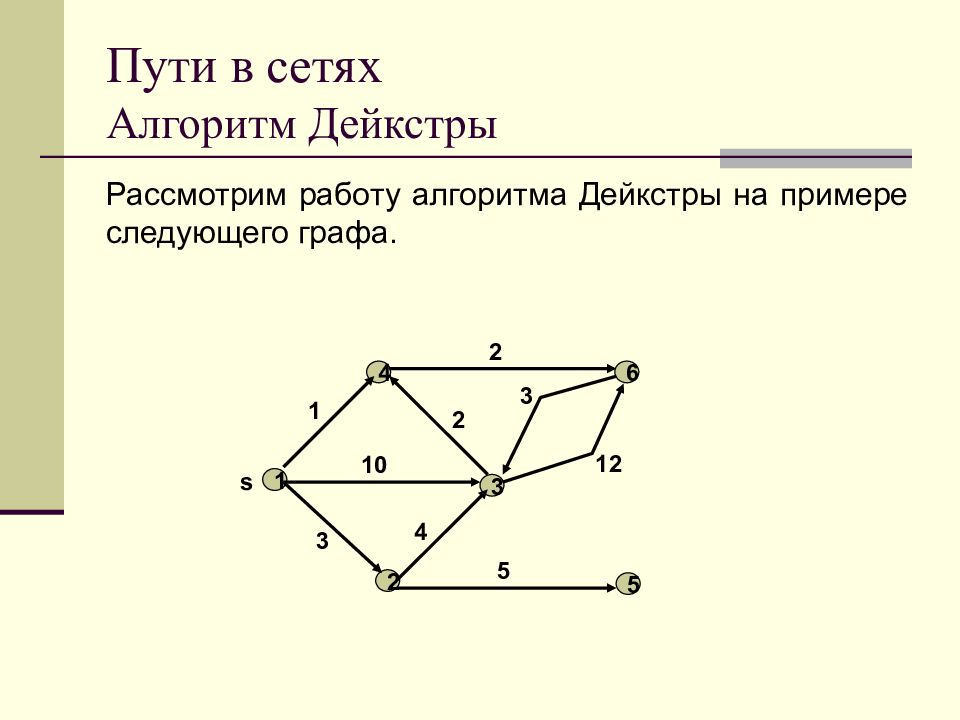
Слайд 62: Пути в сетях Алгоритм Дейкстры
Рассмотрим работу алгоритма Дейкстры на примере следующего графа. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5
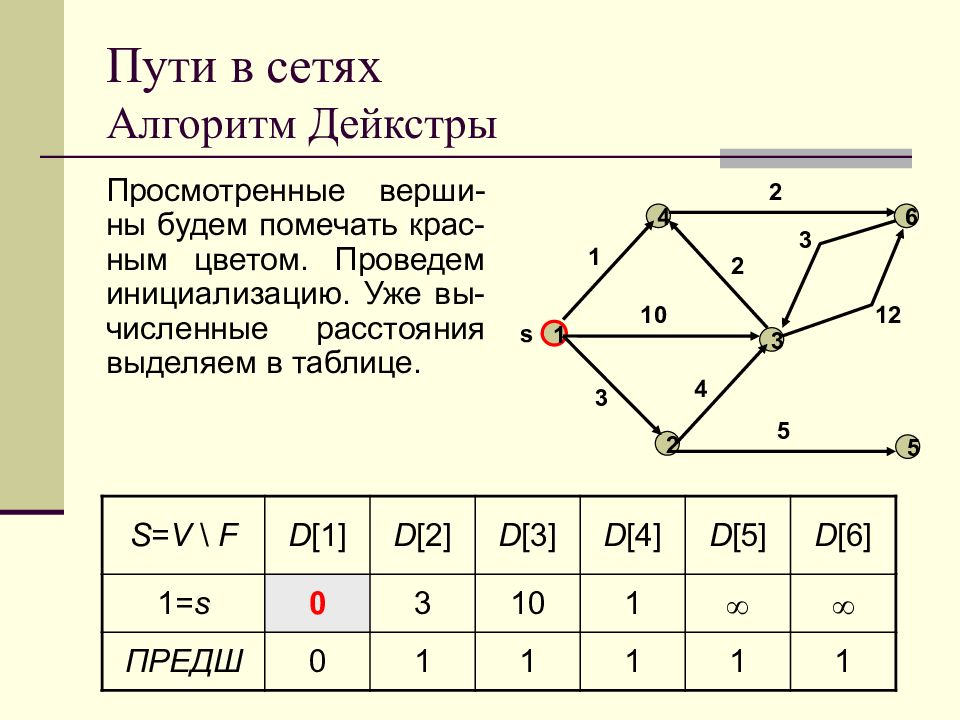
Слайд 63: Пути в сетях Алгоритм Дейкстры
Просмотренные верши-ны будем помечать крас-ным цветом. Проведем инициализацию. Уже вы-численные расстояния выделяем в таблице. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1= s 0 3 10 1 ПРЕДШ 0 1 1 1 1 1
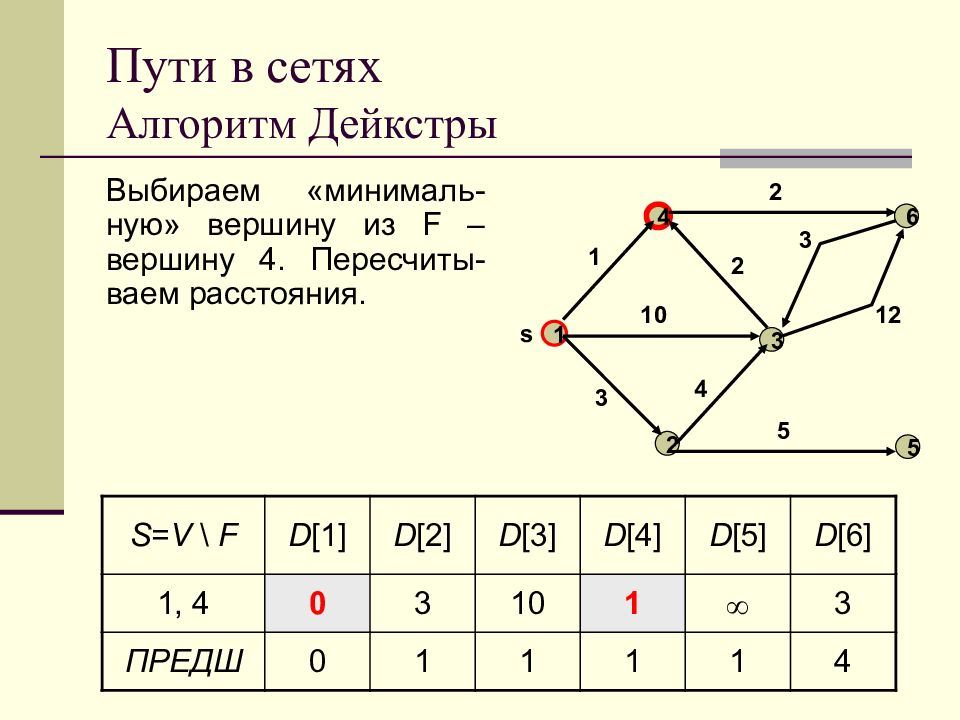
Слайд 64: Пути в сетях Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину 4. Пересчиты-ваем расстояния. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1, 4 0 3 10 1 3 ПРЕДШ 0 1 1 1 1 4
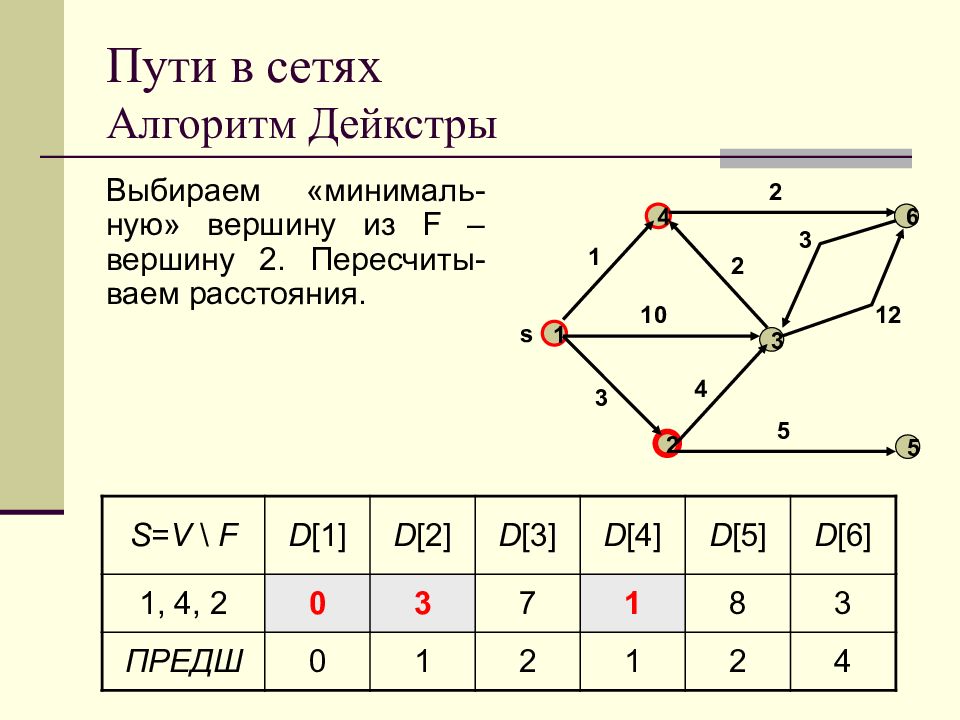
Слайд 65: Пути в сетях Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину 2. Пересчиты-ваем расстояния. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1, 4, 2 0 3 7 1 8 3 ПРЕДШ 0 1 2 1 2 4
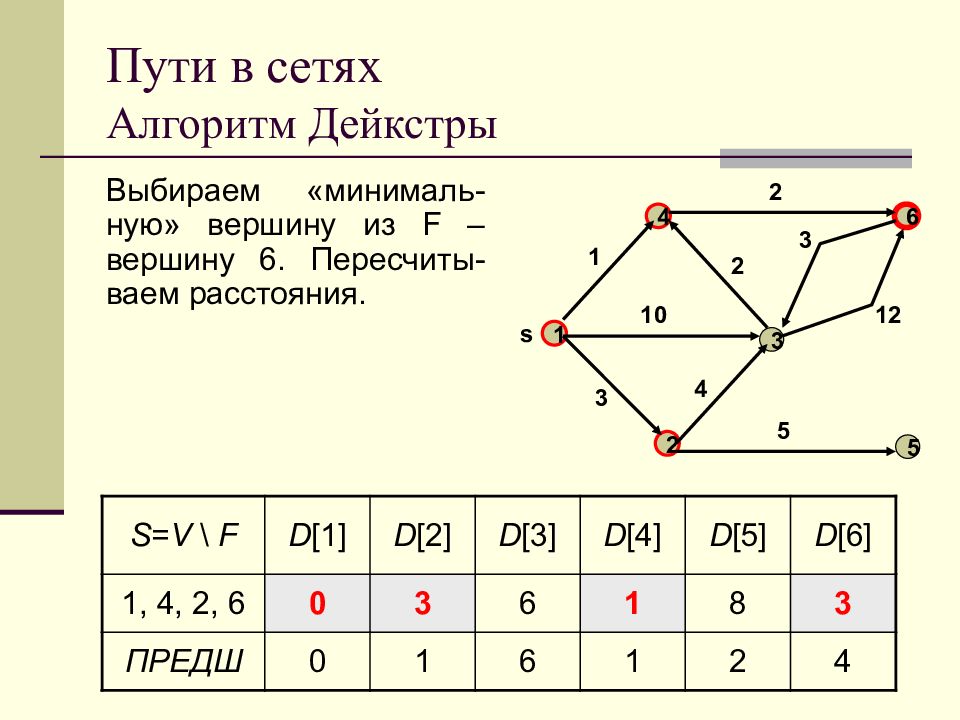
Слайд 66: Пути в сетях Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину 6. Пересчиты-ваем расстояния. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1, 4, 2, 6 0 3 6 1 8 3 ПРЕДШ 0 1 6 1 2 4
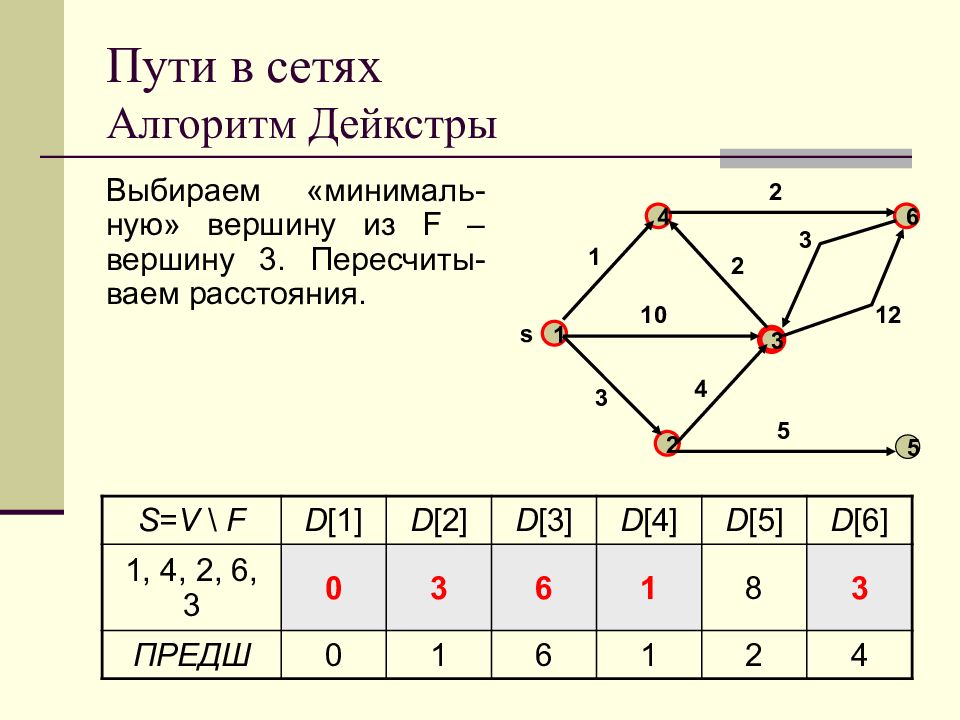
Слайд 67: Пути в сетях Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину 3. Пересчиты-ваем расстояния. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1, 4, 2, 6, 3 0 3 6 1 8 3 ПРЕДШ 0 1 6 1 2 4
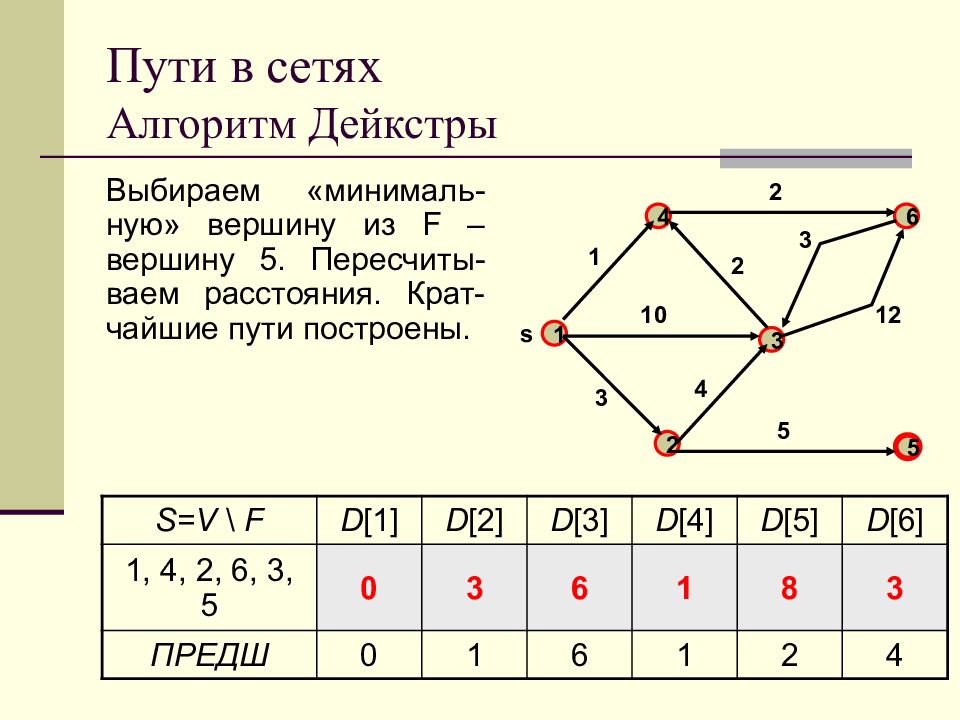
Слайд 68: Пути в сетях Алгоритм Дейкстры
Выбираем «минималь-ную» вершину из F – вершину 5. Пересчиты-ваем расстояния. Крат-чайшие пути построены. 1 2 3 4 5 s 6 1 3 10 4 2 2 3 12 5 S = V \ F D [1] D [2] D [3] D [4] D [5] D [6] 1, 4, 2, 6, 3, 5 0 3 6 1 8 3 ПРЕДШ 0 1 6 1 2 4
Слайд 70: Потоки в сетях
В этом разделе будем рассматривать сети G=(V,E,c;s,t), имеющие единственную вершину с нулевой степенью захода ( s ) и единственную вершину с нулевой степенью исхода ( t ). Будем считать, что веса c ( e ) неотрицательны. Числа c ( e ) будем называть пропускной способностью дуги e.
Слайд 71: Потоки в сетях
Потоком в сети G называется функция f : E R, удовлетворяющая условиям: 0 f ( e ) c ( e ) для всех e E ; f ( v- )= f ( v+ ) для всех v V \ { s,t } Здесь, а
Слайд 72: Потоки в сетях
Величиной потока называется число, рав - ное f ( s + ). Поток f называется максимальным, если для любого потока f* выполняется неравенство:
Слайд 73: Потоки в сетях
Задача о максимальном потоке: в заданной сети найти поток максимальной величины.
Слайд 74: Потоки в сетях
( s,t ) – разрезом (в дальнейшем, просто разре-зом ) ( V s, V t ) в сети G называется пара множеств V s и V t, удовлетворяющих условиям: s V s, t V t ; V s V t = V ; V s V t = .
Слайд 75: Потоки в сетях
Для разреза ( V s, V t ) через E ( V s V t ) обозначим множество всех дуг e, начала которых лежат в V s, а концы — в V t, т.е. Аналогично,
Слайд 76: Потоки в сетях
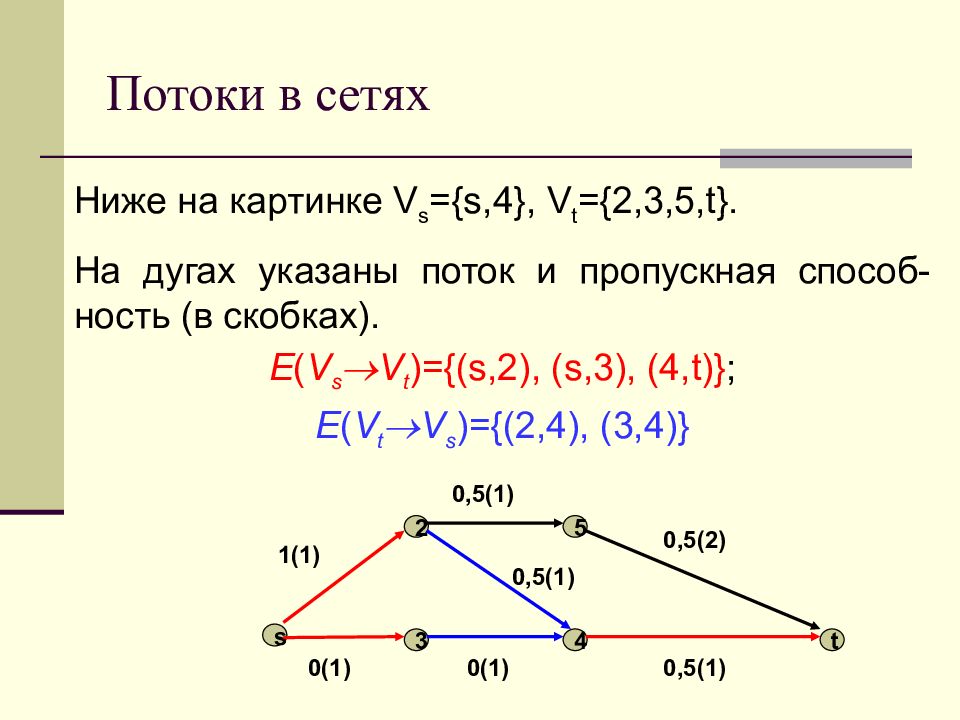
Ниже на картинке V s ={s,4}, V t = {2,3,5,t}. На дугах указаны поток и пропускная способ-ность (в скобках). E ( V s V t )={(s,2), (s,3), (4,t)} ; E ( V t V s )={(2,4), (3,4)} s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1)
Слайд 78: Потоки в сетях
Ниже на рисунке для V s ={s,4}, V t = {2,3,5,t} s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1)
Слайд 79: Потоки в сетях
Справедливы следующие утверждения. Лемма 1. Для любого потока f и любого разреза ( V s, V t ) справедливо равенство s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1) На рисунке
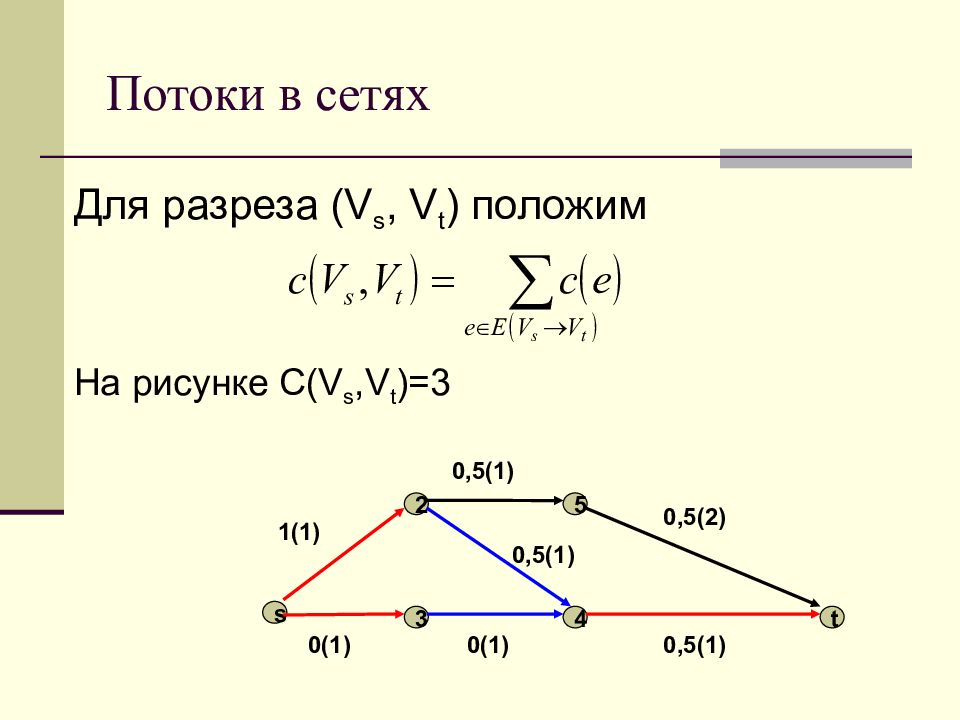
Слайд 80: Потоки в сетях
Для разреза ( V s, V t ) положим s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1) На рисунке C(V s,V t )=3
Слайд 81: Потоки в сетях
Справедливы следующие утверждения. Следствие. Для любого потока f и любого разреза ( V s, V t ) справедливо неравенство s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1) На рисунке
Слайд 82: Потоки в сетях
Разрез ( V s V t ) называется минимальным, если для любого разреза ( V s *,V t * ) справедливо
Слайд 83: Потоки в сетях
Лемма 2. Если для некоторого потока f * и некоторого разреза ( V s *, V t * ) выполняется равенство то поток f* максима-лен, а разрез ( V s *, V t *) минимален. s 4 3 2 5 t 1(1) 1 (1) 1 (2) 0(1) 1 (1) 1 (1) 1 (1) На рисунке
Слайд 84: Потоки в сетях
Цепью из v в w в сети G называется чередую - щаяся последовательность попарно различ - ных вершин и дуг в которой дуга e r либо выходит из v r и входит в v r+1, либо, наоборот, выходит из v r+1 и входит в v r. В первом случае дуга называется прямой, во втором – обратной.
Слайд 85: Потоки в сетях
Пусть P – цепь из v в w. Для каждой дуги цепи P положим Пусть Цепь P из v в w называется f - дополняющей, если h ( P )>0.
Слайд 86: Потоки в сетях
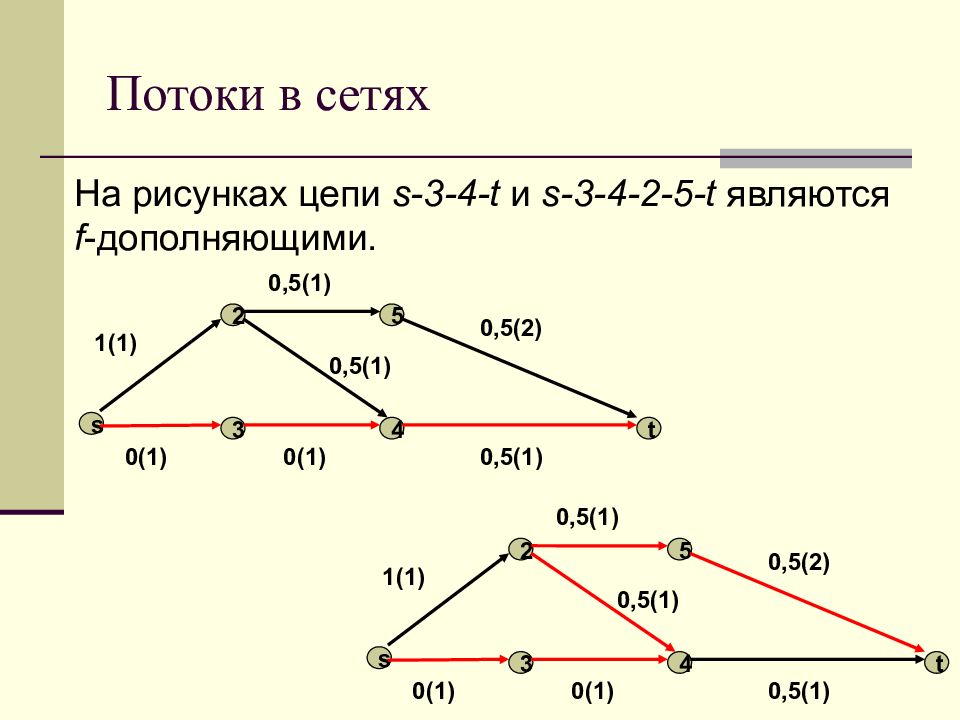
На рисунках цепи s-3-4-t и s-3-4-2-5-t являются f - дополняющими. s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1) s 4 3 2 5 t 1(1) 0,5(1) 0,5(2) 0,5(1) 0(1) 0(1) 0,5(1)
Слайд 87: Потоки в сетях
Лемма 3. Пусть f – поток в сети G и P – f - до-полняющая ( s, t ) - цепь. Тогда в сети G сущест-вует поток f * такой, что Поток f * строится так:
Слайд 88: Потоки в сетях
Теорема (Форда-Фалкерсона, 1956). Для потока f в сети G следующие условия эквивалентны: поток f максимален; не существует f -дополняющей цепи из s в t ; существует разрез ( V s, V t ), для которого
Слайд 90
Дэлберт Рей Фалкерсон (14 августа 1924 10 января 1976) Американский математик. В 1956 году вместе с Лестером Рейнолдсом Фордом младшим разработал алгоритм построения максимального потока в сетях. Получил степень PhD в универси-тете Висконсин-Мэдисон в 1951. В 1979 году была учреждена премия Фалкерсона, вручаемая каждые три года за выдающиеся достижения в области дискретной математики совместно матема-тико-программистским обществом и Американским математическим обществом.
Слайд 91: Потоки в сетях Алгоритм Форда-Фалкерсона
Работа алгоритма Форда-Фалкерсона базируется на идее, подсказанной леммой 3. положить f ( e ) = 0 для всех дуг e E ; для текущего потока f искать f - дополня-ющую ( s,t ) - цепь; если такая цепь P построена, то для всех прямых дуг цепи P положить а для всех обратных и вернуться на шаг 2; иначе СТОП.
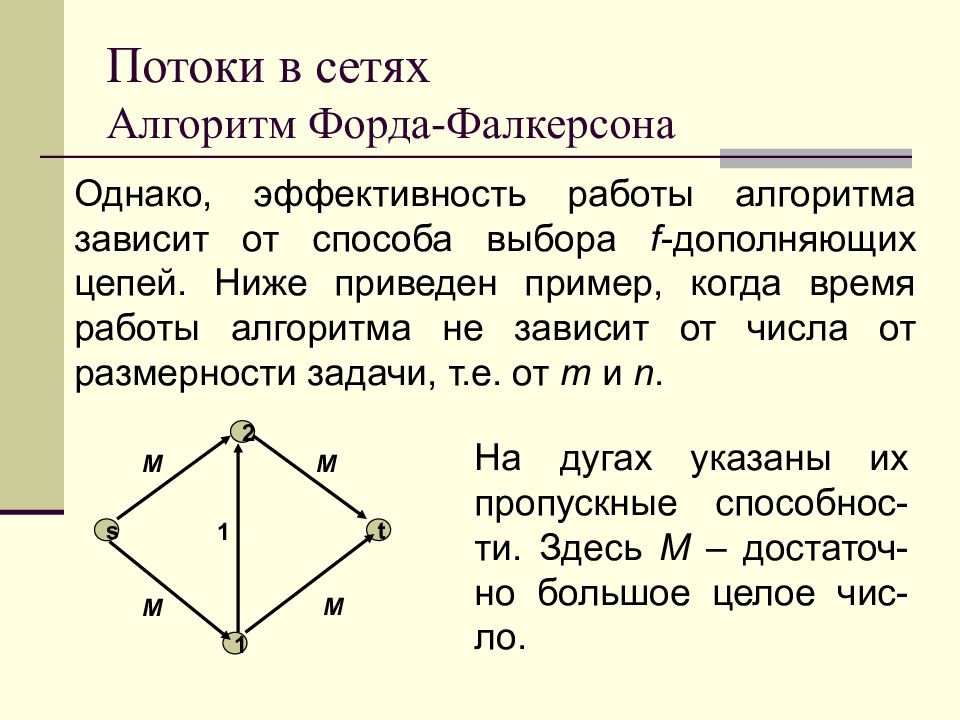
Слайд 92: Потоки в сетях Алгоритм Форда-Фалкерсона
Однако, эффективность работы алгоритма зависит от способа выбора f - дополняющих цепей. Ниже приведен пример, когда время работы алгоритма не зависит от числа от размерности задачи, т.е. от m и n. s 1 2 t M M M M 1 На дугах указаны их пропускные способнос-ти. Здесь M – достаточ-но большое целое чис-ло.
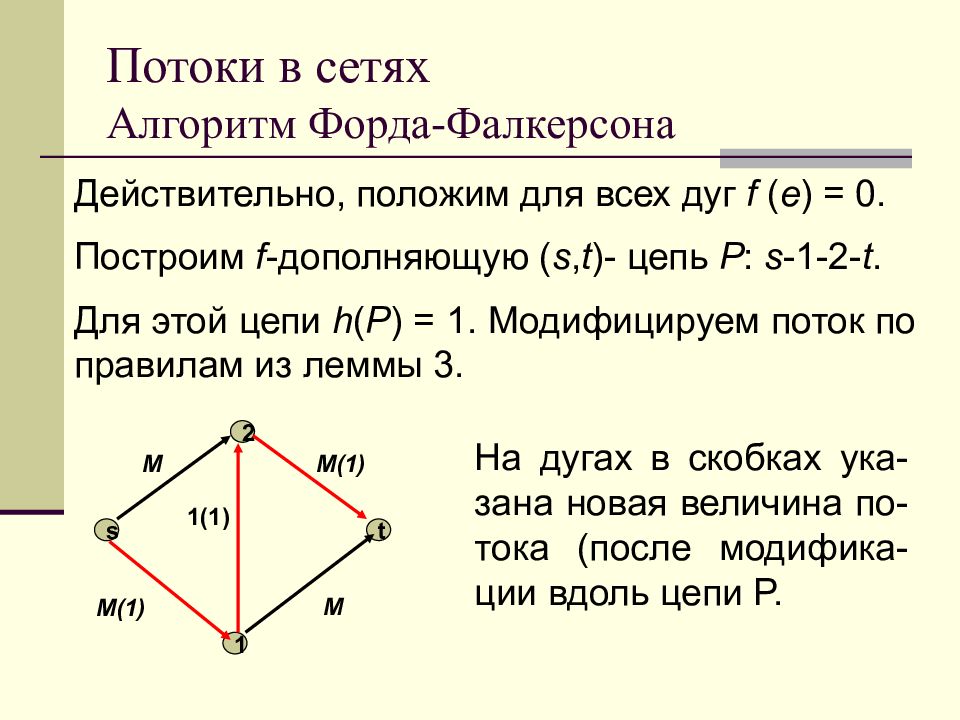
Слайд 93: Потоки в сетях Алгоритм Форда-Фалкерсона
Действительно, положим для всех дуг f ( e ) = 0. Построим f - дополняющую ( s, t )- цепь P : s -1-2- t. Для этой цепи h ( P ) = 1. Модифицируем поток по правилам из леммы 3. s 1 2 t M M(1) M(1) M 1(1) На дугах в скобках ука - зана новая величина по - тока (после модифика - ции вдоль цепи P.
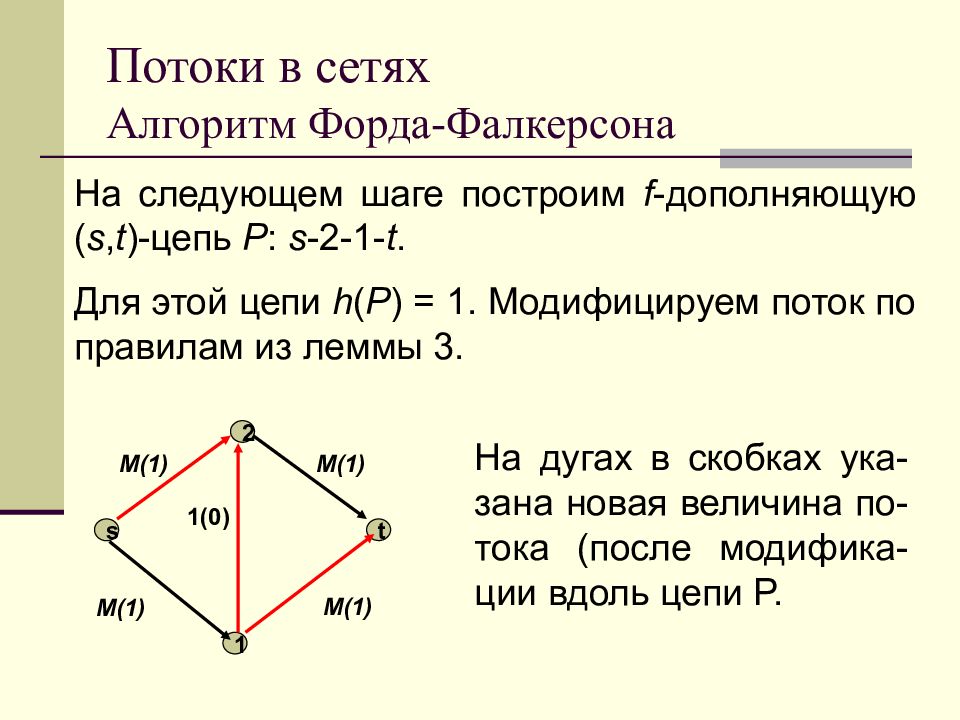
Слайд 94: Потоки в сетях Алгоритм Форда-Фалкерсона
На следующем шаге построим f - дополняющую ( s, t )- цепь P : s -2-1- t. Для этой цепи h ( P ) = 1. Модифицируем поток по правилам из леммы 3. s 1 2 t M (1) M(1) M(1) M (1) 1(0) На дугах в скобках ука - зана новая величина по - тока (после модифика - ции вдоль цепи P.
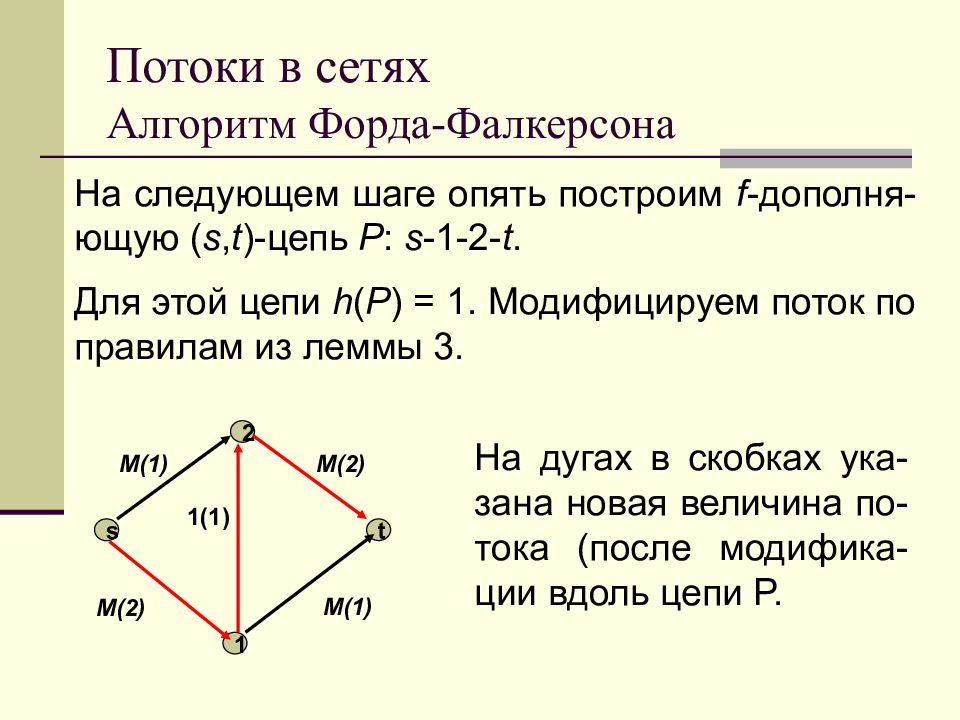
Слайд 95: Потоки в сетях Алгоритм Форда-Фалкерсона
На следующем шаге опять построим f - дополня-ющую ( s, t )- цепь P : s - 1 - 2 - t. Для этой цепи h ( P ) = 1. Модифицируем поток по правилам из леммы 3. s 1 2 t M (1) M( 2 ) M( 2 ) M (1) 1( 1 ) На дугах в скобках ука - зана новая величина по - тока (после модифика - ции вдоль цепи P.
Слайд 96: Потоки в сетях Алгоритм Форда-Фалкерсона
Далее на каждом нечетном шаге выбираем цепь s - 1 - 2 - t, а на каждом четном шаге – цепь s - 2 - 1 - t. Каждый раз поток увеличивается на единицу. Максимальный поток в этой сети равен 2 M. Следовательно понадобится 2 M итераций, т.е. их число не зависит от размерности задачи.
Слайд 97: Потоки в сетях Алгоритм Форда-Фалкерсона
На очередном шаге алгоритма следует отыскивать кратчайшие по числу дуг f - дополняющие ( s, t )- цепи! Они могут быть найдены, например, с помощью поиска в ширину.
Слайд 98: Потоки в сетях Алгоритм Форда-Фалкерсона
Отметим важное свойство: если пропускные способности всех дуг являются целочисленными, то как макси-мальный поток, так и все промежуточные значения потока также являются цело-численными.
Слайд 99: Потоки в сетях Алгоритм Форда-Фалкерсона
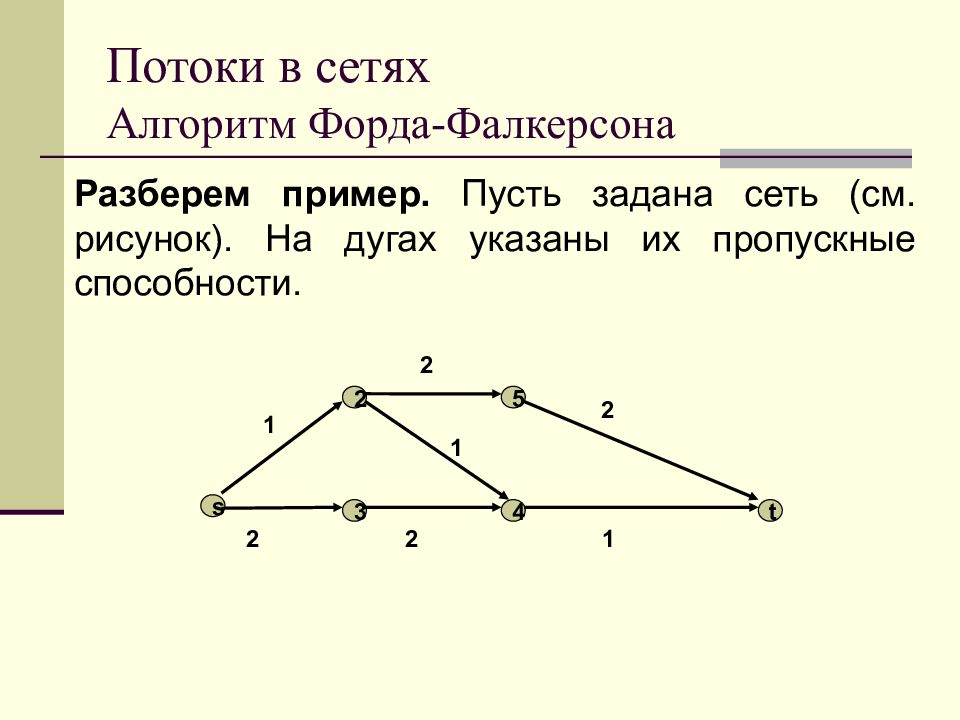
Разберем пример. Пусть задана сеть (см. рисунок). На дугах указаны их пропускные способности. s 4 3 2 5 t 1 2 2 1 2 2 1
Слайд 100: Потоки в сетях Алгоритм Форда-Фалкерсона
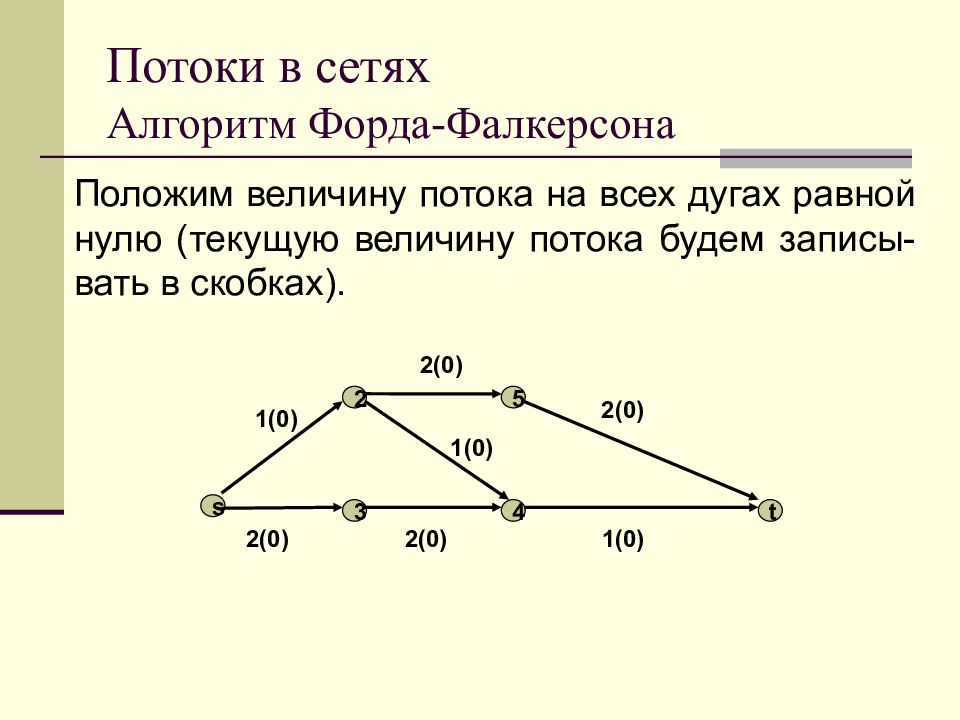
Положим величину потока на всех дугах равной нулю (текущую величину потока будем записы-вать в скобках). s 4 3 2 5 t 1(0) 2(0) 2 (0) 1 (0) 2(0) 2(0) 1 (0)
Слайд 101: Потоки в сетях Алгоритм Форда-Фалкерсона
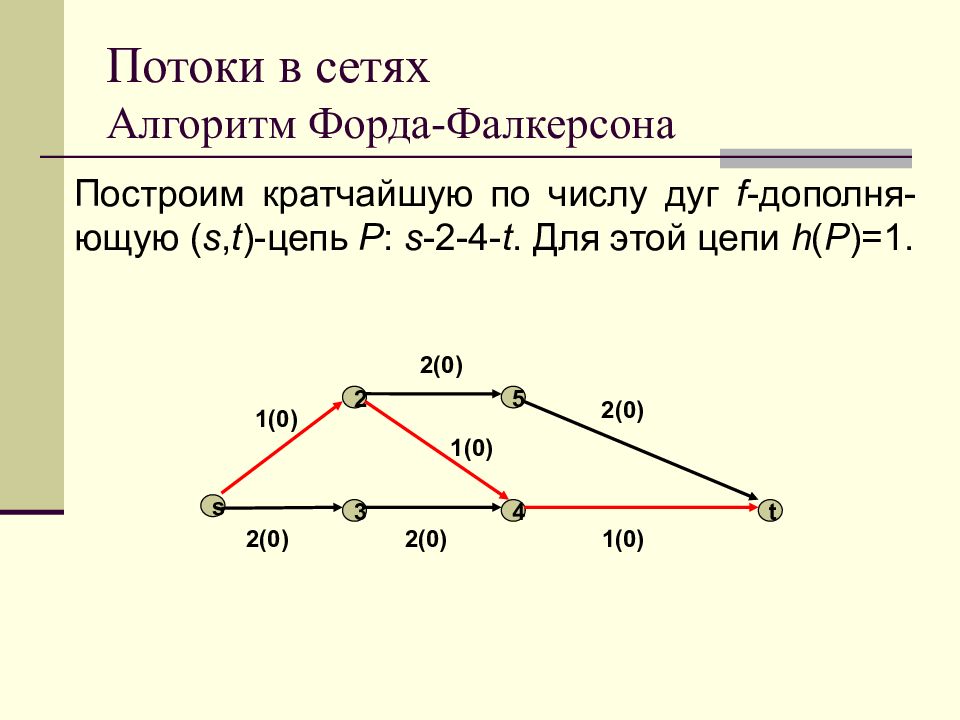
Построим кратчайшую по числу дуг f - дополня-ющую ( s, t )- цепь P : s -2-4- t. Для этой цепи h ( P )=1. s 4 3 2 5 t 1(0) 2(0) 2 (0) 1 (0) 2(0) 2(0) 1 (0)
Слайд 102: Потоки в сетях Алгоритм Форда-Фалкерсона
Скорректируем поток вдоль найденной цепи. s 4 3 2 5 t 1(1) 2( 0 ) 2 ( 0 ) 1 ( 1 ) 2(0) 2(0) 1 ( 1 )
Слайд 103: Потоки в сетях Алгоритм Форда-Фалкерсона
Построим кратчайшую по числу дуг f - дополня-ющую ( s, t )- цепь P : s - 3 - 4 -2-5- t. Для этой цепи h ( P )=1. Дуга 4-2 ― обратная. s 4 3 2 5 t 1(1) 2( 0 ) 2 ( 0 ) 1 ( 1 ) 2(0) 2(0) 1 ( 1 )
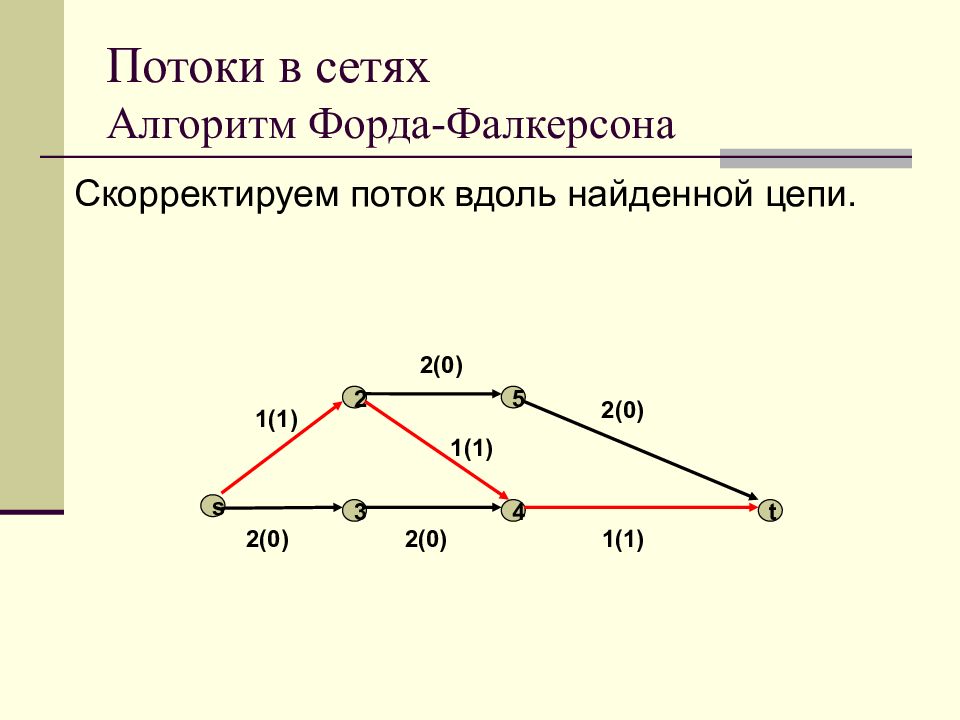
Слайд 104: Потоки в сетях Алгоритм Форда-Фалкерсона
Скорректируем поток вдоль найденной цепи. s 4 3 2 5 t 1(1) 2(1) 2 (1) 1 (0) 2(1) 2(1) 1 (1)
Слайд 105: Потоки в сетях Алгоритм Форда-Фалкерсона
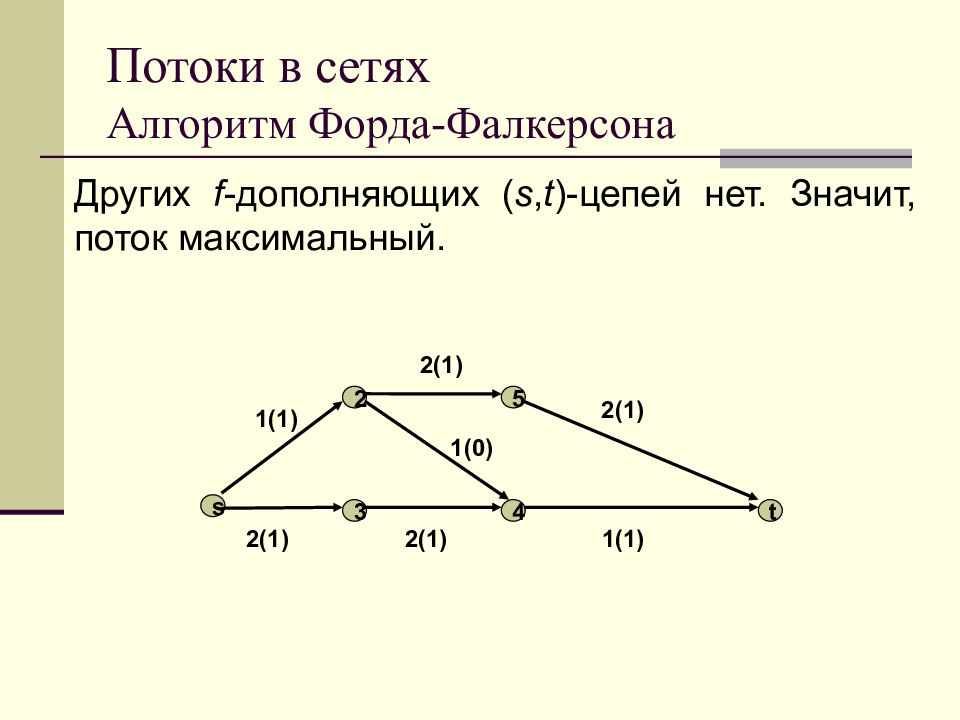
Других f - дополняющих ( s, t )- цепей нет. Значит, поток максимальный. s 4 3 2 5 t 1(1) 2(1) 2 (1) 1 (0) 2(1) 2(1) 1 (1)
Слайд 106: Потоки в сетях Алгоритм Форда-Фалкерсона
Минимальный разрез строится так: V s состоит из концов всех f- дополняющих ( s, v )- цепей. В данном случае V s ={ s,3,4}, V t ={2,5, t }. Из Vs в Vt ведут дуги ( s, 2 ) и ( 4, t ). Значит, с ( V s, V t ) =1+1=2. s 4 3 2 5 t 1(1) 2(1) 2 (1) 1 (0) 2(1) 2(1) 1 (1)
Слайд 107: Потоки в сетях Алгоритм Форда-Фалкерсона
Задача. В стране имеется сеть железных дорог, соединяющих M городов. Для двух заданных горо-дов A и B требуется определить максимально воз-можное число поездов, которое можно пустить из A в B. Из-за конструктивных особенностей поездов и железных дорог никакие два поезда не могут про-езжать через один и от же город, исключая, конеч-но, города A и B. Железные дороги заданы парой городов, которые они соединяют. Проезд по ним возможен в любом направлении. Предложите ма-тематическую модель этой задачи как задачи опти-мизации на графе и опишите неформально алго-ритм ее решения.
Слайд 109: Паросочетания в двудольных графах
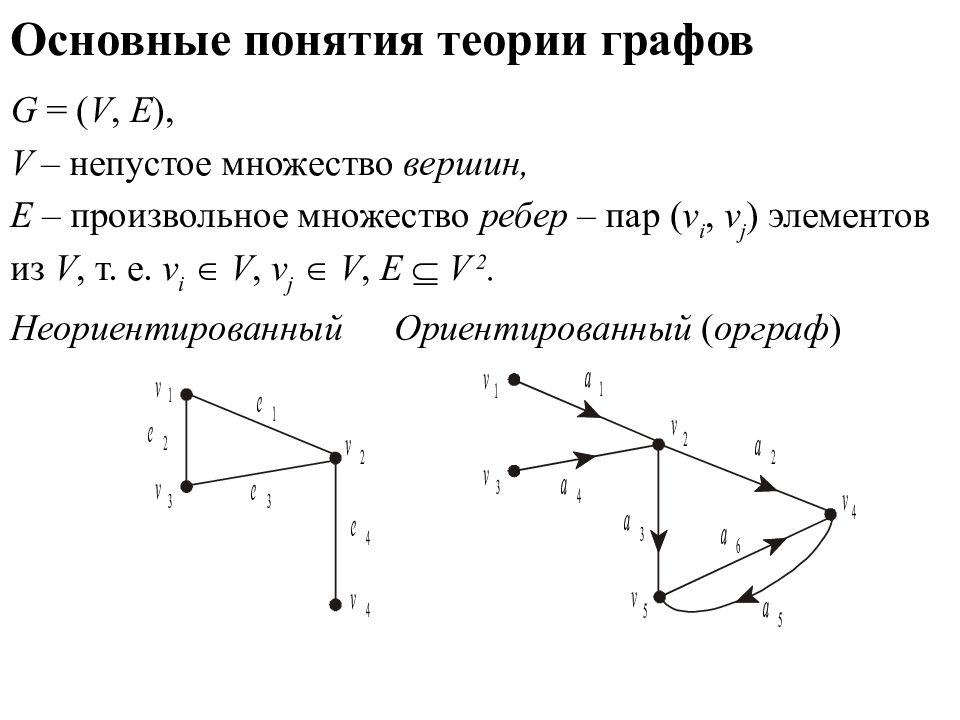
Паросочетанием в графе называется произволь-ное множество его ребер такое, что каждая вер-шина графа инцидентна не более, чем одному реб-ру из этого множества. Граф G =( V, E ) называется двудольным, если мно - жество его вершин V можно разбить на непере - секающиеся множества X и Y такие, что каждое ребро e E имеет вид e = xy, где x X, y Y.
Слайд 110: Паросочетания в двудольных графах
Пусть M – паросочетание в графе G =( X, Y, E ). Говорят, что M сочетает x с y и y с x, если xy M. Вершины, не принадлежащие ни одному ребру из паросочетания, называют свободными относи-тельно M или просто свободными, а все прочие – насыщенными в M или просто насыщенными. Удобно также все ребра, входящие в паросо-четание M называть M- темными или просто темными, а все прочие – M -светлыми или просто светлыми.
Слайд 111: Паросочетания в двудольных графах
Паросочетание, содержащее наибольшее число ребер, называется наибольшим. Паросочетание, не содержащееся ни в каком дру-гом паросочетании, называется максимальным (по включению). Любое наибольшее паросочетание является ма-ксимальным. Обратное неверно. Паросочетание, насыщающее все вершины дву-дольного графа, называется полным.
Слайд 112: Паросочетания в двудольных графах
Пусть M – паросочетание в графе G. M - чередующейся цепью называется такая последо - вательность вершин и ребер вида x 0, x 0 y 1, y 1, y 1 x 2, x 2, …, x k, x k y k+1, y k+1, где k > 0, что все вершины этой цепи различны, x 0 и y k + 1 – свободные, а все остальные вершины насыщенные в паросочетании M, причем каждое второе ребро принадлежит M ( т.е. ребра вида y i x i+1, i=1,…,k-1 входят в M ), а остальные ребра в M не входят.
Слайд 113: Паросочетания в двудольных графах
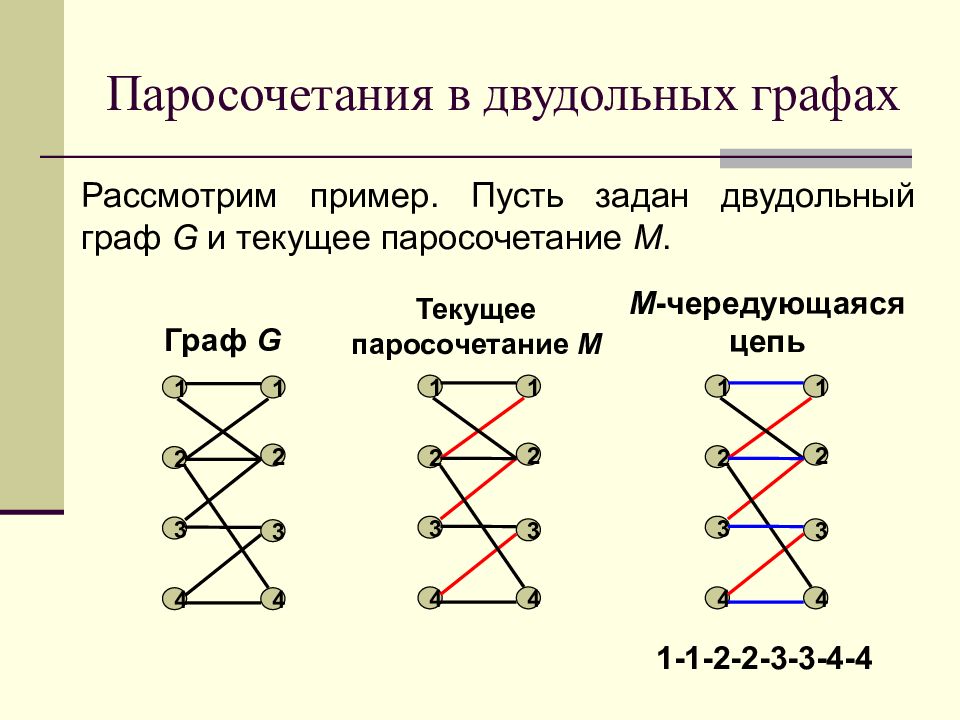
Рассмотрим пример. Пусть задан двудольный граф G и текущее паросочетание M. 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 Граф G Текущее паросочетание M 1 2 3 4 1 2 3 4 1-1-2-2-3-3-4-4 M - чередующаяся цепь
Слайд 114: Паросочетания в двудольных графах
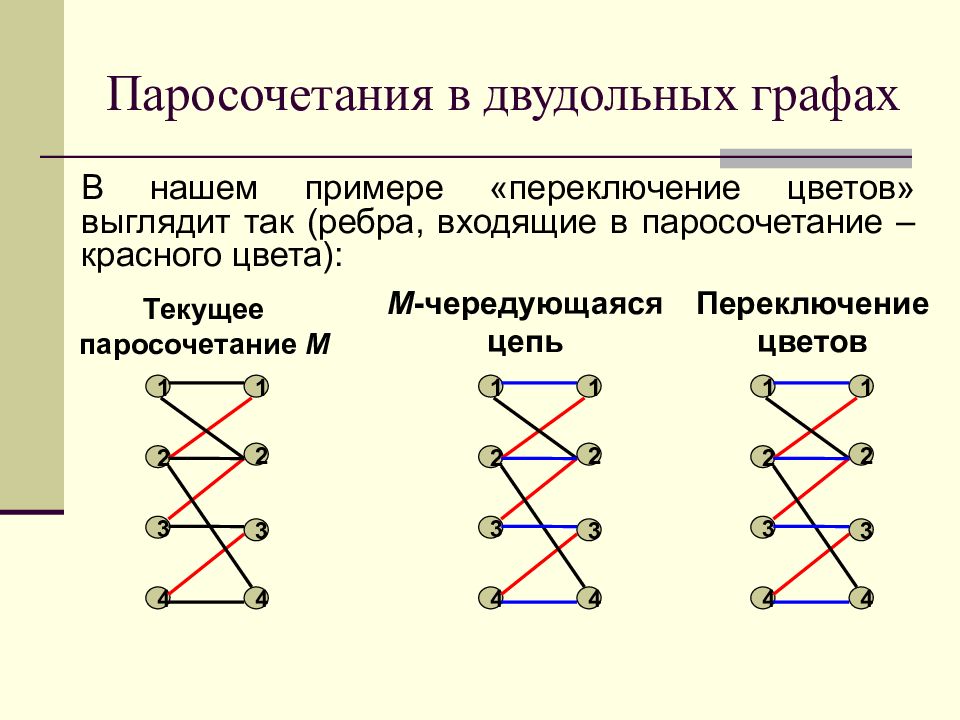
Пусть M – текущее паросочетание и P – построенная M - чередующаяся цепь. Операция M P определяется следующим образом : все ребра из P, входившие в M из паросочетания исключаются, а все ребра из P, не входившие в M, в паросочетание добавляются. Другими словами, В цепи P происходит « переключение цветов ». Светлые ребра становятся темными и, наоборот, темные – светлыми.
Слайд 115: Паросочетания в двудольных графах
В нашем примере «переключение цветов» выглядит так (ребра, входящие в паросочетание – красного цвета): 1 2 3 4 1 2 3 4 Текущее паросочетание M 1 2 3 4 1 2 3 4 M - чередующаяся цепь 1 2 3 4 1 2 3 4 Переключение цветов
Слайд 117
Харольд Уиллиам Кун (род. в 1925 году) Американский математик. Специалист в области теории игр. Профессор Принстонского университета. Автор Венгер - ского алгоритма (1955 год) и соавтор теоремы Куна-Так - кера о необходимых условиях оптимальности в задаче мате-матического программирова-ния. В 1980 году удостоен приза Джона фон Неймана.
Слайд 118
Неформально алгоритм может быть описан следующим образом. Паросочетания в двудольных графах. Алгоритм Куна пустое паросочетание объявить текущим паросо-четанием M ; если все вершины из X насыщены в M, то СТОП ( M – полное паросочетание); иначе выбрать произвольную свободную вершину x X и искать M -чередующуюся цепь, начинающуюся в x ; если такая цепь P найдена, то положить M := M P и вернуться на шаг 2; иначе СТОП (полного паросочетания в заданном графе не существует).
Слайд 119: Паросочетания в двудольных графах. Алгоритм Куна
Рассмотрим работу алгоритма Куна на нашем примере. Пусть дан двудольный граф G 1 2 3 4 1 2 3 4 Граф G Объявляем пустое паросочетание текущим: M =
Слайд 120: Паросочетания в двудольных графах. Алгоритм Куна
Будем просматривать вершины из доли X в ес-тественном порядке. Находим первую M - чере-дующуюся цепь P : 1 – 1. 1 2 3 4 1 2 3 4 Граф G Выполним операцию M P (переключаем цвета). Новое текущее паросоче - тание M = {1-1}.
Слайд 121: Паросочетания в двудольных графах. Алгоритм Куна
Находим M - чередующуюся цепь P : 2 – 1 – 1 – 2. 1 2 3 4 1 2 3 4 Граф G Выполним операцию M P (переключаем цвета). Новое текущее паросоче - тание M = {2-1,1-2}.
Слайд 122: Паросочетания в двудольных графах. Алгоритм Куна
Находим M - чередующуюся цепь P : 3 – 2 – 1 – 1 – 2 – 4. 1 2 3 4 1 2 3 4 Граф G Выполним операцию M P (переключаем цвета). Новое текущее паросоче - тание M = {1-1, 2-4, 3-2}.
Слайд 123: Паросочетания в двудольных графах. Алгоритм Куна
Находим M - чередующуюся цепь P : 4 – 4 – 2 – 1 – 1 – 2 – 3 – 3. 1 2 3 4 1 2 3 4 Граф G Выполним операцию M P (переключаем цвета). Новое текущее паросоче - тание M = {1-2, 2-1, 3-3, 4-4}.
Слайд 124: Паросочетания в двудольных графах. Алгоритм Куна
Ненасыщенных вершин не осталось. Алгоритм построил полное паросочетание. 1 2 3 4 1 2 3 4 Граф G
Слайд 126: Задача о назначениях
Пусть G =( X, Y, E, c ) – взвешенный двудольный граф, | X |=| Y |= n. Весом паросочетания M называется сумма весов входящих в него ребер. Задача о назначениях: в заданном взвешен-ном двудольном графе найти полное паросо-четание минимального веса (оптимальное паросочетание).
Слайд 127: Задача о назначениях
Будем предполагать, что G – полный двудоль-ный граф (т.е. любая пара вершин x X, y Y соединена ребром ). Это не ограничивает общности, т.к. любую пару несмежных вершин можжно соединить ребром очень большого веса (например, большего суммы весов всех оставшихся ребер).
Слайд 129: Задача о назначениях Венгерский алгоритм
Идея работы венгерского алгоритма основана на нескольких утверждениях. Лемма 1. Если веса всех ребер графа, инци-дентных какой-либо вершине, увеличить (уменьшить) на одно и то же число, то всякое оптимальное паросочетание в графе с новыми весами является оптимальным и в графе с исходными весами.
Слайд 130: Задача о назначениях Венгерский алгоритм
Эта лемма позволяет рассматривать только графы с неотрицательными весами. Более того, каждой вершине этого графа оказывается инцидентна хотя бы одна вершина нулевого веса.
Слайд 131: Задача о назначениях Венгерский алгоритм
Пусть X ’ X, Y ’ Y и d . Будем говорить, что к графу G =( X, Y, E, c ) применена операция ( X ’, d, Y ’ ), если сначала из веса каждого ребра, инцидентного вершине из X ’, вычтено число d, а затем к весу каждого ребра, инцидентного вершине из Y ’, прибавлено число d.
Слайд 132: Задача о назначениях Венгерский алгоритм
Справедлива следующая Лемма 2. Пусть G =( X, Y, E, c ) – двудольный взвешенный граф с неотрицательными весами, X ’ X, Y ’ Y и d =min{ c ( x, y )| x X ’, y Y \ Y ’ }. Если к графу G применить операцию ( X ’, d, Y ’ ), то веса всех ребер G останутся неотрицатель-ными; веса ребер вида xy, где x X ’, y Y ’ или x X \ X ’, y Y \ Y ’ не изменятся.
Слайд 133: Задача о назначениях Венгерский алгоритм
Схема применения операции из леммы 2. Y ’ Y \ Y ’ X ’ I II – d X\X ’ IV + d III
Слайд 134: Задача о назначениях Венгерский алгоритм
Следующая лемма очевидна. Лемма 3. Если веса всех ребер графа неотри-цательны, и некоторое полное паросочетание состоит из ребер нулевого веса, то оно явля-ется оптимальным.
Слайд 135: Задача о назначениях Венгерский алгоритм
В 1955 году Харольд Уиллиам Кун предложил алгоритм решения задачи о назначениях, кото-рый принято называть Венгерским.
Слайд 136: Задача о назначениях Венгерский алгоритм
Преобразовать веса ребер так, чтобы веса всех ребер стали неотрицательными и каждой вершине стало инцидентно хотя бы одно ребро нулевого веса; пустое паросочетание объявить текущим паросочетанием M ; если в графе все вершины насыщены относительно текущего паросочетания, то СТОП (текущее паросочетание оптимально); иначе выбрать свободную вершину x X и искать M - чередующуюся цепь, начинающуюся в x, из ребер нулевого веса; если такая цепь построена, то положить M := M P и вернуться на шаг 3;
Слайд 137: Задача о назначениях Венгерский алгоритм
иначе для множества вершин X ’ X, Y ’ Y, помеченных в ходе поиска (это вершины венгерского дерева), положить величину d равной d =min{ c ( x, y )| x X ’, y Y \ Y ’ } и применить к графу операцию ( X ’, d, Y ’ ); из тех вершин x X ’, которым стало инцидентно хотя бы одно ребро нулевого веса, возобновить поиск M- чередующейся цепи по ребрам нулевого веса; если такая цепь P будет найдена, то положить M := M P и вернуться на шаг 3; иначе вернуться на шаг 6 (множества X ’ и Y ’ при этом увеличатся).
Слайд 138: Задача о назначениях Венгерский алгоритм
Рассмотрим пример работы венгерского алгоритма. Пусть двудольный граф задан своей матрицей весов: На месте w ij этой матрицы стоит вес ребра, соединяющего верши - ны x i и y j.
Слайд 139: Задача о назначениях Венгерский алгоритм
Преобразуем веса так, чтобы каждой вершине оказа-лось инцидентно ребро нулевого веса. Для этого из каждой строки матрицы вычтем минимальный эле-мент строки. Видим, что вершине y 2 не инци-дентна ни одно ребро нулевого веса. Вычитаем из всех элемен-тов второго столбца его мини-мальный элемент.
Слайд 140: Задача о назначениях Венгерский алгоритм
Мы добились того, что каждой вершине инцидентно как минимум одно ребро нулевого веса, и веса всех ребер неотрицательны.
Слайд 141: Задача о назначениях Венгерский алгоритм
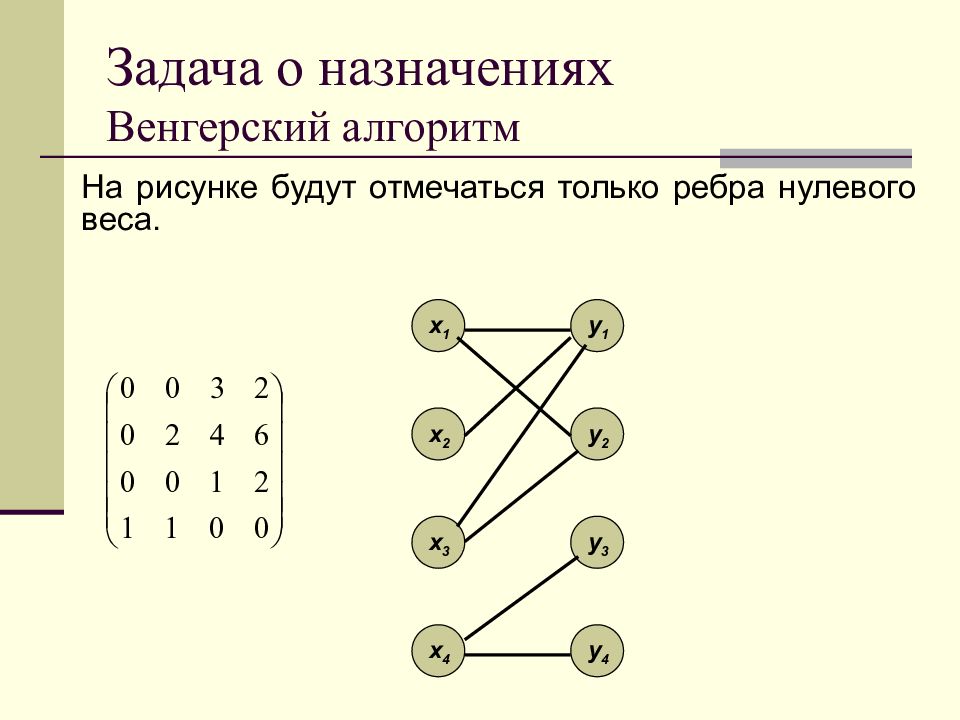
На рисунке будут отмечаться только ребра нулевого веса. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 142: Задача о назначениях Венгерский алгоритм
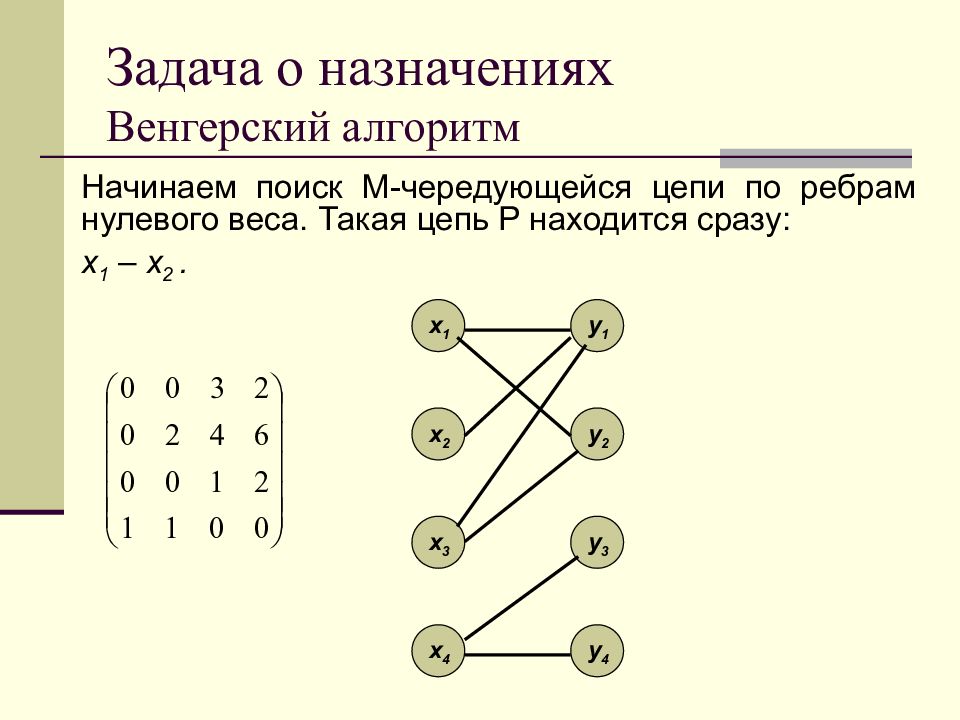
Начинаем поиск M- чередующейся цепи по ребрам нулевого веса. Такая цепь P находится сразу: x 1 – x 2. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 143: Задача о назначениях Венгерский алгоритм
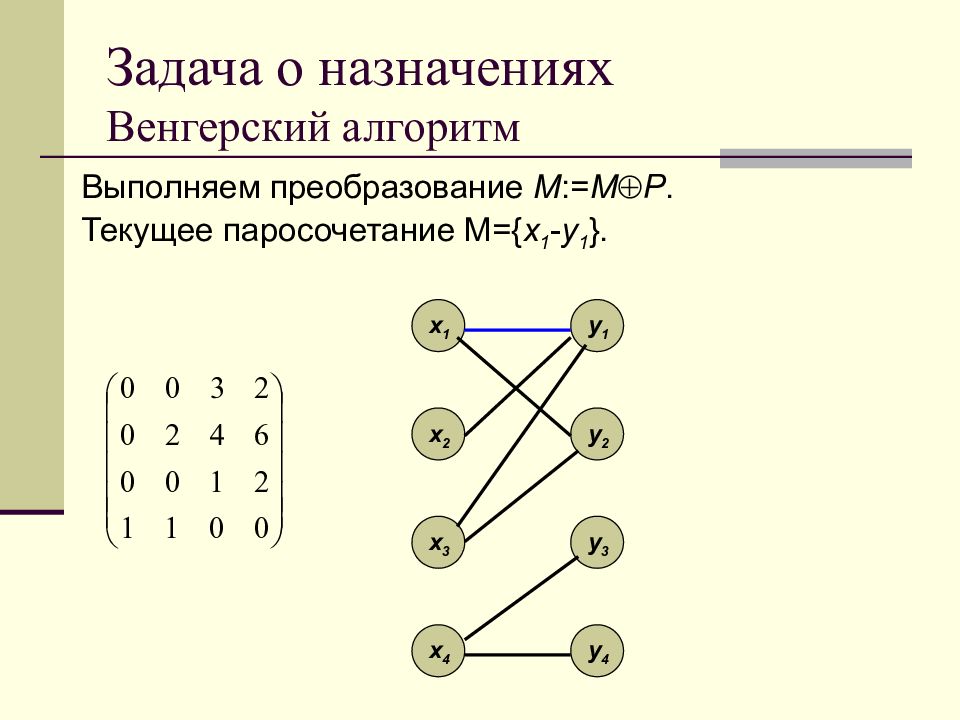
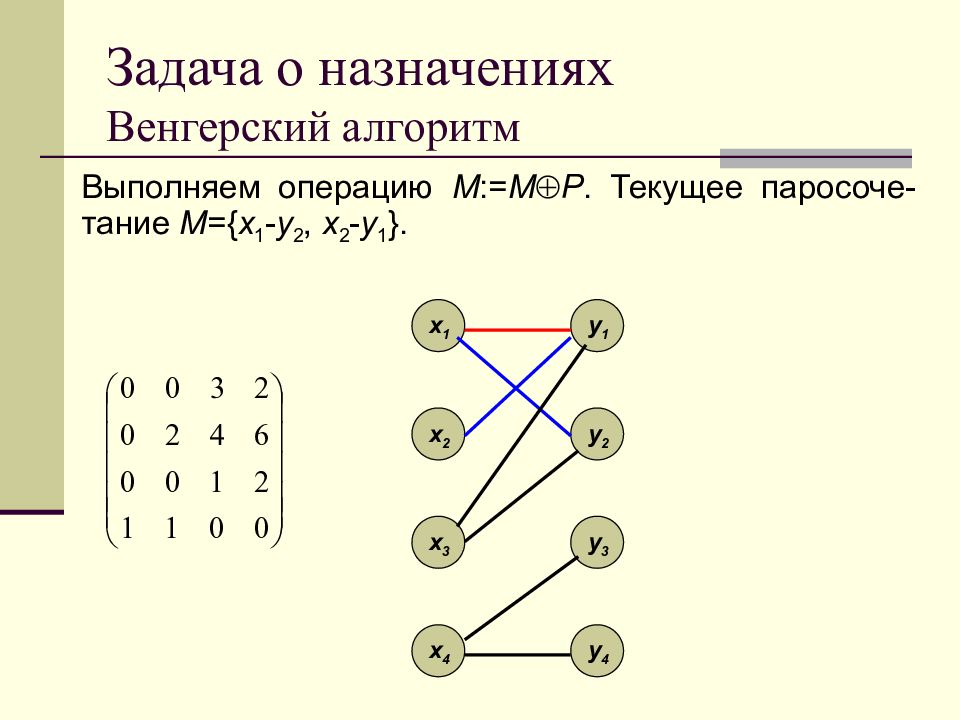
Выполняем преобразование M := M P. Текущее паросочетание M={ x 1 - y 1 }. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 144: Задача о назначениях Венгерский алгоритм
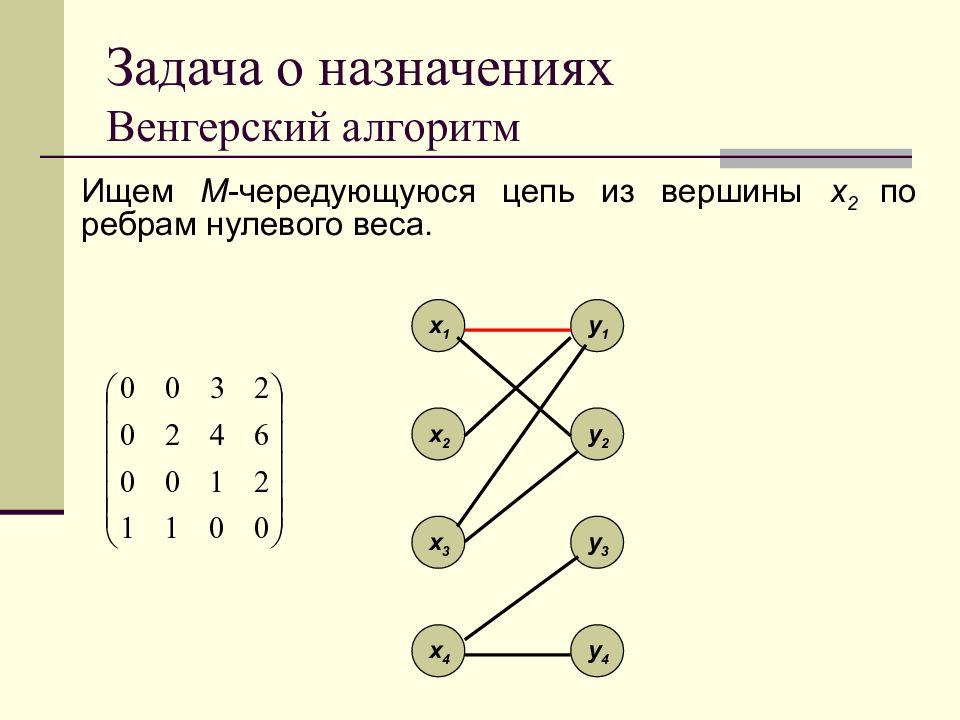
Ищем M -чередующуюся цепь из вершины x 2 по ребрам нулевого веса. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 145: Задача о назначениях Венгерский алгоритм
Выполняем операцию M := M P. Текущее паросоче - тание M ={ x 1 - y 2, x 2 - y 1 }. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 146: Задача о назначениях Венгерский алгоритм
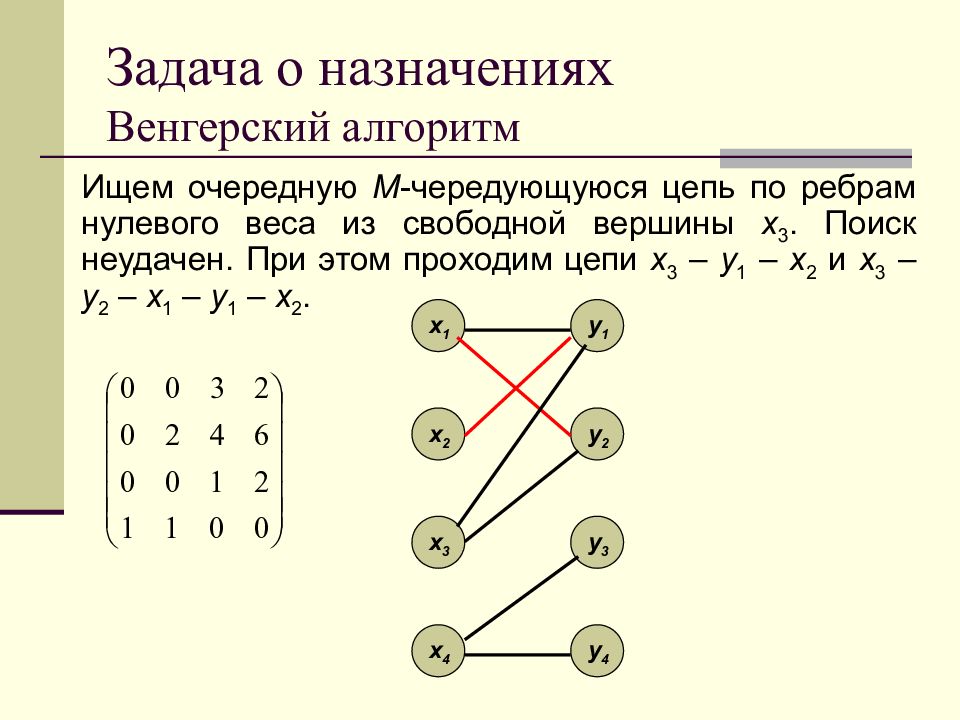
Ищем очередную M - чередующуюся цепь по ребрам нулевого веса из свободной вершины x 3. Поиск неудачен. При этом проходим цепи x 3 – y 1 – x 2 и x 3 – y 2 – x 1 – y 1 – x 2. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 147: Задача о назначениях Венгерский алгоритм
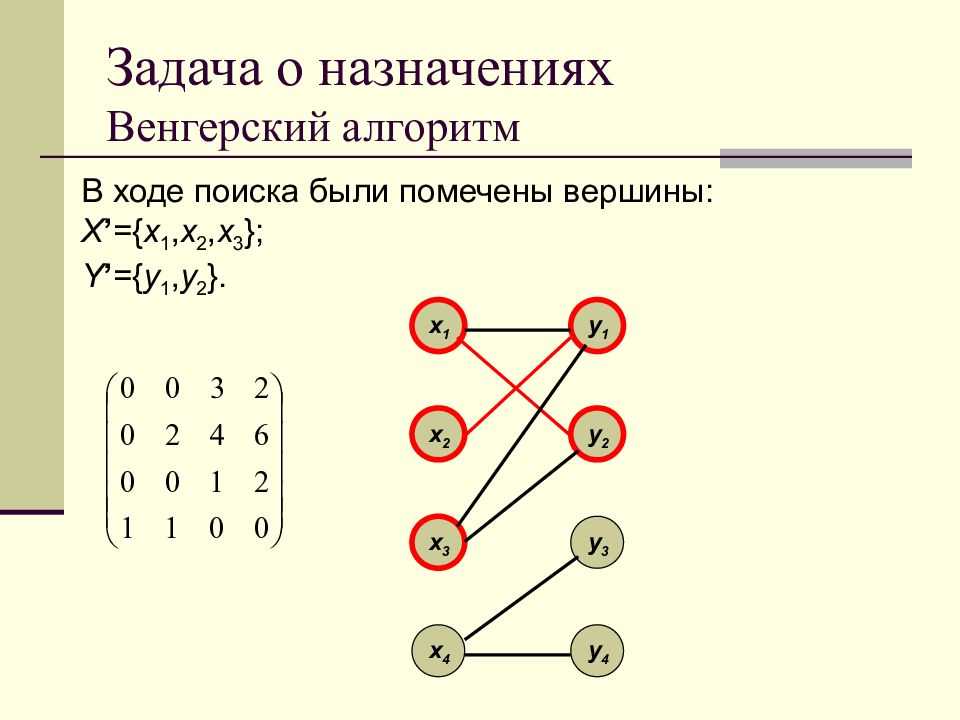
x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 В ходе поиска были помечены вершины: X ’ ={ x 1, x 2, x 3 }; Y ’ ={ y 1, y 2 }.
Слайд 148: Задача о назначениях Венгерский алгоритм
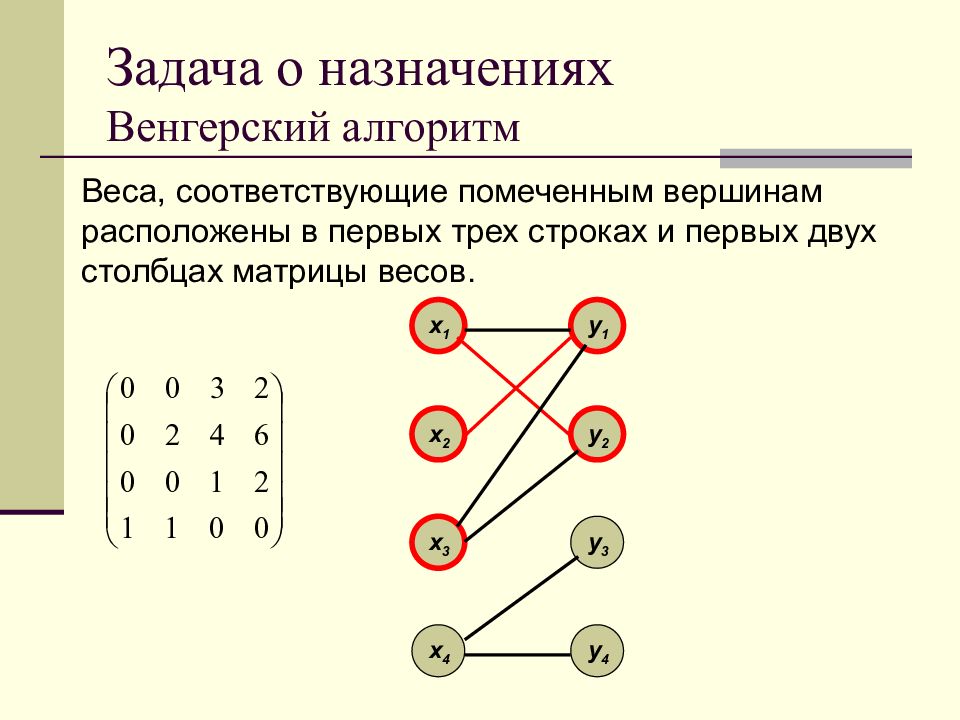
x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 Веса, соответствующие помеченным вершинам расположены в первых трех строках и первых двух столбцах матрицы весов.
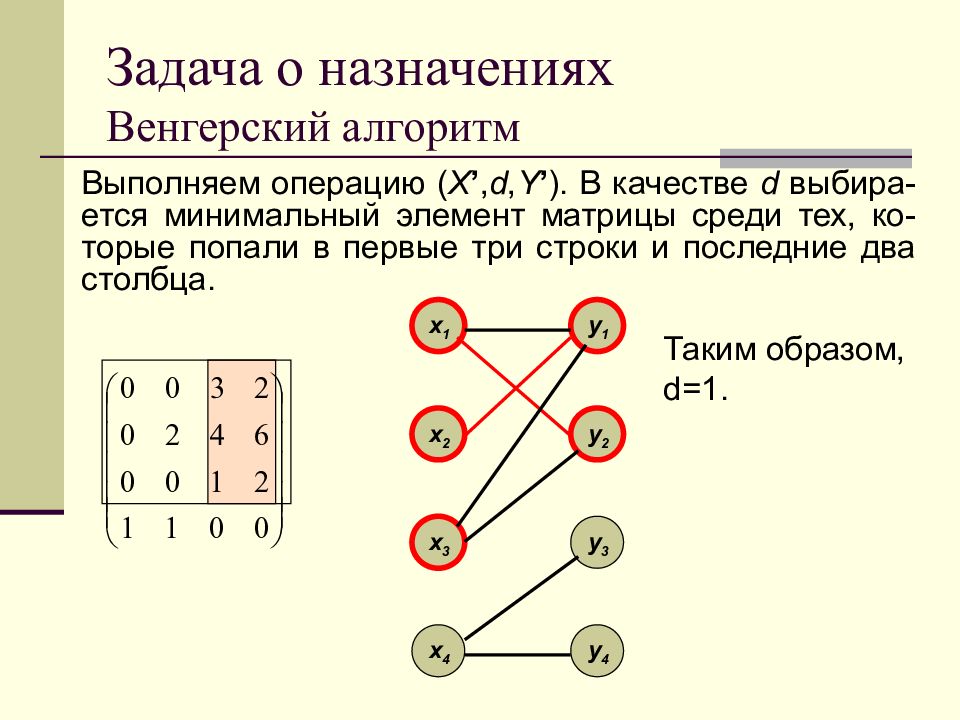
Слайд 149: Задача о назначениях Венгерский алгоритм
x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 Выполняем операцию ( X ’, d, Y ’ ). В качестве d выбира-ется минимальный элемент матрицы среди тех, ко-торые попали в первые три строки и последние два столбца. Таким образом, d = 1.
Слайд 150: Задача о назначениях Венгерский алгоритм
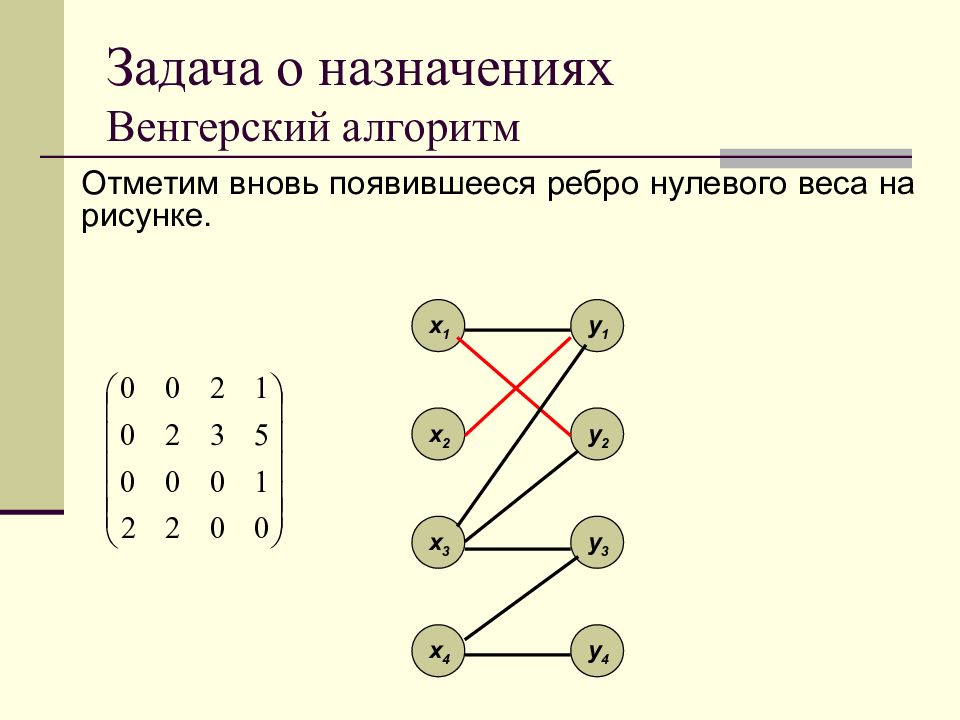
В результате применения операции ( X ’, d, Y ’ ) матрица весов преобразуется к следующему виду: Множество ребер нулевого ве - са пополнилось. Появилось ребро x3-y3.
Слайд 151: Задача о назначениях Венгерский алгоритм
Отметим вновь появившееся ребро нулевого веса на рисунке. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 152: Задача о назначениях Венгерский алгоритм
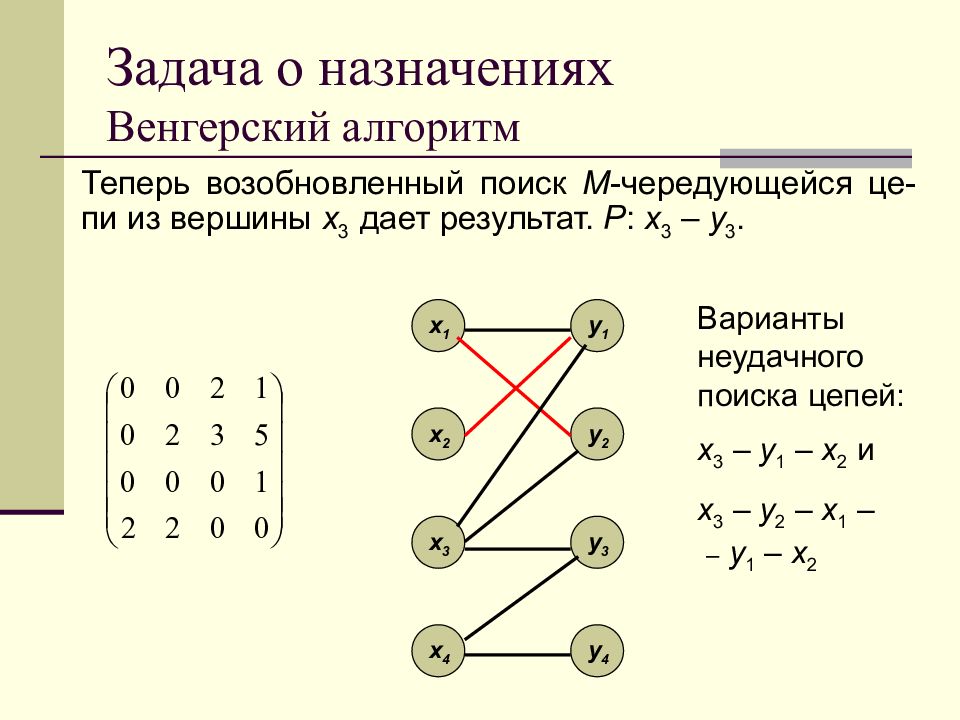
Теперь возобновленный поиск M -чередующейся це-пи из вершины x 3 дает результат. P : x 3 – y 3. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 Варианты неудачного поиска цепей: x 3 – y 1 – x 2 и x 3 – y 2 – x 1 – – y 1 – x 2
Слайд 153: Задача о назначениях Венгерский алгоритм
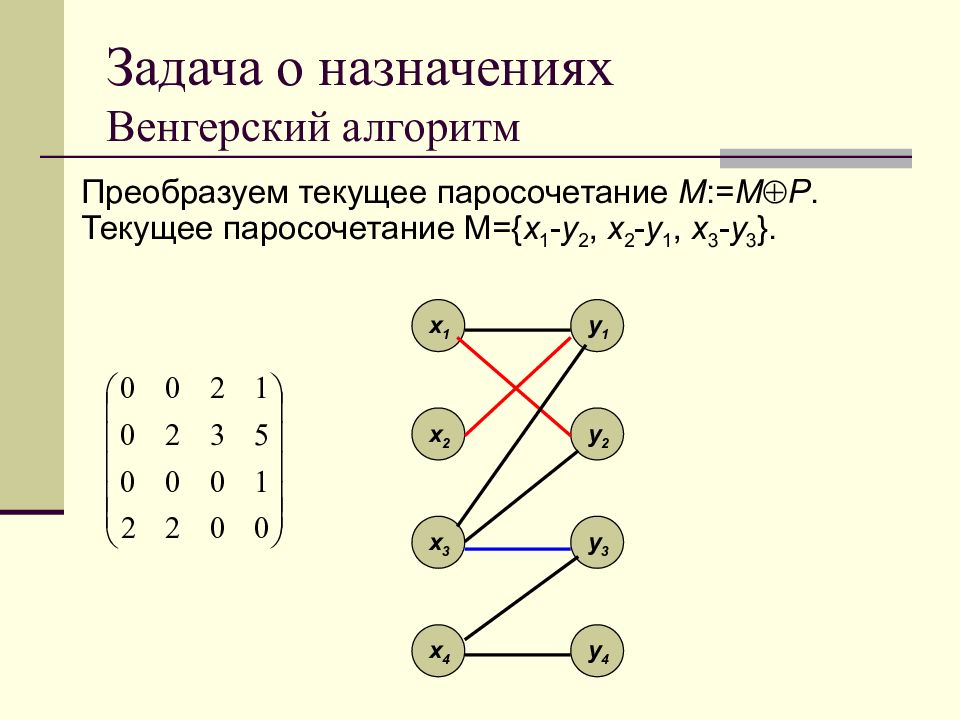
Преобразуем текущее паросочетание M := M P. Текущее паросочетание M={ x 1 - y 2, x 2 - y 1, x 3 - y 3 }. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4
Слайд 154: Задача о назначениях Венгерский алгоритм
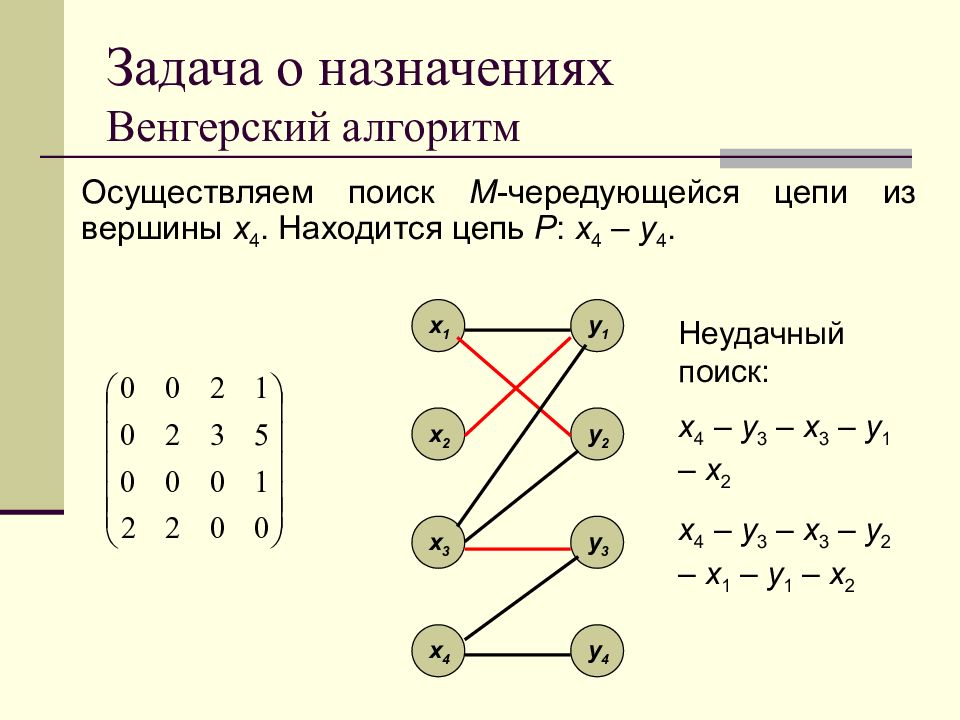
Осуществляем поиск M -чередующейся цепи из вершины x 4. Находится цепь P : x 4 – y 4. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 Неудачный поиск: x 4 – y 3 – x 3 – y 1 – x 2 x 4 – y 3 – x 3 – y 2 – x 1 – y 1 – x 2
Слайд 155: Задача о назначениях Венгерский алгоритм
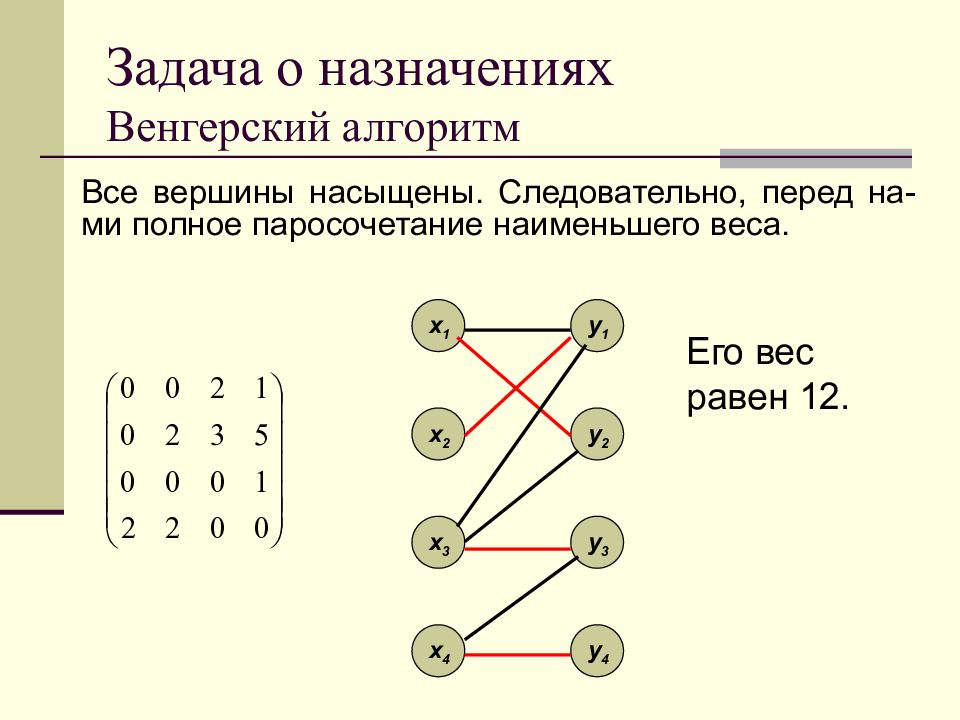
Все вершины насыщены. Следовательно, перед на-ми полное паросочетание наименьшего веса. x 1 x 2 x 3 x 4 y 1 y 2 y 3 y 4 Его вес равен 12.
Последний слайд презентации: Комбинаторные алгоритмы: Задача о назначениях Венгерский алгоритм
Рассмотрим задачу. Требуется выполнить n видов работ, для выполнения которых имеется n видов станков. Каждая работа должна быть выполнена на каком-нибудь одном станке, и на каждом станке можно выполнить не более одной работы. Для каждой пары ( i -ая работа – j -ый станок) известно время выполнения c ij.Требуется распределить работы по станкам так, чтобы все работы были выполнены, и суммарное время выполнения работ было минимальным. Предложите математическую модель этой задачи как задачи оптимизации на графе и опишите в неформализованном виде алгоритм ее решения.