Слайд 3
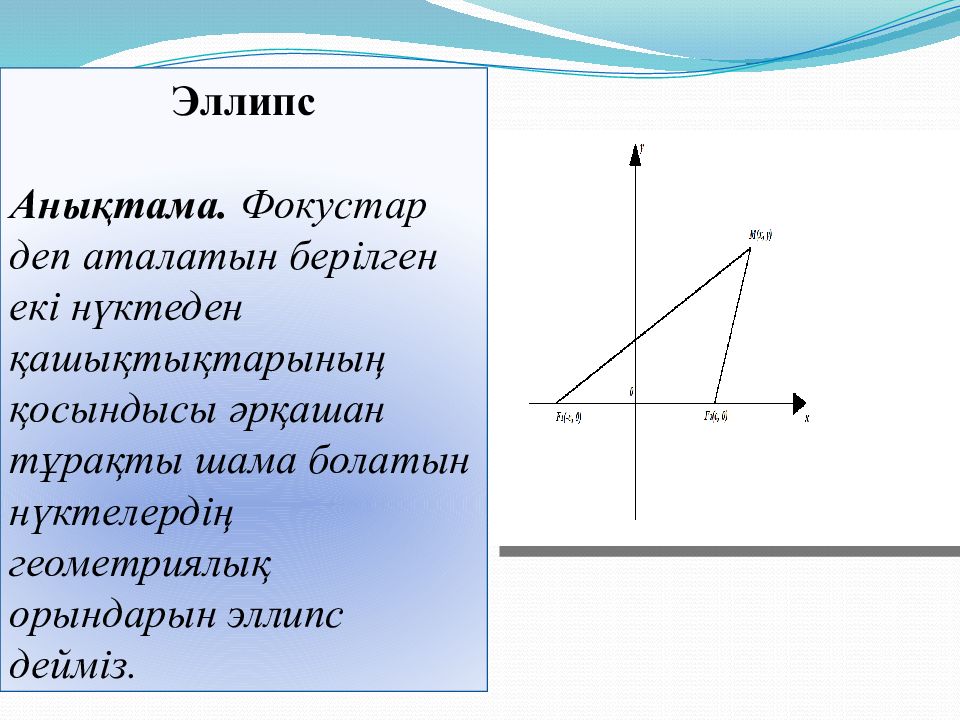
Эллипс Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын эллипс дейміз.
Слайд 4
егер а>с болса, а 2 — с 2 >0 болады, сондықтан (2) деп белгілейік, олай болса b 2 х 2 + а 2 у 9 = а 2 b 2, осыдан (3) мұндағы х пен у — эллипстің бойындағы кез келген нүктелердің координаталары, а — зллипстің үлкен жарты осі, b — оның кіші жарты осі. Бұл теңдеу эллипстің жабайы теңдеуі деп аталады. Эллипстің жабайы теңдеуі.
Слайд 5
Радиус-вектор және эксцентриситет. 1-параграфта эллипстің жабайы теңдеуін шығарумен байланысты мынадай теңдік шық ты:. Бүл теңдіктің сол жағы +у 2 = сонда. Анықтама бойынша R 2 -нің мәнін осы анықтамаға қойып, -ді табайық: = 2а- Сонымен, мынадай екі теңдік шықты: -, (4) мұндағы және эллипстің радиус-векторлары деп аталады. (4) теңдік — осы эллипстің радиус-векторларының формуласы. қатынасы эллипстің эксцентриситеті деп аталады. Эксцентриситет е әрпімен белгіленеді.
Слайд 6
Шеңбер — эллипстің дербес жағдайы. Эллипстің жабайы теңдеуі. Егер а = b болса, онда шеңбердің теңдеуі шығады: х 2 +у 2 = а 2. Бұл — центрі координаталардың бас нүктесінде жатқан, радиусы а-ға тең шеңбердің теңдеуі. Алдыңғы параграфта а 2 = b 2 + с 2 теңдігі үш кесіндінің байланысын көрсетеді дегенбіз. Бұл жағдайда а= b болғаңдықтан, с=0. Ендеше шеңбердің эксцентритеті нольге тең, яғни 38-сызбада эллипстің жабайы теңдеуі мен шеңбердің х 2 +у 2 = а 2 теңдеуіне сәйкес келетін график керсетілген.
Слайд 7
Эллипске жүргізілген жанама мен нормальдың теңдеулері. Эллипстің теңдеуі және оның бойында жатқан бір нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін қорытып шығарайық. теңдеуі, нүктесі берілген. Енді (Ж) жанамасы мен (N) нормалының теңдеулерін іздейік (40-сызба). нүктесінен қиюшы (Қ) түзуін жүргізейік. Берілген нүктесі қозғалмайтын, М 2 нүктесі қозғалатын нүктелер болсын. М 2 нүктесі берілген нүктесіне ұмтылғанда, қиюшы (Қ) түзуі жанамаға ұмтылады, яғни М 2 нүктесінің координаталары нүктесінің координаталарына тең болғанда =, = яғни қиюшы түзу жанама болады. Қиюшы түзудің (екі нүктеден өтетін түзудің) теңдеуін жазайық:
Слайд 8
Осы теңдіктің оң жағындағы қосынды эллипстің жабайы формуласы бойынша бірге тең. Сонда іздеген жанаманың жабайы теңдеуі шығады: 4. Нормальдың теңдеуін екінші түрге келтірейік. Ол үшін (8) теңдеуді түрлендірейік : 1-параграфтағы (2) формула бойынша: а 2 — b 2 = с 2, сонда =
Слайд 9
Эллипстің түйіндес диаметрлері. Эллипстің центрінен өтетін түзулерді эллипстің диаметрлері дейміз. Эллипстің екі нүктесінен өтетін түзуді эллипстің хордасы, ал центрден өтетін хорданы оның диаметрі дейміз. Сонымен, эллипске көптеген диаметрлер мен хордалар жүргізуге болады. Эллипстің осындай диаметрлерінің ішіндегі түйіндес екі диаметрін қарастырайық. Аны қ тама. Бір диаметрге параллель жүргізілген хордаларды екінші диаметр қ ақ бөлсе, онда осы екі диаметрді ( А 2 және В 1 В 2, 42- сызба ) түйіндес диаметрлер дейміз.
Слайд 10
Ордината осіне параллель түзулердің ішіндегі бір түзудің эллипстің кіші осшен қашықтығы әрқашан да d = катынасына тең тұрақты шама болса, онда мұндай түзуді эллипстің директрисасы деп атайды. Бұл d = жағдаиында =е қатынасы х-ке тәуелді емес. Сондықтан ол эллипстің эксцентриситетіне тең. Бұл — эллипстің оң жағындағы директриса, ал оның сол жағындағы директрисаның таңбасы теріс болады, яғни d =-. Эллипстің директрисалары.
Слайд 11
Сонымен, эллипстің әрбір нүктесінен фокусқа дейінгі қашықтықтың сол нүктеден директрисаға дейінгі қашықтыққа қатынасы әрқашан да тұрақты шама, ол эксцентриситетке тең: =е (14 ) Директрисаның ордината осінен қашықтығының формуласы d = ± (15) Эллипстің эксцентриситеті е =. Осыны (15) формулаға.қойсақ: (15 ´ ) Эллипстің үлкен осі (2а), оның екі фокусының арасындағы қашықтықтан (2с) артық, яғни 2а>2с, а>с. Сондықтан >а.
Слайд 12
Эллипс пен шеңбердің параметрлік теңдеулері F ( x, y ) (18 ) Енді эллипстің жабайы теңдеуін алайық : Эллипстің бойыннан кез келген М(х, у) нүктесін алып, оны координаталардың бас нүктесімен қосып, осы М нүктесінен абсцисса осіне М D перпендикулярын түсіріп, эллипске іштей және сырттай екі шеңбер жүргізейік. OM 1 D тік бұрышты үшбұрышыннан: OM 2 B тік бұрышты үшбұрышынан: у= эллипстің параметрлік теңдеулері мынадай болады: Егер а болса, онда эллипс шеңберге айналады. Шеңбердің параметрлік теңдеулері мынадай болады: (20) теңдеудегі а мен эллипстің жарты осьтері, t – өзгеріліп отыратын бұрыш. Ал (21) теңдеудегі a-шеңбердің радиусы, t параметрі- абсцисса осі мен радиустың арасындағы бұрыш.
Слайд 13
Гипербола Гиперболаның жабайы теңдеуі. Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырымы өрқашанда турақты шама болатын нүктелердің геометриялық орындарын гипербола дейміз. Анықтама бойынша (47-сызба): 2а = М-Ғ 2 М, (1) Ғ 2 = 2С, ОҒ 2 = С болсын. Екі нүктенің ара қашықтығынның формуласы бойынша . Осы мен -нің мәндерін анықтамаға қойып, алгебралық түрлендіру арқылы гиперболаның жабайы теңдеуін табайық: М = Ғ 2 М =.
Слайд 14
Гиперболаның жабайы теңдеуі х 2 — а 2 у 2 = а 2, осыдан Б ұ л теңдеу гиперболаның жабайы теңдеуі деп аталады. Мұндағы х, у — гиперболаның бойындағы кез келген нүктенің ағымдық координаталары, а - гиперболаның нақты жарты осі, b — жорымал жарты ось. Гиперболаның түрін оның жабайы теңдеуі бойынша зерттеу. Гиперболаның жабайы. теңдеуін у арқылы өрнектейік :
Слайд 15
Р адиус-вектор және эксцентриситет. Осы тараудың 1-параграфында гиперболанық жабайы теңдеуін дәлелдегенде мынадай теңдік шықты: = а. (47) сызбадан: Ғ 2 М = R 2 = х—а. Анықтама бойынша — R 2 = 2а. Осыдан -ді табайық: = 2а + R 2 = 2а+ х — а, = а + х. Сонымен, мен -нің мәндері мынадай болады: = х+а, R 2 = х-а. (4) Бұл теңдіктер гиперболаның радиус-векторларының формулалары деп аталады. Гиперболаның екі фокусының ара қашықтығының нақты осіне қатынасы гиперболаның эксцентриситеті деп аталады. Эксцентриситет е әрпімен белгіленеді: е=. (5) с 2 — а 2 = b 2 формуласынан с>а, яғни с-тің а-дан артық екенін көреміз. Сондықтан гиперболаның эксцентриситеті әрқашанда бірден артық болады: е>1 ( - бұрыс бөлшек).
Слайд 16
Гиперболаның асимптоталары. Анықтама. Гиперболаның асимптотасы деп, координатаның бас нүктесінен өтетін және гиперболаның тармақтарымен шексіз алыстағы нүктелерде кездесетін түз у ді айтамыз. Гиперболаның теңдеуі және координаталардың бас нүктесінен өтетін түзудің Ү = х теңдеуі берілген. Гиперболаның теңдеуін у арқылы шешіп у= ± оның плюс таңбалы мәнін алайық: y =+
Слайд 17
Гиперболаға жүргізілген жанама мен нормальдың теңдеулері. гиперболаға жүргізілген нормальдың теңдеуі мынадай болады : ( 11) гиперболаға жүргізілген жанаманың қолайлы теңдеуі шығады :
Слайд 18
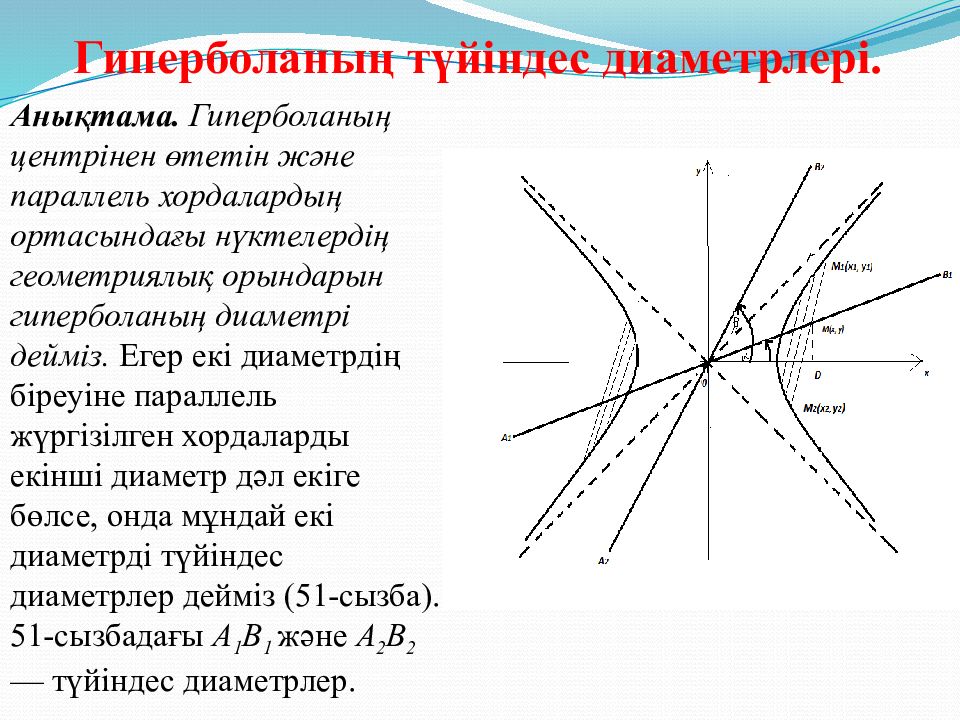
Аны қ тама. Гиперболаның центрінен өтетін және параллель хордалардың ортасындағы нүктелердің геометриялық орындарын гиперболаның диаметрі дейміз. Егер екі диаметрдің біреуіне параллель жүргізілген хордаларды екінші диаметр дәл екіге бөлсе, онда мұндай екі диаметрді түйіндес диаметрлер дейміз (51-сызба). 51-сызбадағы А 1 В 1 және А 2 В 2 — түйіндес диаметрлер. Гиперболаның түйіндес диаметрлері.
Слайд 19
Директрисалардың теңдеулері былайша жазылады : ( 16) немесе d = ( 16’) а 2 + b 2 = с 2 теңдігінен гипербола үшін с>а, < a. Сондықтан директрисалар гиперболаның екі тармағының арасында және центрдің екі жағында жатады. Гиперболаның директрисалары.
Слайд 20
Гиперболаның теңдеуі мен түзудің у = кх + l теңдеуі берілген. Осы екі теңдеуді біріктіріп шығарып, х- тің мәнін белгілі шамалар арқылы (а, b, к, l ) іздейік. Дискриминант D= болсын. х-тің шешуі осы дискриминанттың мәніне байланысты болады. Мұнда үш түрлі жағдай болады: 1) D>0; 2) D = 0; 3) D 0. Бірінші жағдайда х-тің екі түрлі мәніне y-тің екі мәні сәйкес келеді. Мұнда түзу гиперболаны екі нүктеден қияды. Екінші жағдайда лхгің бір мәніне у-тің бір мәні сәйкес келеді. Мұнда түзу гиперболаға жанама болады. Бұл жағдайдағы түзудің гиперболаға жанама болу шартын табу үшін теңдігіне р мен q - дің жоғарғы мәндерін қоямыз : Осы теңдеуді түрлендіріп, мынаны табамыз : Бұл теңдік түзудің гиперболаға жанама болу шартын көрсетеді. Енді жанасу нүктесінің координаталарын табу үшін 7- параграфтағы (12) және (13) теңдіктерге l- дің мәнін қояйық : Осыдан жанасу нүктесінің координаталары табылады : М 1 М 2 хордасы жанама болу үшін М1(х 1 у 1 ), М 2 (х 2, у 2 ) нүктелері беттесуге тиіс, яғни х 1 =х 2 = х, = = у. Гиперболаның түзумен қиылысуы
Слайд 21
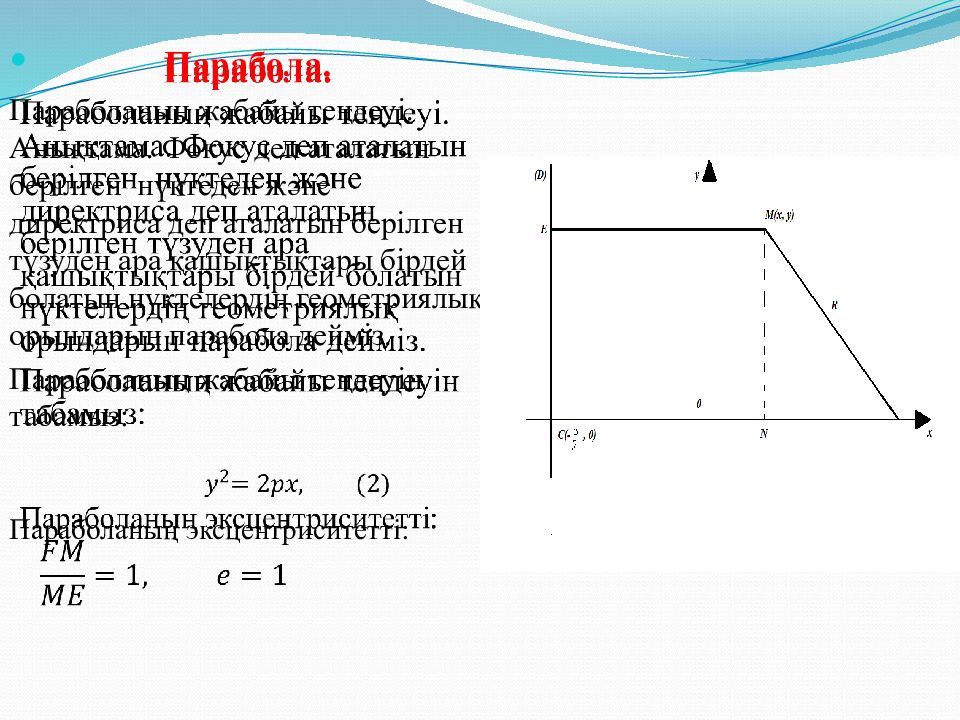
Парабола. Параболаның жабайы теңдеуі. Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын нүктелердің геометриялық орындарын парабола дейміз. Параболаның жабайы теңдеуін табамыз: Параболаның эксцентриситетті:
Слайд 22
Бұл - параболаға жүргізілген жанаманың тедеуі. Екі түзудің перпендикулярлық шарты бойынша нормальдық теңдеуі мынадай болады:
Слайд 23
Параболаның диаметрлері. Анықтама. Берілген ба- ғытқа параллель хордалардың ортасындағы нүктелердің геомет-риялық орындарын параболаның осы бағытқа түйіндес диаметрі дейміз. параболаның диаметрі мынадай болады :
Слайд 24
Параболаның түзумен қиылысуы. Параболаның у 2 = 2рх теңдеуі мен түзудің у = b х+ l теңдеуі берілген. Мұндағы дискриминанттың мәніне байланысты үш түрлі жағда й болуы мүмкін: р>0 оң таңбалы сан. Бірінші жағдайда түзу параболаны екі нүктеден қияды. Мұндағы х-т ің нақты екі мәніне у-т ің нақты екі мәні сәйкес келеді. Екінші жағдайда түзу парабодаға жанама болады, яғни түз у мен парабола бір нүктеде қиылысады. Түзудің параболаға жанама болу шарты : р — 2 kl = 0, осыдан р = 2 kl. (13) Бұл жағдайдағы жанасу нүктесінің координаталары : M. Ү шінші жагдаида түзу параболаға қиюшы да және жанама да болмайды, яғни түзу параболаның сыртынан өтеді.
Слайд 25
Қорытынды Қорыта айтқанда «Екінші ретті қисықтар» тақырыбына байланысты курстық жұмыста мен эллипс, гипербола, параболаға байланысты практикалық есептер мен мысалдар келтірдім. Практикалық есептердің арқасында теореманы кеңірек ашуға болатынына көзім жетті. Әр бір тақырыптың қажетті негізгі анықтамалар мен формулалар келтірілген және есептер шығарылып, формулаларды және теориялық тұжырымдамаларды қолдану мүмкіндіктері мен ерекшеліктері айқын көрсетілген. Тақырыптың негізгі бөлімде бұл курыстық жұмыстың тақырыбын нақты ашуға тырыстым. Бұл бөлім «екінші ретті қисықтар» тақырыбына анықтамалар, формулалар келтірілген, графиктер мен мысалдар берілген. Сондай-ақ, эллипс гипербола, парабола тақырыптарына байланысты есептерді қарастыру анықталады. Қорыта айтқанда «Екніші ретті қисықтар» тақырыбына байланысты практикалық есептердің арқасында теореманы кеңірек ашуға болатынына көзім жетті. Әр бір тақырыптың қажетті негізгі анықтамалар, теоремалар мен формулалар келтірілген және есептер шығарылып, формулаларды және теориялық тұжырымдамаларды қолдану мүмкіндіктері мен ерекшеліктері айқын көрсетілген. Қорыта айтқанда, бұл жұмыстың тақырыбын нақты әрі толық ашып, нақты дәлелдеулер келтіруге тырыстым. Аналитикалық геометрияға байланысты әр түрлі кітаптар, есептер жинағы менің курстық жұмысыма үлкен көмегін тигізді.