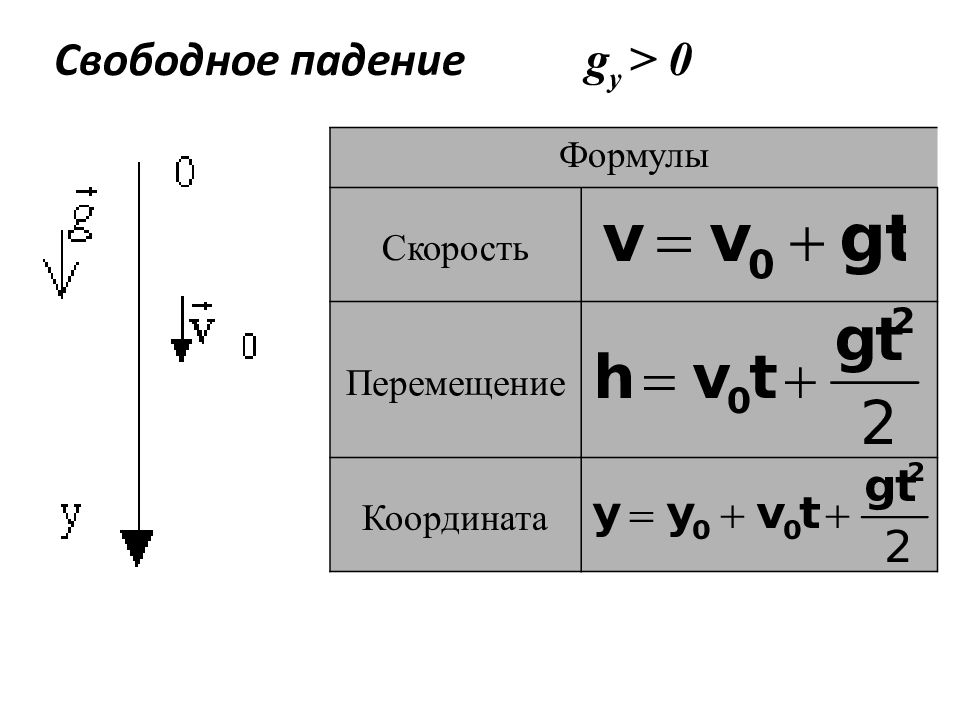
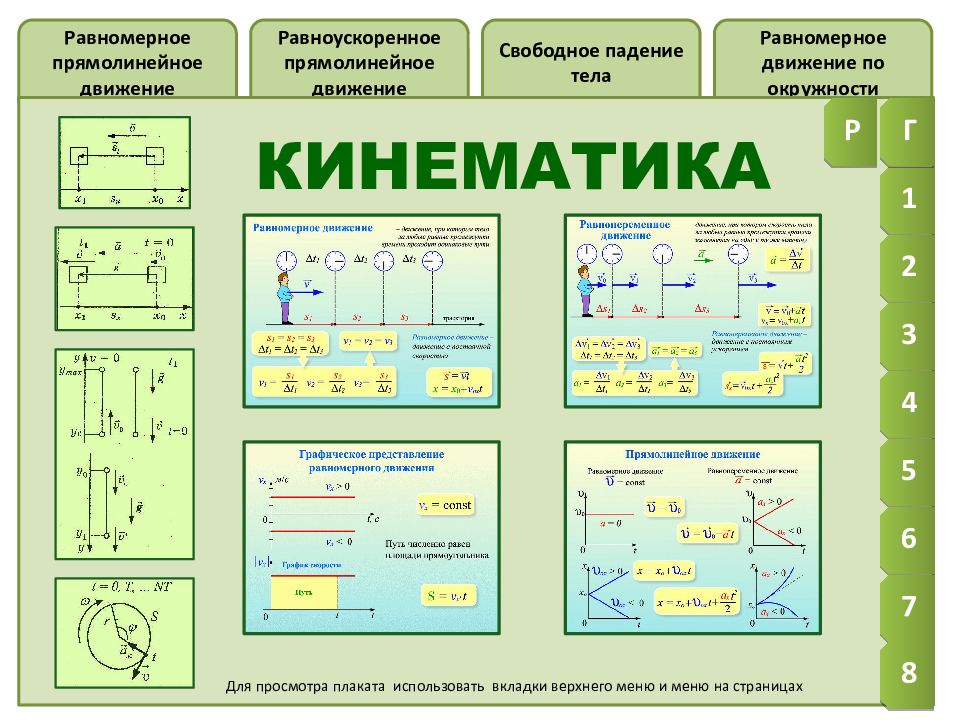
Формулы Скорость Перемещение Координата Свободное падение g y > 0
Формулы Скорость Перемещение Координата Тело брошено вертикально вверх g y < 0
Свободное падение без начальной скорости ( υ 0 = 0) При выбранной системе координат движение тела описывается уравнениями: Из последней формулы можно найти время падения тела с высоты h: Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения:
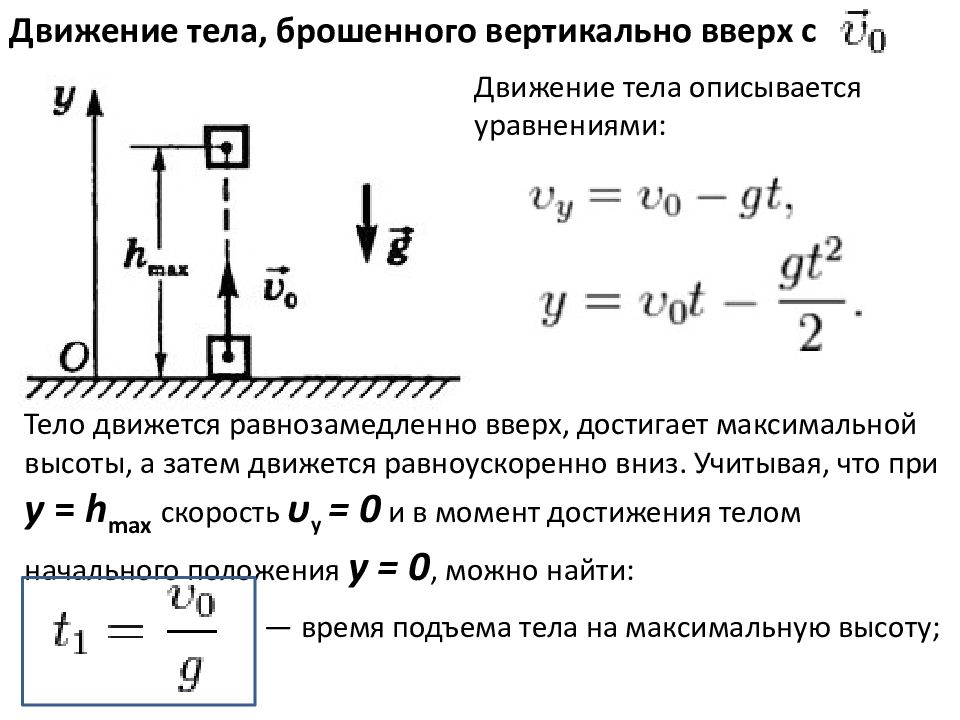
Движение тела, брошенного вертикально вверх с Движение тела описывается уравнениями: Тело движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при y = h max скорость υ y = 0 и в момент достижения телом начального положения y = 0, можно найти: — время подъема тела на максимальную высоту;
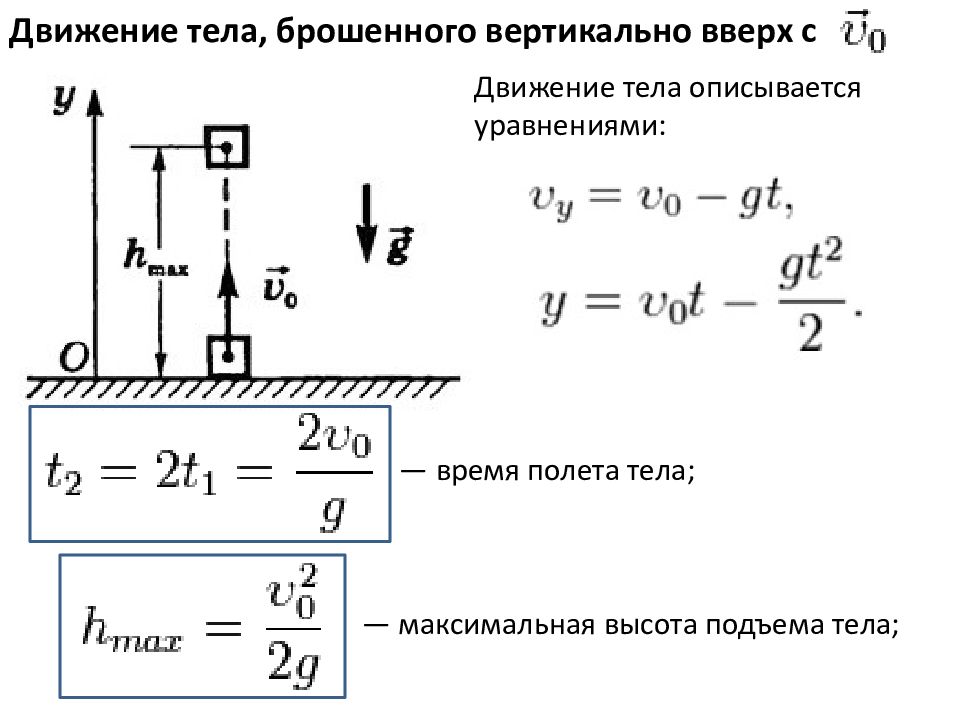
Движение тела, брошенного вертикально вверх с Движение тела описывается уравнениями: — время полета тела; — максимальная высота подъема тела;
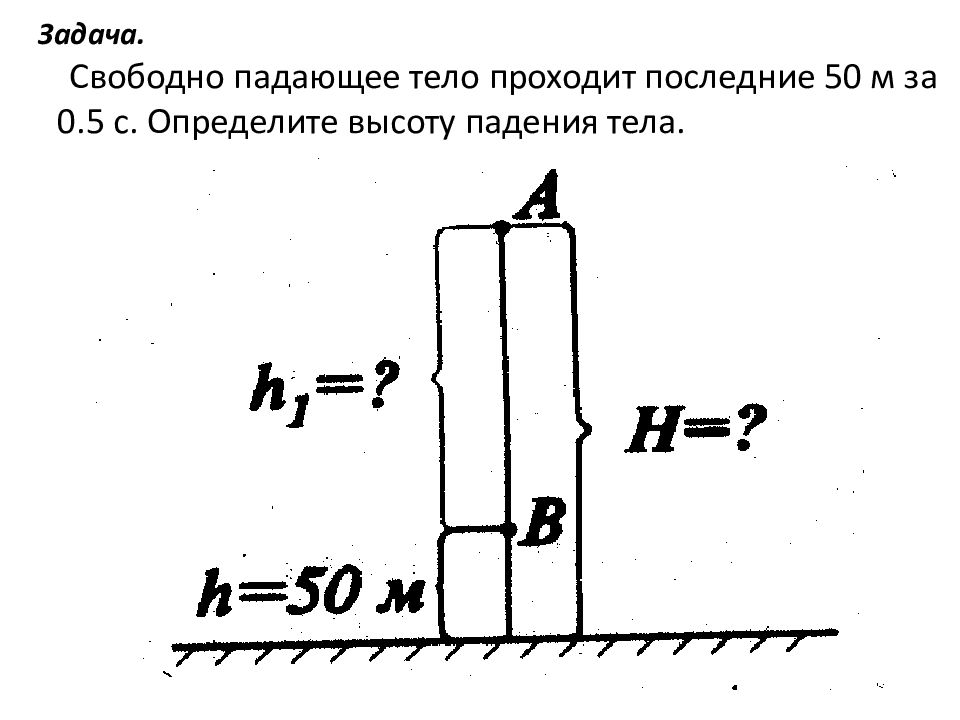
Задача. Свободно падающее тело проходит последние 50 м за 0.5 с. Определите высоту падения тела.
Решение Пусть в точке В тело имеет скорость v.
Решение задач Задача 1 Тело падает с высоты 57,5 м ( v 0 = 0). Сколько времени падает тело и какова его скорость при ударе о землю? Задача 2 Стрела выпущена из лука вертикально вверх с начальной скоростью v 0 = 30 м/с. На какую макси - мальную высоту поднимется стрела? Задача 3 Тело свободно падает с высоты 20 м над землей. Какова скорость тела в момент удара о землю? На какой высоте его скорость вдвое меньше?
Движение тела, брошенного горизонтально
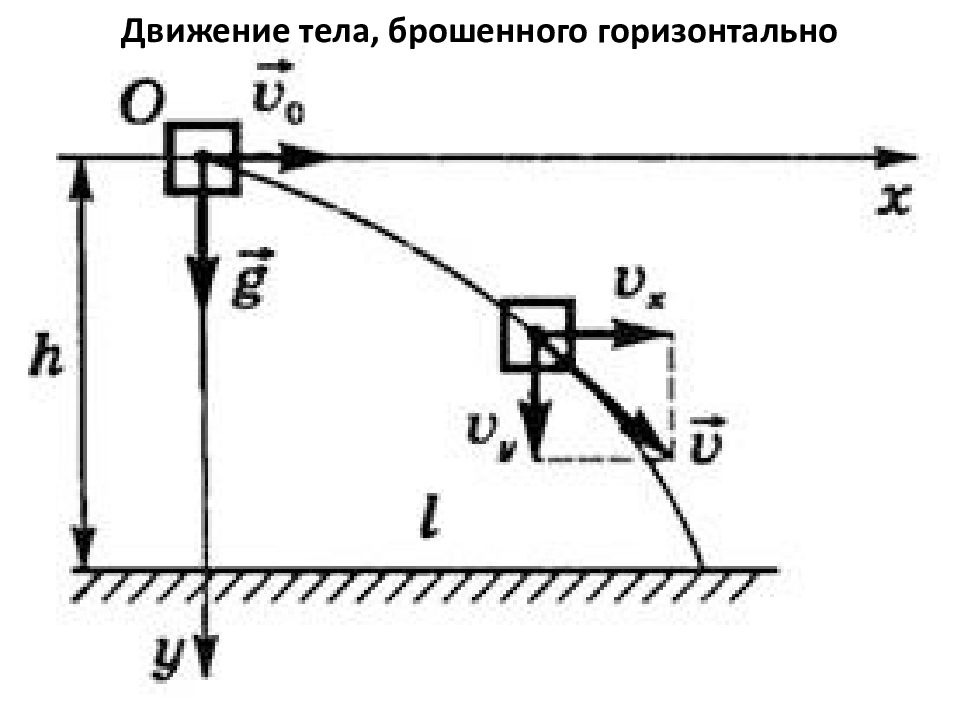
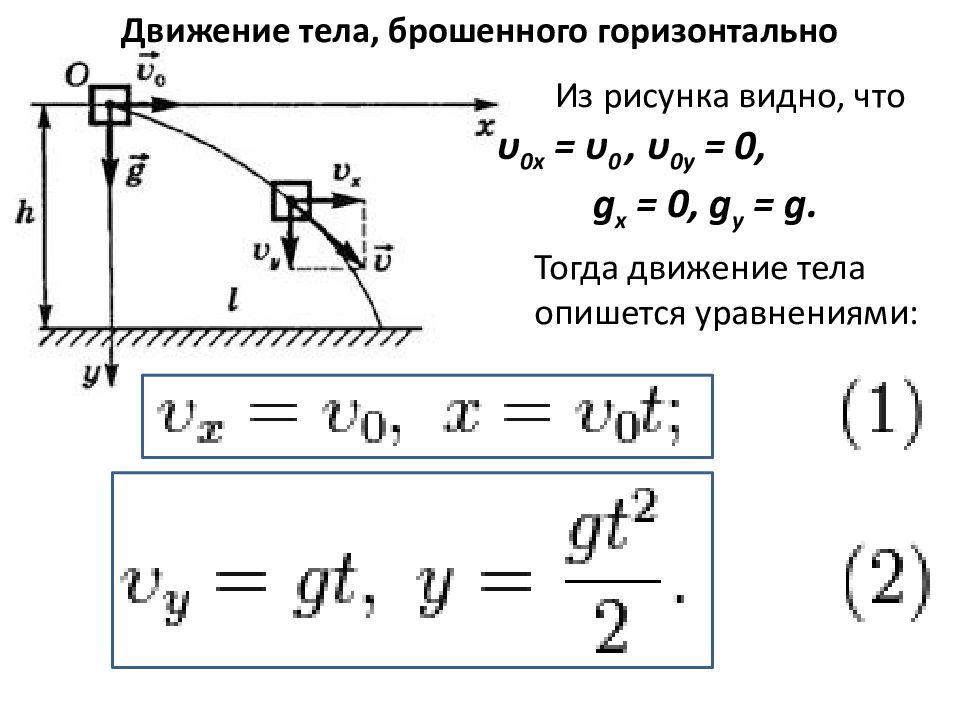
Движение тела, брошенного горизонтально Из рисунка видно, что υ 0x = υ 0, υ 0y = 0, g x = 0, g y = g. Тогда движение тела опишется уравнениями:
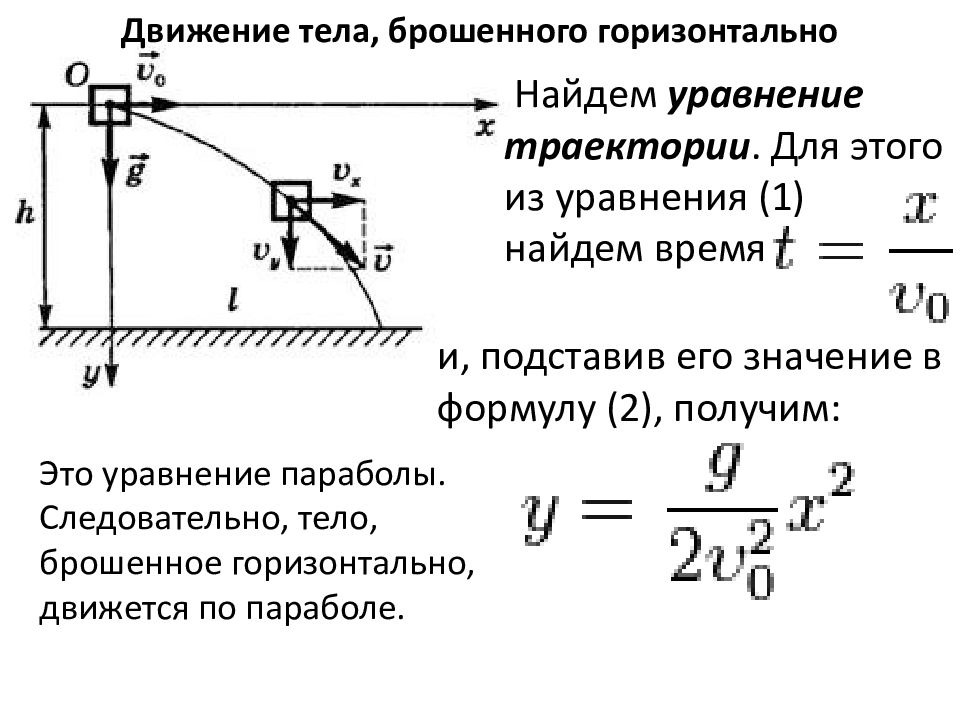
Движение тела, брошенного горизонтально Найдем уравнение траектории. Для этого из уравнения (1) найдем время и, подставив его значение в формулу (2), получим: Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе.
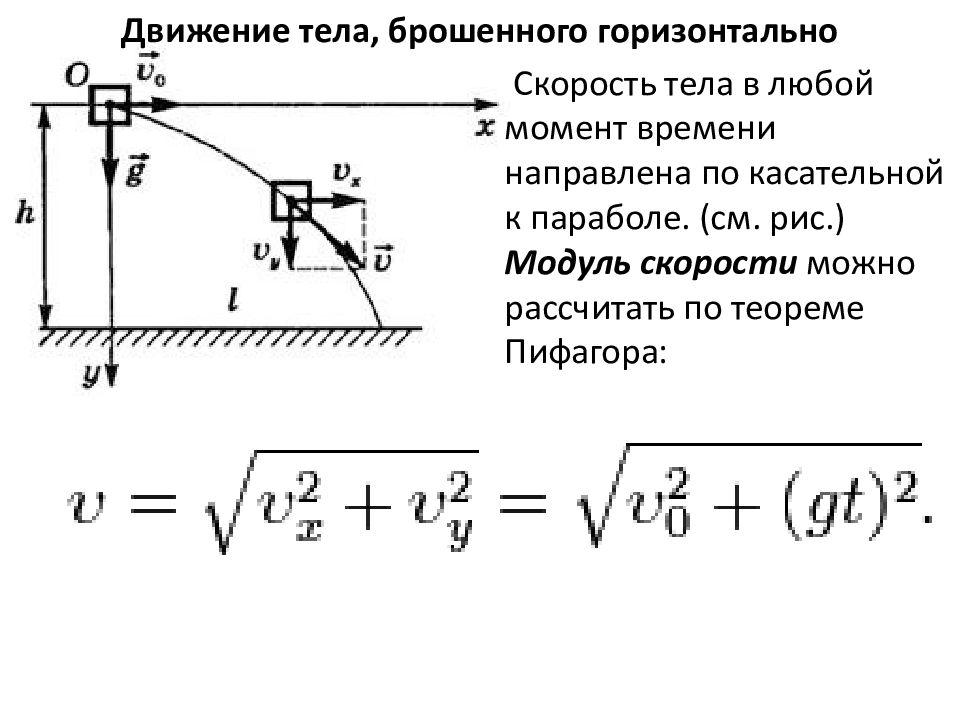
Движение тела, брошенного горизонтально Скорость тела в любой момент времени направлена по касательной к параболе. (см. рис.) Модуль скорости можно рассчитать по теореме Пифагора:
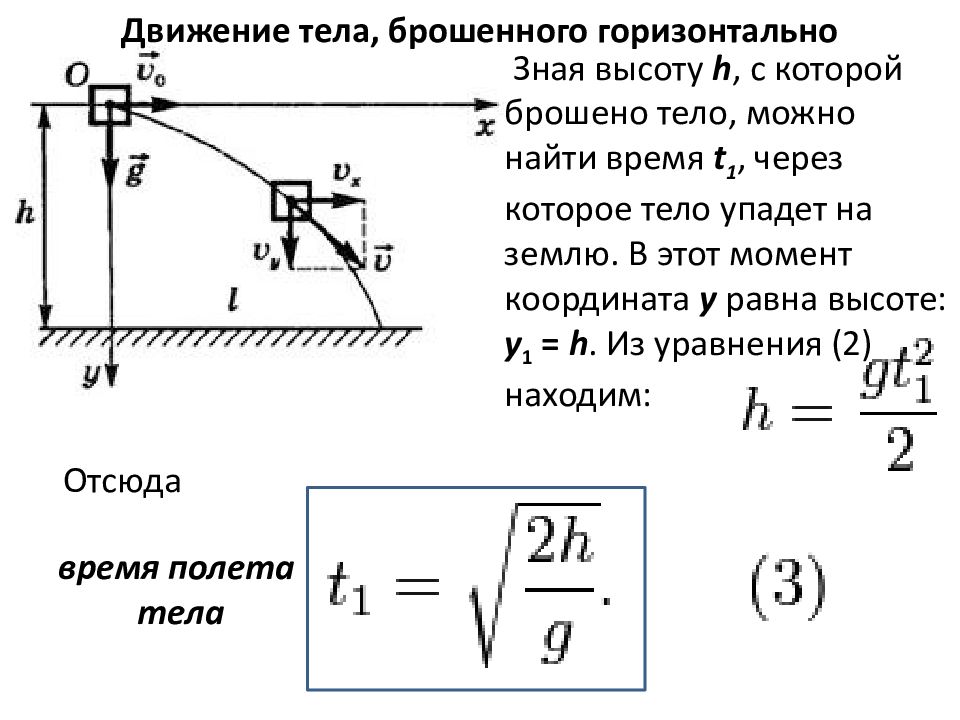
Движение тела, брошенного горизонтально Зная высоту h, с которой брошено тело, можно найти время t 1, через которое тело упадет на землю. В этот момент координата y равна высоте: y 1 = h. Из уравнения (2) находим: Отсюда время полета тела
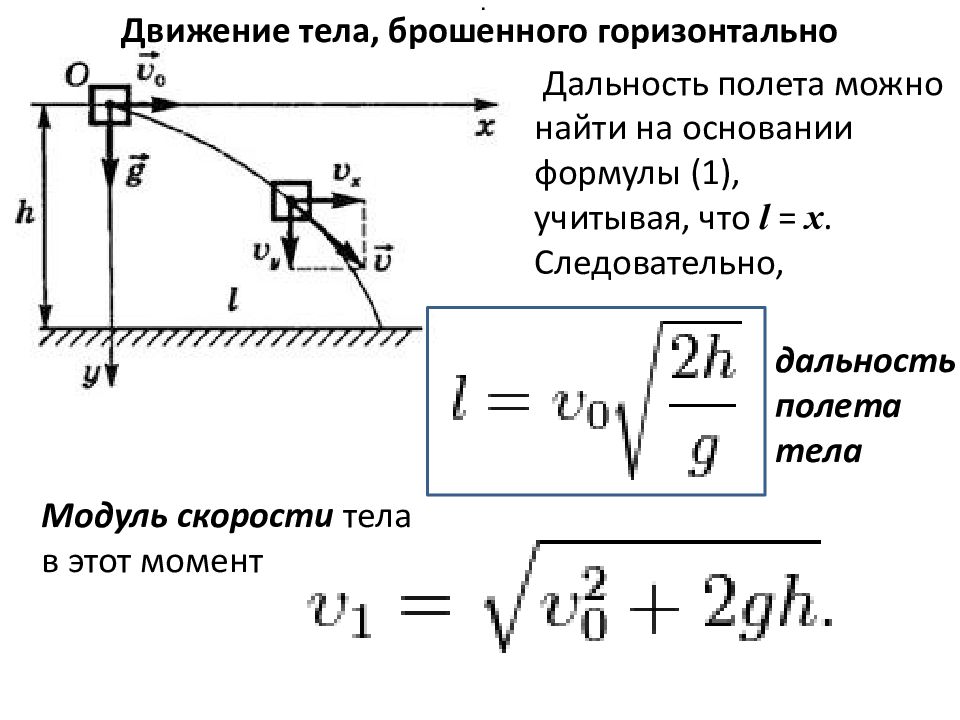
Движение тела, брошенного горизонтально Дальность полета можно найти на основании формулы (1), учитывая, что l = x. Следовательно, Модуль скорости тела в этот момент дальность полета тела .
