Первый слайд презентации: Геометрияның негізгі ұғымдары
Слайд 2: Геометрия- фигуралардың қасиеттерін зерттейтін ғылым
«гео» - жер, « метрео »- өлшеймін деген сөздерінен шыққан
Слайд 4: Геометрияның қолданысы
Өмірге байланысы бар есептерде; Қоршаған ортаны тануда; Логикалық ойлау қабілетін дамытуда; Көптеген маңызды мамандықтардың негізі болып табылады Мысалы: Архитектура, құрылыс инженериясында, скульптор т.б.
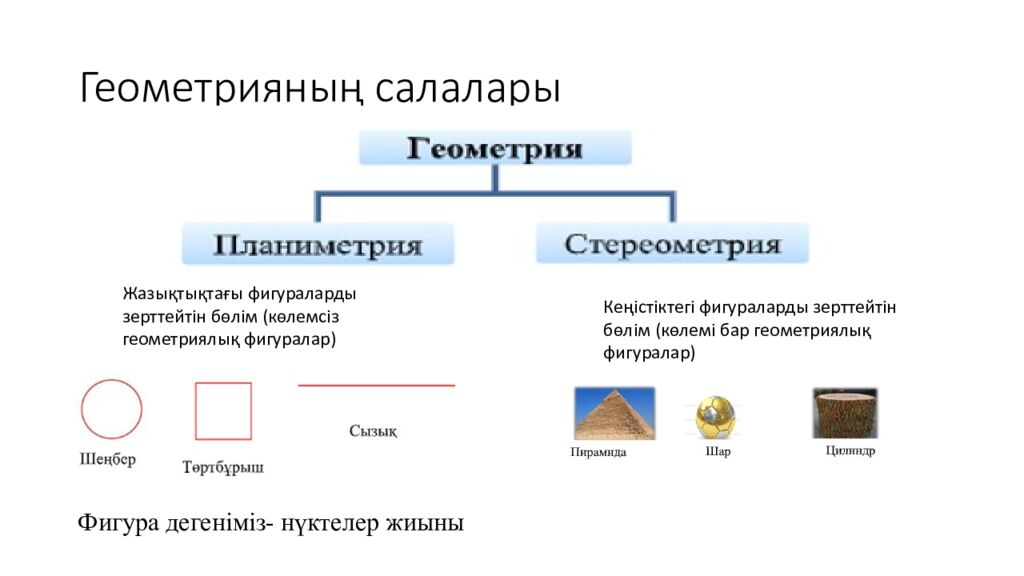
Слайд 5: Геометрияның салалары
Жазықтықтағы фигураларды зерттейтін бөлім (көлемсіз геометриялық фигуралар) Кеңістіктегі фигураларды зерттейтін бөлім (көлемі бар геометриялық фигуралар) Фигура дегеніміз- нүктелер жиыны
Слайд 6: Геометриялық есептер мынадай түрлерге бөлінеді:
Есептеуге берілген есептер; Дәлелдеуге берілген есептер; Салу есептері. Геометриялық есептерді шығару үшін анықтамаларды, аксиомаларды және теоремаларды білу қажет
Слайд 7: Анықтама
Жаңа ұғымдардың мағынасын бұрыннан белгілі ұғымдар арқылы түсіндіретін сөйлемді анықтама деп атаймыз. Мысалы: үшбұрыштың анықтамасы
Слайд 8: Негізгі ұғымдар
Анықтамасыз қабылданатын ұғымдар негізгі ұғымдар деп аталады.
Слайд 9: Нүкте
Нүкте- өте кішкентай нысандар бейнесі. А Нүкте латынның бір бас әріпімен белгіленеді
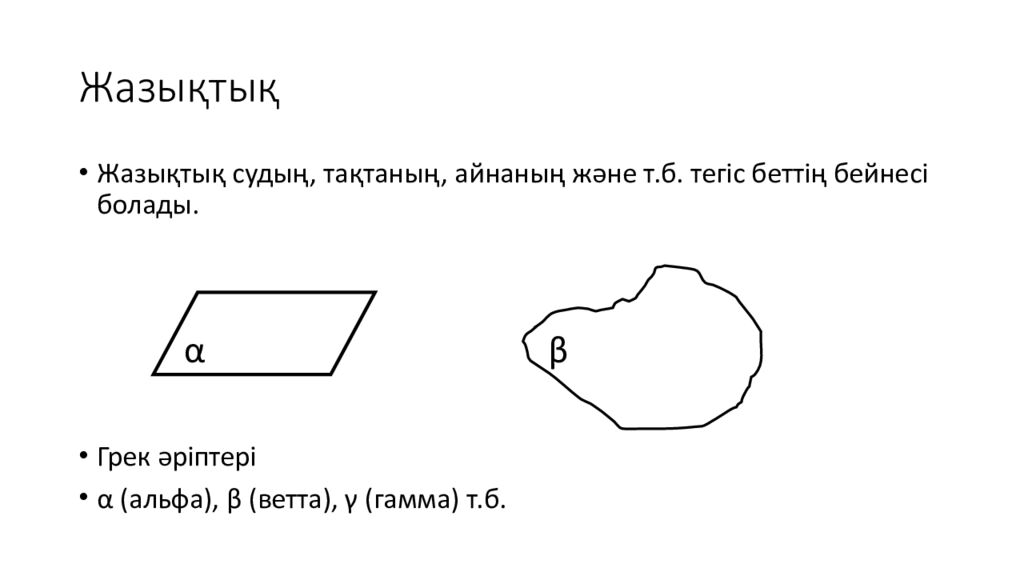
Слайд 11: Жазықтық
Жазықтық судың, тақтаның, айнаның және т.б. тегіс беттің бейнесі болады. Грек әріптері α (альфа), β ( ветта ), γ (гамма) т.б. β α
Слайд 12: Дәлелдеу
Берілген тұжырымдаманы ретімен талдау арқылы ақиқаттығына көз жеткізуді дәлелдеу деп атаймыз.
Слайд 13: Аксиома
Ақиқаттығы дәлелдеусіз қабылданатын сөйлем аксиома деп аталады.
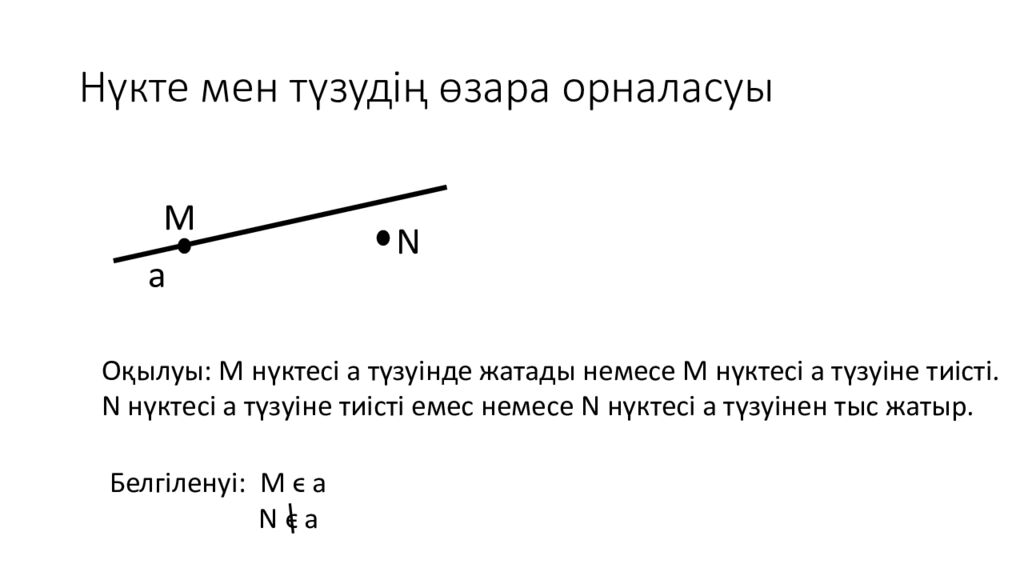
Слайд 14: Нүкте мен түзудің өзара орналасуы
а М N Оқылуы: М нүктесі а түзуінде жатады немесе М нүктесі а түзуіне тиісті. N нүктесі а түзуіне тиісті емес немесе N нүктесі а түзуінен тыс жатыр. Белгіленуі: М ϵ а N ϵ а
Последний слайд презентации: Геометрияның негізгі ұғымдары: Жазықтықтағы нүктелер мен түзулердің бір-біріне тиісті болатыны туралы қасиеттерге тоқталайық. Олар геометрияда тиістілік аксиомалары деп аталады
І.І Қандай түзуді алсақ та, ол түзуге тиісті нүктелер де, оған тиісті емес нүктелер де бар болады. І.ІІ Кез келген екі нүкте арқылы бір ғана түзу жүргізуге болады. С Д