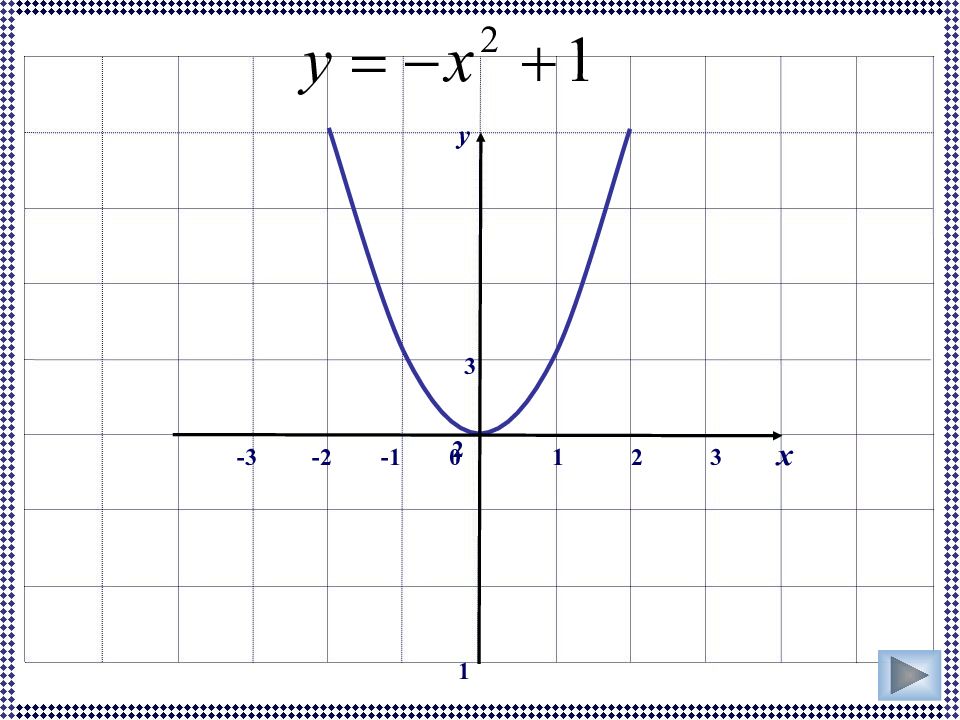
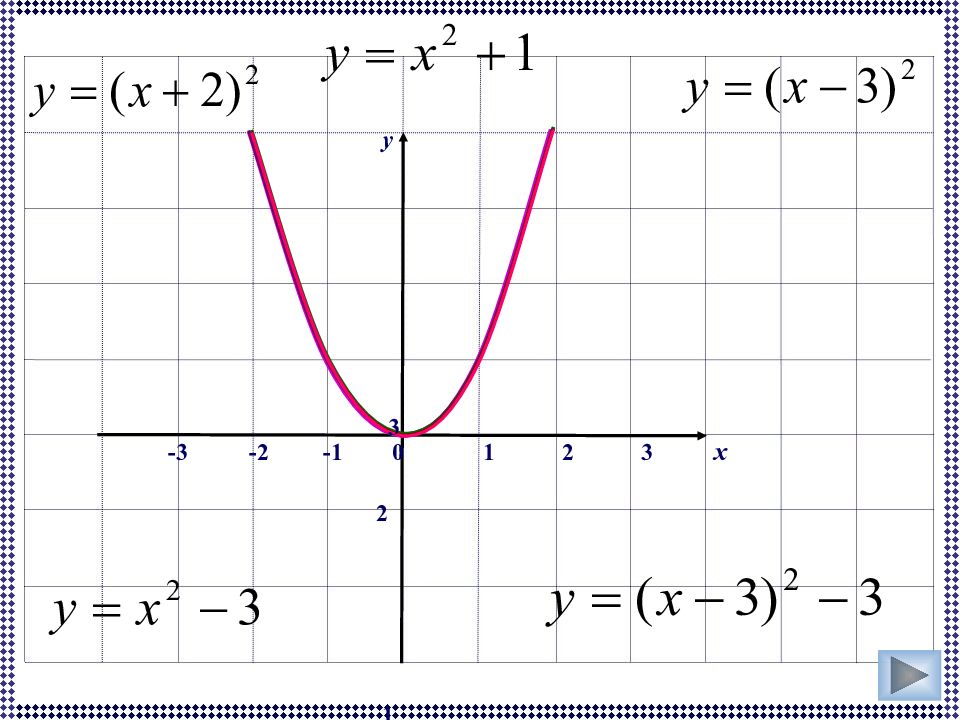
Первый слайд презентации
График функции квадратичной Работа выполнена учителем ГОУ центр образования №170 КУПРЯШИНОЙ Л.А.
Слайд 2: Торговый центр
Форма параболы иногда используется в архитектуре для строительства крыш и куполов
Слайд 10: Парабола в науке и технике
По эллиптическим, параболическим и гиперболическим орбитам движутся тела в поле тяготения. Параболическое зеркало используется в большинстве телескопов-рефлекторов, а также в антеннах радаров и специальных микрофонах с параболическими отражателями, в мощных прожекторах и автомобильных фарах. Парабола в науке и технике
Слайд 12
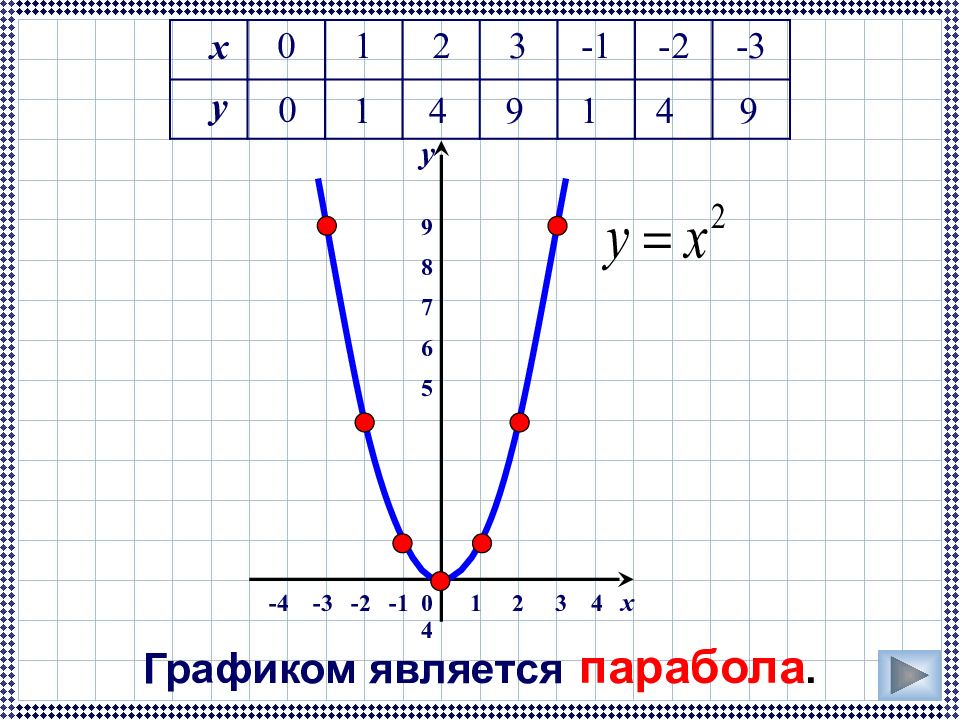
Графиком является парабола. -4 -3 -2 -1 0 1 2 3 4 x х 0 1 2 3 -1 -2 -3 y 4 1 4 0 1 9 9 y 9 8 7 6 5 4 3 2 1
Слайд 13: Знак коэффициента а задаёт направление ветвей
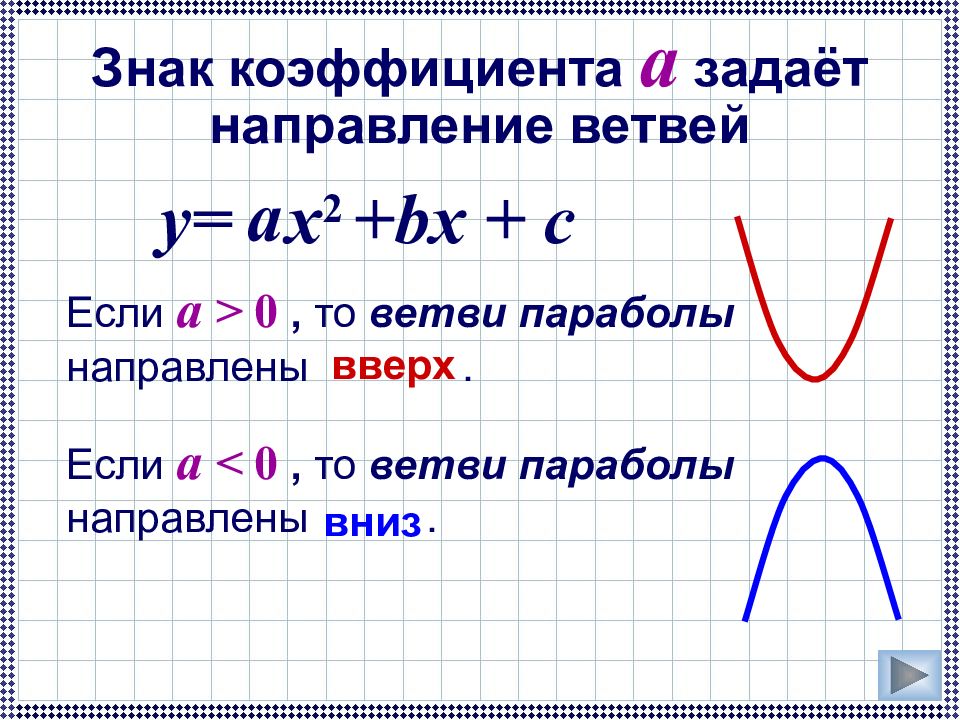
Если a < 0, то ветви параболы направлены. Если a > 0, то ветви параболы направлены. y= x 2 +bx + c Знак коэффициента а задаёт направление ветвей вверх вниз a
Слайд 15
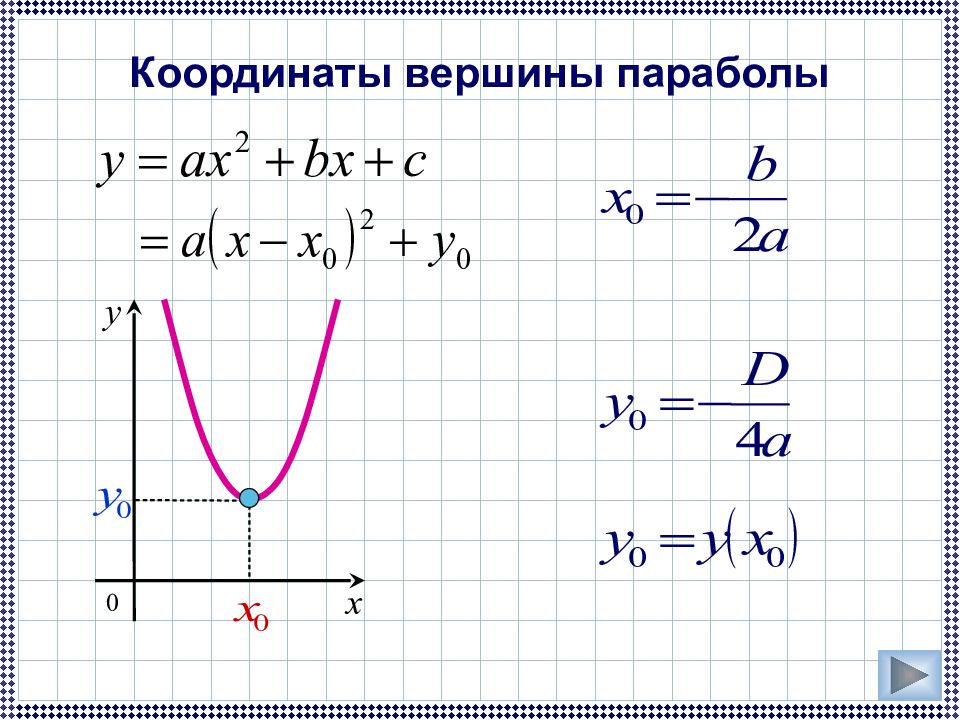
Укажите координаты вершины параболы y = -3( x -2) 2 +5 Сделай клик мышкой по правильному ответу 1) (-2 ; -5) 2) (2 ; -5) 3) (2 ; 5) 4) (-2 ; 0) 5 2 Проверка
Слайд 16: Укажите координаты вершины параболы y = 2 x 2 + 4 x + 5 :
4) (-1 ; 3 ) Укажите координаты вершины параболы y = 2 x 2 + 4 x + 5 : Проверка (2) 1) (-3 ; - 1 ) 2) (3 ; 1 ) 3) (-1 ; -3 ) Сделай клик мышкой по правильному ответу
Слайд 17: Нули квадратичной функции
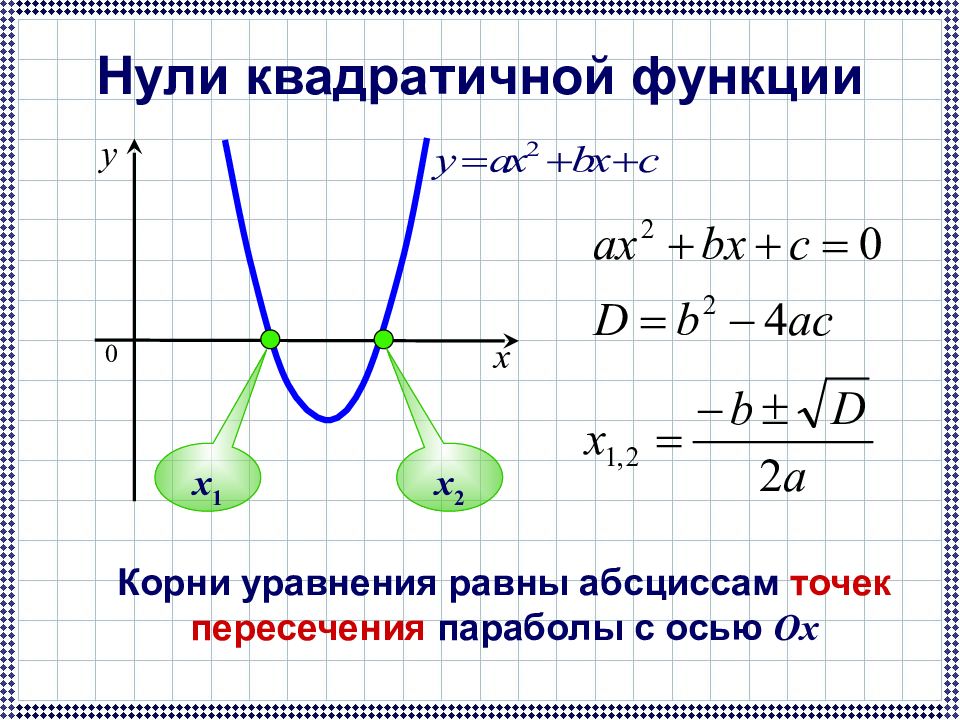
Корни уравнения равны абсциссам точек пересечения параболы с осью Ox x 1 x 2
Слайд 18: Определите нули функции y = x 2 +4 x -5
Проверка (2) Сделай клик мышкой по правильному ответу 1) 1 и 5 2) -5 и 1 3) -2 и -3 4) -1 и 5 -5 4 -
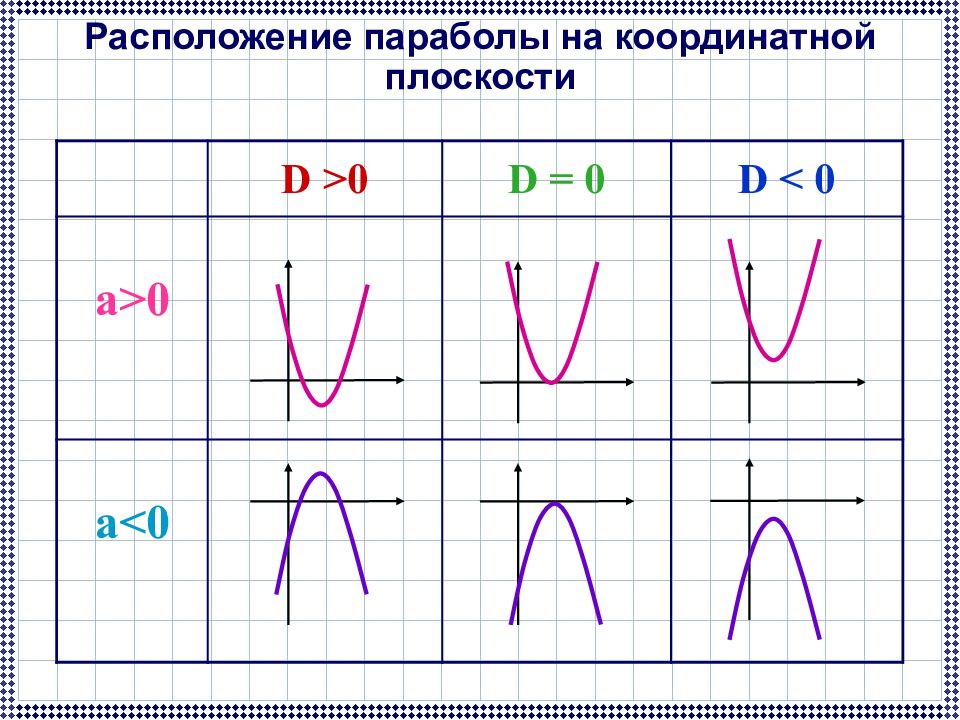
Слайд 19: Расположение параболы на координатной плоскости
D >0 D = 0 D < 0 а >0 а <0 Расположение параболы на координатной плоскости
Слайд 20: Замечательные свойства параболы
Если дискриминант, то парабола пересекает ось абсцисс в двух точках. Если дискриминант, то парабола касается оси абсцисс. Если дискриминант, то парабола не пересекает ось абсцисс. Замечательные свойства параболы D < 0 D > 0 D = 0
Слайд 21
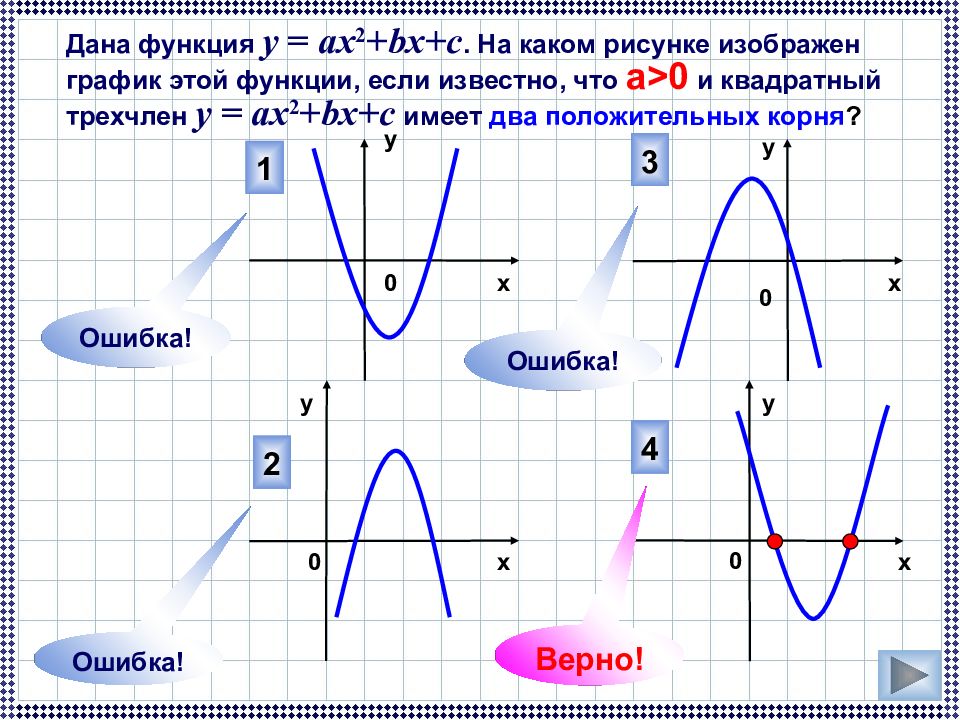
Дана функция у = ах 2 +bx+c. На каком рисунке изображен график этой функции, если известно, что а >0 и квадратный трехчлен у = ах 2 +bx+c имеет два положительных корня ? 4 3 2 1 Ошибка! Ошибка! Верно! 0 0 х у у х х х у у 0 0 Ошибка!
Слайд 22
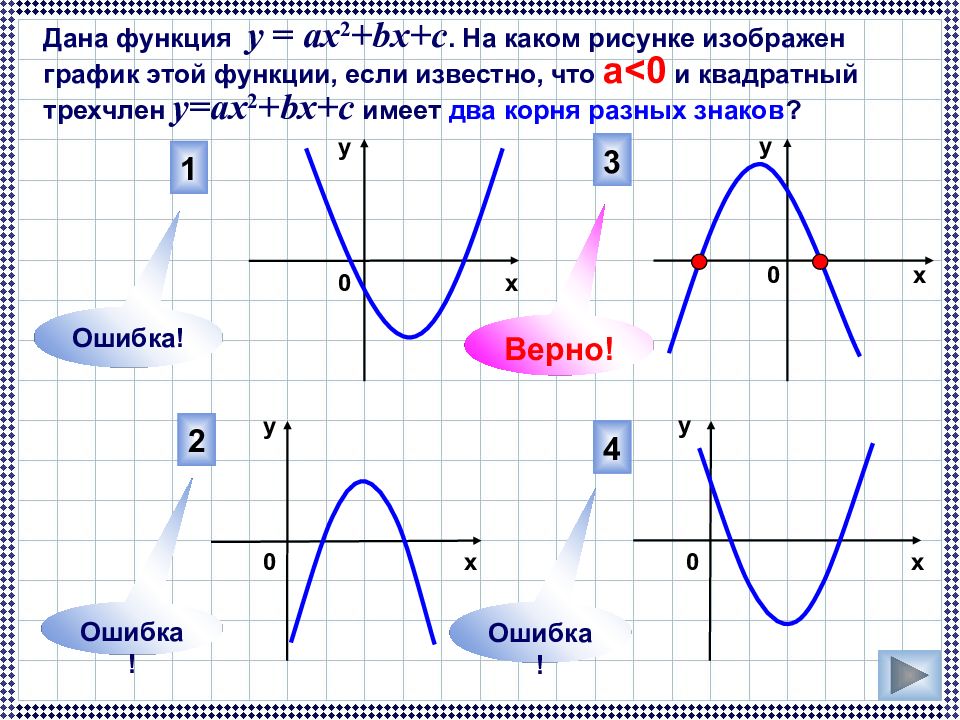
Дана функция у = ах 2 +bx+c. На каком рисунке изображен график этой функции, если известно, что а <0 и квадратный трехчлен у=ах 2 +bx+c имеет два корня разных знаков ? 3 4 2 1 Ошибка! Ошибка! Ошибка! 0 0 х у у х х х у у 0 0 Верно!
Слайд 23
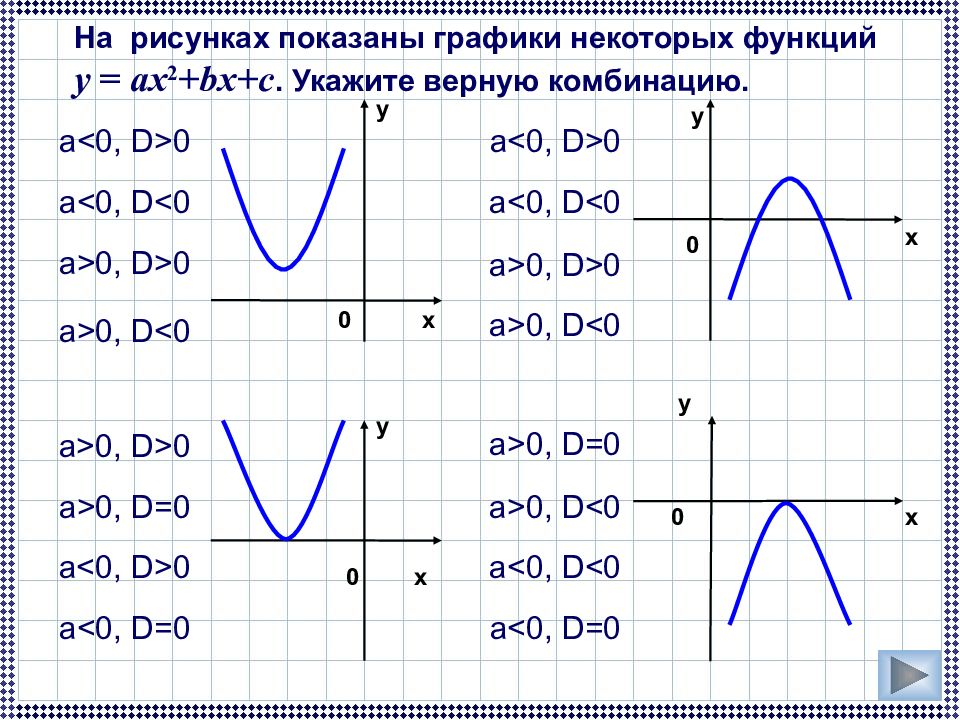
х у у х у 0 х 0 0 у х На рисунках показаны графики некоторых функций у = a х 2 + bx +с. Укажите верную комбинацию. а <0, D>0 a<0, D<0 a>0, D>0 a>0, D<0 a>0, D<0 a<0, D<0 a>0, D>0 a<0, D>0 a>0, D>0 a<0, D=0 a<0, D>0 a>0, D=0 a>0, D=0 a>0, D<0 a<0, D<0 a<0, D=0 0
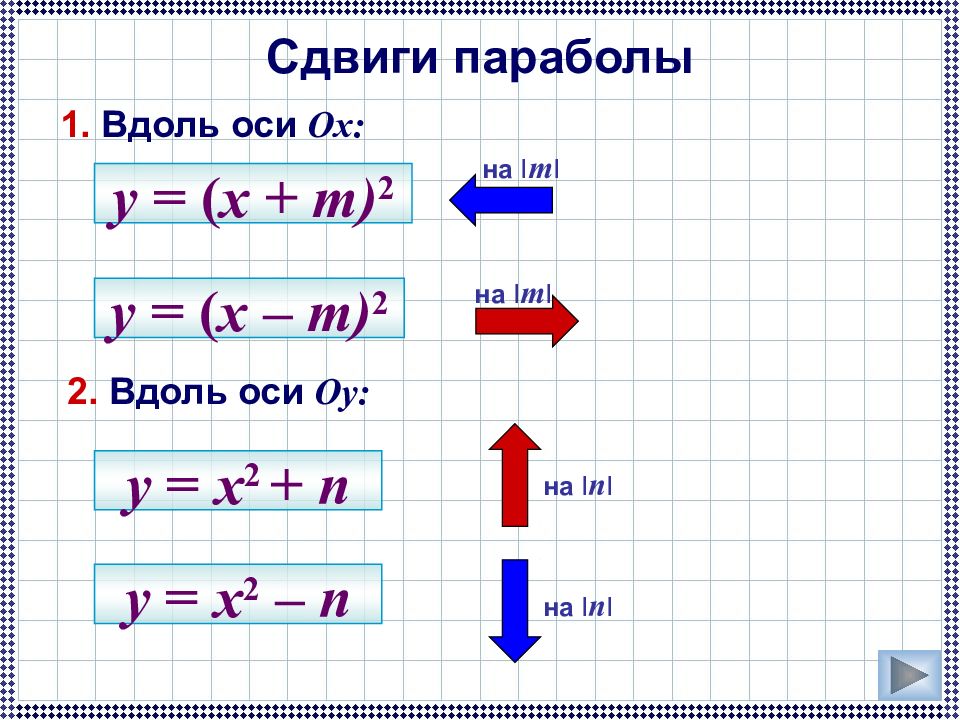
Слайд 24: Сдвиги параболы
1. Вдоль оси Ox : 2. Вдоль оси Oy : на I m I на I m I y = ( x + m) 2 y = ( x – m) 2 на I n I на I n I y = x 2 + n y = x 2 – n
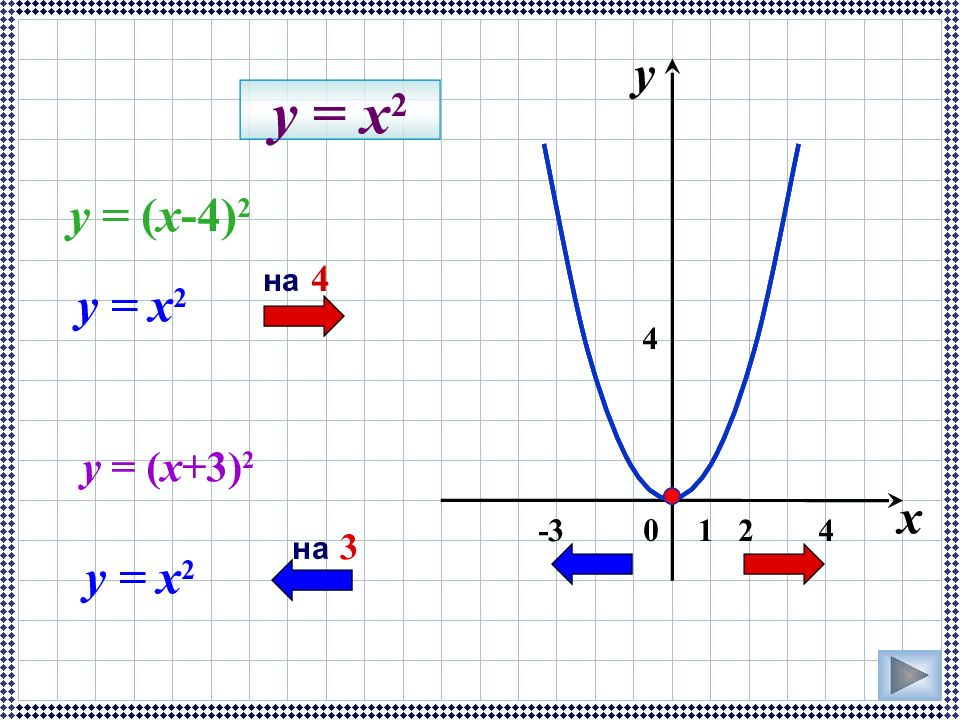
Слайд 25: y = x 2
y x 1 0 2 4 4 -3 y = ( x -4) 2 y = ( x +3) 2 на 4 y = x 2 на 3 y = x 2
Слайд 26
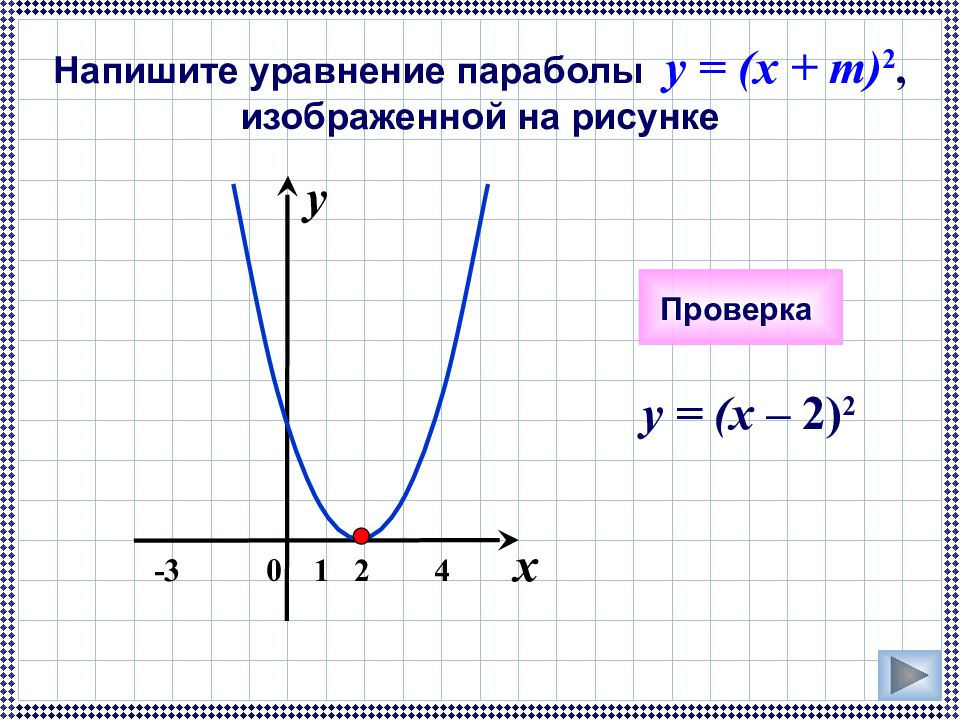
y = (x – 2 ) 2 x 0 y 1 2 4 -3 Напишите уравнение параболы y = (x + m) 2, изображенной на рисунке Проверка
Слайд 27
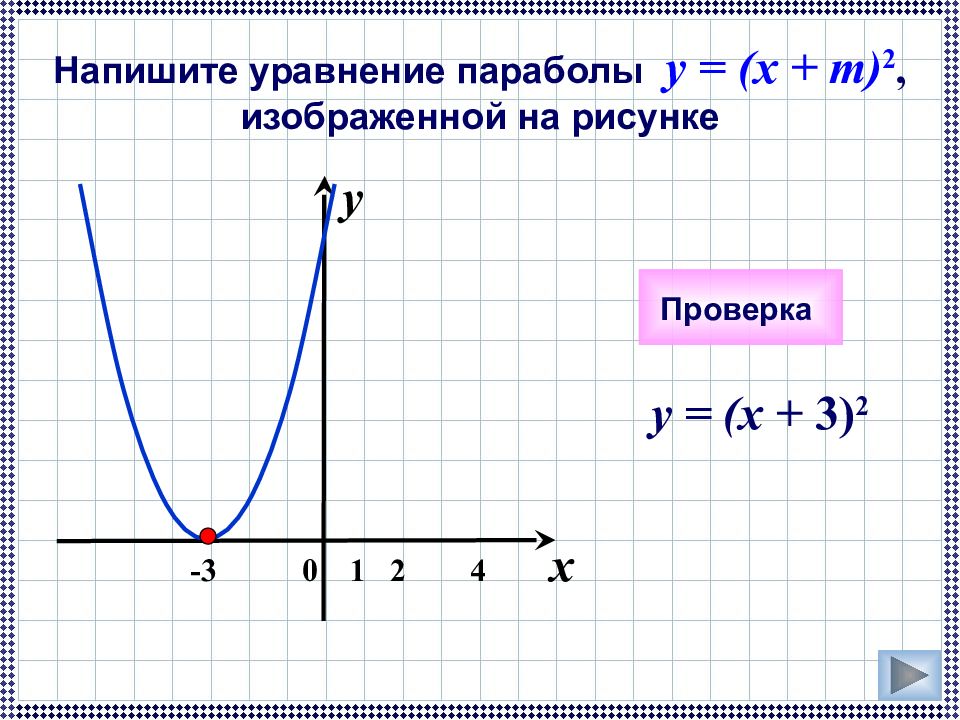
y = (x + 3 ) 2 x 0 y 1 2 4 -3 Напишите уравнение параболы y = (x + m) 2, изображенной на рисунке Проверка
Слайд 29
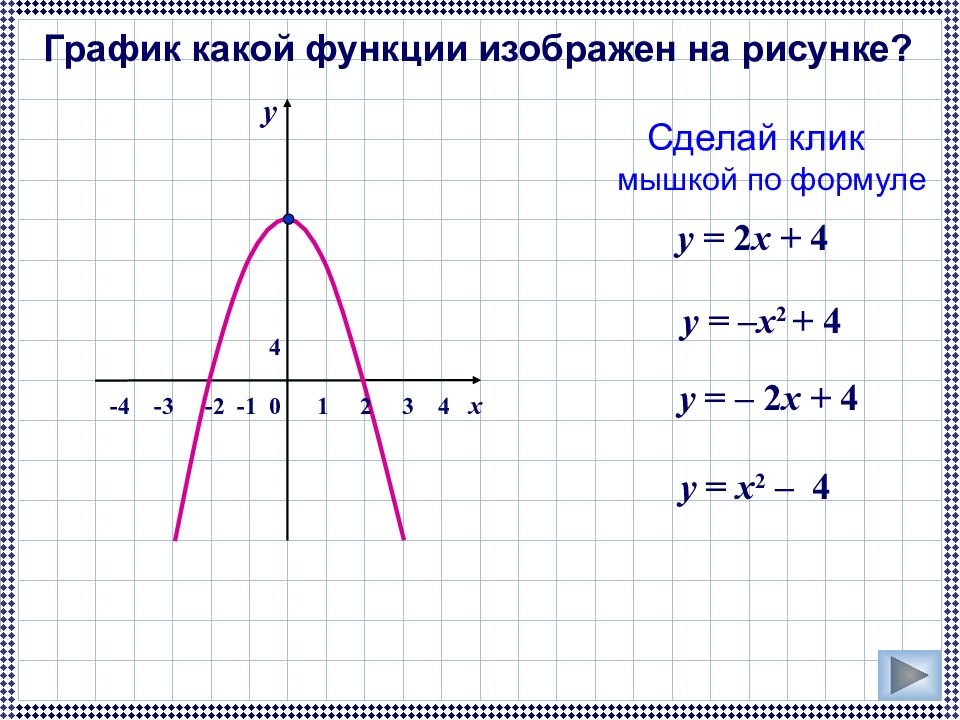
График какой функции изображен на рисунке? Сделай клик мышкой по формуле у = 2 x + 4 у = – x 2 + 4 у = – 2 x + 4 у = x 2 – 4 -4 -3 -2 -1 0 1 2 3 4 x y 4
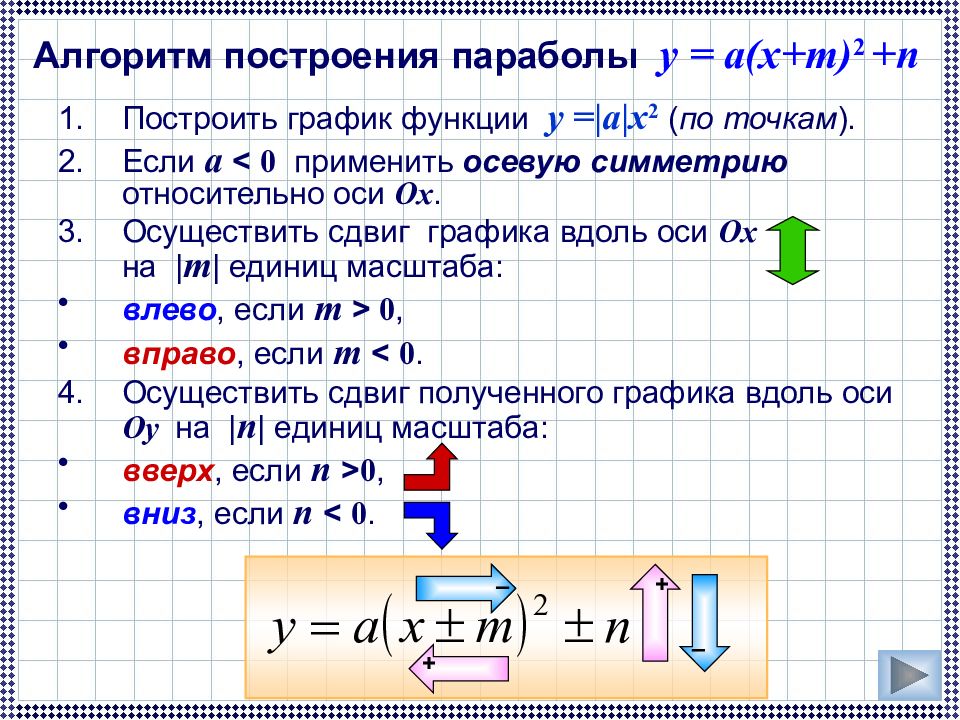
Слайд 30: Алгоритм построения параболы y = a(x+m) 2 +n
Построить график функции у =| a | x 2 ( по точкам ). Если а < 0 применить осевую симметрию относительно оси Ox. Осуществить сдвиг графика вдоль оси Ox на | m | единиц масштаба: влево, если m > 0, вправо, если m < 0. Осуществить сдвиг полученного графика вдоль оси Oy на | n | единиц масштаба: вверх, если n > 0, вниз, если n < 0. Алгоритм построения параболы y = a(x+m) 2 +n + – + –
Слайд 32
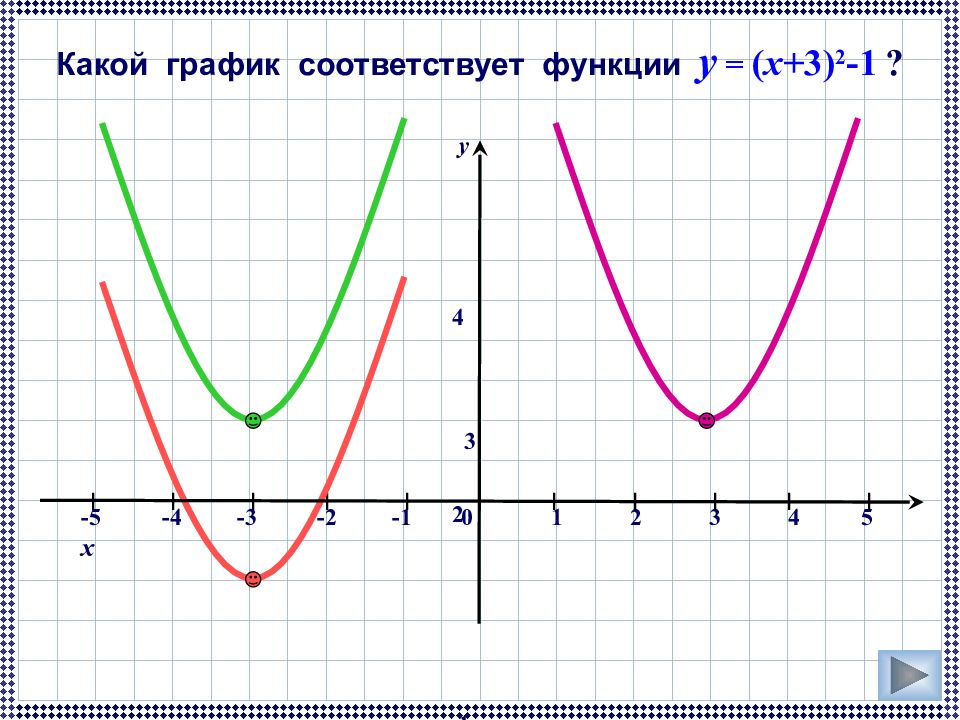
-5 -4 -3 -2 -1 0 1 2 3 4 5 x I I I I I I I I I I Какой график соответствует функции y = ( x +3) 2 -1 ? y 4 3 2 1 -1
Слайд 33
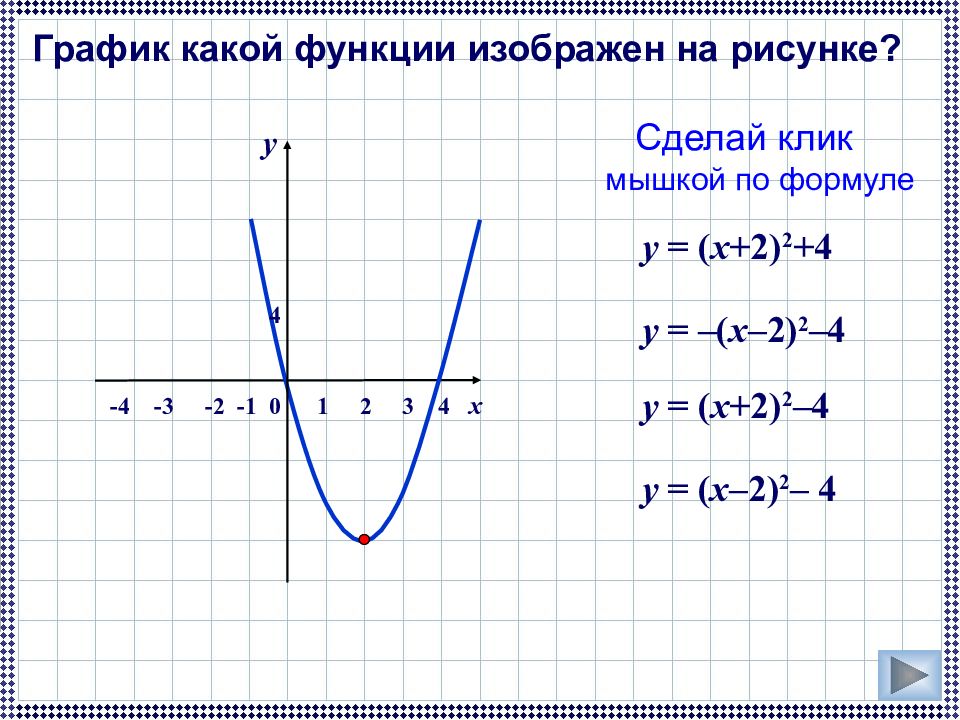
График какой функции изображен на рисунке? Сделай клик мышкой по формуле у = ( x +2) 2 +4 у = ( x –2) 2 – 4 у = ( x +2) 2 – 4 у = –( x –2) 2 – 4 -4 -3 -2 -1 0 1 2 3 4 x y 4
Слайд 34
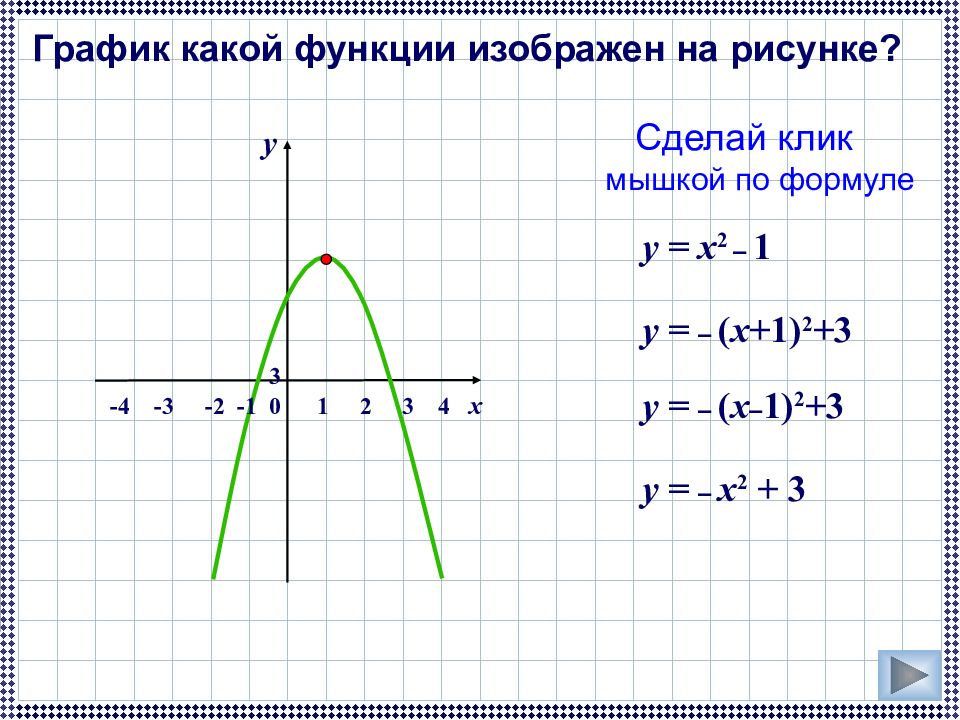
График какой функции изображен на рисунке? Сделай клик мышкой по формуле у = x 2 – 1 у = – x 2 + 3 у = – ( x – 1) 2 +3 у = – ( x +1) 2 +3 -4 -3 -2 -1 0 1 2 3 4 x y 3
Слайд 35
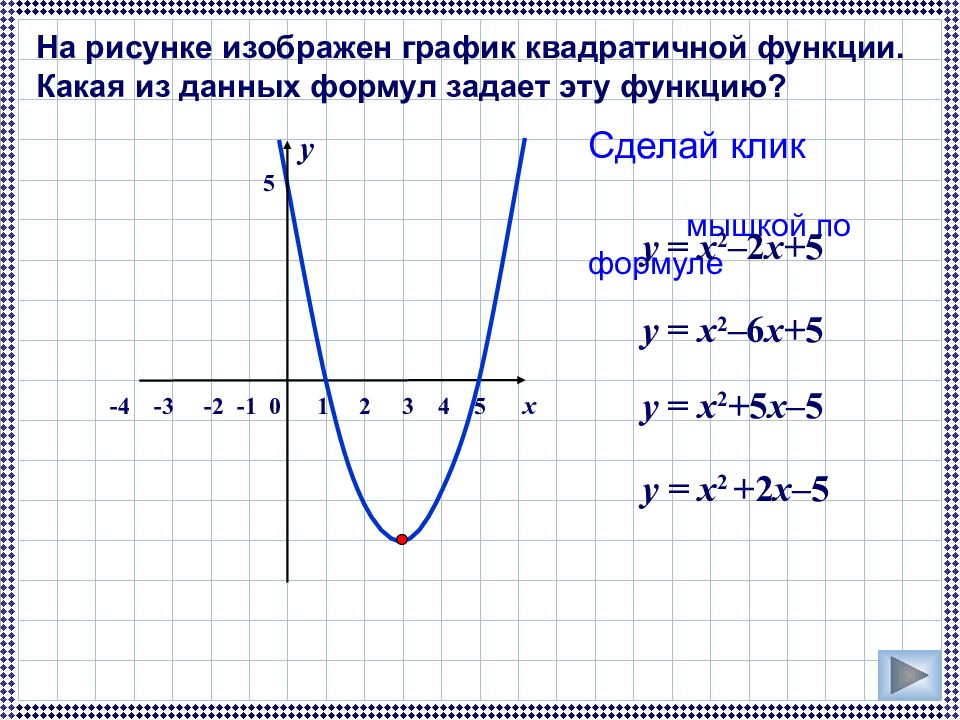
Сделай клик мышкой по формуле у = x 2 – 2 x +5 у = x 2 +2 x – 5 у = x 2 +5 x – 5 у = x 2 – 6 x+ 5 -4 -3 -2 -1 0 1 2 3 4 5 x y На рисунке изображен график квадратичной функции. Какая из данных формул задает эту функцию? 5
Слайд 36
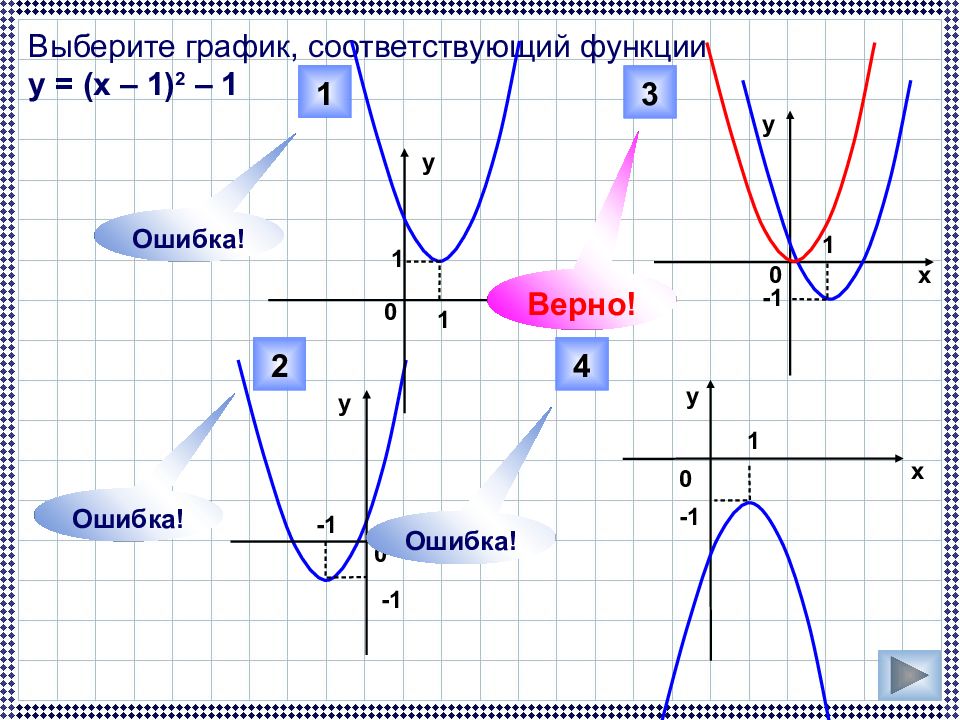
Выберите график, соответствующий функции у = (х – 1) 2 – 1 3 4 2 0 0 х у у х х х у у 0 0 1 -1 1 1 -1 -1 -1 1 1 Верно! Ошибка! Ошибка! Ошибка!
Слайд 37: Уравнение параболы y =2( x -3) 2 +4 получено из параболы y =2 x 2 …
Сдвигом вдоль оси Ох на 3 единицы вправо и сдвигом вдоль оси O у на 4 единицы вверх. Сдвигом вдоль оси Ох на 3 единицы вправо и сдвигом вдоль оси O у на 4 единицы вниз. Сдвигом вдоль оси Ох на 3 единицы влево и сдвигом вдоль оси O у на 4 единицы вниз. Сдвигом вдоль оси Ох на 4 единицы влево и сдвигом вдоль оси O у на 3 единицы вниз.
Слайд 38
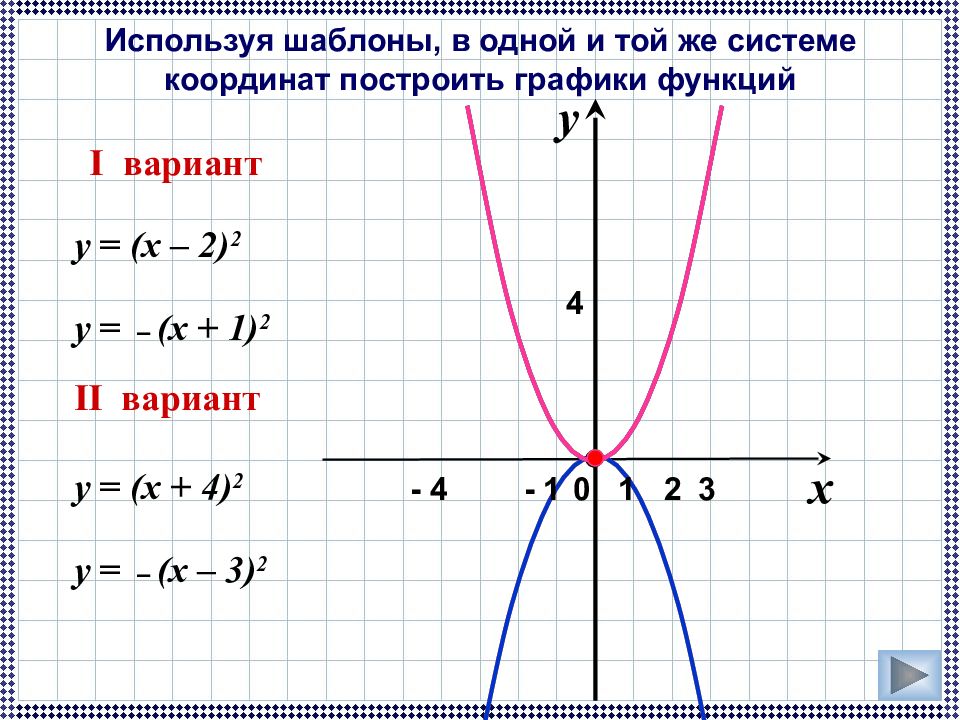
y = (x – 2) 2 I вариант y = (x + 4 ) 2 y = – (x – 3 ) 2 y = – (x + 1 ) 2 x 0 y 1 2 - 4 4 3 - 1 II вариант Используя шаблоны, в одной и той же системе координат построить графики функций
Слайд 39: Алгоритм построения параболы у = ах 2 + b х + с
Определить направление ветвей параболы. Найти координаты вершины параболы. Провести ось симметрии параболы. Найти точку пересечения параболы с осью Oy при x = 0. Найти нули функции при у = 0 и точки пересечения параболы с осью Ox. Найти дополнительные точки.
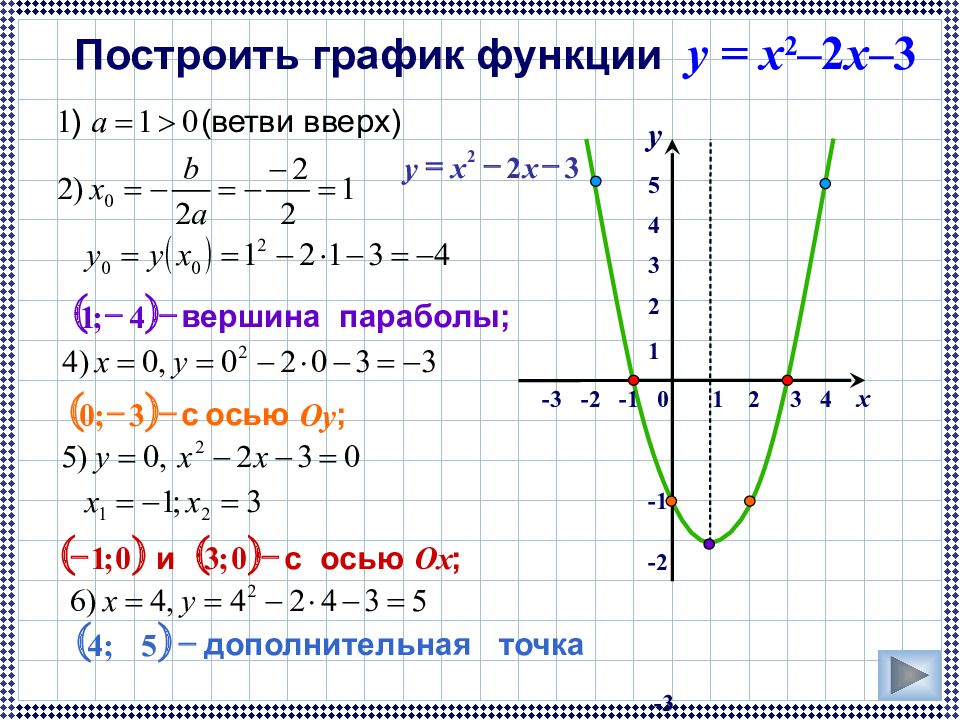
Слайд 40: Построить график функции y = x 2 – 2 x– 3
y 5 4 3 2 1 -1 - 2 -3 -4 Построить график функции y = x 2 – 2 x– 3 -3 -2 -1 0 1 2 3 4 x 3 2 2 - - = x x y ( ) параболы; вершина - - 4 ; 1 ( ) ; осью с O y - - 3 ; 0 ( ) ( ) ; осью с и O x - - 0 ; 3 0 ; 1 ( ) точка ьная дополнител - 5 ; 4
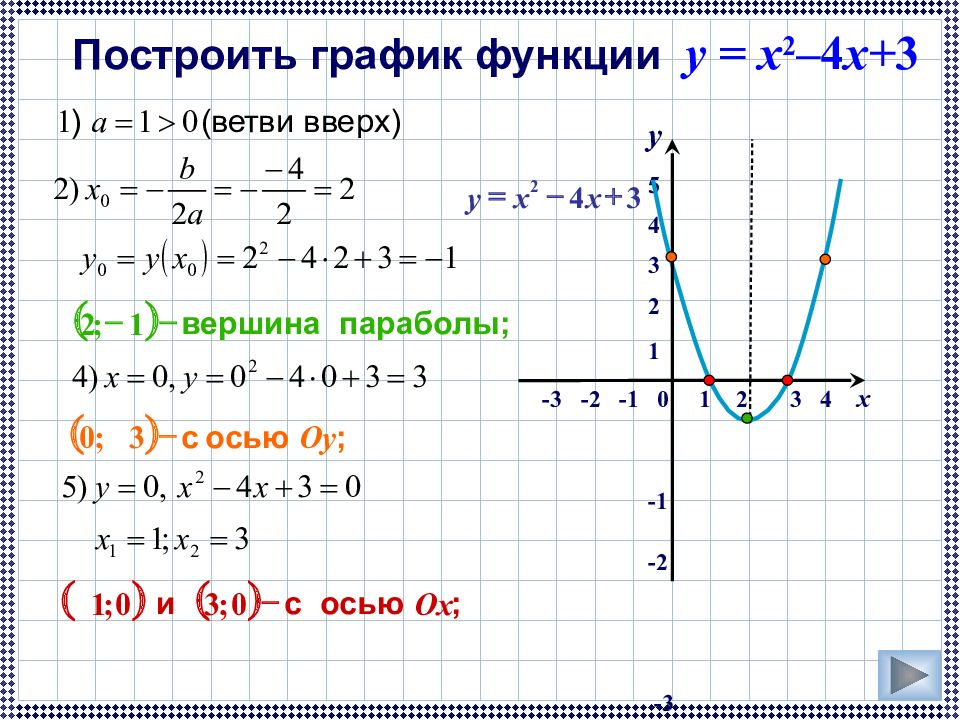
Слайд 41: Построить график функции y = x 2 – 4 x+ 3
y 5 4 3 2 1 -1 - 2 -3 -4 Построить график функции y = x 2 – 4 x+ 3 -3 -2 -1 0 1 2 3 4 x 3 4 2 + - = x x y ( ) параболы; вершина - - 1 ; 2 ( ) ; осью с O y - 3 ; 0 ( ) ( ) ; осью с и O x - 0 ; 3 0 ; 1