Слайд 2: Data Mining
кластерный анализ 1. метод главных компонент 2. факторный анализ 3.
Слайд 3: Классификация и кластеризация
Классификация (от лат. classis — разряд, класс и facio — делаю, раскладываю) система соподчиненных понятий (классов объектов) какой-либо области знания или деятельности человека, часто представляемая в виде различных по форме схем (таблиц) и используемая как средство для установления связей между этими понятиями или классами объектов, а также для точной ориентировки в многообразии понятий или соответствующих объектов.
Слайд 4: Классификация
Классификация - упорядочение по некоторому принципу множество объектов, которые имеют сходные классификационные признаки (одно или несколько свойств), выбранных для определения сходства или различия между этими объектами
Слайд 5: Процесс классификации
Цель процесса классификации состоит в том, чтобы построить модель, которая использует прогнозирующие атрибуты в качестве входных параметров и получает значение зависимого атрибута. Процесс классификации заключается в разбиении множества объектов на классы по определенному критерию.
Слайд 6
Животные подразделяются на : а) принадлежащих императору; б) набальзамированных; в) дрессированных; г) молочных поросят; д) сирен; е) сказочных; ж) бродячих собак; з) включённых в данную классификацию; и) дрожащих, как сумасшедшие; к) неисчислимых; л) нарисованных самой лучшей верблюжьей кисточкой; м) других; н) тех, которые только что разбили цветочную вазу и о) тех, которые издалека напоминают мух. (Хорхе Луис Борхес, Другие исследования: 1937—1952). Древняя китайская классификация животных
Слайд 7: Классификация
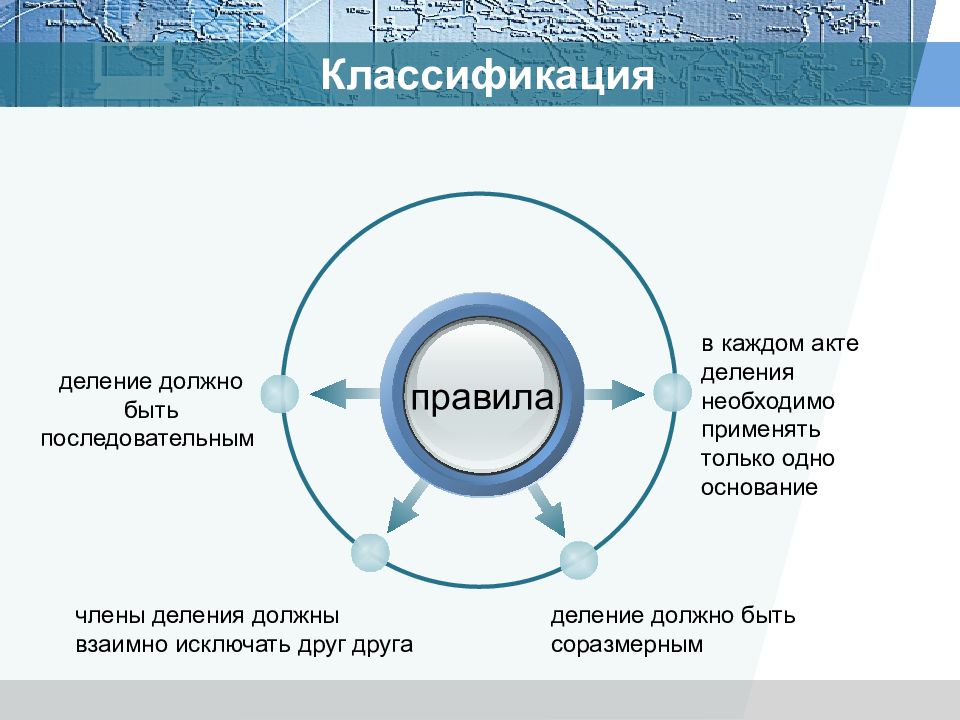
правила в каждом акте деления необходимо применять только одно основание деление должно быть соразмерным члены деления должны взаимно исключать друг друга деление должно быть последовательным
Слайд 8: Кластеризация
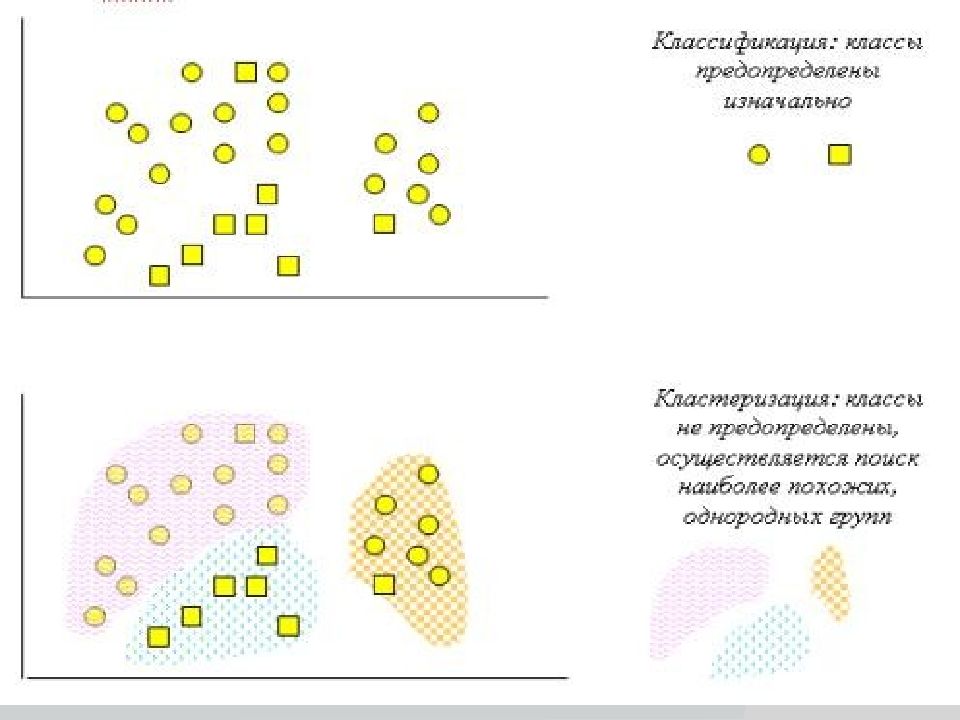
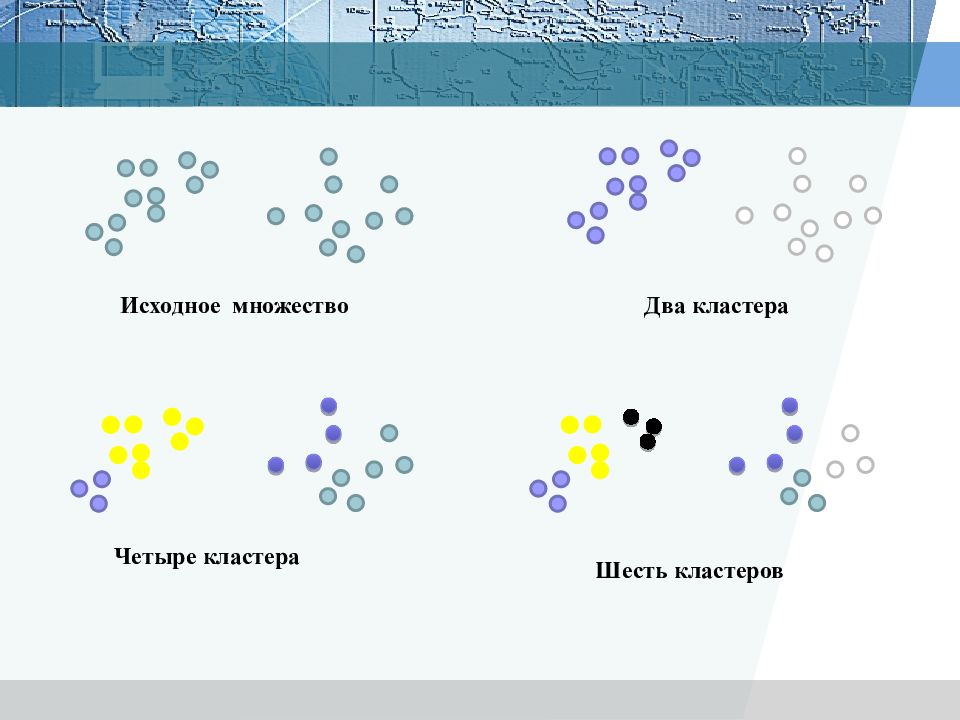
Кластеризация предназначена для разбиения совокупности объектов на однородные группы ( кластеры или классы). Если данные выборки представить как точки в признаковом пространстве, то задача кластеризации сводится к определению "сгущений точек".
Слайд 10
Цель кластеризации - поиск существующих структур путем: понимания данных путём выявления кластерной структуры. Разбиение выборки на группы схожих объектов позволяет упростить дальнейшую обработку данных и принятия решений, применяя к каждому кластеру свой метод анализа; сжатия данных. Если исходная выборка избыточно большая, то можно сократить её, оставив по одному наиболее типичному представителю от каждого кластера; обнаружения новизны. Выделяются нетипичные объекты, которые не удаётся присоединить ни к одному из кластеров.
Слайд 11
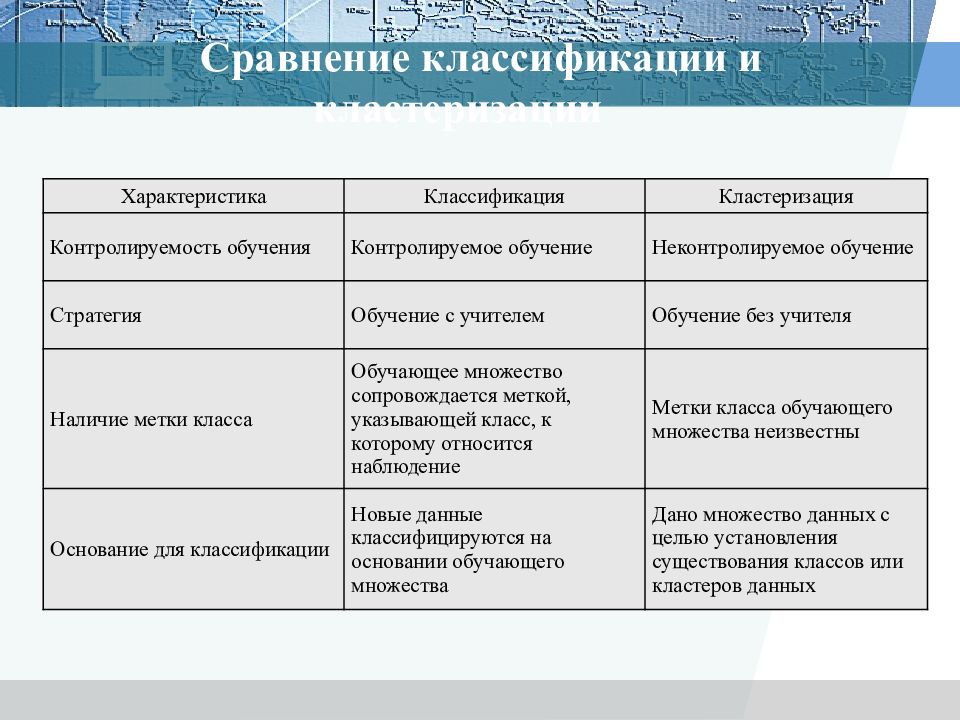
Характеристика Классификация Кластеризация Контролируемость обучения Контролируемое обучение Неконтролируемое обучение Стратегия Обучение с учителем Обучение без учителя Наличие метки класса Обучающее множество сопровождается меткой, указывающей класс, к которому относится наблюдение Метки класса обучающего множества неизвестны Основание для классификации Новые данные классифицируются на основании обучающего множества Дано множество данных с целью установления существования классов или кластеров данных Сравнение классификации и кластеризации
Слайд 13: Кластерный анализ
Кластерный анализ – это способ группировки многомерных объектов, основанный на представлении результатов отдельных наблюдений точками подходящего геометрического пространства с последующим выделением групп как «сгустков» этих точек (кластеров, таксонов). «Кластер» (cluster) в английском языке означает «сгусток», «гроздь винограда», «скопление звезд» и т.д. Термин кластерный анализ, впервые введенный Трионом (Tryon) в 1939 году.
Слайд 14
Первые работы, описывающие методы кластерного анализа относятся к концу 30-х годов. Считается, что термин «кластерный анализ» первым в употребление ввёл американский психолог из университета Беркли Роберт Трайон ( Robert C. Tryon ) в 1939. Однако активный интерес к данной теме пришёлся на период 60-80 гг. Импульсом для разработки многих кластерных методов послужила книга « Начала численной таксономии », опубликованная в 1963 г. двумя биологами — Робертом Сокэлом и Петером Снитом
Слайд 16
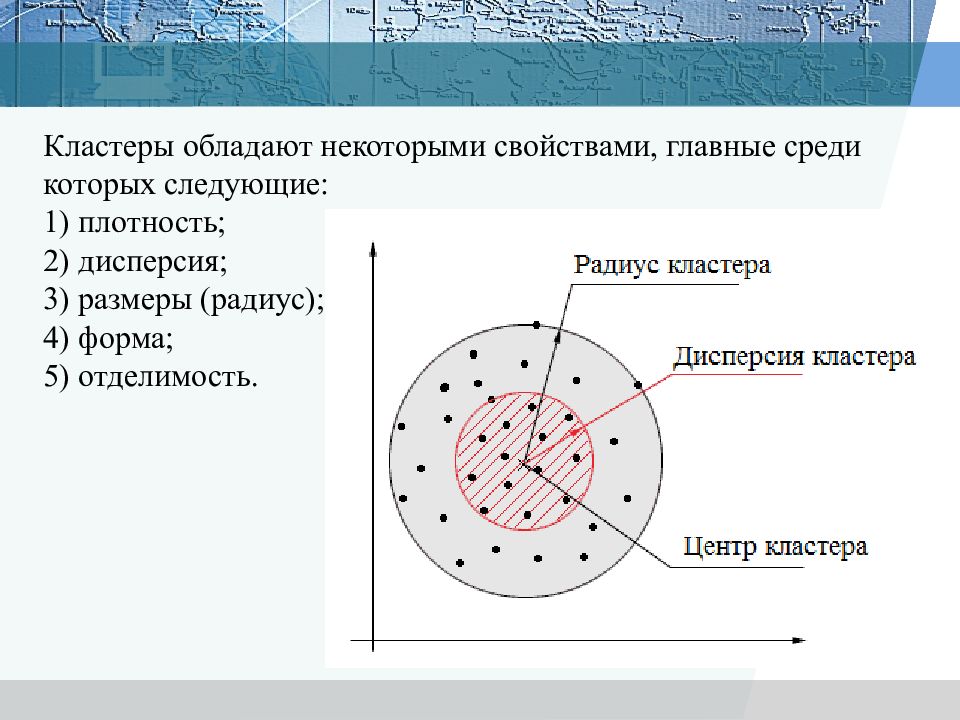
Кластеры обладают некоторыми свойствами, главные среди которых следующие: 1) плотность; 2) дисперсия; 3) размеры (радиус); 4) форма; 5) отделимость.
Слайд 17
внутрикластерные расстояния, как правило, меньше межкластерных ленточные кластеры кластеры с центром
Слайд 18
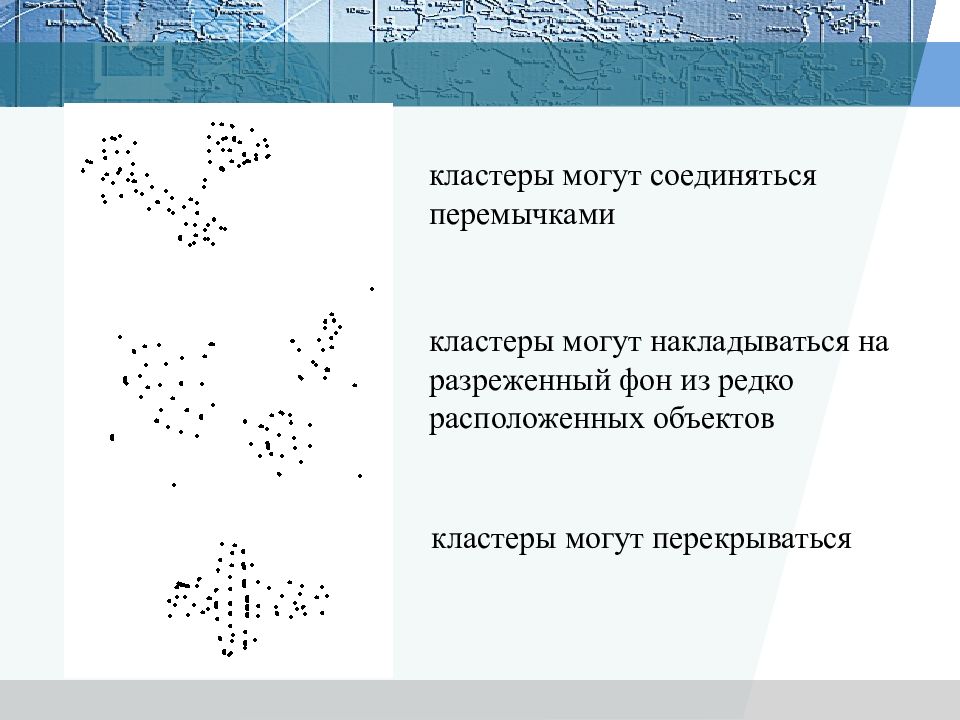
кластеры могут соединяться перемычками кластеры могут накладываться на разреженный фон из редко расположенных объектов кластеры могут перекрываться
Слайд 19
кластеры могут образовываться не по сходству, а по иным типам регулярностей кластеры могут вообще отсутствовать Каждый метод кластеризации имеет свои ограничения и выделяет кластеры лишь некоторых типов. Понятие «тип кластерной структуры» зависит от метода и также не имеет формального определения
Слайд 20
Н есмотря на различия в целях, типах данных и примененных методах, все исследования, использующие кластерный анализ, характеризуют следующие пять основных шагов : 1) отбор выборки для кластеризации; 2) определение множества признаков, по которым будут оцениваться объекты в выборке; 3) вычисление значений той или иной меры сходства между объектами; 4) применение метода кластерного анализа для создания групп сходных объектов; 5) проверка достоверности результатов кластерного решения.
Слайд 21
ПРЕДОСТЕРЕЖЕНИЙ ОТНОСИТЕЛЬНО КЛАСТЕРНОГО АНАЛИЗА 1) Многие методы кластерного анализа — довольно простые процедуры, которые, как правило, не имеют достаточного статистического обоснования 2) Методы кластерного анализа разрабатывались для многих научных дисциплин, а потому несут на себе отпечатки специфики этих дисциплин. 3) Разные кластерные методы могут порождать и порождают различные решения для одних и тех же данных.
Слайд 22
Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся во множестве Х, разбить множество объектов G на m (m – целое) кластеров (подмножеств) Q 1, Q 2, …, Q m, так, чтобы каждый объект G j принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие одному и тому же кластеру, были сходными, в то время, как объекты, принадлежащие разным кластерам были разнородными.
Слайд 23
Различные приложения кластерного анализа можно свести к четырем основным задачам : 1) разработка типологии или классификации; 2) исследование полезных концептуальных схем группирования объектов; 3) порождение гипотез на основе исследования данных; 4) проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.
Слайд 24
Формулировка задачи кластерного анализа Пусть множество I={I 1,I 2,…, I n } обозначает n объектов. Результат измерения i-й характеристики Ij объекта обозначают символом x ij, а вектор X j =[ x ij ] отвечает каждому ряду измерений (для j- го объекта). Таким образом, для множества I объектов исследователь располагает множеством векторов измерений X={X 1, X 2,…, X n }, которые описывают множество I. Множество X может быть представлено как n точек в p-мерном евклидовом пространстве Е р. Пусть m – целое число, меньшее чем n. Задача кластерного анализа заключается в том, чтобы на основании данных, содержащихся во множестве, разбить множество объектов I на m кластеров (подмножеств) π 1,π 2,…, π m так, чтобы каждый объект I j принадлежал одному и только одному подмножеству разбиения и чтобы объекты, принадлежащие разным кластерам, были разнородными (несходными).
Слайд 25
Алгоритмы кластеризации Имеется обучающая выборка X ℓ = {x 1,...,x ℓ } ⊂ X и функция расстояния между объектами ρ( x,x ′). Требуется разбить выборку на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике ρ, а объекты разных кластеров существенно отличались. При этом каждому объекту x i ∈ X ℓ приписывается метка (номер) кластера y i. Алгоритм кластеризации - это функция a: X → Y, которая любому объекту x ∈ X ставит в соответствие метку кластера y ∈ Y. Множество меток Y в некоторых случаях известно заранее, однако чаще ставится задача определить оптимальное число кластеров, с точки зрения того или иного критерия качества кластеризации.
Слайд 27: Основные понятия кластерного анализа
Матрица расстояний d i i =0 для i=1, 2,…,n.
Слайд 28: Основные понятия кластерного анализа
Мерой близости между объектами X i и X j является вещественная функция μ(X i,X j )=μ ij со свойствам : Пары значений мер близости можно объединить в матрицу близости:
Слайд 29
R=(r ij ), i,j=1, 2,..., n, элемент r ij который определяет степень близости i-го объекта к j-му.
Слайд 30: Стандартизация
Стандартизация (standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака.
Слайд 31
Меры сходства 1) коэффициенты корреляции; 2) меры расстояния; 3) коэффициенты ассоциативности; 4) вероятностные коэффициенты сходства Количественное оценивание сходства отталкивается от понятия метрики. При этом подходе к сходству события представляются точками координатного пространства, причем замеченные сходства и различия между точками находятся в соответствии с метрическими расстояниями между ними
Слайд 32
1 ) Симметрия. Даны два объекта х и у; расстояние между ними удовлетворяет условию d ( x, y )= d ( y, x )≥0. 2) Неравенство треугольника. Даны три объекта х, у, г; расстояния между ними удовлетворяют условию d ( x, y )≤ d ( x, z )+ d ( y, z ). Очевидно, это просто утверждение, что длина любой стороны треугольника меньше или равна сумме двух других сторон. Полученное выражение также называется метрическим неравенством. 3) Различимость нетождественных объектов. Даны два объекта х и у: если d ( x, y )≠0, то x ≠ y. 4) Неразличимость идентичных объектов. Для двух идентичных объектов x и x' d ( x, x')=0 т. е. расстояние между этими объектами равно нулю. Критерии для мер сходства
Слайд 39: меры расстояния
C тепенное расстояние Минковского Степенное расстояние Квадрат евклидового расстояния Расстояние Чебышева
Слайд 40: меры расстояния
где S ковариационная матрица выборки Х=(Х 1, Х 2,….. X n ) Манхэттенское расстояние Расстояние Махаланобиса Расстояние Хемминга
Слайд 41
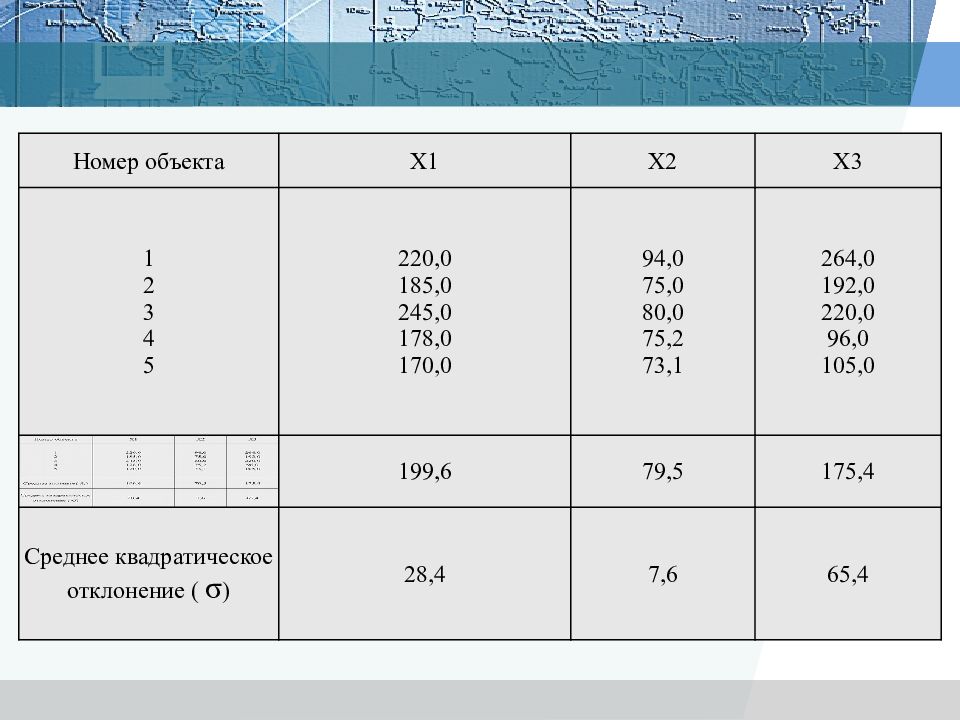
Номер объекта X1 X2 X3 1 2 3 4 5 220,0 185,0 245,0 178,0 170,0 94,0 75,0 80,0 75,2 73,1 264,0 192,0 220,0 96,0 105,0 199,6 79,5 175,4 Среднее квадратическое отклонение ( σ ) 28,4 7,6 65,4
Слайд 42
Перед тем как вычислять матрицу расстояний, нормируем исходные данные по формуле .
Слайд 44
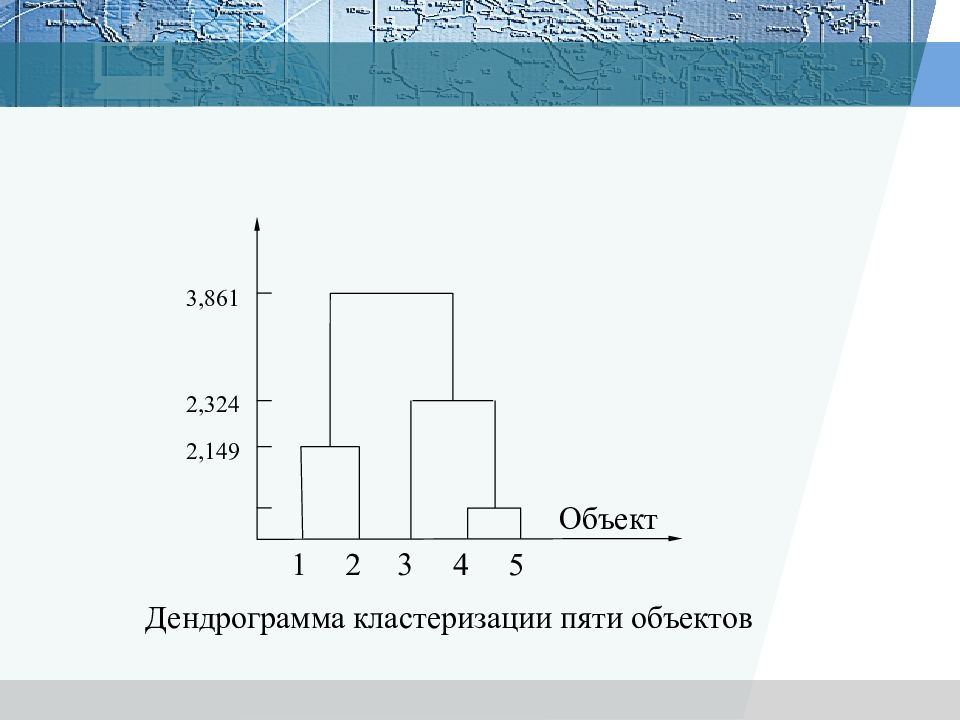
1 2 3 4 5 Объект 2,149 2,324 3,861 Дендрограмма кластеризации пяти объектов
Слайд 45
Коэффициенты ассоциативности 1 0 1 a b 0 c d простой коэффициент совстречаемости ; коэффициент Жаккара ; коэффициент Гауэра
Слайд 47
Объект 2 Объект 1 1 0 1 1 1 0 2 4 Два объекта имеют только один общий признак, и различаются по 4 признакам. Таким образом, S = 0,625 (=5/8). Тем не менее J = 0,250 ( = 1/4).
Слайд 48
Коэффициент Гауэра — единственный в своем роде, так как при оценке сходства допускает одновременное использование переменных, измеренных по различным шкалам. Коэффициент был предложен Гауэром (1971) и имеет вид где W ijk — весовая переменная, принимающая значение 1, если сравнение объектов по признаку k следует учитывать, и 0 — в противном случае; S ijk — «вклад» в сходство объектов, зависящий от того, учитывается ли признак k при сравнении объектов i и j. В случае бинарных признаков W ijk = 0, если признак k отсутствует у одного или обоих сопоставляемых объектов
Слайд 49: Методы объединения или связи
6. Методы объединения или связи Метод ближнего соседа или одиночная связь 1. 3. 2. Метод наиболее удаленных соседей Метод Варда 4. Метод невзвешенного попарного среднего 5. Метод взвешенного попарного среднего 7. Невзвешенный центроидный метод Взвешенный центроидный метод
Слайд 51
Одиночная связь (метод ближайшего соседа (single linkage или nearest neighbor )).
Слайд 52: меры расстояния, дендрограмма
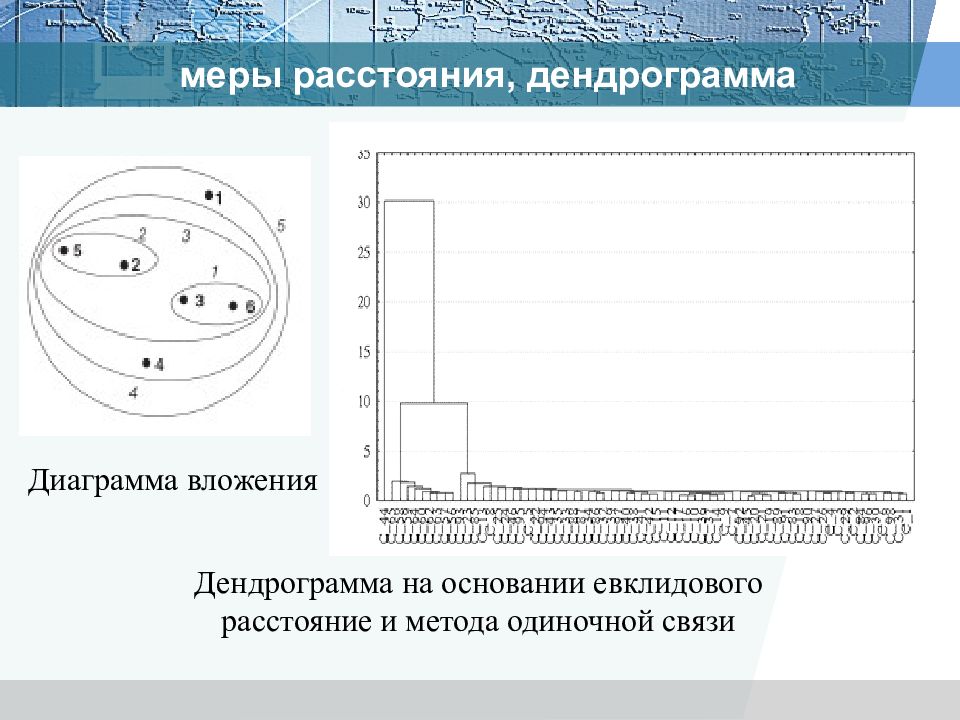
Дендрограмма на основании евклидового расстояние и метода одиночной связи Диаграмма вложения
Слайд 54: меры расстояния, дендрограмма
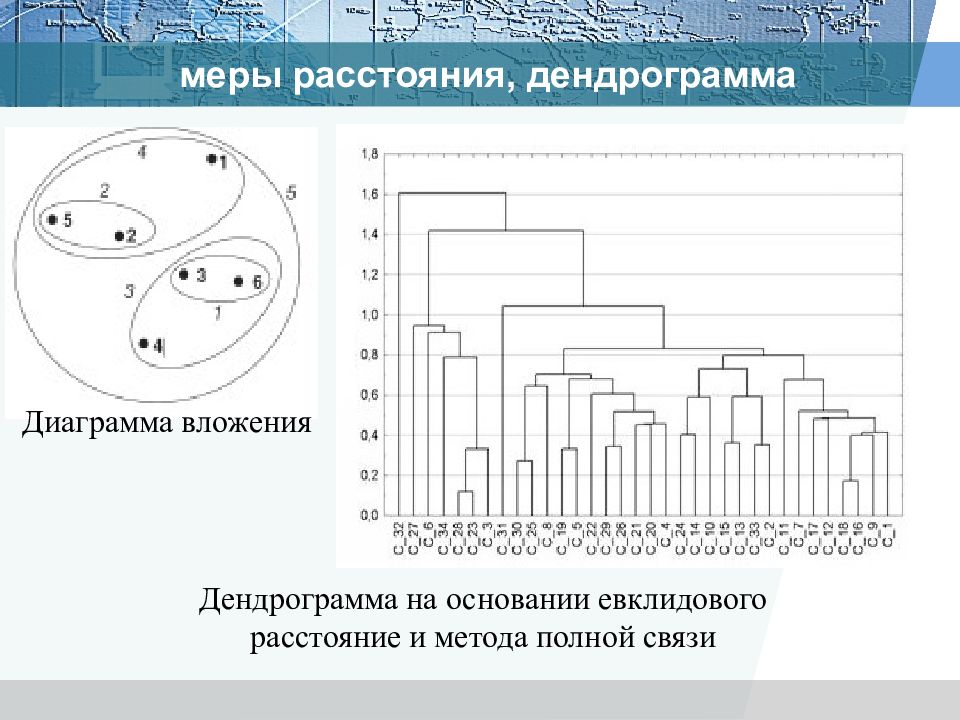
Дендрограмма на основании евклидового расстояние и метода полной связи Диаграмма вложения
Слайд 55
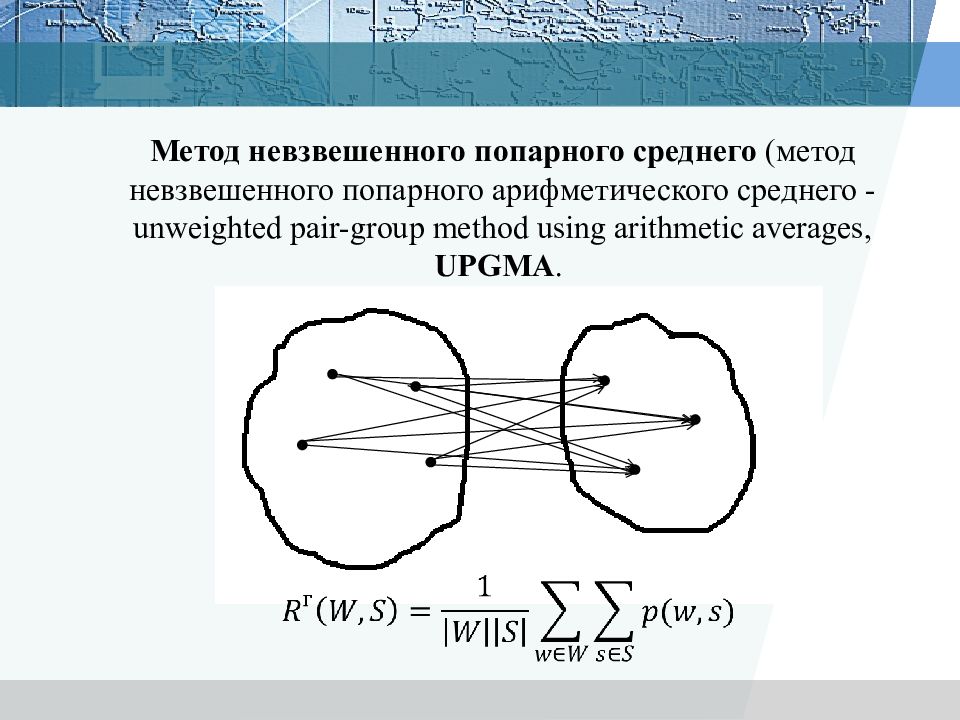
Метод невзвешенного попарного среднего (метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages, UPGMA.
Слайд 56: меры расстояния, дендрограмма
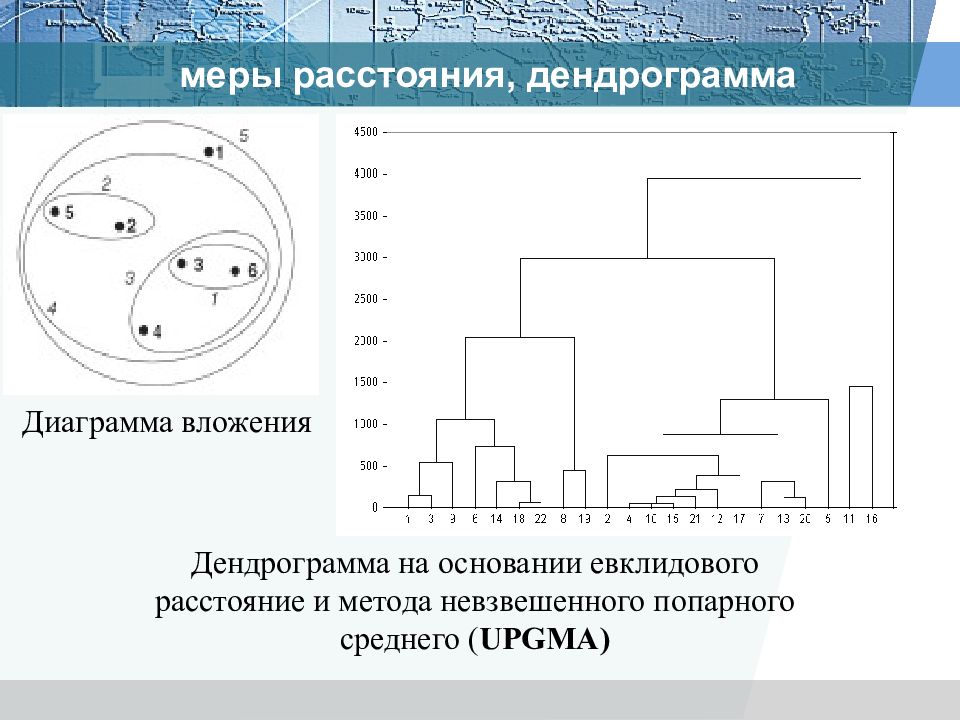
Дендрограмма на основании евклидового расстояние и метода невзвешенного попарного среднего ( UPGMA) Диаграмма вложения
Слайд 57
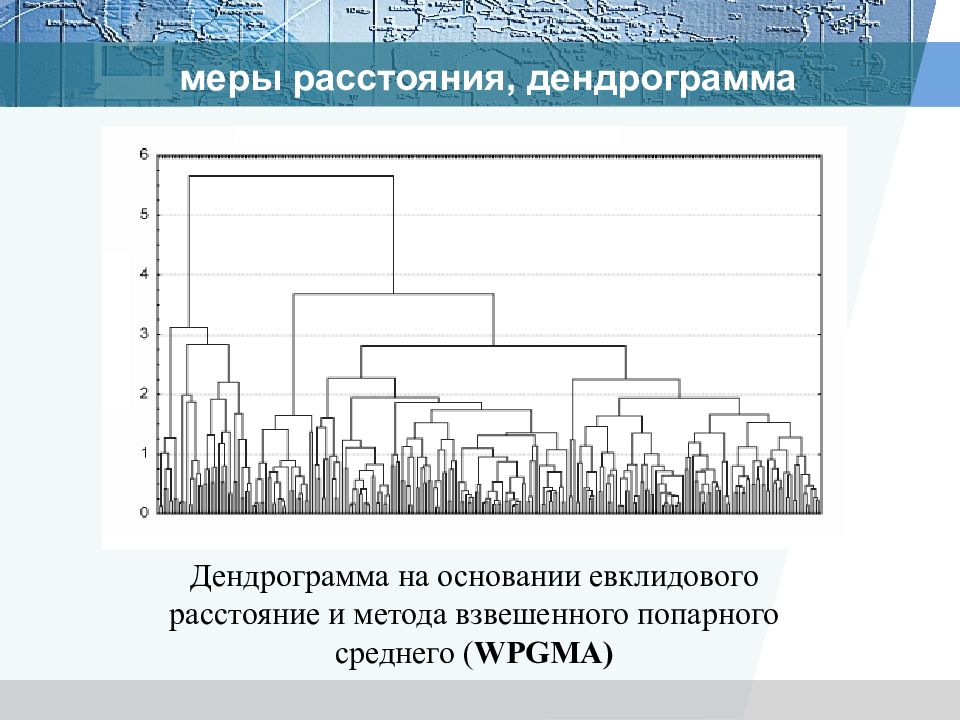
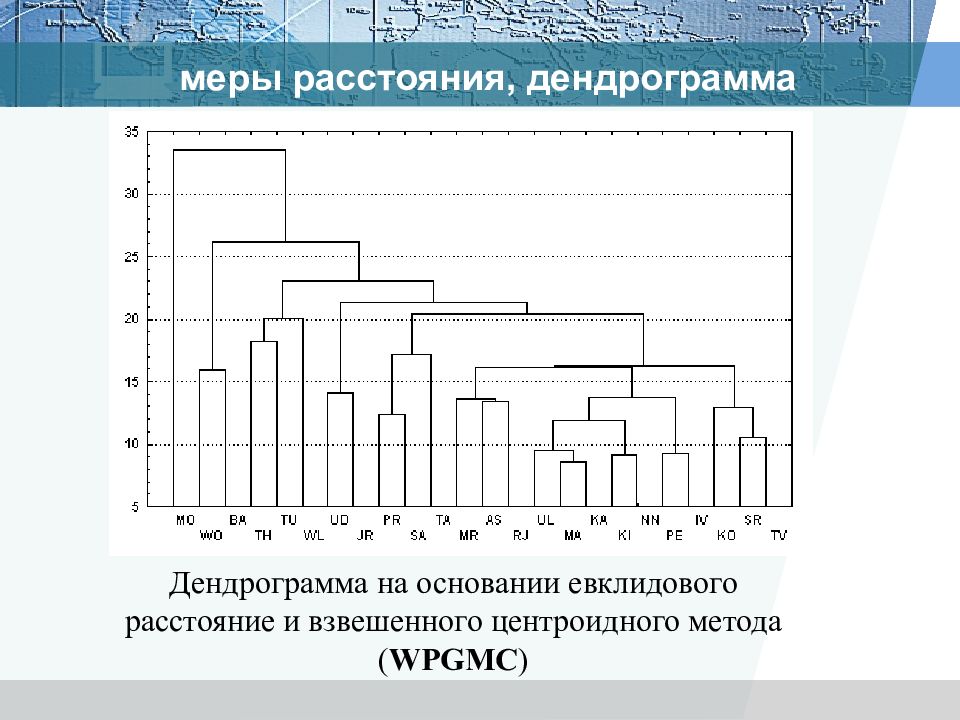
Дендрограмма на основании евклидового расстояние и метода взвешенного попарного среднего ( WPGMA) меры расстояния, дендрограмма
Слайд 58
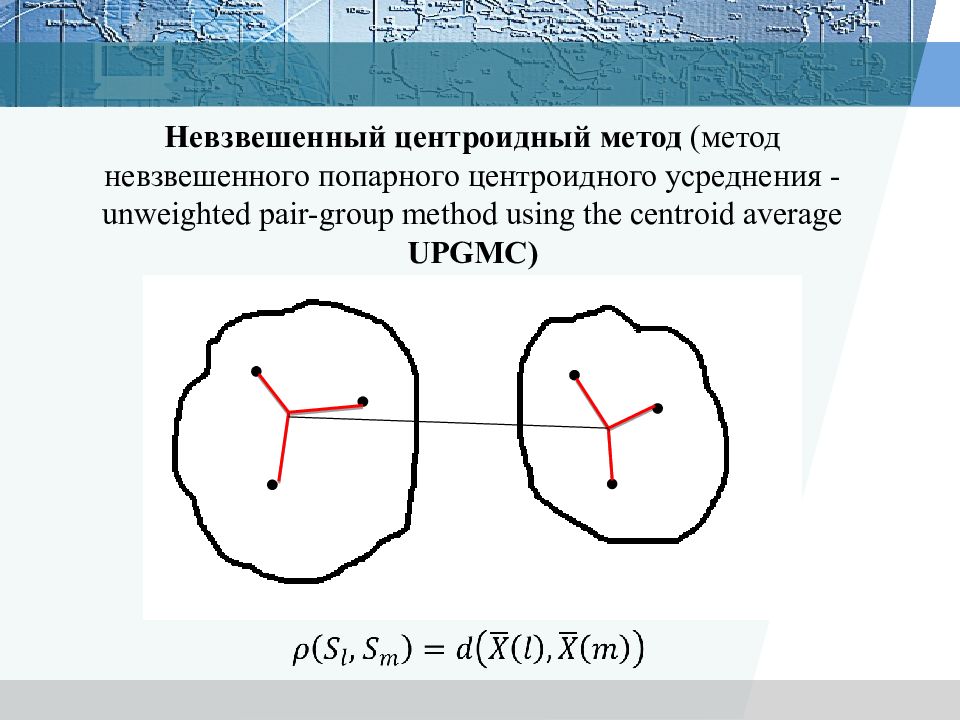
Невзвешенный центроидный метод (метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average UPGMC)
Слайд 59
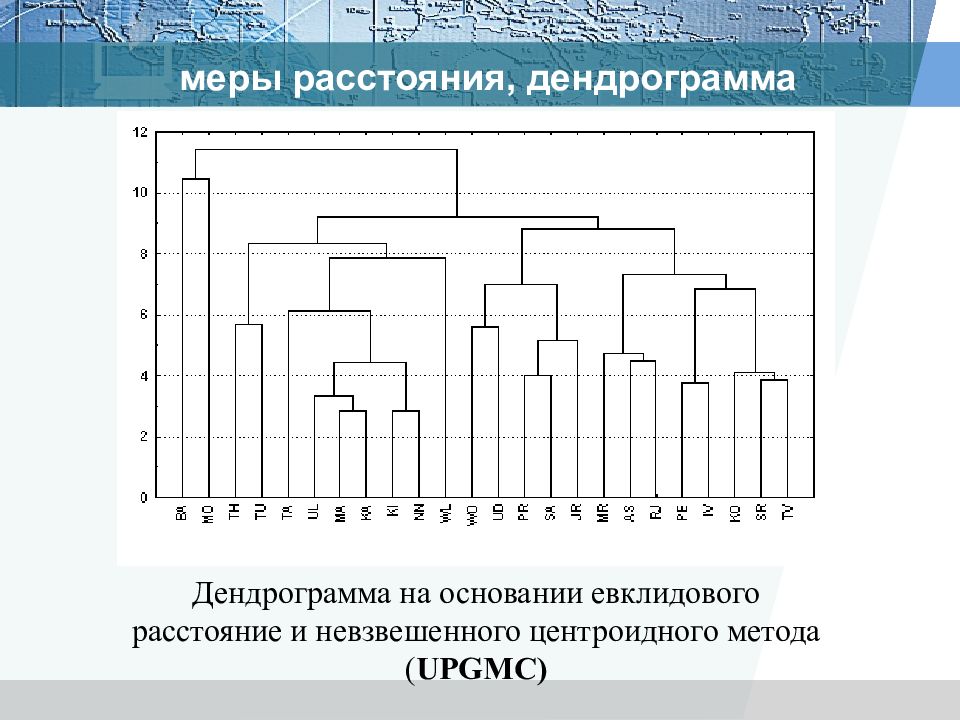
меры расстояния, дендрограмма Дендрограмма на основании евклидового расстояние и невзвешенного центроидного метода ( UPGMC)
Слайд 60
Дендрограмма на основании евклидового расстояние и взвешенного центроидного метода ( WPGMC ) меры расстояния, дендрограмма
Слайд 62
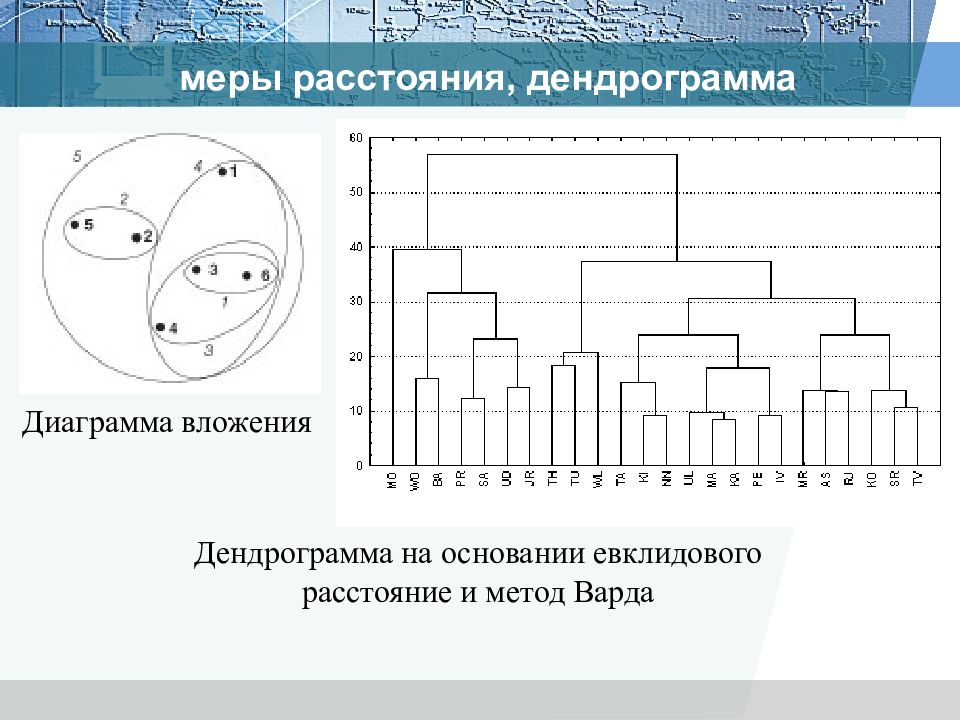
Дендрограмма на основании евклидового расстояние и метод Варда меры расстояния, дендрограмма Диаграмма вложения
Слайд 63
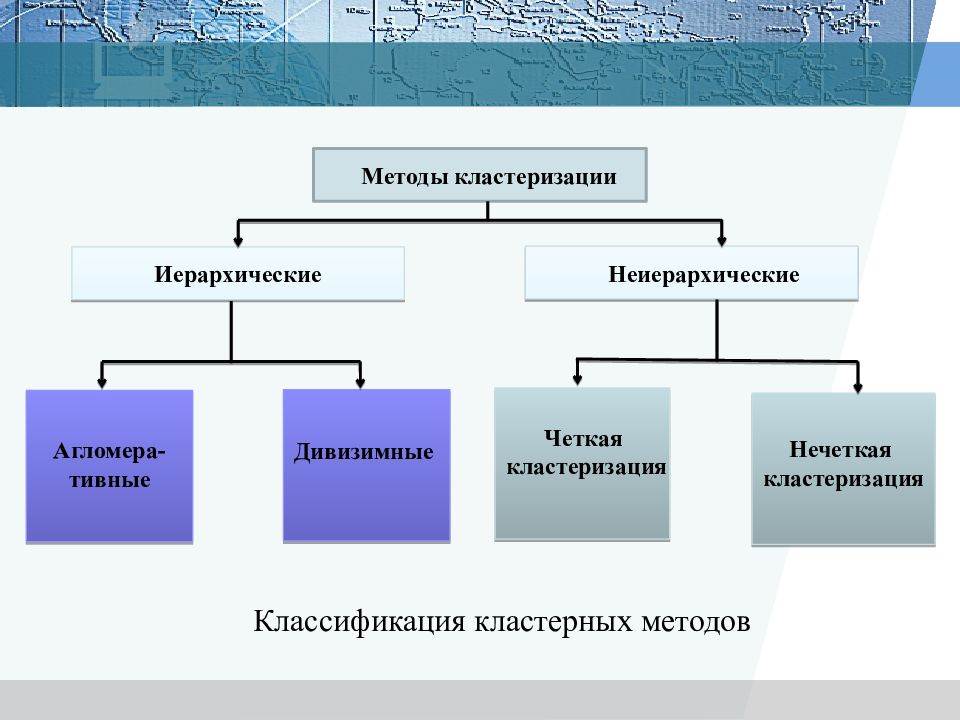
Методы кластеризации Иерархические Неиерархические Агломера- тивные Дивизимные Четкая кластеризация Нечеткая кластеризация Классификация кластерных методов
Слайд 64: Методы кластеризации
методы, основывающиеся на иерархической апроцедуре (итерационные процедуры, которые пытаются найти наилучшее разбиение, ориентируясь на заданный критерий оптимизации, не строя при этом полного дерева: наиболее популярный — алгоритм метод k–средних Мак–Кина
Слайд 65: Методы кластеризации
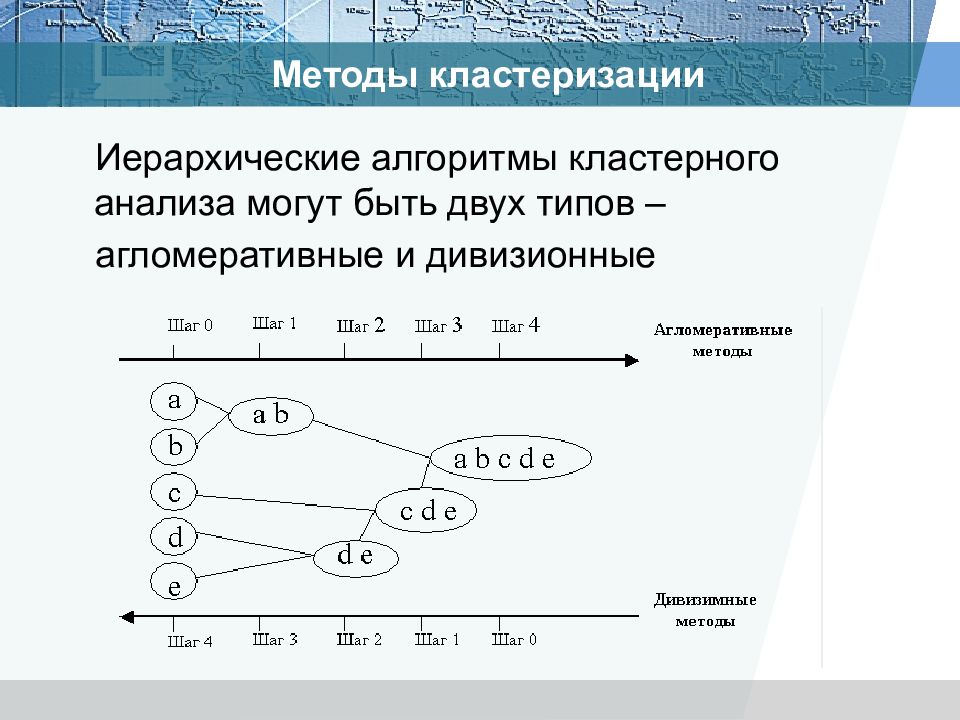
Иерархические алгоритмы кластерного анализа могут быть двух типов – агломеративные и дивизионные
Слайд 68: Методы кластеризации
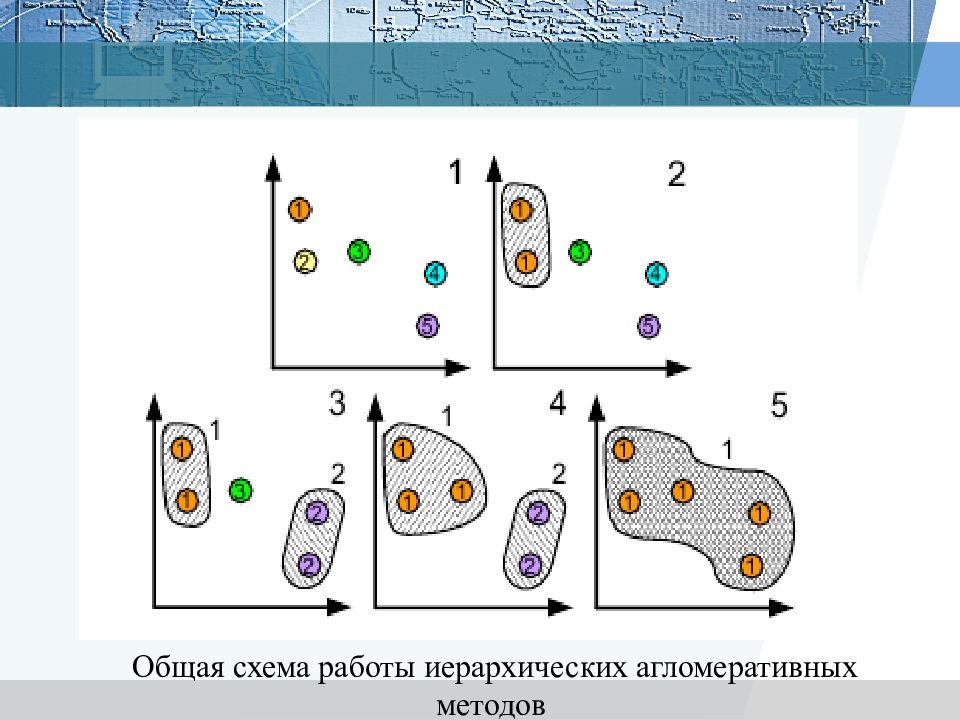
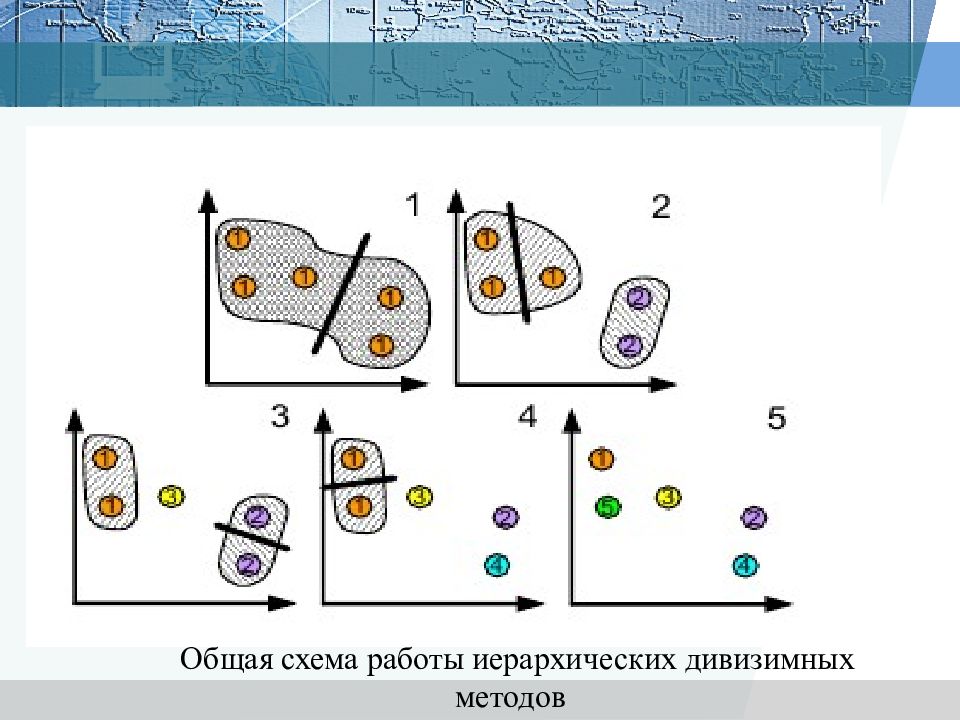
Иерархические алгоритмы связаны с построением дендрограмм (от греческого dendron - "дерево"), которые являются результатом иерархического кластерного анализа. Дендрограмма описывает близость отдельных точек и кластеров друг к другу, представляет в графическом виде последовательность объединения (разделения) кластеров. Дендрограмма (dendrogram) - древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров. Дендрограммой также называют древовидной схемой, деревом объединения кластеров, деревом иерархической структуры. Дендрограмма представляет собой вложенную группировку объектов, которая изменяется на различных уровнях иерархии.
Слайд 69
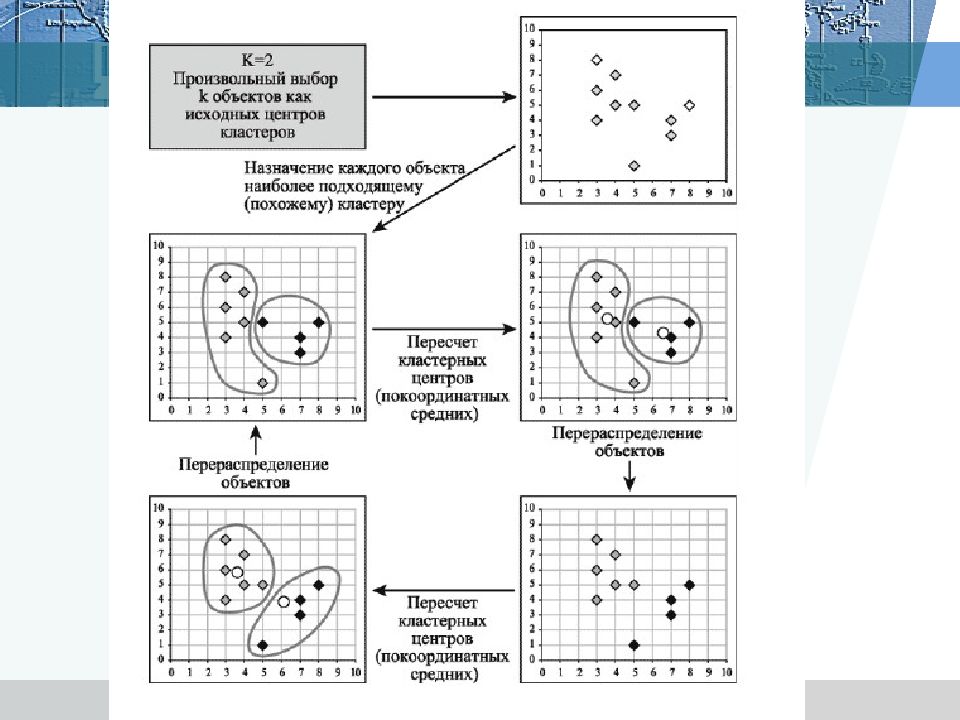
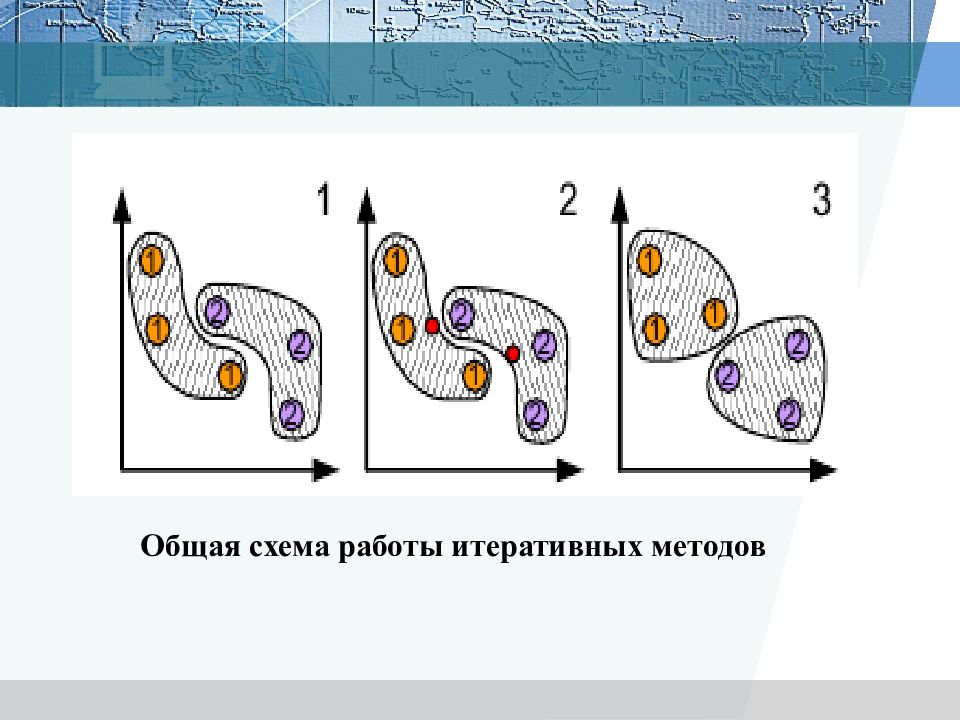
Итеративные методы Алгоритм: 1. начать с исходного разбиения данных на некоторое заданное число кластеров; вычислить центры тяжести этих кластеров; 2. поместить каждую точку данных в кластер с ближайшим центром тяжести; 3. вычислить новые центры тяжести кластеров; кластеры не заменяются на новые до тех пор, пока не будут просмотрены полностью все данные; 4. шаги 2 и 3 повторяются до тех пор, пока не перестанут меняться кластеры.
Слайд 70
Алгоритм метод k–средних Мак–Кина 1. Случайно выбрать k точек, являющихся начальными координатами «центрами масс» кластеров (любые k из n объектов, или вообще k случайных точек). 2. Определяем центр каждого кластера µ j, j ∈{1,..., m }как элемент, компоненты которого вычисляются как среднее арифметическое входящих в этот кластер элементов. В центре кластера достигается минимум функции суммы квадратов расстояний от элементов кластера до точки. 3. Отнести каждый объект к кластеру с ближайшим «центром масс». 4. Пересчитать «центры масс» кластеров согласно текущему членству. 5. Если критерий остановки не удовлетворен, вернуться к шагу 2.
Слайд 74: Нумерическая таксономия
Фенотипический коэффициент простого соответствия (подобия) равен: S = (а + d) / (а + b +c+d) Дендрограмма, построенная на основе коэффициентов подобия между шестью видами бактерий
Слайд 75
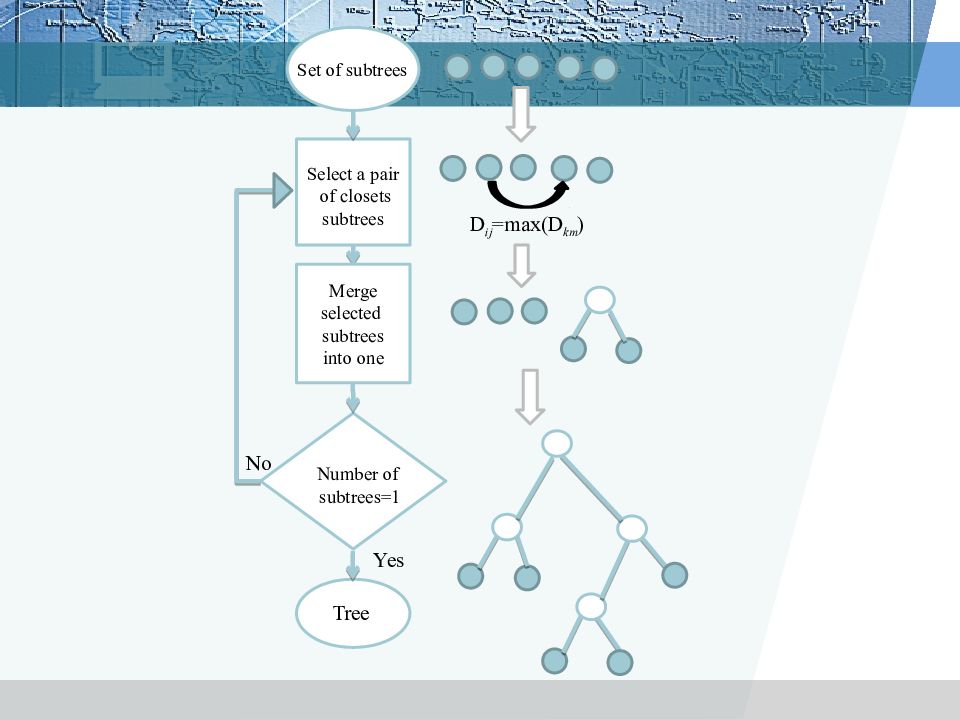
Set of subtrees Select a pair of closets subtrees Merge selected subtrees into one Number of subtrees=1 Tree Yes No D ij =max(D km )
Слайд 76
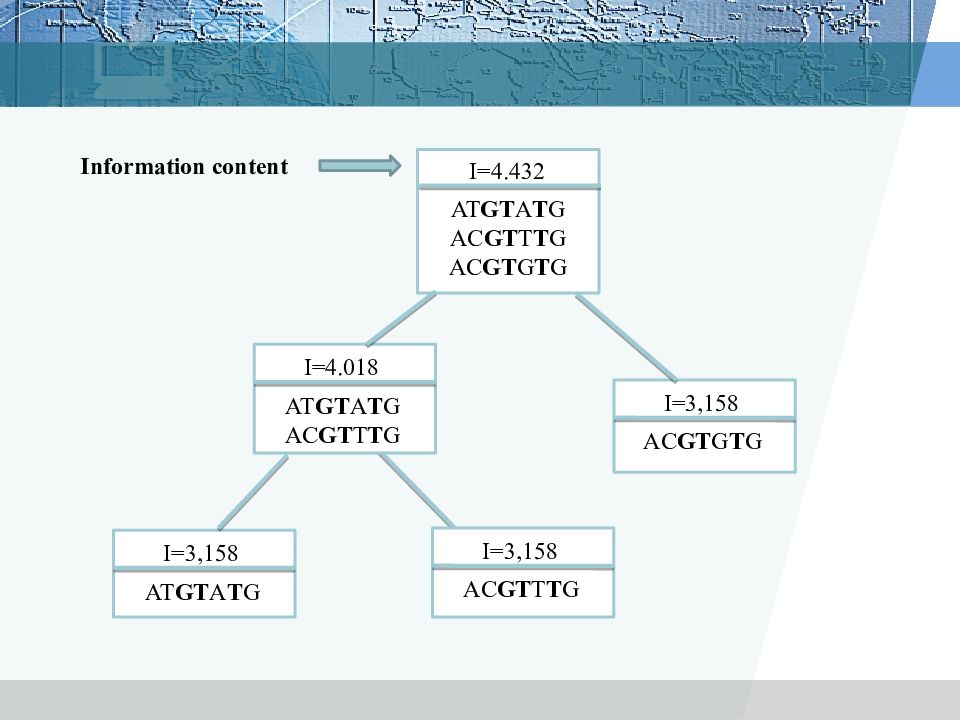
I=4.432 AT GT A T G AC GT T T G AC GT G T G I=4. 018 AT GT A T G AC GT T T G I= 3,158 AC GT G T G I= 3,158 AT GT A T G I= 3,158 AC GT T T G Information content
Слайд 77: Нумерическая таксономия
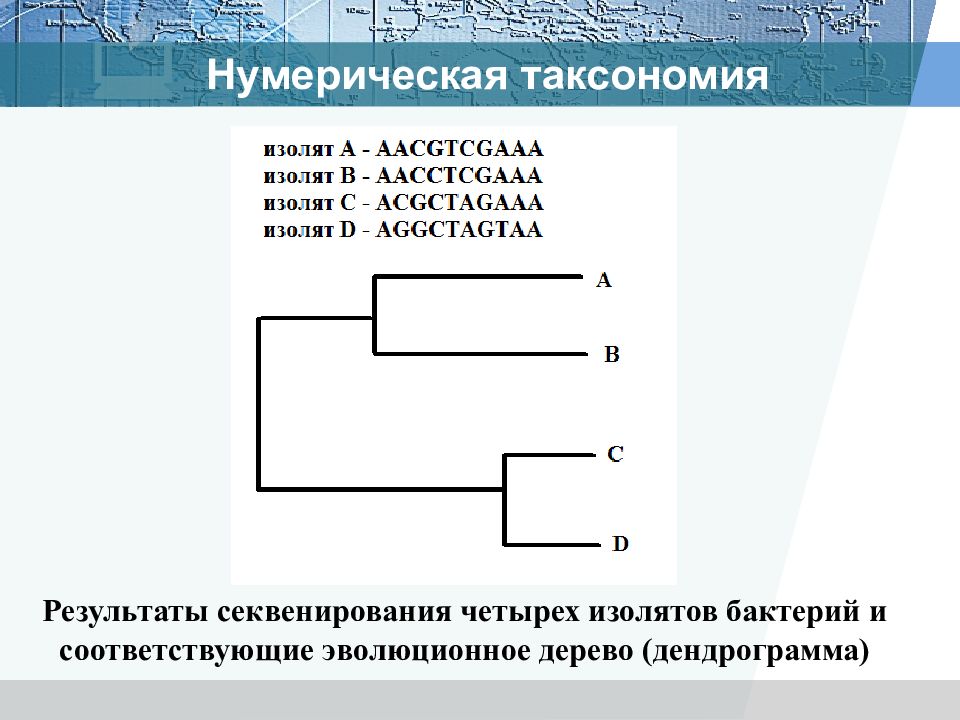
Результаты секвенирования четырех изолятов бактерий и соответствующие эволюционное дерево (дендрограмма)
Слайд 78
Литературные источники использованные при подготовке: Айвазян С. А., Бухштабер В. М., Енюков И. С., Мешалкин Л. Д. Прикладная статистика: классификация и снижение размерности. — М.: Финансы и статистика, 1989. Дорофеюк А. А. Алгоритмы автоматической классификации // Проблемы расширения возможностей автоматов (Труды Ин-та пробл. управ. АН СССР). Вып 1. – М.: ИПУ АН СССР, 1971. С. 5-41. Дюран Б., Оделл П. Кластерный анализ. – М.: Статистика, 1977. – 128 с Жамбю М. Иерархический кластер-анализ и соответствия. – М.: Финансы и статистика, 1988. – 342 с. Ким Дж.О., Мьюллер Ч.У, Клекка У.Р. и др. Факторный, дискриминантный и кластерный анализ. – М.: Финансы и статистика, 1989. – 215 с. Классификация и кластер / Под ред. Дж. Вэн- Райзина. – М.: Мир, 1980. – 390 с. Кольцов П.П. Математические модели теории распознавания образов // Компьютер и задачи выбора. – М.: Наука, 1989. С. 89-119. Кузнецов Д. Ю, Трошкина Т.Л. Кластерный анализ и его применение http://elibrary.ru/item.asp?id=10365372 Мандель И.Д. Кластерный анализ. – М.: Финансы и статистика, 1988. – 176 с. Методы кластерного анализа. Иерархические методы http://www.intuit.ru/department/database/datamining/13/4.html
Слайд 79
11. Миркин Б.Г., Черный Л.Б. Об измерении близости между различными разбиениями конечного множества объектов // Автоматика и телемеханика. 1970. № 5. С. 6-18. 12. Мхитарян В.С., Архипова М.Ю., Сиротин В.П. ЭКОНОМЕТРИКА: Учебно-методический комплекс. – М.: Изд. центр ЕАОИ. 2008. – 144 с. 13. Николаенко С. Курс лекций «Алгоритмы кластеризации I I» http : // logic. pdmi. ras. ru /∼ sergey / index. php ? page = teaching 14. Розенберг Г.С. О сравнении различных методов автоматической классификации // Автоматика и телемеханика. 1975. № 9. С. 145-148. 15. Чубукова И. А. Лекция «Data Mining». 16. Факторный, дискриминантный и кластерный анализ: Пер с англ./Дж.-О. Ким, Ч. У. Мьюллер, У. Р. Клекка и др.; Под ред. И. С. Енюкова. — М.: Финансы и статистика, 1989.— 215 с. 17. Фрей Т.Э.-А. О математико-фитоценотических методах классификации растительности: Автореф. дис. … докт. биол. наук. – Тарту: ТартГУ, 1967. – 32 с. 18. Воронов К. В. « Машинное обучение (курс лекций, К.В.Воронцов) » -http://www.MachineLearning.ru/wiki 19. Dallwitz, M.J. 1988. A flexible clustering method based on UPGMA and ISS http://delta-intkey.com 20. Geoff Bohling. Dimension reduction and cluster analysis.- 2006. – 22 p.
Слайд 80
21. Chamundeswari1 G., Pardasaradhi G., Satyanarayana Ch. An Experimental Analysis of K-means Using Matlab //International Journal of Engineering Research & Technology (IJERT).- Vol. 1 Issue 5, July – 2012. PP. 1 – 5. 22. Jain, Murty, Flynn Data clustering: a review. // ACM Comput. Surv. 31 (3), 1999 23. Joe H. Ward (1963). Hierarchical Grouping to optimize an objective function. Journal of American Statistical Association, 58(301), 236-244. 24. Sokal R., Sneath P. Principles of Numerical Taxonomy. - San Francisco: W.H. Freeman, 1963. - 573 р 25. Ward J.H. Hierarchical grouping to optimize an objective function // J. Amer. Statist. Assoc. 1963. V. 58. № 301. Р. 236-244.
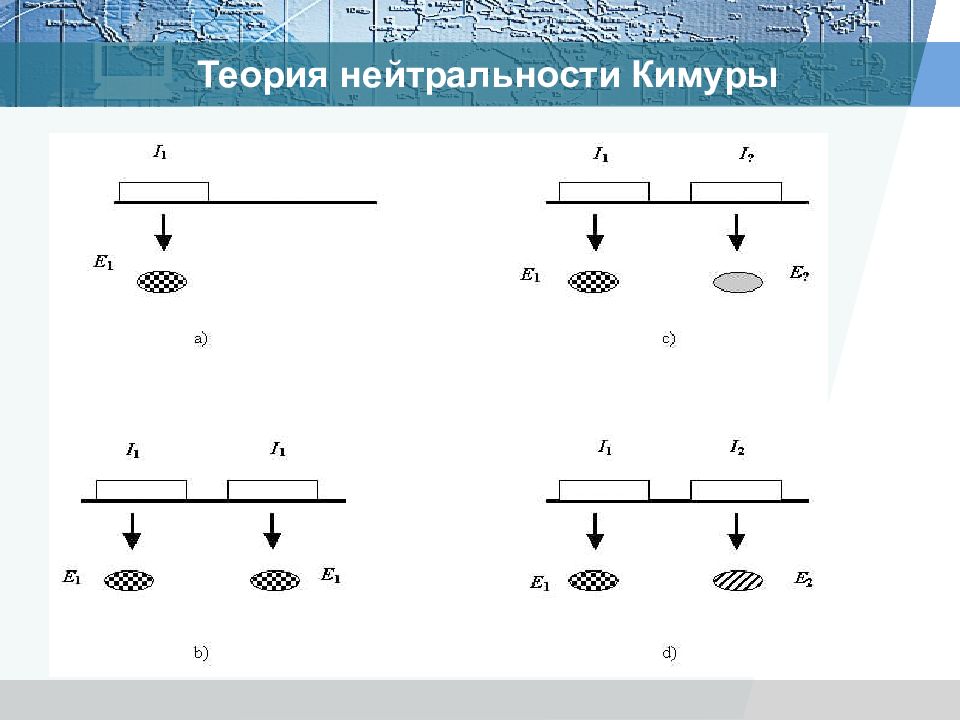
Слайд 82: Теория нейтральности Кимуры
Основное предположение этой теории состоит в следующем: на молекулярном уровне мутации (замены аминокислот или нуклеотидов) преимущественно нейтральны или слабо вредны (существенно вредные мутации также возможны, но они элиминируются из популяции селекцией).