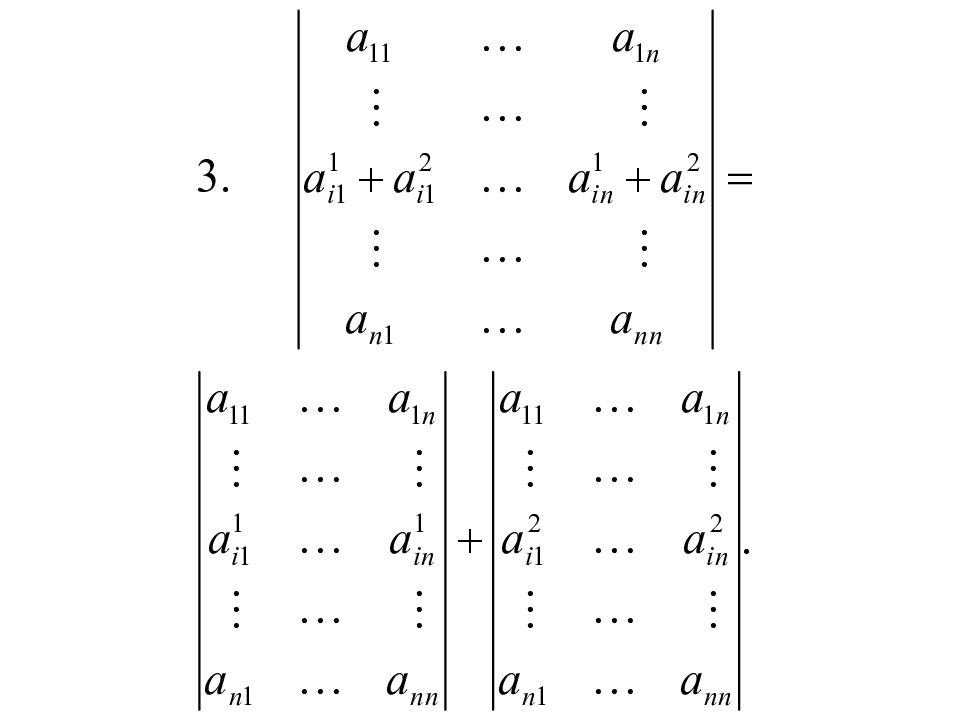
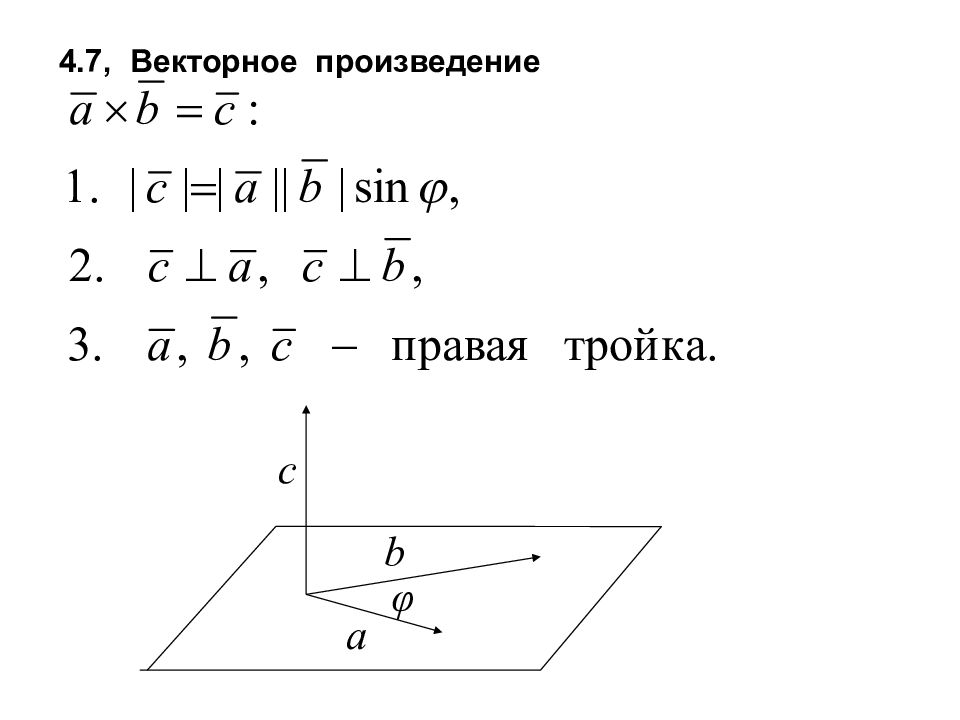
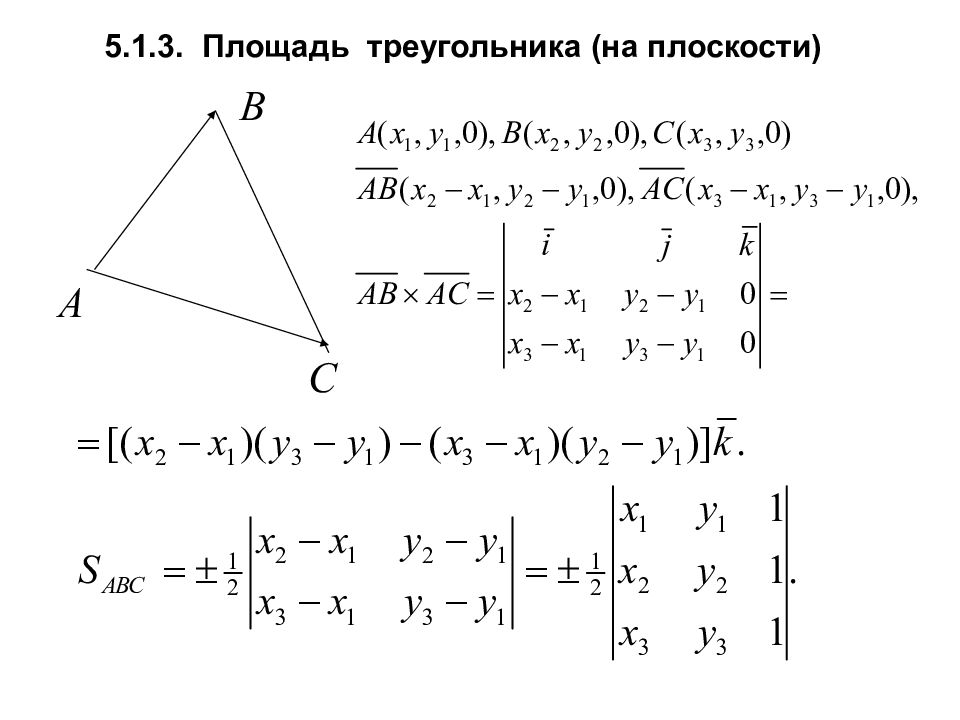
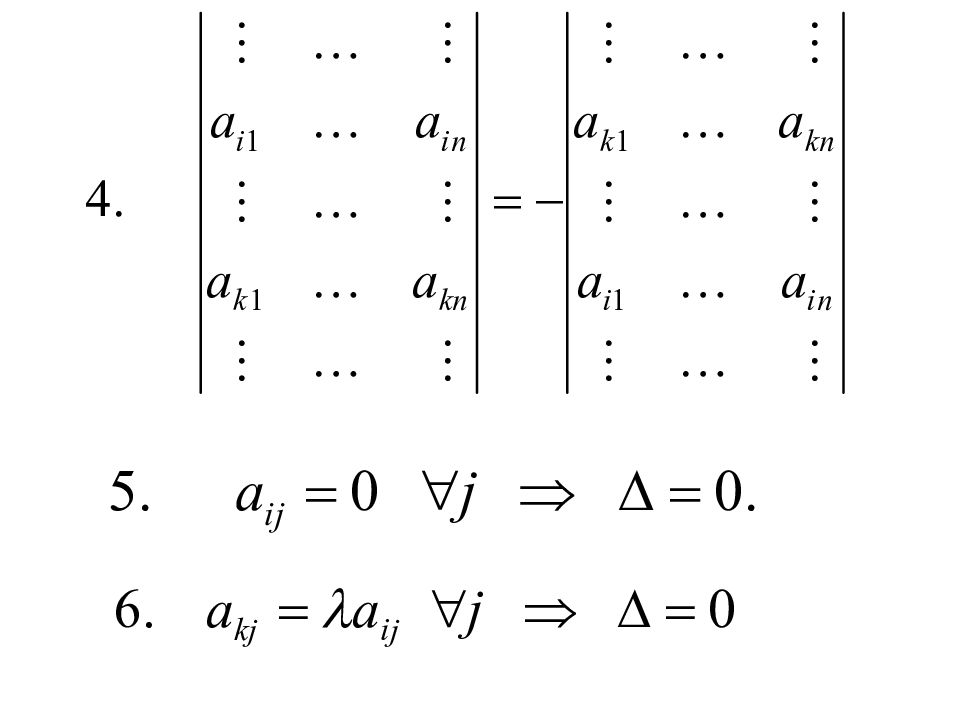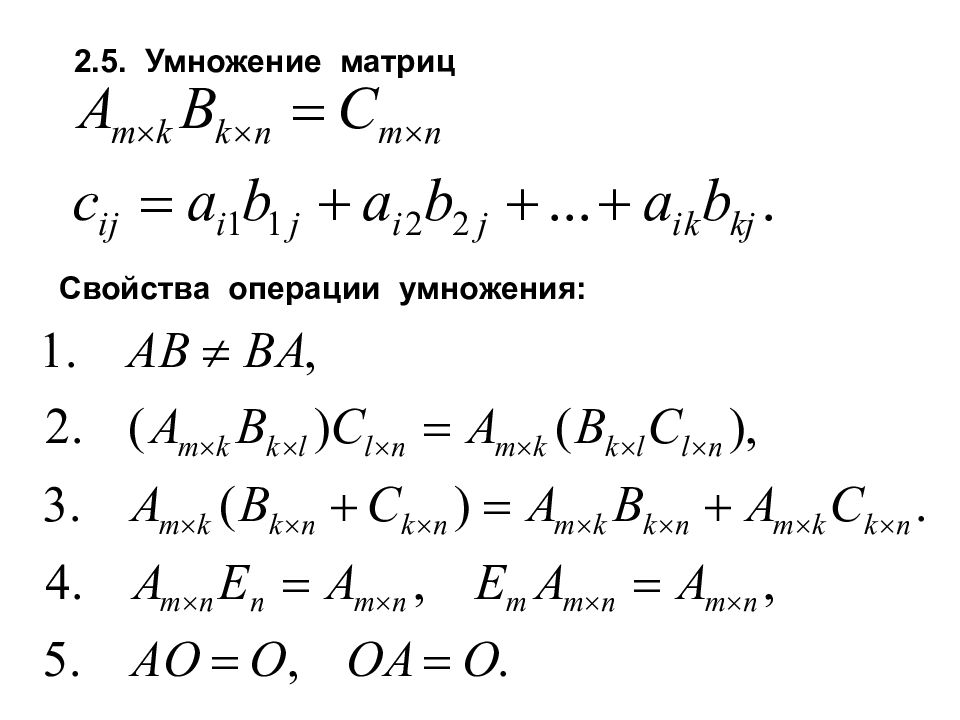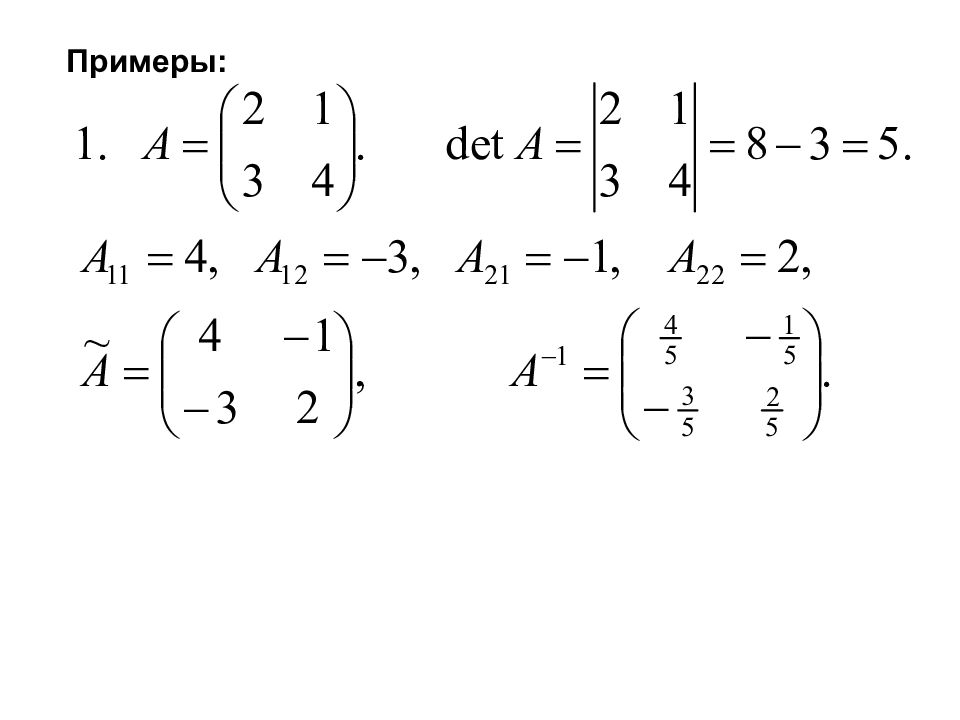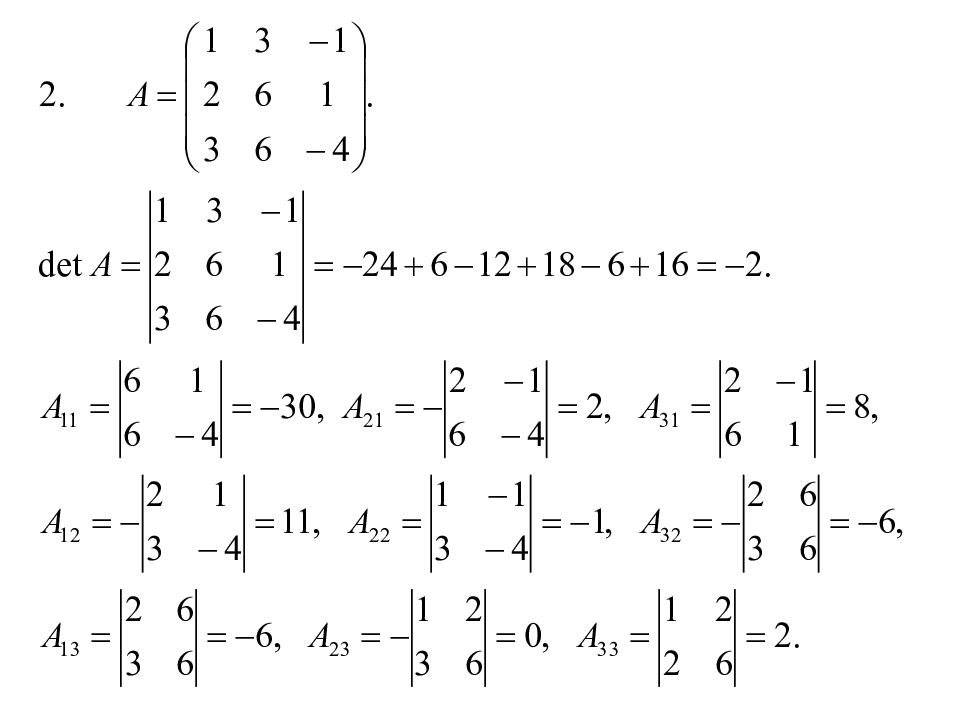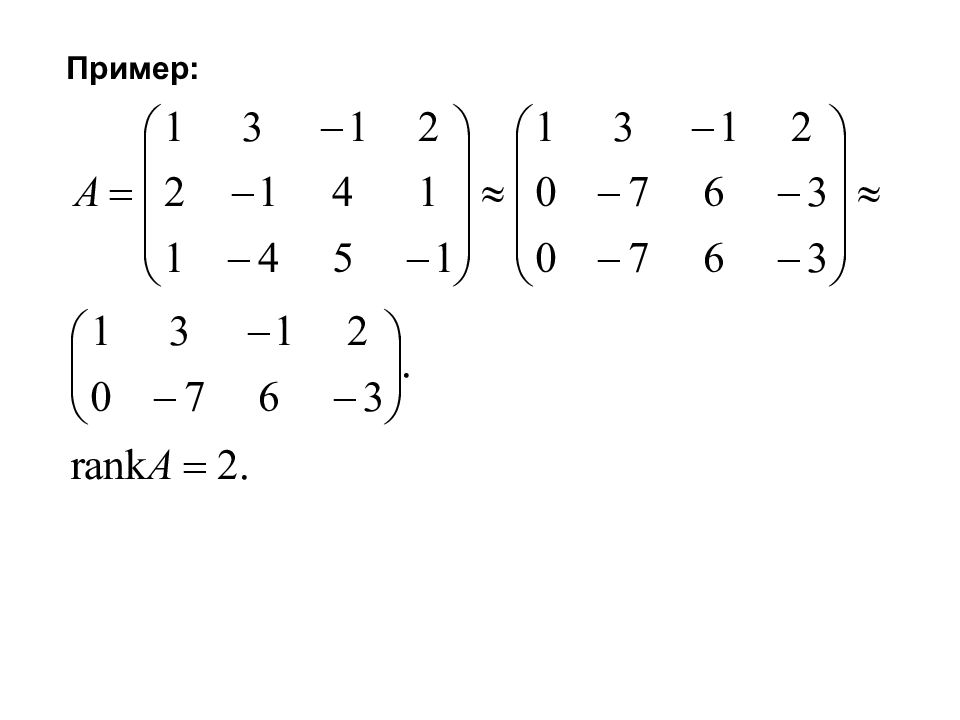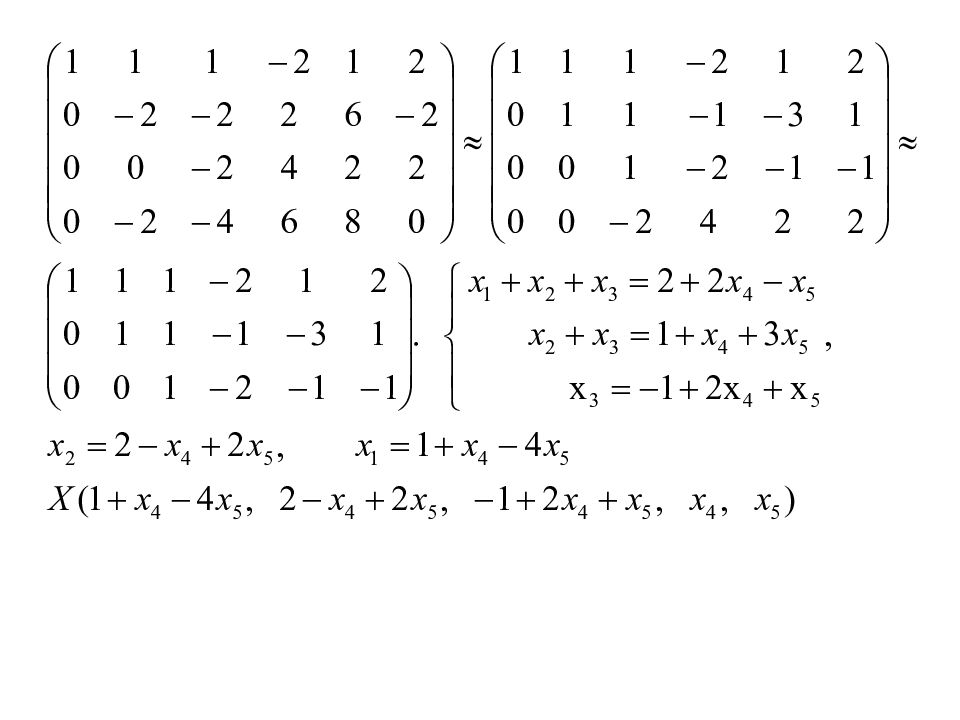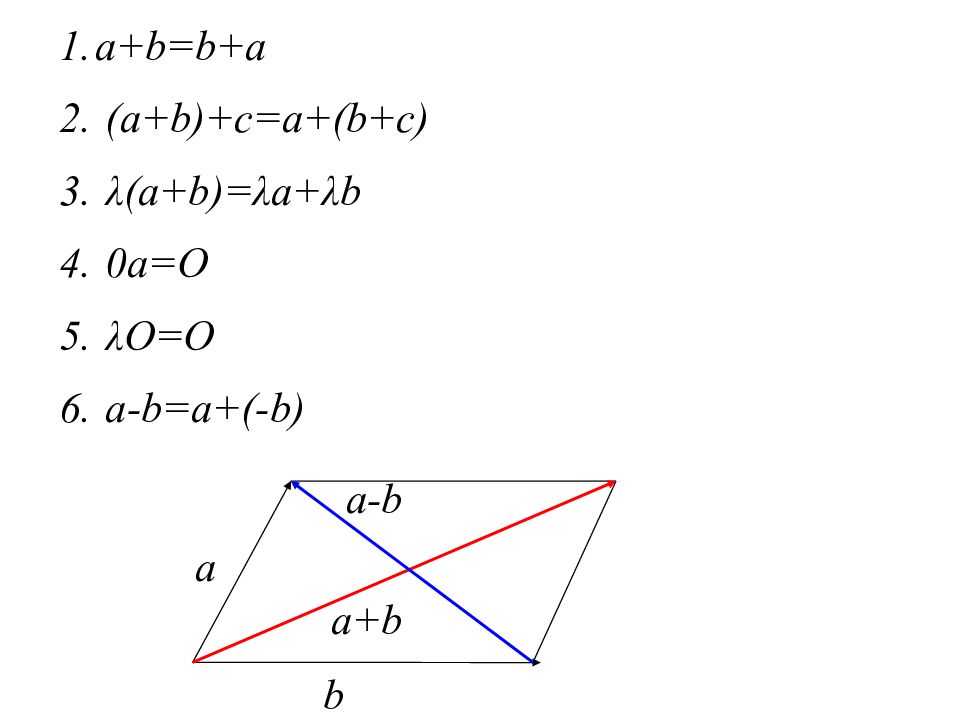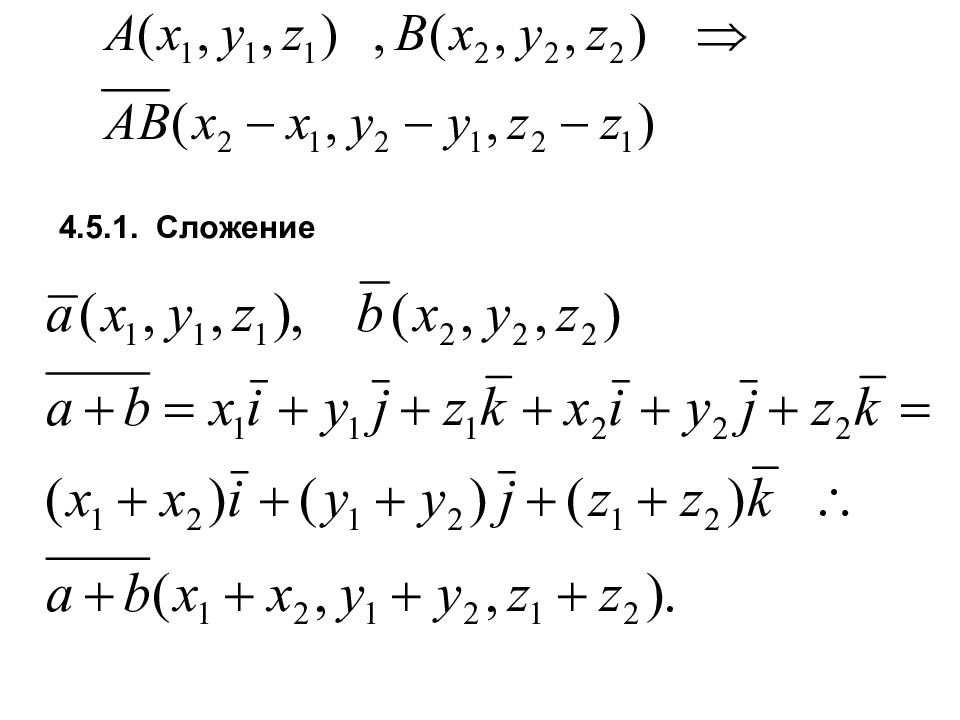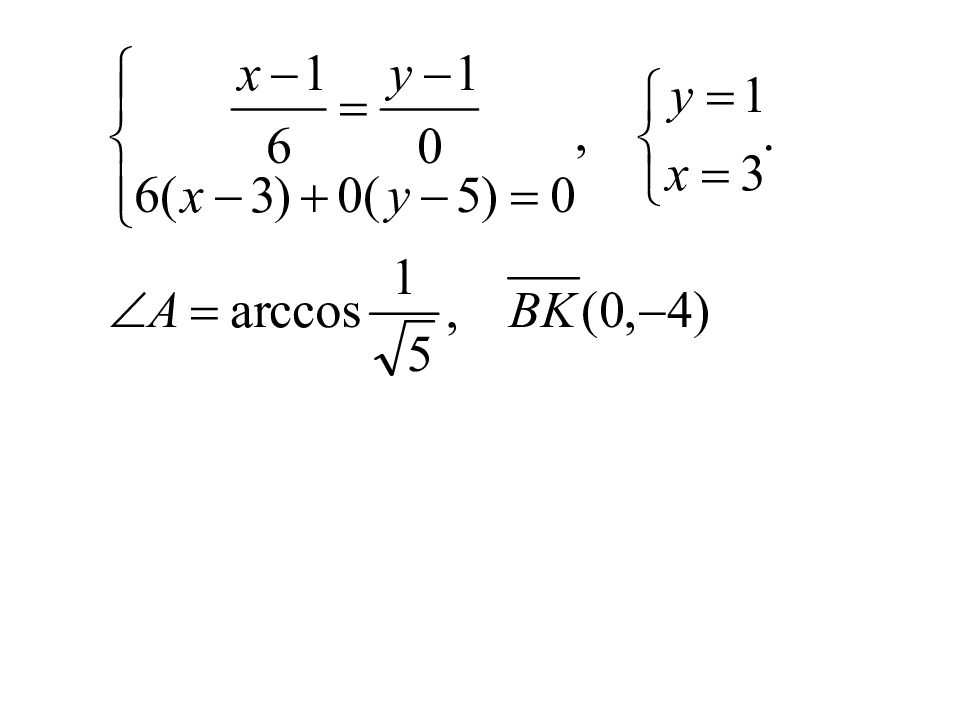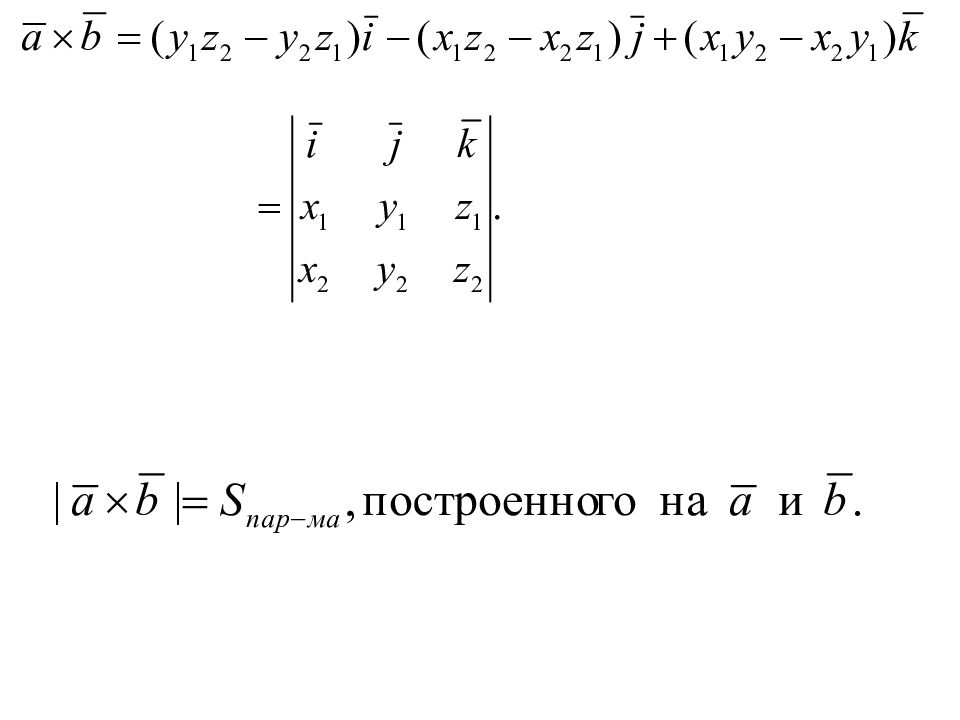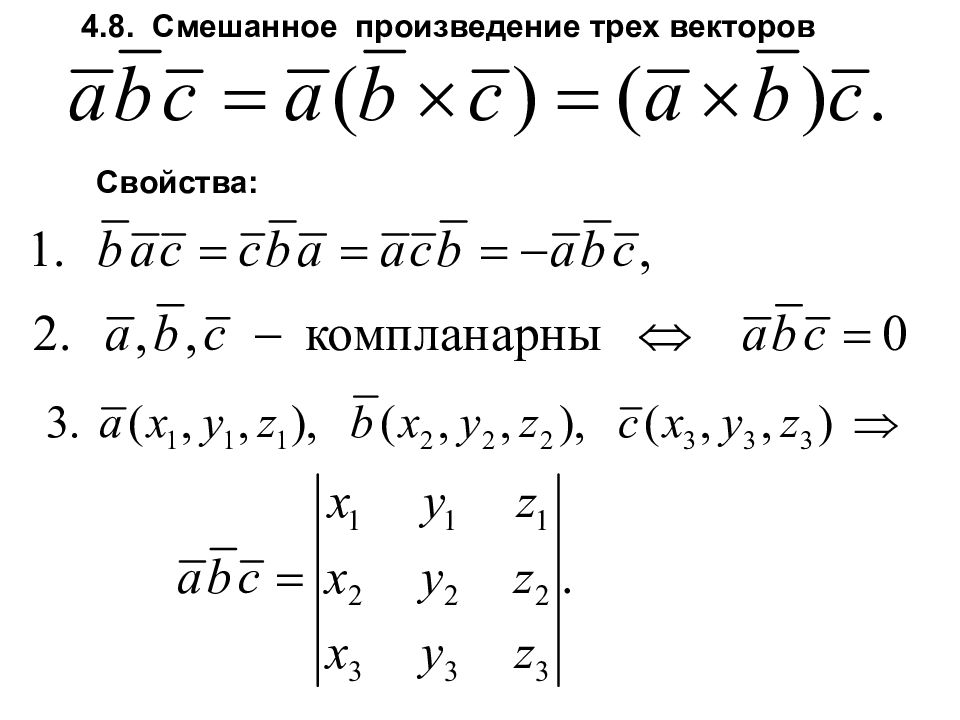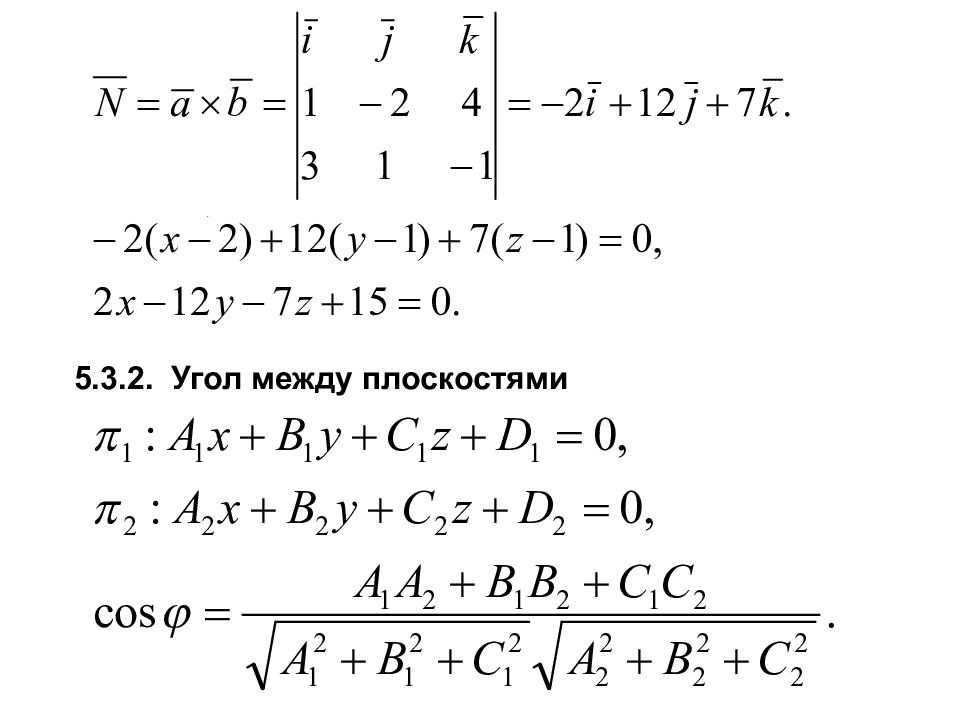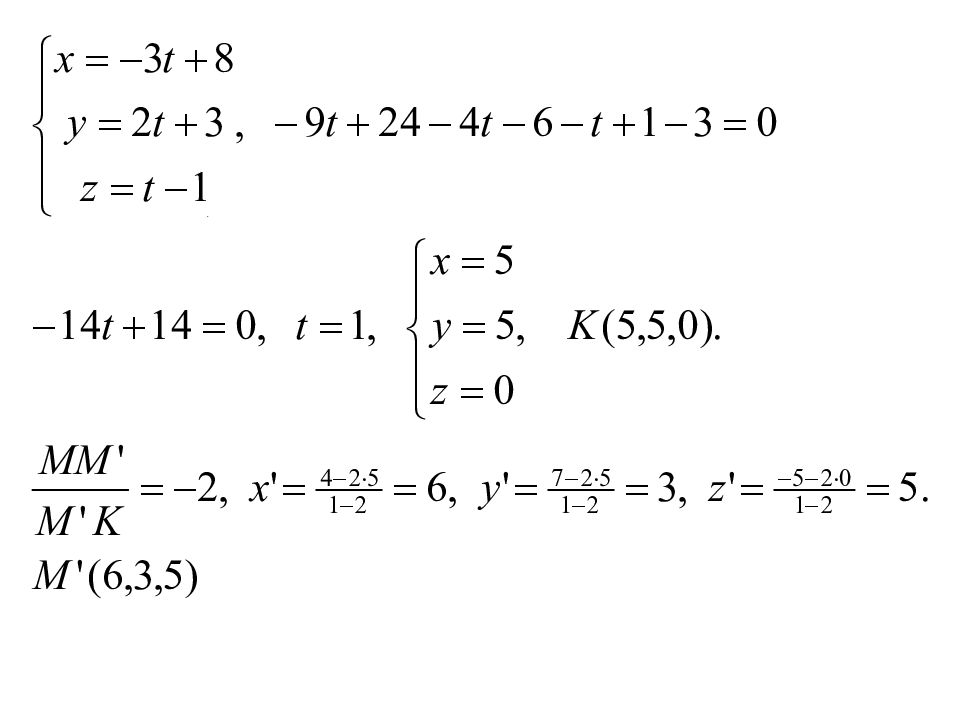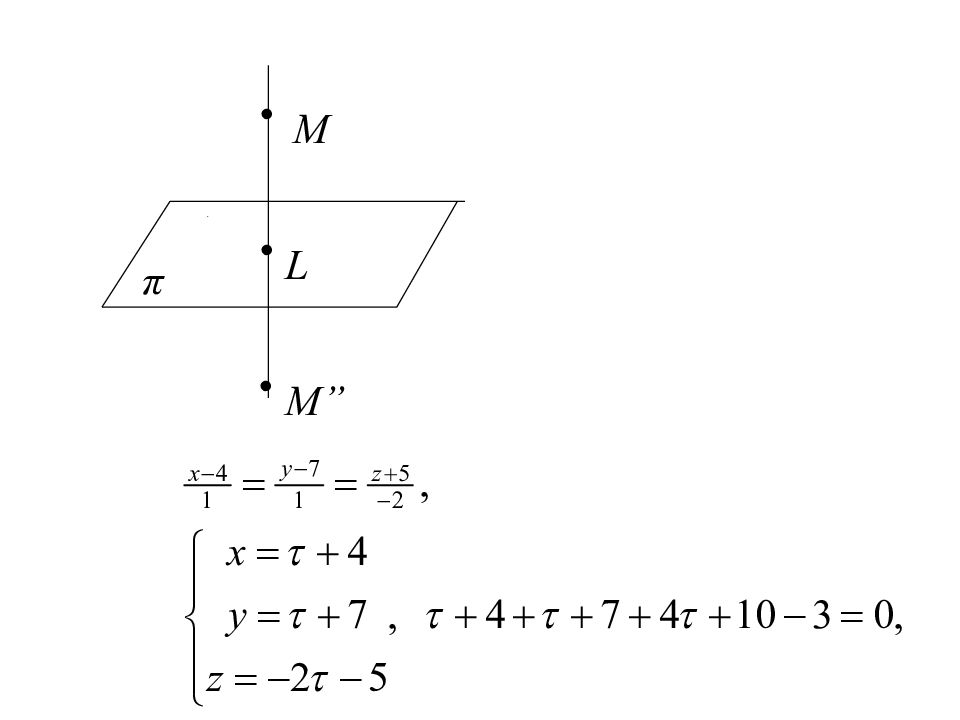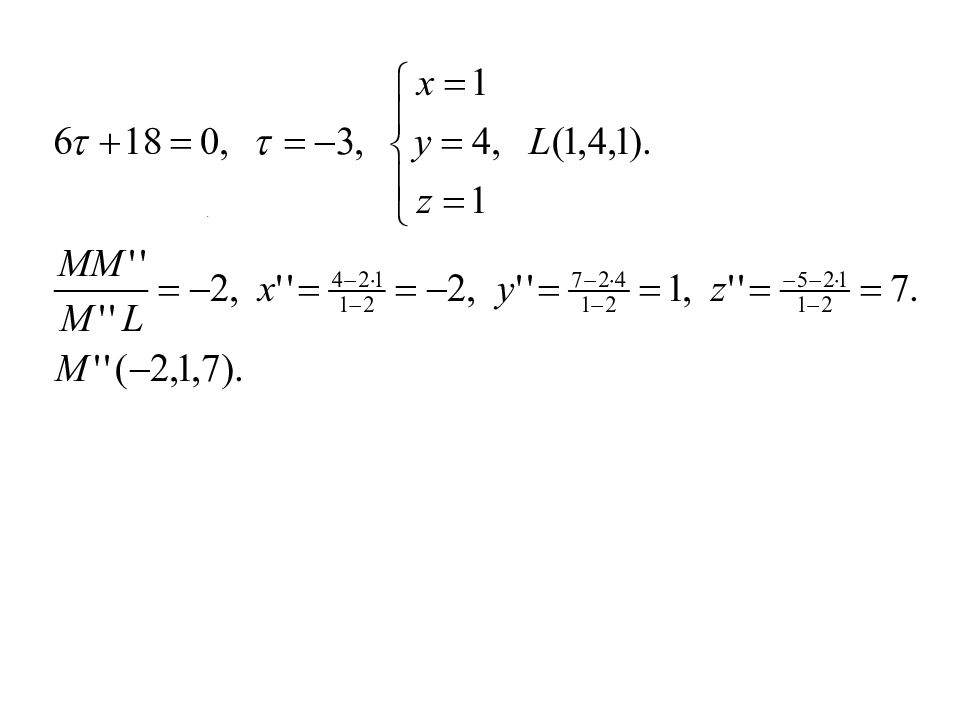Первый слайд презентации
Лекции по линейной алгебре для студентов 1 курса ИЭФ 1-ый семестр
Слайд 2
Определители n- го порядка Определитель 2-го порядка Пример: Определитель 3-го порядка
Слайд 3
Пример: Минор ( n-1)- го порядка M ij Алгебраическое дополнение элемента a ij
Слайд 10
Верхняя (нижняя) треугольная матрица: Диагональная матрица: Единичная матрица: Нулевая маерица:
Слайд 12
2. 3. Свойства линейных операций 2.4. Линейная комбинация Если -- числа, и -- матрицы одного порядка, то определена
Слайд 21
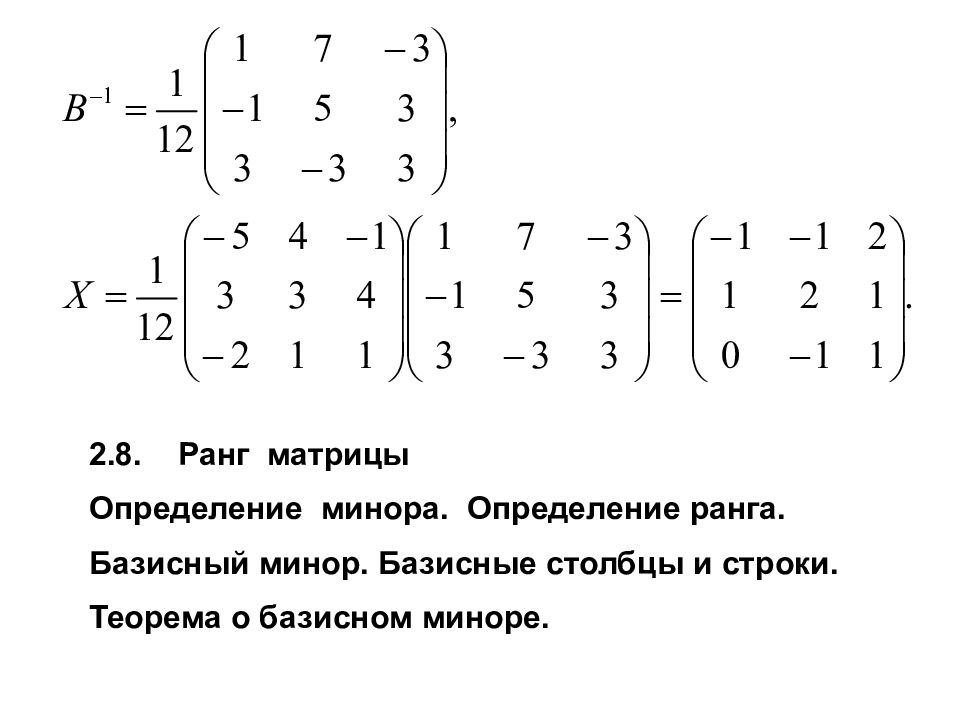
2.8. Ранг матрицы Определение минора. Определение ранга. Базисный минор. Базисные столбцы и строки. Теорема о базисном миноре.
Слайд 22
Элементарные преобразования Транспонирование Изменение порядка строк Умножение строки на число отличное от нуля Вычеркивание нулевой строки Вычеркивание одной из двух пропорциональных строк Прибавление к какой-либо строке линейной комбинации остальных строк Элементарные преобразования не меняют ранга матрицы.
Слайд 27
3.3. Общая теория линейных систем Опр. решения, совместности Пусть m -- число уравнений, n -- число неизвестных r -- ранг системы
Слайд 33
Векторная алгебра 4.1. Основные определения Коллинеарность, ортогональность, нулевой вектор, равенство векторов A B a AB c d e e↑↑d e ↑↓c • f o o ||f o f
Слайд 34
4.2. Линейные операции над векторами Сложение a b c= a+b Умножение на число a λ a, λ >0 μ a, μ <0
Слайд 35
a+b=b+a (a+b)+c=a+(b+c) λ (a+b)= λ a+ λ b 0a=O λ O=O a-b=a+(-b) a b a+b a-b
Слайд 36
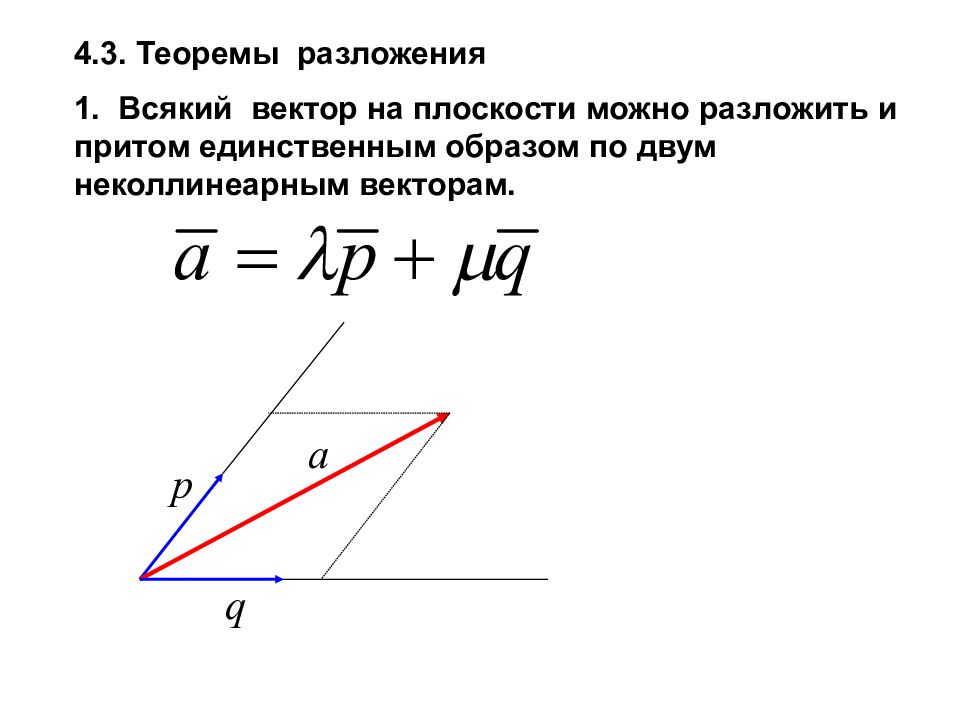
4.3. Теоремы разложения 1. Всякий вектор на плоскости можно разложить и притом единственным образом по двум неколлинеарным векторам. p q a
Слайд 37
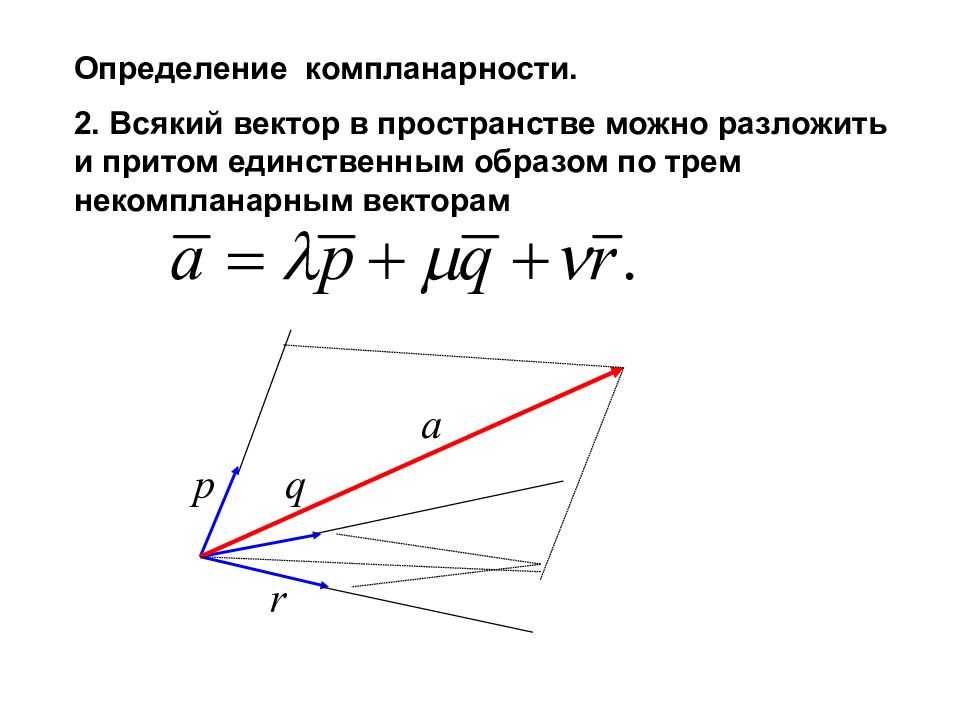
Определение компланарности. 2. Всякий вектор в пространстве можно разложить и притом единственным образом по трем некомпланарным векторам a p q r
Слайд 38
4. 4. Проекция вектора на ось Определение оси, угол между вектором и осью, компонента вектора по оси, проекция вектора на ось • O 1 l A B A 1 B 1 φ A 1 B 1 -- компонента вектора AB по оси l |A 1 B 1 |= Пр l AB -- проекция вектора на ось l
Слайд 40
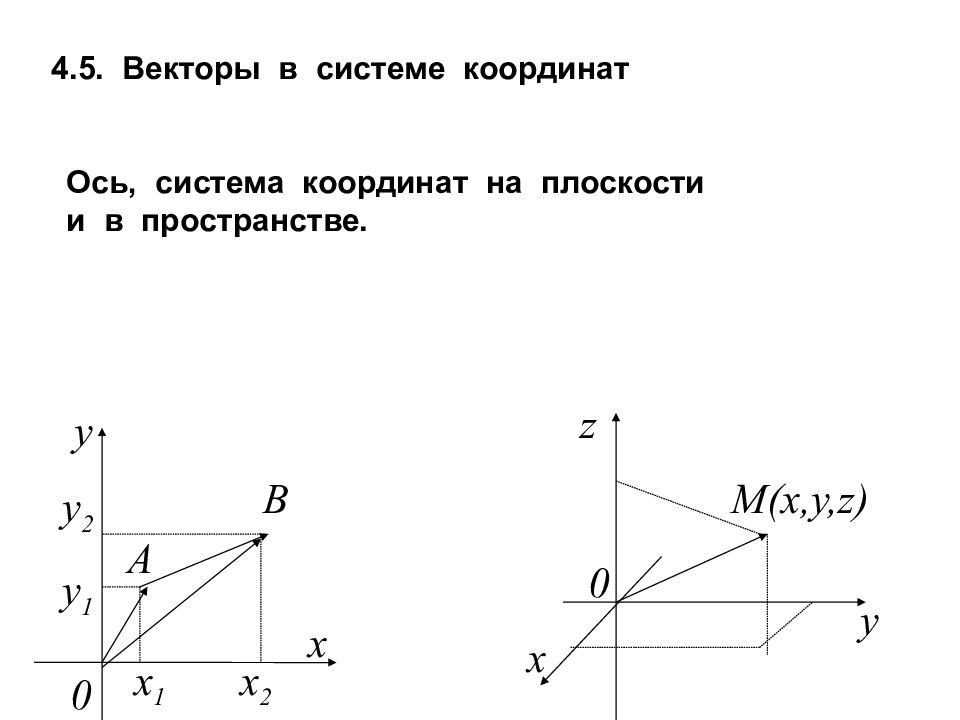
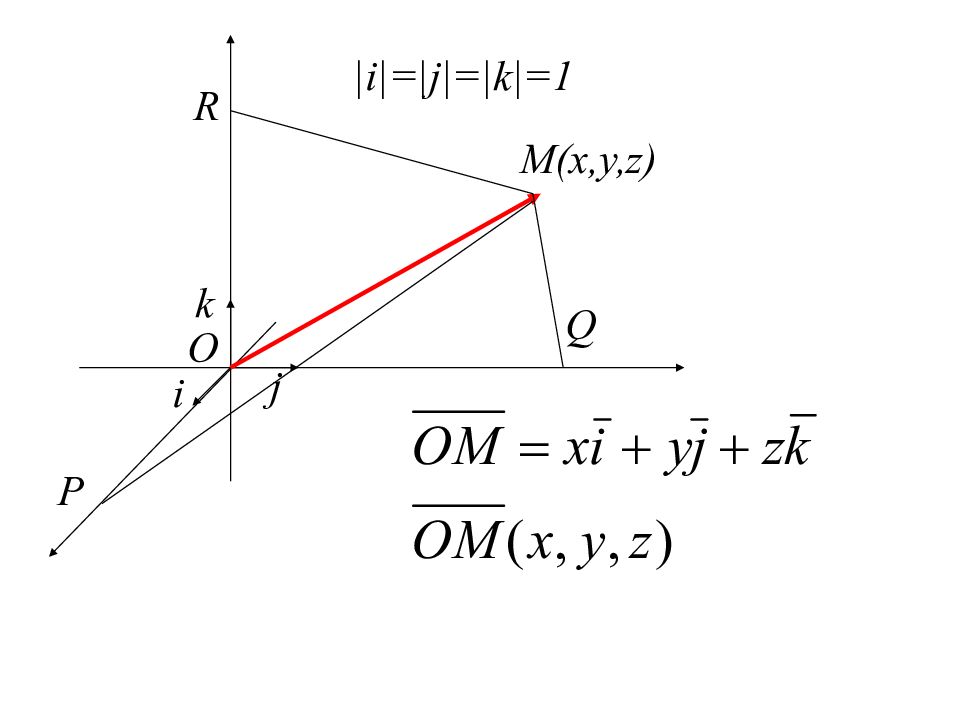
A B y y 2 y 1 0 x 1 x 2 x 0 x y z M(x,y,z) Ось, система координат на плоскости и в пространстве. 4.5. Векторы в системе координат
Слайд 57
Аналитическая геометрия 5.1. Основные задачи аналитической геометрии 5.1.1. Расстояние между двумя точками 5.1.2. Деление отрезка в заданном отношении • • •
Слайд 60
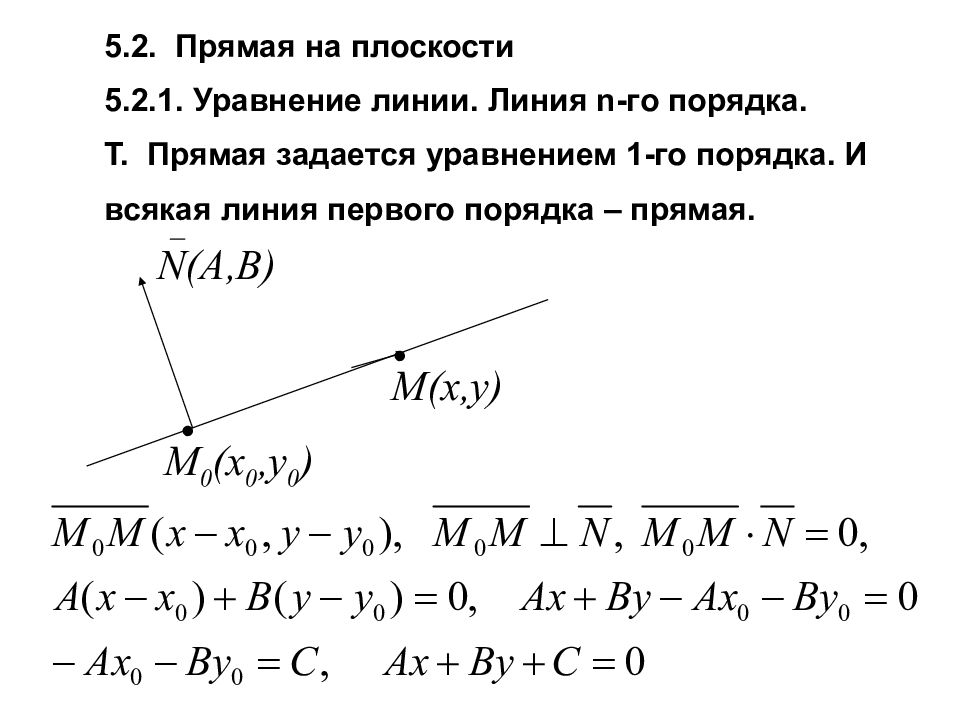
5.2. Прямая на плоскости 5.2.1. Уравнение линии. Линия n- го порядка. Т. Прямая задается уравнением 1-го порядка. И всякая линия первого порядка – прямая. • • N(A,B) M 0 (x 0,y 0 ) M(x,y)
Слайд 62
5.2. 3. Уравнение прямой, проходящей через две точки • M 1 (x 1,y 1 ) M(x,y) M 2 (x 2,y 2 )
Слайд 63
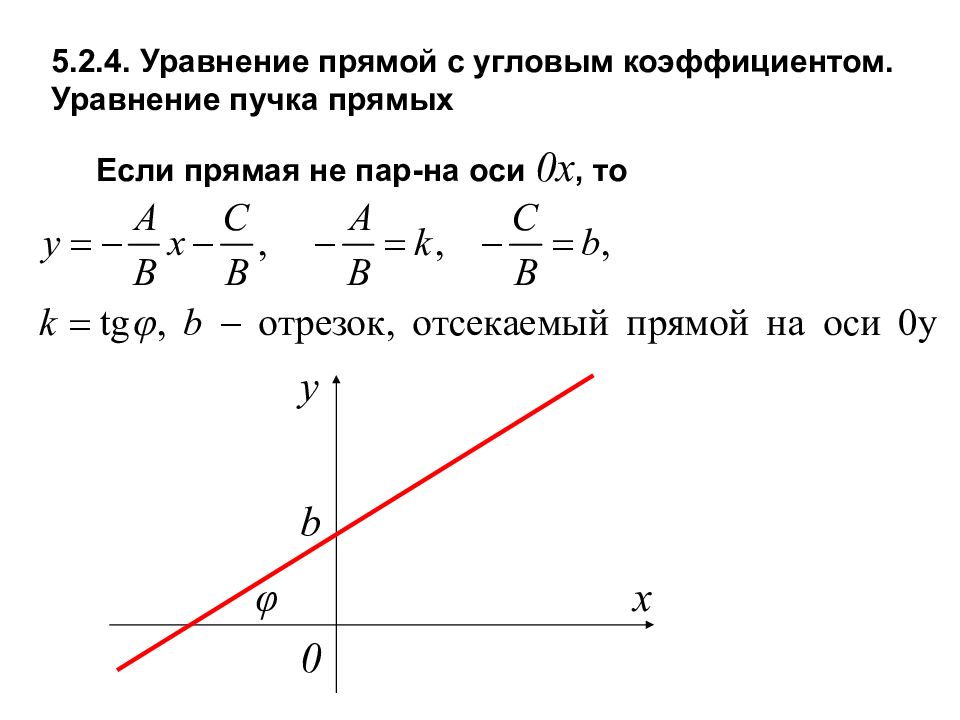
5.2.4. Уравнение прямой с угловым коэффициентом. Уравнение пучка прямых Если прямая не пар-на оси 0x, то φ y 0 b x
Слайд 65
Пример. Написать уравнения стороны AC медианы BM высоты BK и биссектрисы BD в тр-ке ABC
Слайд 68
Пример: Написать ур-ния прямых пар-ной и перп-ной l и проходящих через т. М(3,-1) 5.2.6. Точка пересечения прямых
Слайд 70
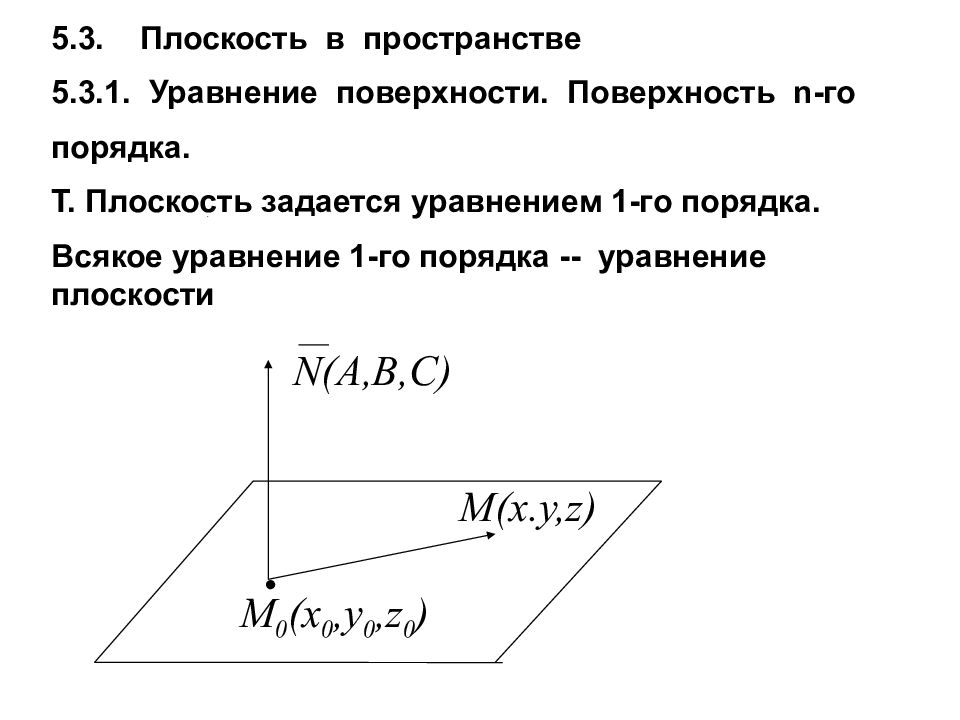
5.3. Плоскость в пространстве 5.3.1. Уравнение поверхности. Поверхность n -го порядка. Т. Плоскость задается уравнением 1-го порядка. Всякое уравнение 1-го порядка -- уравнение плоскости • N(A,B,C) M 0 (x 0,y 0,z 0 ) M(x.y,z)
Слайд 71
Пример. Написать ур-ние плоскости, проход. через данную точку параллельно векторам
Слайд 73
Условие параллельности Условие перпендикулярности 5.3.3. Точка пересечения трех плоскостей
Слайд 74
5.4. Прямая в пространстве 5.4.1. Общие уравнения прямой 5.4.2. Канонические уравнения прямой
Слайд 75
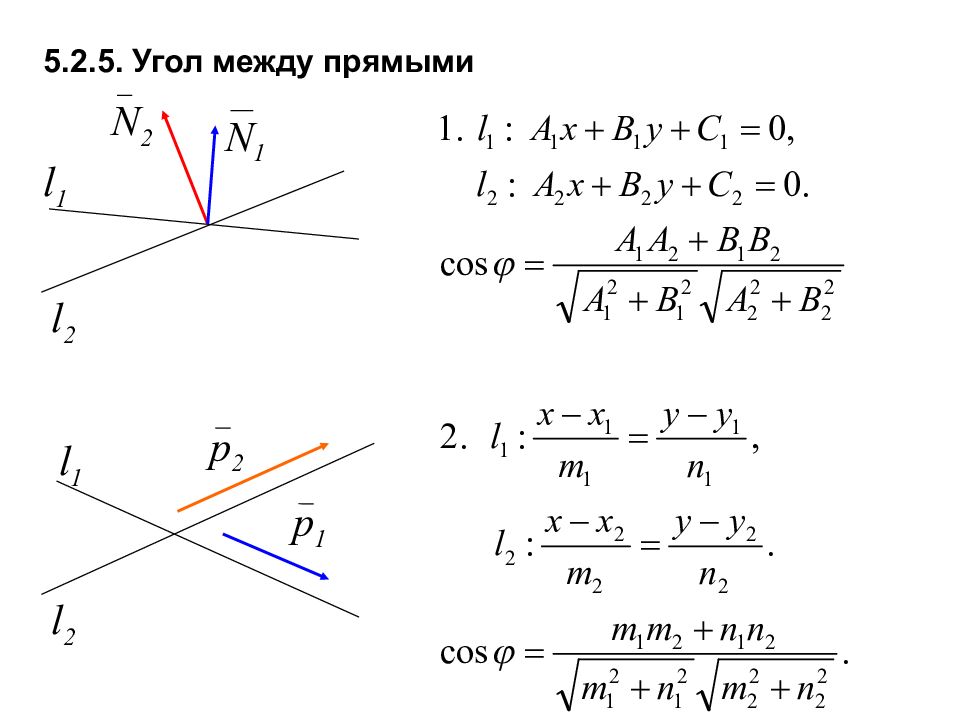
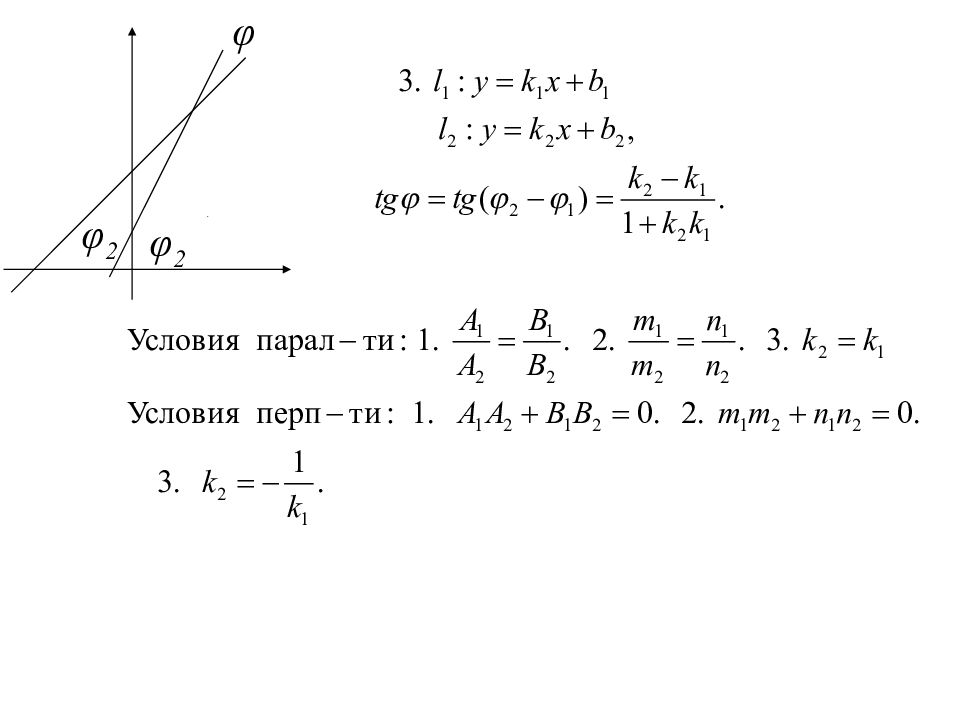
5.4. 3. Угол между прямыми Условие параллельности Пример. Через т. М провести прямую парал. прямой Условие перпендикулярности
Слайд 78
5.5. Прямая и плоскость 5.5.1. Проекция прямой на плоскость -- геом. место осн. пер-ров π l φ p N
Слайд 79
5.5.2. Угол между прямой и плоскостью 5.5.3. Точка пересечения прямой и плоскости
Слайд 80
Пример: Найти точки, симметричный т. M(4,7,-5) относительно прямой l и плоскости π • • l M M’ K •