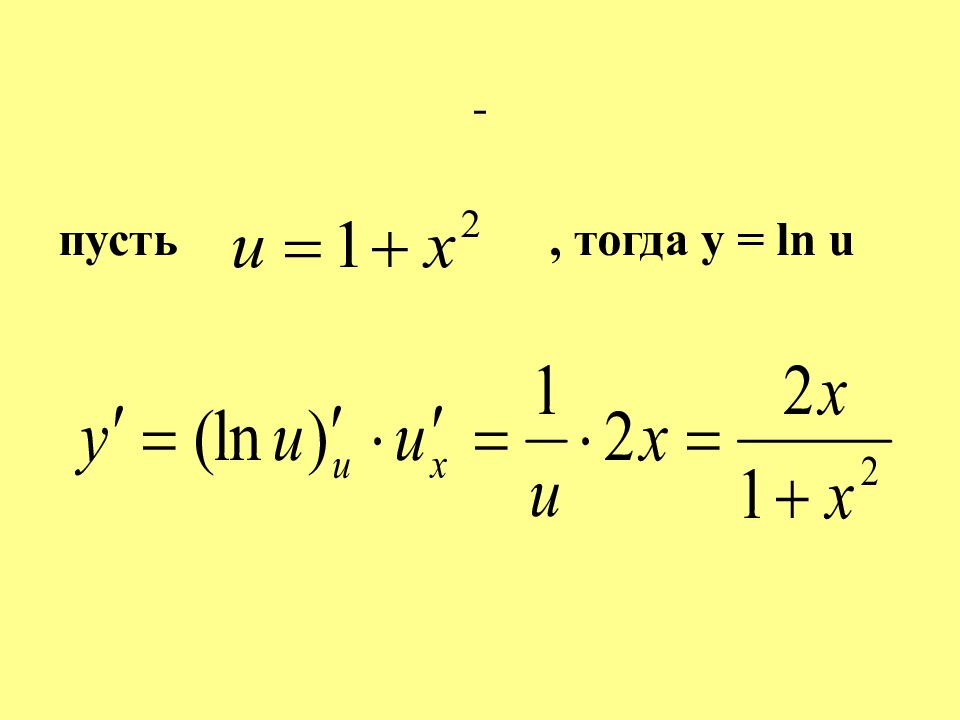Слайд 2: План лекции:
Дифференциальное исчисление Интегральное исчисление Дифференциальные уравнения
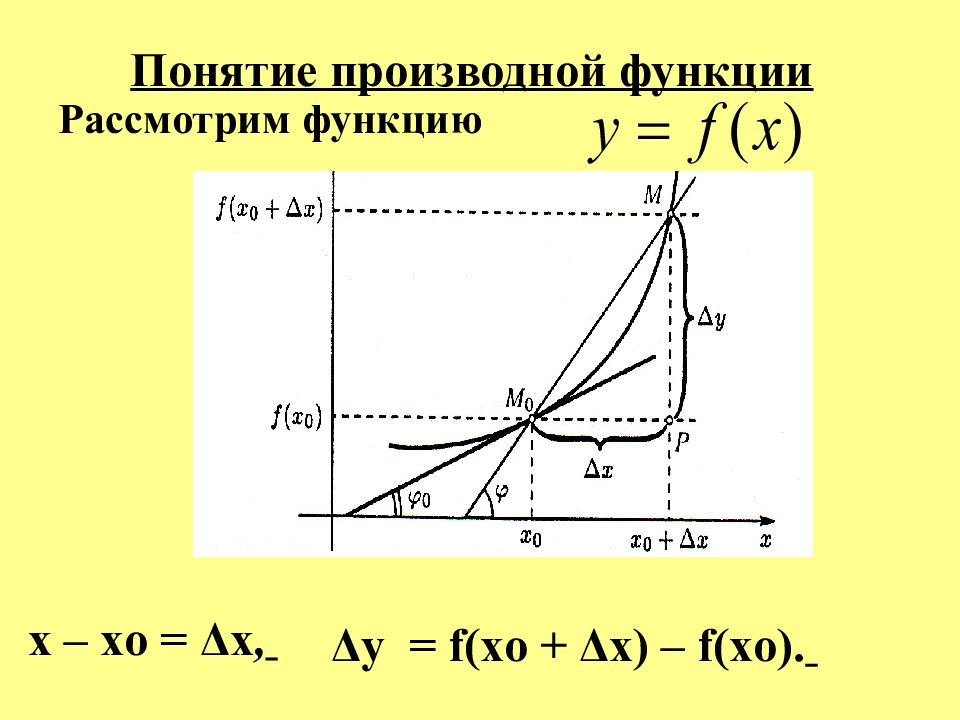
Слайд 3: Понятие производной функции
Рассмотрим функцию x – xo = Δ x, Δ y = f ( xo + Δ x ) – f (х o ).
Слайд 4
Если существует, то этот предел называется производной от функции по переменной x в точке x 0 у ' x =
Если x = f ( t ) есть уравнение прямолинейного движения точки, то производная представляет собой скорость точки в момент времени t. Производная f '(х) функции геометрически представляет собой угловой коэффициент касательной к графику этой функции в точке с абсциссой x.
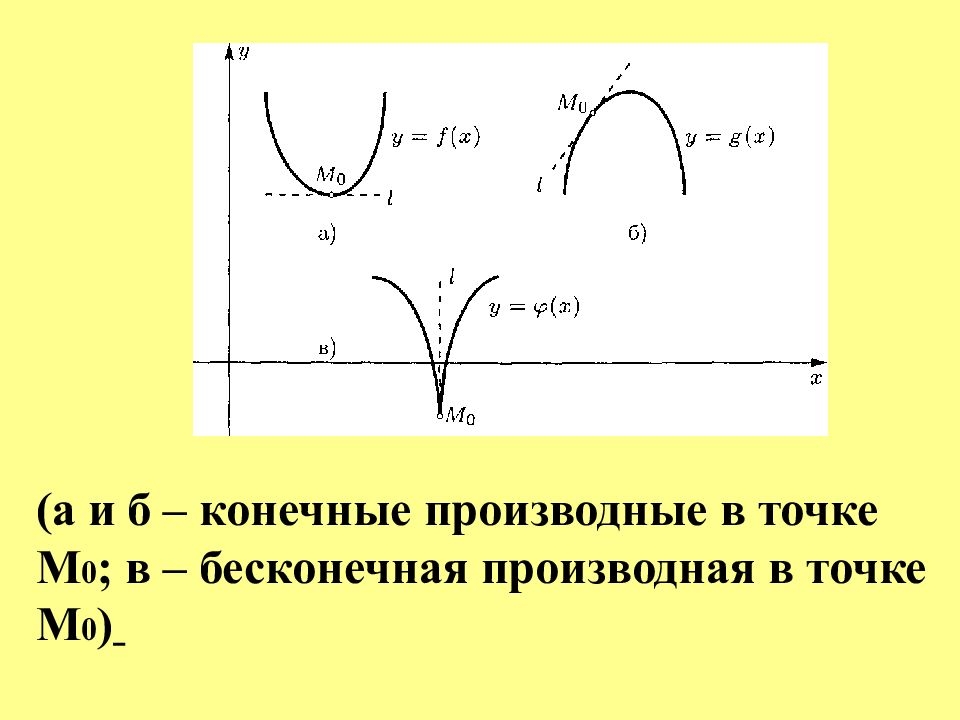
Слайд 6
(а и б – конечные производные в точке М 0 ; в – бесконечная производная в точке М 0 )
Слайд 7: Правила дифференцирования
Производная от постоянной величины равна нулю, т. е. если у = C, то y ' = 0: C ' = 0. 2. Производная алгебраической суммы конечного числа функций равна сумме производных слагаемых: (u + v + w +...)' = u' + v' + w' +...
Слайд 8
3.Производная произведения двух функций определяется формулой: ( u ∙ v )' = u ' ∙ v + u ∙ v ' 4. Производная частного от деления двух функций определяется формулой:
Слайд 12: Дифференцирование сложной функции
Производная сложной функцииопределяется по формуле: y ' x = y ' u ∙ u ' x Пример. Найти производную функции Используя правило дифференцирования сложной функции, получим:
Слайд 14: Понятие дифференциала функции
На основании определения предела Δу/Δх = у' + α (Δх), отсюда Δу = у' ∙ Δх + Δх ∙ α (Δх). Первое слагаемое в правой части этого равенства стремится к нулю, как Δх (если у' 0), а второе слагаемое кроме Δх содержит в себе множитель α (Δх), который тоже стремится к нулю при Δх.
Слайд 15
Таким образом, первое слагаемое стремится к нулю медленнее второго, и поэтому его называют главной частью приращения функции Δу.
Слайд 16
Главная часть приращения функции Δу, равная произведению у' ∙ Δх, называется дифференциалом первого порядка от функции, соответствующим выбранным значениям х и Δх. Обозначается так: dy = у' ∙ Δх ( первая форма записи дифференциала)
Слайд 18
Дифференциал dy равен приращению ординаты касательной к графику, соответствующему значениям x и x + Δ x. Вторая форма записи дифференциала: dy = у' ∙ dx
Слайд 19: Приближенные вычисления с помощью дифференциала
Теорема: Если функция дифференцируема в точке x, причем f '( x ) 0, то при Δ x —> 0 приращение Δ y и дифференциал dy функции являются эквивалентными бесконечно малыми.
Слайд 20
Следовательно, Δ y ≈ dy. Абсолютная и относительная погрешности этого равенства могут быть сделаны сколь угодно малыми при достаточно малом. Структура дифференциала обычно значительно проще структуры приращения функции, в силу чего формула широко применяется в приближенных вычислениях.
Пусть ( x, у) — произвольная фиксированная точка из области определения z = f ( x, у). Рассмотрим предел Этот предел (если он существует) называется частной производной (1-го порядка) данной функции z по переменной x в точке ( x, у).
Слайд 22
Аналогично, Таким образом, частная производная функции z = f ( x, у) по аргументу x есть производная этой функции по x при постоянном значении у. Аналогично, есть производная функции z = f ( x, у) по у в предположении, что x является константой.
Слайд 24: Понятие неопределенного интеграла
Дифференцируемая функция F (х) называется первообразной для функции f ( x ) на ( a, b ), если F '(х) = f ( x ) на (а, b ). Например, для f(x) = cos x первообразной будет F(x) = sin x, так как F '(х) = ( sin x) ' = cos x
Слайд 25
Выражение F (х) + С, где С - произвольная постоянная величина, определяющее множество первообразных для функции f ( x ), называется неопределенным интегралом и обозначается символом,т.е. = F (х) + С, где знак - знак неопределенного интеграла, f ( x ) — называется подынтегральной функцией, f ( x ) dx - подынтегральным выражением, x - переменной интегрирования.
Слайд 30
Свойства неопределенных интегралов 1. Производная от неопределенного интеграла равна подынтегральной функции: 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
Слайд 31: Свойства неопределенных интегралов
3. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной: Пример 1. Пример 2.
Слайд 32: Свойства неопределенных интегралов
Постоянный множитель можно выносить за знак интеграла: Пример 3. 5. Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
Слайд 34: Методы интегрирования
Непосредственное интегрирование Этот метод заключается в прямом использовании табличных интегралов и свойств. Пример.
Слайд 35: Методы интегрирования
Метод разложения Этот метод заключается в разложении подынтегральной функции в линейную комбинацию более простых функций с использованием известных формул. Пример.
Слайд 36: Методы интегрирования
Метод подведения под знак дифференциала Для приведения данного интеграла к табличному бывает удобно сделать преобразования дифференциала. Пример.
Слайд 37: Методы интегрирования
Метод замены переменной Существуют две формулы замены переменной в неопределенном интеграле: , где x = φ ( t ) 2., где φ ( x ) = t
Слайд 38: Методы интегрирования
Пример. Здесь следует ввести новую переменную t так, чтобы избавиться от квадратного корня. Положим,тогда, а dx = 2t dt
Слайд 39
Методы интегрирования Метод интегрирования по частям Дифференциал произведения двух функций определяется формулой
Слайд 40: Методы интегрирования
Интегрируя это равенство, получим выражение: Отсюда.
Слайд 42
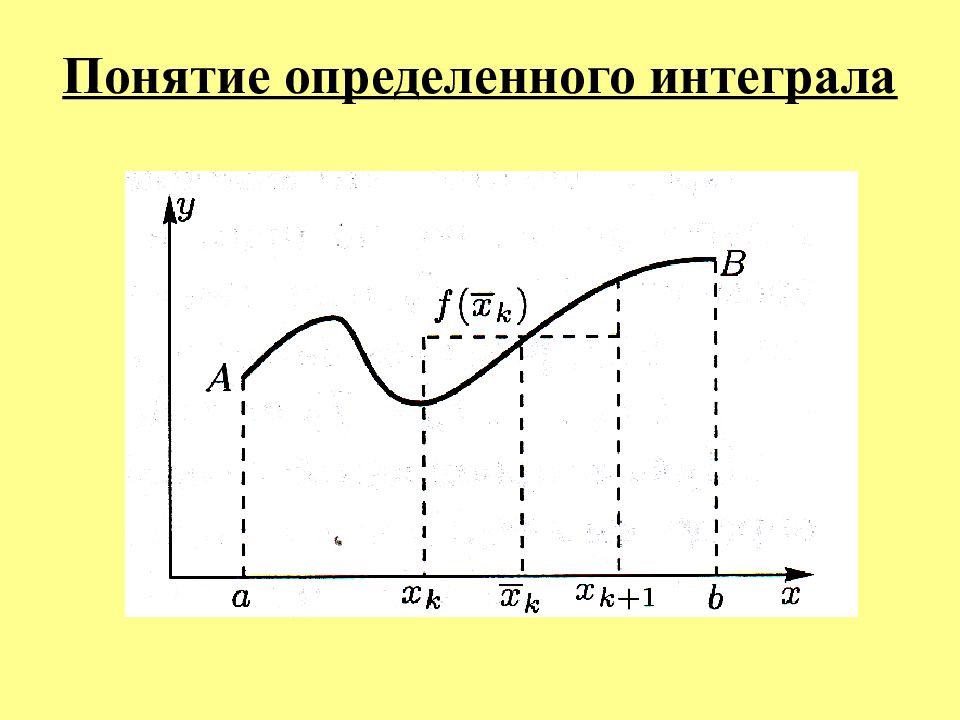
Понятие определенного интеграла Вычисление площади криволинейной трапеции Криволинейной трапецией будем называть плоскую фигуру, ограниченную осью ОХ, графиком непрерывной функции у = f ( x ) и двумя вертикальными прямыми х = а и х = b
Слайд 44: Понятие определенного интеграла
Учитывая, что площадь фигуры, составленной из нескольких непересекающихся фигур, равна сумме площадей этих фигур, получим Предел этой суммы называется определенным интегралом от функции f ( x ) в пределах от a до b и обозначается
Слайд 45: Понятие определенного интеграла
Определенным интегралом называется предел, к которому стремится интегральная сумма при стремлении к нулю длины наибольшего частичного интервала Δх.
Слайд 46: Свойства определенного интеграла
Интеграл от суммы конечного числа функций равен сумме интегралов от слагаемых: Постоянный множитель подынтегральной функции можно выносить за символ интеграла:
Слайд 47: Свойства определенного интеграла
3.Если верхний и нижний пределы интеграла поменять местами, то интеграл изменит знак:
Слайд 48: Свойства определенного интеграла
4.Если интервал интегрирования [а, b ] разбить на две части [а, с] и [с, b ], то 5. Если подынтегральная функция в интервале интегрирования не меняет знака, то интеграл представляет собой число того же знака, что и функция
Слайд 49: Формула Ньютона-Лейбница
Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятых при верхнем и нижнем пределах интеграла: , где F `( x ) = f ( x ) Разность значений функции часто записывают так:
Слайд 50: Дифференциальные уравнения
Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные различных порядков, называется дифференциальным. Если функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным. Общий вид обыкновенного дифференциального уравнения: или
Слайд 51
Порядком дифференциального уравнения называется порядок старшей производной, входящей в него. Пример. ху' – у = 0, у' + sin х = 0 - уравнения первого порядка, у" + 2у' + 5у = х - уравнение второго порядка.
Слайд 52
Решением дифференциального уравнения называется такая функция, которая обращает уравнение в тождество после подстановки этой функции и ее производных в уравнение. При решении дифференциальных уравнений используется операция интегрирования, что связано с появлением произвольной постоянной
Слайд 53: Дифференциальные уравнения первого порядка
Общий вид дифференциального уравнения 1-го порядка определяется выражением Общим решением дифференциального уравнения 1-го порядка является множество решений у = f ( x, С), где С - произвольная постоянная.
Слайд 54
График решения дифференциального уравнения называется интегральной кривой. Придавая произвольной постоянной С различные значения, можно получить частные решения. На плоскости ХОУ общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.
Слайд 55
Если задать точку A ( x 0,у 0 ), через которую должна проходить интегральная кривая, то, как правило, из множества функций у = φ(х, С) можно выделить одну - частное решение. Частным решением дифференциального уравнения называется его решение, не содержащее произвольных постоянных.
Слайд 56
Если функция у = φ (х, С) является общим решением, то из условия y 0 = φ (х 0, С) можно найти постоянную С. Условие у = у 0 при x = x 0 называют начальным условием. Задача нахождения частного решения дифференциального уравнения, удовлетворяющего начальному условию у = у 0 при x = x 0 называется задачей Коши.
Слайд 57: Теорема Коши (теорема существования и единственности решения)
Пусть в дифференциальном уравнении у' = f ( x, у) функция f ( x,у) и ее частная производная f y '(х,у) определены и непрерывны в некоторой области D, содержащей точку A ( x 0, y 0 ). Тогда в области О существует единственное решение этого уравнения, удовлетворяющее начальному условию у = у 0 при x = x 0.
Слайд 58: Дифференциальное уравнение первого порядка с разделяющимися переменными
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно представить в виде y ' = f 1 ( x ) ∙ f 2 ( y ) Правая часть уравнения представляет собой произведение двух функций, каждая из которых зависит только от одной переменной.
Слайд 59
Пример. Уравнение у' = является уравнением с разделяющимися переменными ( f 1 ( x ) =, f 2 ( y ) = y ), а уравнение не является таким
Слайд 60
Учитывая, что, перепишем y ' = f 1 ( x ) ∙ f 2 ( y ) в виде. Из этого уравнения получим дифференциальное уравнение с разделяющимися переменными, в котором при дифференциалах стоят функции, зависящие от соответствующей переменной:
Слайд 61
Интегрируя почленно, имеем: где С = С 2 – С 1 – произвольная постоянная. Выражение представляет собой общий интеграл уравнения
Слайд 62
Пример 1. Найти решение у' =, удовлетворяющее условию: у = 6 при х = 2 (у(2) = 6). Заменим у' на, тогда Умножим обе части на dx, так как при дальнейшем интегрировании нельзя оставлять dx в знаменателе:
Слайд 63
Разделив обе части на у ( ), получим уравнение Интегрируем: Потенцируя, получим у = С(х + 1) - общее решение.
Слайд 64
По начальным данным определяем произвольную постоянную, подставив их в общее решение 6 = С(2 + 1) => С = 2. Окончательно получаем у = 2(х + 1) — частное решение.
Слайд 65
Однородные дифференциальные уравнения первого порядка Дифференциальное уравнение 1-го порядка называется однородным, если его можно представить в виде у' = f ( y / x ). Введем новую функцию u = y / x или y = u ∙ x. Отсюда у' = u 'х + u или dy = u dx + x du. Свели к диф. уравнению с разделяющимися переменными
Слайд 66: Линейные дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка называется линейным, если его можно представить в виде y ' + p ( x ) y = q ( x ) Здесь у, у' — входят в 1-й степени, р(х), q (х) — неизвестные функции, в частности, они могут быть постоянными величинами.
Слайд 67
Уравнение решается методом Бернулли с помощью специального приема. Представим у в виде произведения двух функций у = u ( x ) υ( x ), где u, υ — неизвестные функции, причем одну из них можно выбрать произвольно. Если у = u υ, то у' = u ' υ + u υ' и, подставляя в ур-ие, получим u ' υ + u υ ' + р(х) u υ = q ( x ), u ' υ + u (υ' + р(х) υ) = q (х).
Слайд 68
Функции u, υ нам неизвестны, определим одну из них, например υ, из условия υ' + р(х) υ = 0 (1) Учитывая это, придем к уравнению u ' υ = q (х) (2) Найдем υ( x ) из (1): υ ' = - p ( x ) υ,
Слайд 70
Некоторые приложения дифференциальных уравнений первого порядка 1. Задача о радиоактивном распаде Скорость распада R а (радия) в каждый момент времени пропорциональна его наличной массе. Найти закон радиоактивного распада R а, если известно, что в начальный момент имелось m 0 R а и период полураспада R а равен 1590 лет.
Слайд 71
Пусть в момент t масса R а составляет x г. Тогда скорость распада R а равна По условию задачи где k – коэффициент пропорциональности
Слайд 72
Разделяя в последнем уравнении переменные и интегрируя, получим ln x = - kt + lnC, откуда Для определения С используем начальное условие: при t = 0 x = m 0. Тогда С = m 0 и, значит, Коэффициент пропорциональности k определяем из дополнительного условия: при t = 1590 x = m 0 /2.
Слайд 74
2. Задача о скорости размножения бактерий Скорость размножения бактерий пропорциональна их количеству. В начальный момент имелось 100 бактерий. В течение 3 часов их число удвоилось. Найти зависимость количества бактерий от времени. Во сколько раз увеличится количество бактерий в течение 9 часов?