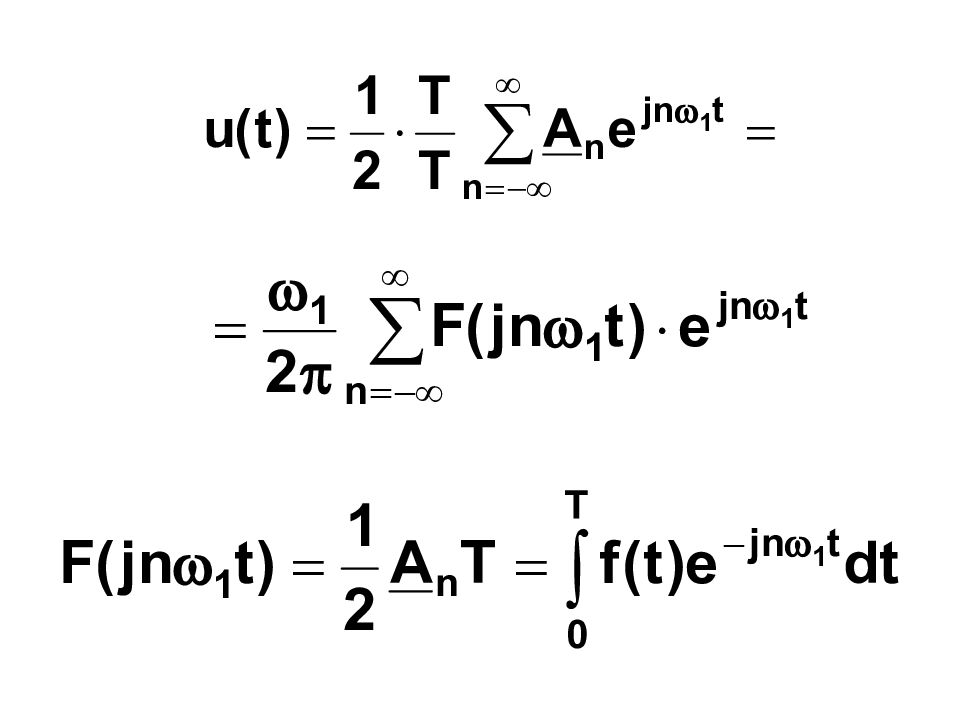Первый слайд презентации: Лекция №19 Спектры непериодических сигналов
Слайд 2
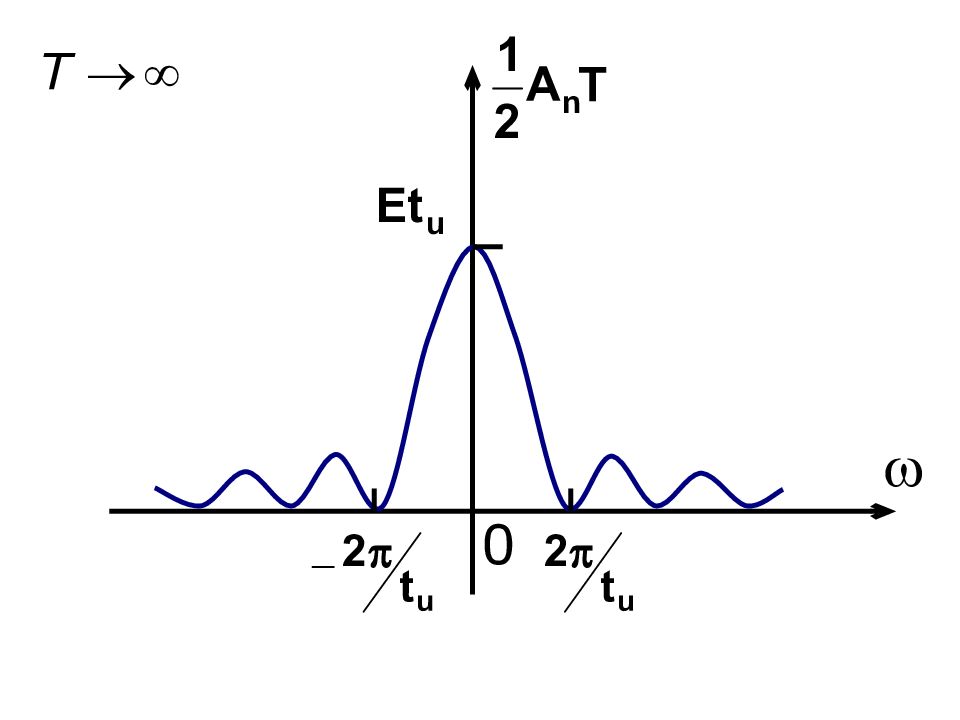
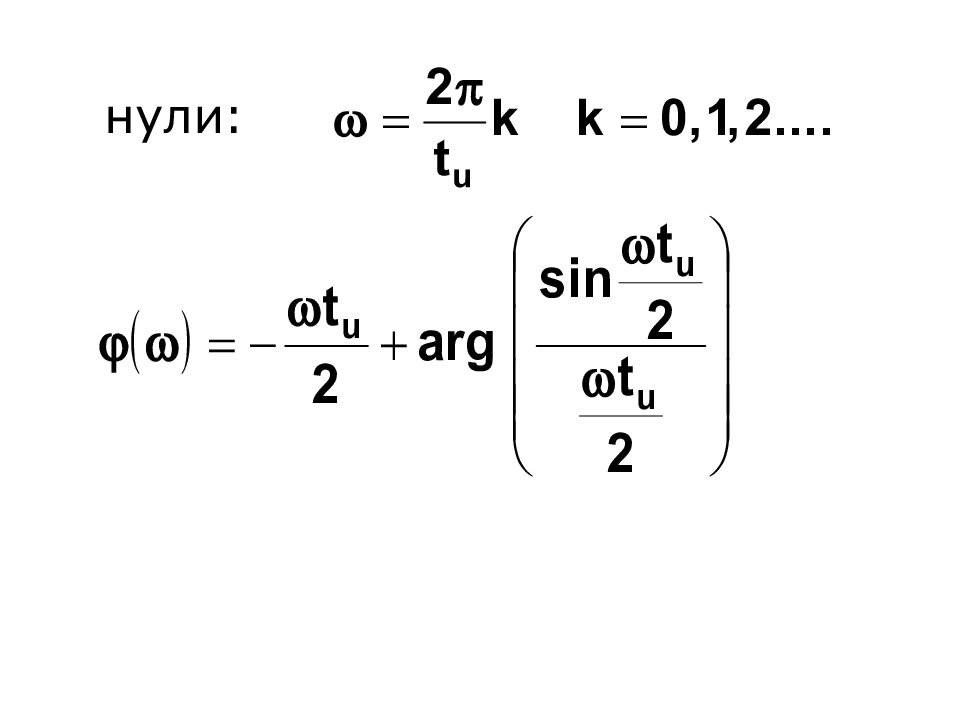
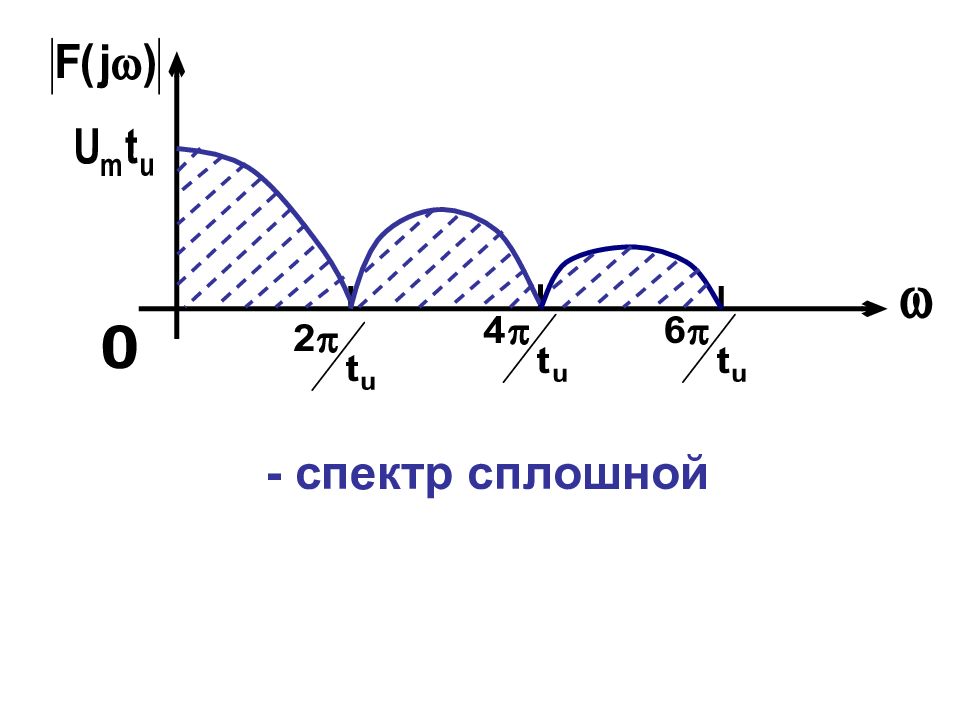
С увеличением периода сигнала Т спектральные линии сгущаются а их амплитуды уменьшаются. При периодическая последовательность переходит в одиночный импульс. Спектральные линии такого импульса сольются друг с другом и спектр станет сплошным (такой спектр содержит бесконечное число гармоник с бесконечно малыми амплитудами).
Слайд 6: Прямое преобразование Фурье:
позволяет определить спектральную плотность сигнала
Слайд 7: Обратное преобразование Фурье:
позволяет определить сигнал по его спектральной плотности
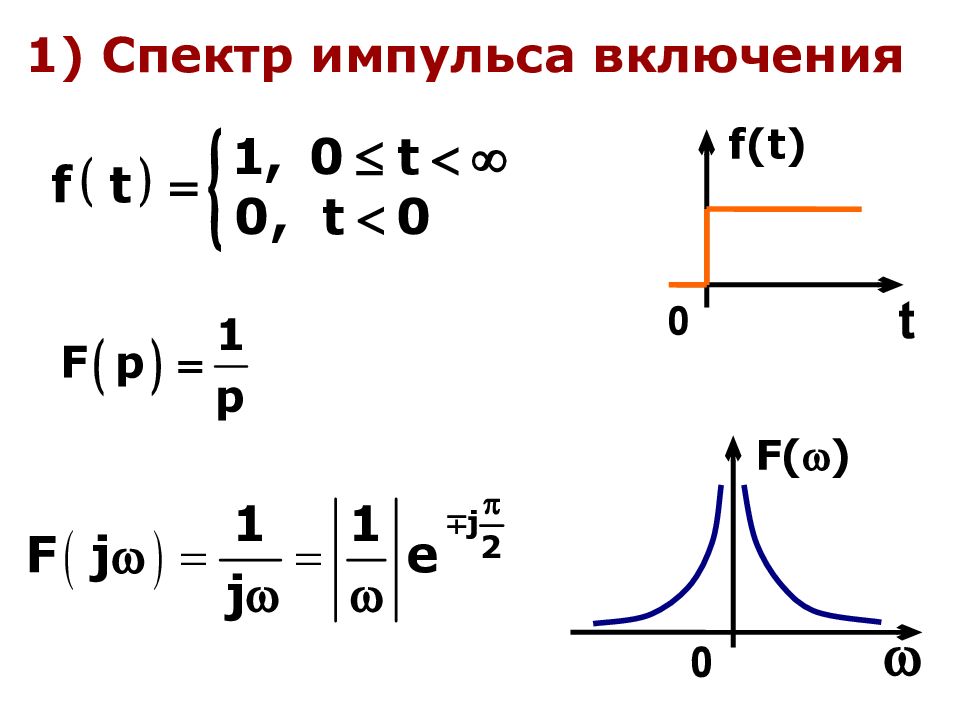
Слайд 13: Одностороннее преобразование Фурье. Связь с преобразованием Лапласа
Если при - одностороннее преобразование Фурье
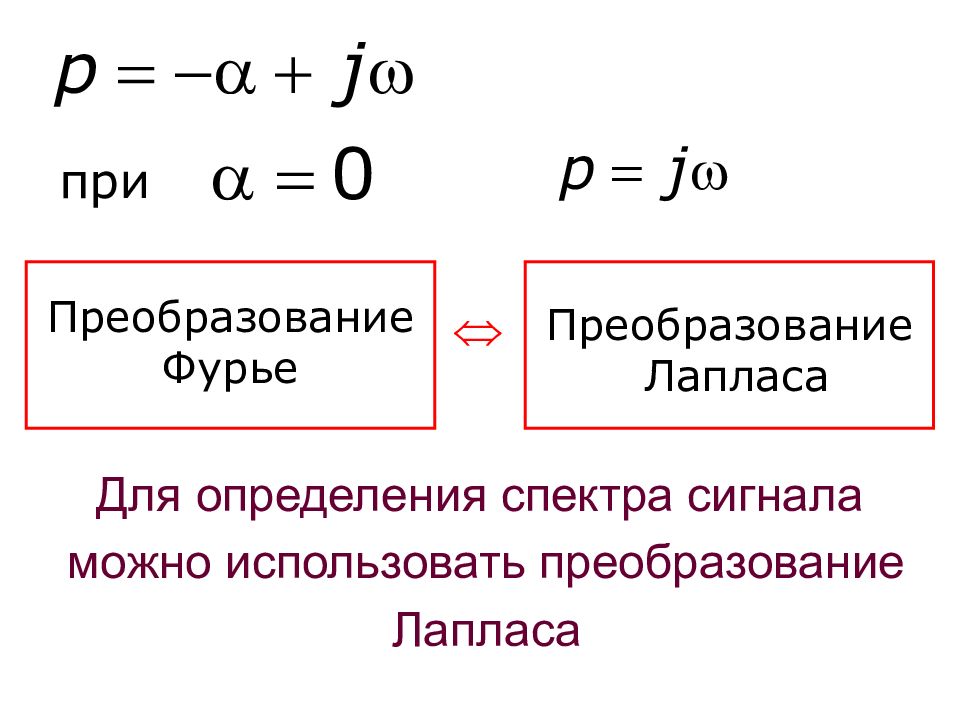
Слайд 15: при
Преобразование Лапласа Преобразование Фурье Для определения спектра сигнала можно использовать преобразование Лапласа
Слайд 18: ТЕОРЕМЫ О СПЕКТРАХ
1. теорема линейности 2. теорема запаздывания Спектральная плотность амплитуд не меняется, меняется только спектральная плотность фаз
Слайд 19
3. теорема дифференцирования - если - если Дифференцирование сигнала ведет к расширению его спектра
Слайд 20
4. теорема интегрирования - нулевые начальные условия - ненулевые начальные условия Интегрирование сигнала ведет к сужению его спектра
Слайд 21
5. Теорема подобия 6. Теорема смещения Чем короче импульс, тем шире его спектр При умножении сигнала на гармоническое колебание его спектр смещается по шкале частот на величину, равную частоте гармонического колебания.
Слайд 23: 8. Равенство Парсеваля (теорема Релея)
Энергия сигнала во временной области равна энергии сигнала в частотной области
Слайд 24
энергия электрического сигнала, рассеиваемая на сопротивлении R =1Ом спектральная плотность энергии сигнала (энергетический спектр) показывает, какая доля энергии заключена в каждой полоске частот шириной в окрестности частоты и
позволяет судить об распределении энергии в спектре непериодического сигнала Равенство Парсеваля применяют для выбора полосы пропускания канала
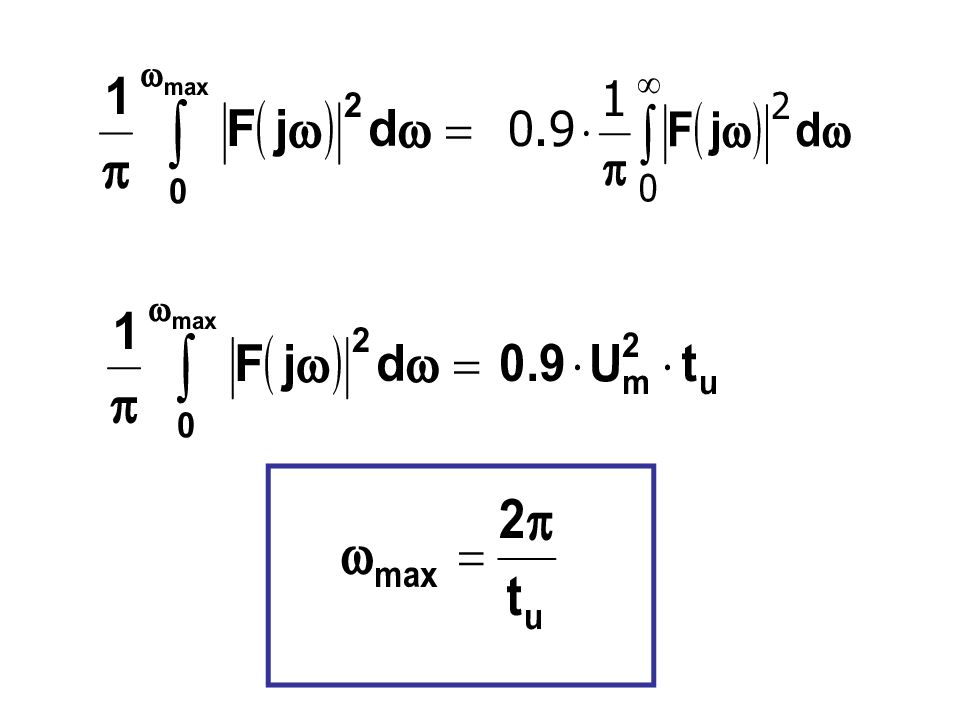
Слайд 26
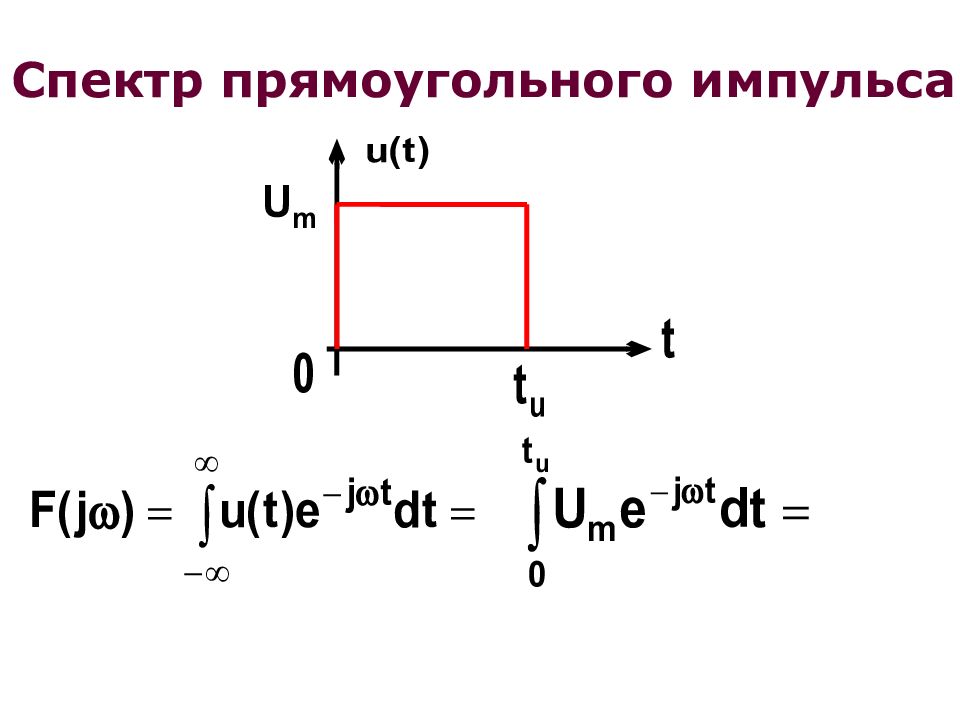
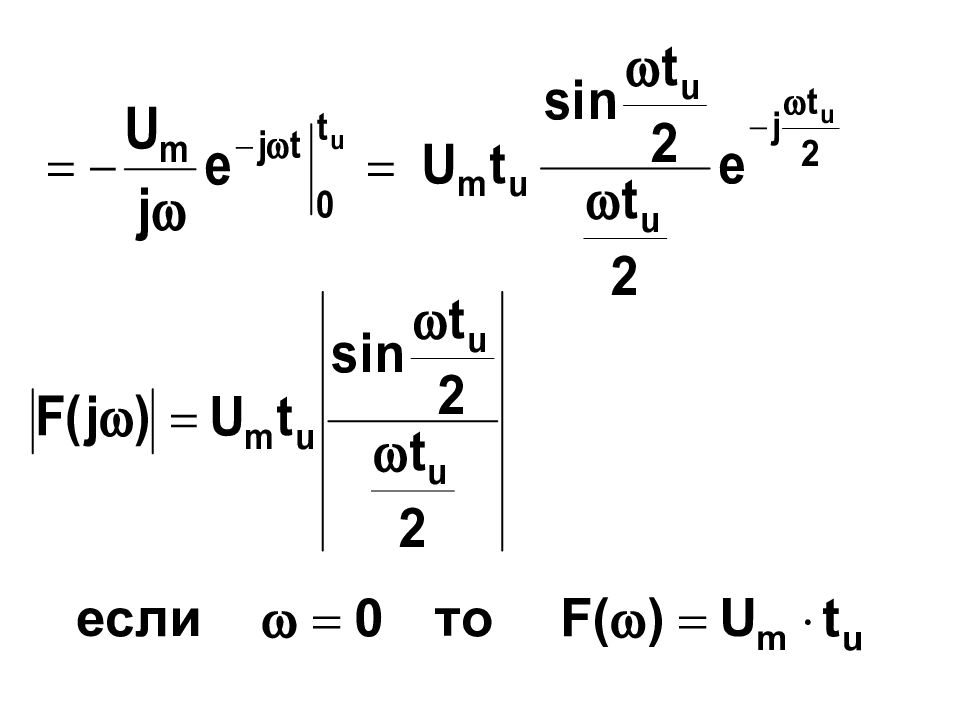
выбирают из условия передачи 90% энергии сигнала Найдем для прямоугольного импульса