Преподаватель: Солодухин Андрей Геннадьевич
1. Маршруты, цепи, циклы 2. Расстояния и метрические характеристики 3. Связность графов
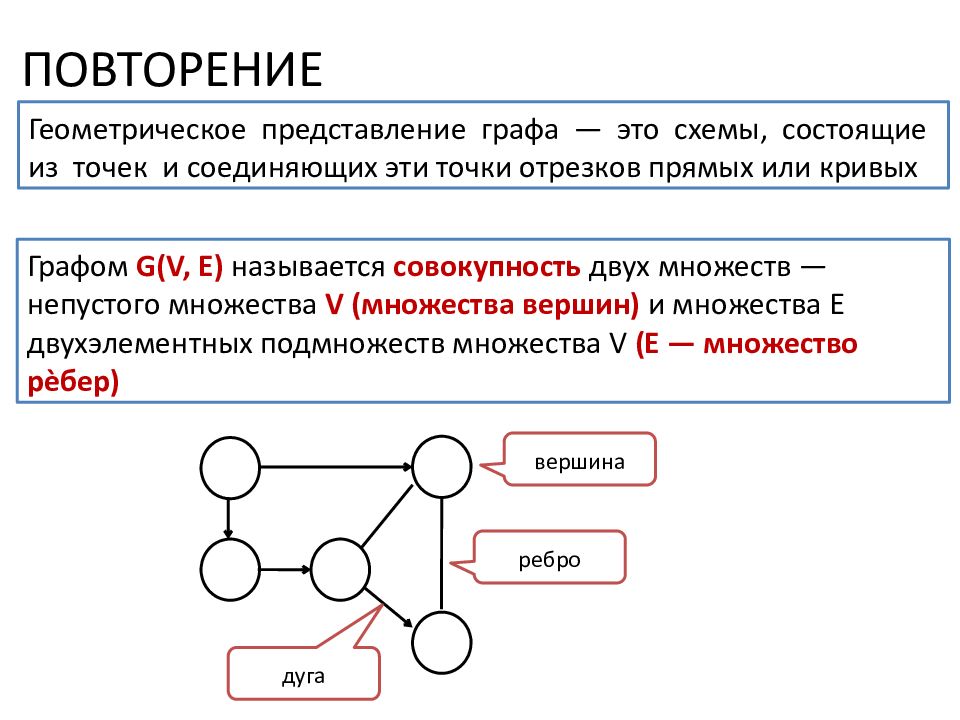
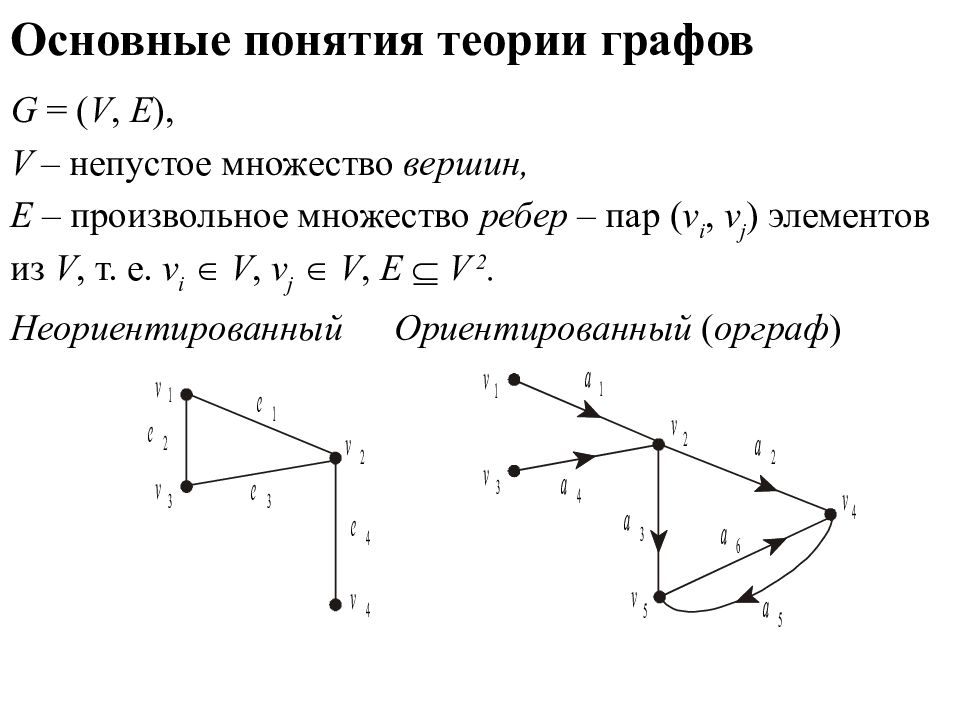
ПОВТОРЕНИЕ Геометрическое представление графа — это схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых Графом G(V, E) называется совокупность двух множеств — непустого множества V (множества вершин) и множества E двухэлементных подмножеств множества V (E — множество рѐбер ) вершина ребро дуга
МАРШРУТЫ, ЦЕПИ, ЦИКЛЫ: ОПРЕДЕЛЕНИЯ Маршрутом в графе называется последовательность вершин и ребер, начинающаяся и заканчивающаяся вершиной Маршрут в котором все ребра различны, называется цепью Цепь называется простой, если и все вершины в ней различны Длиной пути называется число ребер в нем Путь – это … ориентированная цепь, в которой дуги имеют одинаковое направление
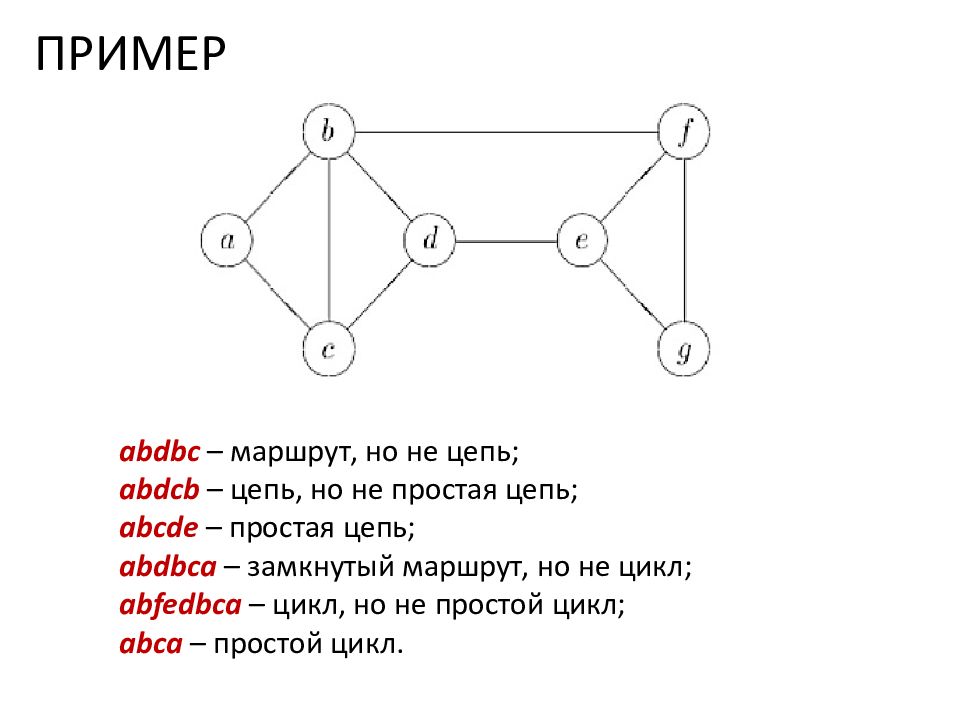
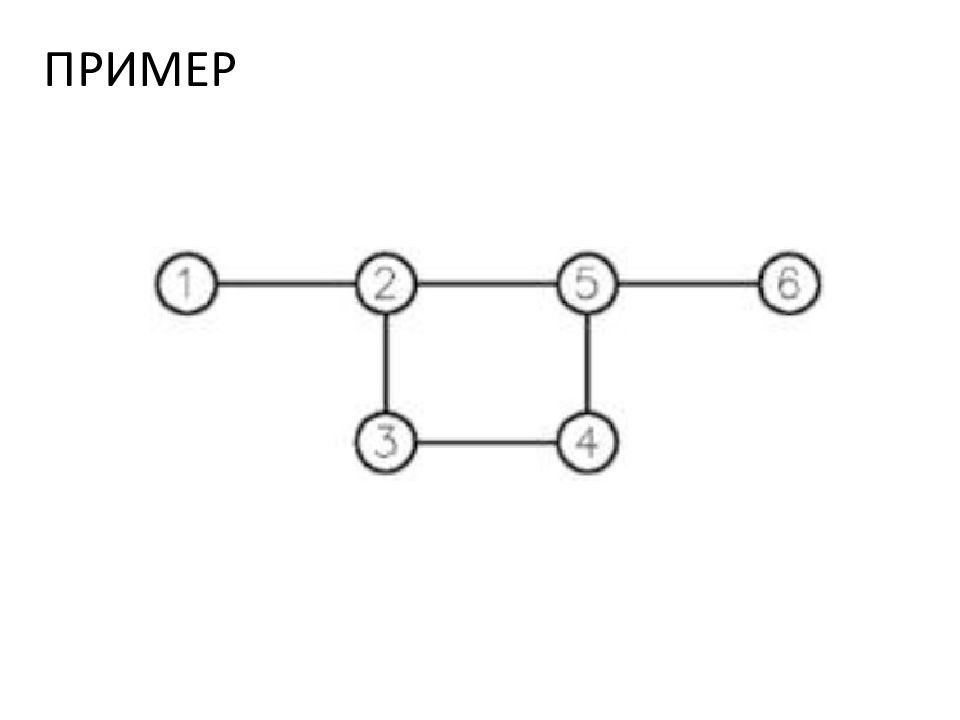
ПРИМЕР abdbc – маршрут, но не цепь; abdcb – цепь, но не простая цепь; abcde – простая цепь; abdbca – замкнутый маршрут, но не цикл; abfedbca – цикл, но не простой цикл; abca – простой цикл.
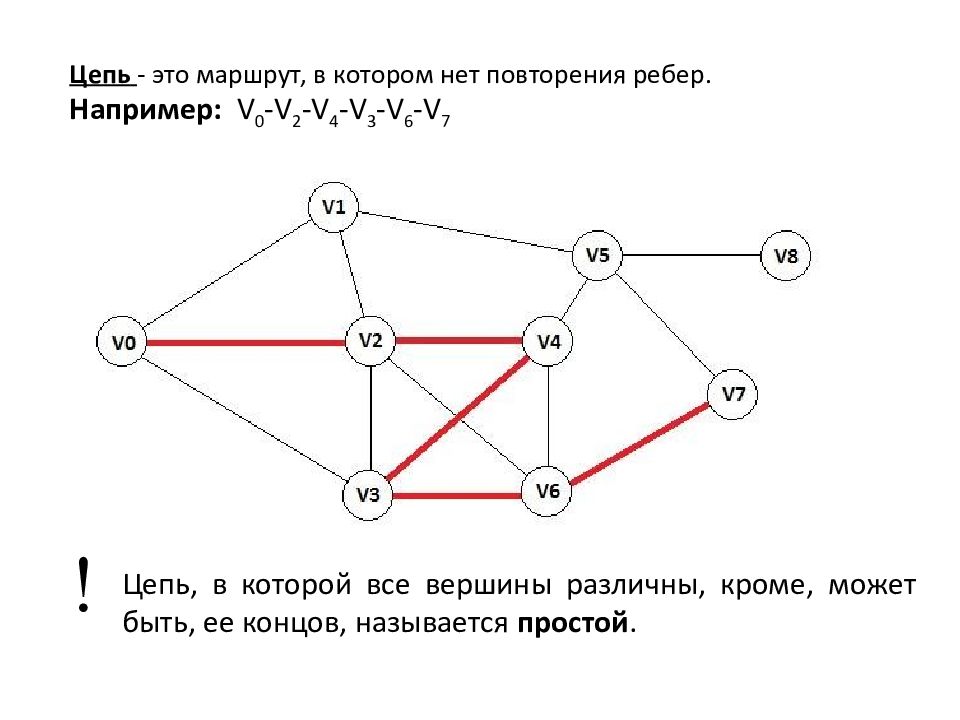
Цепь - это маршрут, в котором нет повторения ребер. Например: V 0 - V 2 - V 4 - V 3 - V 6 - V 7 Цепь, в которой все вершины различны, кроме, может быть, ее концов, называется простой.
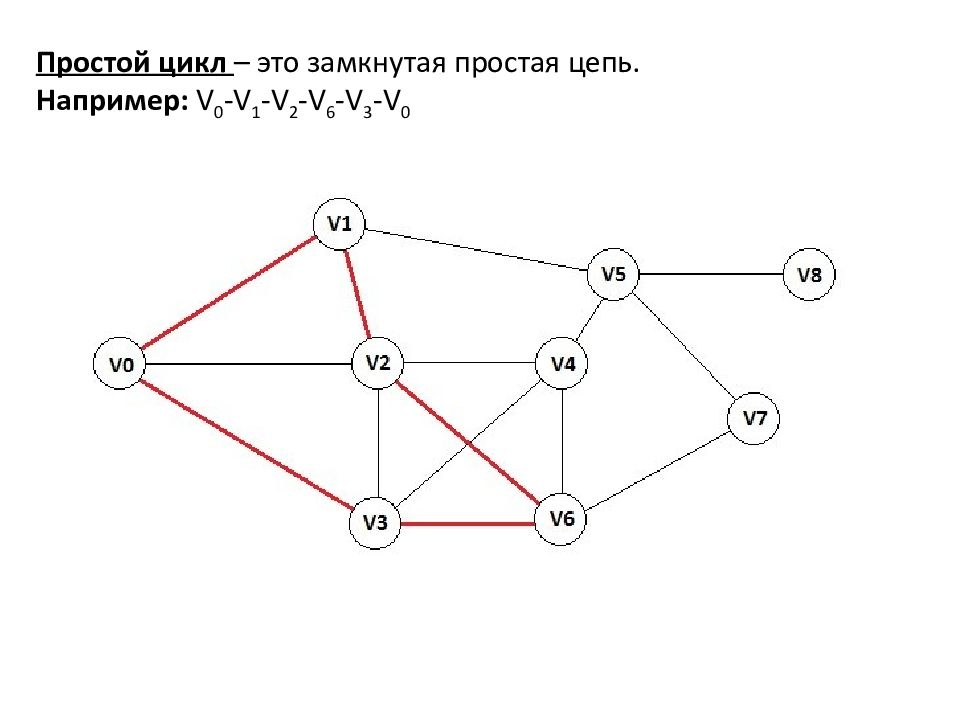
Простой цикл – это замкнутая простая цепь. Например: V 0 -V 1 -V 2 -V 6 -V 3 -V 0
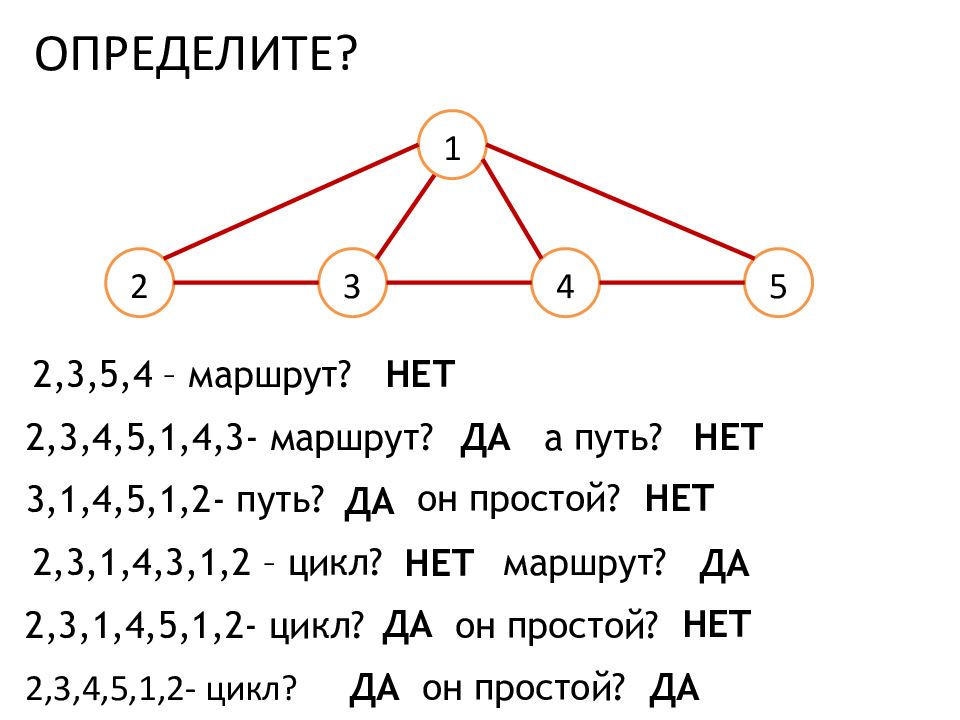
ОПРЕДЕЛИТЕ? 1 2 3 4 5 2,3,4,5,1,2- цикл? 2,3,5,4 – маршрут? НЕТ 2,3,4,5,1,4,3- маршрут? ДА а путь? НЕТ 3,1,4,5,1,2- путь? ДА он простой? НЕТ 2,3,1,4,3,1,2 – цикл? НЕТ маршрут? ДА 2,3,1,4,5,1,2- цикл? ДА он простой? НЕТ ДА он простой? ДА
СВОЙСТВА МАРШРУТОВ Вершина u i называется достижимой из вершины u j, если существует маршрут из u i в u j. В любом маршруте, соединяющем две различные вершины, содержится простой путь, соединяющий те же вершины. В любом цикле, проходящем через некоторое ребро, содержится простой цикл, проходящий через это ребро. Если в графе степень каждой вершины не меньше 2, то в нем есть цикл Если есть цепь, соединяющая вершины u, v, то есть и простая цепь, соединяющая вершины u, v
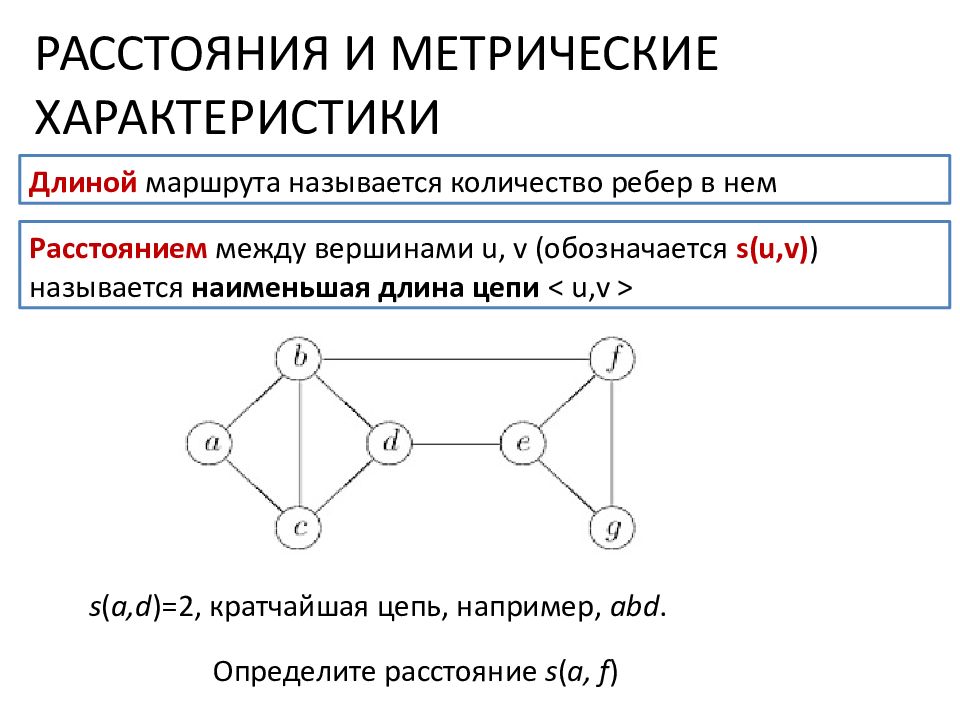
РАССТОЯНИЯ И МЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ Длиной маршрута называется количество ребер в нем Расстоянием между вершинами u, v (обозначается s( u,v ) ) называется наименьшая длина цепи < u,v > s ( a, d )=2, кратчайшая цепь, например, abd. Определите расстояние s ( a, f )
ДИАМЕТР, РАДИУС, ЦЕНТР ГРАФА Диаметр графа – максимальное расстояние между двумя вершинами: то есть наибольший эксцентриситет : Радиус графа R ( G ) – наименьший эксцентриситет Центральная вершина – вершина, эксцентриситет которой равен радиусу графа. Центр – множество всех центральных вершин Эксцентриситет вершины – расстояние от нее до самой удаленной вершины ecc ( x ) = max s (x, y)
Центром графа G называется такая вершина v, что максимальное расстояние между v и любой другой вершиной графа является наименьшим из всех возможных; это расстояние называется радиусом r. Таким образом, Граф может иметь много центров и может не иметь их совсем
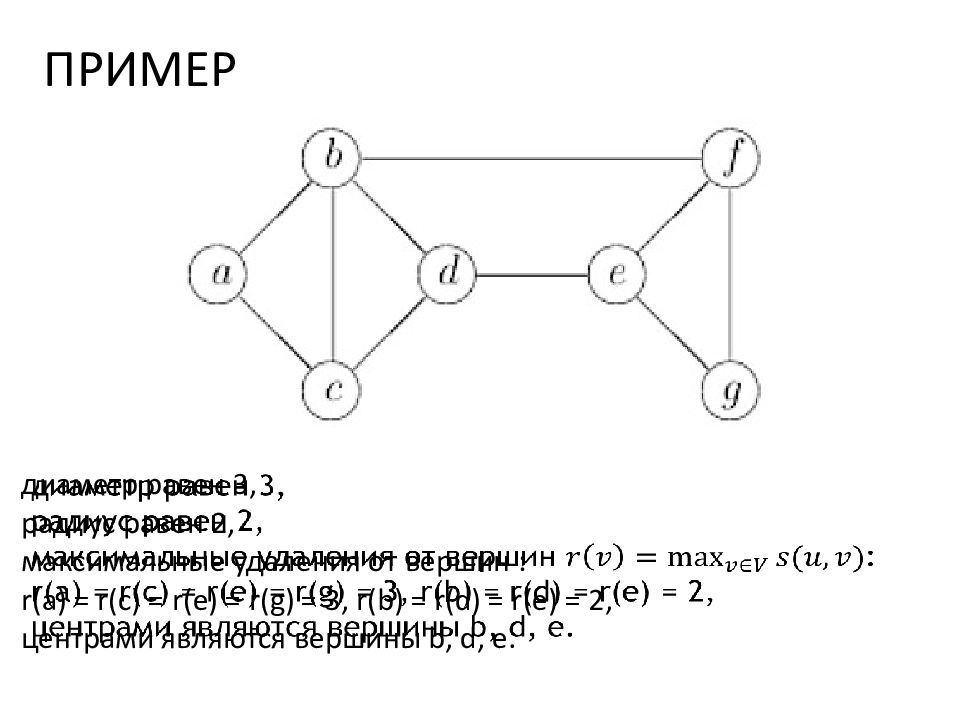
ПРИМЕР диаметр равен 3, радиус равен 2, максимальные удаления от вершин : r ( a ) = r ( c ) = r ( e ) = r ( g ) = 3, r ( b ) = r ( d ) = r ( e ) = 2, центрами являются вершины b, d, e.
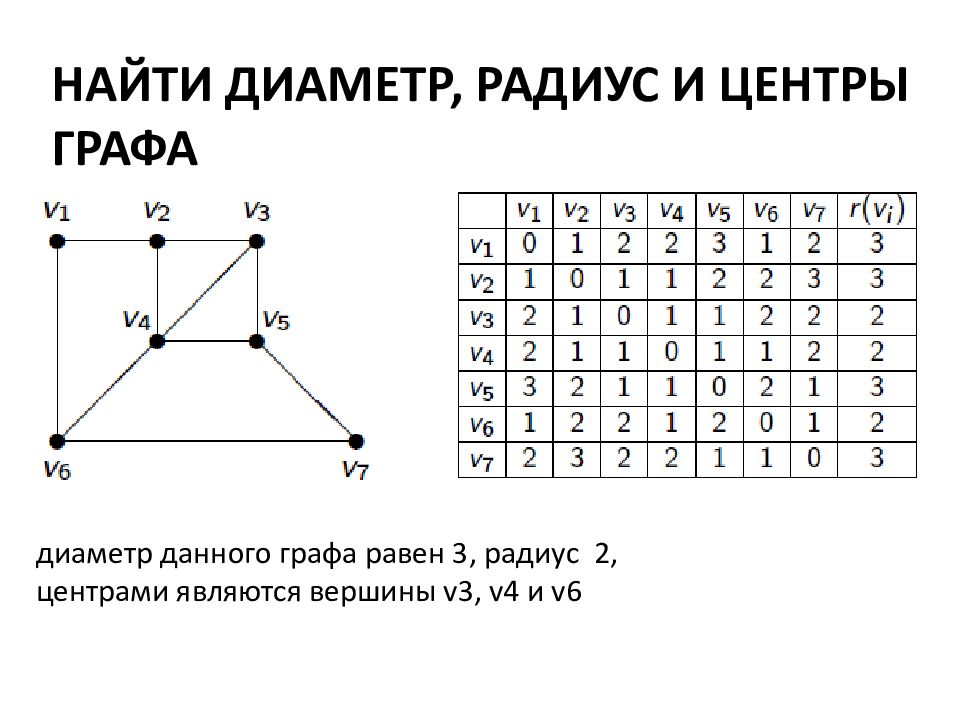
НАЙТИ ДИАМЕТР, РАДИУС И ЦЕНТРЫ ГРАФА диаметр данного графа равен 3, радиус 2, центрами являются вершины v3, v4 и v6
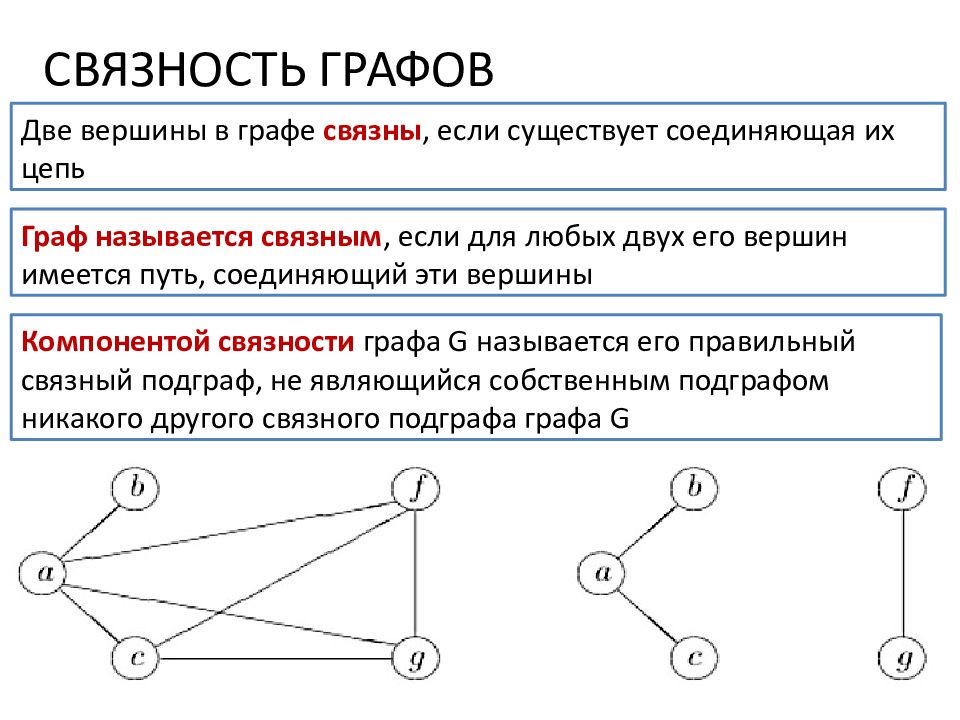
СВЯЗНОСТЬ ГРАФОВ Две вершины в графе связны, если существует соединяющая их цепь Граф называется связным, если для любых двух его вершин имеется путь, соединяющий эти вершины Компонентой связности графа G называется его правильный связный подграф, не являющийся собственным подграфом никакого другого связного подграфа графа G
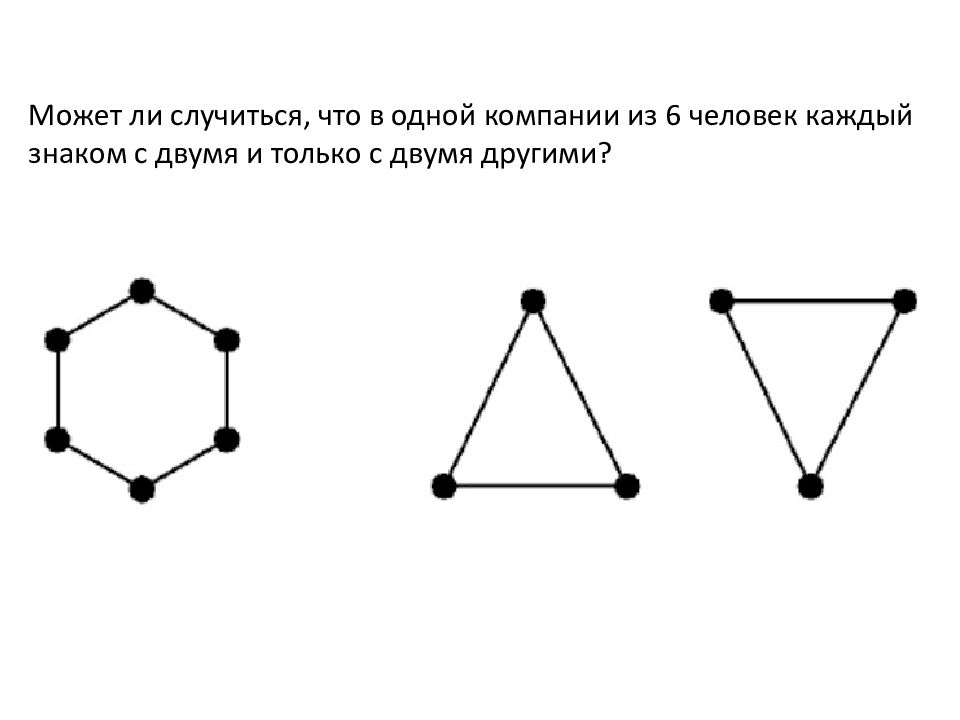
Может ли случиться, что в одной компании из 6 человек каждый знаком с двумя и только с двумя другими?
Граф G, изображенный на рисунке, имеет три компоненты связности.
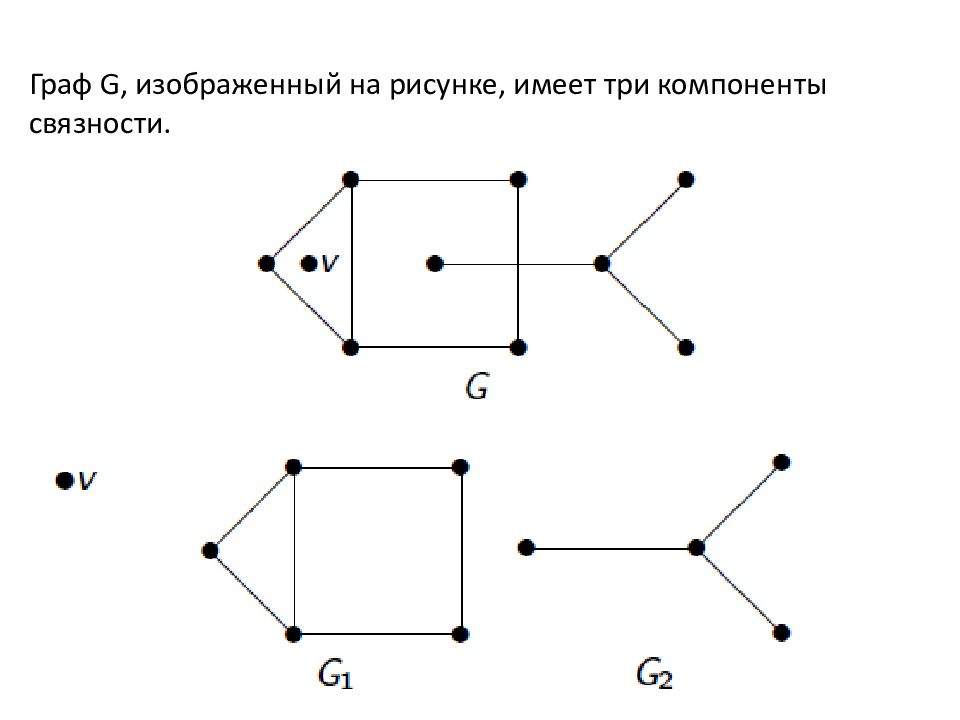
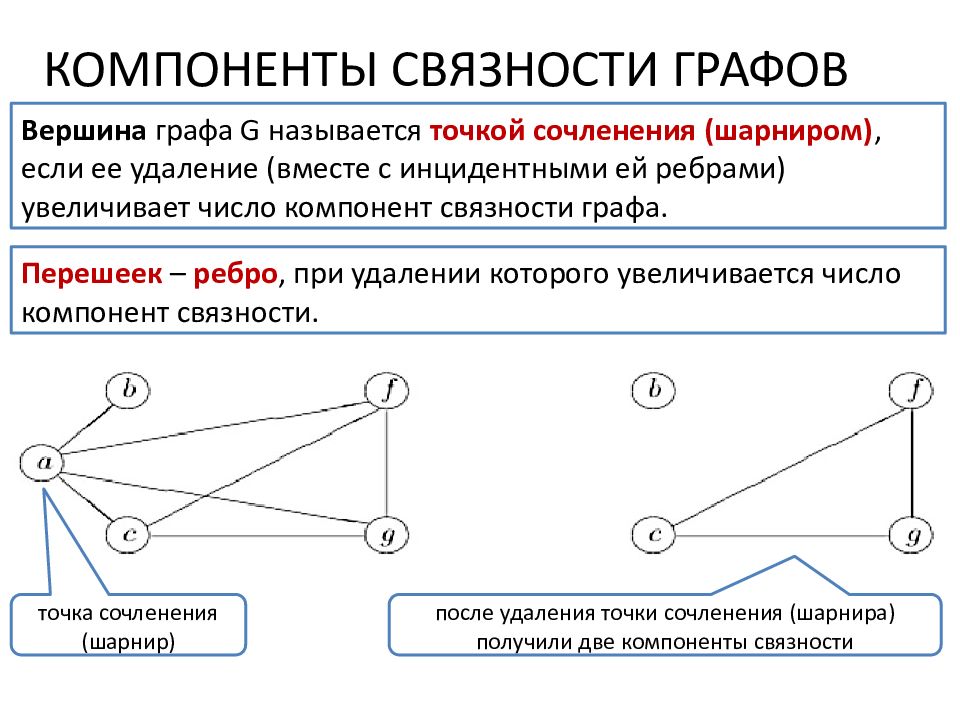
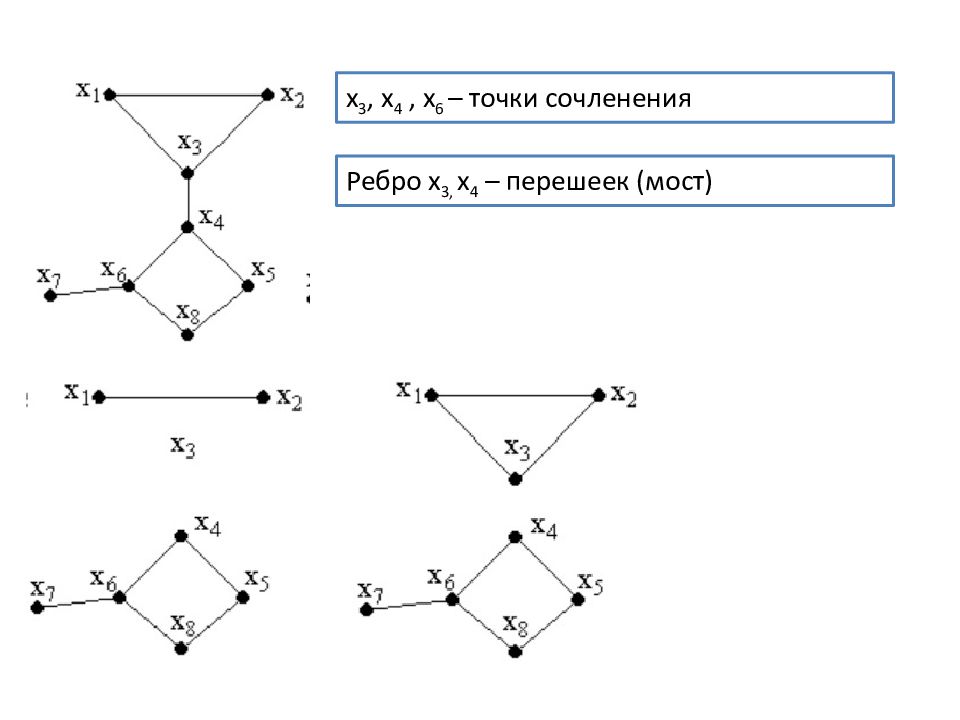
КОМПОНЕНТЫ СВЯЗНОСТИ ГРАФОВ Вершина графа G называется точкой сочленения (шарниром), если ее удаление (вместе с инцидентными ей ребрами) увеличивает число компонент связности графа. Перешеек – ребро, при удалении которого увеличивается число компонент связности. точка сочленения (шарнир) после удаления точки сочленения (шарнира) получили две компоненты связности
x 3, x 4, х 6 – точки сочленения Ребро x 3, x 4 – перешеек (мост)
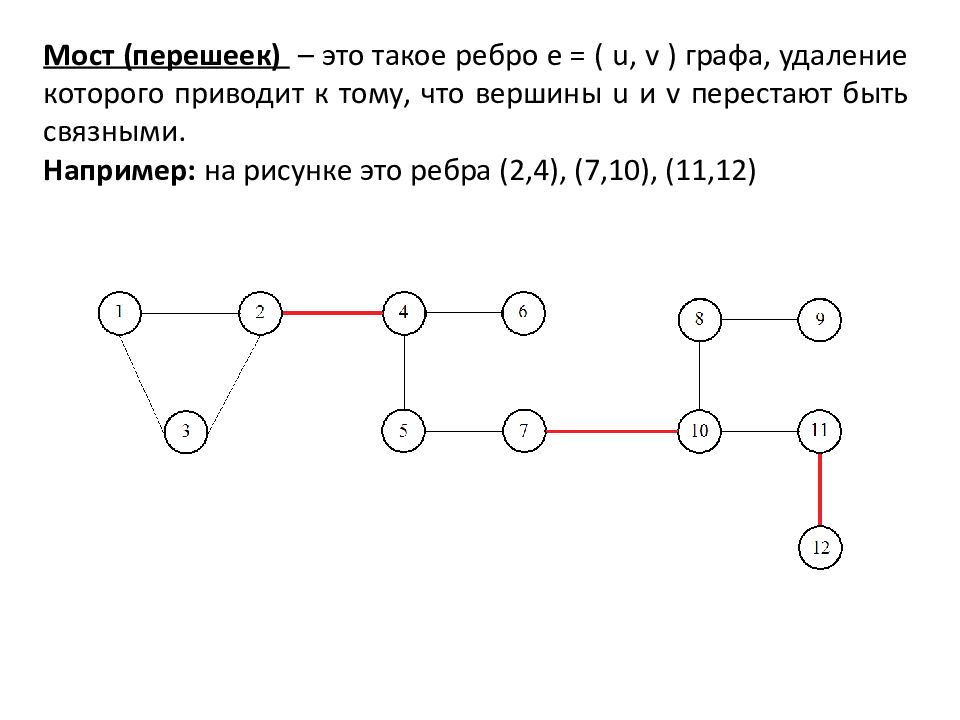
Мост (перешеек) – это такое ребро е = ( u, v ) графа, удаление которого приводит к тому, что вершины u и v перестают быть связными. Например: на рисунке это ребра (2,4), (7,10), (11,12)
МАРШРУТЫ В ОРИЕНТИРОВАННЫХ ГРАФАХ Для ориентированного графа можно определить два типа маршрутов: неориентированный (просто маршрут ) и ориентированный ( ормаршрут ) при движении вдоль маршрута в орграфе ребра могут проходиться как в направлении ориентации, так и в обратном направлении, а при движении вдоль ормаршрута - только в направлении ориентации Будем говорить, что маршрут соединяет вершины x 1 и x k, а ормаршрут ведет из x 1 в x k
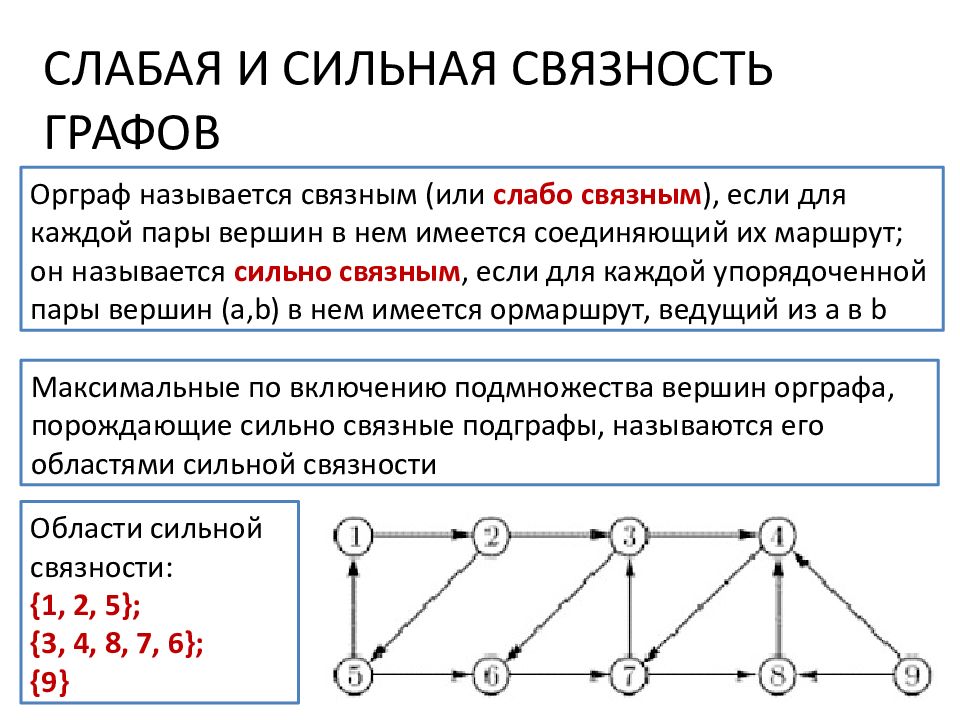
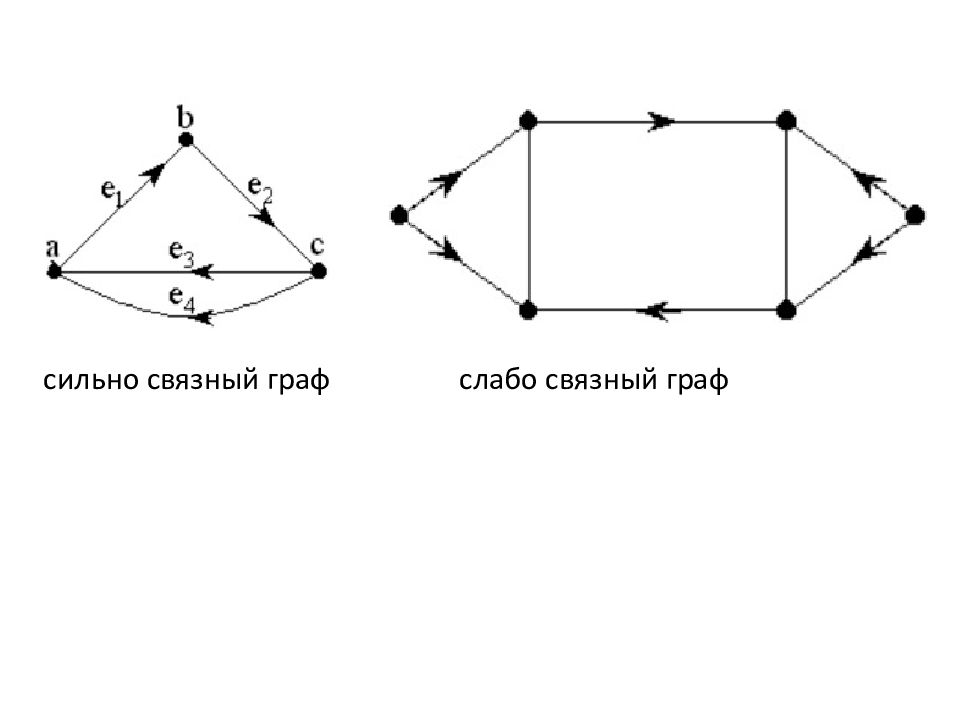
СЛАБАЯ И СИЛЬНАЯ СВЯЗНОСТЬ ГРАФОВ Орграф называется связным (или слабо связным ), если для каждой пары вершин в нем имеется соединяющий их маршрут; он называется сильно связным, если для каждой упорядоченной пары вершин ( a, b ) в нем имеется ормаршрут, ведущий из a в b Максимальные по включению подмножества вершин орграфа, порождающие сильно связные подграфы, называются его областями сильной связности Области сильной связности: {1, 2, 5}; { 3, 4, 8, 7, 6 }; { 9}
сильно связный граф слабо связный граф
ПРИМЕР
Что такое маршрут? В чем измеряется длина маршрута? Что такое цепь? Простая цепь? Что такое путь? Чем он отличается от цепи? Что такое цикл? Простой цикл? Что такое контур? Чем он отличается от цикла? Поясните понятия связности и достижимости. Что такое сильная связность, слабая связность, просто связность, вершинная связность, реберная связность? Чем отличается компонента связности от компоненты сильной связности? Какая вершина называется точкой сочленения? Какое ребро (дуга) называется мостом (перешейком)? ВОПРОСЫ
Программирование, компьютеры и сети https ://progr-system.ru /
