Одиннадцатое октября. Классная работа. Свойства нуля при сложении и умножении, свойства единицы при умножении.
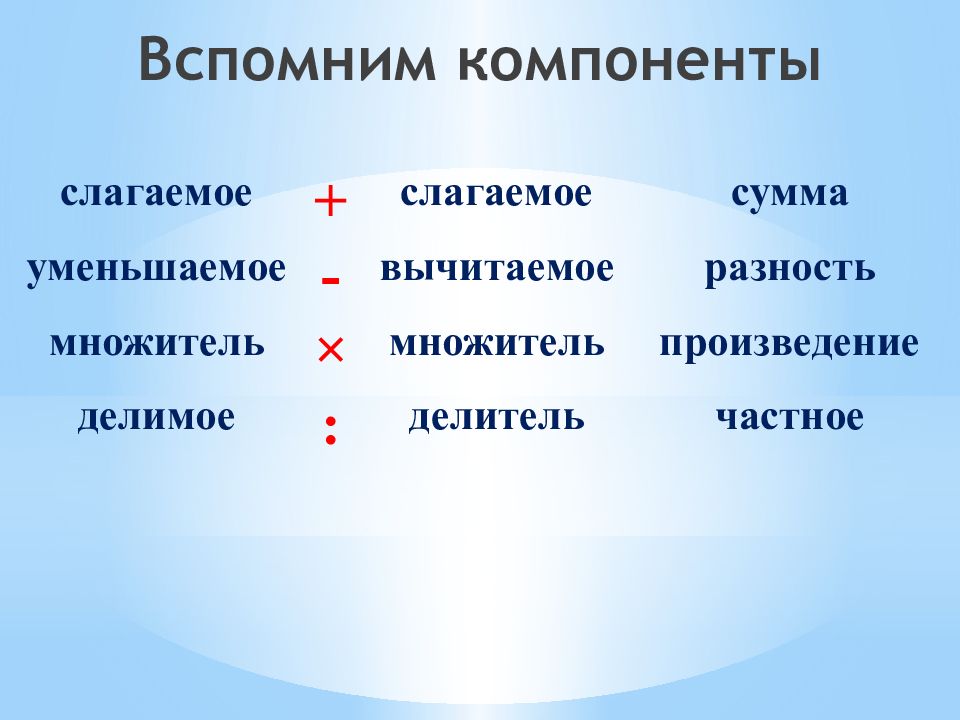
Вспомним компоненты слагаемое + слагаемое сумма уменьшаемое - вычитаемое разность множитель × множитель произведение делимое : делитель частное
Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число. Число 0 имеет два названия: НУЛЬ и НОЛЬ.
Если к числу прибавить нуль, получится само число. a + 0 = 0 + a = a 0+0+0+0+0+0+0+0 = 0 Так как в равенстве все слагаемые одинаковые, сложение можно заменить умножением. 0+0+0+0+0+0+0+0 = 0 × 8 = 0
При умножении 0 на любое число получается 0: 0 × a = 0 где a — любое число Пример: 0 ×3 = 0, 0 × 4 = 0, 0 × 10 = 0. Число умножаем на ноль (переместительный закон умножения) 3 × 0 = 0× 3 = 0.
При умножении любого числа на 0 получается 0: a × 0 = 0 где a — любое число Из приведённых примеров следует, что для любого числа a верны равенства: 0 × a = 0 a × 0 = 0 Произведение двух множителей, один из которых равен нулю, всегда будет равно нулю. Число «0» — это единственное действительное число, которое не является ни положительным, ни отрицательным.
При умножении единицы на любое число в результате получится данное число. 1 × a = a × 1 = а Пример. 1 × 3 = 3 потому что сумма 1 + 1 + 1 = 3. При умножении любого числа на единицу результат будет равен этому числу. Пример. 5 × 1 = 5, если число 5 взять 1 раз, то получится 5.
Из приведённых примеров следует, что для любого числа a верны равенства: 1 × a = a a × 1 = a Произведение двух множителей, один из которых равен единице, всегда будет равно другому множителю.
Индивидуальная работа. Первый множитель 15 второй 10. Найдите значение произведения. Делимое 0, делитель 50. Найти значение частного. Первый множитель 23, второй 100. Найдите значение произведения. Делимое 180, делитель 180. Найти значение частного. Делимое 70, делитель 2. Найти значение частного. Первый множитель 2 030, второй 0. Найдите значение произведения. Делимое 86 123, делитель 1. Найти значение частного.
№ 1. Решите примеры: 1. (6 · 4 – 3 · 8) + 3 2. 7 · (2· 7 + 34 - 48) 3. 0 + (4 ·4 – 3 · 5) 4. 8 · (30 – 3 · 3 - 21) 5. 3 + (7 · 7 – 20 - 29) 6. (36 – 9 ·4) · (39 + 46)
