Первый слайд презентации
Окружность, описанная около правильного многоугольника и вписанная в правильный многоугольник.
Слайд 4
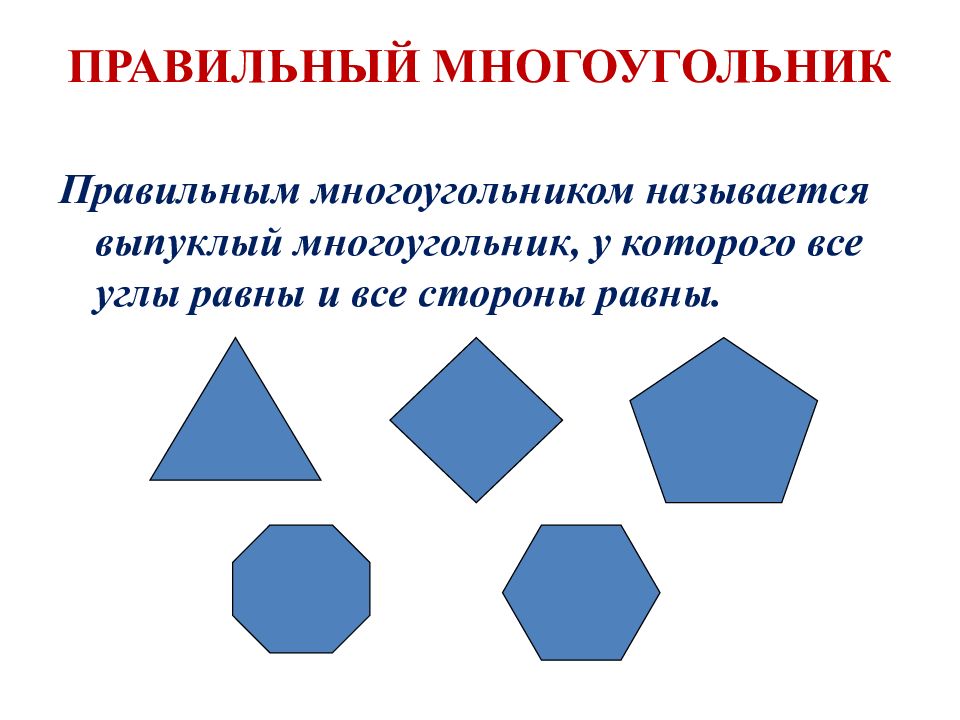
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Слайд 6
Вписанная и описанная окружность Окружность называется описанной около многоугольника, если все его вершины лежат на этой окружности. Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну. Центр описанной окружности – точка пересечения биссектрис
Слайд 7
Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Вписанная и описанная окружность Теорема: В любой правильный многоугольник можно вписать окружность, и притом только одну. Центр вписанной окружности – точка пересечения серединных перпендикуляров.
Слайд 8
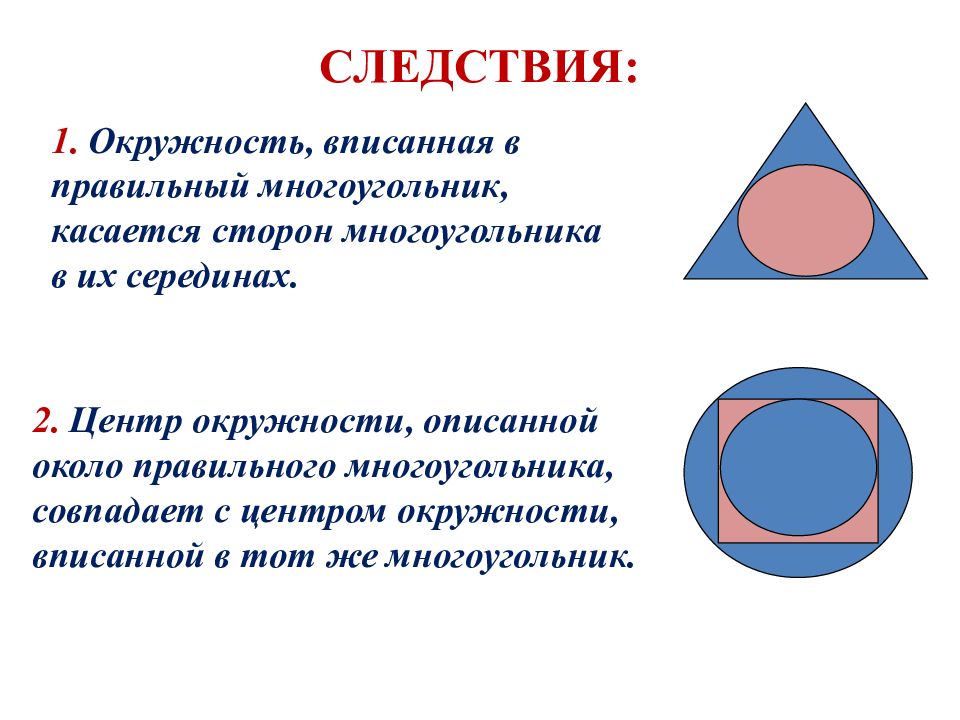
1. Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. 2. Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник. СЛЕДСТВИЯ:
Слайд 9
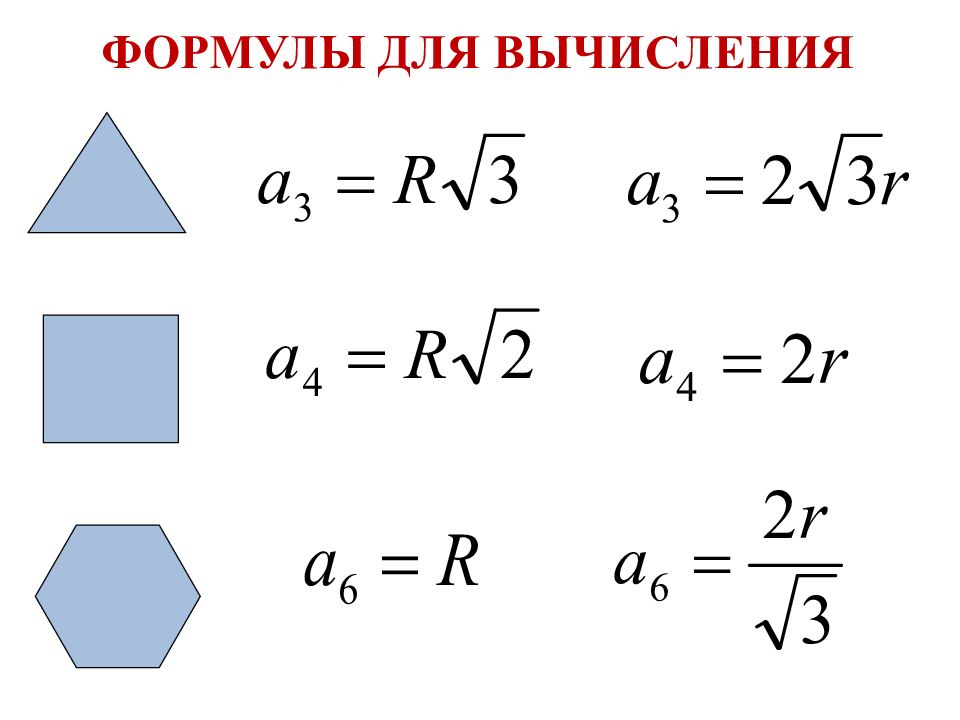
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ Площадь правильного многоугольника Сторона правильного многоугольника Радиус вписанной окружности
Слайд 10
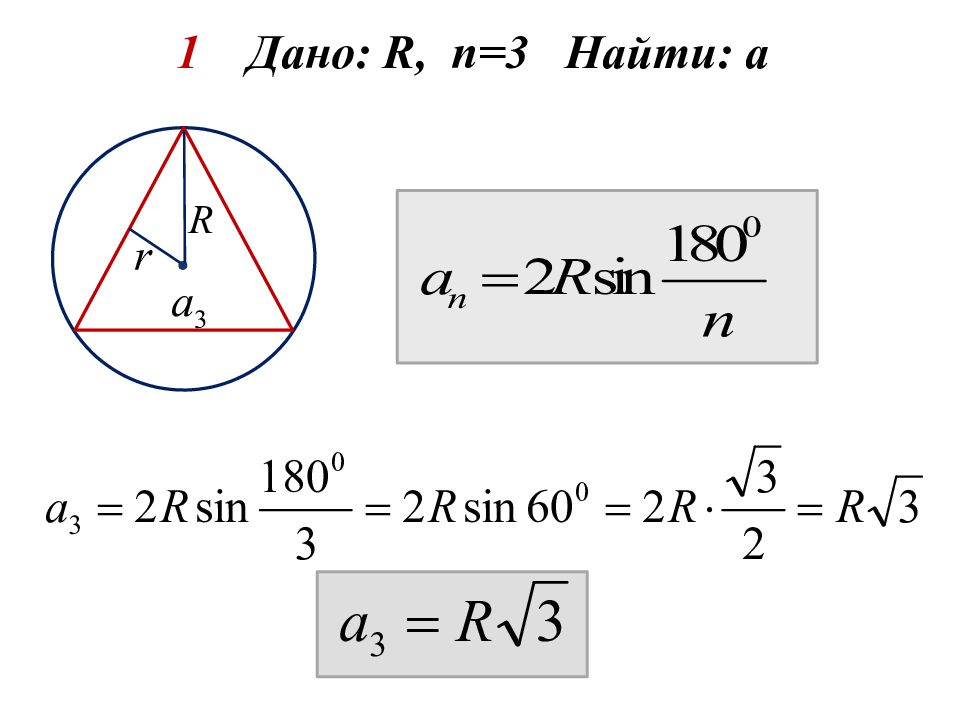
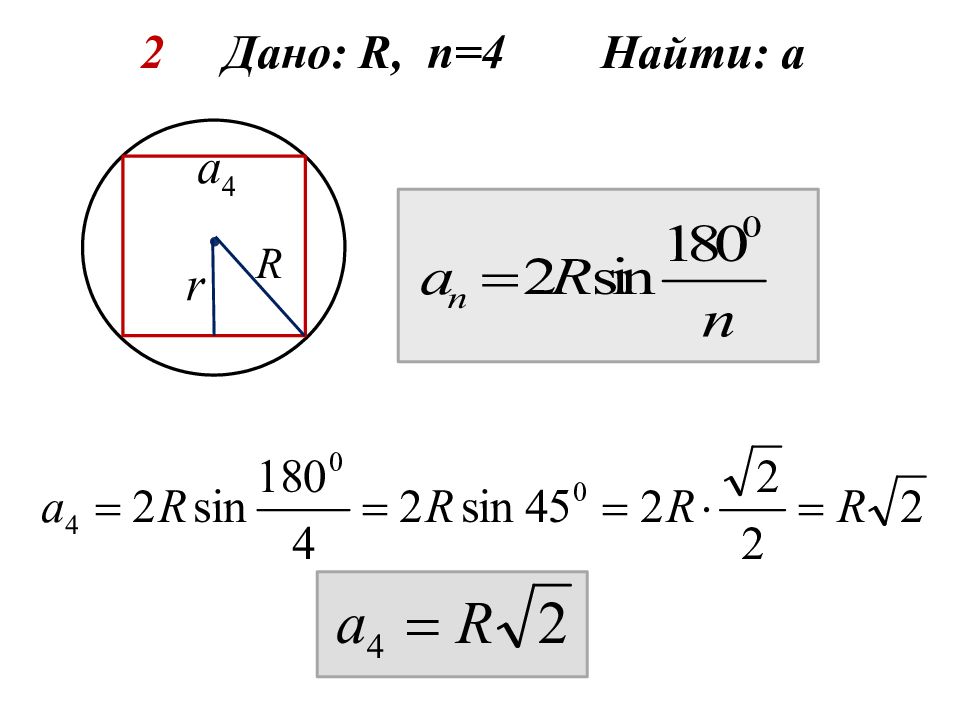
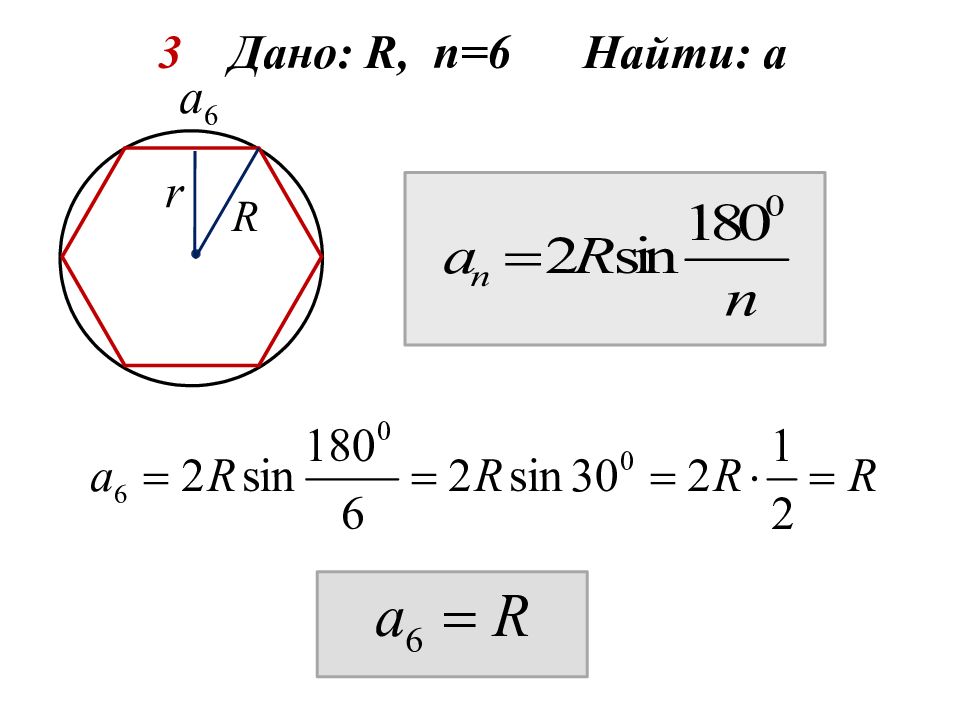
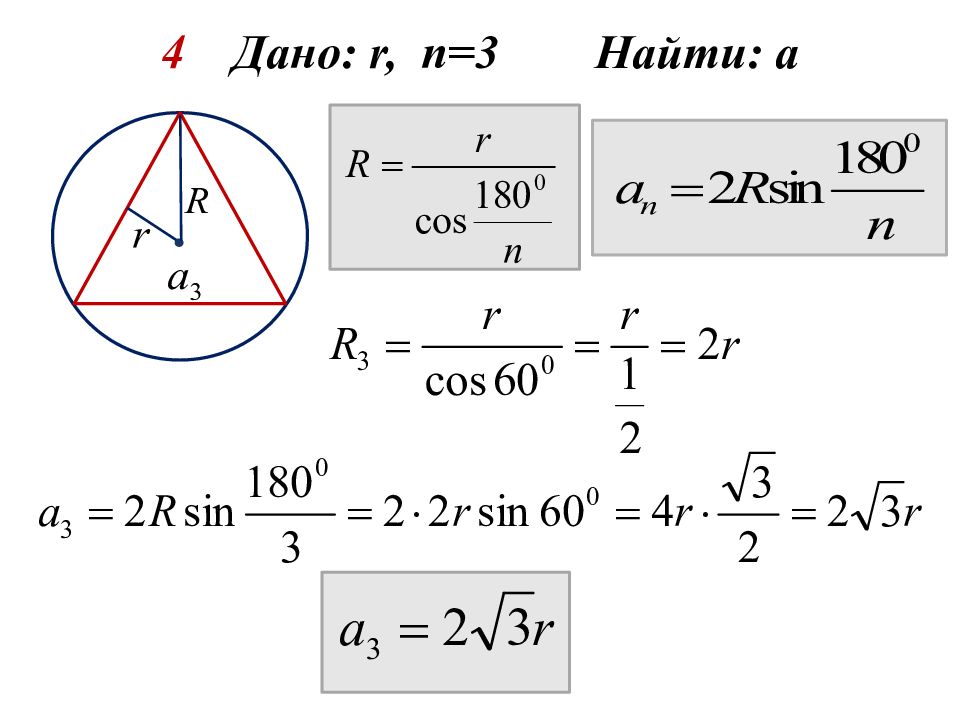
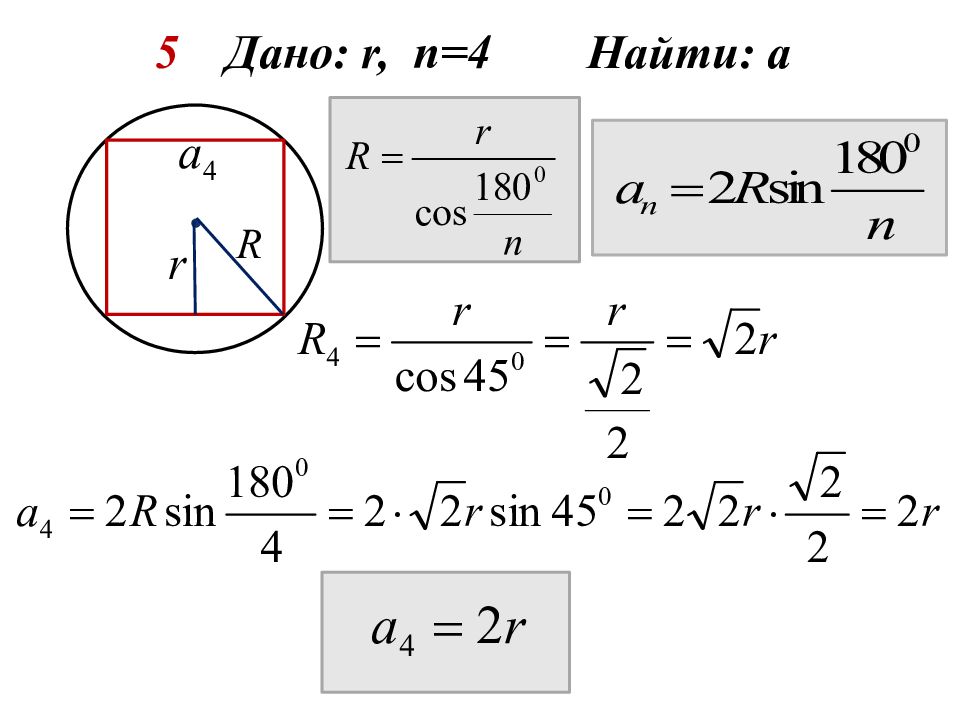
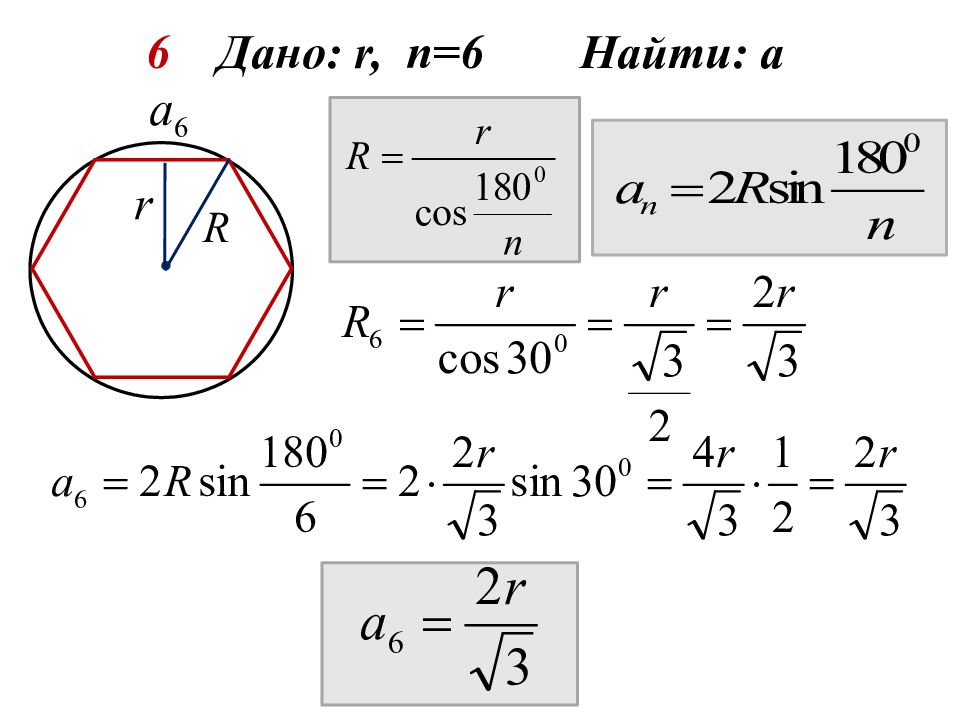
1 Дано: R, n =3 Найти: а 2 Дано: R, n =4 Найти: а 3 Дано: R, n =6 Найти: а 4 Дано: r, n =3 Найти: а 5 Дано: r, n = 4 Найти: а 6 Дано: r, n = 6 Найти: а