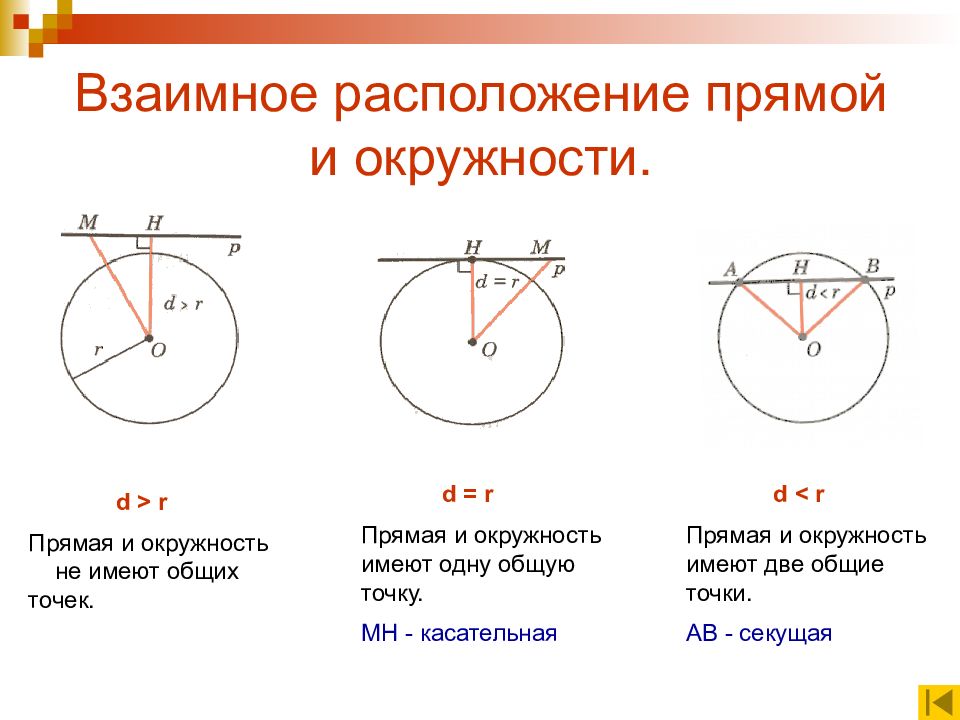
d > r Прямая и окружность не имеют общих точек. d = r Прямая и окружность имеют одну общую точку. МН - касательная d < r Прямая и окружность имеют две общие точки. АВ - секущая
Слайд 3: Углы, связанные с окружностью
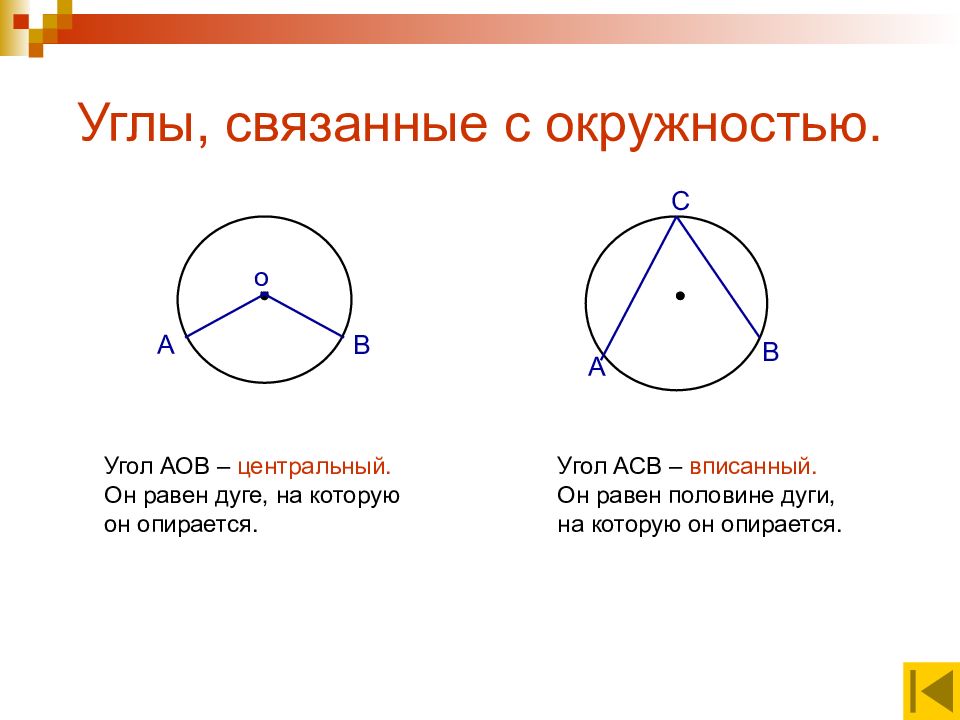
о А В А В С Угол АОВ – центральный. Он равен дуге, на которую он опирается. Угол АСВ – вписанный. Он равен половине дуги, на которую он опирается.
Слайд 4: Свойства вписанных углов
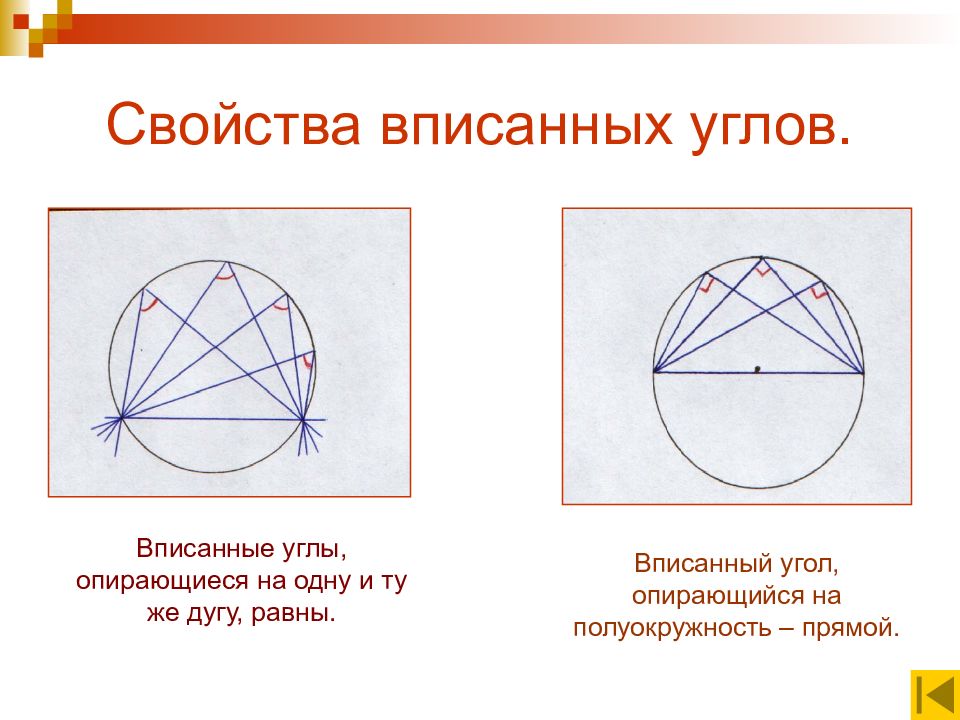
Вписанные углы, опирающиеся на одну и ту же дугу, равны. Вписанный угол, опирающийся на полуокружность – прямой.
Слайд 5: Свойство отрезков касательных
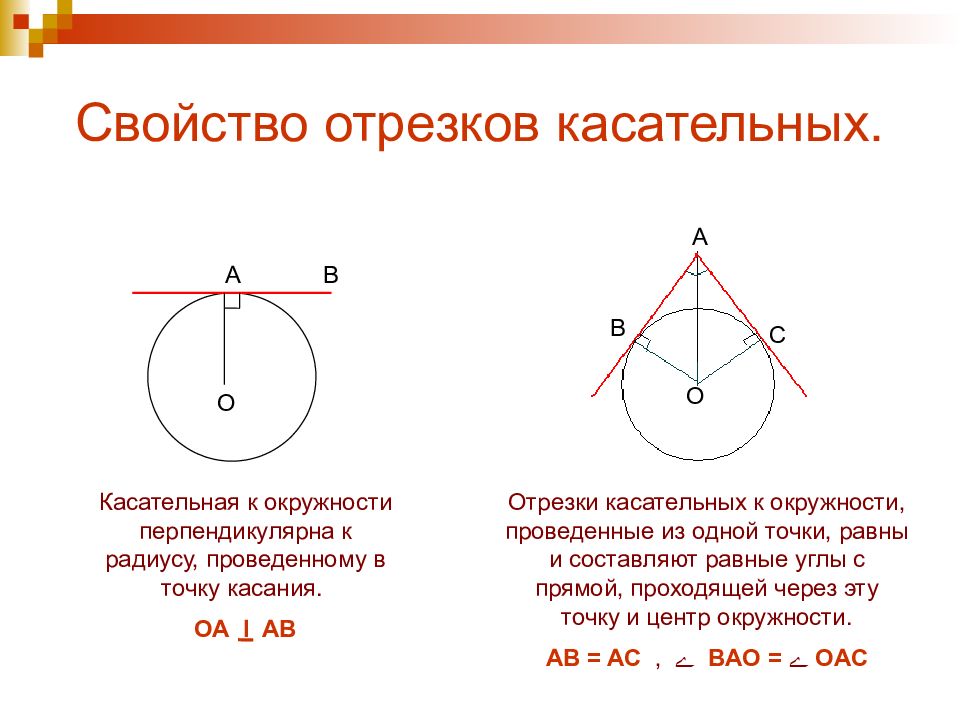
А В О Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. ОА I AB А О С В Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. AB = AC, ے BA О = ے OAC
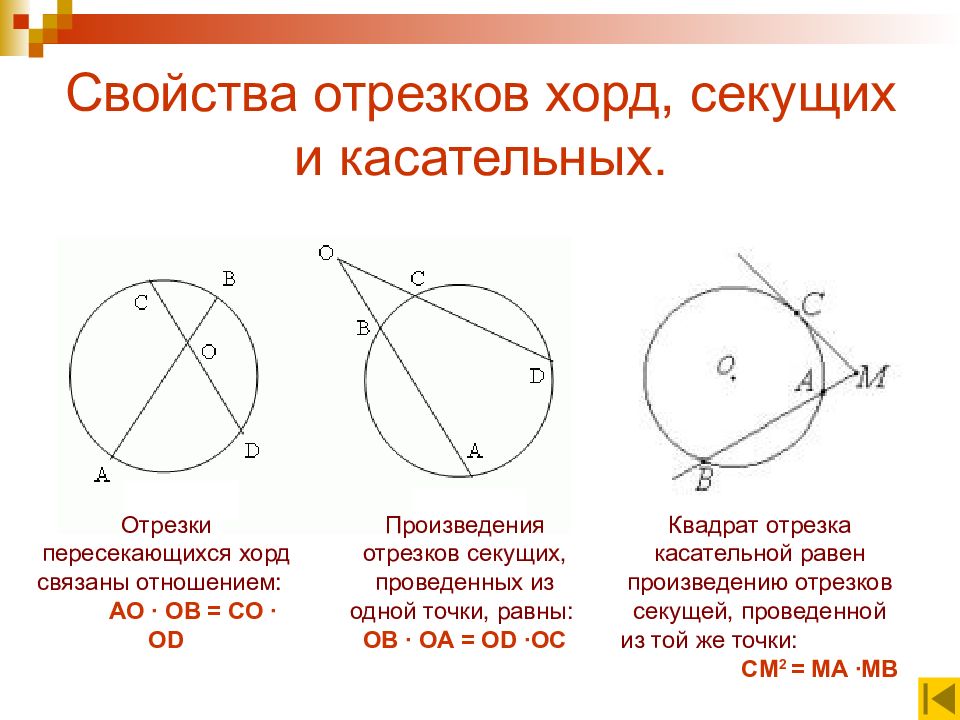
Слайд 6: Свойства отрезков хорд, секущих и касательных
Отрезки пересекающихся хорд связаны отношением: AO ∙ OB = СО ∙ OD Произведения отрезков секущих, проведенных из одной точки, равны: OB ∙ OA = OD ∙OC Квадрат отрезка касательной равен произведению отрезков секущей, проведенной из той же точки: CM 2 = MA ∙MB
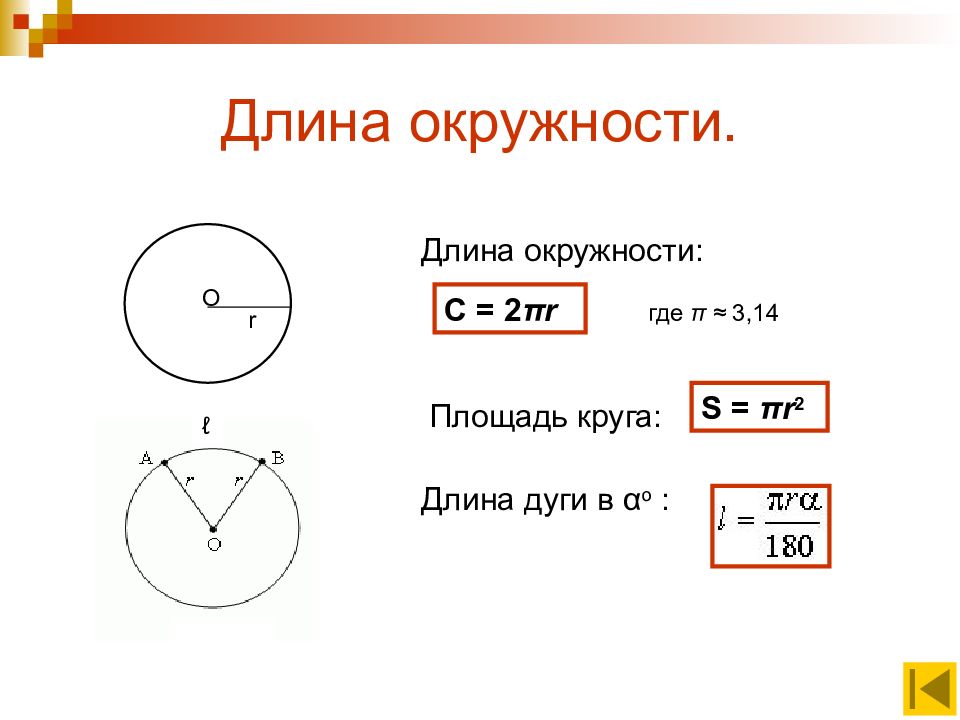
Слайд 7: Длина окружности
О r Длина окружности: Длина дуги в α o : C = 2 π r где π ≈ 3,14 ℓ Площадь круга: S = π r 2
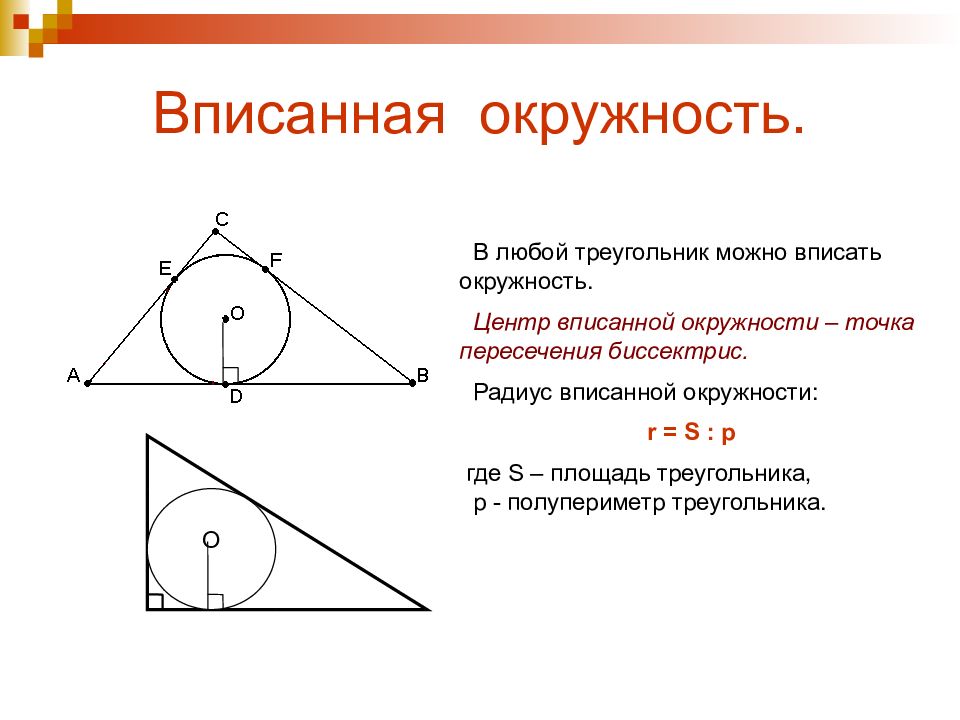
Слайд 8: Вписанная окружность
В любой треугольник можно вписать окружность. Центр вписанной окружности – точка пересечения биссектрис. Радиус вписанной окружности: r = S : р где S – площадь треугольника, р - полупериметр треугольника. О
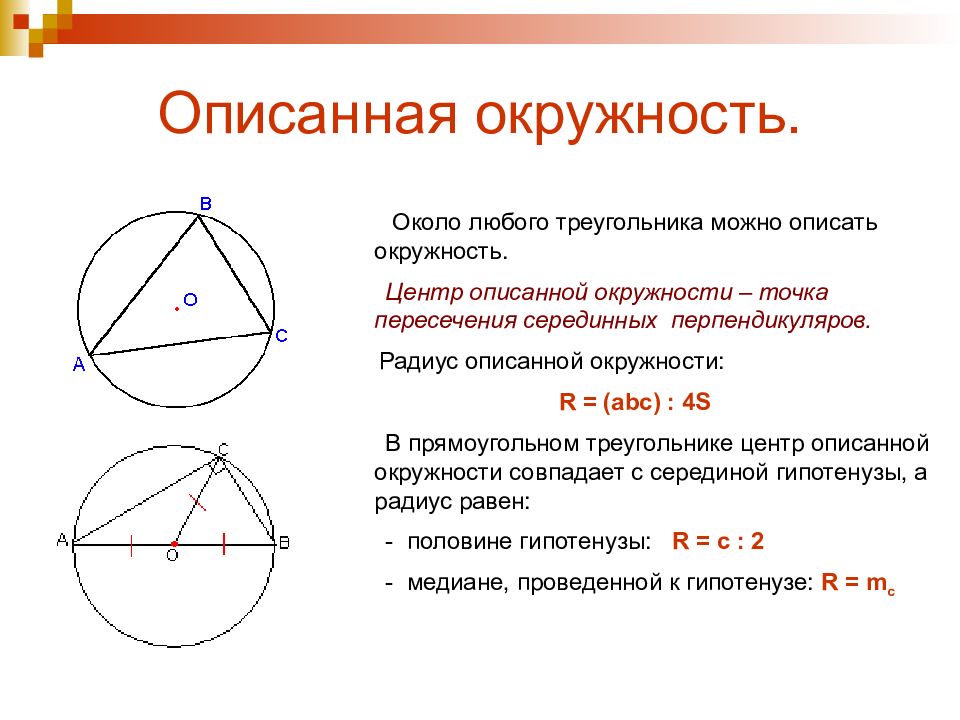
Слайд 9: Описанная окружность
Около любого треугольника можно описать окружность. Центр описанной окружности – точка пересечения серединных перпендикуляров. Радиус описанной окружности: R = (abc) : 4 S В прямоугольном треугольнике центр описанной окружности совпадает с серединой гипотенузы, а радиус равен: - половине гипотенузы: R = c : 2 - медиане, проведенной к гипотенузе: R = m c
Слайд 10: Вписанная и описанная окружности
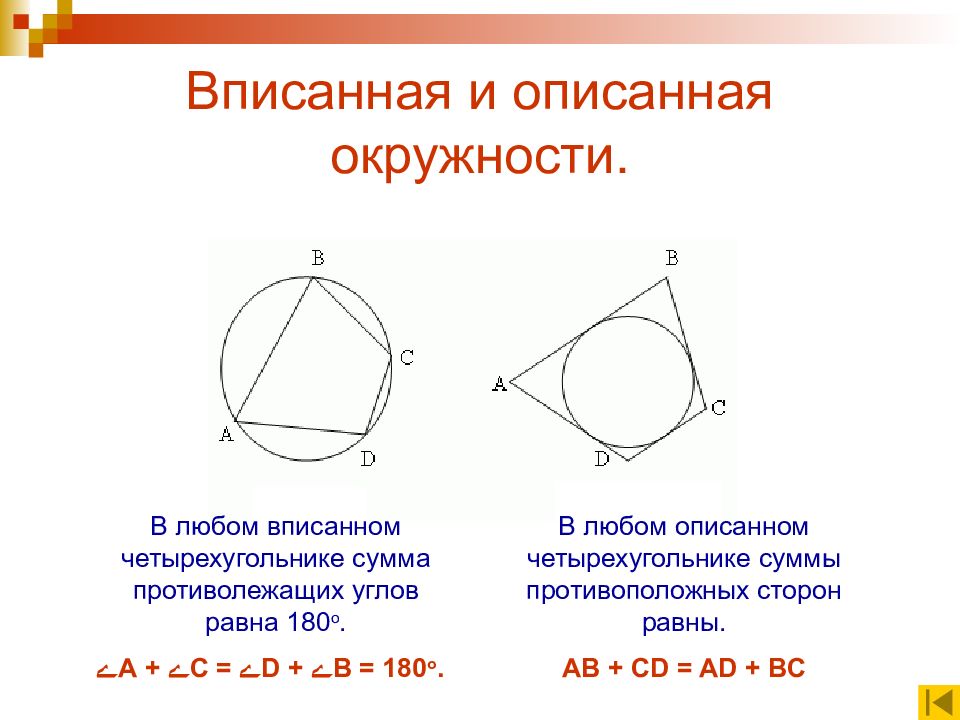
В любом вписанном четырехугольнике сумма противолежащих углов равна 180 о. ے A + ے C = ے D + ے B = 180 о. В любом описанном четырехугольнике суммы противоположных сторон равны. АВ + CD = AD + BC
Слайд 11: Задача № 1
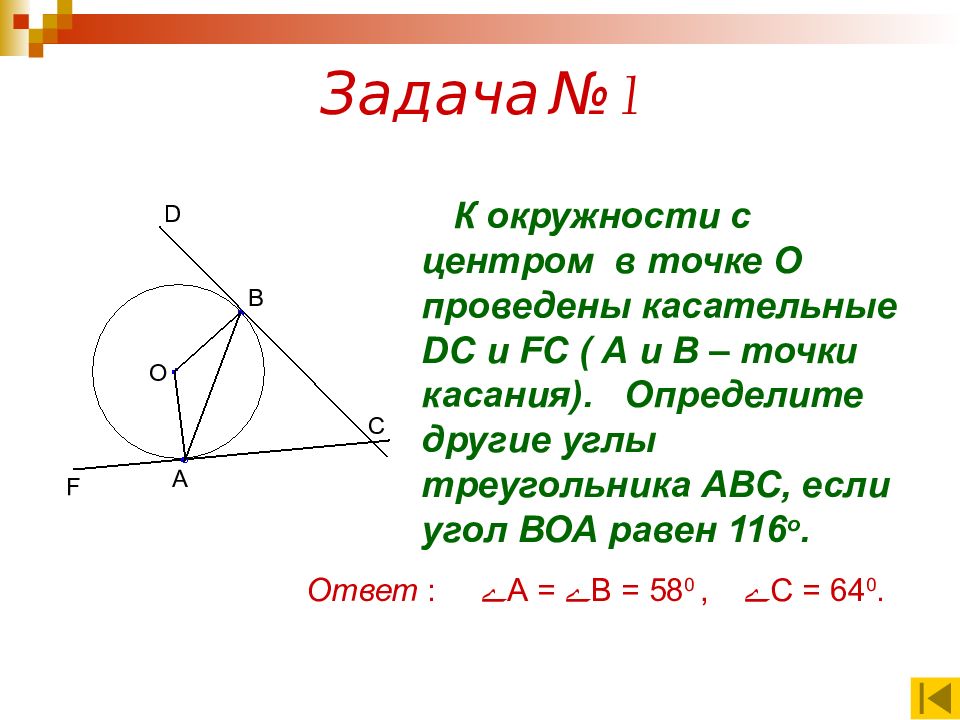
О В А С D F К окружности с центром в точке О проведены касательные DC и FC ( А и В – точки касания). Определите другие углы треугольника АВС, если угол ВОА равен 116 о. Ответ : ے А = ے В = 58 0, ے С = 64 0.
Слайд 12: Задача № 2
А В О С Окружность с центром в точке О касается сторон угла А (В и С – точки касания). Отрезок АВ равен радиусу окружности. Определите градусную меру угла А. Ответ : ے А = 90 0.
Слайд 13: Задача № 3
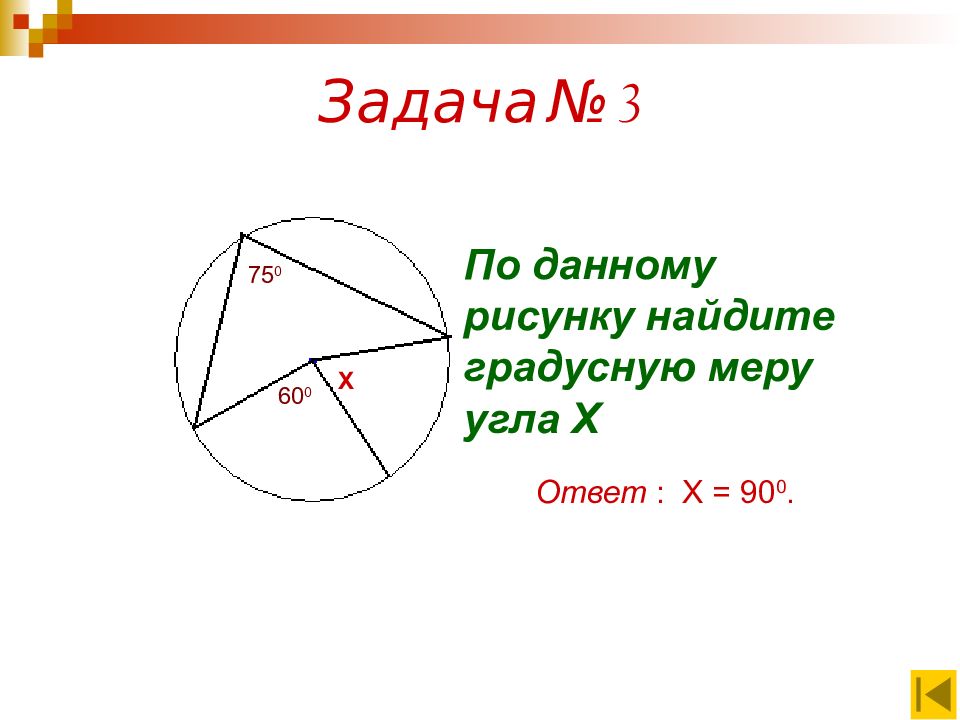
75 0 60 0 Х По данному рисунку найдите градусную меру угла Х Ответ : Х = 90 0.
Слайд 14: Задача № 4
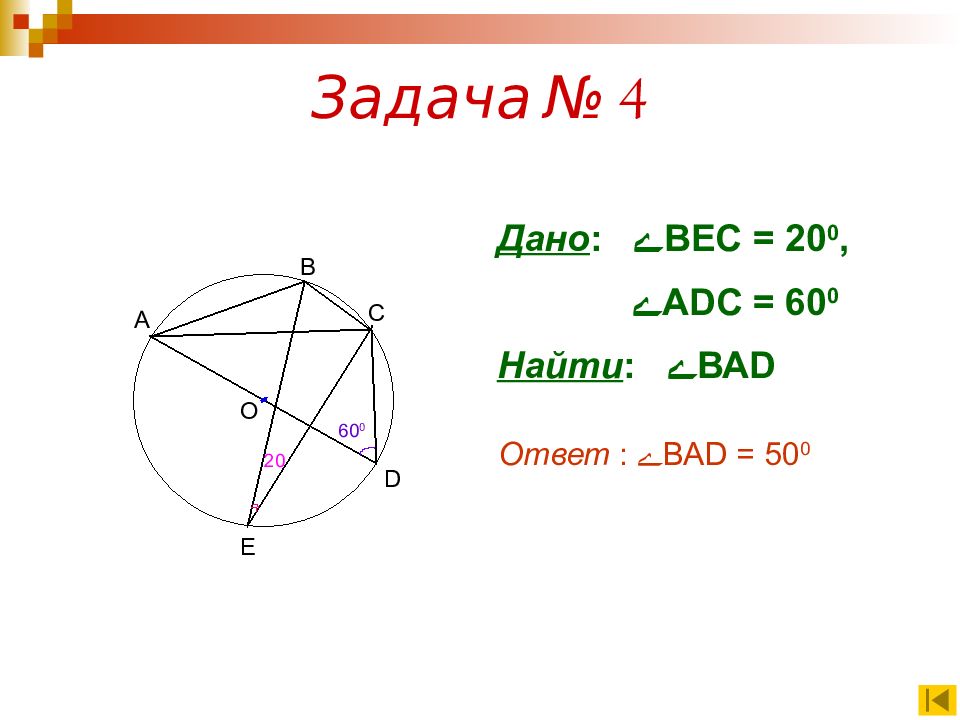
О 60 0 А В С D Е 20 Дано : ے ВЕС = 20 0, ے А DC = 60 0 Найти : ے ВА D Ответ : ے ВА D = 50 0
Слайд 15: Задача № 5
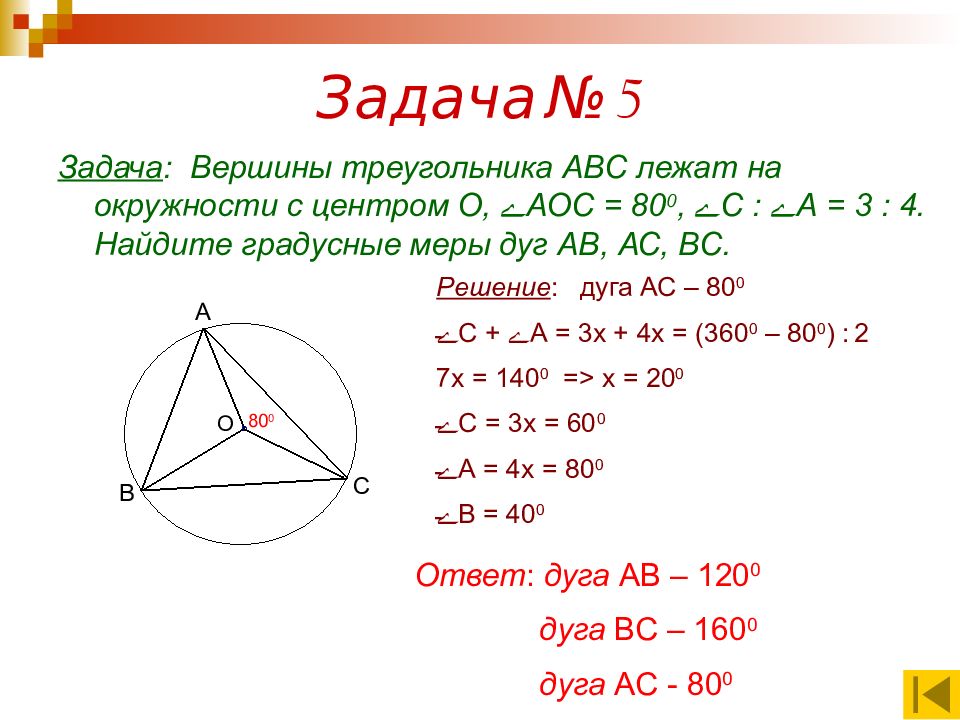
Задача : Вершины треугольника АВС лежат на окружности с центром О, ے АОС = 80 0, ے С : ے А = 3 : 4. Найдите градусные меры дуг АВ, АС, ВС. О А В С 80 0 Решение : дуга АС – 80 0 ے С + ے А = 3х + 4х = (360 0 – 80 0 ) : 2 7х = 140 0 => х = 20 0 ے С = 3х = 60 0 ے А = 4х = 80 0 ے В = 40 0 Ответ : дуга АВ – 120 0 дуга ВС – 160 0 дуга АС - 80 0
Слайд 16: Задача № 6
Задача : Хорды АВ и С D пересекаются в точке Е. АЕ = 8см, ВЕ = 6см, С D = 16 см. В каком отношении точка Е делит отрезок С D ? А В С D Е 8 6 Х 16-х Решение : АЕ ∙ ВЕ = СЕ ∙ D Е Х(16 – Х) = 48 Х 2 – 16Х + 48 = 0 Х 1 = 12, Х 2 = 4 Х 2 : Х 1 = 4 : 12 = ⅓ Ответ: ⅓
Слайд 17: Задача № 7
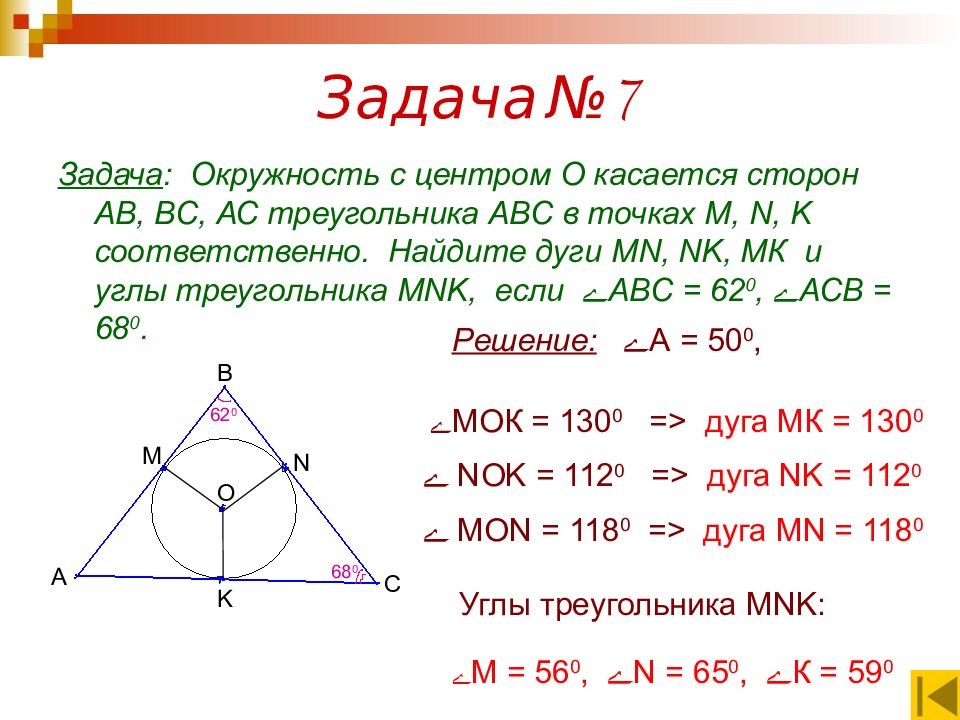
Задача : Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС в точках M, N, K соответственно. Найдите дуги MN, NK, M К и углы треугольника MNK, если ے АВС = 62 0, ے АСВ = 68 0. А В С О М N K 62 0 68 0 Решение: ے А = 50 0, ے МОК = 130 0 => дуга МК = 130 0 ے NOK = 112 0 => дуга NK = 112 0 ے MON = 118 0 => дуга MN = 118 0 Углы треугольника MNK : ے М = 56 0, ے N = 65 0, ے К = 59 0
Слайд 18: Задача № 8
Задача : Точка С делит хорду АВ на отрезки 15см и 8см. Найдите диаметр окружности, если расстояние от точки С до центра окружности равно 1см. А В С О 15 8 1 Решение : воспользуемся теоремой о произведении длин отрезков пересекающихся хорд Х Х+1 Х (Х + 2) = 15 ∙ 8 Х 2 + 2Х – 120 = 0 Х 1 =10 Х 2 = - 12(не удовл.) r = Х + 1 => r = 11см Ответ: d = 22 см
Слайд 19: Задача № 9
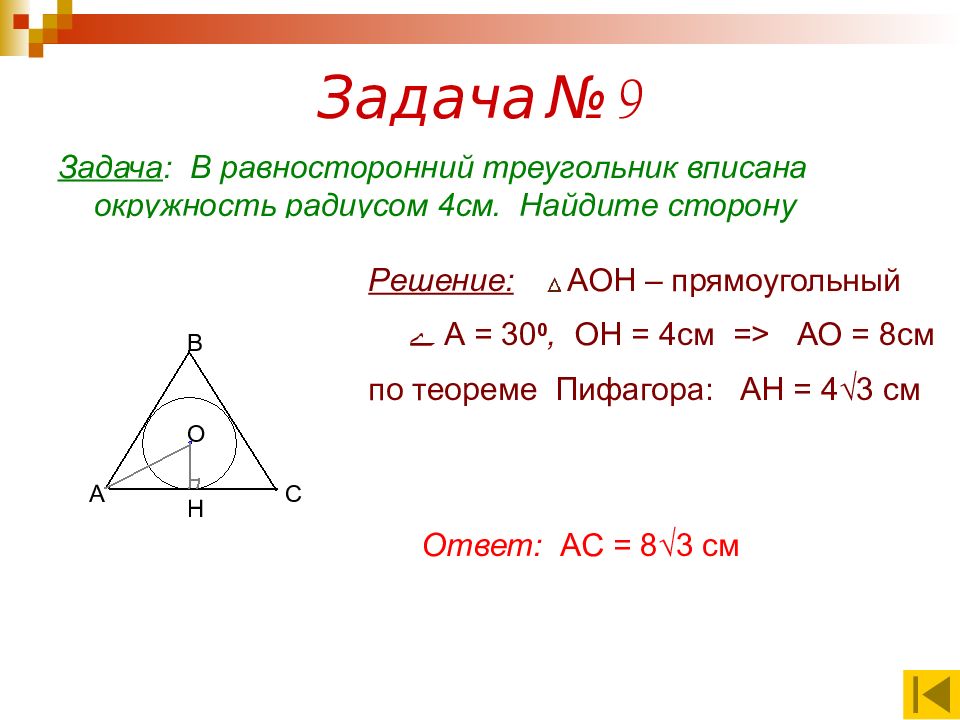
Задача : В равносторонний треугольник вписана окружность радиусом 4см. Найдите сторону треугольника. А В С О Н Решение: АОН – прямоугольный ے А = 30 0, ОН = 4см => АО = 8см по теореме Пифагора: АН = 4 √3 см Ответ: АС = 8 √3 см
Слайд 20: Задача № 10
Задача : В равнобедренной трапеции разность оснований равна 20см, а радиус вписанной в нее окружности равен 2 √14 см. Найдите стороны трапеции. А В С D Н Решение : ВН = 2 r = 4 √14 см АН = (А D – ВС) : 2 = 10 см по т. Пифагора: АВ = 18 см => С D = 18 см так как окружность вписанная, то ВС + А D = АВ + С D = 36 см Х + Х + 20 = 36 Х = 8 Х Х + 20 Ответ : АВ = CD = 18 см ВС = 8см, А D = 28 см
Слайд 21: Задача № 11
Задача : Равнобедренный треугольник с основанием 8см вписан в окружность радиуса 5см. Найдите площадь этого треугольника и его боковую сторону. О А С В Н 8 5 Решение : треугольник АОН – прямоуг. АО = 5см, АН = 4см => ОН = 3см h = 8 см, а = 8см => S =32см 2 по теореме Пифагора АВ = 4√5 см Ответ : S = 32 см 2, бок. ребро - 4 √5 см
Последний слайд презентации: Решение задач по теме:: Задача № 12
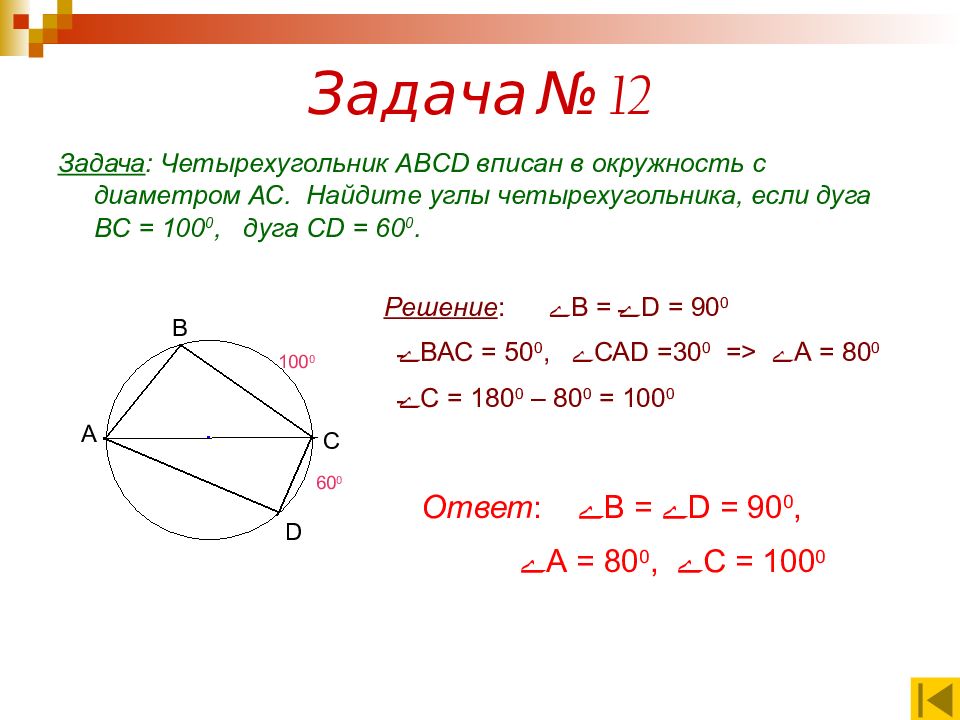
Задача : Четырехугольник АВС D вписан в окружность с диаметром АС. Найдите углы четырехугольника, если дуга ВС = 100 0, дуга С D = 60 0. А В С D Решение : ے В = ے D = 90 0 ے ВАС = 50 0, ے СА D =30 0 => ے А = 80 0 ے С = 180 0 – 80 0 = 100 0 100 0 60 0 Ответ : ے В = ے D = 90 0, ے А = 80 0, ے С = 100 0