Преподаватель: Солодухин Андрей Геннадьевич
1. Бинарные операции. 2. Унарные операции.
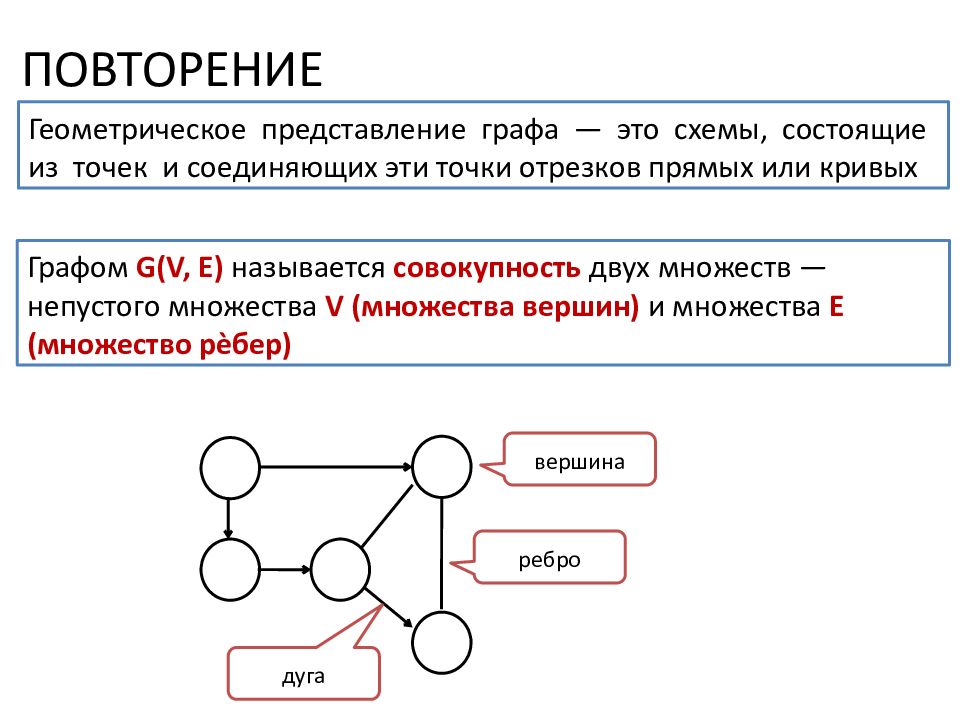
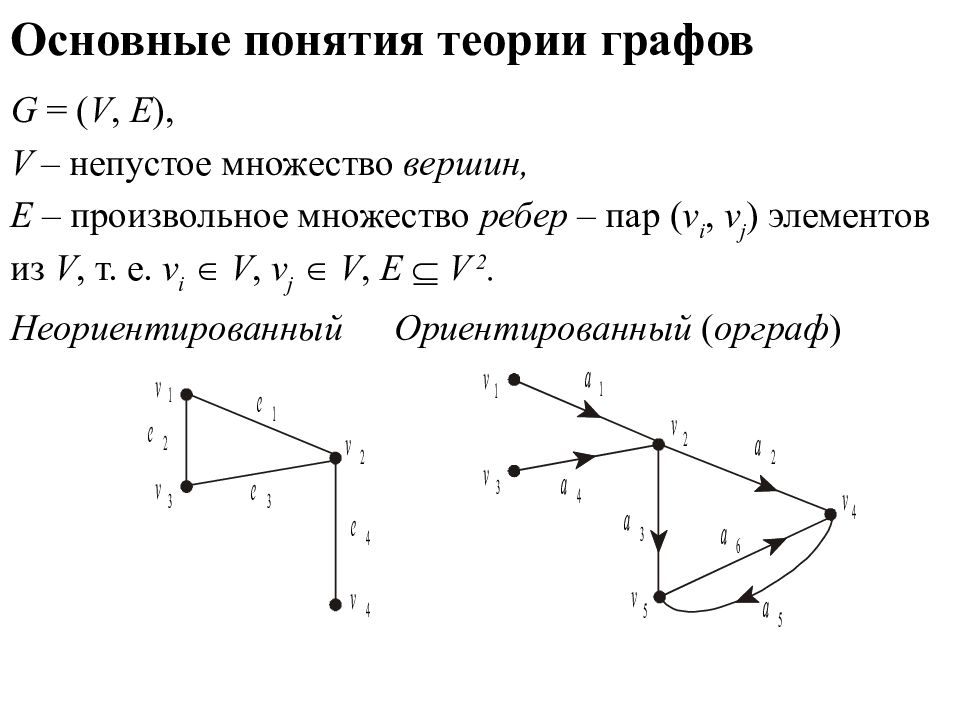
ПОВТОРЕНИЕ Геометрическое представление графа — это схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых Графом G(V, E) называется совокупность двух множеств — непустого множества V (множества вершин) и множества E (множество рѐбер ) вершина ребро дуга
СПОСОБЫ ОПИСАНИЯ ГРАФОВ Способы описания графов Перечисление элементов Изображение Матрица смежности Матрица инциденций Списки смежности ; ; ;
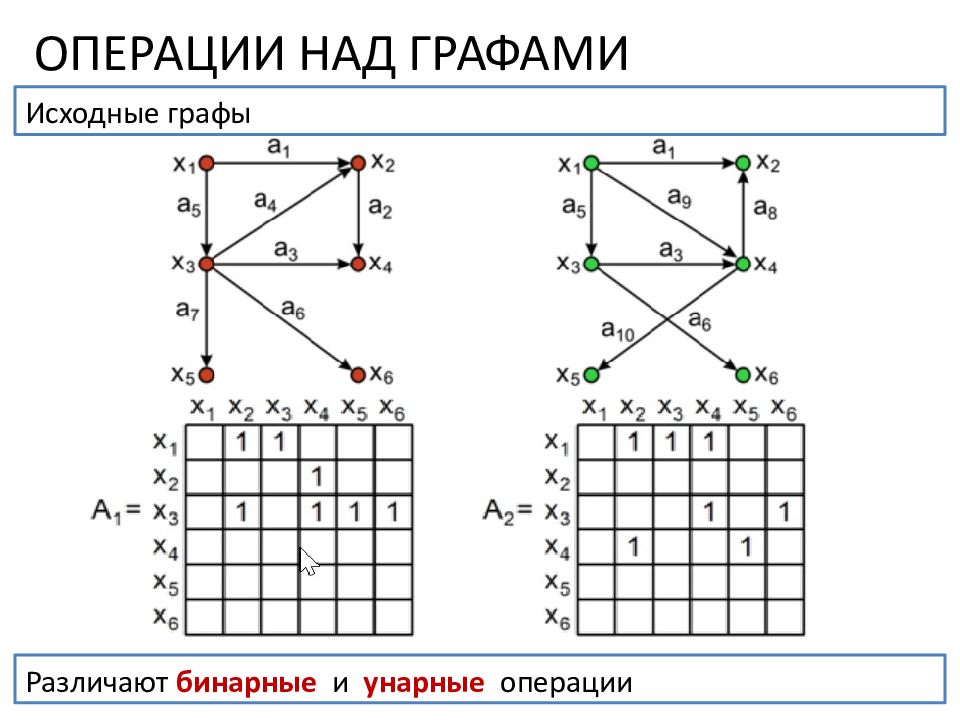
ОПЕРАЦИИ НАД ГРАФАМИ Исходные графы Различают бинарные и унарные операции
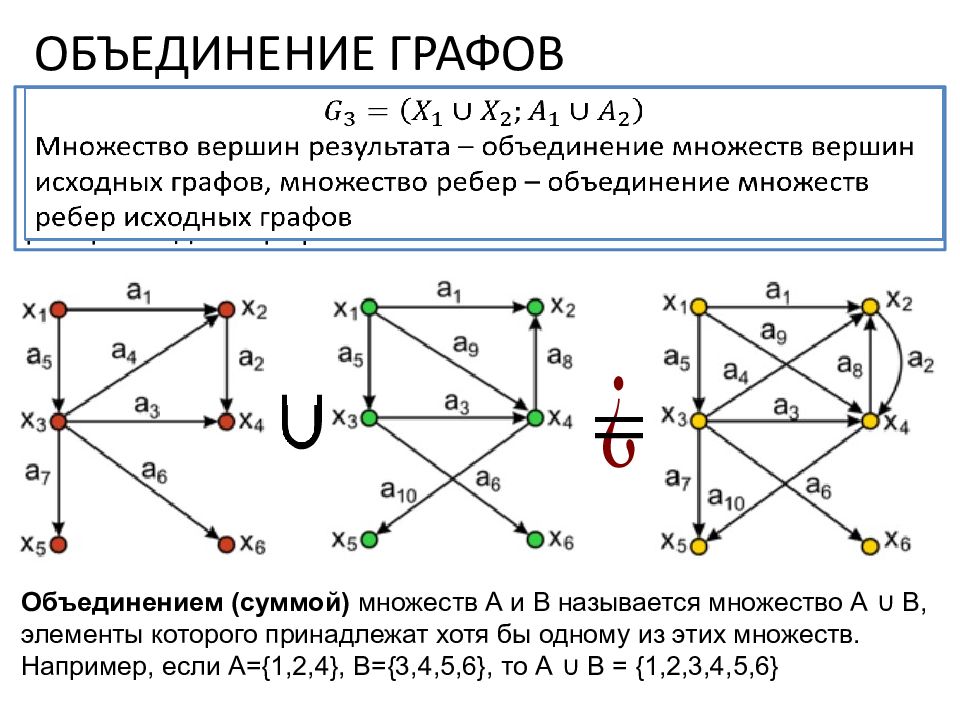
ОБЪЕДИНЕНИЕ ГРАФОВ Множество вершин результата – объединение множеств вершин исходных графов, множество ребер – объединение множеств ребер исходных графов Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
ОБЪЕДИНЕНИЕ ГРАФОВ При объединении графов матрица смежности результата получается операцией поэлементного логического сложения матриц смежности исходных графов G 1 и G 2.
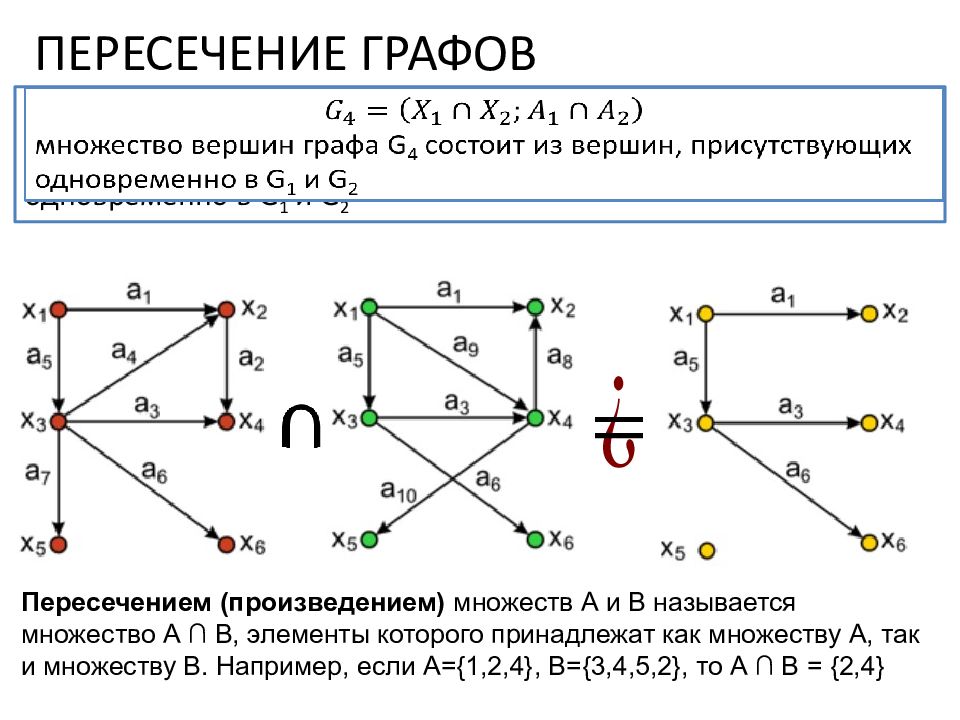
ПЕРЕСЕЧЕНИЕ ГРАФОВ множество вершин графа G 4 состоит из вершин, присутствующих одновременно в G 1 и G 2 Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
ПЕРЕСЕЧЕНИЕ ГРАФОВ результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G 1 и G 2
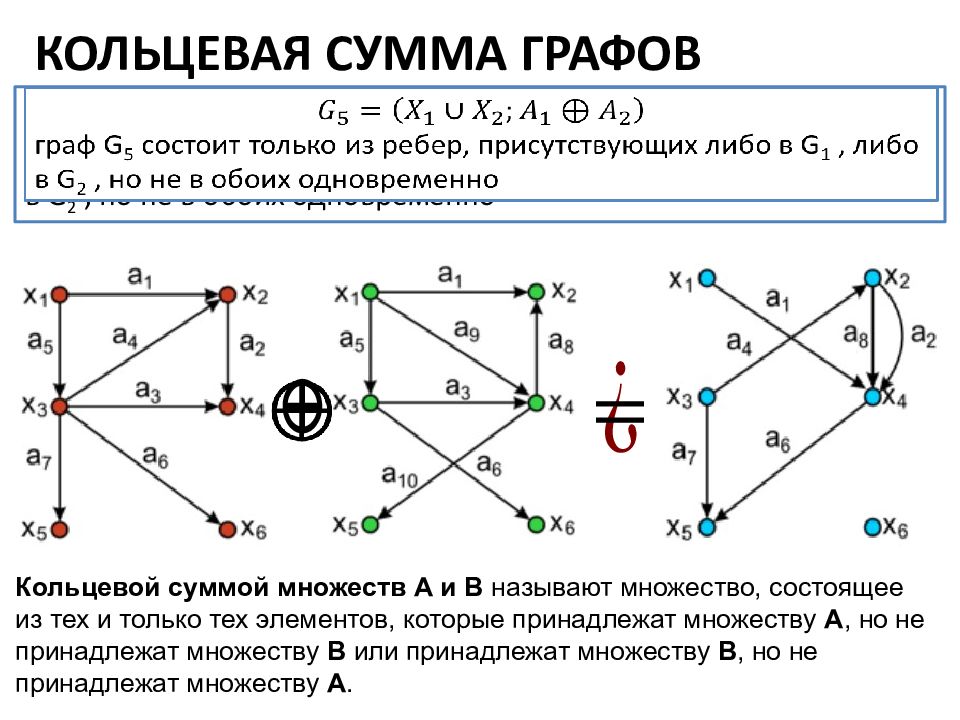
КОЛЬЦЕВАЯ СУММА ГРАФОВ граф G 5 состоит только из ребер, присутствующих либо в G 1, либо в G 2, но не в обоих одновременно Кольцевой суммой множеств А и В называют множество, состоящее из тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В или принадлежат множеству В, но не принадлежат множеству А.
КОЛЬЦЕВАЯ СУММА ГРАФОВ результирующая матрица смежности получается операцией поэлементного логического сложения матриц смежности исходных графов
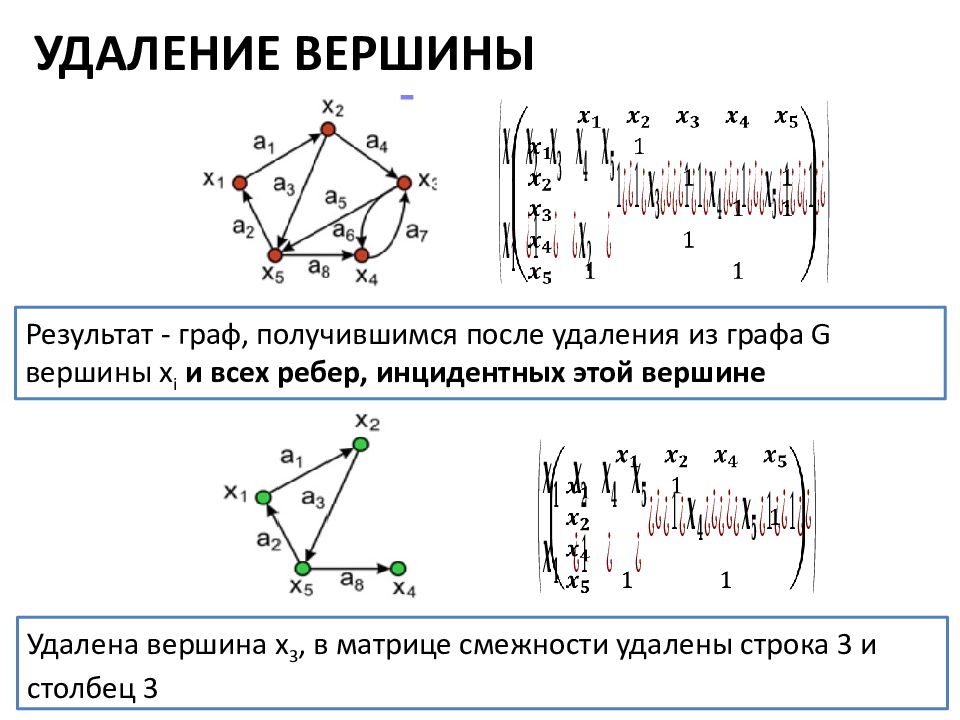
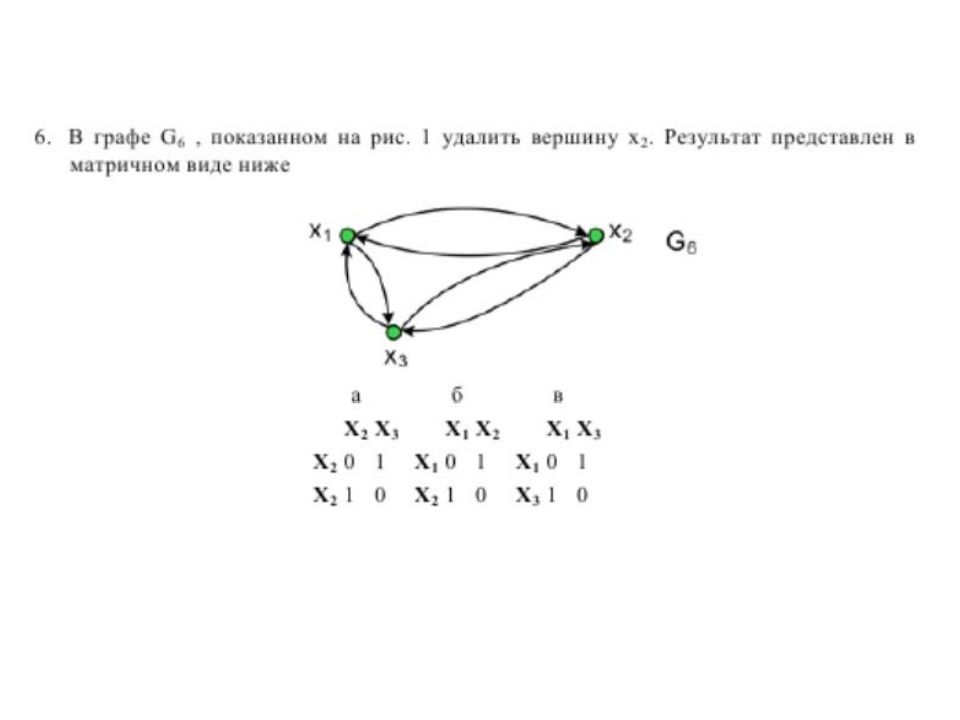
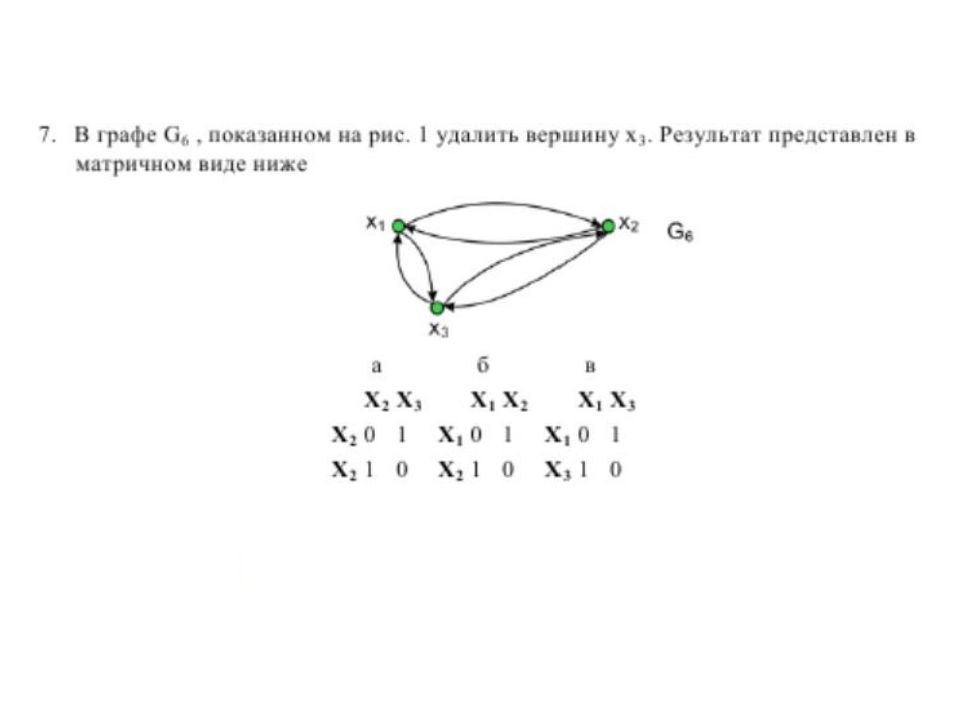
УДАЛЕНИЕ ВЕРШИНЫ Результат - граф, получившимся после удаления из графа G вершины х i и всех ребер, инцидентных этой вершине Удалена вершина x 3, в матрице смежности удалены строка 3 и столбец 3
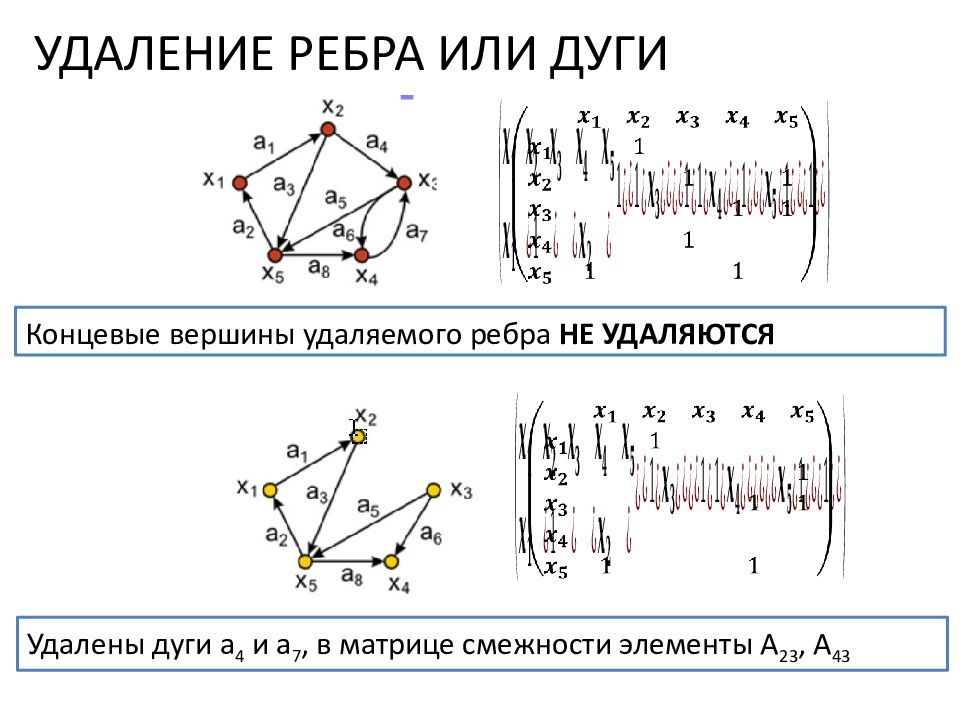
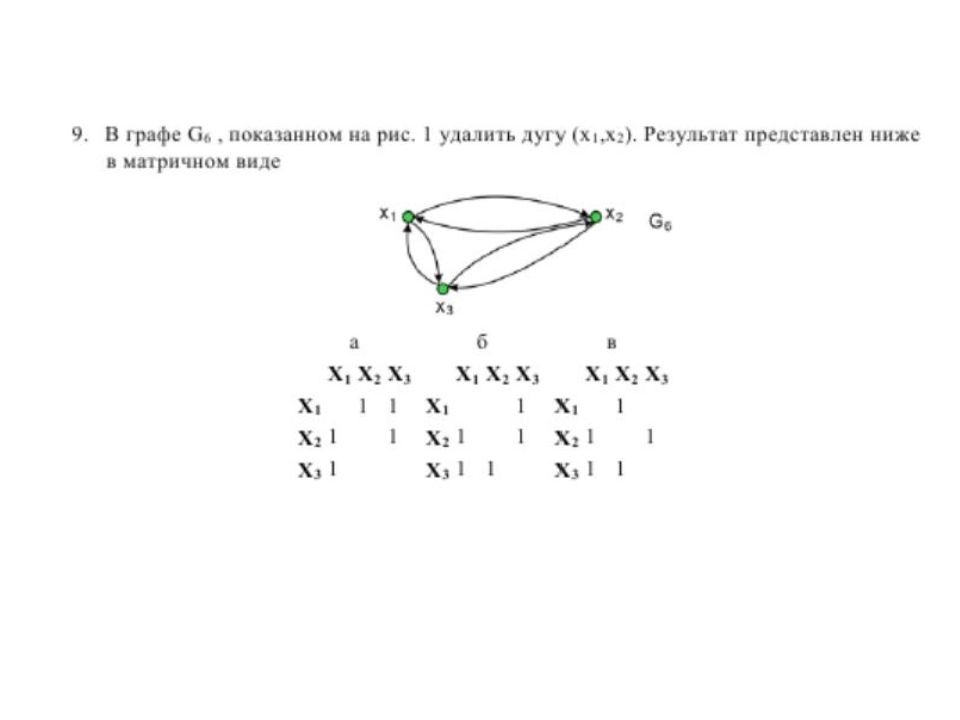
УДАЛЕНИЕ РЕБРА ИЛИ ДУГИ Концевые вершины удаляемого ребра НЕ УДАЛЯЮТСЯ Удалены дуги a 4 и a 7, в матрице смежности элементы A 2 3, A 43
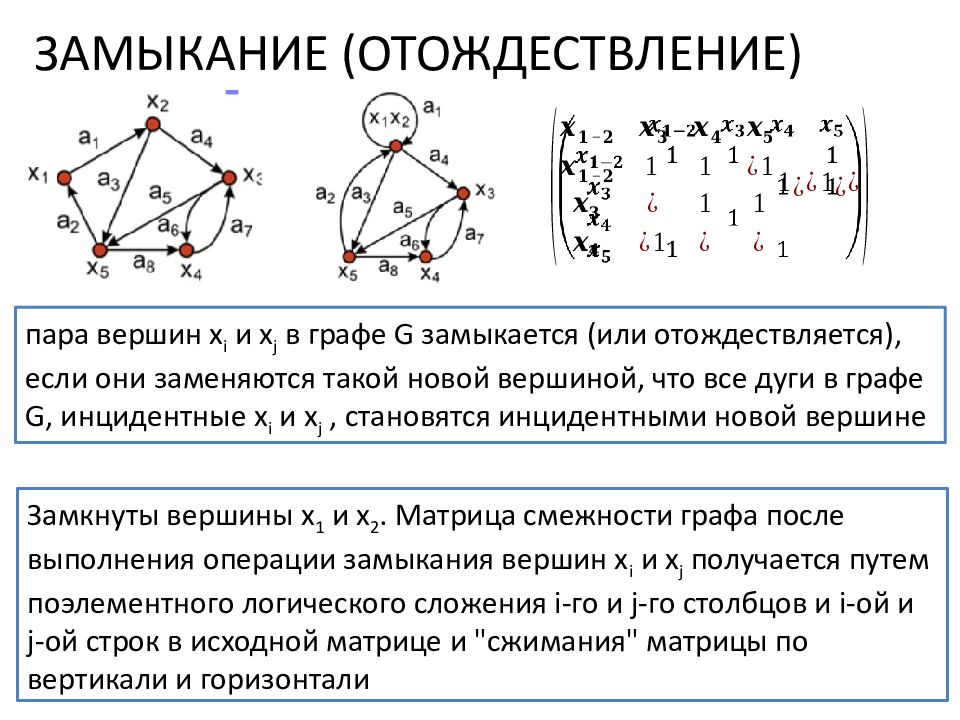
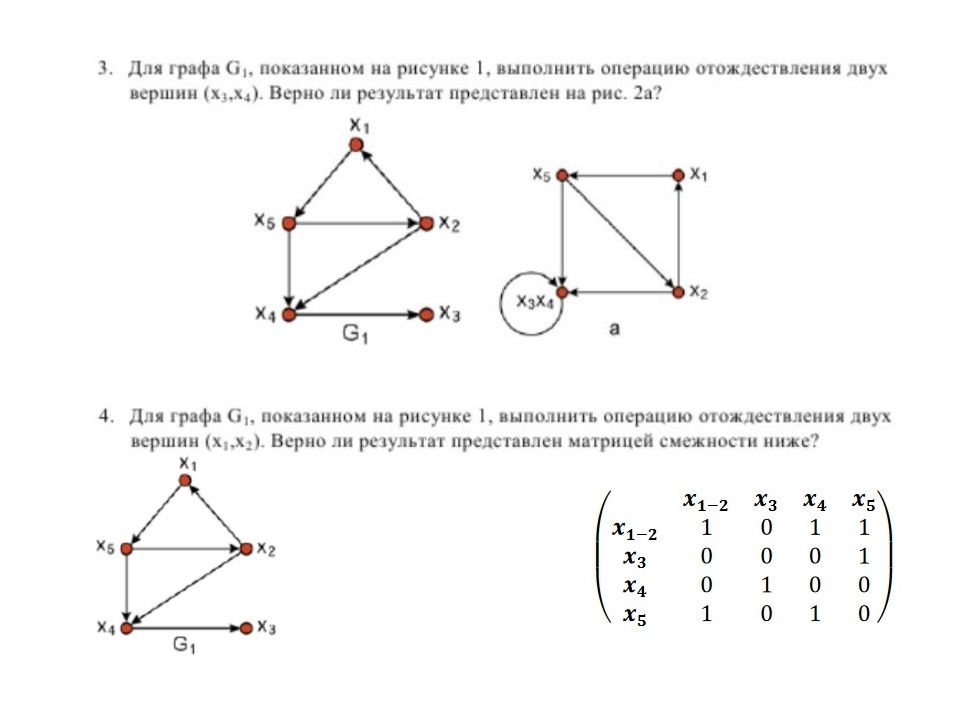
ЗАМЫКАНИЕ (ОТОЖДЕСТВЛЕНИЕ) пара вершин х i и x j в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные х i и x j, становятся инцидентными новой вершине Замкнуты вершины x 1 и x 2. Матрица смежности графа после выполнения операции замыкания вершин х i и x j получается путем поэлементного логического сложения i- го и j- го столбцов и i-ой и j-ой строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали
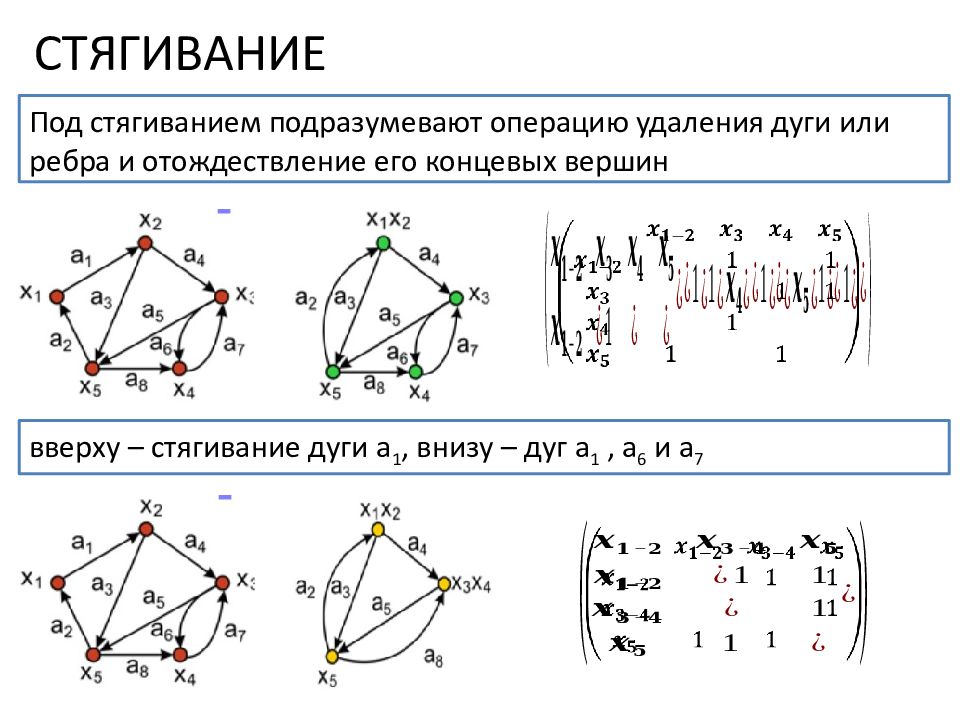
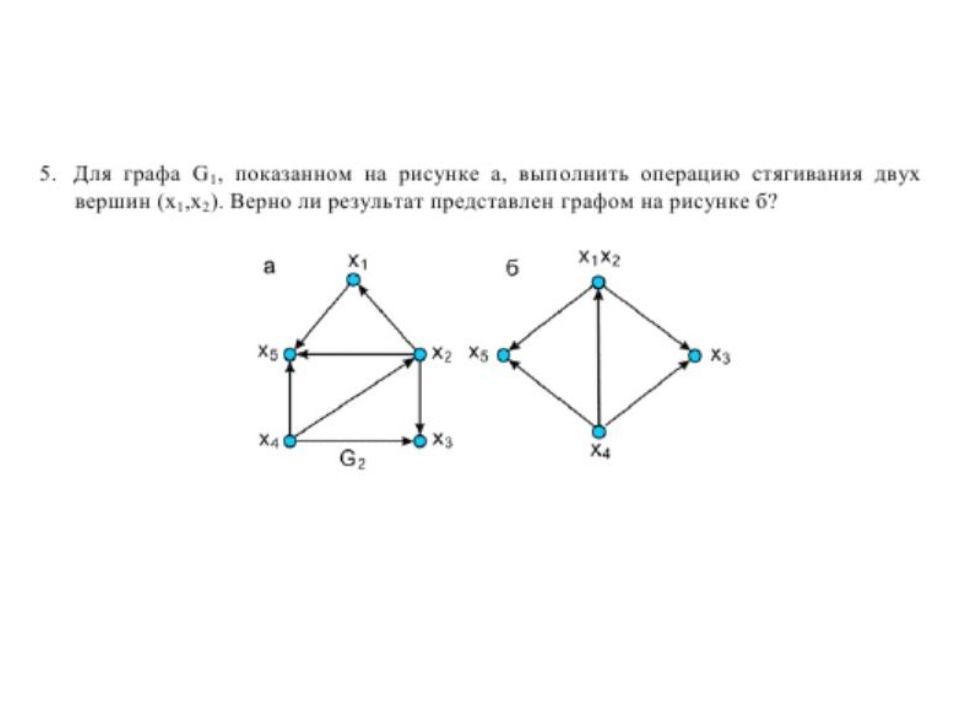
СТЯГИВАНИЕ вверху – стягивание дуги a 1, внизу – дуг a 1, a 6 и a 7 Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин
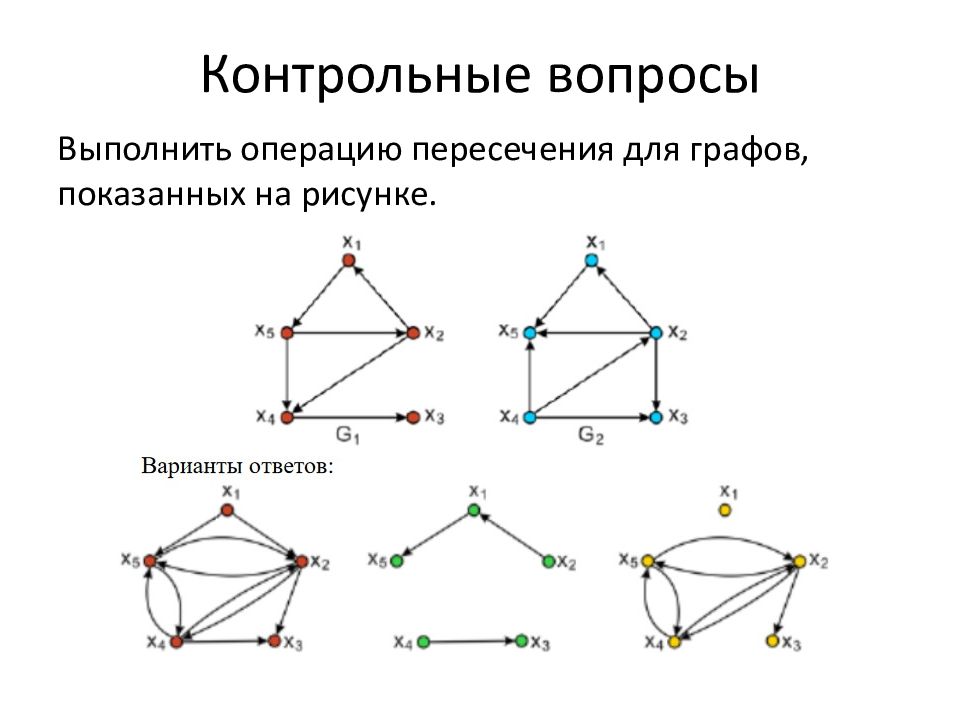
Контрольные вопросы Выполнить операцию пересечения для графов, показанных на рисунке.
Контрольные вопросы Выполнить операцию пересечения для графов, представленных матрицами смежности смежности.
Программирование, компьютеры и сети https ://progr-system.ru /
