Первый слайд презентации: Множества. Операции над множествами
Слайд 2
«Множество есть многое, мыслимое нами как единое». Основоположник теории множеств немецкий математик Георг Кантор (1845-1918)
Понятие множества является одним из фундаментальных понятий математики, которому трудно дать определение. Дело в том, что определить понятие – это значит найти такое родовое понятие, в которое это понятие входит в качестве вида, но понятие «множество» - это самое широкое понятие математики и математической логики, т.е. категория, а для категории нельзя найти более широкое, т.е. родовое понятие. Ограничимся описательным объяснением этого понятия. Основные определения теории множеств. Примеры
Множество – это набор, совокупность каких-либо вполне различаемых объектов, называемых его элементами, обладающими общими для всех их и только их свойствами, и рассматриваемых как единое целое. Основные определения теории множеств. Примеры Примеры: множество людей, живущих сейчас в России, множество точек данной геометрической фигуры, множество решений данного уравнения. невозможно говорить о множестве капель в стакане воды, так как невозможно четко и ясно указать каждую отдельную каплю.
Слайд 5: Структура множества
Каждое множество состоит из того или иного набора объектов, которые называются элементами множества. Факт, что элемент а принадлежит множеству Х будем обозначать: а Х. Порядок элементов в множестве несущественен. Множества { а, в, с } и { а, с, в } одинаковы. При этом, нужно иметь ввиду, что элемент а и множество { а } – это не одно и то же. Первое – это объект, обозначенный а, второе – это множество, состоящее из единственного элемента а. Поэтому можно сказать, что « а принадлежит { а }» – это истинное суждение. В то время как, «{ а } принадлежит а » - это ложное суждение. Структура множества
Слайд 6: Способы задания множества
Перечисление элементов множества. Обычно перечислением задают конечные множества. Описание свойств, общих для всех элементов этого множества, и только этого множества. Это свойство называется характеристическим свойством, а такой способ задания множества описанием. Таким образом, можно задавать как конечные, так и бесконечные множества. Способы задания множества
Слайд 7
Примерами множеств могут служить: а) множество всех натуральных чисел, б) множество всех целых чисел (положительных, отрицательных и нуля), в) множество всех рациональных чисел, г) множество всех действительных чисел, д) множество площадей треугольников, е)множество четырехугольников,
Слайд 8: Числовые множества
Множество НАТУРАЛЬНЫХ чисел N, N={1, 2, 3, 4, 5, …} Множество ЦЕЛЫХ чисел Z, Z={…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} Множество РАЦИОНАЛЬНЫХ чисел Q, Q={x| x=p/q, где p Z, q N } Множество ИРРАЦИОНАЛЬНЫХ чисел I -, бесконечные непериодические дроби, (, =3,141592…, e =2,718281, …) Множество ДЕЙСТВИТЕЛЬНЫХ чисел R получено объединением РАЦИОНАЛЬНЫХ и ИРРАЦИОНАЛЬНЫХ чисел. Множество КОМПЛЕКСНЫХ чисел C, содержащих в себе мнимую единицу і, которая является квадратным корнем из –1. Построены для извлечения корня из отрицательных чисел. Эти виды чисел используются в современной математике. Причем комплексные числа включают в себя все остальные виды чисел. Это множество чисел наиболее широкое, хотя и оно также может расширяться. Числовые множества
Слайд 9: Количество элементов множества
Множества бывают конечными или бесконечными. Если число элементов множества конечно – множество называется конечным. Определение: Количество элементов, составляющих множество, называется мощностью множества. Определение: Если между элементами бесконечного множества можно установить взаимооднозначное соответствие с элементами множества положительных целых чисел, то говорят, что множество счетно. Например : множество действительных чисел - бесконечное множество. множество чисел, делящихся без остатка на 3 – счетное множество, множество букв русского алфавита, множество отличников вашей группы – конечно. Количество элементов множества
Слайд 10: Равенство множеств
Определение: Два множества равны между собой, если они состоят из одних и тех же элементов. Т.е. любой элемент множества Х является элементом множества Y, и любой элемент множества Y является элементом множества Х. Равенство множеств
Слайд 11: Диаграммы Эйлера-Венна
Для наглядного представления (графического изображения ) множеств и результатов операций над ними удобно пользоваться так называемыми диаграммами Эйлера-Венна (кругами Эйлера). При этом множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника. Элементы множества – точки внутри соответствующего круга. Диаграммы Эйлера-Венна
Слайд 12
«Парадокс брадобрея". Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.
Слайд 13: Подмножество. Включение
Определение: Множество A является подмножеством B, если любой элемент множества A принадлежит множеству B. Это еще называется нестрогим включением A B. Например : Пусть Х – множество студентов некоторой группы, Е – множество отличников этой же группы. E X т.к. группа может состоять только из отличников. Когда хотят подчеркнуть, что в множестве B есть обязательно элементы, отличные от элементов множества A, то пишут A B. Это называется строгим включением. Например : Пусть Х – множество всех студентов ВлГУ, Е – множество студентов педагогического института. E X т.к. в множестве всех студентов ВлГУ обязательно есть элементы E. Подмножество. Включение
Слайд 14: Пустое множество
Если характеристическим свойством, задающим множество, А не обладает ни один объект, то говорят, что множество А пустое. Понятие пустого множества очень важное понятие. Оно позволяет описательно задавать множества, не заботясь, есть ли в этом множестве элементы и совершенно спокойно оперировать с этими множествами. Пустое множество будем считать конечным множеством. Например : множество действительных корней уравнения пустое. Пустое множество
Слайд 16: 1. Пересечение множеств А∩В
Пересечением множества А и В называют множество, состоящие из всех общих элементов множеств А и В (А∩В). Например, а) А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, то А∩В = {3; 9}; б) А = {10; 20; …; 100} и В = {6; 12; 18;…}, то А∩В = {30; 60; 90}. 1. Пересечение множеств А∩В
Слайд 17: Непересекающиеся множества
Определение : Множества называются непересекающимися, если не имеют общих элементов, т.е. их пересечение равно пустому множеству. Например : а) непересекающимися множествами являются множества отличников группы и неуспевающих. б ) непересекающимися множествами являются множества А = {3; 9; 12} и В = {1; 5; 7; 11}. Непересекающиеся множества
Слайд 18: Свойства пересечения
X∩Y = Y∩X – коммутативность; (X∩Y) ∩Z =X∩ (Y∩Z)=X∩Y∩Z – ассоциативность; X∩ = ; X∩ I = Х; Свойства пересечения
Слайд 19: 2. Объединение множеств АUВ
Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств. Например, А = {3; 9; 12} и В = {1; 3; 5; 7; 9; 11}, АUВ=? АUВ = {1; 3; 5; 7; 9; 11; 12}. 2. Объединение множеств АUВ
Слайд 20: Свойства объединения
X UY = Y UY - коммутативность; (X UY ) U Z =X U (Y U Z)=X U Y U Z – ассоциативность; XU = X ; XU I = I. Свойства объединения
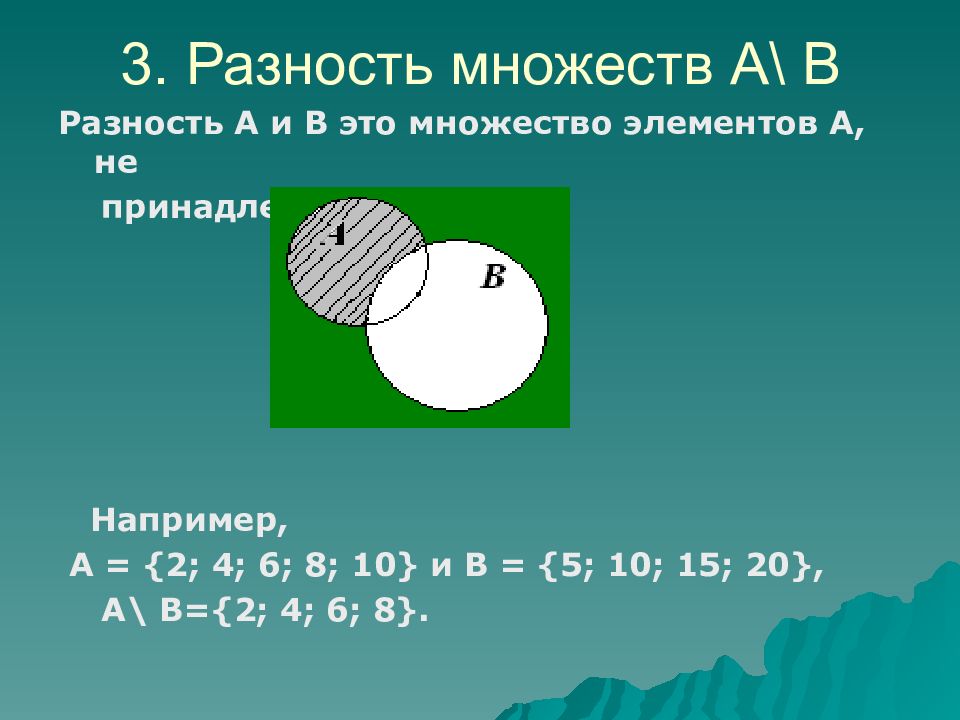
Слайд 21: 3. Разность множеств А\ В
Разность А и В это множество элементов А, не принадлежащих В. Например, А = {2; 4; 6; 8; 10} и В = {5; 10; 15; 20}, А\ В={2; 4; 6; 8}. 3. Разность множеств А\ В
Слайд 22: Свойства операции разности
А\В ≠ В\А; А\А=∅; А\∅=А; I \А= Ā. Свойства операции разности
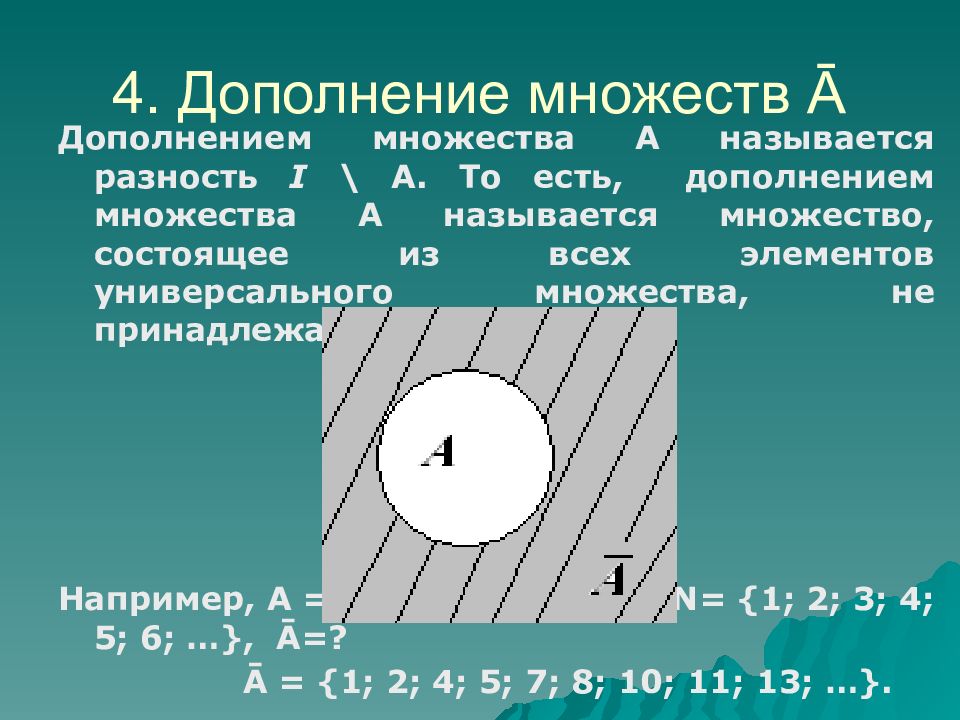
Слайд 23: 4. Дополнение множеств Ā
Дополнением множества А называется разность I \ А. То есть, дополнением множества А называется множество, состоящее из всех элементов универсального множества, не принадлежащих множеству А. Например, А = {3; 6; 9; 12} и I =N = {1; 2; 3; 4; 5; 6; …}, Ā =? Ā = {1; 2; 4; 5; 7; 8; 10; 11; 13; …}. 4. Дополнение множеств Ā
Слайд 24: Свойства дополнения
1. Множество X и его дополнение не имеют общих элементов 2. Любой элемент I принадлежит или множеству Х или его дополнению. 3. Закон двойного отрицания Свойства дополнения
Слайд 25: Декартово произведение множеств
Фабрика верхнего трикотажа изготовляет мужские пуловеры, женские костюмы, кофты и платья следующих расцветок: бордо, синяя, голубая, зеленая, коричневая, серая. Посмотрим, какие изделия можно получить, учитывая возможные для них расцветки. Обозначим через А множество видов изделий: А={мужской пуловер, женский костюм, кофта, платье}, через В – множество предлагаемых расцветок: В={бордо, синяя, голубая, зеленая, коричневая, серая}. C оставим список всех пар из элементов множества А и элементов множества В таким образом, что сначала будем записывать элемент множества А, затем элемент множества В. получим множество С упорядоченных пар элементов множеств А и В. Возможные изделия можно перечислить с помощью таблицы.
Слайд 26: Декартово произведение множеств
A B Мужской пуловер Женский костюм Кофта Платье Бордо Пуловер-бордо костюм-бордо Кофта-бордо Платье-бордо Синяя Пуловер-синий Голубая Зеленая Кофта-зеленая Коричневая Платье-коричневое Серая Костюм-серый Декартово произведение множеств
Слайд 27: Определение декартова произведения
Декартовым (или прямым) произведением А×В множества А на множество В называется множество всех упорядоченных пар, в которых первая компонента – элемент множества А, а вторая – элемент множества В. А×В={( x, y ) | x∈A, y∈B }. Количество элементов в декартовом произведении двух множеств: если m (А) =n, m (B) =k, то m (А×В) =n⋅k. Определение декартова произведения
Слайд 28: Пример декартова произведения
Вычислить количество двухзначных чисел. Двухзначное число можно принять за упорядоченную пару, где на первом месте может стоять цифра из множества А={1, 2, 3, 4, 5, 6, 7, 8, 9}, а на втором – из множества В={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, т.е. за элемент прямого произведения этих множеств, тогда получаем: m (А)=9, m (B)=10, то m (А×В)=9⋅10=90. Итак, всего имеется 90 различных двухзначных чисел. Пример декартова произведения
Слайд 29: Соответствие множеств
Определение. Будем говорить, что между элементами двух множеств А и В установлено соответствие ρ, если в их произведении А×В выделено некоторое подмножество Ω. Если пара ( a,b )∈Ω⊆Α×Β, это означает по определению, что элементы a и b множеств А и В находятся в отношении ρ (пишется aρb ). Пример соответствия. Пусть даны множества А – студентов и В – множество групп. Утверждение “студент a учится в группе b ” задает соответствие между множеством студентов и множеством групп. Здесь а пробегает множество значений А, b – множество значений В. Такое соотношение называется бинарным соответствием, т.е. соответствием между двумя множествами А и В. Соответствие множеств
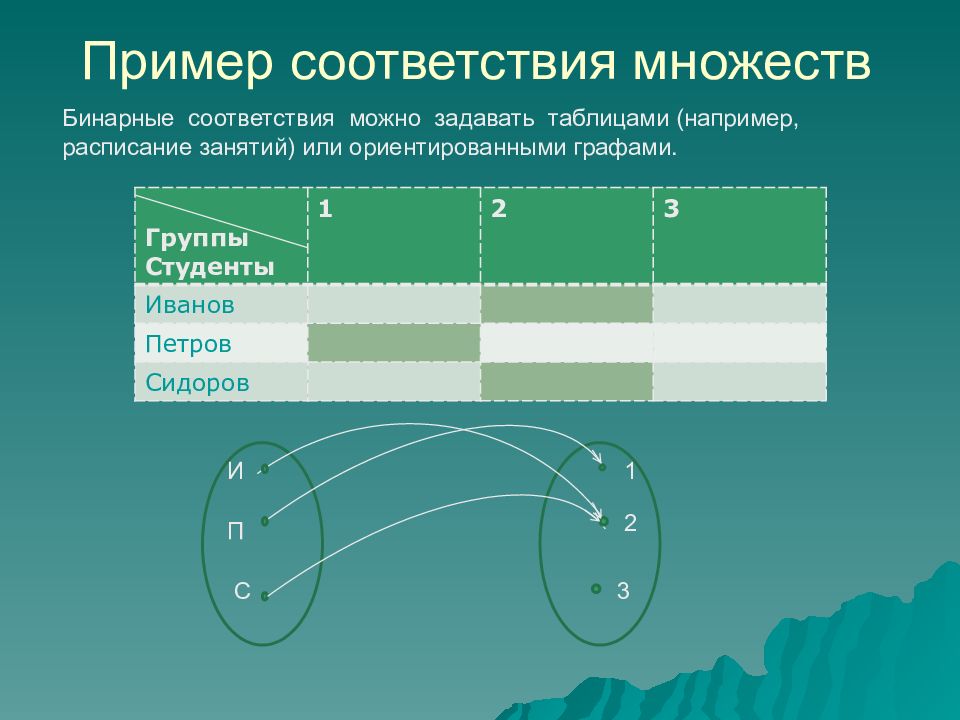
Слайд 30: Пример соответствия множеств
Группы Студенты 1 2 3 Иванов Петров Сидоров Пример соответствия множеств И П С 1 2 3 Бинарные соответствия можно задавать таблицами (например, расписание занятий) или ориентированными графами.
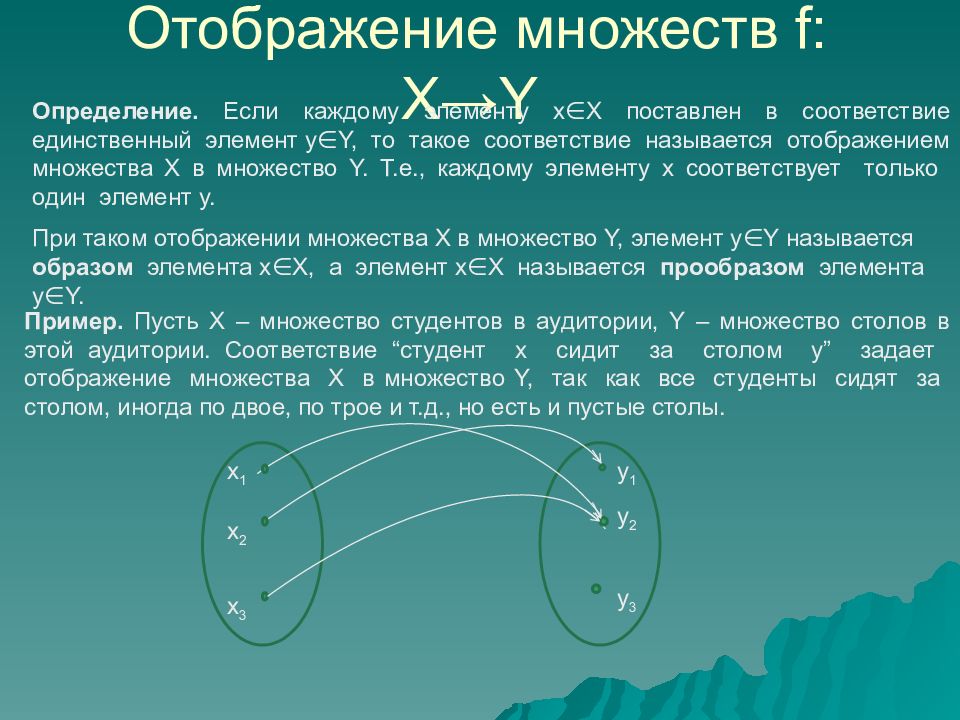
Слайд 31: Отображение множеств f: X→Y
x 1 x 2 x 3 y 1 y 2 y 3 Определение. Если каждому элементу x∈X поставлен в соответствие единственный элемент y∈Y, то такое соответствие называется отображением множества Х в множество Y. Т.е., каждому элементу х соответствует только один элемент y. При таком отображении множества Х в множество Y, элемент y∈Y называется образом элемента x∈X, а элемент x∈X называется прообразом элемента y∈Y. Пример. Пусть Х – множество студентов в аудитории, Y – множество столов в этой аудитории. Соответствие “студент х сидит за столом y” задает отображение множества Х в множество Y, так как все студенты сидят за столом, иногда по двое, по трое и т.д., но есть и пустые столы.
Слайд 36
Задание 1 1) Задайте множество цифр, с помощью которых записывается число: а) 3254; б) 8797; в) 11000; г) 555555. 2) Задайте множество А описанием: а) А = {1, 3, 5, 7, 9}; б) А = {- 2, - 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}; г) А = {0,1; 0,01; 0,001; 0,0001; …}; д ) А = {1/2, 2/3, 3/4, 4/5, … }. 3) Задание с выбором ответа. Даны множества: М = {5,4,6 }, Р = {4,5,6}, Т = {5,6,7}, S = {4, 6}. Какое из утверждений неверно? а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.
Слайд 37
Задание 2 1. Запишите на символическом языке следующее утверждение: а) число 10 – натуральное; б) число – 7 не является натуральным; в) число – 100 является целым; г) число 2,5 – не целое. 2. Верно ли, что: а) – 5 N ; б) -5 Z ; в) 2,(45) Q ? 3. Верно ли, что: а) 0,7 {х | х 2 – 1 < 0}; б) – 7 {х | х 2 + 16х ≤ - 64}?
Слайд 38
Задание 3 1. Даны множества: А = {10}, В = {10, 15}, С = {5, 10, 15}, D = {5, 10, 15, 20}. Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А … D ; б ) А … В; в) С … А; г) С … В. 2. Даны три множества А = {1, 2, 3, …, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16, …, 36}. Верно ли, что: а) А В; б) В С; в) С А; г) С В?
Слайд 39
Задание 4 1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите: 1) А∩В; 2) А∩С; 3) С∩В. 2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}. Найдите А∩В. 3. Даны множества: А = { a, b, c, d }, B = { c, d, e, f }, C = { c, e, g, k }. Найдите (А∩В)∩С.
Слайд 40
Задание 5 1. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5; 11}. Найдите : 1 ) АUВ ; 2 ) АUС ; 3) СUВ. 2. Даны множества: А = { a, b, c, d }, B = { c, d, e, f }, C = { c, e, g, k }. Найдите (АUВ)UС.
Слайд 41: Решение задач с помощью кругов Эйлера
ЭЙЛЕР Леонард (1707-1783), российский ученый — математик, механик, физик и астроном.
Слайд 42: Задача 1
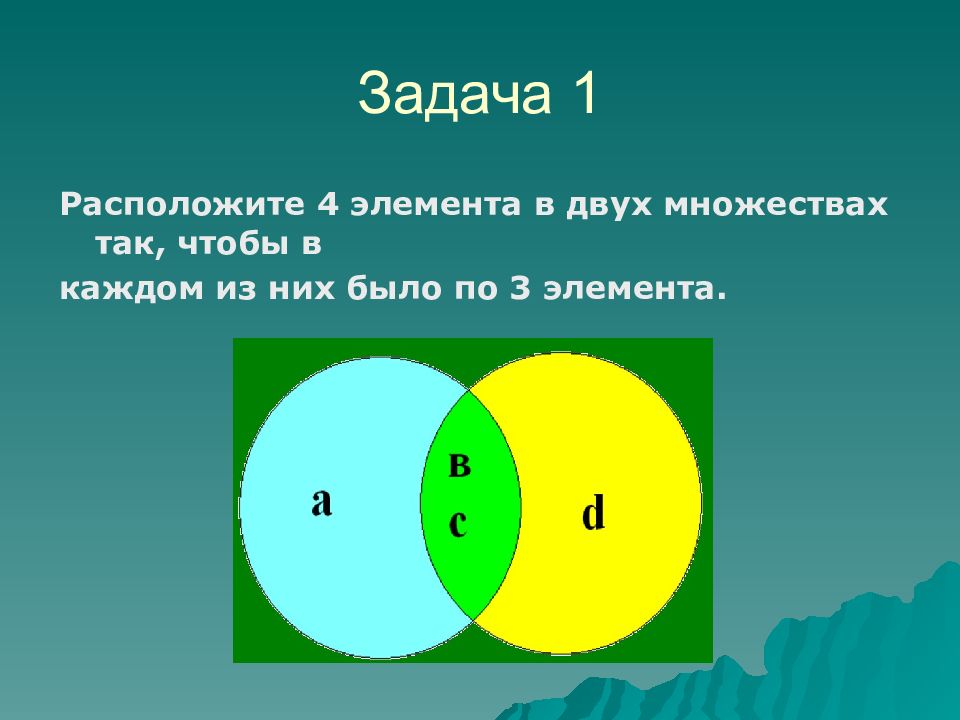
Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента. Задача 1
Слайд 43: Задача 2
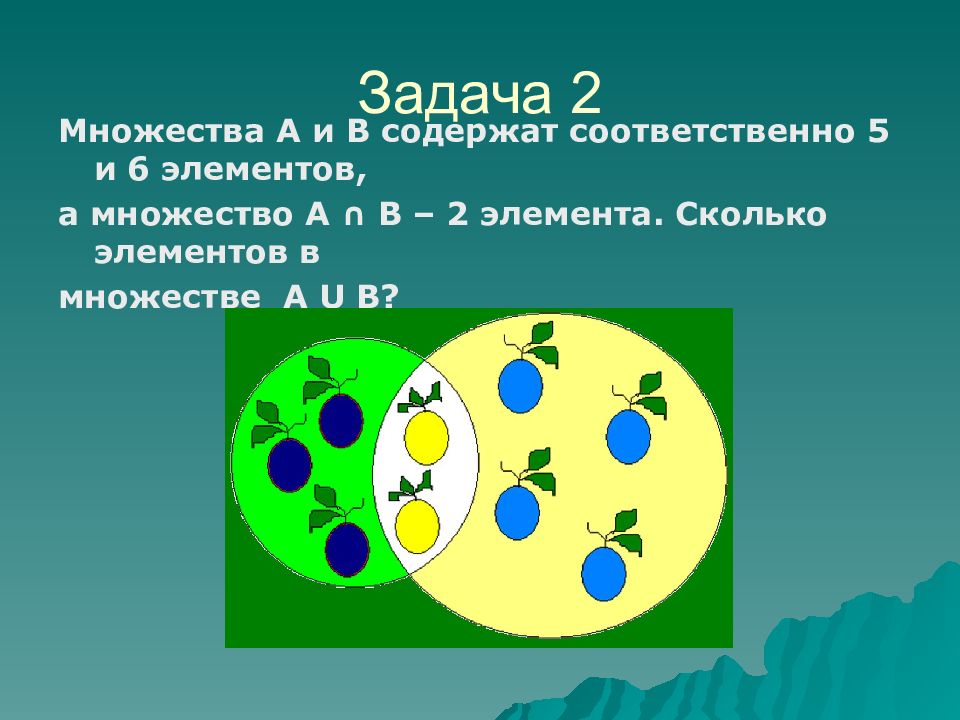
Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В? Задача 2
Слайд 44: Задача 3
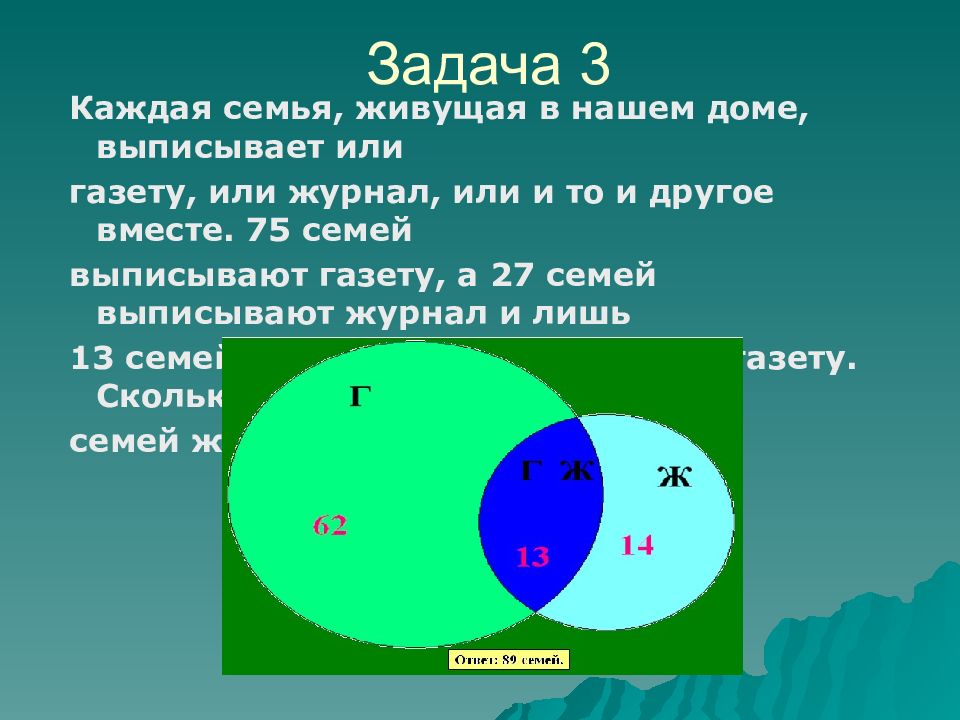
Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме? Задача 3
Слайд 45: Задача 4
На школьной спартакиаде каждый из 25 учеников 9 –го класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу? Задача 4
Слайд 46: Задача 5
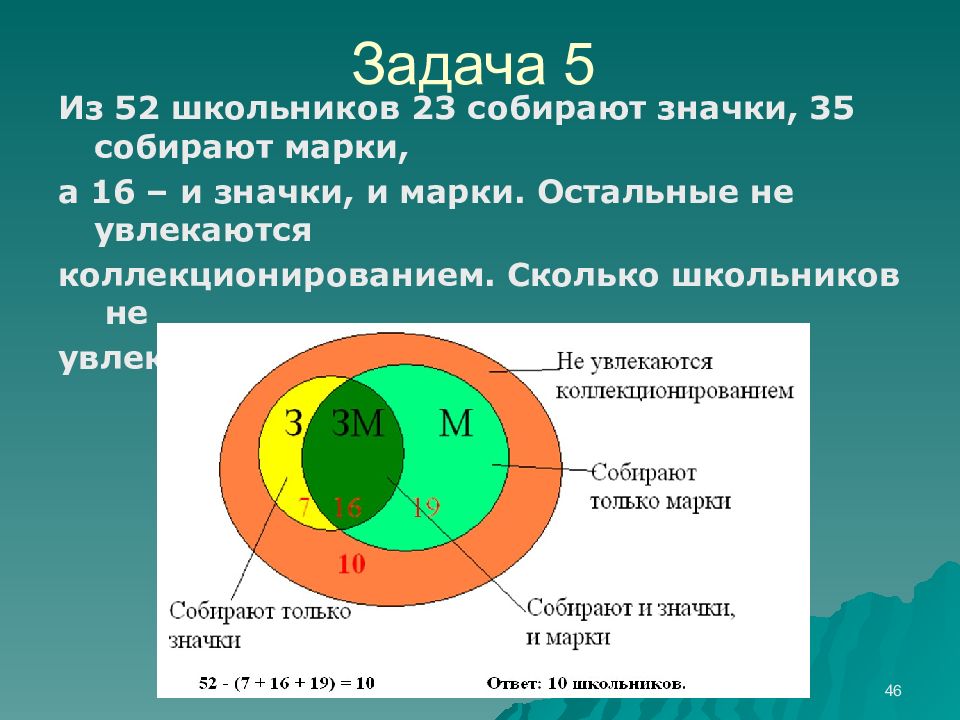
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием? 46 Задача 5
Слайд 47: Задача 6
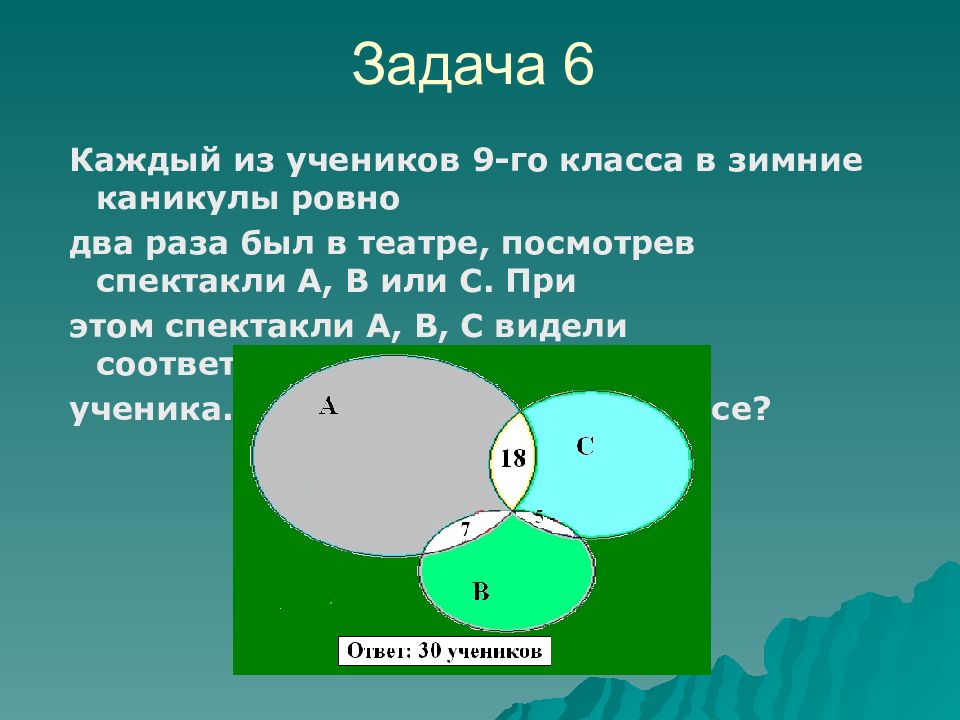
Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе ? Задача 6
Слайд 48: Задача 7
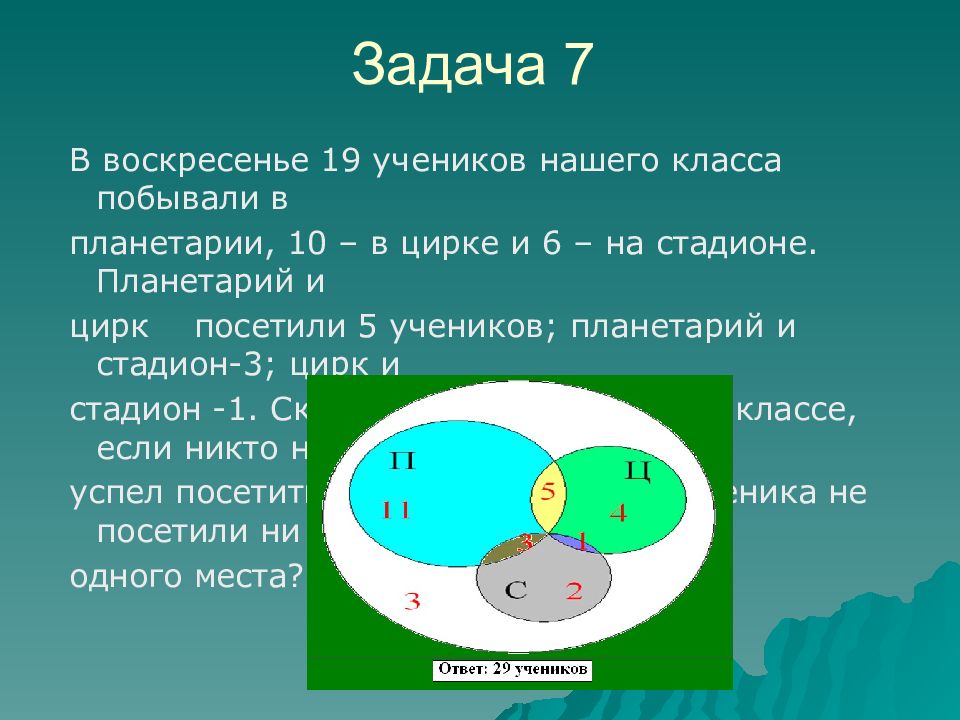
В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников ; планетарий и стадион-3 ; цирк и стадион -1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места? Задача 7
Слайд 49: Задача 8
В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика, которые любят всё и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки? Задача 8
Слайд 50: Задача 9
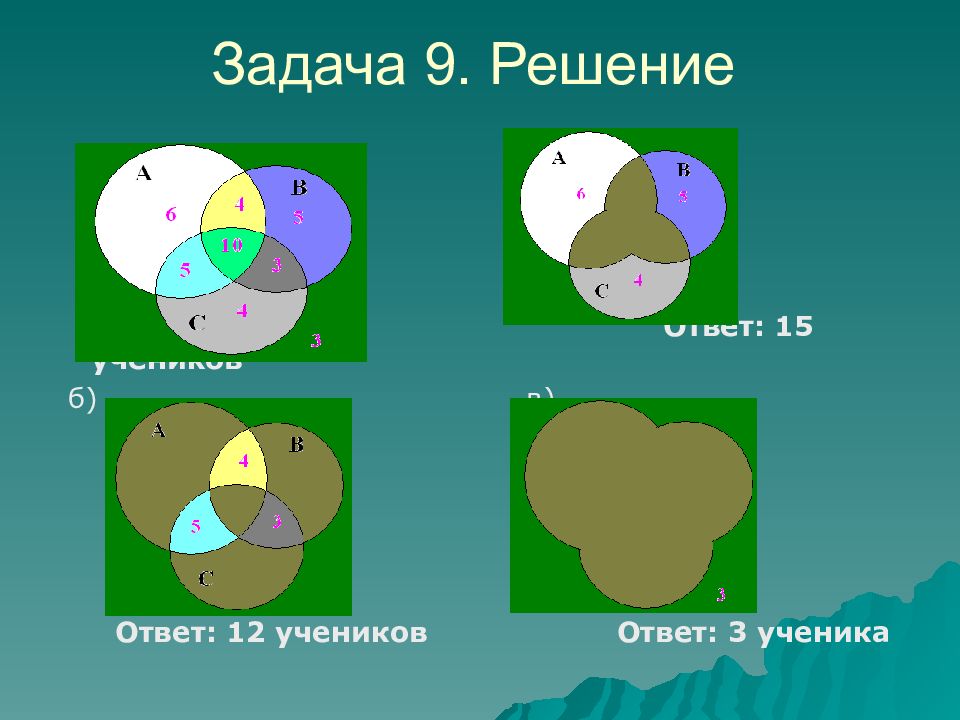
На уроке литературы учитель решил узнать, кто из 40 учеников 9 – го класса читал книги А, В, С. Результаты опроса выглядели так : книгу А прочитали 25 учеников, книгу В – 22 ученика, книгу С – 22 ученика; одну из книг А или В прочитали 33 ученика, одну из книг А или С прочитали 32 ученика, одну из книг В или С – 31 ученик. Все три книги прочитали 10 учеников. Сколько учеников: а) прочитали только по одной книге; б ) прочитали ровно две книги; в) не прочили ни одной из указанных книг? Задача 9
Слайд 51: Задача 9. Решение
а) Ответ: 15 учеников б) в) Ответ: 12 учеников Ответ: 3 ученика Задача 9. Решение
Слайд 52: Задача 10
На зимних каникулах из 36 учащихся класса только двое просидели дома, а 25 ребят ходили в кино, 15 – в театр, 17 – в цирк. Кино и театр посетили 11 человек, кино и цирк – 10, театр и цирк – 4. Сколько ребят побывало и в кино, и в театре, и в цирке? Задача 10
Слайд 53
Литература [1 ] Алгебра, 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / [А. Г. Мордкович, Л.А. Александрова и др.] -12-е изд., испр. - М.: Мнемозина, 2010. [2 ] Занимательная математика. 5 – 11 классы. Авт.- сост. Т.Д. Гаврилова. – Волгоград : Учитель, 2005. – 96 с. [3 ] Математика 6 класс : учеб. для общеобразоват. учреждений / Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др./; под ред. Г.В. Дорофеева, И.Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение». – 11 –е изд. - М.: Просвещение, 2010. – 303 с.: ил. 53
Слайд 54: Связь между алгеброй логики и теорией множеств
Дело в том, что термин алгебра в своем роде имя нарицательное. Под ним понимается раздел математики, изучающий алгебраические операции, а природа объектов, к которым применяются эти операции, не важна. Говоря об алгебре логики или об алгебре множеств, мы более всего уделяли внимание операциям, определенным над допустимыми в данной теории объектами, свойствам этих операций. Еще одним хорошо известным вам примером алгебры, является алгебра чисел, к которой все выписанные законы также применимы. Проводя аналогии между этими алгебрами, мы можем сказать Связь между алгеброй логики и теорией множеств
Слайд 55
№ 5. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
Слайд 56: Решение 1
Пусть А - это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В - множество учеников, умеющих танцевать. Количество элементов в нём - m = 18. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. - это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k. Согласно формуле доказанной выше n + m- k = 17+ 19- k = 30 k = 6. Ответ: 6 учеников в классе поют и танцуют одновременно.
Слайд 57: Решение 2
Сначала заметим, что из 30 человек не умеют петь 30 - 17 = 13 человек. Все они умеют танцевать, т.к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
Слайд 58: 6
На фирме работают 67 человек. Из них 47 знают английский язык, 35 - немецкий язык, а 23 - оба языка. Сколько человек в фирме не знают ни английского, ни немецкого языков?
Слайд 59: Решение
n ( А) = 47 – знают английский язык n ( В) = 35- знают немецкий язык n ( C)= x – не знают ни английский, ни немецкий язык n (A B ) = 23 – знают английский и немецкий языки n ( A ) = 67 – работники фирмы 67 = 47 +35 – 23 + x x = 8 Ответ: 8 человек не знают ни английский, ни немецкий язык.
Слайд 60
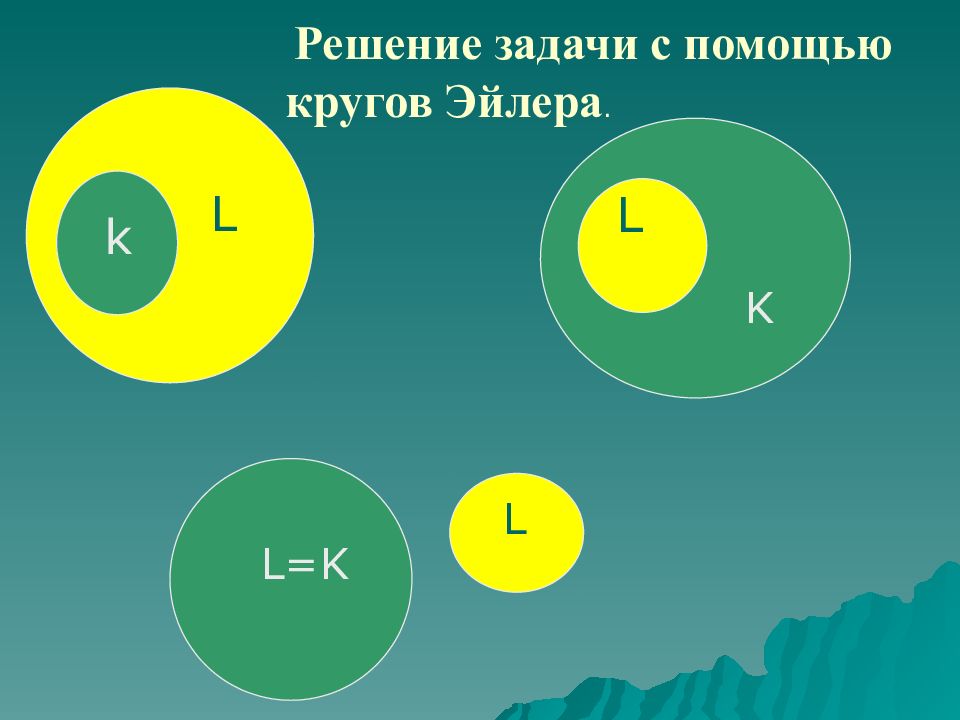
№ 7. Изобразите с помощью кругов Эйлера пересечение множеств K и M, если: а) K L б) L K в) K = L г) K L =