Определенный интеграл, как предел интегральной суммы Геометрический смысл определенного интеграла Физический смысл определенного интеграла Формула Ньютона – Лейбница Свойства определенного интеграла Замена переменной в определенном интеграле Интегрирование по частям 1
Пусть функция y = f(x) определена на отрезке [a; b]. Выполним следующие действия: С помощью точек x 0 = a; x 1 ; x 2 ;…;x n = b разобьем отрезок [a; b] на n частичных отрезков: a b x 1 x 2 х i -1 х i x n - 1 … … В каждом частичном отрезке [ x i - 1 ; x i ] выберем произвольную точку: и найдем значение функции в ней, то есть величину f(c i ). с 1 с 2 с i с n Умножим найденное значение функции f(c i ) на длину соответствующего частичного отрезка : 2
Составим сумму всех таких произведений Если при этом интегральная сумма S n имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции f(x) на отрезке [a; b] и обозначается: Интегральная сумма функции y = f(x) на [ a; b ] Обозначим длину наибольшего частичного отрезка: Найдем предел интегральной суммы, когда, так что 3
Теорема (существования определенного интеграла) Нижний предел интегрирования Верхний предел интегрирования [a; b] - область (отрезок) интегрирования Если функция y = f(x) непрерывна на отрезке [a; b], то определенный интеграл существует. Непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций ( например для ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва) 4
Пусть непрерывная неотрицательная функция y = f(x) задана на отрезке [a; b]. Фигура, ограниченная сверху графиком функции y = f(x), снизу – осью OX, сбоку прямыми x = a; x = b, называется криволинейной трапецией. Найдем площадь этой трапеции. Составим для функции f( х ) интегральную сумму на отрезке [a; b]. Найдем геометрический смысл этой суммы. : 5
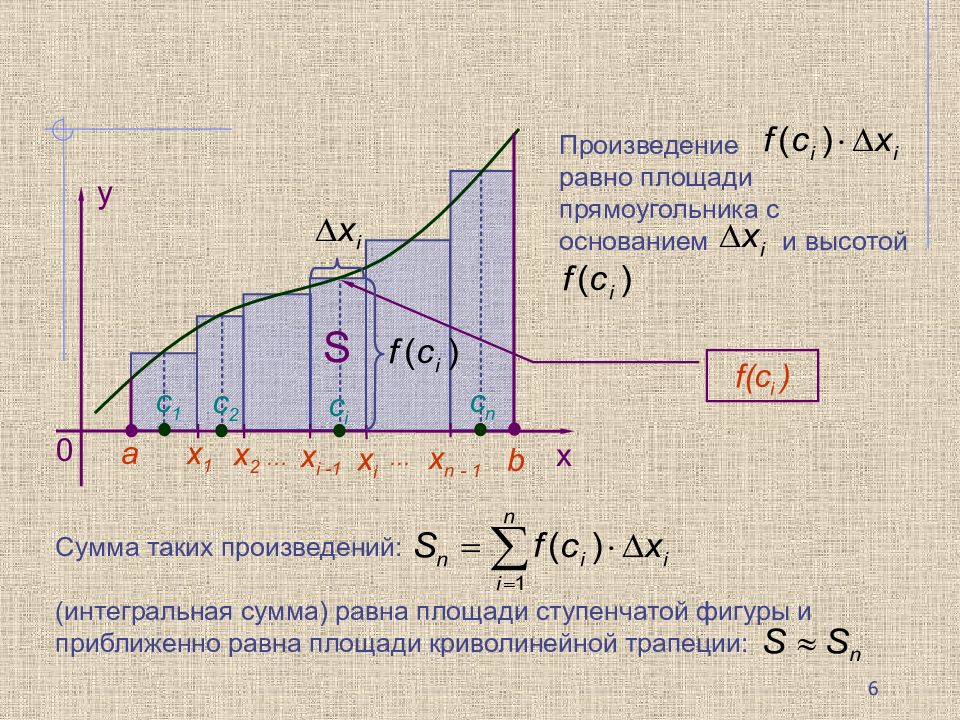
x y 0 a b x 1 x 2 х i -1 х i x n - 1 … … с 1 с 2 с i с n f(c i ) Произведение равно площади прямоугольника с основанием и высотой Сумма таких произведений: (интегральная сумма) равна площади ступенчатой фигуры и приближенно равна площади криволинейной трапеции: S 6
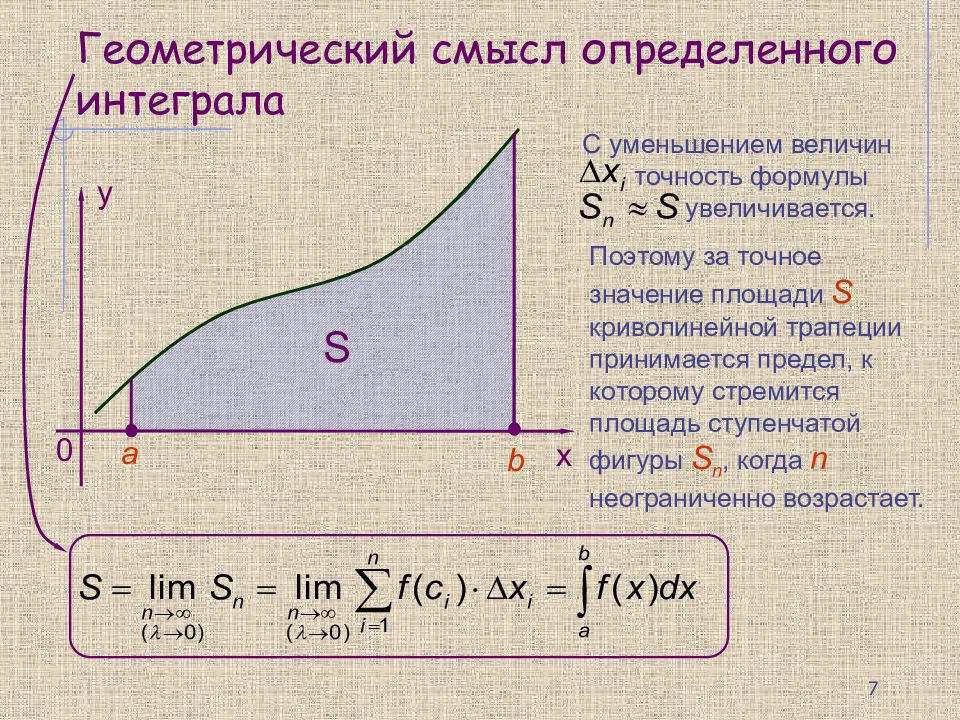
x y 0 Геометрический смысл определенного интеграла a b С уменьшением величин точность формулы увеличивается. Поэтому за точное значение площади S криволинейной трапеции принимается предел, к которому стремится площадь ступенчатой фигуры S n, когда n неограниченно возрастает. x y 0 a b S 7
a b x 1 x 2 х i -1 х i x n - 1 … … с i Пусть материальная точка М перемещается по воздействием силы , направленной вдоль оси OX и имеющей переменную величину Найдем работу А силы по перемещению точки М вдоль оси OX из точки х = а в точку х = b. М Но если длина отрезка достаточно мала, то силу на этом отрезке можно считать постоянной, равной значению функции в произвольно выбранной точке Поэтому работа, совершенная этой силой на отрезке равна: Сила, действующая на отрезке [ x i - 1 ; x i ] меняется от точки к точке. 8
Приближенное значение работы А силы на всем отрезке [a; b] : Точное значение работы А : Аналогично можно показать, что путь S, пройденный точкой за промежуток времени от t = a до t = b, равен определенному интегралу от скорости: Масса неоднородного стержня на отрезке [a; b] равна определенному интегралу от плотности: 9
Теорема Если функция y = f(x) непрерывна на отрезке [a; b] и F(x) какая либо ее первообразная, то имеет место формула: Формула Ньютона - Лейбница 10
Если функция f интегрируема на каждом из отрезков [ a, c ] и [ c, b ] ( a < c < b ), то она интегрируема на [ a, b ] и 11
Если функция f непрерывна на отрезке [ a, b ] то существует точка такая, что Теорема о среднем Это свойство имеет при f(x) > 0 следующий геометрический смысл: x y 0 a b с Значение определенного интеграла S равно при некотором площади прямоугольника с высотой f(c) и основанием b – a. Число: называется средним значением функции f(x) на отрезке [ a, b ]. 12
Если функция f сохраняет знак на отрезке [ a, b ] то интеграл на этом отрезке имеет тот же знак, что и функция: Оценка интеграла : если m и М – соответственно наименьшее и наибольшее значения функции f (х) на отрезке [ a, b ] то : x y 0 a b S М m Площадь криволинейной трапеции заключена между площадями прямоугольников, основания которых есть отрезок [ a, b ], а высоты равны m и М. 13
Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом: х Это означает также, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции. 14
Пусть для вычисления интеграла от непрерывной функции сделана подстановка: Теорема Если: 1) Функция x = φ(t) и ее производная непрерывны при ; 2) Множеством значений функции x = φ(t) при является отрезок [a; b] ; 3), то Замечания: 1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не нужно. 2) Иногда вместо подстановки x = φ(t) применяют подстановку t = q(x) 15
16
Теорема Если функции u = u(x) и v = v(x) имеют непрерывные производные на отрезке [a; b], то имеет место формула: 17
