Первый слайд презентации: Площадь криволинейной трапеции и интеграл (урок-практикум)
Слайд 3
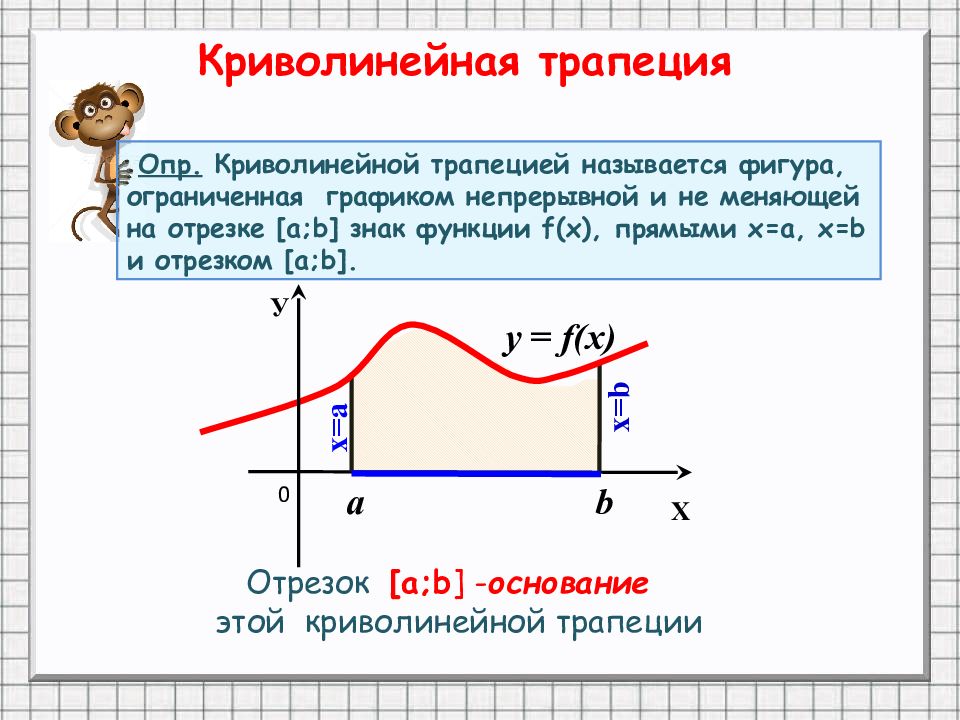
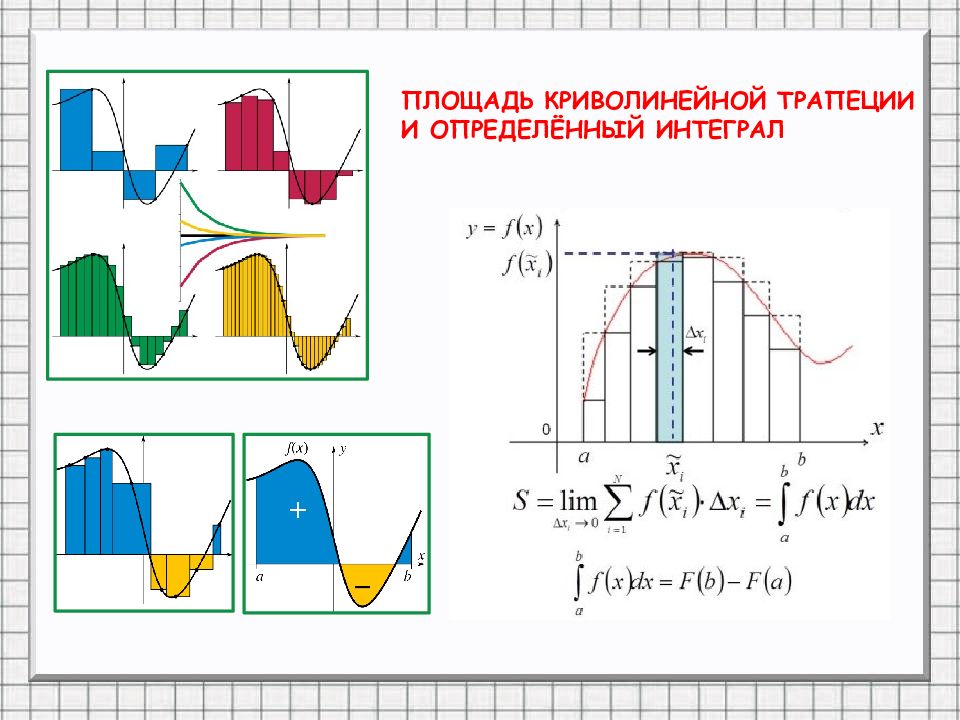
a b х=а x=b 0 y = f(x) Х У Криволинейная трапеция Отрезок [ a;b ] - основание этой криволинейной трапеции Опр. Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [ а;b ] знак функции f ( х ), прямыми х=а, x=b и отрезком [ а;b ].
Слайд 4
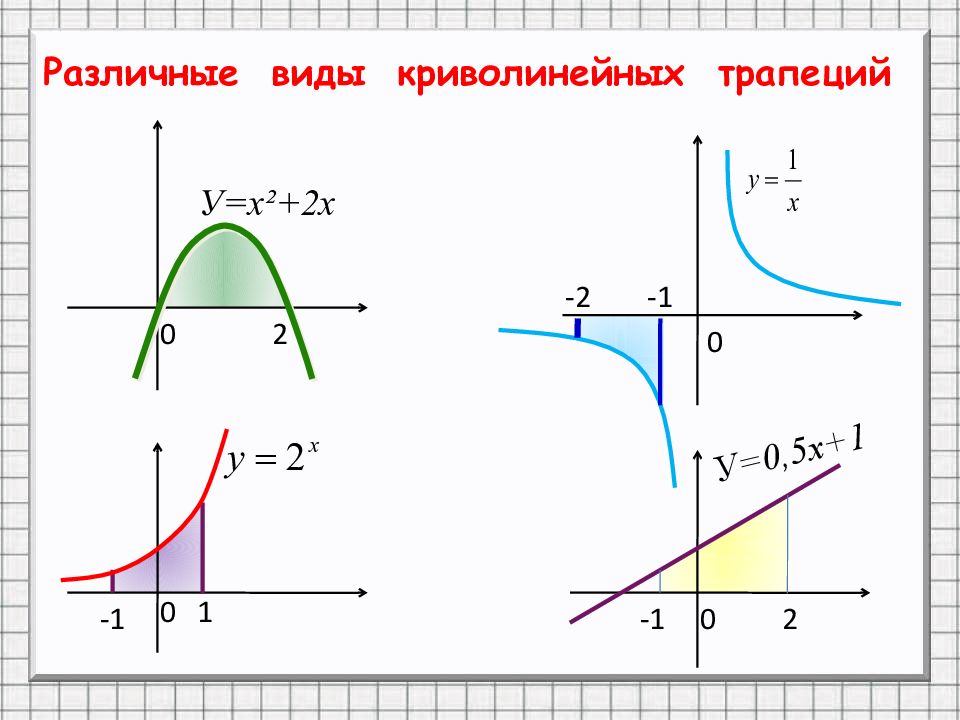
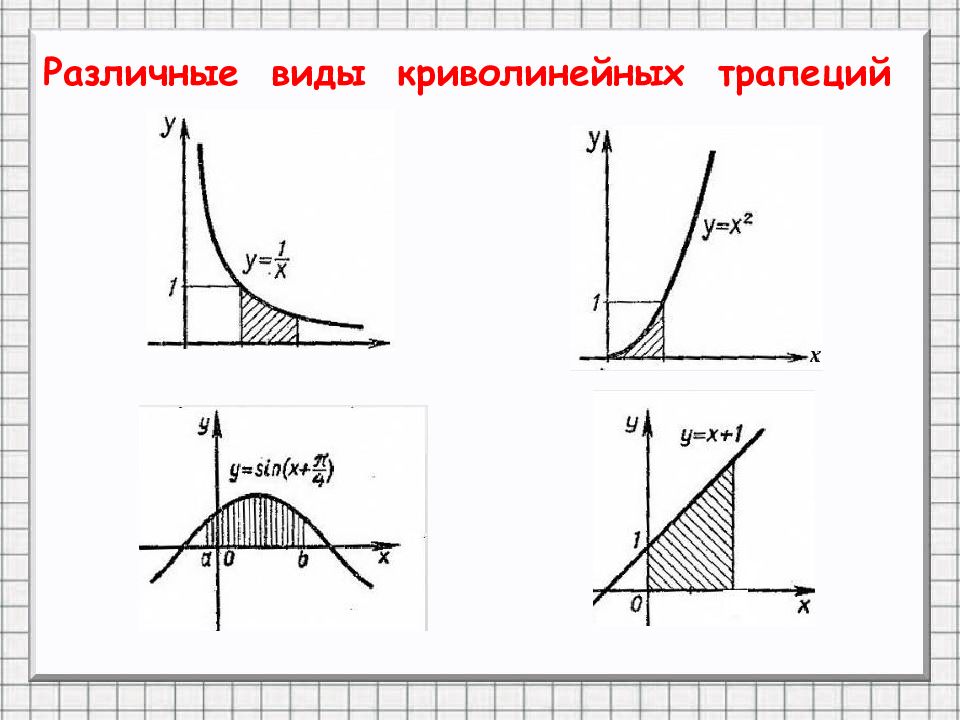
Различные виды криволинейных трапеций 0 2 0 0 0 1 -1 -1 2 -1 -2 У=х²+2х У=0,5х+1
Слайд 6
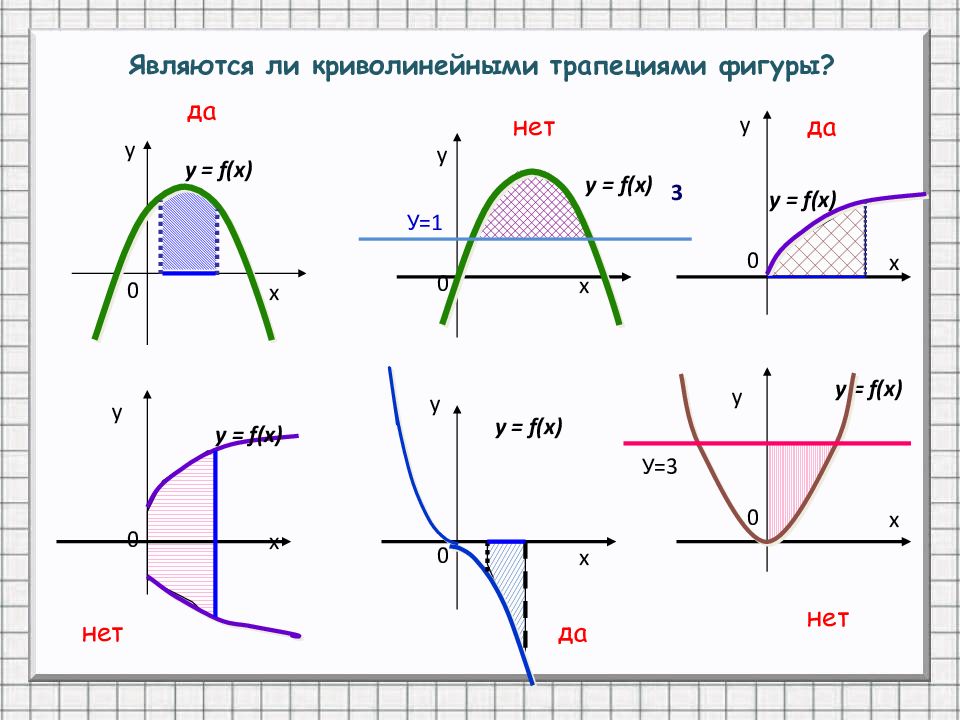
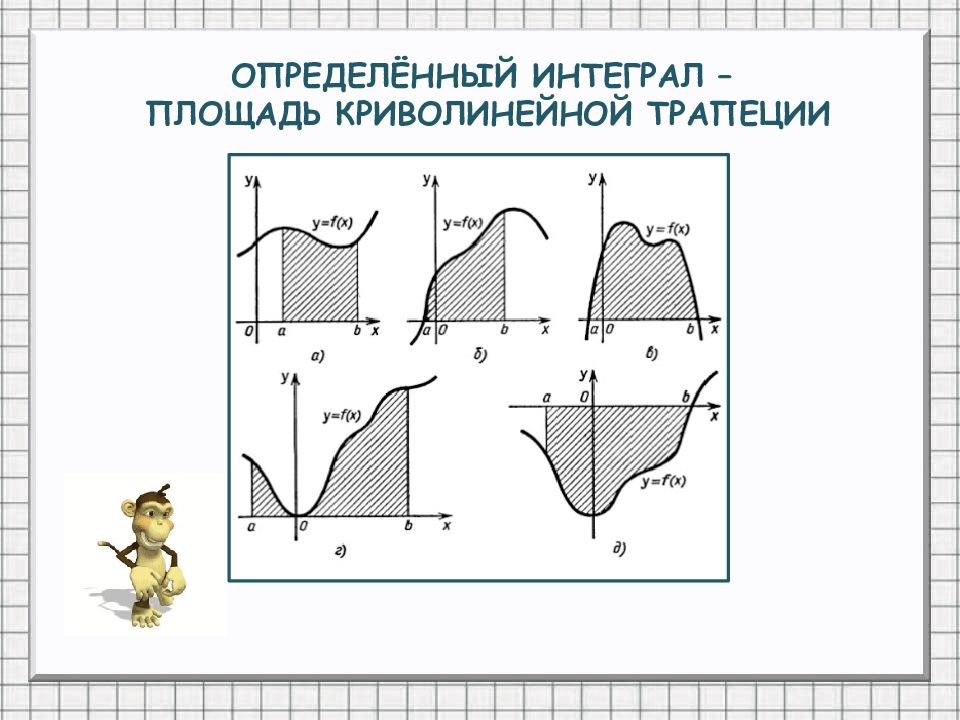
0 х у 0 х 0 х 0 х 0 х 0 х у у у у у У=1 3 y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) y = f(x ) У=3 да да да нет нет нет Являются ли криволинейными трапециями фигуры?
Слайд 7
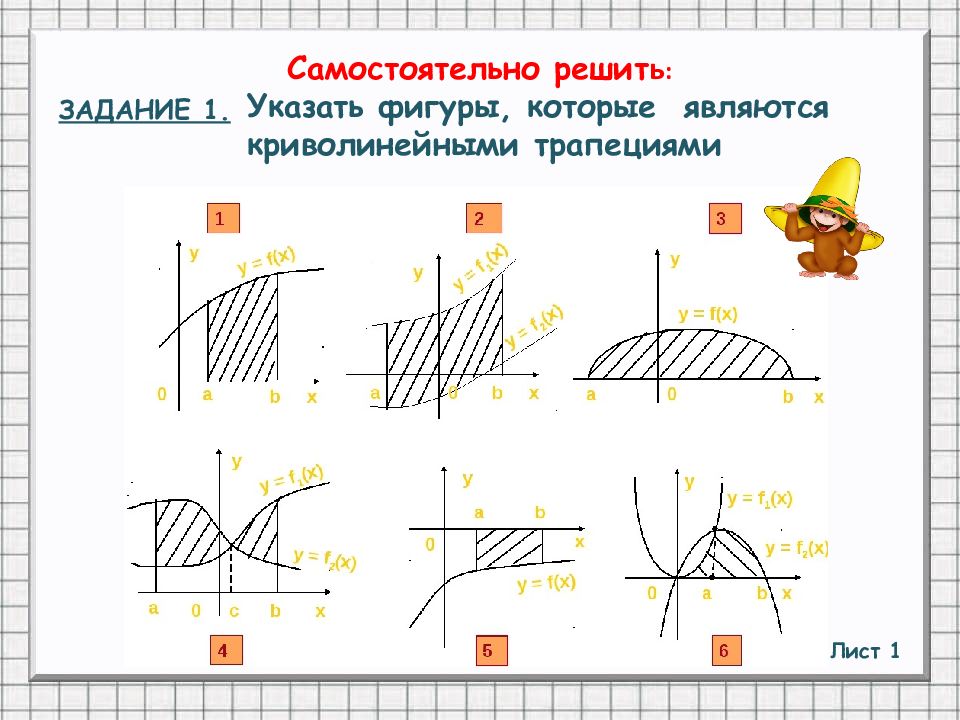
Самостоятельно решит ь : Лист 1 ЗАДАНИЕ 1. Указать фигуры, которые являются криволинейными трапециями
Слайд 8
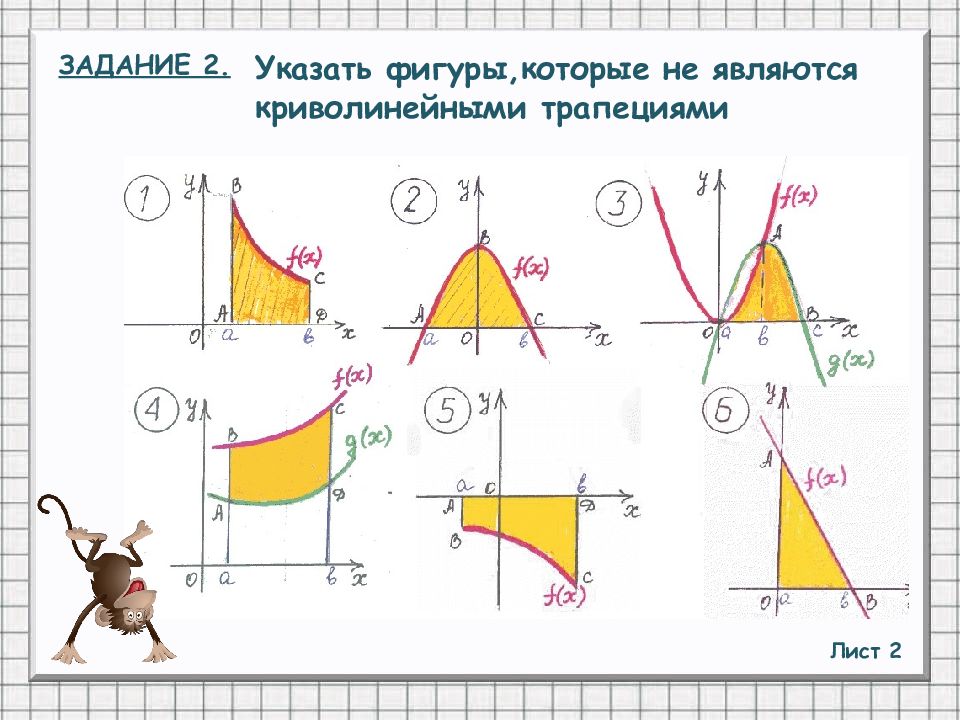
Лист 2 ЗАДАНИЕ 2. Указать фигуры,которые не являются криволинейными трапециями
Слайд 9
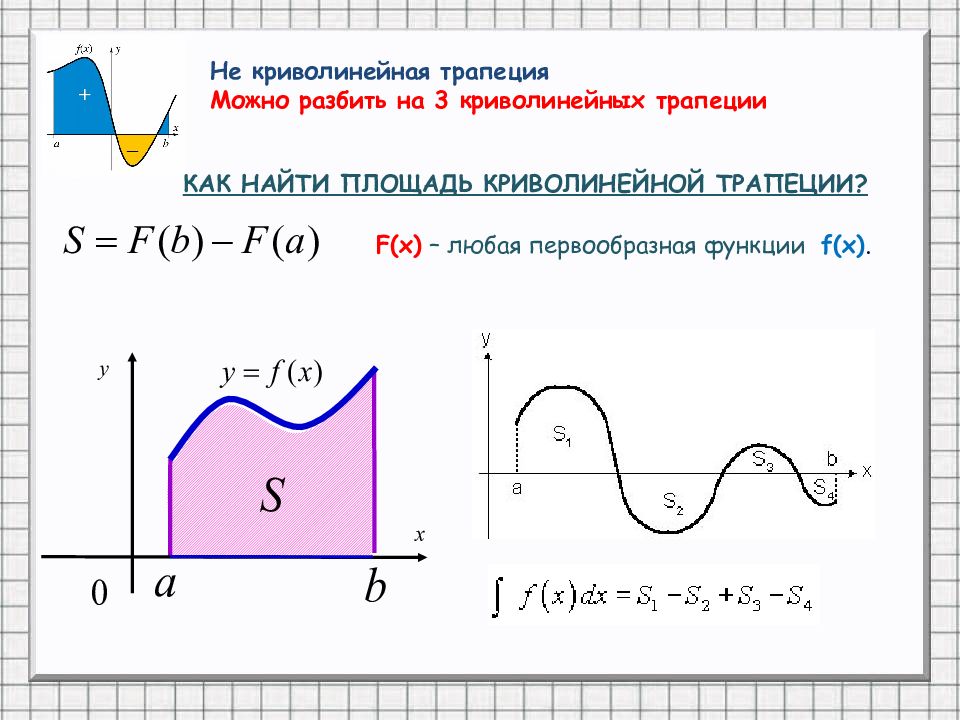
F(x) – любая первообразная функции f(x). Не криволинейная трапеция Можно разбить на 3 криволинейных трапеции КАК НАЙТИ ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ?
Слайд 10
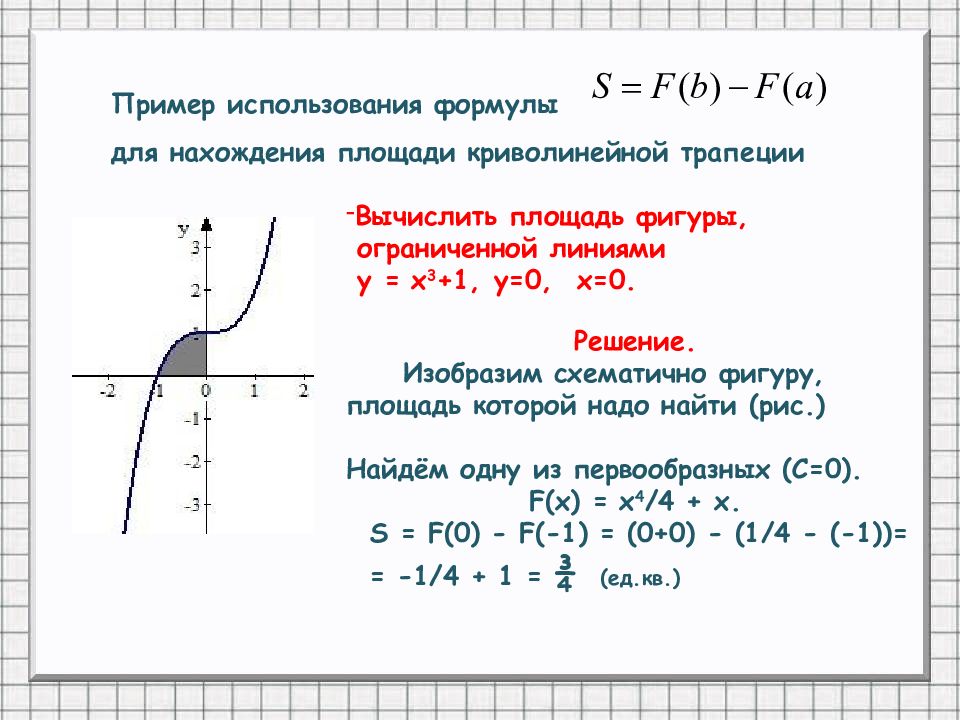
Вычислить площадь фигуры, ограниченной линиями у = x 3 +1, у=0, x=0. Решение. Изобразим схематично фигуру, площадь которой надо найти (рис.) Найдём одну из первообразных (С=0). F( x ) = x 4 /4 + x. S = F(0) - F(-1) = (0+0) - (1/4 - (-1))= = -1/4 + 1 = ¾ (ед.кв.) Пример использования формулы для нахождения площади криволинейной трапеции
Слайд 15: СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Слайд 17
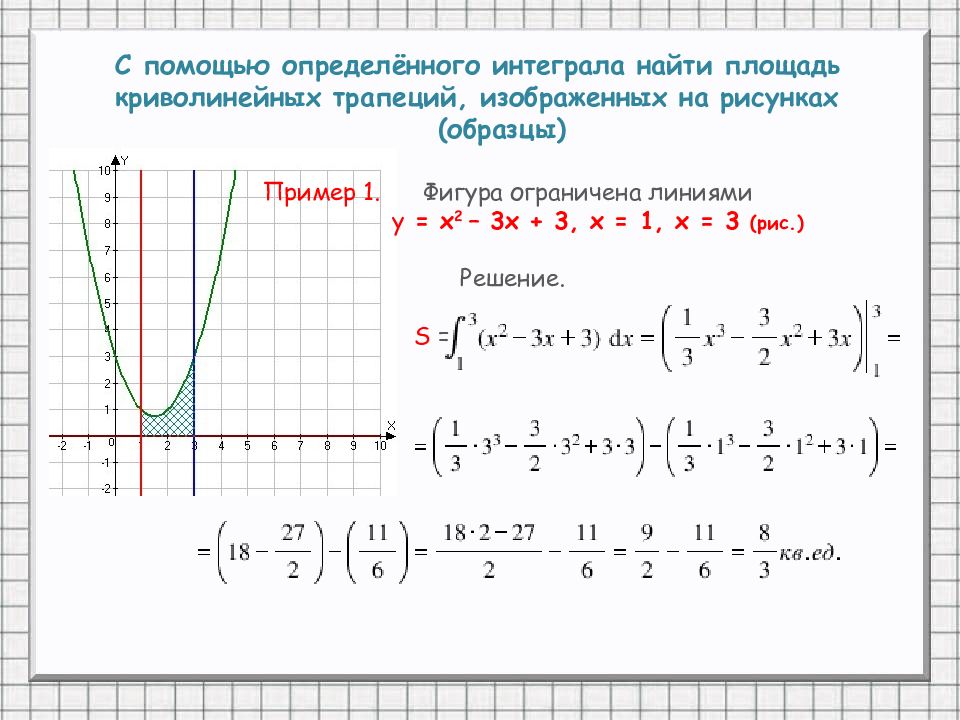
С помощью определённого интеграла найти площадь криволинейных трапеций, изображенных на рисунках (образцы) Пример 1. Фигура ограничена линиями у = х 2 – 3х + 3, х = 1, х = 3 (рис.) Решение. S =
Слайд 18
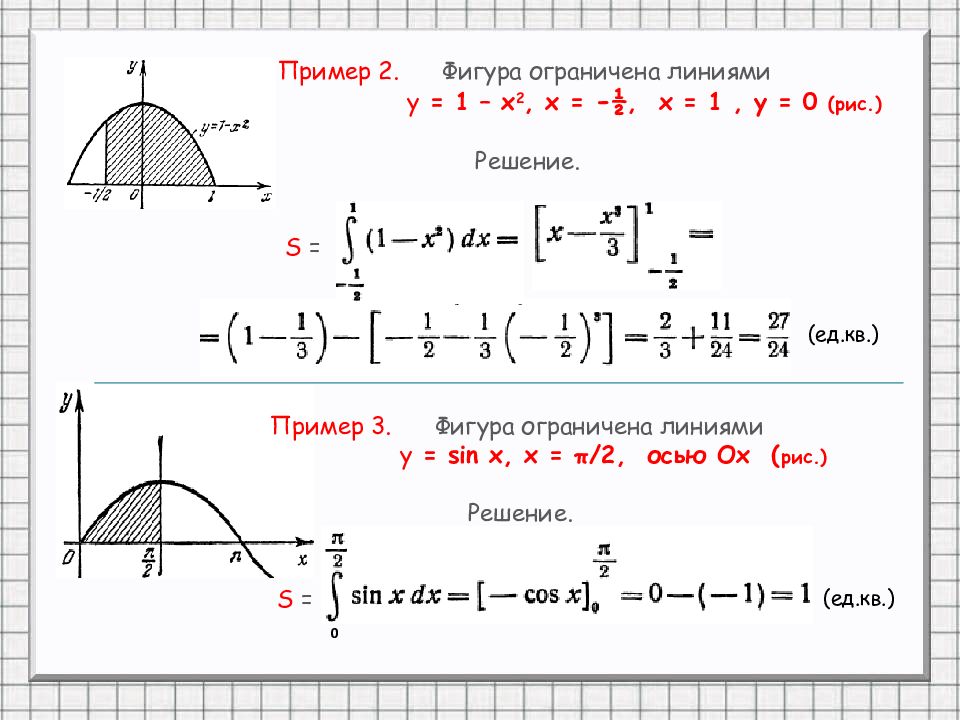
Пример 2. Фигура ограничена линиями у = 1 – х 2, х = -½, х = 1, у = 0 (рис.) Решение. S = (ед.кв.) Пример 3. Фигура ограничена линиями у = sin x, x = π /2, осью Ох ( рис.) Решение. S = (ед.кв.) 0
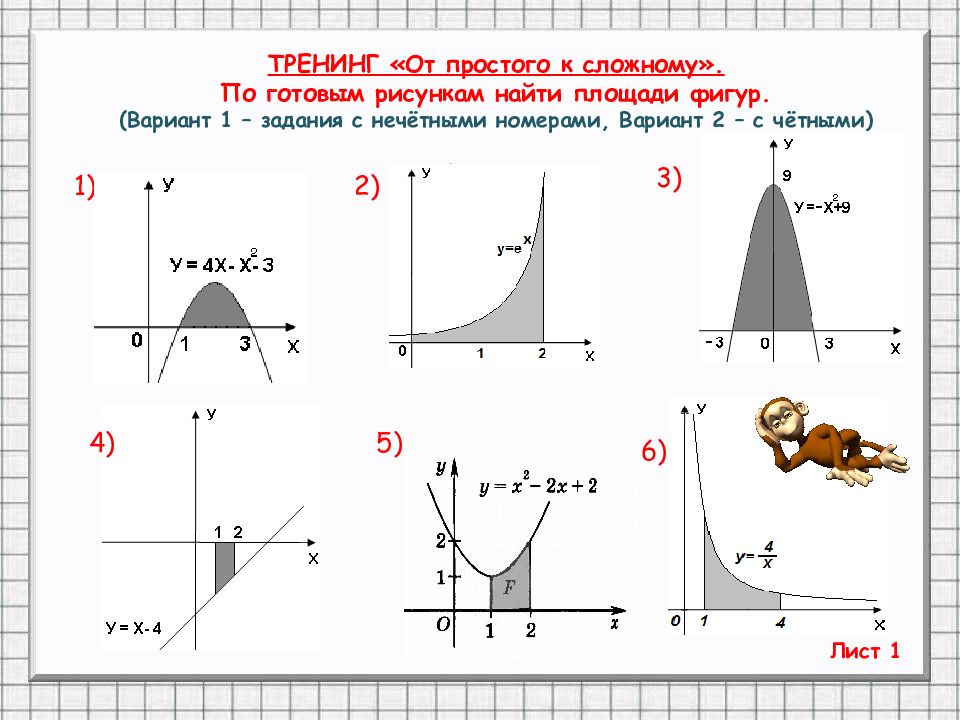
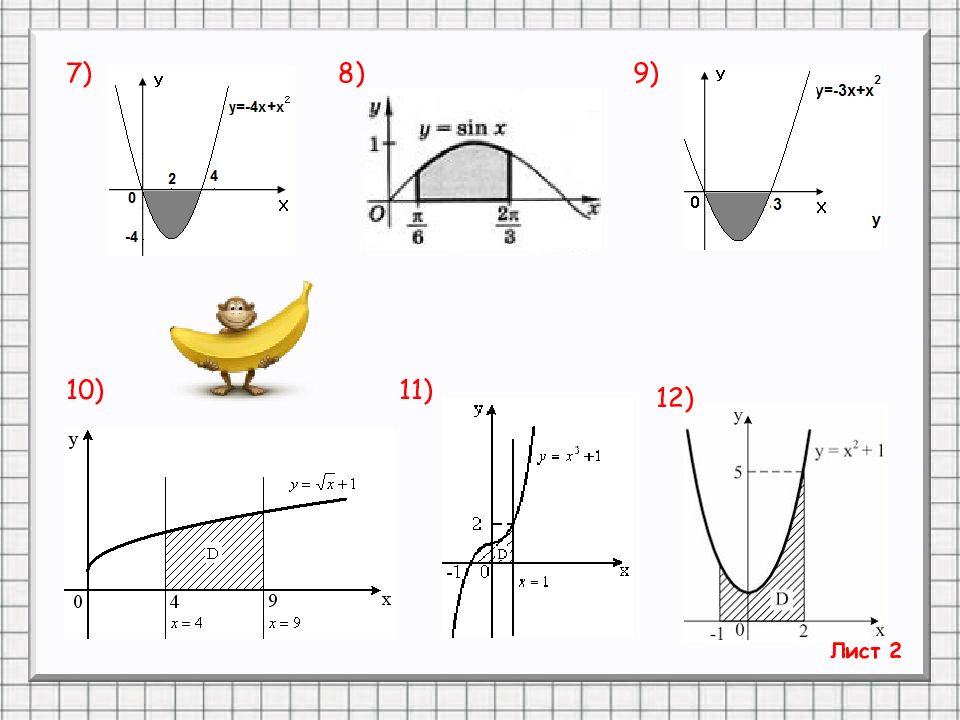
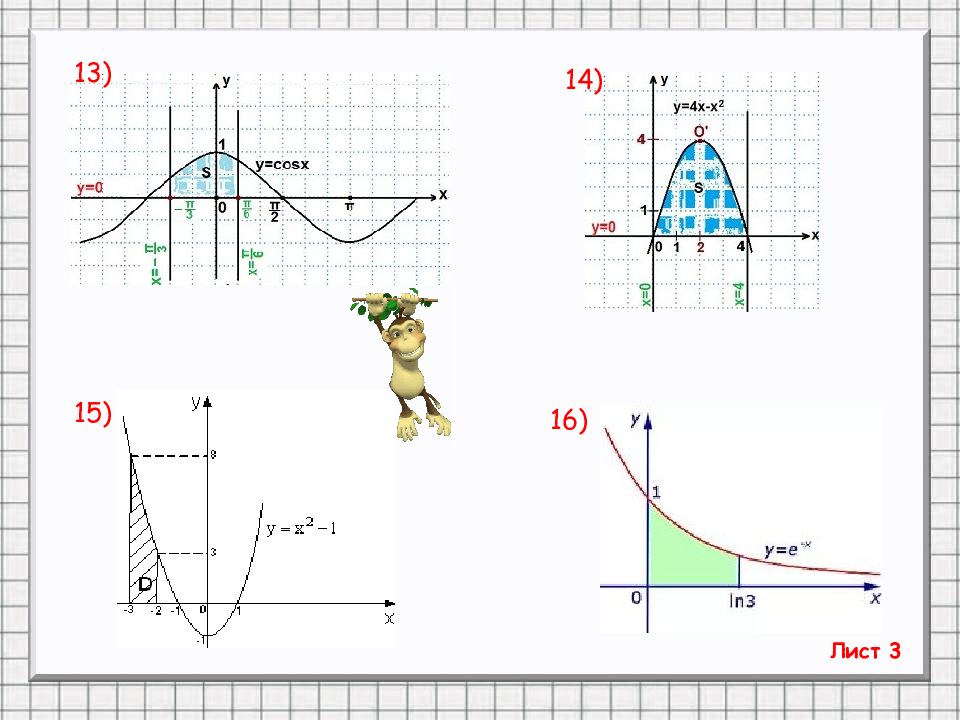
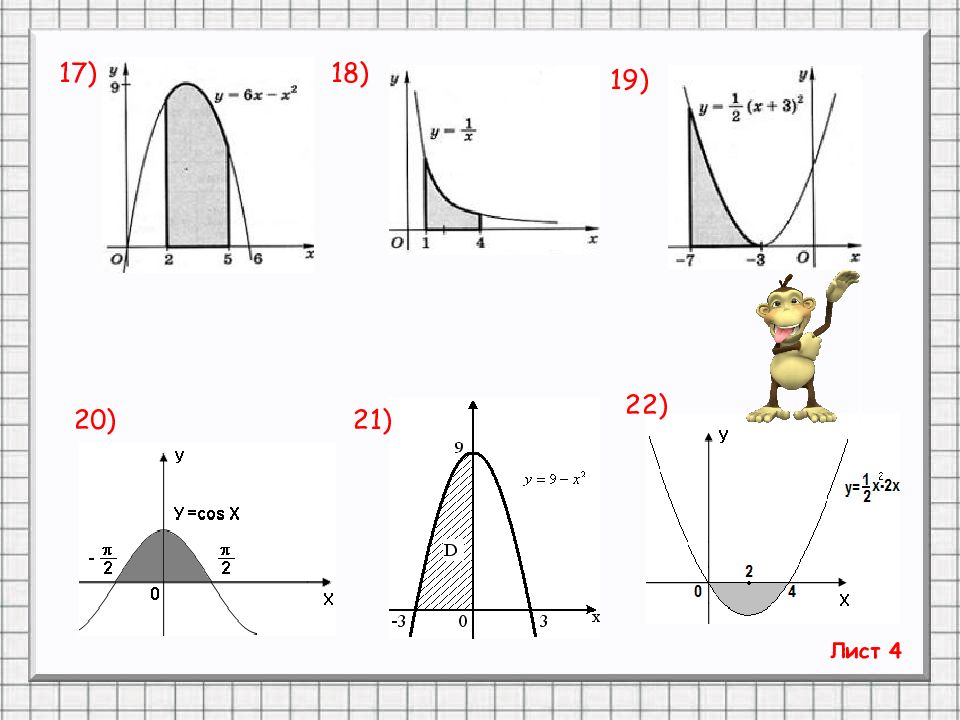
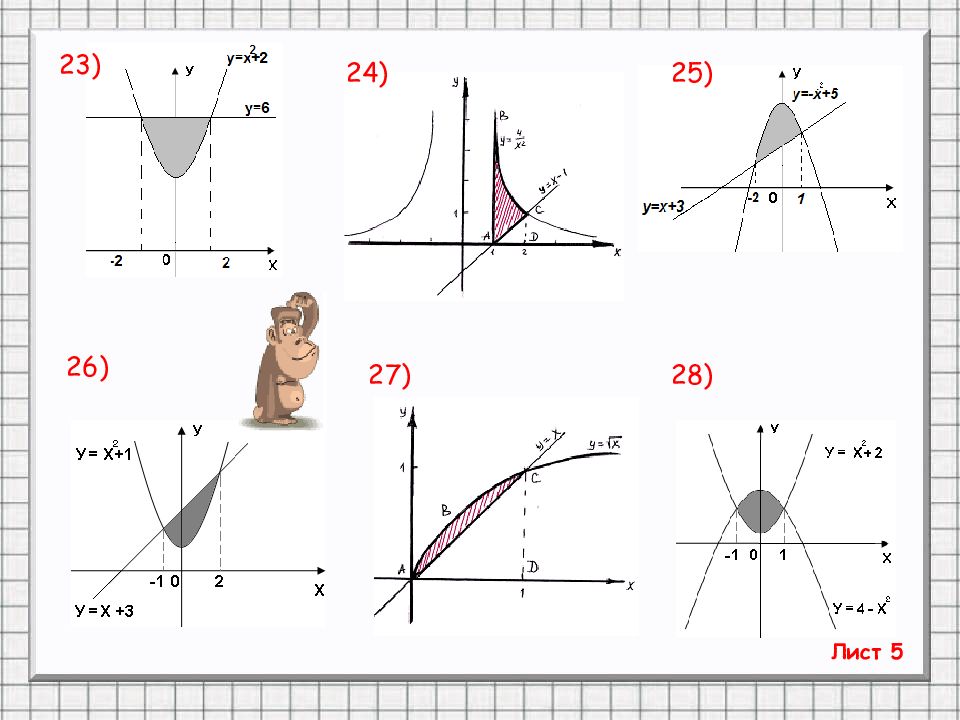
Слайд 19: ТРЕНИНГ «От простого к сложному». По готовым рисункам найти площади фигур. (Вариант 1 – задания с нечётными номерами, Вариант 2 – с чётными)
1) 2) 3) Лист 1 6) 5) 4)
Слайд 24
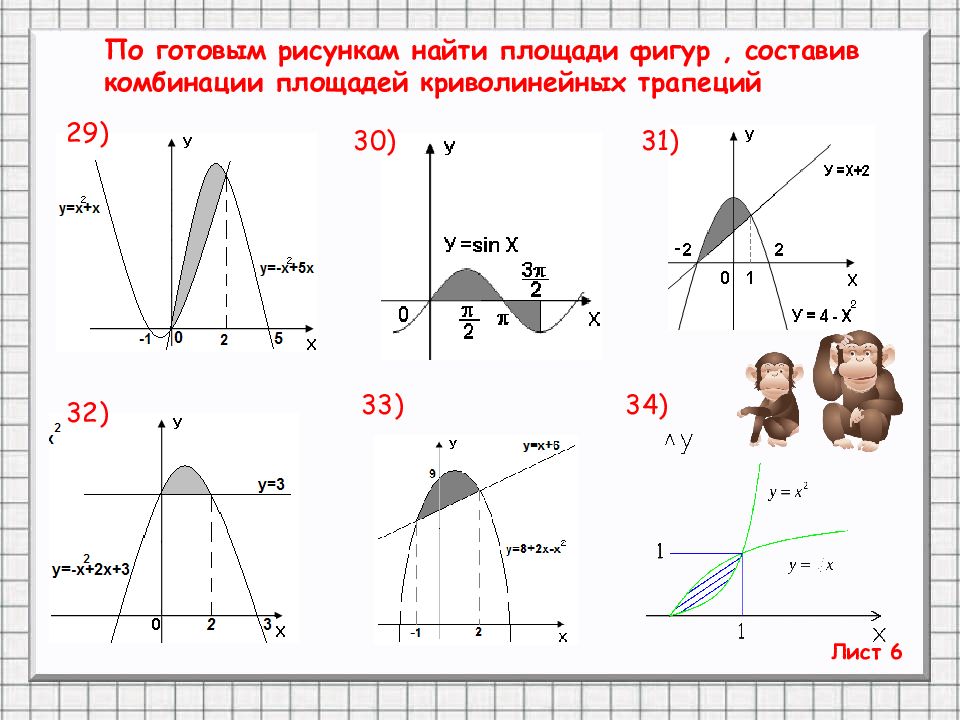
Лист 6 30) 31) 32) 33) 34) 29) По готовым рисункам найти площади фигур, составив комбинации площадей криволинейных трапеций