Урюпинский филиал ГАПОУ “Волгоградский медицинский колледж”
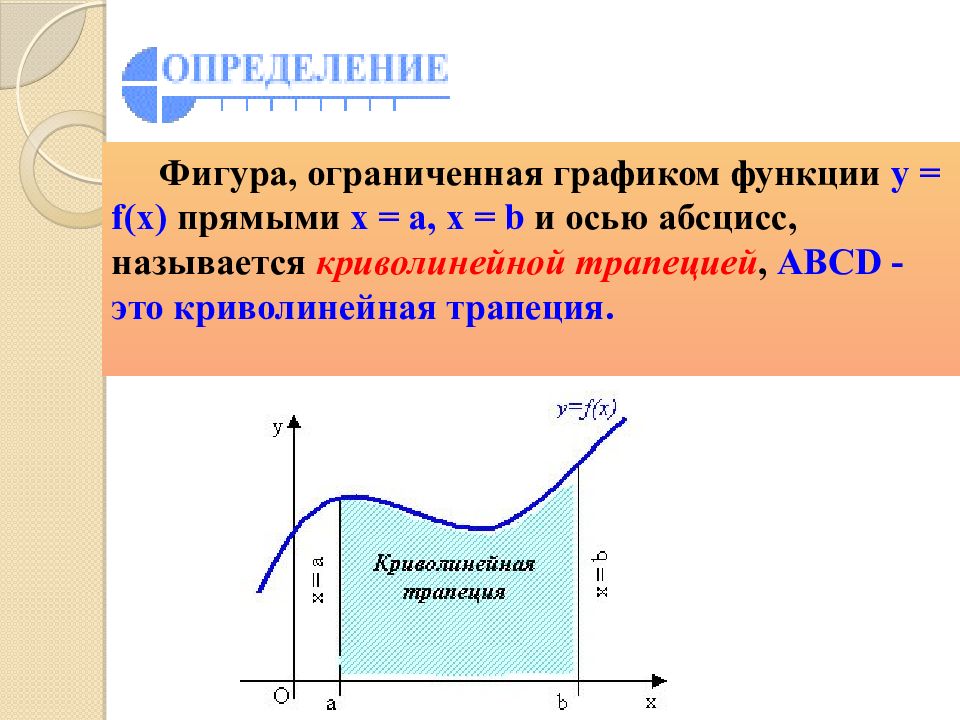
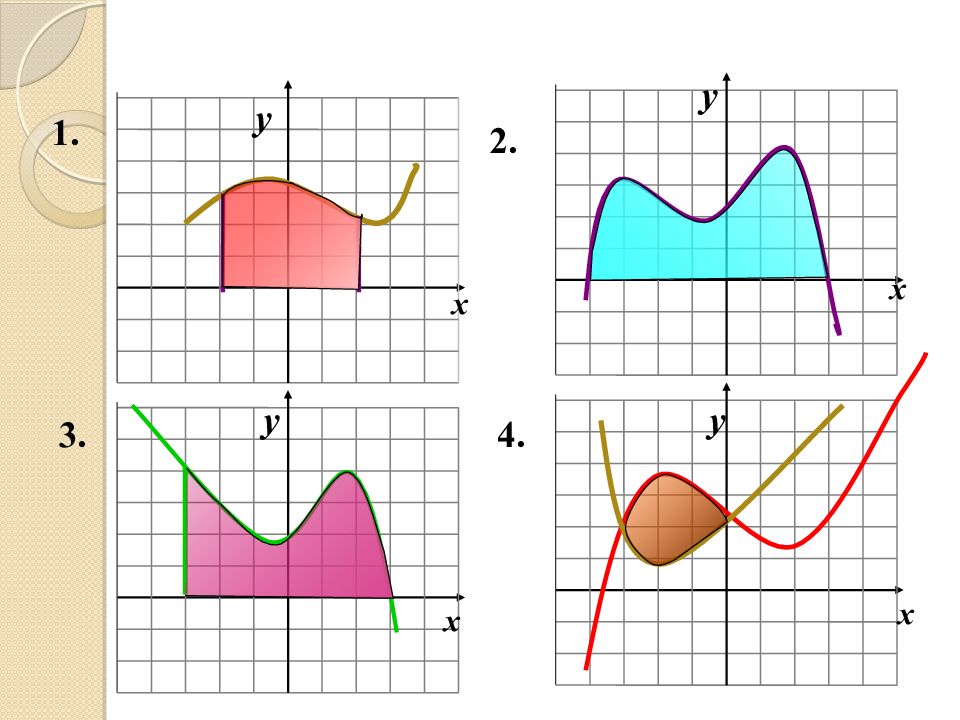
Фигура, ограниченная графиком функции y = f ( x ) прямыми x = a, x = b и осью абсцисс, называется криволинейной трапецией, ABCD -это криволинейная трапеция.
y y y y x x x x 1. 4. 3. 2.
Если f ( x ) на отрезке [ a ; b ] неотрицательна, то определенный интеграл равен площади криволинейной трапеции, ограниченной графиком функции f ( x ), осью абсцисс и прямыми x = a, x = b,т.е.
Если f (х ) – непрерывная и неотрицательная на отрезке [ a ; b ] функция, а F (х) – ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [ a ; b ], т.е.
1. Метод разложения (непосредственное интегрирование).
Вычислить.
Пример
Используя понятие определенного интеграла, дадим общий метод вычисления площадей плоских фигур. Как известно, определенный интеграл от неотрицательной непрерывной функции есть площадь соответствующей криволинейной трапеции. В этом заключается геометрический смысл определенного интеграла, на этом основано его применение к вычислению площадей плоских фигур. Площадь криволинейной трапеции, ограниченной неотрицательной функцией f ( x ), осью абсцисс и прямыми x = a, x = b, определяется как
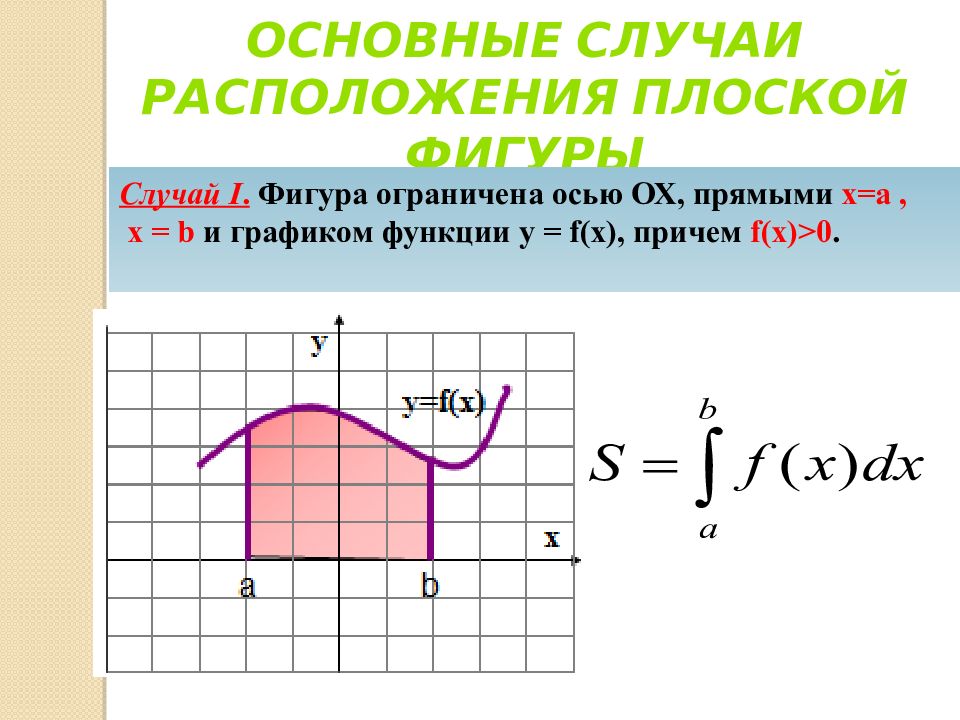
Основные случаи расположения плоской фигуры Случай I. Фигура ограничена осью ОХ, прямыми х=а, х = b и графиком функции у = f ( x ), причем f ( x )>0.
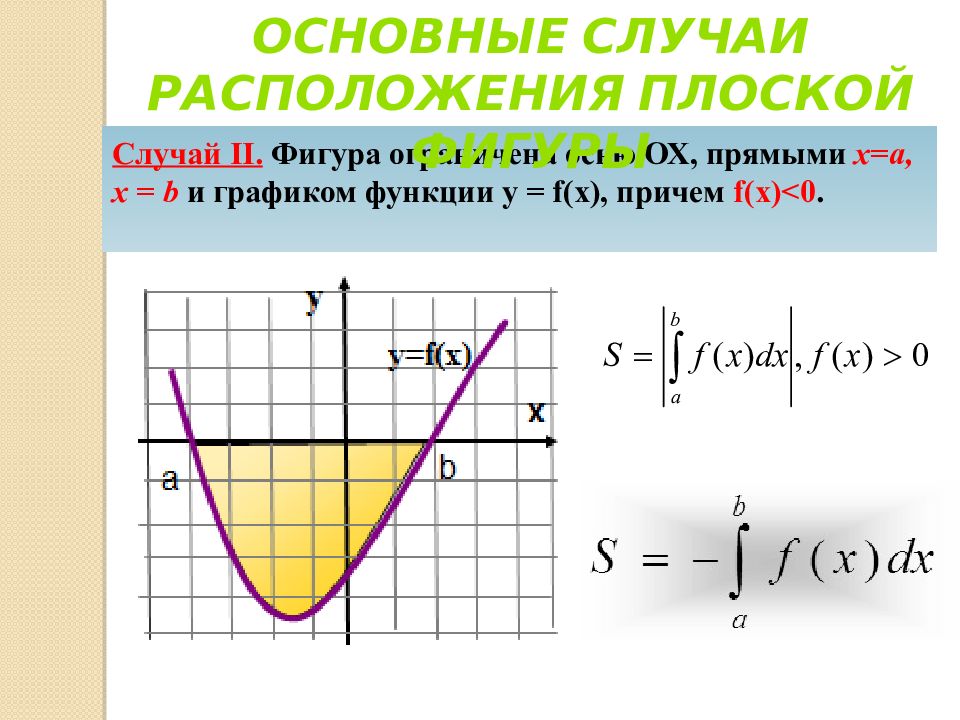
Случай II. Фигура ограничена осью ОХ, прямыми х=а, х = b и графиком функции у = f ( x ), причем f ( x )<0. Основные случаи расположения плоской фигуры
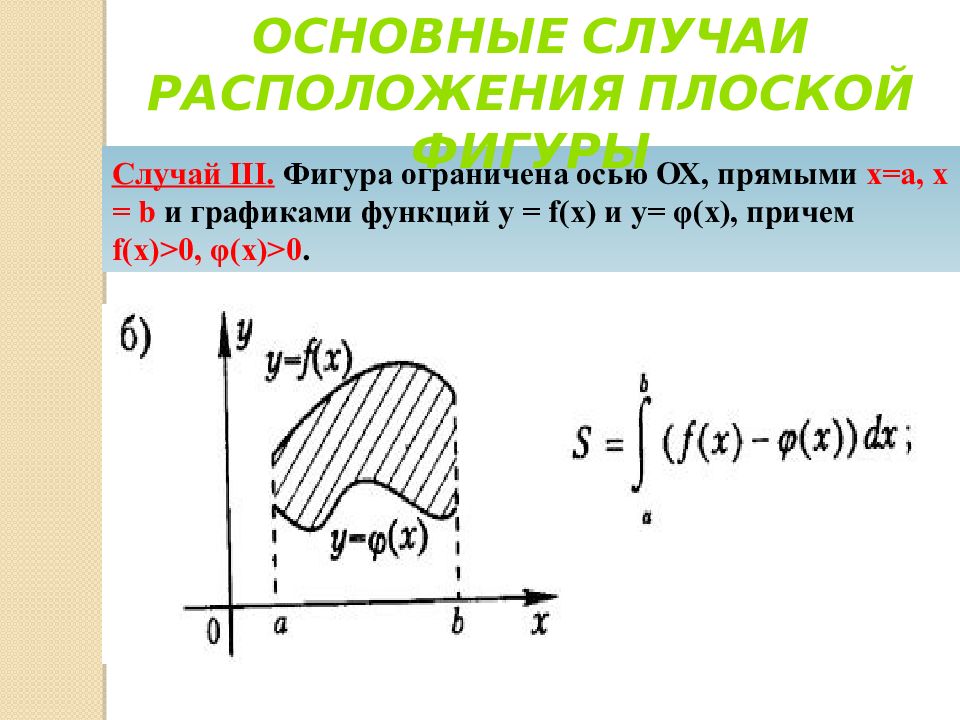
Случай III. Фигура ограничена осью ОХ, прямыми х=а, х = b и графиками функций у = f ( x ) и y = φ ( x ), причем f ( x )>0, φ ( x )>0. Основные случаи расположения плоской фигуры
Случай IV. Если f ( x ) 0, φ ( x ) 0, то графики функций расположены ниже оси абсцисс, а условие f ( x ) ≥ φ ( x ), означает, что график f ( x ) расположен выше графика φ ( x )>0. Основные случаи расположения плоской фигуры
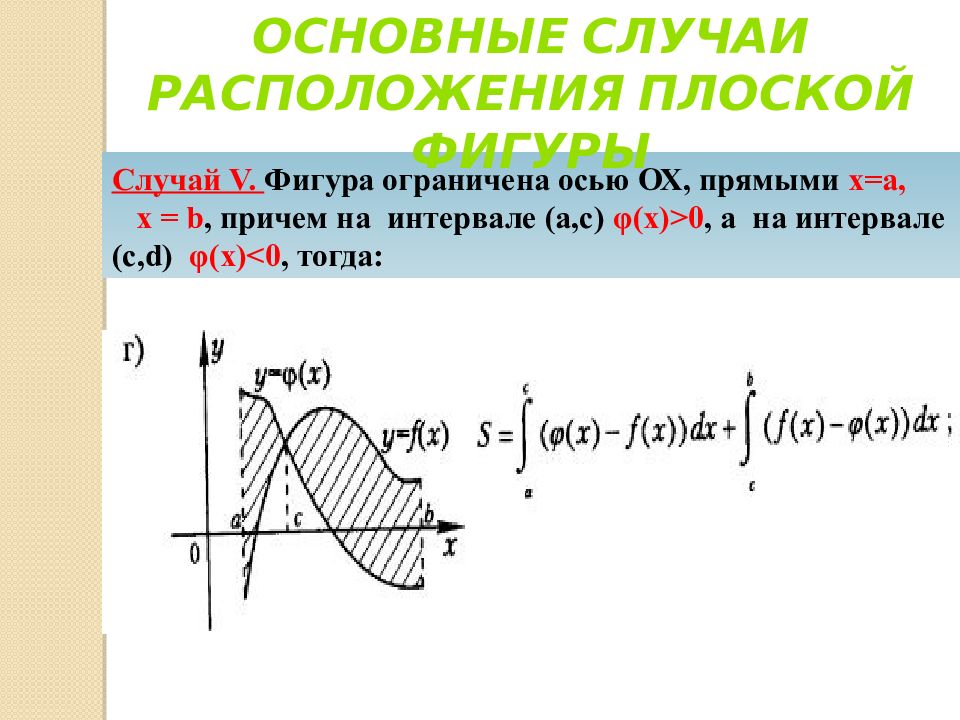
Случай V. Фигура ограничена осью ОХ, прямыми х=а, х = b, причем на интервале ( а,с ) φ ( x )>0, а на интервале ( c, d ) φ ( x )<0, тогда: Основные случаи расположения плоской фигуры
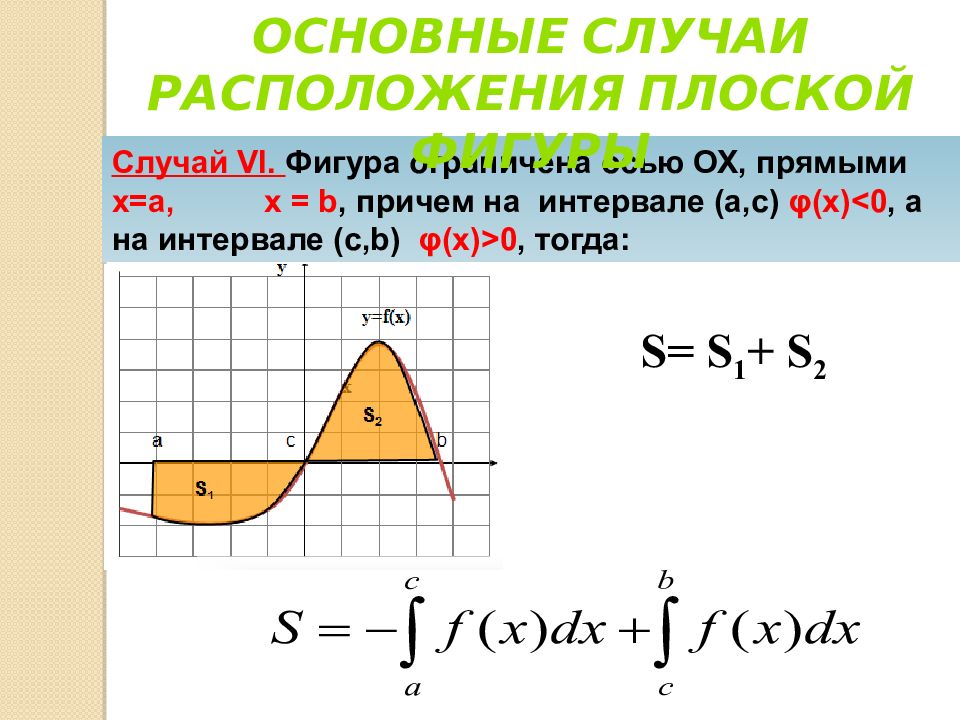
Случай VI. Фигура ограничена осью ОХ, прямыми х=а, х = b, причем на интервале ( а,с ) φ ( x ) < 0, а на интервале ( c, b ) φ ( x ) > 0, тогда: Основные случаи расположения плоской фигуры S= S 1 + S 2
Сделать чертеж графиков заданных функций, ограничивающих площадь плоских фигур. Найти пределы интегрирования. Выяснить какой формулой площади плоской фигуры удобно пользоваться в данном случае. Вычислить площадь заданной фигуры. АЛГОРИТМ решения задач на вычисление площадей :
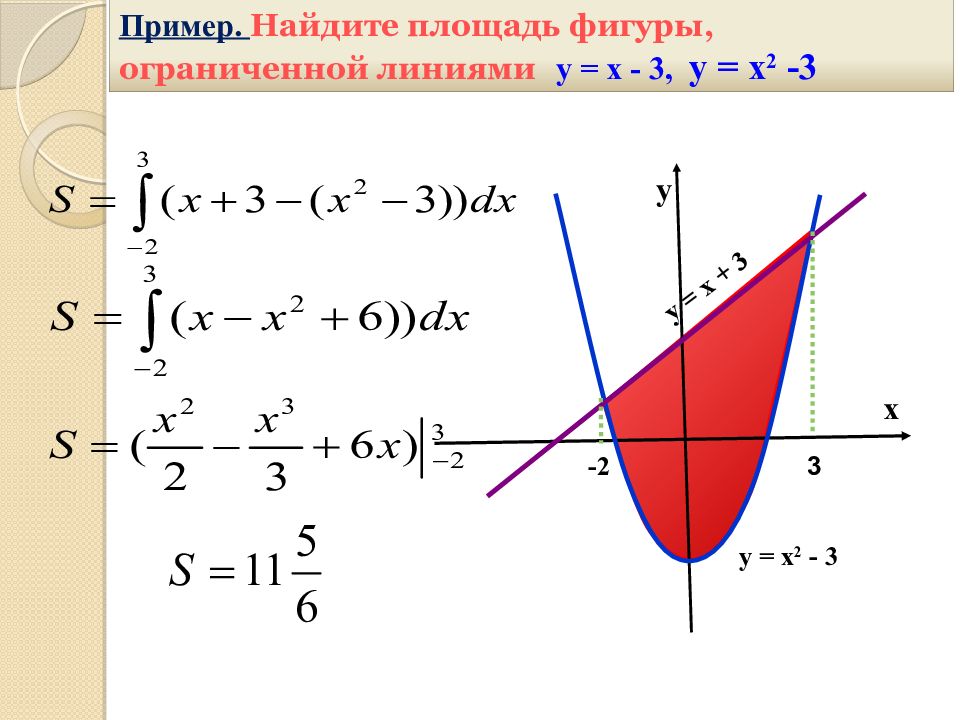
х у = х 2 - 3 -2 3 у у = х + 3 Пример. Найдите площадь фигуры, ограниченной линиями у = х - 3, у = х 2 -3
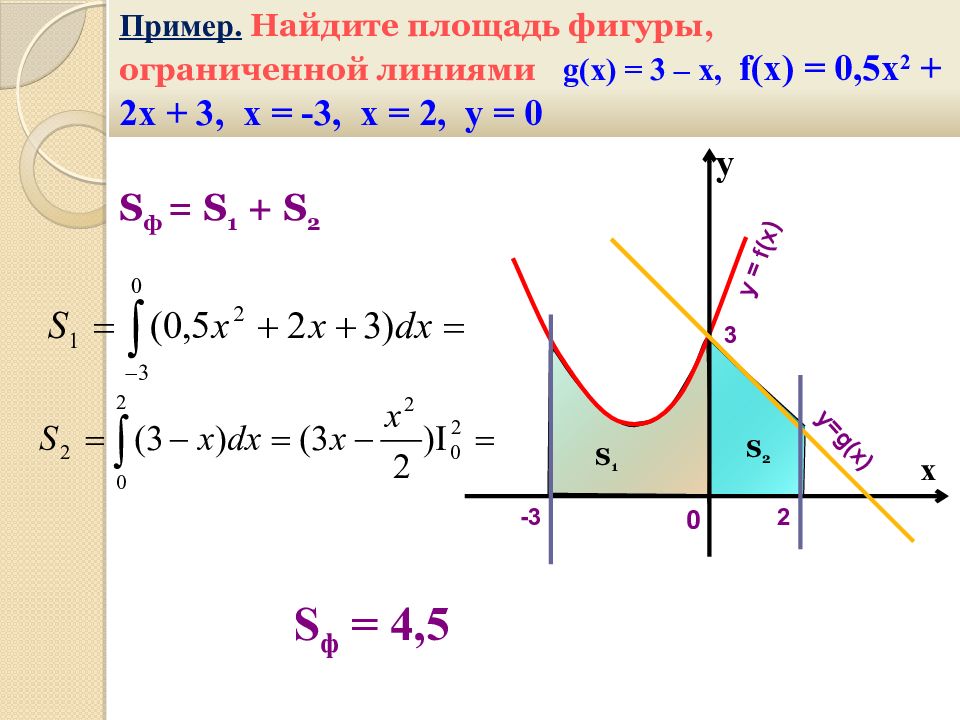
Пример. Найдите площадь фигуры, ограниченной линиями g(x) = 3 – х, f(x) = 0,5х 2 + 2х + 3, х = -3, х = 2, у = 0 у х -3 2 3 у= g(x) у = f(x) 0 S 1 S 2 S ф = S 1 + S 2 S ф = 4,5
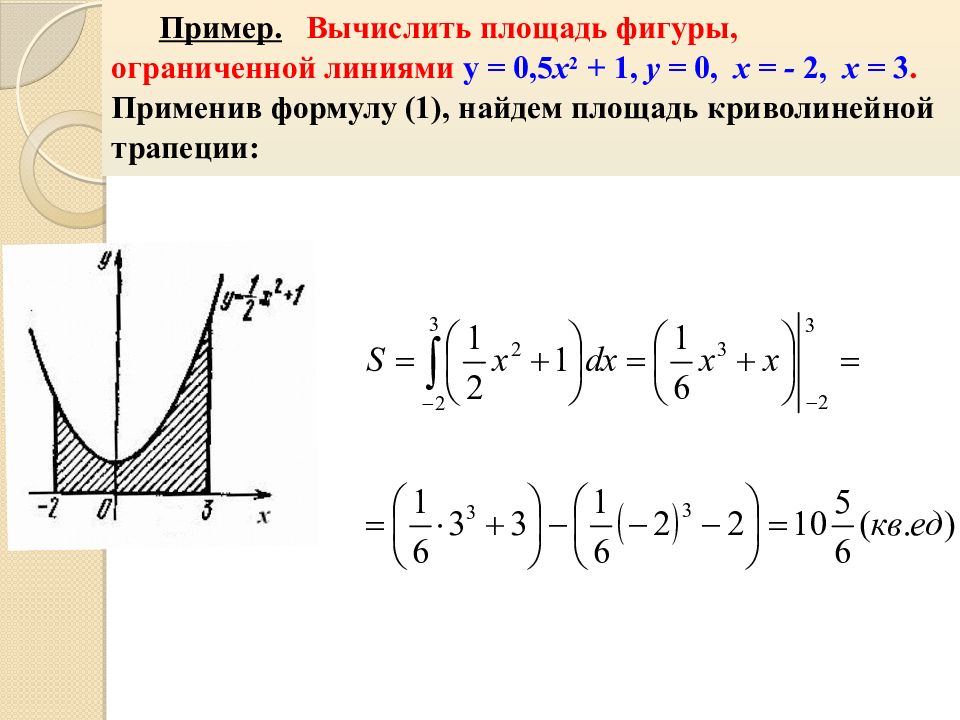
Пример. Вычислить площадь фигуры, ограниченной линиями y = 0,5 х 2 + 1, y = 0, х = - 2, x = 3. Применив формулу (1), найдем площадь криволинейной трапеции:
Пример. Вычислить площадь фигуры, ограниченной линиями y = - х 2 - 1, у = 0, х = -1, х = 2. По формуле (2) находим
Пример. Вычислить площадь фигуры, ограниченной линиями у = sin х, y = 0, х = - π / 2, х = π. Очевидно, что sin х ≤ 0 для всех х ∈ [ - π /2; 0] и sin х ≥ 0 для всех х ∈ [0; π ]. Поэтому
Пример. Вычислить площадь фигуры,ограниченной линиями Пределы интегрирования а и b находим из системы уравнений : Отсюда, т. е. x 2 - Зх - 18 = 0, откуда х = - 3 и х = 6. Следовательно, а = - 3 и b = 6. Так как на отрезке [ - 3; 6] для имеем f(x) ≥ g(x), то по формуле (3) находим
Федотова Тамара Валентиновна СПАСИБО ЗА ВНИМАНИЕ!
