"Основные понятия и аксиомы стереометрии.
Планиметрия Стереометрия
Стереометрия изучает свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов « стереос » объемный, пространственный, « метрео » – мерить.
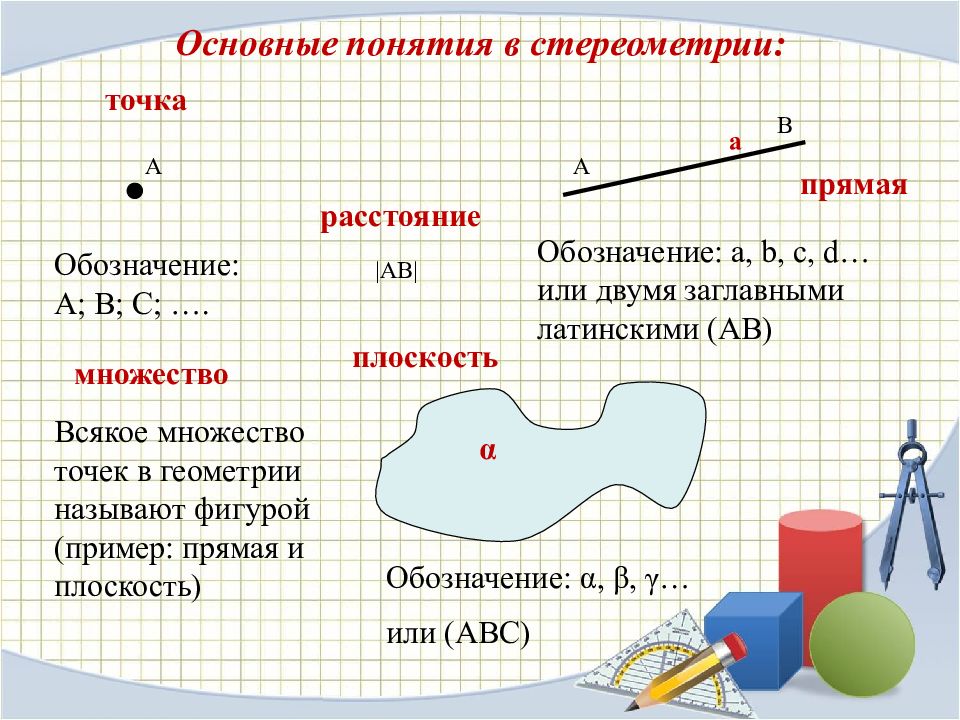
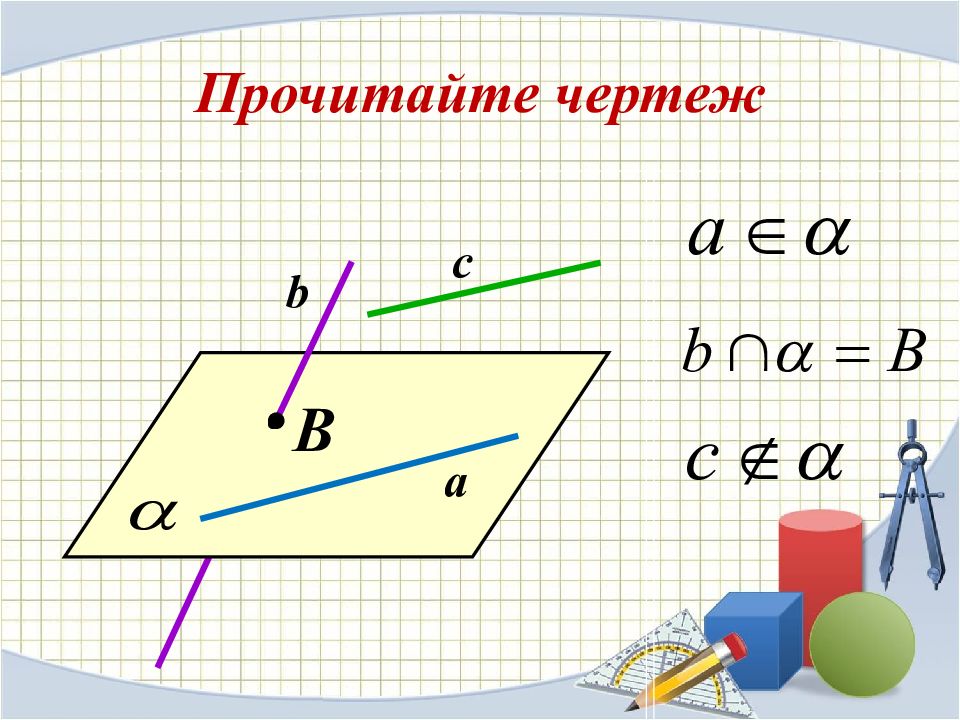
Основные понятия в стереометрии : точка α Обозначение: А; В; С ; …. Обозначение: a, b, с, d… или двумя заглавными латинскими (АВ) Обозначение: α, β, γ … или (АВС) плоскость множество расстояние Всякое множество точек в геометрии называют фигурой (пример: прямая и плоскость) А а А В прямая |АВ|
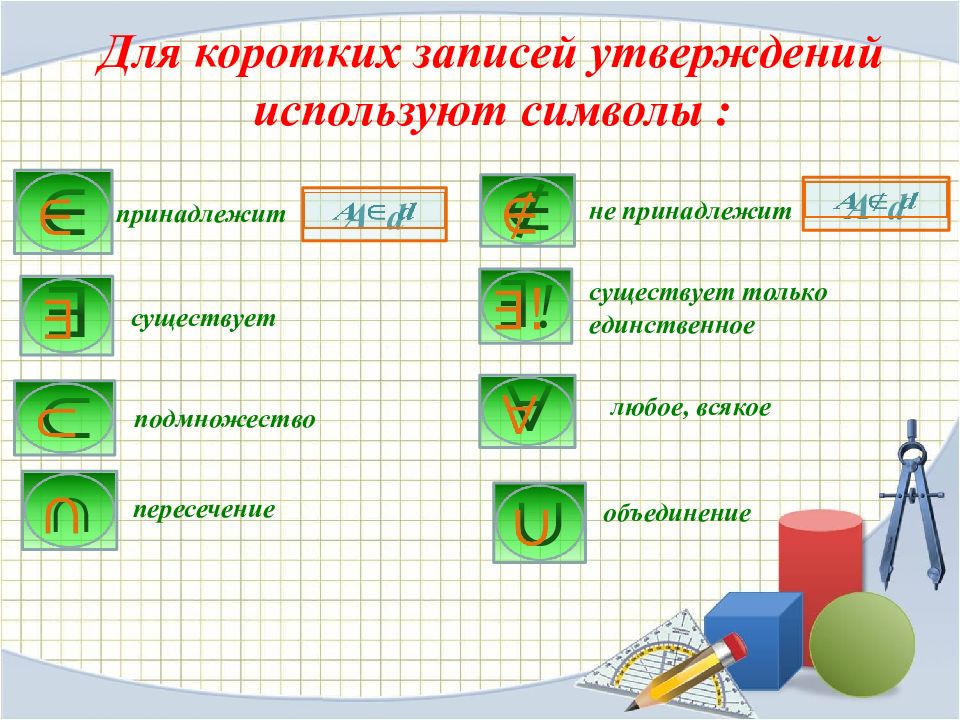
Для коротких записей утверждений используют символы : принадлежит н е принадлежит подмножество A d A d пересечение объединение существует только единственное существует любое, всякое
Для коротких записей утверждений используют символы : параллельны н е параллельны перпендикулярны скрещивающиеся равносильны следует
A С
B c b a
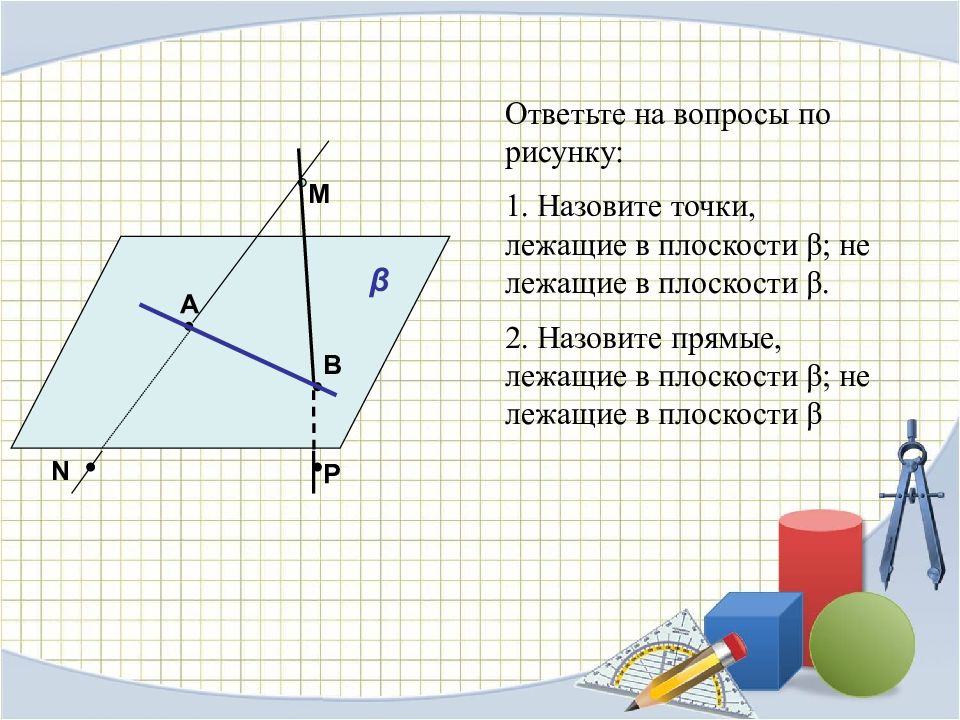
β А В М N Р Ответьте на вопросы по рисунку: 1. Назовите точки, лежащие в плоскости β ; не лежащие в плоскости β. 2. Назовите прямые, лежащие в плоскости β ; не лежащие в плоскости β
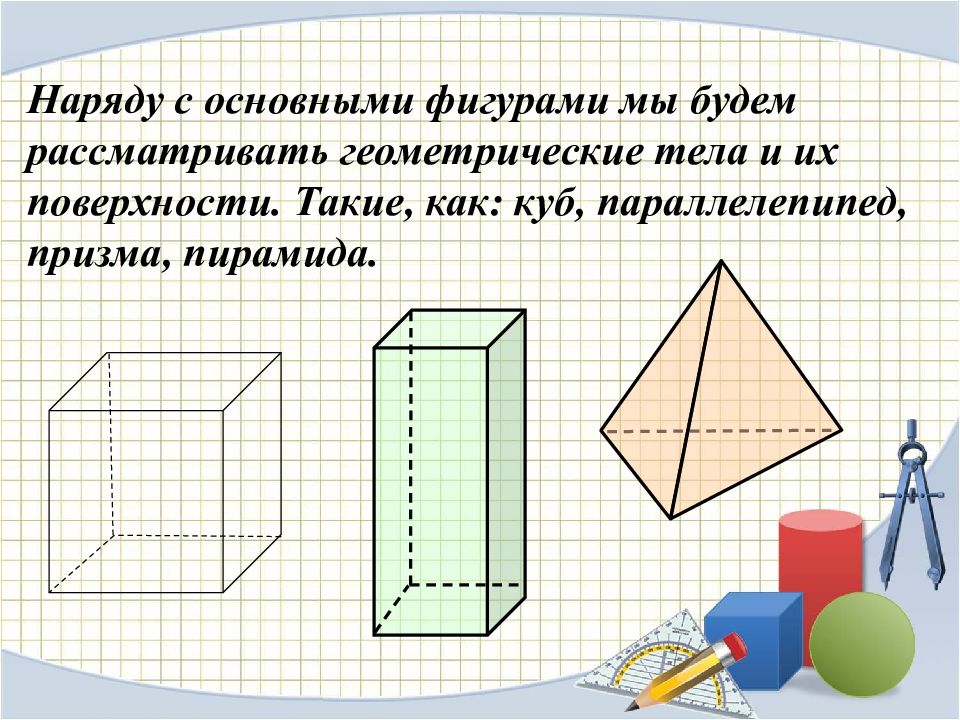
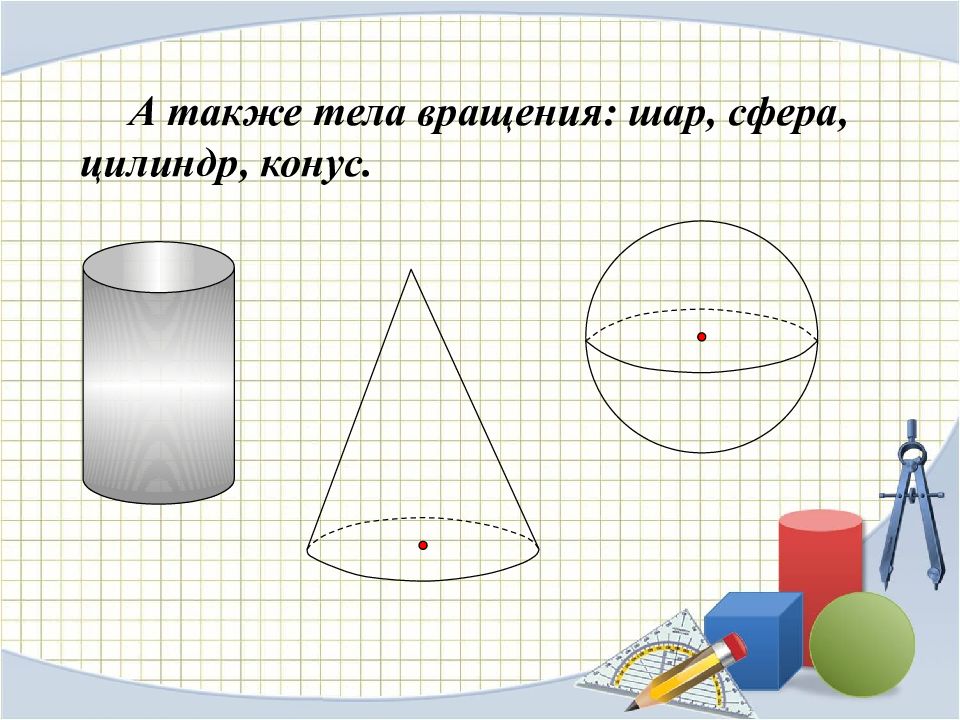
Наряду с основными фигурами мы будем рассматривать геометрические тела и их поверхности. Такие, как: куб, параллелепипед, призма, пирамида.
А также тела вращения: шар, сфера, цилиндр, конус.
В аксиомах стереометрии выражены основные свойства неопределяемых понятий: точки, прямой, плоскости и расстояния. Аксиома – это предложение не требующее доказательство.
Существует хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек. а α Для любой плоскости α и прямой а существует хотя бы одна не принадлежащая им точка.
Через любые две различные точки проходит одна и только одна прямая. А В Если прямые имеют по две общие точки, то эти прямые совпадают: а = b
Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости А В α
Аксиома 4 Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость. А В С Если плоскости имеют три общие точки, не принадлежащие одной прямой, то эти плоскости совпадают ( α = β )
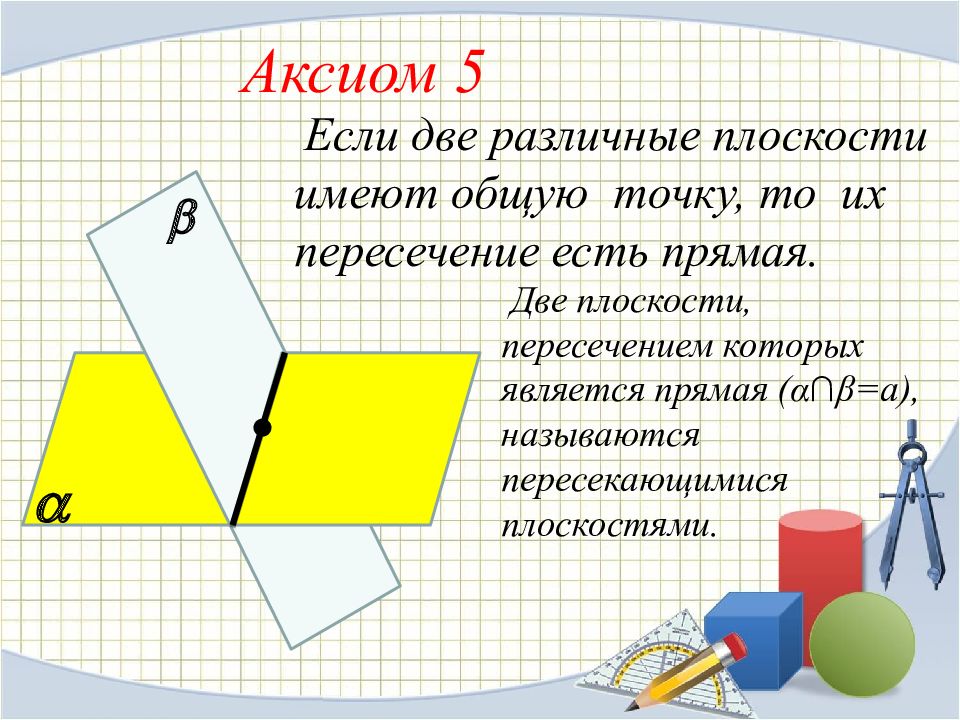
Аксиом 5 Если две различные плоскости имеют общую точку, то их пересечение есть прямая. Две плоскости, пересечением которых является прямая ( α∩β =а), называются пересекающимися плоскостями.
Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние |АВ| равно нулю в том и только в том случае, если точки А и В совпадают. А В А В
Расстояние от точки А до точки В равно расстоянию от точки В до точки А: |АВ|=|ВА| А В
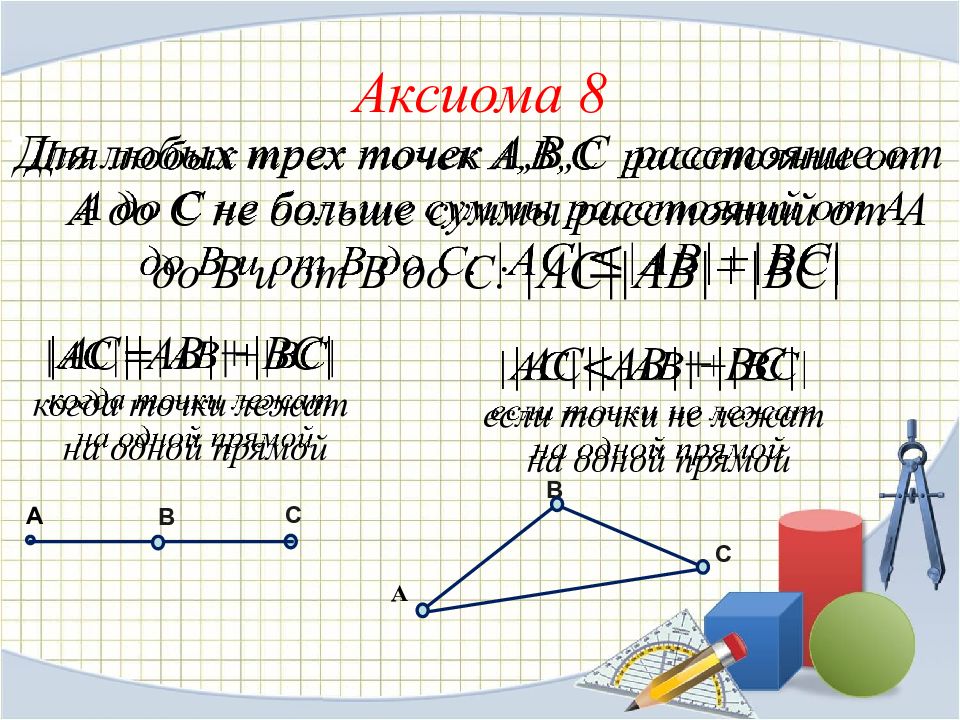
Для любых трех точек А,В,С расстояние от А до С не больше суммы расстояний от А до В и от В до С: |АС| |АВ|+|ВС| А В С |АС| |АВ|+|ВС| когда точки лежат на одной прямой |АС| |АВ|+|ВС| если точки не лежат на одной прямой А В С
Для каждой плоскости выполняются известные из планиметрии аксиомы порядка, подвижности плоскости и параллельных прямых Из принятых выше аксиом вытекает, что в каждой плоскости можно применять теоремы планиметрии. Например, в каждой плоскости выполняется теорема Пифагора, сумма углов любого треугольника равна 180°
Следствие 1 Через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость. М a Q P
1) 2) (АВС) = α – единст. (через три точки, не лежащие на одной прямой проведем плоскость α ) 3) В α ; С α ⇒ (ВС) α (ВС) α ( т.к. две точки прямой а принадлежат плоскости, то и вся прямая лежит в этой плоскости) 4) α - единственная (т. к. через три точки, не лежащие на одной прямой проходит только одна плоскость ) а А В С α Дано: а, Доказать : 1) α ; а ; А α 2) α - единственная
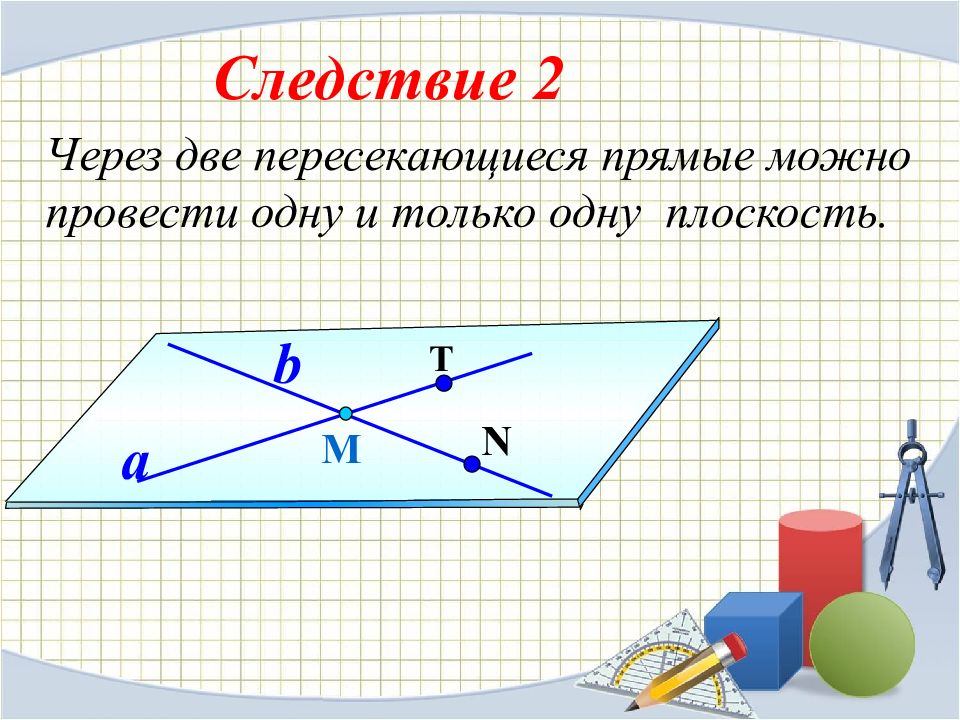
Через две пересекающиеся прямые можно провести одну и только одну плоскость. М a b N Следствие 2 Т
М М В 2) (АВС) = α – единст. ( через точку А и прямую b проведем плоскость α ) 3) А М (АМ) = α В М (ВМ) = α 4) α - единственная (т. к. через три точки, не лежащие на одной прямой проходит только одна плоскость) Доказательство Дано: а ∩ b= М Доказать : 1 ) α ;а 2 ) α - единственная а b M А В
b a α Определение: Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общей точки.
Следствие 3 Через две различные параллельные прямые можно провести только одну плоскость. b a
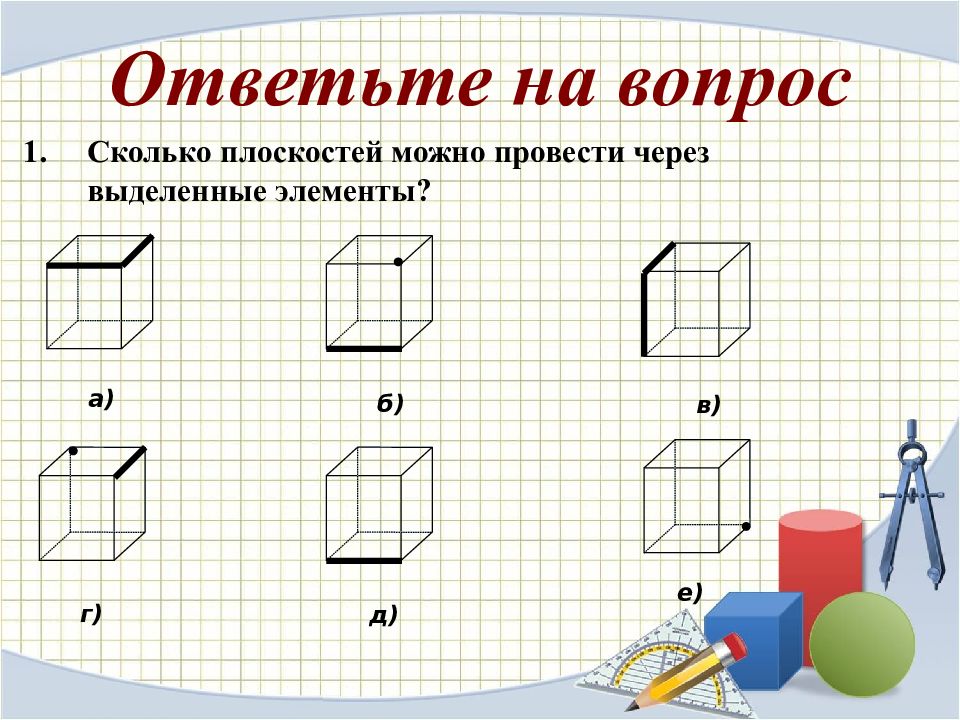
Сколько плоскостей можно провести через выделенные элементы? а) б) в) г) д) е) Ответьте на вопрос
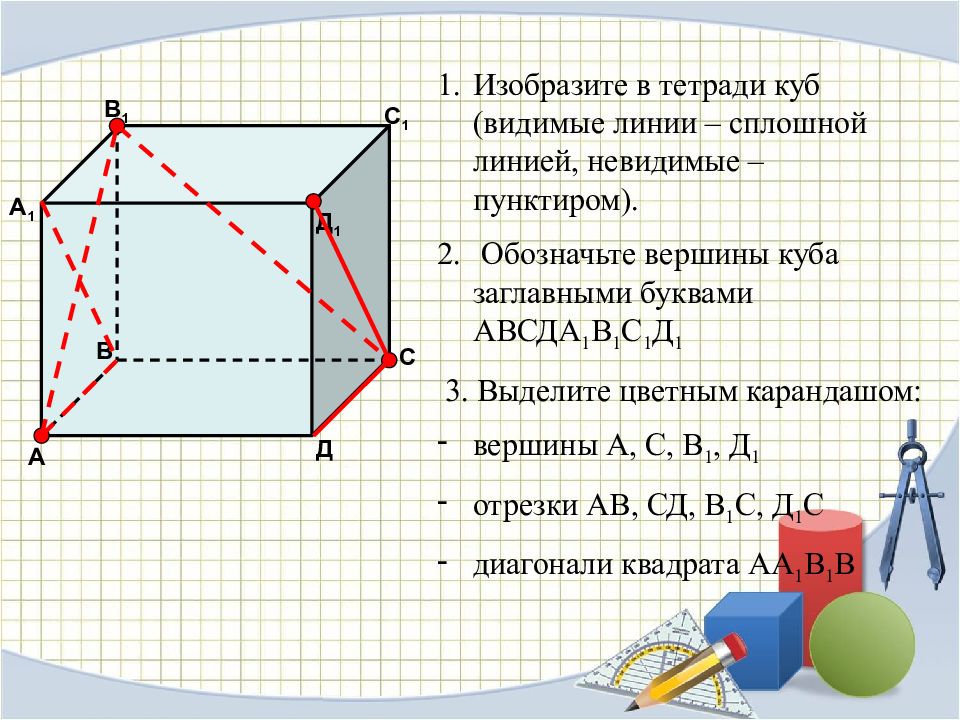
Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром). Обозначьте вершины куба заглавными буквами АВСДА 1 В 1 С 1 Д 1 3. Выделите цветным карандашом: вершины А, С, В 1, Д 1 отрезки АВ, СД, В 1 С, Д 1 С диагонали квадрата АА 1 В 1 В А В С Д Д 1 С 1 В 1 А 1
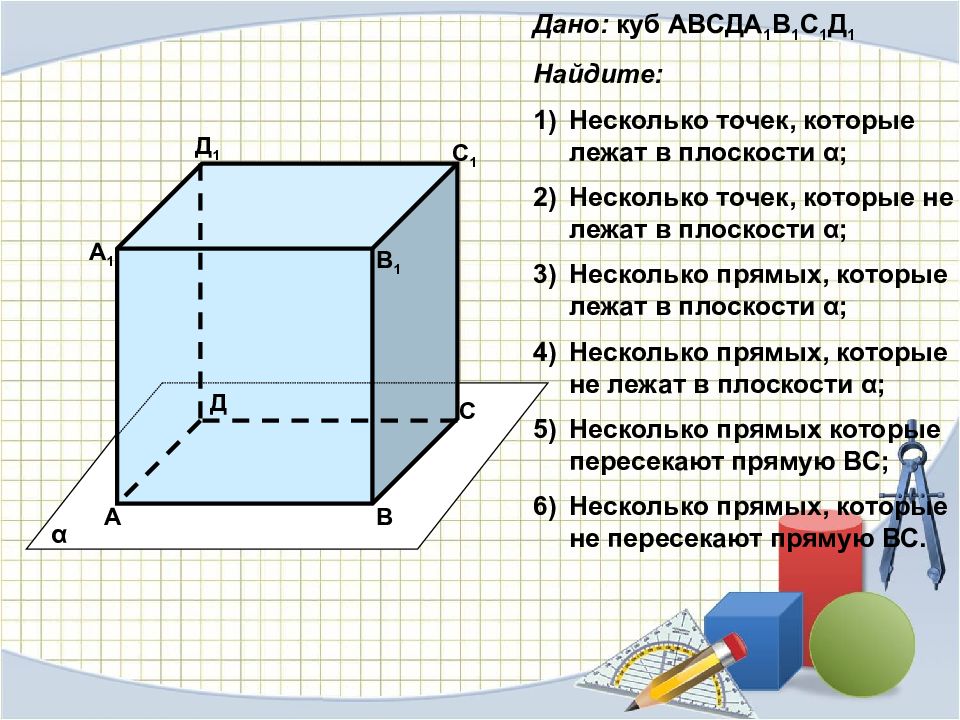
А В С Д А 1 В 1 С 1 Д 1 α Дано: куб АВСДА 1 В 1 С 1 Д 1 Найдите: Несколько точек, которые лежат в плоскости α ; Несколько точек, которые не лежат в плоскости α ; Несколько прямых, которые лежат в плоскости α ; Несколько прямых, которые не лежат в плоскости α ; Несколько прямых которые пересекают прямую ВС; Несколько прямых, которые не пересекают прямую ВС.
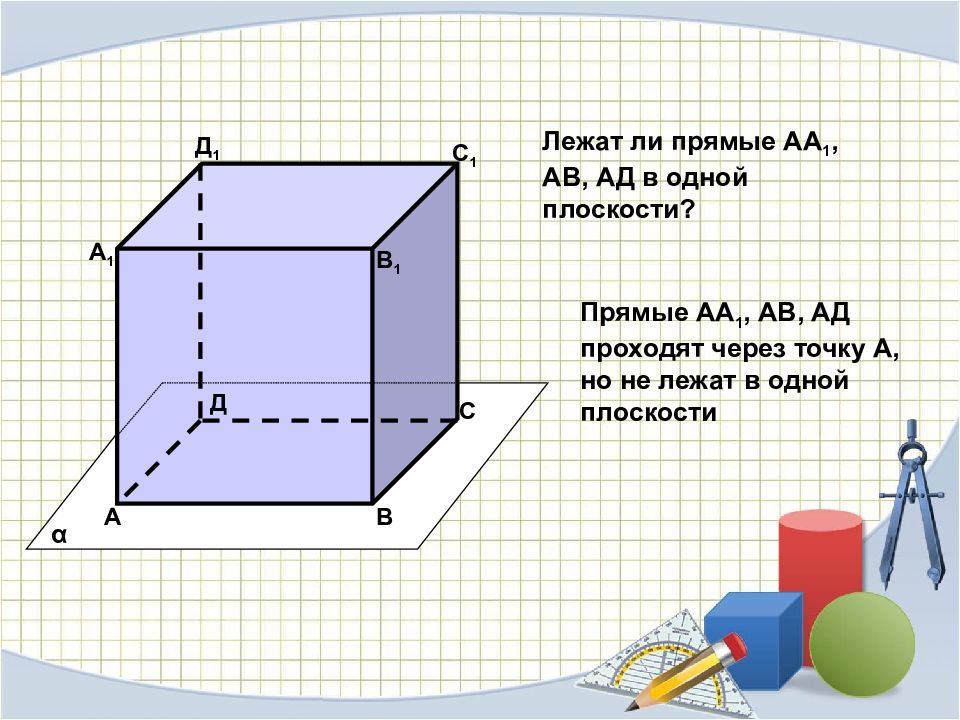
А В С Д А 1 В 1 С 1 Д 1 α Прямые АА 1, АВ, АД проходят через точку А, но не лежат в одной плоскости Лежат ли прямые АА 1, АВ, АД в одной плоскости?
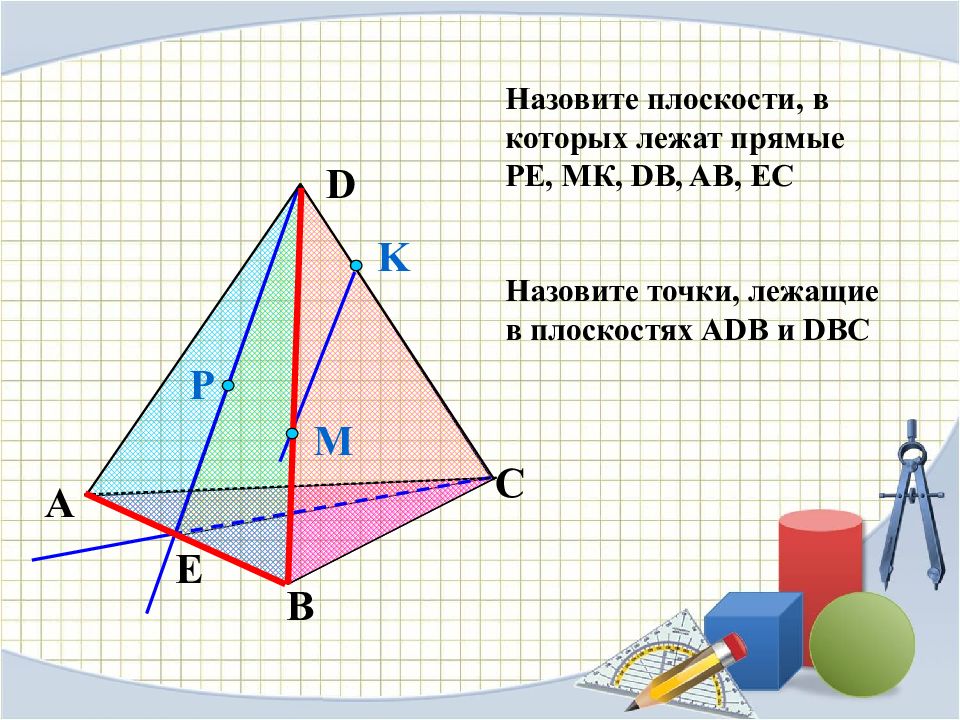
Назовите плоскости, в которых лежат прямые РЕ, МК, DB, AB, EC Назовите точки, лежащие в плоскостях А DB и DBC P E A B C D M K
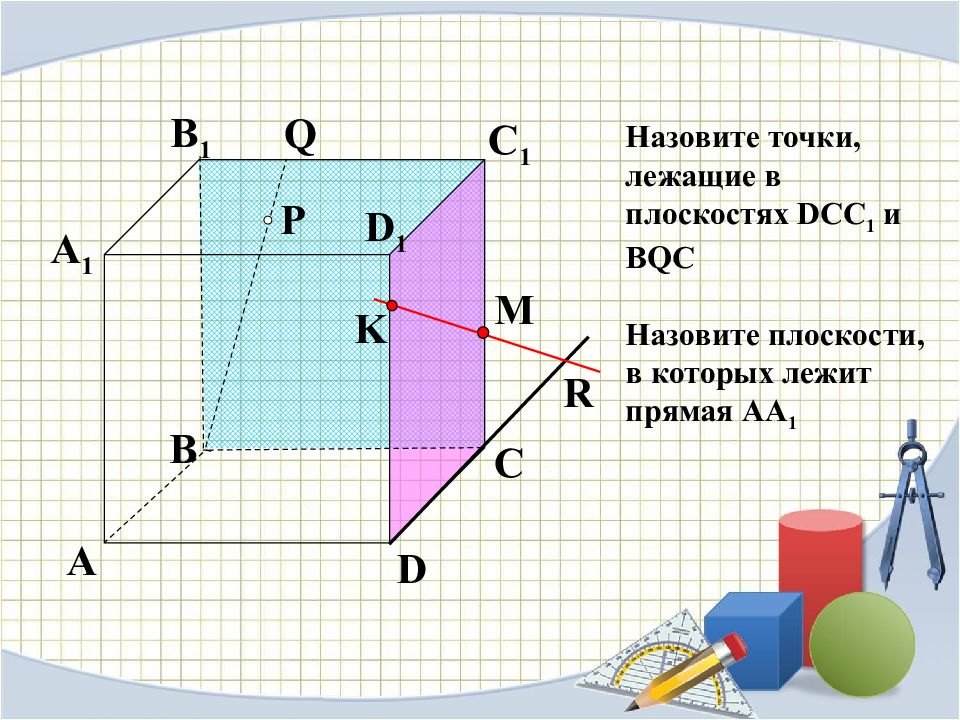
P A B C D A 1 B 1 C 1 D 1 R M K Q Назовите точки, лежащие в плоскостях DCC 1 и BQC Назовите плоскости, в которых лежит прямая АА 1
Задания для самостоятельной работы: Задание 1. Запишите с помощью символов взаимное расположение точек, прямых и плоскостей, изображенных на рисунке. P K A a b α
Задания для самостоятельной работы: Задание 2. Дан куб ABCDA 1 B 1 C 1 D 1. Запишите с помощью символики ответы на вопросы: а ) По какой прямой пересекаются плоскости: ( ABC) и (AA 1 D 1 ); (AA 1 B 1 ) и (AA 1 D ); (BB 1 C 1 ) и (CC 1 D 1 ). б ) Каким плоскостям принадлеж а т точки: A, C 1, D ? в) Принадлежит ли B 1 плоскости: 1) ( ABC) ; 2) (BB 1 C 1 ) ; 3) ( A 1 B 1 C 1 ) ? A 1 B A C 1 B 1 D 1 D C
