Аксиомы стереометрии 1 10 класс геометрия 1. Аксиомы стереометрии и их следствия.
Планиметрия Стереометрия Изучает свойства геометрических фигур на плоскости Изучает свойства фигур в пространстве В переводе с греческого слово «геометрия» означает «землемерие» « гео » – по-гречески земля, « метрео » – мерить Слово «стереометрия» происходит от греческих слов « стереос » объемный, пространственный, « метрео » – мерить Изучение нового материала.
Планиметрия Стереометрия Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности. Например, многогранники. Куб, параллелепипед, призма, пирамида. Тела вращения. Шар, сфера, цилиндр, конус. Основные фигуры: точка, прямая Основные фигуры: точка, прямая, плоскость Другие фигуры: отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n- угольники, круг, окружность, дуга и др. Изучение нового материала.
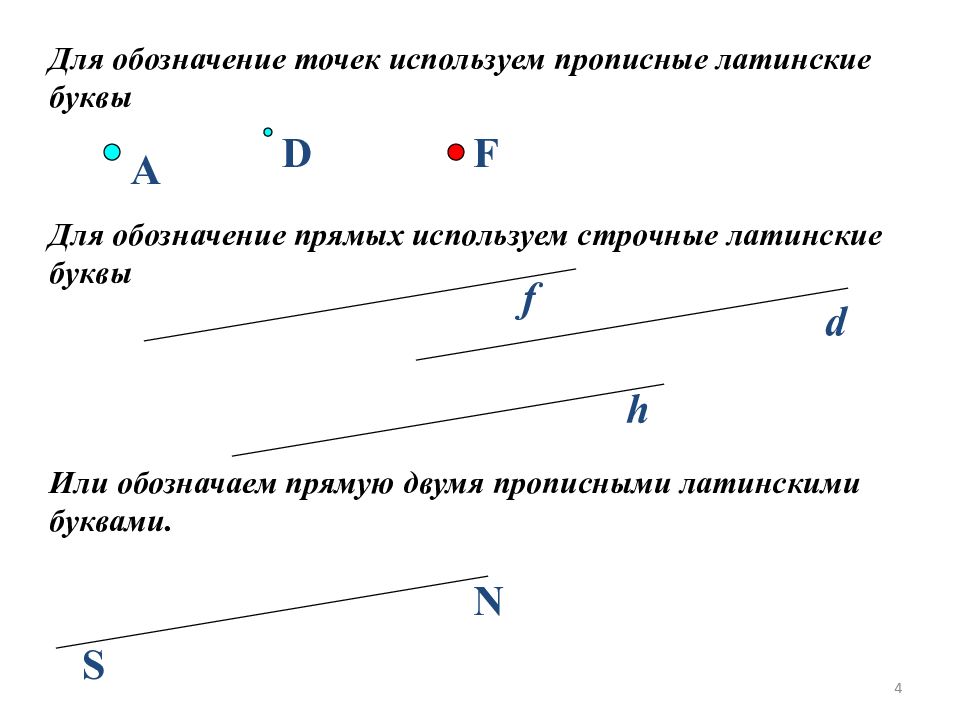
Для обозначение точек используем прописные латинские буквы A D F Для обозначение прямых используем строчные латинские буквы f d h Или обозначаем прямую двумя прописными латинскими буквами. S N 4
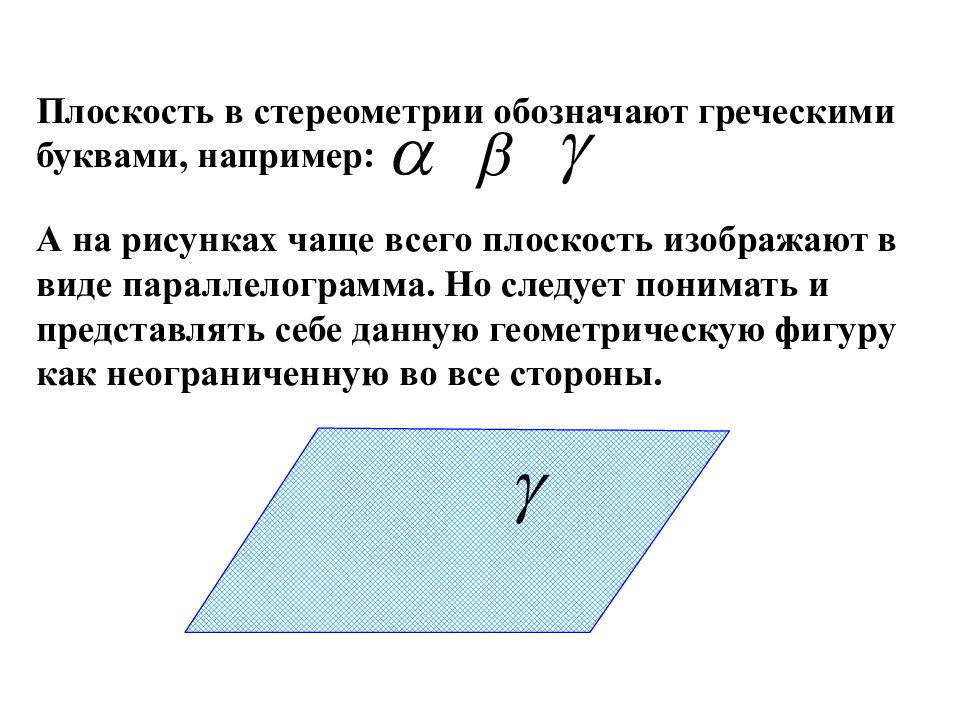
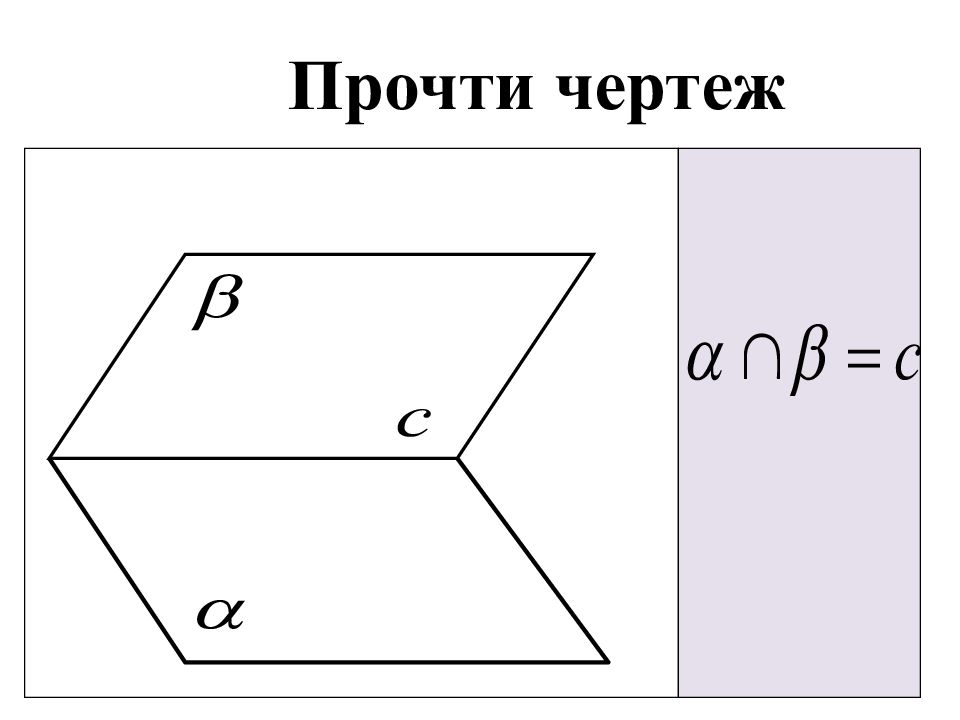
Плоскость в стереометрии обозначают греческими буквами, например: А на рисунках чаще всего плоскость изображают в виде параллелограмма. Но следует понимать и представлять себе данную геометрическую фигуру как неограниченную во все стороны.
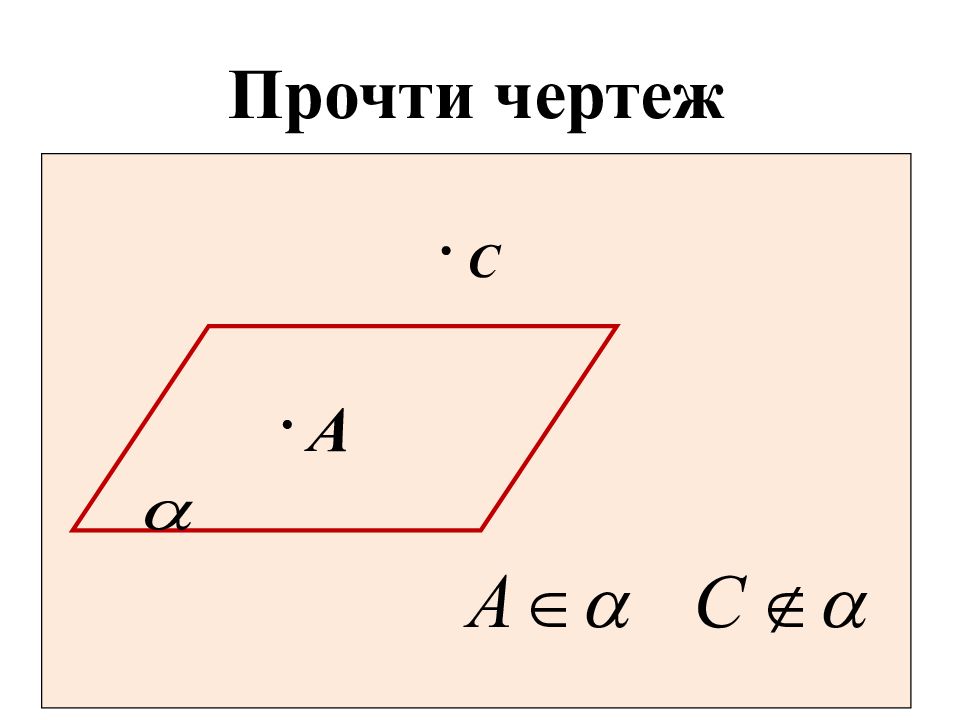
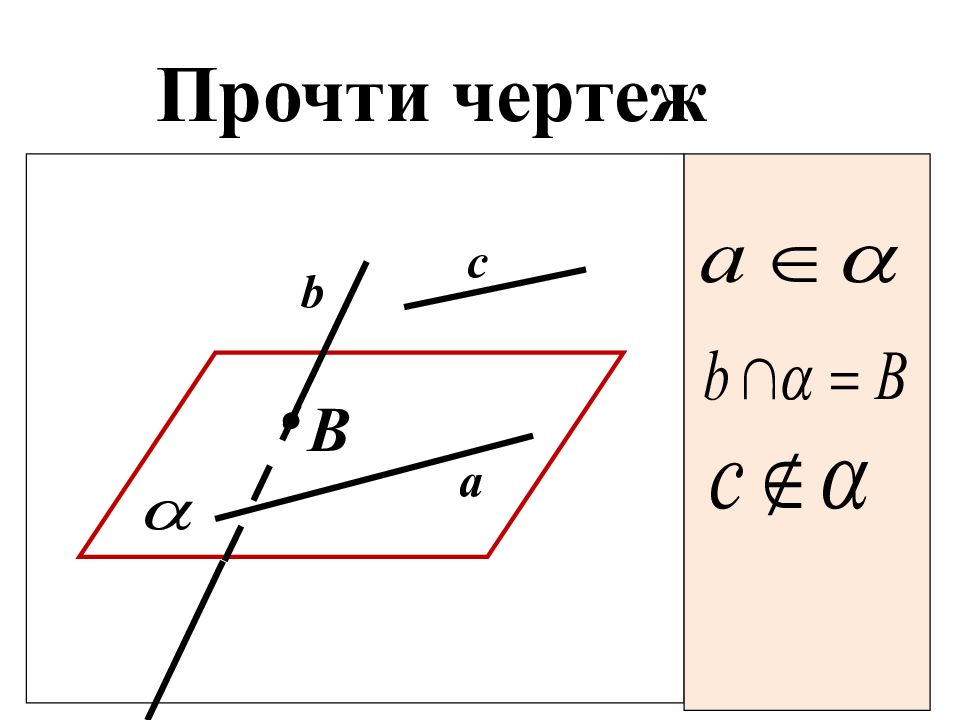
Точка A принадлежит прямой a Точка B не принадлежит прямой a Точка A принадлежит плоскости Прямая a лежит в плоскости Прямая b не лежит в плоскости Точка B не принадлежит плоскости Прямая b пересекает плоскость в точке A Плоскости и пересекаются по прямой c
A С
B c b a
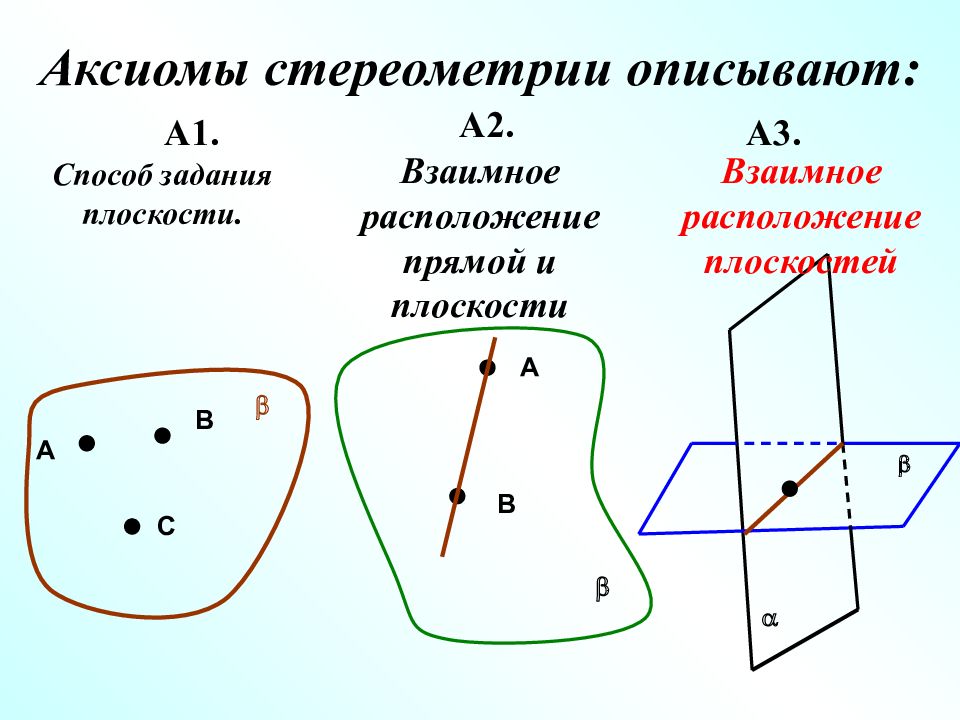
Аксиомы стереометрии описывают: А1. А2. А3. А В С b Способ задания плоскости. b А В Взаимное расположение прямой и плоскости a b Взаимное расположение плоскостей
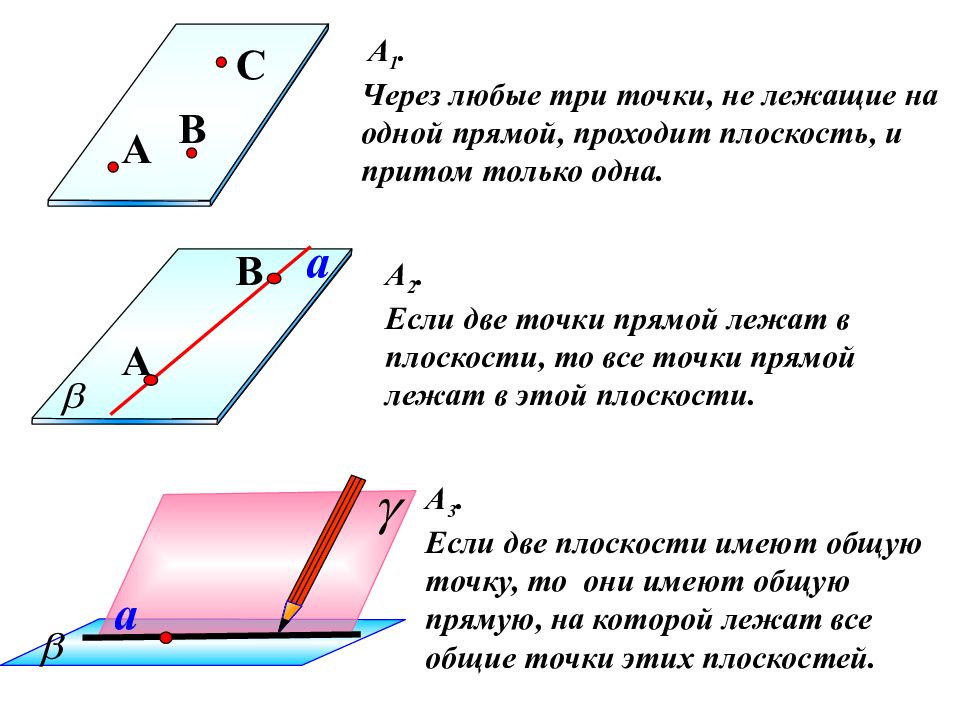
А 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. C A B А 2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. a A B a А 3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
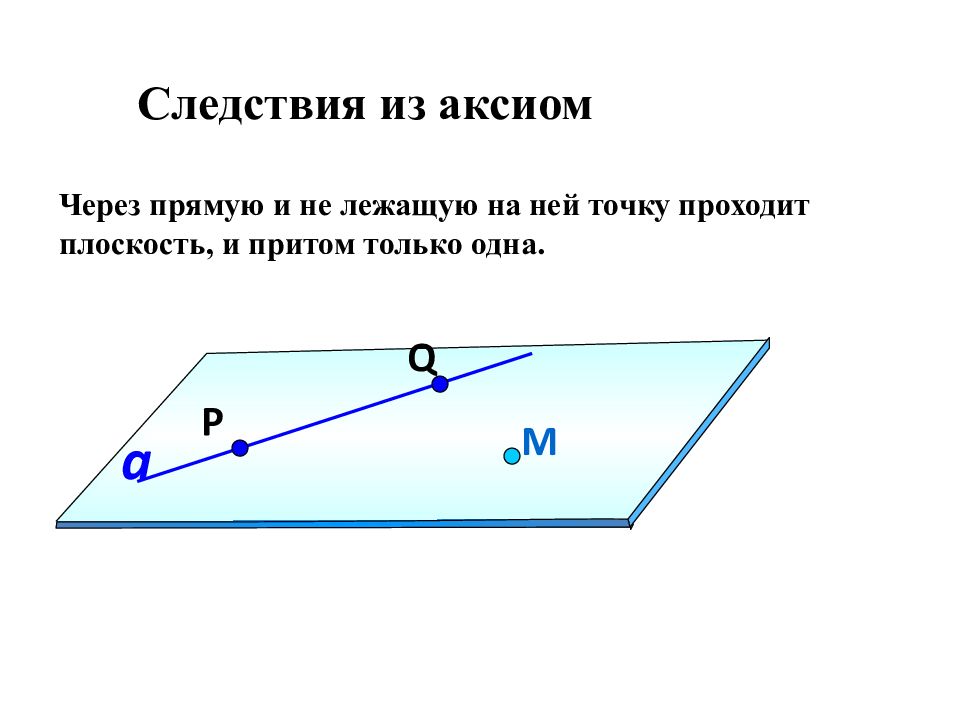
Следствия из аксиом Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. М a Q P
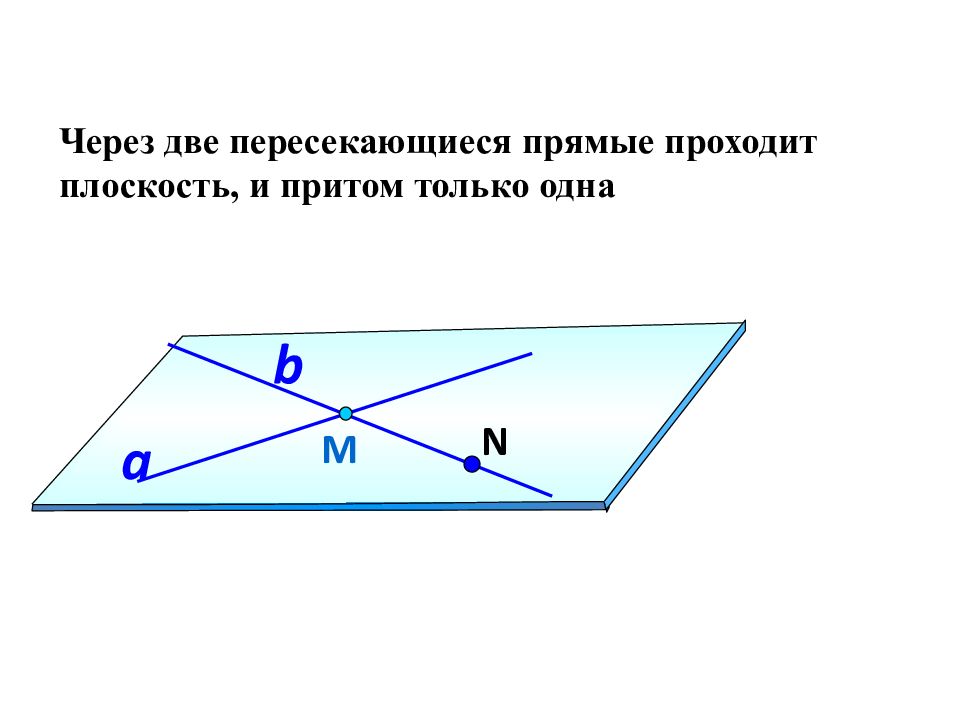
Через две пересекающиеся прямые проходит плоскость, и притом только одна М a b N
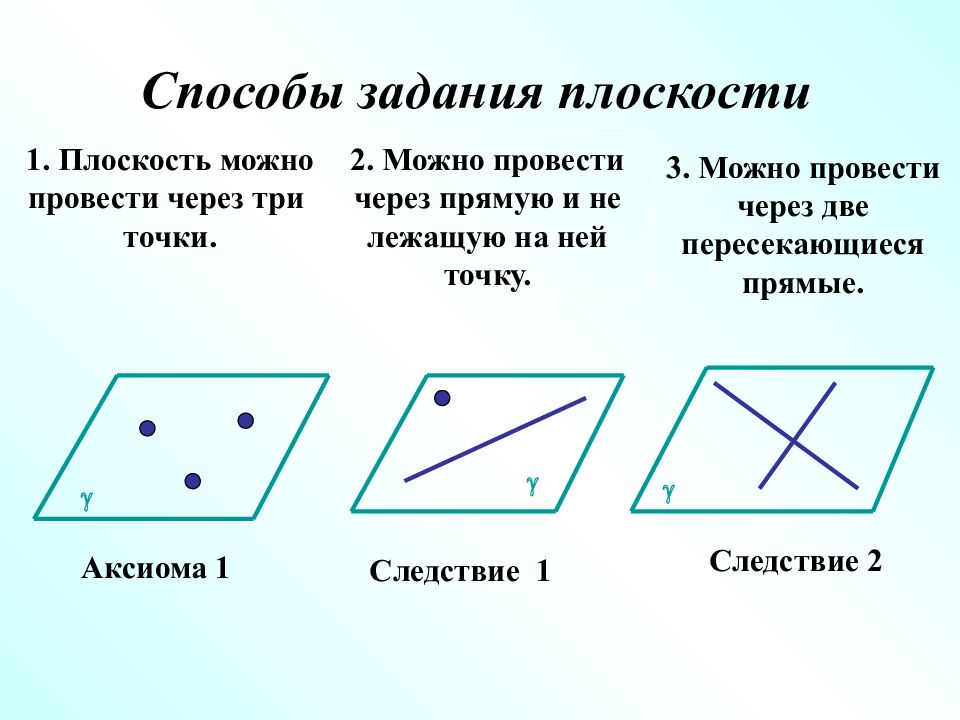
Способы задания плоскости g 1. Плоскость можно провести через три точки. g 2. Можно провести через прямую и не лежащую на ней точку. Аксиома 1 Следствие 1 g Следствие 2 3. Можно провести через две пересекающиеся прямые.
Любые три точки лежат в одной плоскости. Любые четыре точки лежат в одной плоскости. Любые четыре точки не лежат в одной плоскости. Через любые три точки проходит плоскость и при том только одна. Если прямая пересекает 2 стороны треугольника, то она лежит в плоскости треугольника. Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника. Если прямые не пересекаются, то они параллельны. Если плоскости не пересекаются, то они параллельны. В стереометрии мы будем рассматривать ситуации, задающие различные расположения в пространстве основных фигур относительно друг друга ДА ДА ДА НЕТ НЕТ НЕТ НЕТ НЕТ
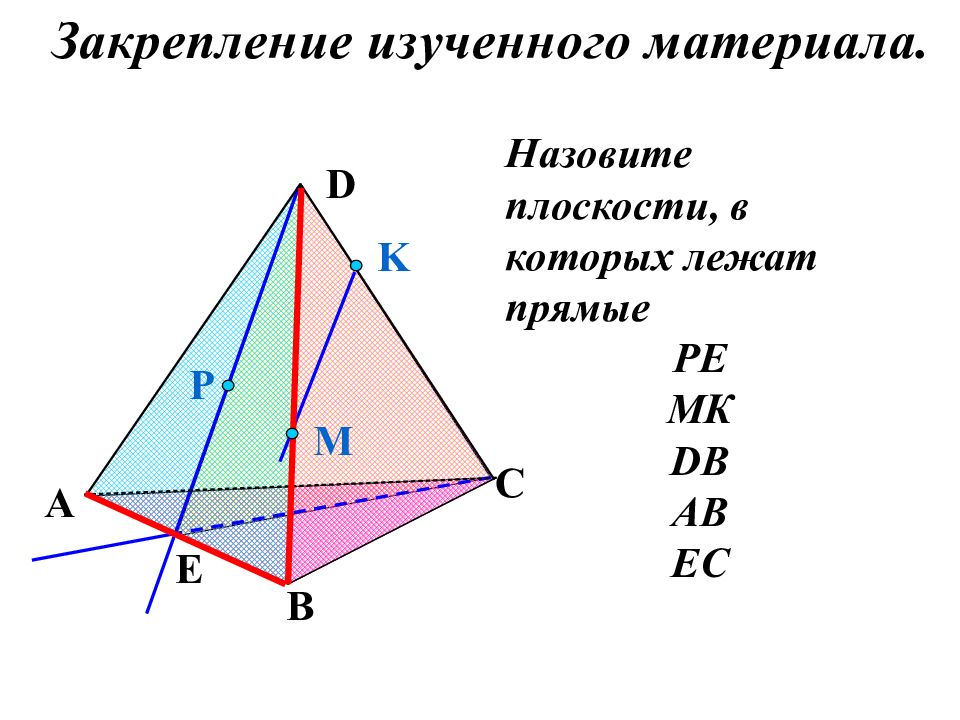
Назовите плоскости, в которых лежат прямые РЕ МК DB AB EC P E A B C D M K Закрепление изученного материала.
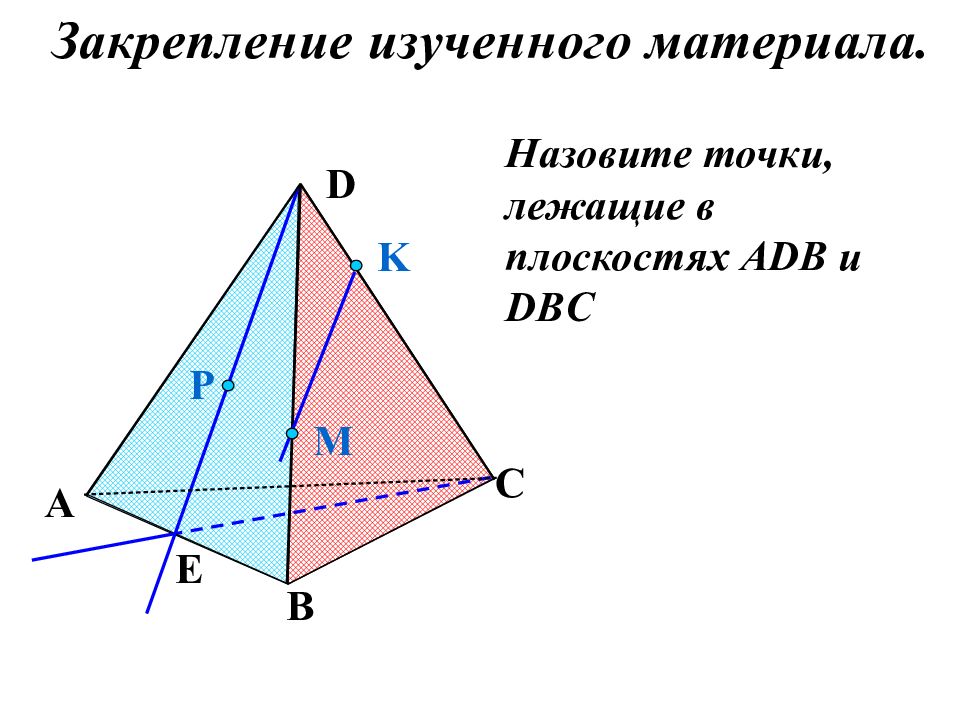
Назовите точки, лежащие в плоскостях А DB и DBC P E A B C D M K Закрепление изученного материала.
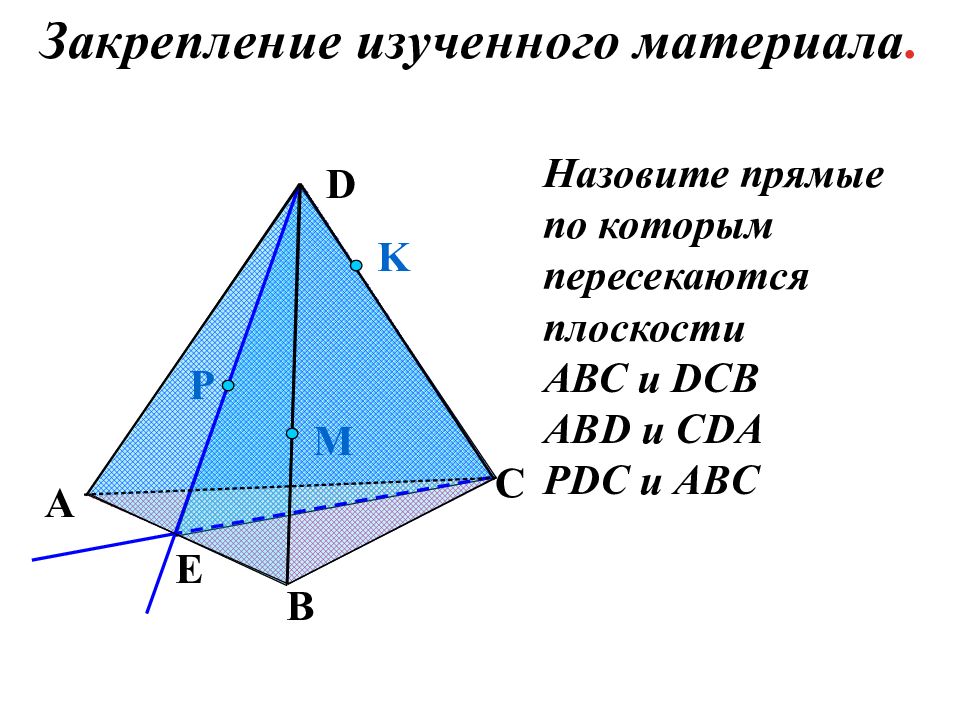
Назовите прямые по которым пересекаются плоскости АВС и DCB ABD и CDA PDC и ABC P E A B C D M K Закрепление изученного материала.
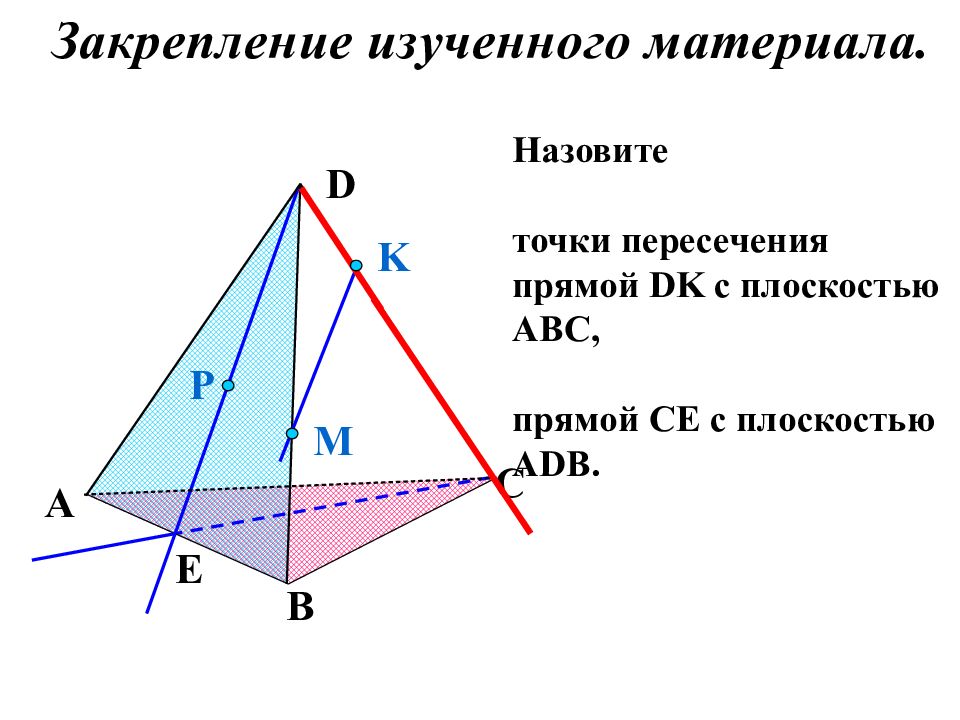
Назовите точки пересечения прямой DK с плоскостью АВС, прямой СЕ с плоскостью А DB. P E A B C D M K Закрепление изученного материала.
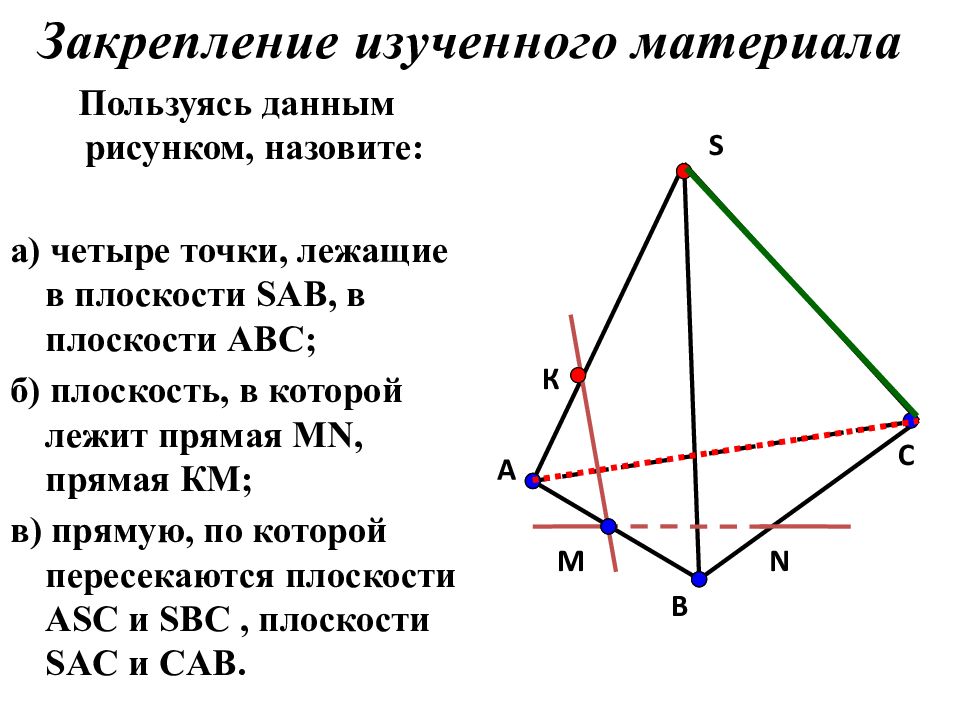
Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость, в которой лежит прямая MN, прямая КМ; в) прямую, по которой пересекаются плоскости ASC и SBC, плоскости SAC и CAB. К А В М S N C Закрепление изученного материала
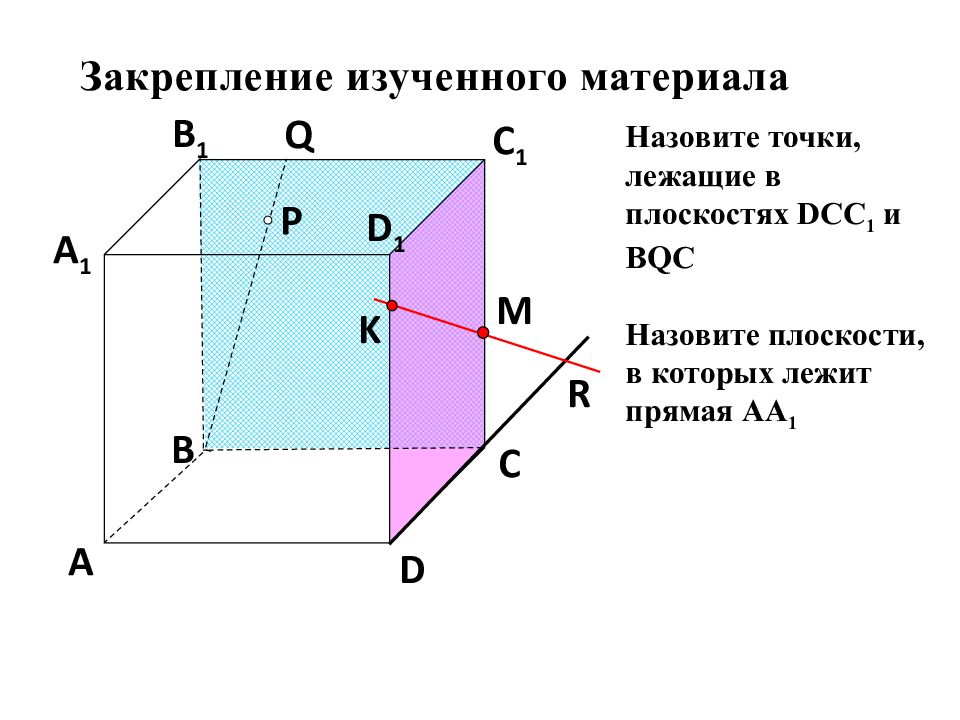
P A B C D A 1 B 1 C 1 D 1 R M K Q Назовите точки, лежащие в плоскостях DCC 1 и BQC Назовите плоскости, в которых лежит прямая АА 1 Закрепление изученного материала
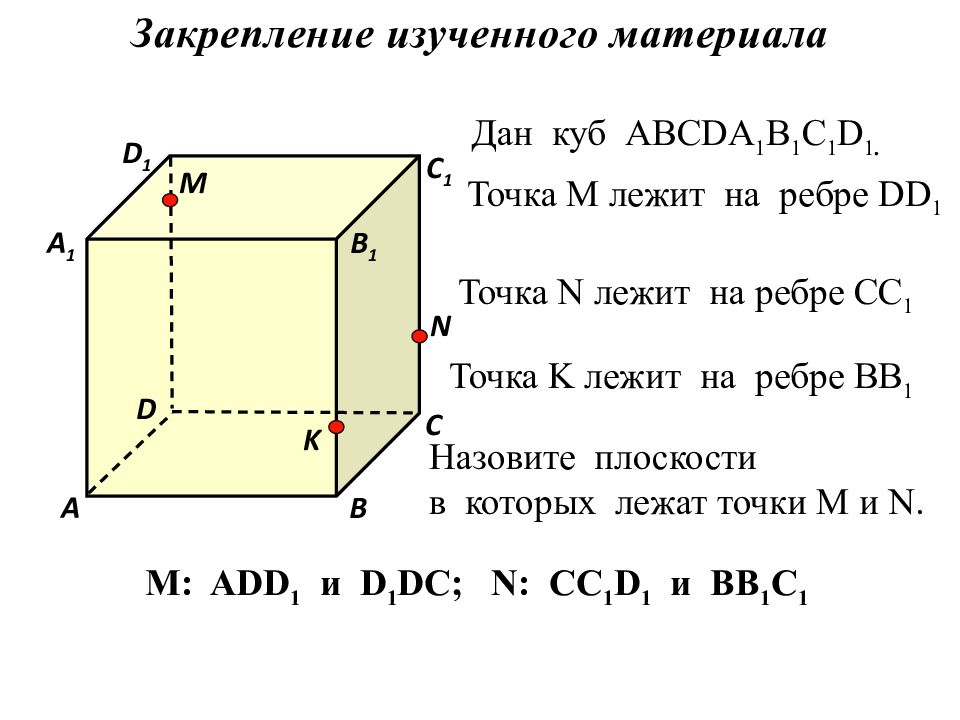
Дан куб АВС DA 1 B 1 C 1 D 1. Точка М лежит на ребре DD 1 Точка N лежит на ребре CC 1 Точка K лежит на ребре BB 1 D 1 В А 1 А D С 1 С В 1 M N K Назовите плоскости в которых лежат точки М и N. M: ADD 1 и D 1 DC; N: CC 1 D 1 и BB 1 C 1 Закрепление изученного материала
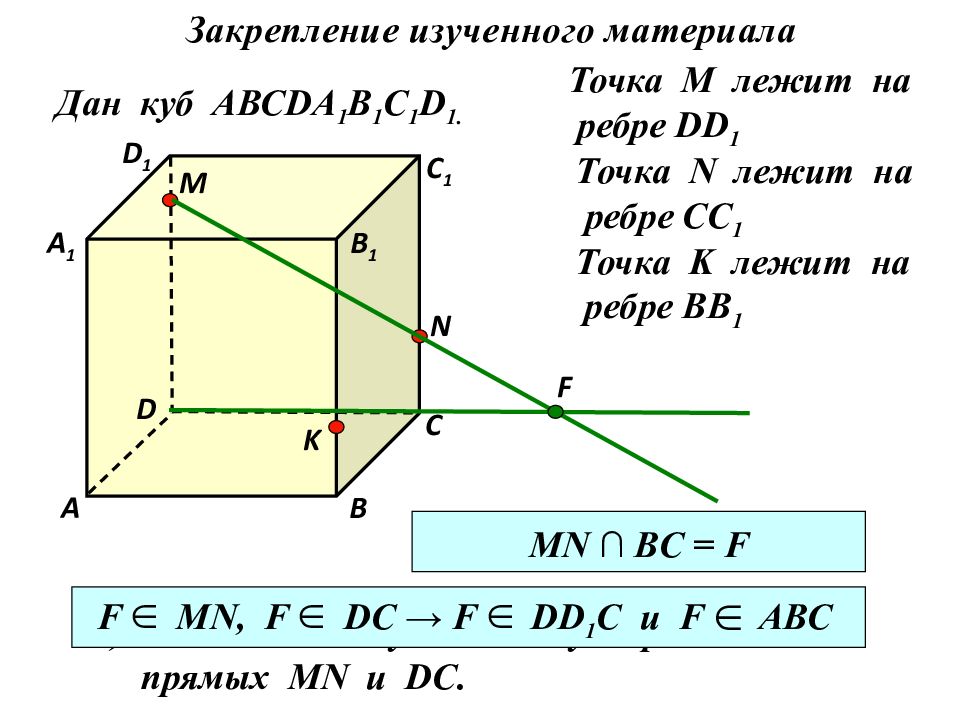
Дан куб АВС DA 1 B 1 C 1 D 1. D 1 D С 1 С В 1 В А 1 А M Точка М лежит на ребре DD 1 N Точка N лежит на ребре CC 1 K Точка K лежит на ребре BB 1 2) Найдите точку F – точку пересечения прямых MN и D С. F Каким свойством обладает точка F? MN ∩ BC = F F MN, F DC → F DD 1 C и F АВС Закрепление изученного материала
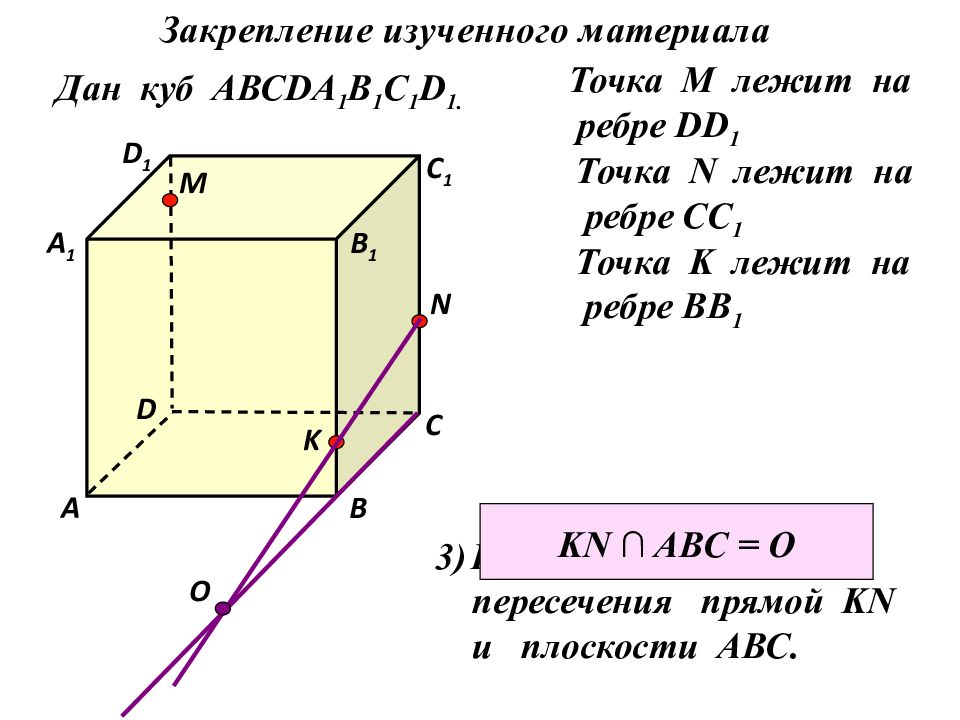
Дан куб АВС DA 1 B 1 C 1 D 1. D 1 D С 1 С В 1 В А 1 А M Точка М лежит на ребре DD 1 N Точка N лежит на ребре CC 1 K Точка K лежит на ребре BB 1 Найдите точку пересечения прямой KN и плоскости АВС. О KN ∩ ABC = O Закрепление изученного материала
