Первый слайд презентации
Пәні : Сынып : Тоқсан : Алгебра 9 I Астана қаласы әкімдігінің « Әдістемелік орталығы »
Слайд 2
Бүгінгі сабақта : екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін шешуді үйренесіз. Екі айнымалысы бар сызықтық емес теңсіздіктер жүйелері
Слайд 3
Бір немесе бірнеше теңсіздігі сызықтық емес болатын екі айнымалысы бар сызықтық емес теңсіздіктер жүйесін қарастырайық. екі айнымалысы бар сызықтық емес теңсіздіктер жүйелері Мысалы:
Слайд 4
x және у айнымалылардың мәндері болатын мына сандар жұбының қайсысы теңсіздіктер жүйесінің шешімі болады: 1 ) Шешуі: болады болады болмайды болмайды Мысал: Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесінің шешімі деп жүйенің әрбір теңсіздігін дұрыс сандық теңсіздікке айналдыратын сандар жұбын атайды.
Слайд 5
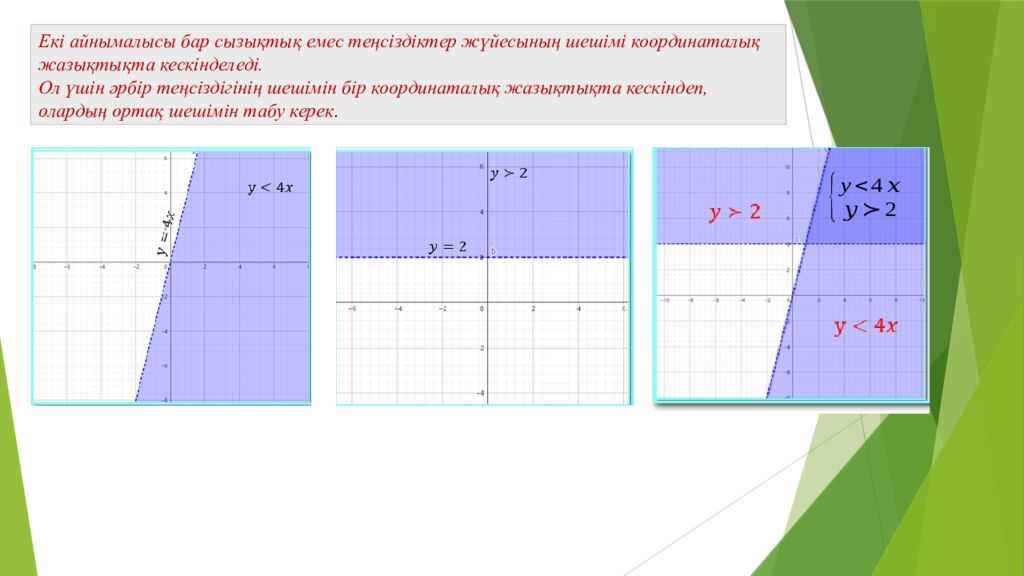
теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз. Мысал: Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесының шешімі координаталық жазықтықта кескінделеді. Ол үшін әрбір теңсіздігінің шешімін бір координаталық жазықтықта кескіндеп, олардың ортақ шешімін табу керек.
Слайд 6
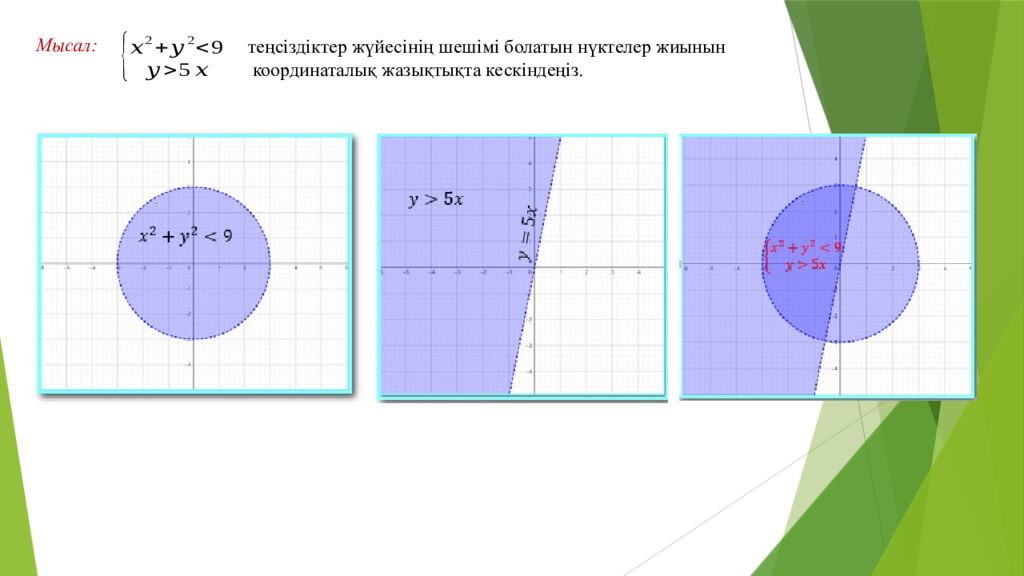
теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз. Мысал:
Слайд 7
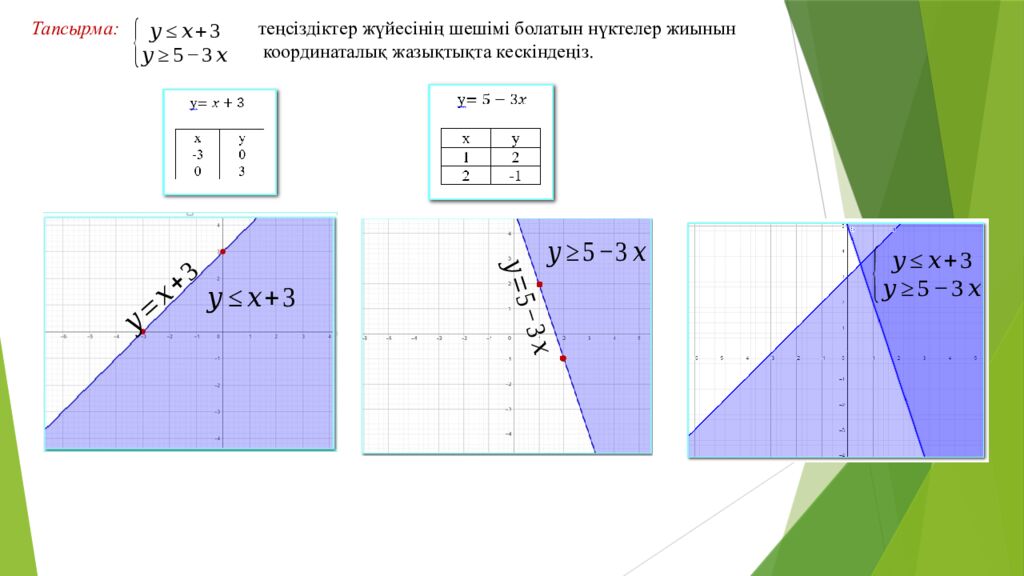
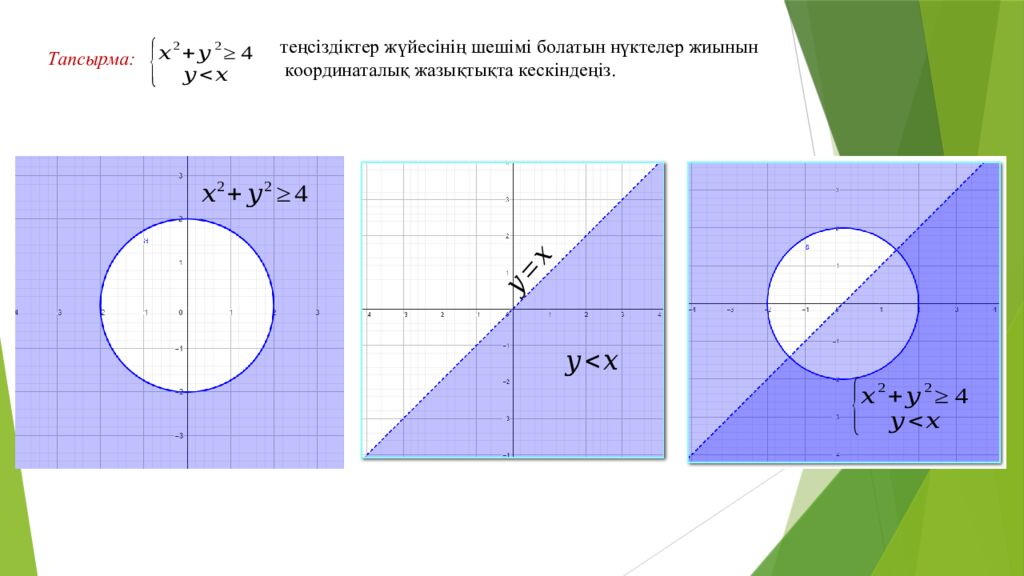
Тапсырма: теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз.
Слайд 8
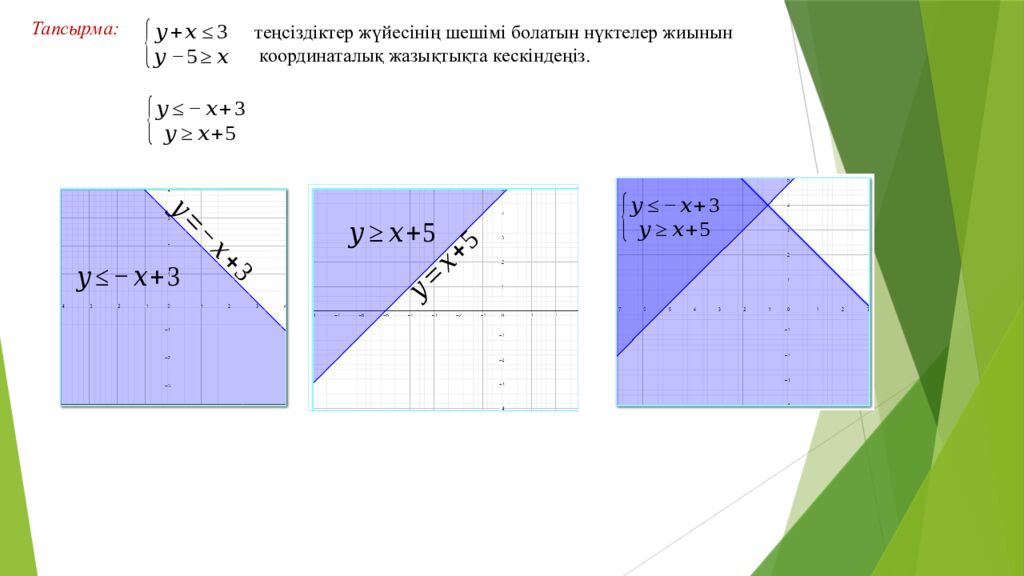
теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз. Тапсырма:
Слайд 9
теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз. Тапсырма:
Слайд 10
Екі айнымалысы бар сызықтық емес теңсіздіктер жүйесінің шешімі болмауы мүмкін бе? Жауабыңызды негіздеңіз. теңсіздіктер жүйесінің шешімі болатын нүктелер жиынын координаталық жазықтықта кескіндеңіз. Жауабы : шешімі жоқ Бекіту: