Первый слайд презентации: Платоновы тела, 10 класс
Правильные выпуклые многогранники Платоновы тела, 10 класс
Слайд 2
«Математика владеет не только истиной, но и высокой красотой – красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства». Бертран Рассел
Слайд 3
Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления.
Слайд 4
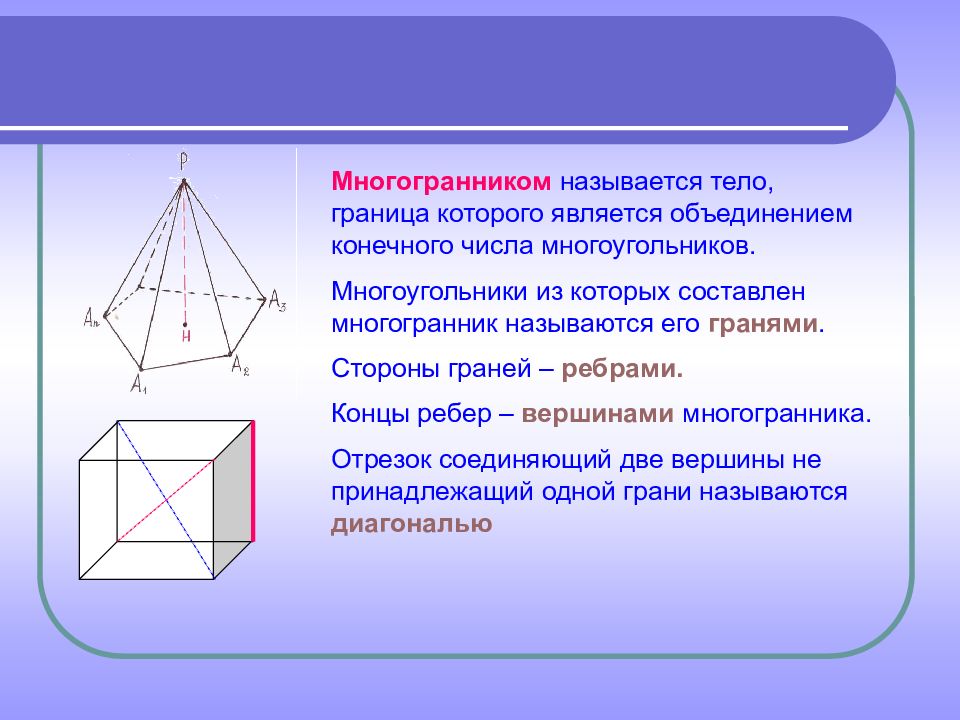
Многогранником называется тело, граница которого является объединением конечного числа многоугольников. Многоугольники из которых составлен многогранник называются его гранями. Стороны граней – ребрами. Концы ребер – вершинами многогранника. Отрезок соединяющий две вершины не принадлежащий одной грани называются диагональю
Слайд 5
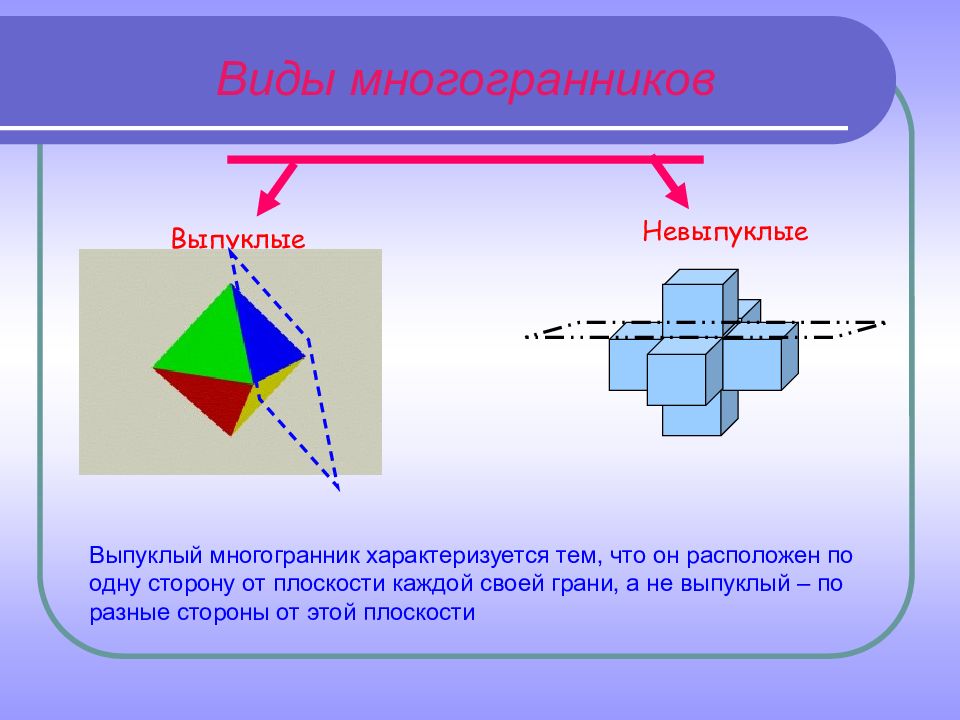
Виды многогранников Выпуклые Невыпуклые Выпуклый многогранник характеризуется тем, что он расположен по одну сторону от плоскости каждой своей грани, а не выпуклый – по разные стороны от этой плоскости
Слайд 6
Букет Пуансо Букет Платона Букет Архимеда Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед
Слайд 7
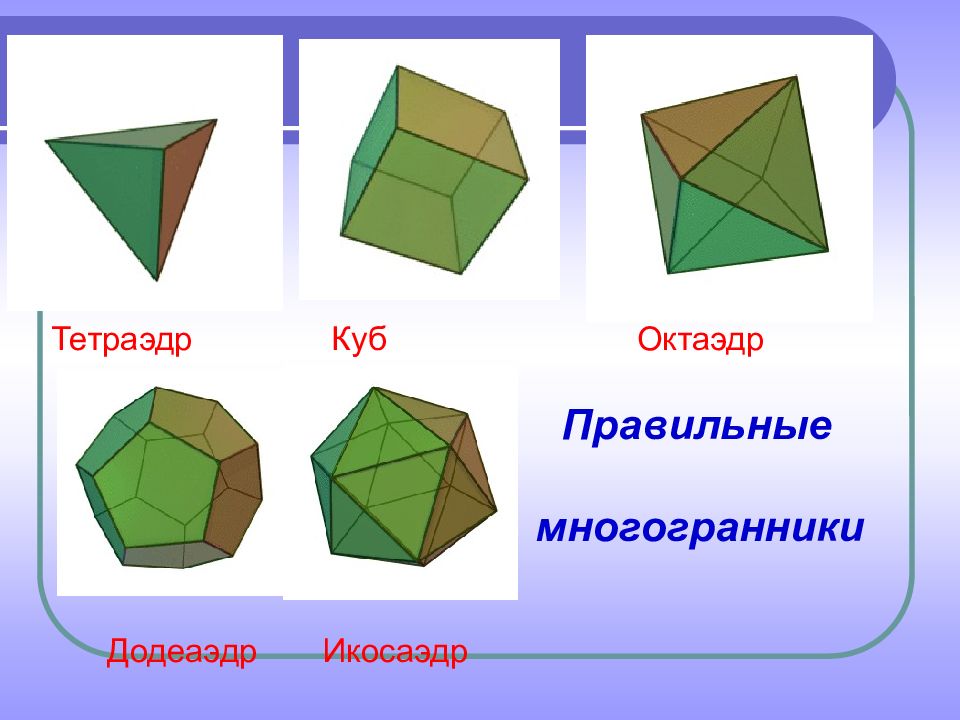
Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук. Л. Кэрролл
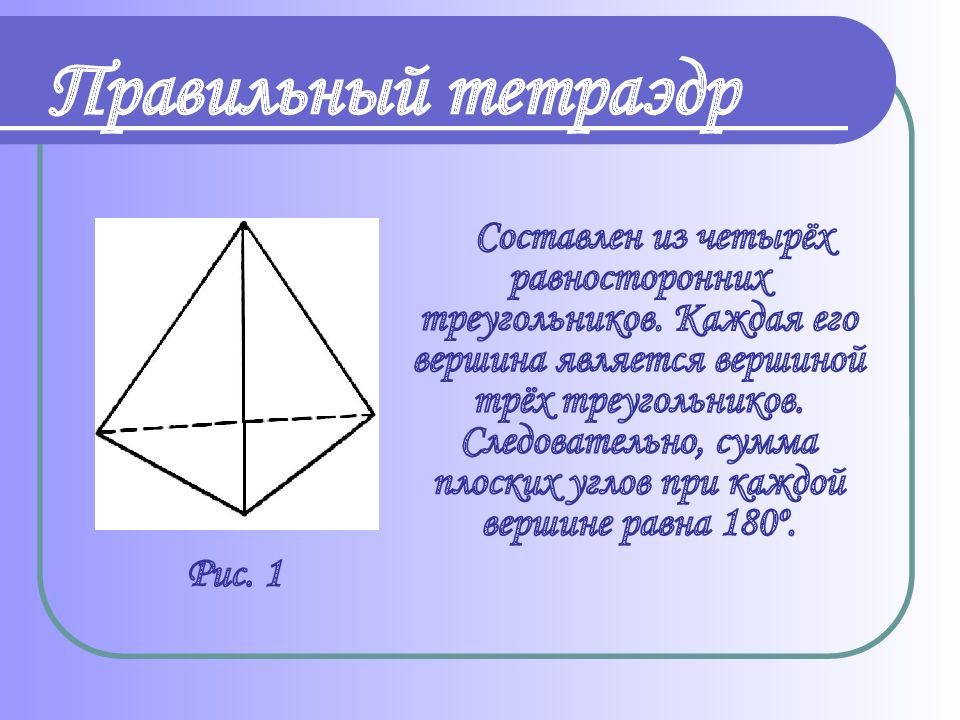
Слайд 10: Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180 º. Рис. 1
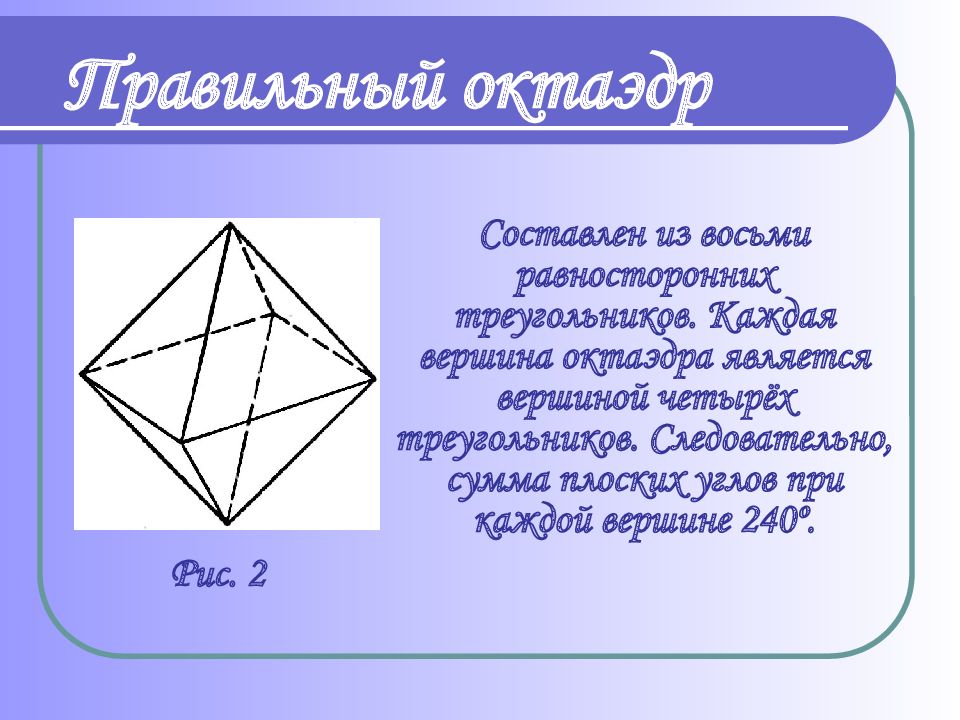
Слайд 11
Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов при каждой вершине 240 º. Правильный октаэдр Рис. 2
Слайд 12
Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300 º. Рис. 3
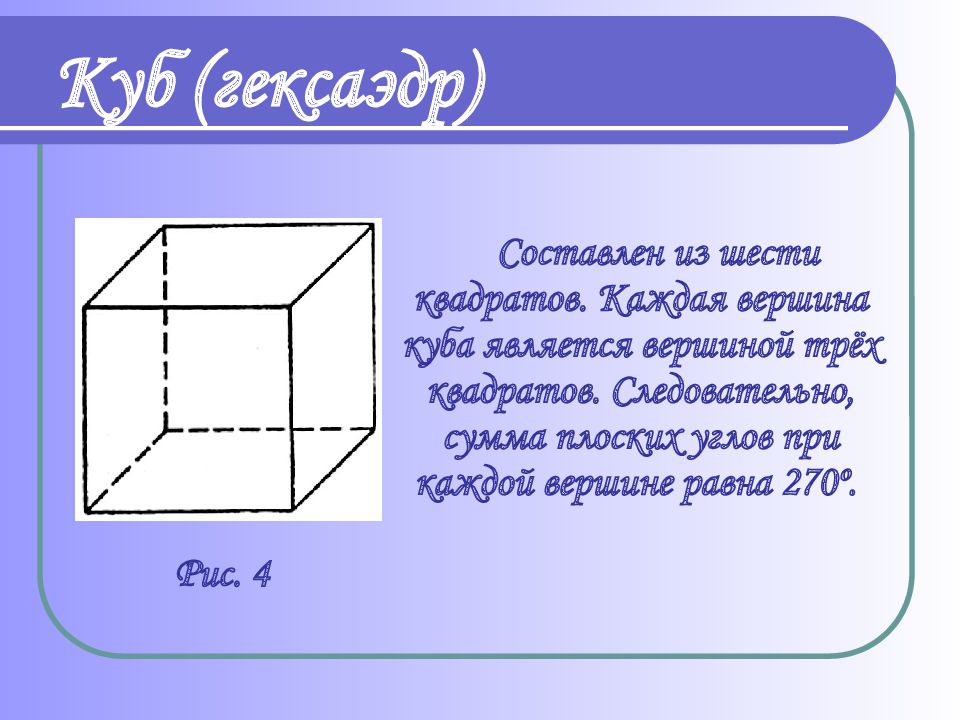
Слайд 13: Куб (гексаэдр)
Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270 º. Куб (гексаэдр) Рис. 4
Слайд 14
Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324 º. Рис. 5
Слайд 15: Названия многогранников
пришли из Древней Греции, в них указывается число граней: «эдра» грань; «тетра» 4; «гекса» 6; «окта» 8; «икоса» 20; «додека» 12. Названия многогранников
Слайд 17
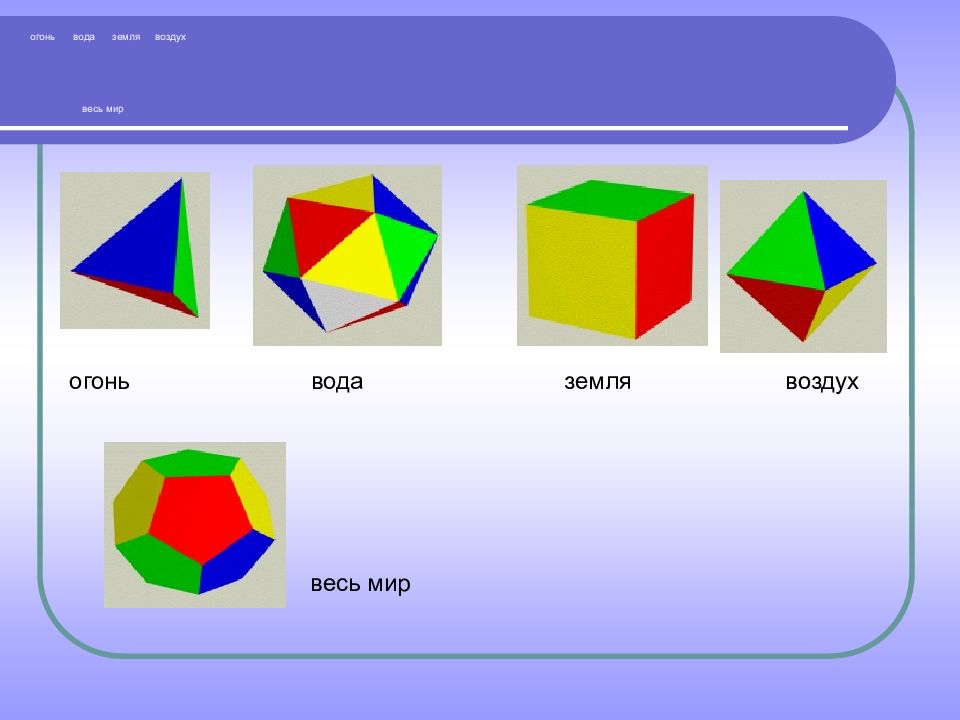
Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.). Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени. Икосаэдр – как самый обтекаемый – воду. Куб – самая устойчивая из фигур – землю. Октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Это была одна из первых попыток ввести в науку идею систематизации. Правильные многогранники в философской картине мира Платона
Слайд 19
«Космический кубок» Кеплера Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца. Модель Солнечной системы И. Кеплера Рис. 6
Слайд 20
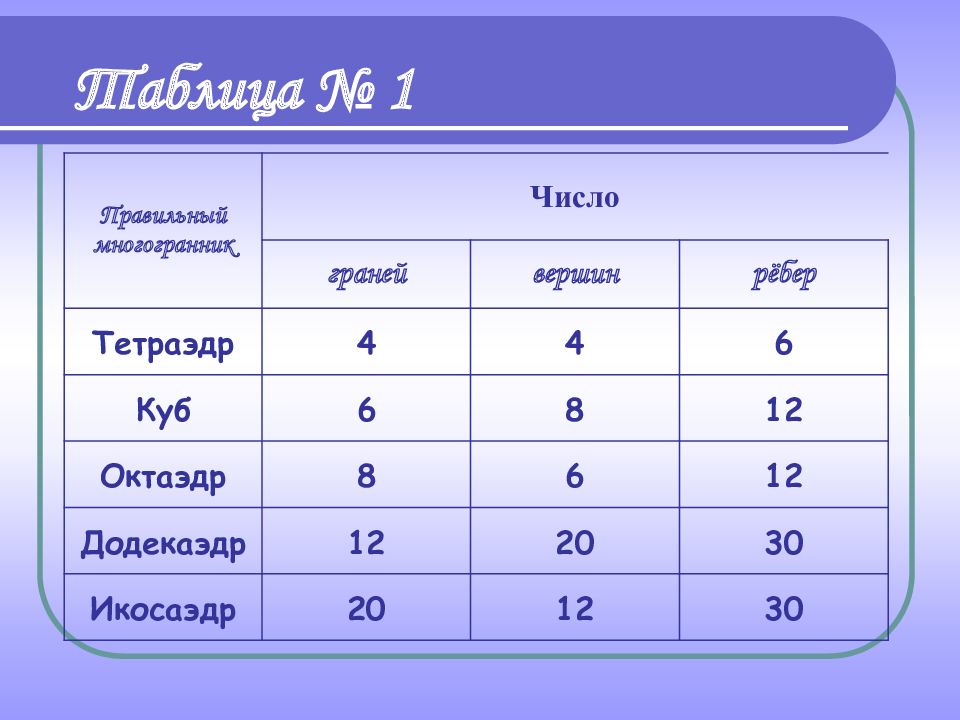
Правильный многогранник Число граней вершин рёбер Тетраэдр 4 4 6 Куб 6 8 12 Октаэдр 8 6 12 Додекаэдр 12 20 30 Икосаэдр 20 12 30 Таблица № 1
Слайд 21
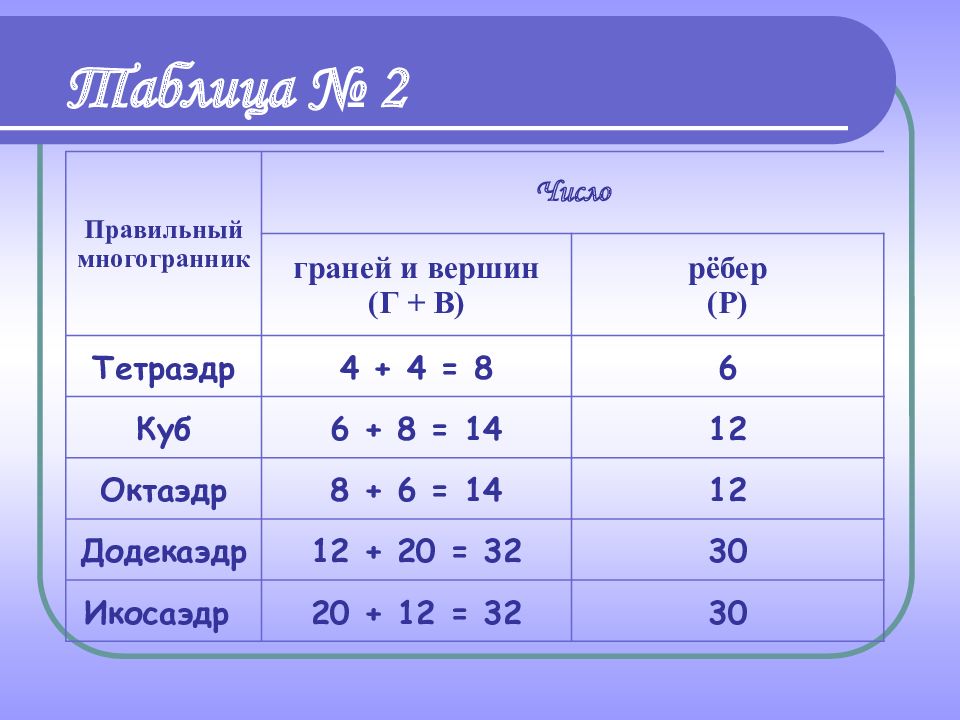
Правильный многогранник Число граней и вершин (Г + В) рёбер (Р) Тетраэдр 4 + 4 = 8 6 Куб 6 + 8 = 14 12 Октаэдр 8 + 6 = 14 12 Додекаэдр 12 + 20 = 32 30 Икосаэдр 20 + 12 = 32 30 Таблица № 2
Слайд 22
Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2 Формула Эйлера Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В Р = 2
Слайд 23
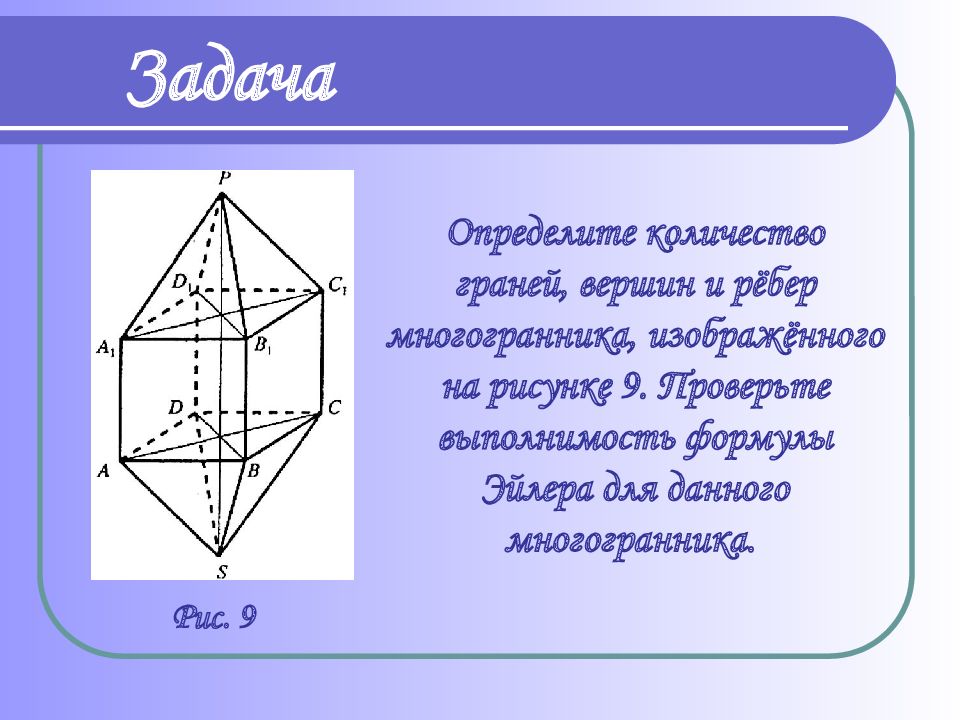
Определите количество граней, вершин и рёбер многогранника, изображённого на рисунке 9. Проверьте выполнимость формулы Эйлера для данного многогранника. Задача Рис. 9
Слайд 25
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.
Слайд 26: Икосаэдро- додекаэдровая структура Земли
…Ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра. Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки… В. Макаров, В. Морозов.
Слайд 28
Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр. Два из них знал И. Кеплер (1571 – 1630 гг.). В 1812 году французский математик О. Коши доказал, что кроме пяти « платоновых тел» и четырех «тел Пуансо » больше нет правильных многогранников.
Слайд 29: БОЛЬШОЙ ИКОСАЭДР
Грани большого икосаэдра - пересекающиеся треугольники. Вершины большого икосаэдра совпадают с вершинами описанного икосаэдра. Большой икосаэдр был впервые описан Луи Пуансо в 1809 г.
Слайд 30: МАЛЫЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР
Грани малого звездчатого додекаэдра - пентаграммы, как и у большого звездчатого додекаэдра. У каждой вершины соединяются пять граней. Вершины малого звездчатого додекаэдра совпадают с вершинами описанного икосаэдра. Малый звездчатый додекаэдр был впервые описан Кеплером в 1619 г.
Слайд 31: БОЛЬШОЙ ДОДЕКАЭДР
Грани большого додекаэдра - пересекающиеся пятиугольники. Вершины большого додекаэдра совпадают с вершинами описанного икосаэдра. Большой додекаэдр был впервые описан Луи Пуансо в 1809 г.
Слайд 32: БОЛЬШОЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР
Грани большого звездчатого додекаэдра - пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра. Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г.
Слайд 33
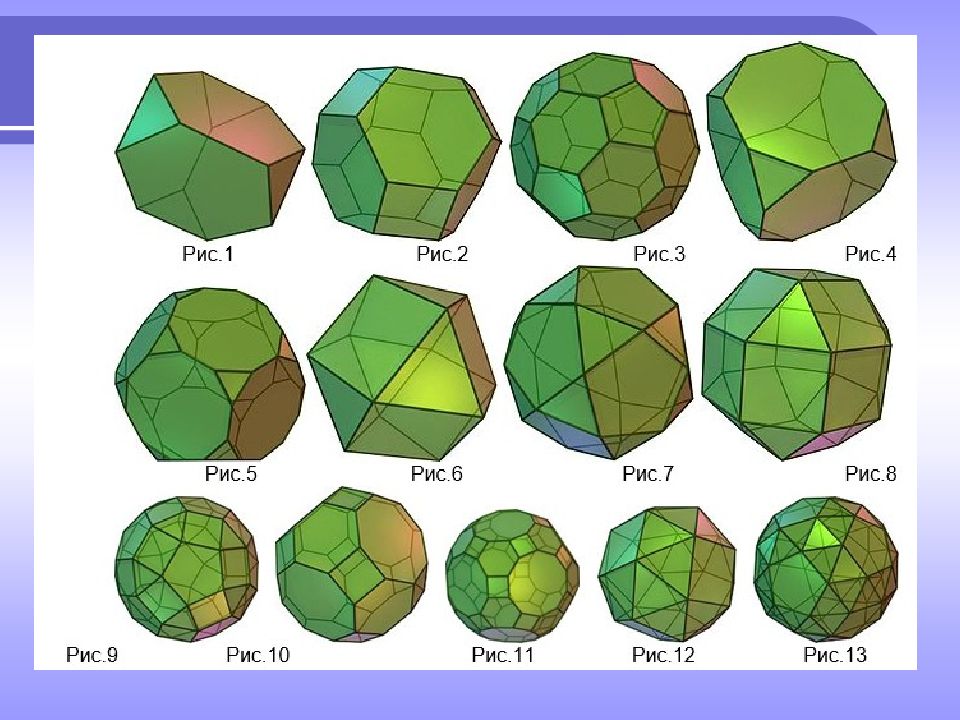
Кроме правильных, существует тринадцать многогранников, которые впервые открыл и описал Архимед – это тела Архимеда. Все многогранные углы у них равны, а грани – правильные многоугольники разных видов. (этим они отличаются от платоновых тел). Причем в каждой вершине сходится одно и тоже количество граней.
Слайд 34
Древнегреческий ученый, математик, физик, механик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда практически важных изобретений Архимед около 287 – 212 гг. до нашей эры Открытие тринадцати полуправильных выпуклых многогранников приписывается Архимеду, впервые перечислившего их в недошедшей до нас работе. Ссылки на эту работу имеются в трудах математика Паппа.
Слайд 36
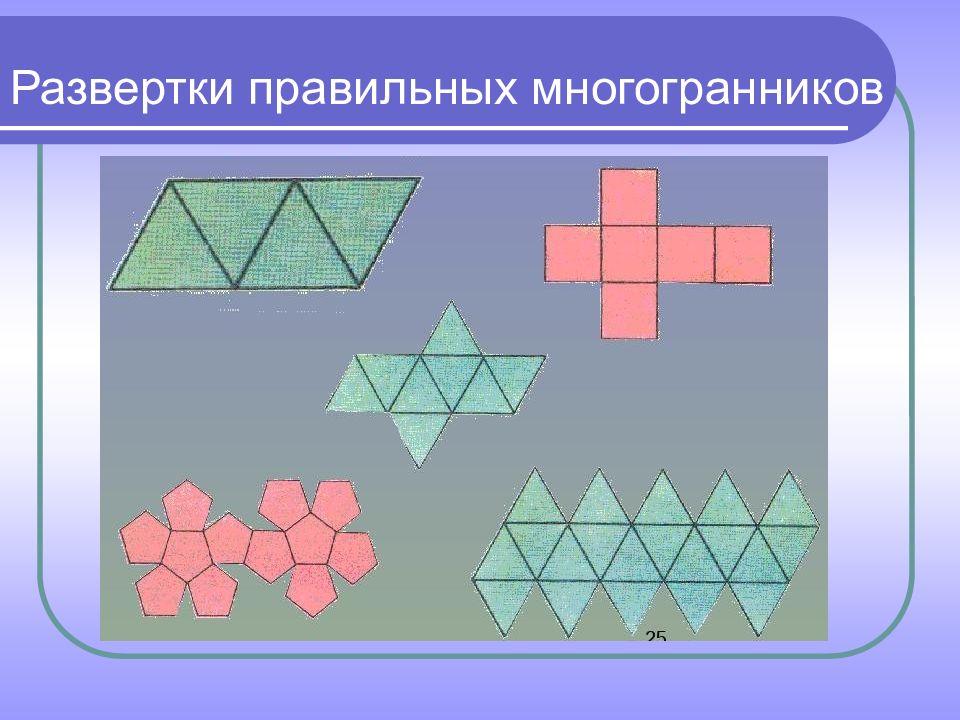
Первую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения: усеченный тетраэдр, усеченный куб, усеченный октаэдр, усеченный додекаэдр, усеченный икосаэдр. Множество архимедовых тел можно разбить на пять групп
Слайд 37
Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются кубоктаэдр икосододекаэдр.
Слайд 38
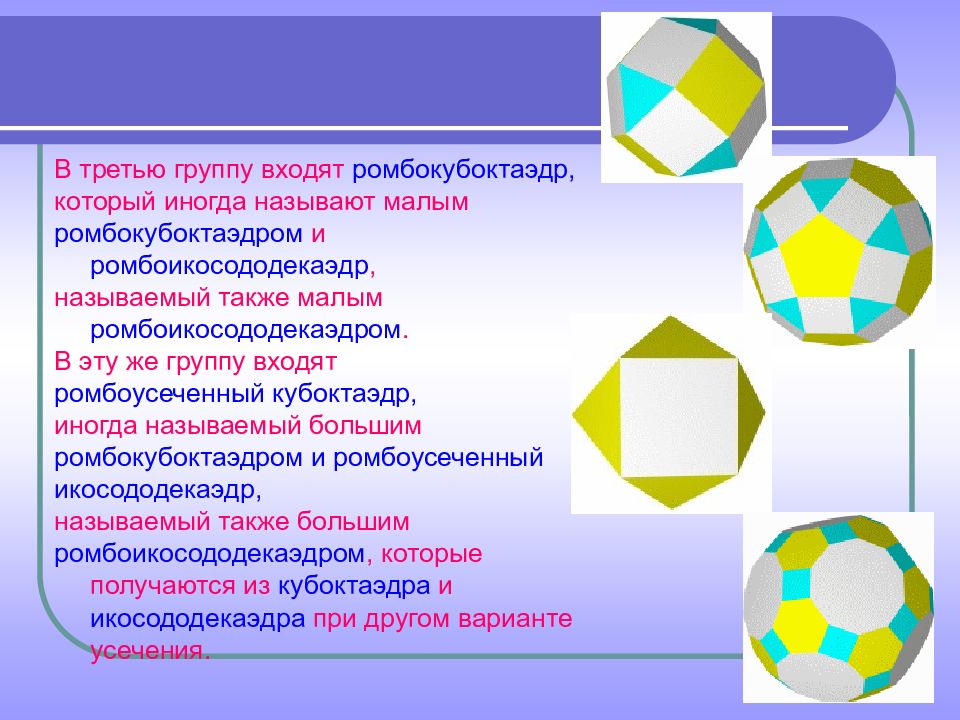
В третью группу входят ромбокубоктаэдр, который иногда называют малым ромбокубоктаэдром и ромбоикосододекаэдр, называемый также малым ромбоикосододекаэдром. В эту же группу входят ромбоусеченный кубоктаэдр, иногда называемый большим ромбокубоктаэдром и ромбоусеченный икосододекаэдр, называемый также большим ромбоикосододекаэдром, которые получаются из кубоктаэдра и икосододекаэдра при другом варианте усечения.
Слайд 39
В четвертую группу входят две курносые модификации - курносый куб и курносый додекаэдр. Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки.
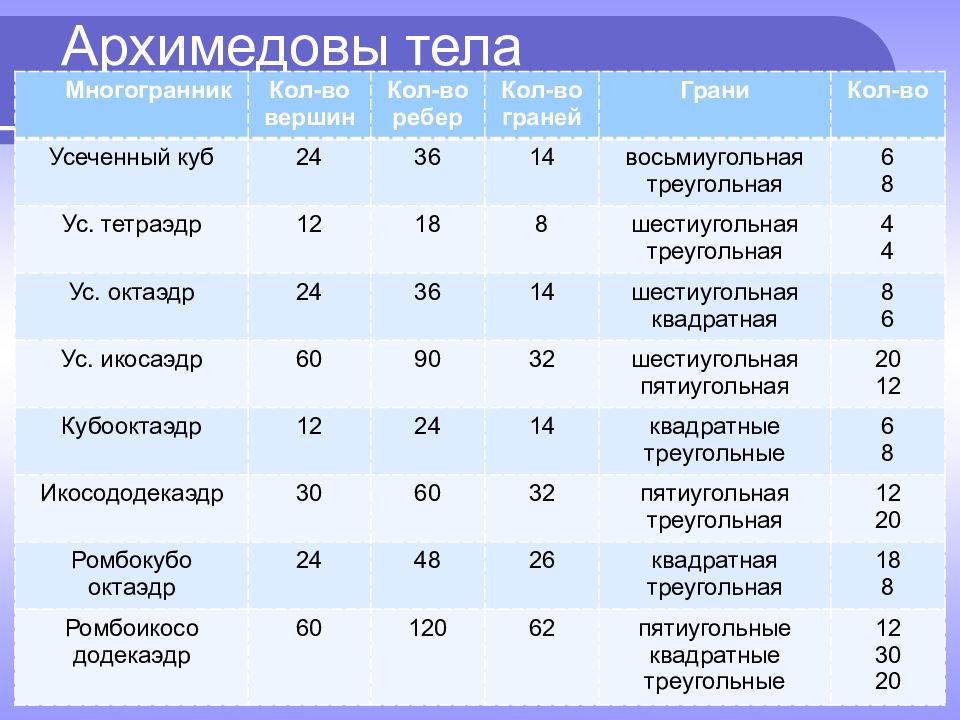
Слайд 40: Архимедовы тела
Многогранник Кол-во вершин Кол-во ребер Кол-во граней Грани Кол-во Усеченный куб 24 36 14 восьмиугольная треугольная 6 8 Ус. тетраэдр 12 18 8 шестиугольная треугольная 4 4 Ус. октаэдр 24 36 14 шестиугольная квадратная 8 6 Ус. икосаэдр 60 90 32 шестиугольная пятиугольная 20 12 Кубооктаэдр 12 24 14 квадратные треугольные 6 8 Икосододекаэдр 30 60 32 пятиугольная треугольная 12 20 Ромбокубо октаэдр 24 48 26 квадратная треугольная 18 8 Ромбоикосо додекаэдр 60 120 62 пятиугольные квадратные треугольные 12 30 20
Слайд 41
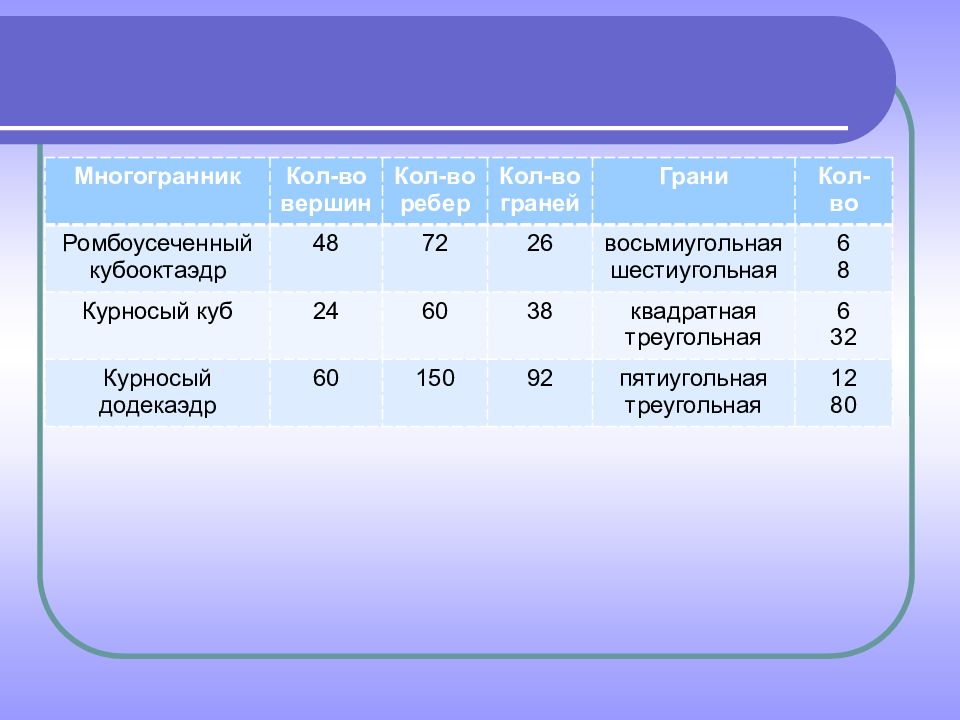
Многогранник Кол-во вершин Кол-во ребер Кол-во граней Грани Кол-во Ромбоусеченный кубооктаэдр 48 72 26 восьмиугольная шестиугольная 6 8 Курносый куб 24 60 38 квадратная треугольная 6 32 Курносый додекаэдр 60 150 92 пятиугольная треугольная 12 80
Слайд 42
Кроме «архимедовых тел» к полуправильным многогранникам относятся все правильные n -угольные призмы, все ребра которых равны.