Первый слайд презентации: ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
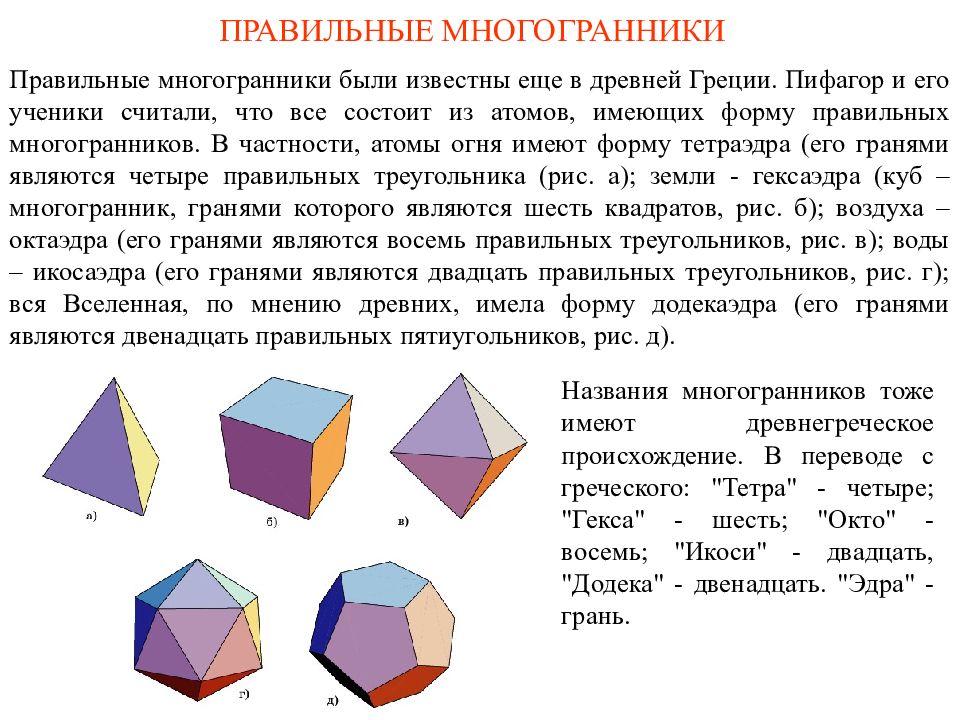
Правильные многогранники были известны еще в древней Греции. Пифагор и его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы ог ня имеют форму тетраэдр а (его гранями являются четыре правильных треугольника (рис. а); земл и - гексаэдр а (куб – многогранник, гранями которого являются шесть квадратов, рис. б ); воздух а – октаэдр а (его гранями являются восемь правильных треугольников, рис. в ); вод ы – икосаэдр а (его гранями являются двадцать правильных треугольников, рис. г ); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д). Названия многогранников тоже имеют древнегреческое происхождение. В переводе с греческого: "Тетра" - четыре; "Гекса" - шесть; "Окто" - восемь; "Икоси" - двадцать, "Додека" - двенадцать. "Эдра" - грань.
Слайд 2: Кубок Кеплера
Иоганн Кеплер (1571 – 1630) в одной из первых своих работ "Тайна мироздания" в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по Кеплеру, заключалась в следующем: "Земля (имеется в виду орбита Земли) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг куба сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия". Такая модель Солнечной системы получила название "Космического кубка" Кеплера. Впоследствии, проведя более точные измерения, Кеплер пришел к выводу, что орбиты планет являются не окружностями, а эллипсами, при этом Солнце находится в одном из фокусов этих эллипсов. В этом состоит 1-ый закон Кеплера.
Слайд 3: ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
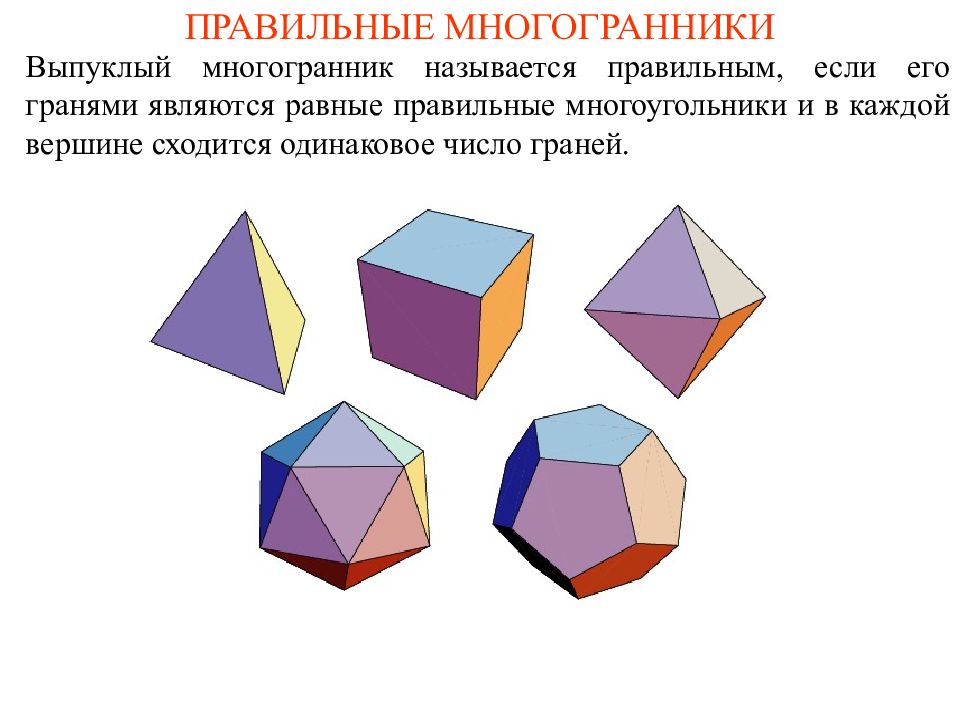
Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники и в каждой вершине сходится одинаковое число граней.
Слайд 4: ТЕТРАЭДР
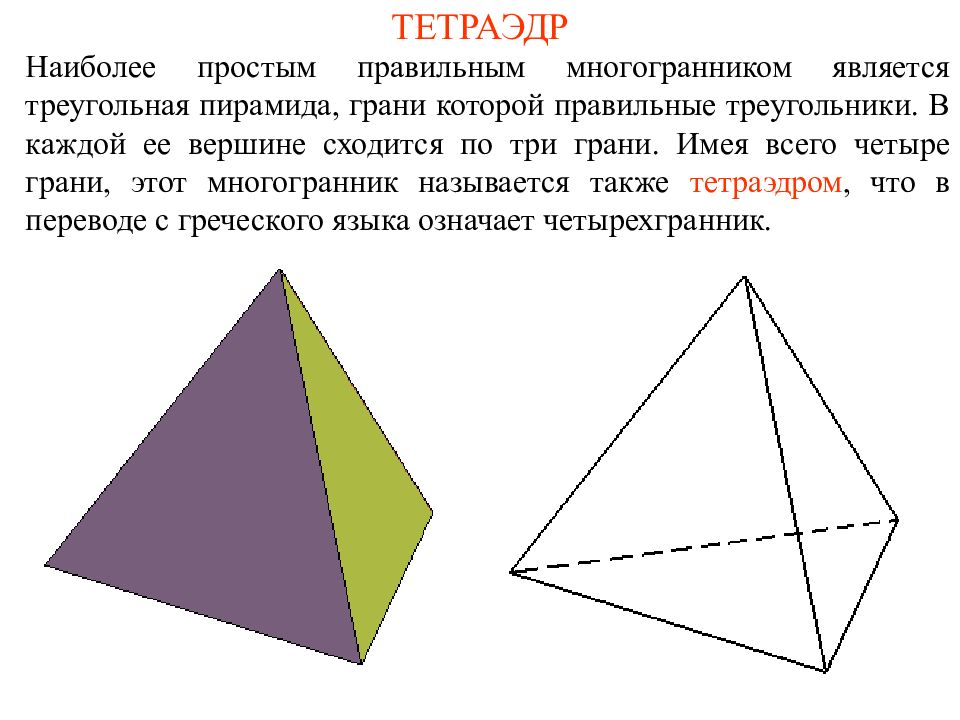
Наиболее простым правильным многогранником является треугольная пирамида, грани которой правильные треугольники. В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.
Слайд 5: Упражнение 1
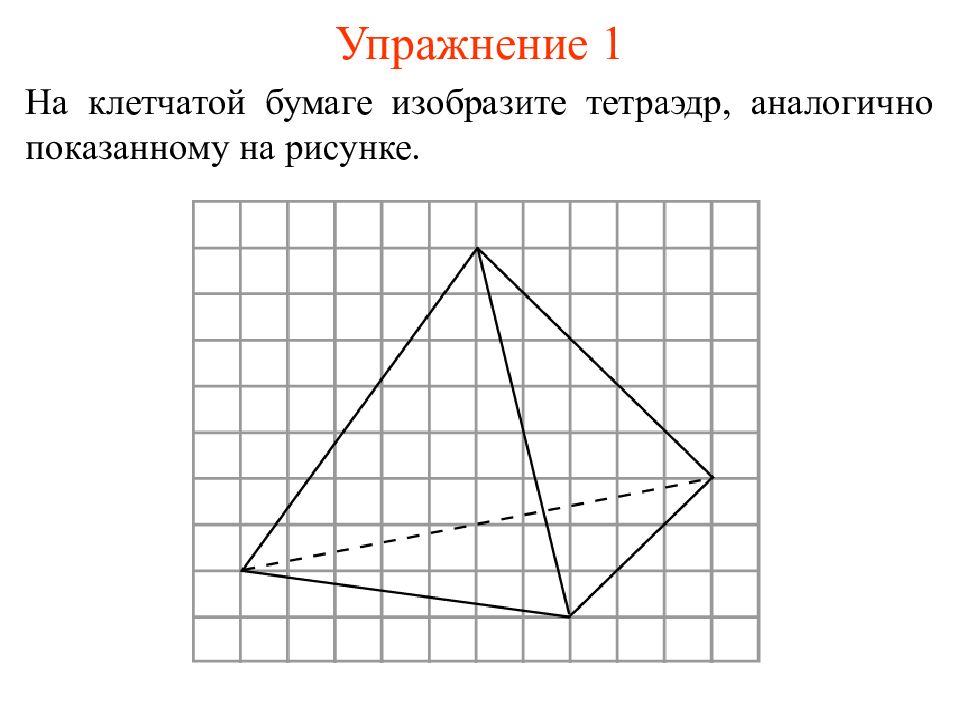
На клетчатой бумаге изобразите тетраэдр, аналогично показанному на рисунке.
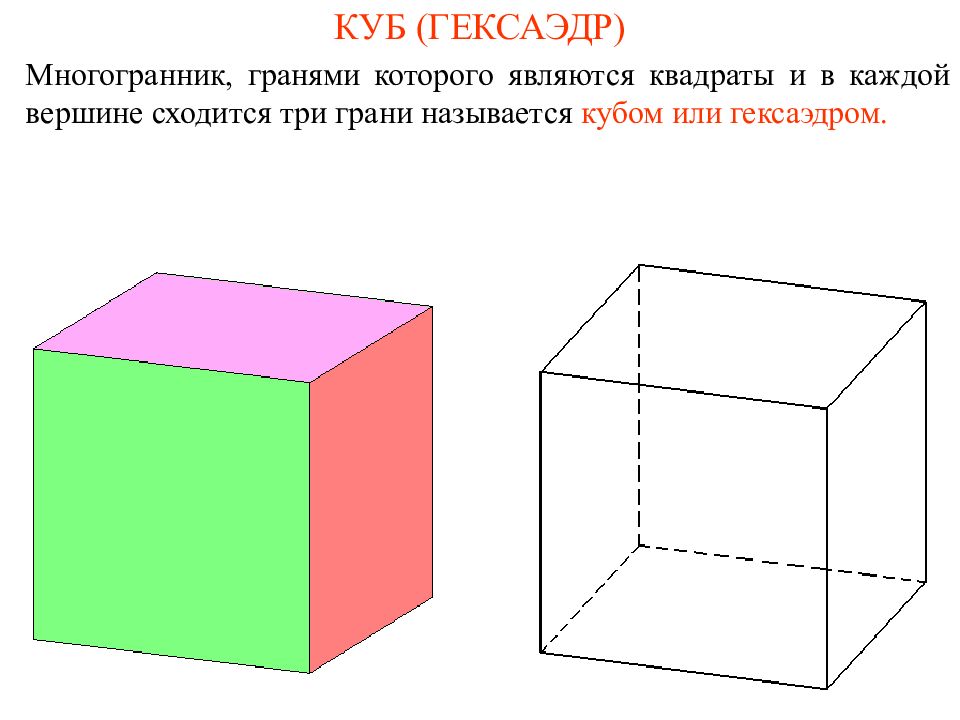
Слайд 6: КУБ (ГЕКСАЭДР)
Многогранник, гранями которого являются квадраты и в каждой вершине сходится три грани называется кубом или гексаэдром.
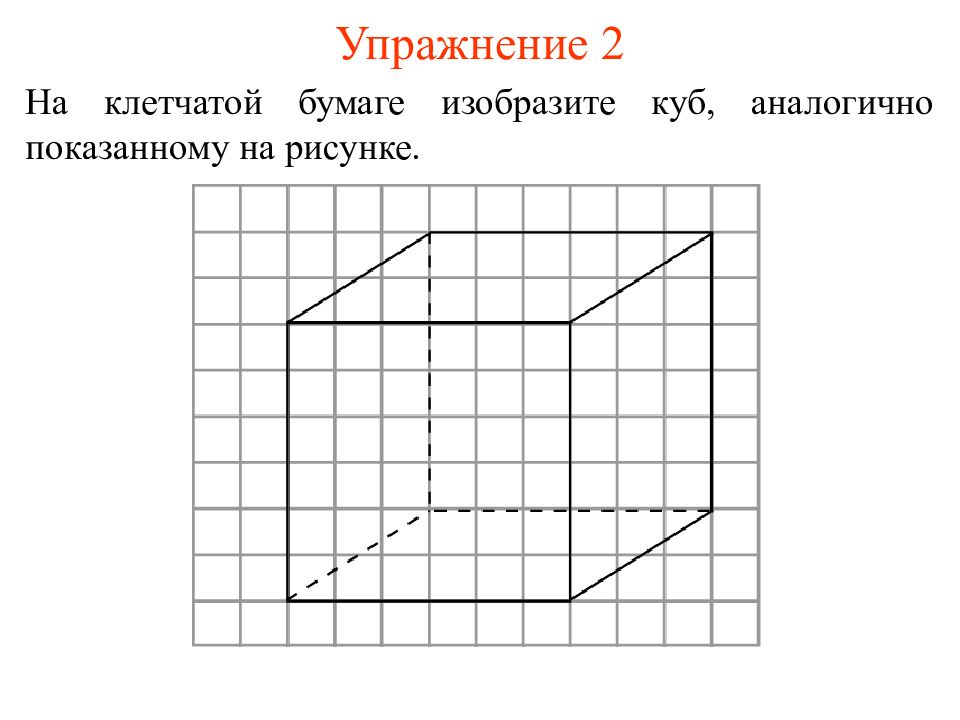
Слайд 7: Упражнение 2
На клетчатой бумаге изобразите куб, аналогично показанному на рисунке.
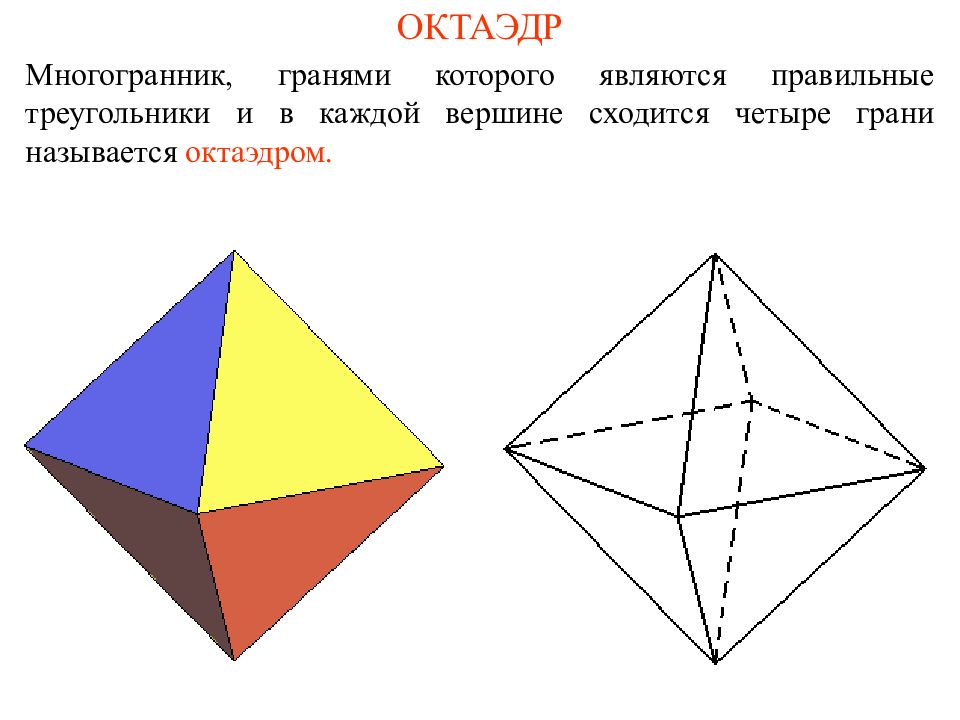
Слайд 8: ОКТАЭДР
Многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится четыре грани называется октаэдром.
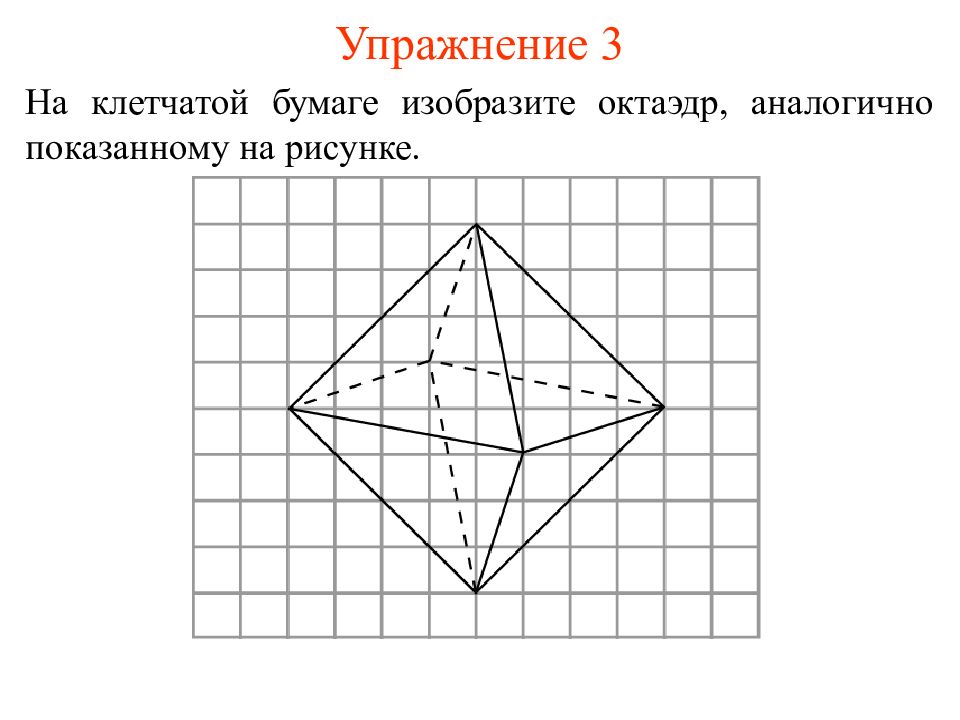
Слайд 9: Упражнение 3
На клетчатой бумаге изобразите октаэдр, аналогично показанному на рисунке.
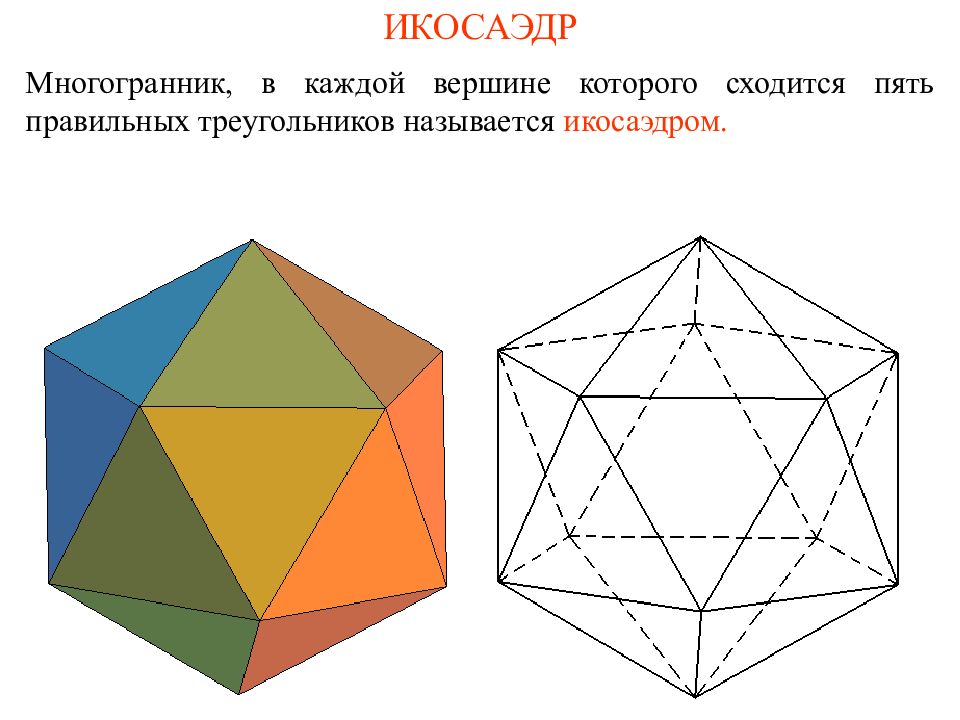
Слайд 10: ИКОСАЭДР
Многогранник, в каждой вершине которого сходится пять правильных треугольников называется икосаэдром.
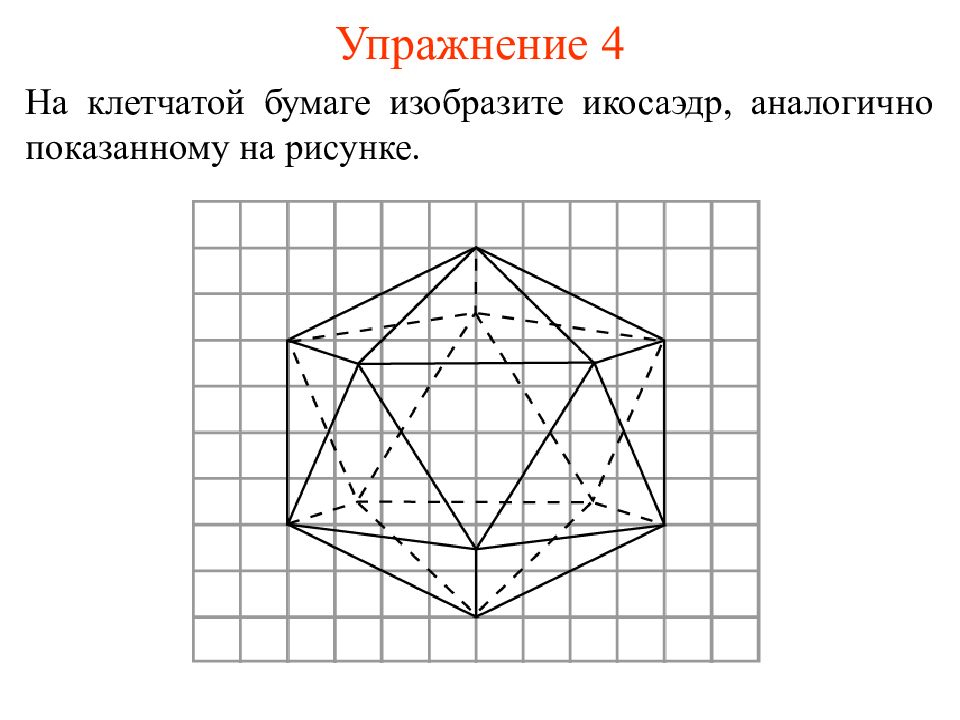
Слайд 11: Упражнение 4
На клетчатой бумаге изобразите икосаэдр, аналогично показанному на рисунке.
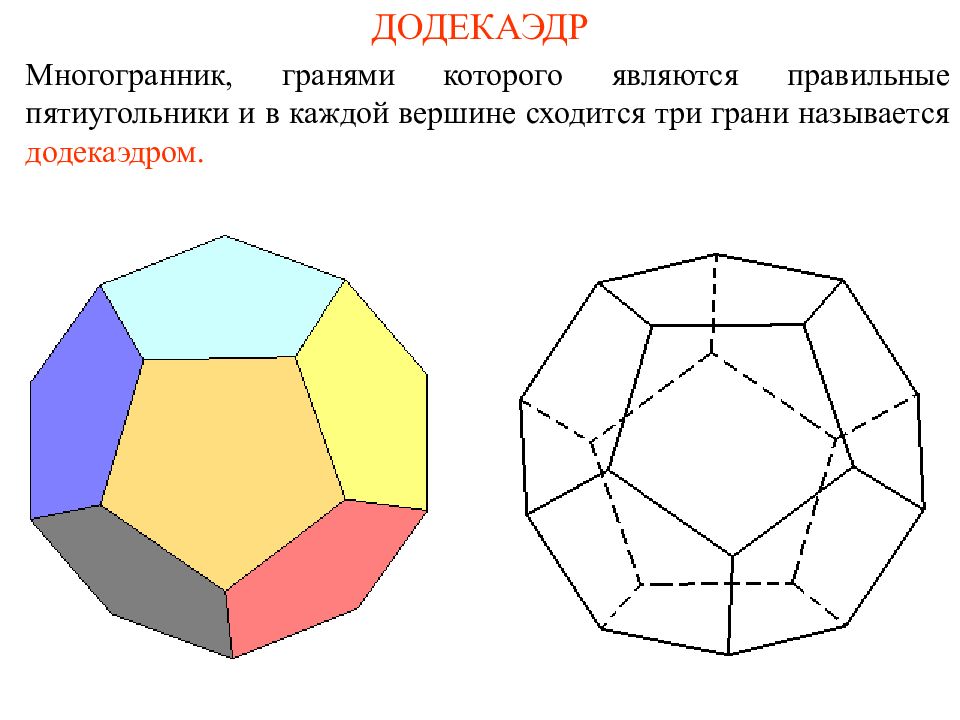
Слайд 12: ДОДЕКАЭДР
Многогранник, гранями которого являются правильные пятиугольники и в каждой вершине сходится три грани называется додекаэдром.
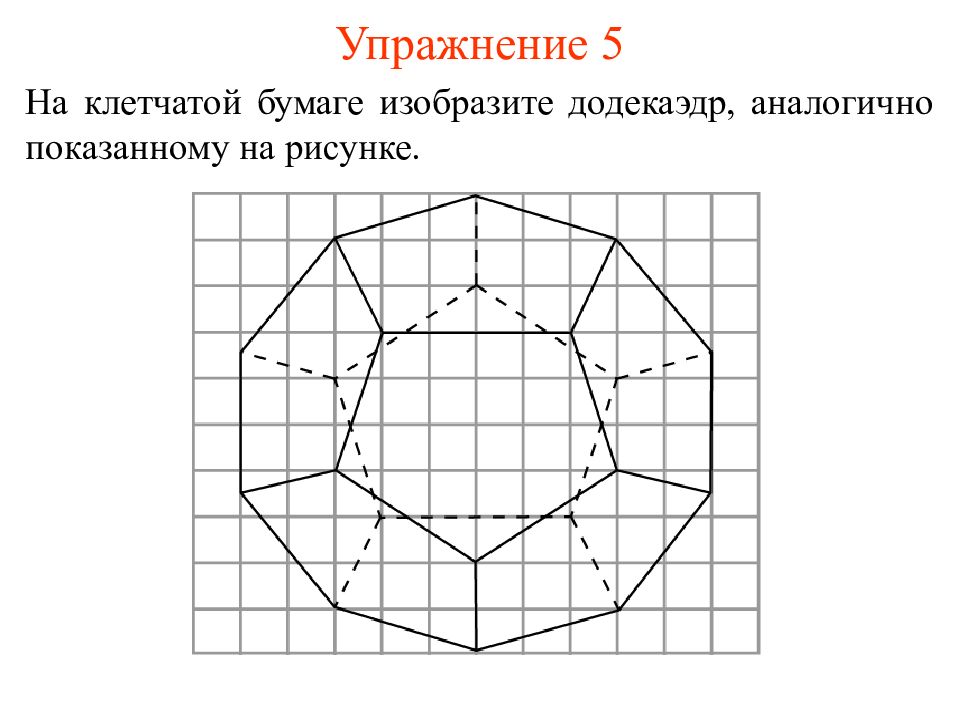
Слайд 13: Упражнение 5
На клетчатой бумаге изобразите додекаэдр, аналогично показанному на рисунке.
Слайд 14: Упражнение 6
Почему гранями правильного многогранника не могут быть правильные шестиугольники? Ответ: Потому что в этом случае сумма плоских углов при вершинах будет больше или равна 360 о.
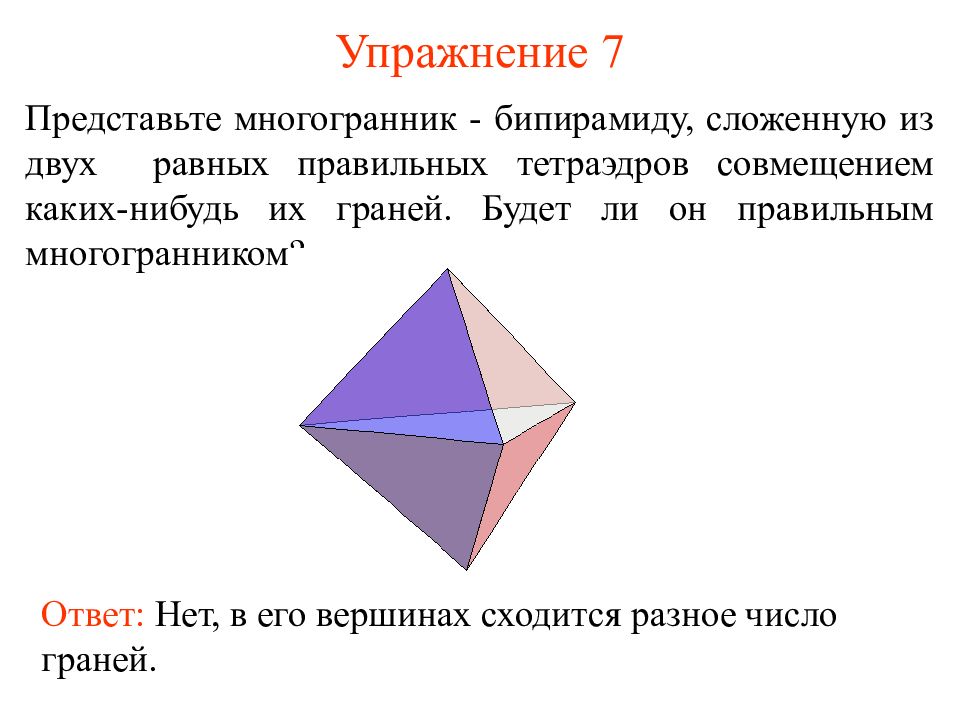
Слайд 15: Упражнение 7
Представьте многогранник - бипирамиду, сложенную из двух равных правильных тетраэдров совмещением каких-нибудь их граней. Будет ли он правильным многогранником? Ответ: Нет, в его вершинах сходится разное число граней.
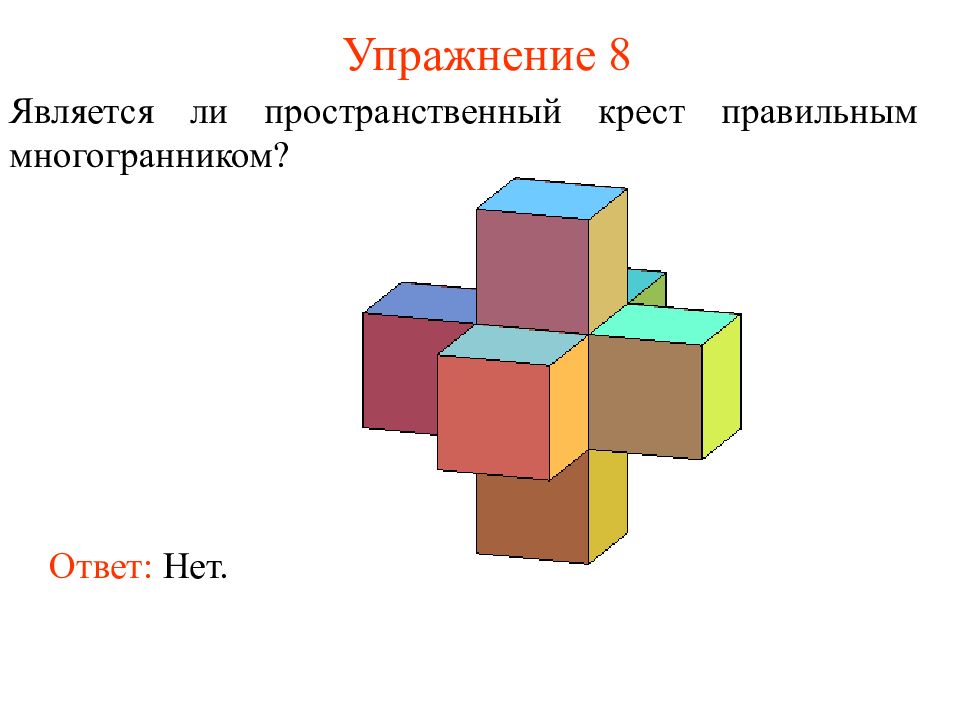
Слайд 16: Упражнение 8
Является ли пространственный крест правильным многогранником? Ответ: Нет.
Слайд 20: Упражнение 12
Соединение каких двух многогранников изображено на рисунке ? Ответ: Икосаэдра и додекаэдра.
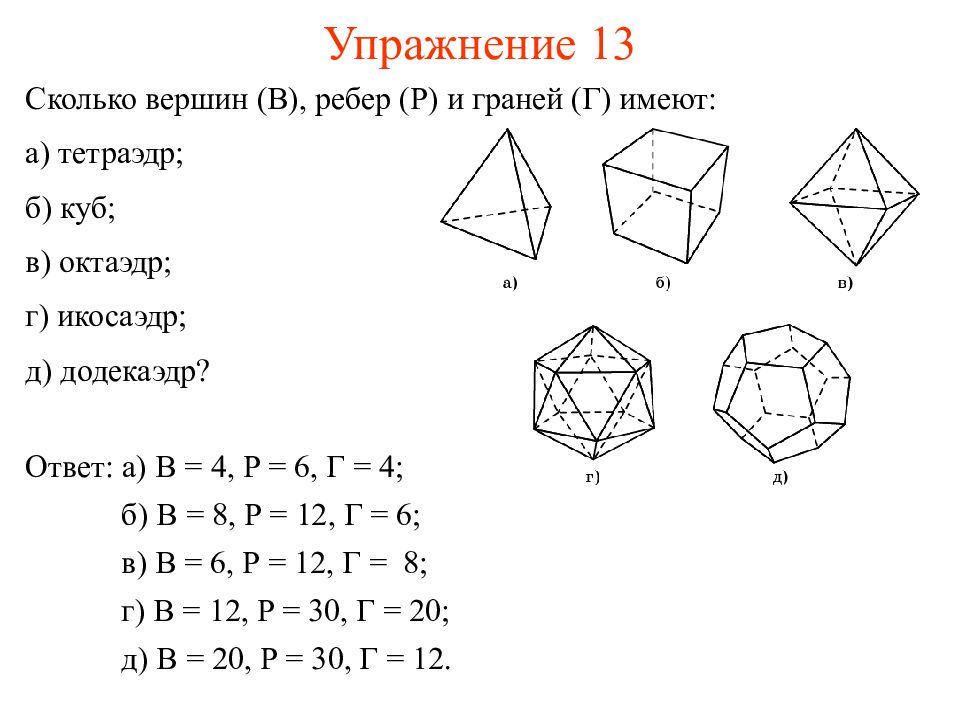
Слайд 21: Упражнение 13
Сколько вершин (В), ребер (Р) и граней (Г) имеют: а) тетраэдр; б) куб; в) октаэдр; г) икосаэдр; д) додекаэдр? Ответ: а) В = 4, Р = 6, Г = 4; б) В = 8, Р = 12, Г = 6; в) В = 6, Р = 12, Г = 8; г) В = 12, Р = 30, Г = 20; д) В = 20, Р = 30, Г = 12.
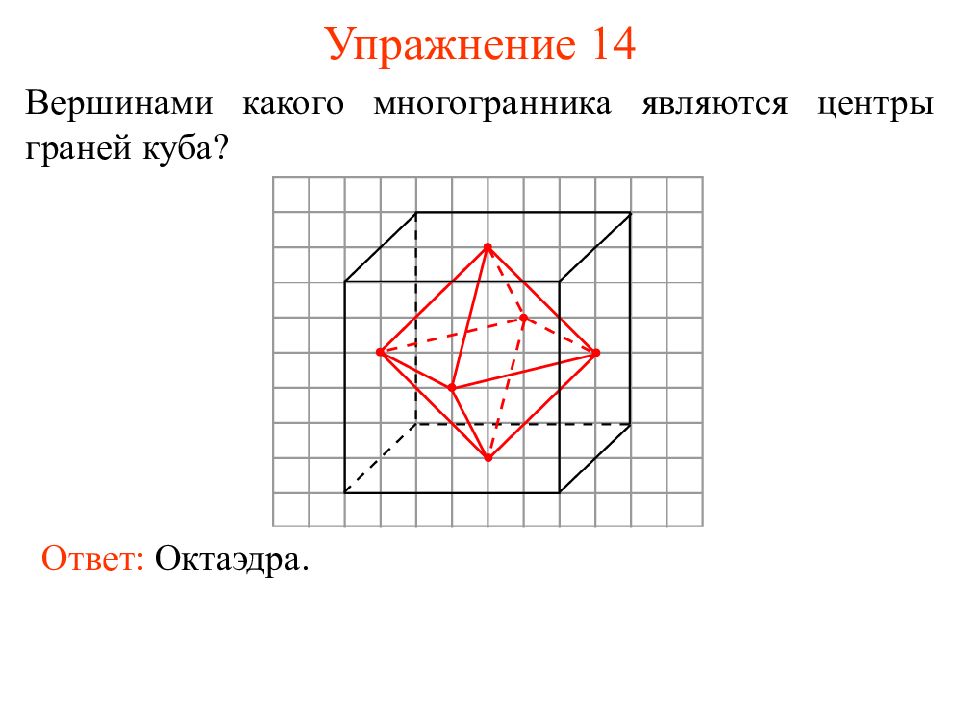
Слайд 22: Упражнение 14
Вершинами какого многогранника являются центры граней куба? Ответ: Октаэдра.
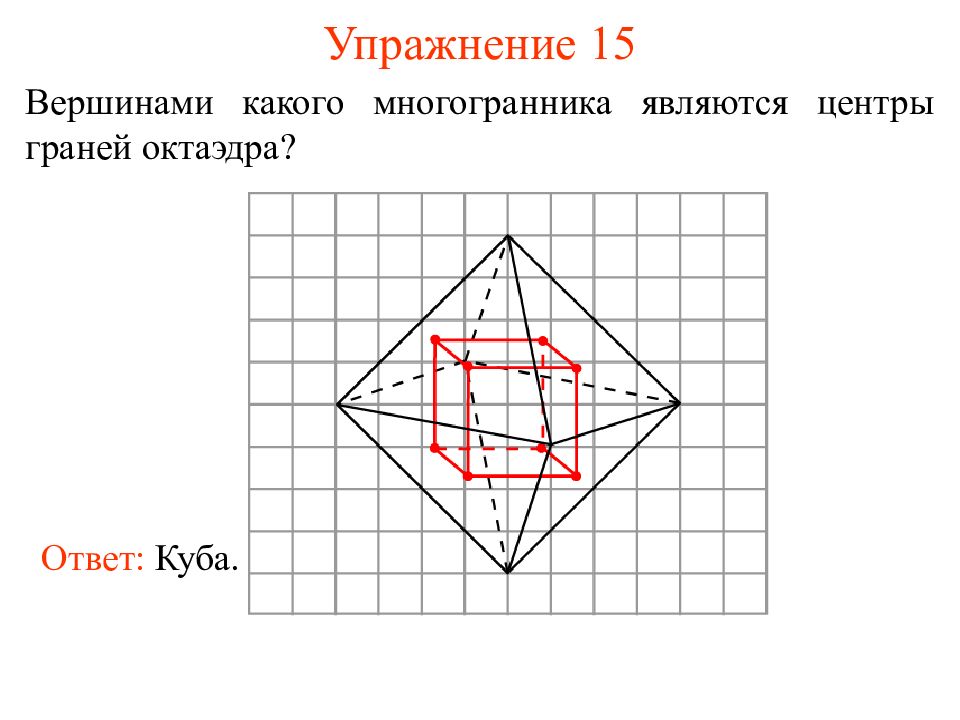
Слайд 23: Упражнение 15
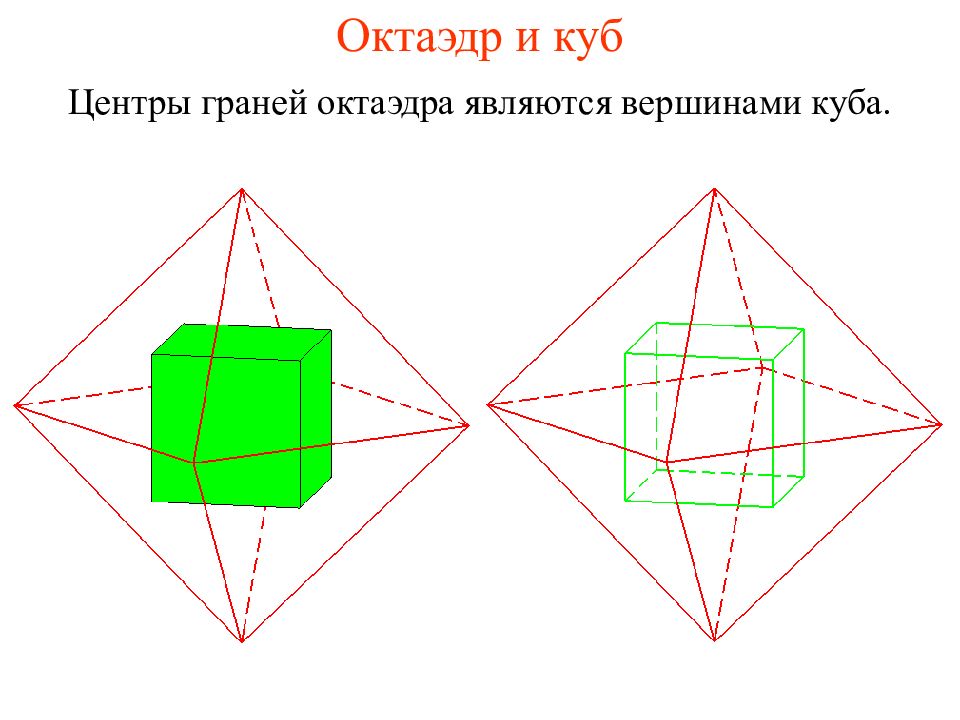
Вершинами какого многогранника являются центры граней октаэдра? Ответ: Куба.
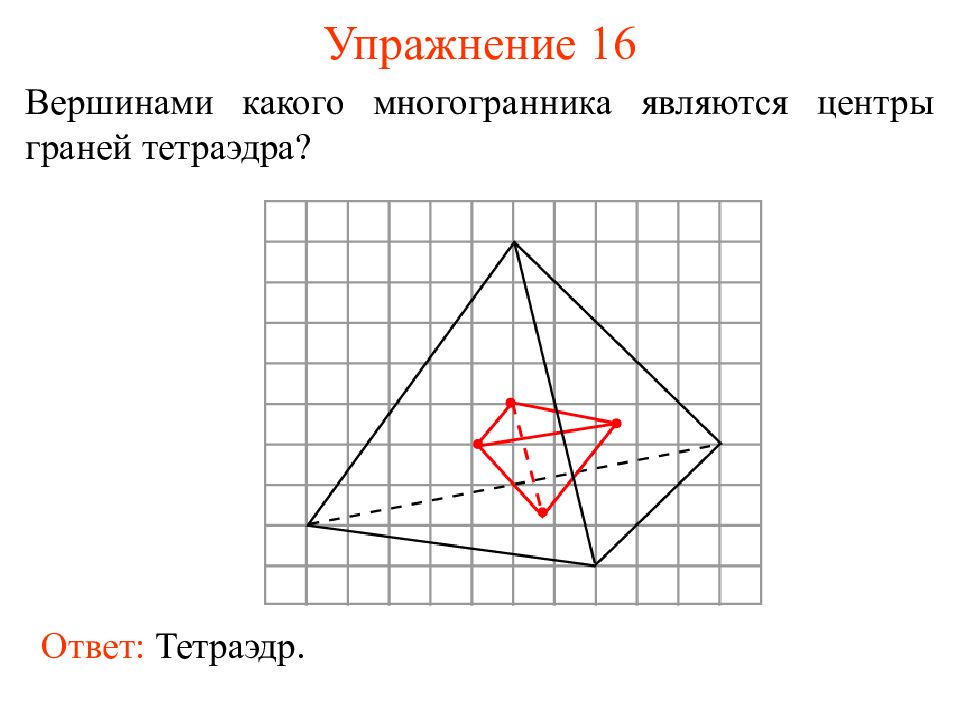
Слайд 24: Упражнение 16
Вершинами какого многогранника являются центры граней тетраэдра? Ответ: Тетраэдр.
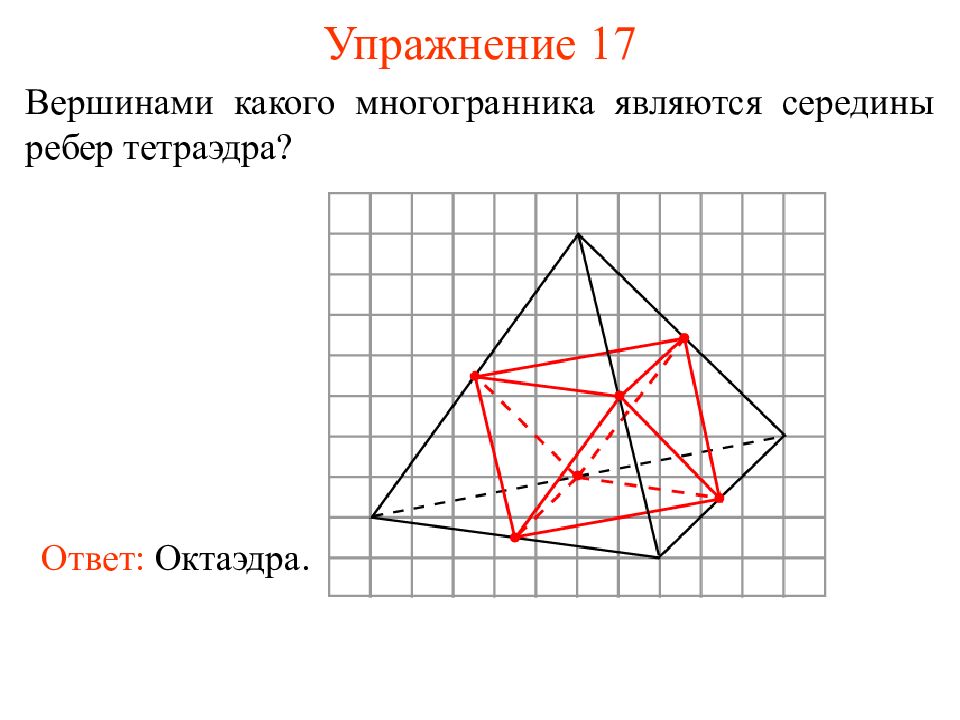
Слайд 25: Упражнение 17
Вершинами какого многогранника являются середины ребер тетраэдра? Ответ: Октаэдра.
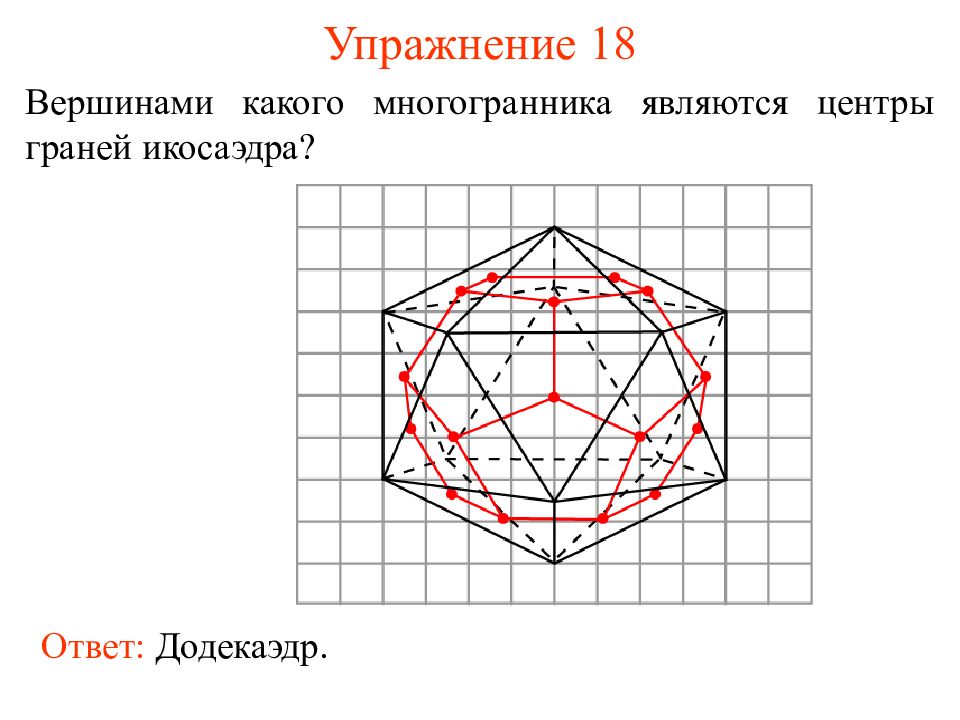
Слайд 26: Упражнение 18
Вершинами какого многогранника являются центры граней икосаэдра? Ответ: Додекаэдр.
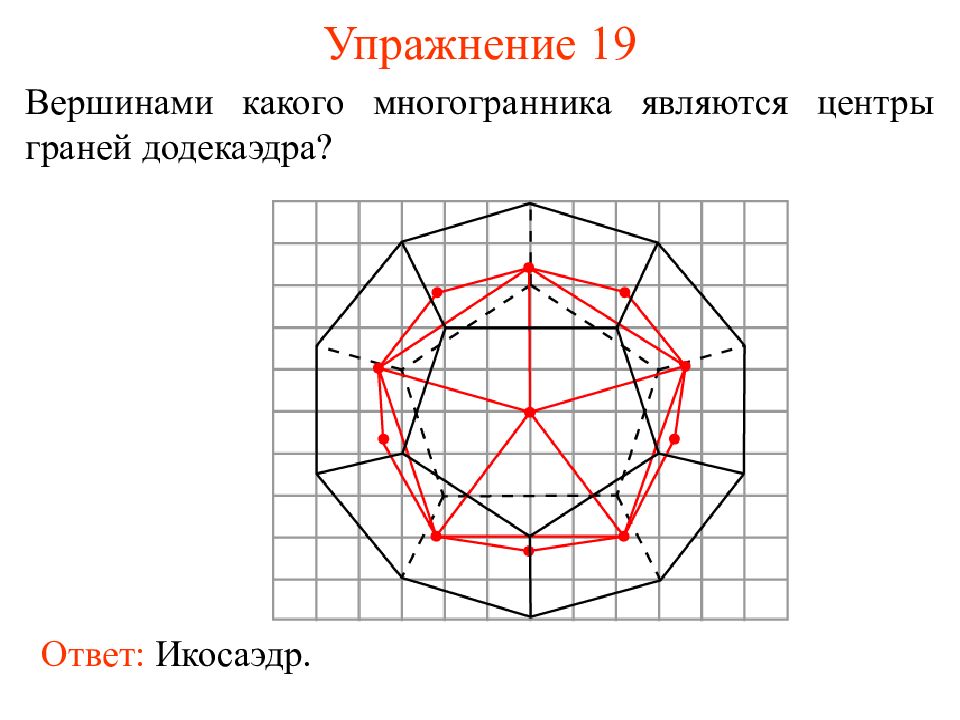
Слайд 27: Упражнение 19
Вершинами какого многогранника являются центры граней додекаэдра? Ответ: Икосаэдр.
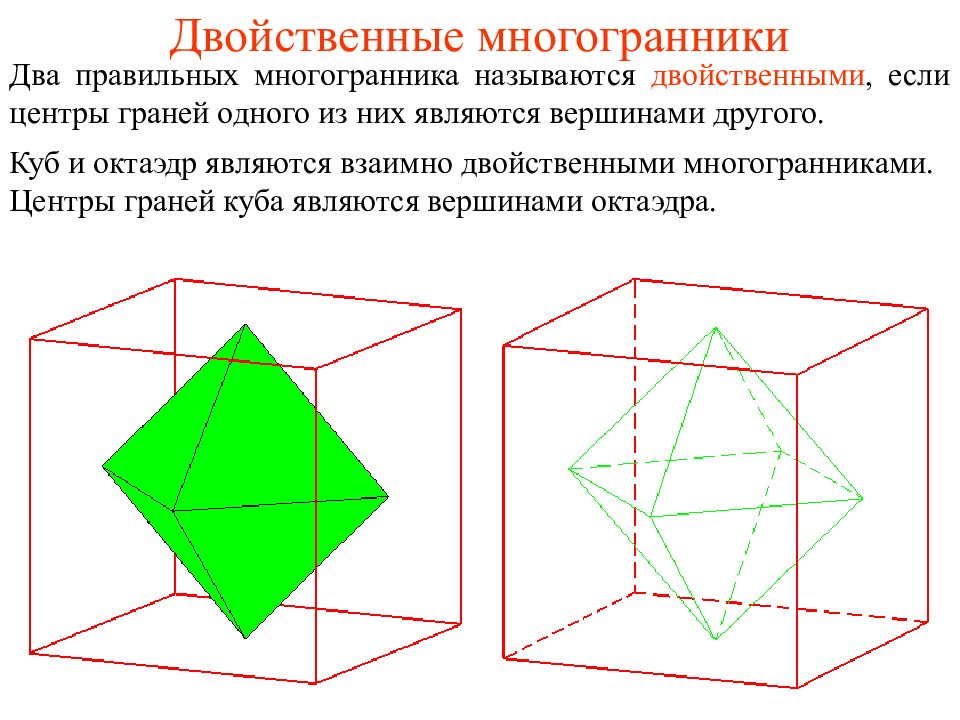
Слайд 28: Двойственные многогранники
Два правильных многогранника называются двойственными, если центры граней одного из них являются вершинами другого. Куб и октаэдр являются взаимно двойственными многогранниками. Центры граней куба являются вершинами октаэдра.
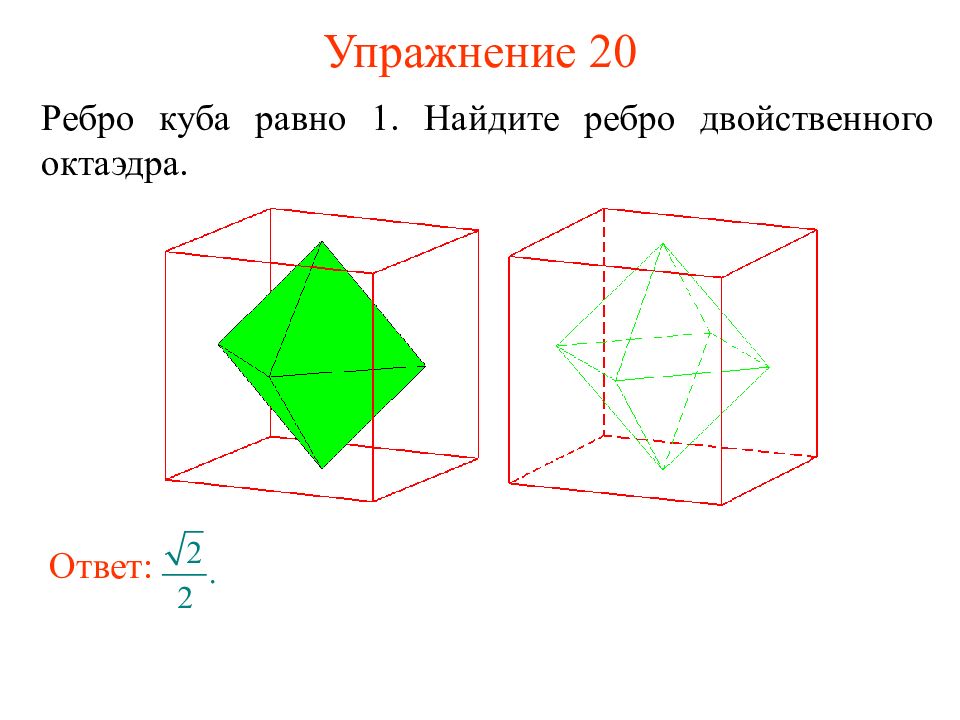
Слайд 29: Упражнение 20
Ребро куба равно 1. Найдите ребро двойственного октаэдра. Ответ:
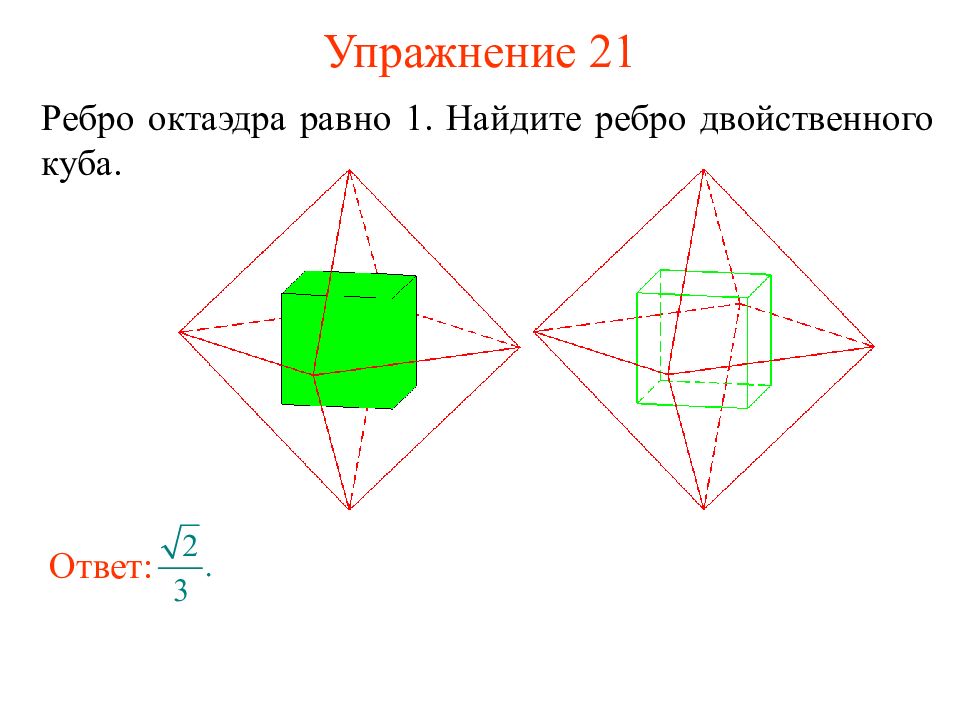
Слайд 31: Упражнение 21
Ребро октаэдра равно 1. Найдите ребро двойственного куба. Ответ:
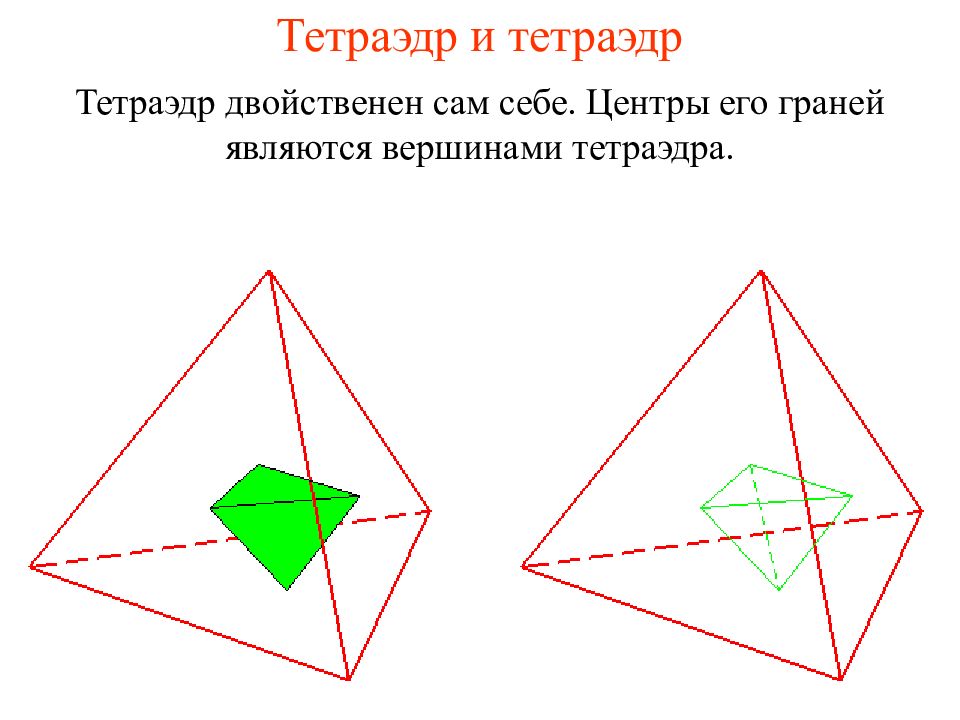
Слайд 32: Тетраэдр и тетраэдр
Тетраэдр двойственен сам себе. Центры его граней являются вершинами тетраэдра.
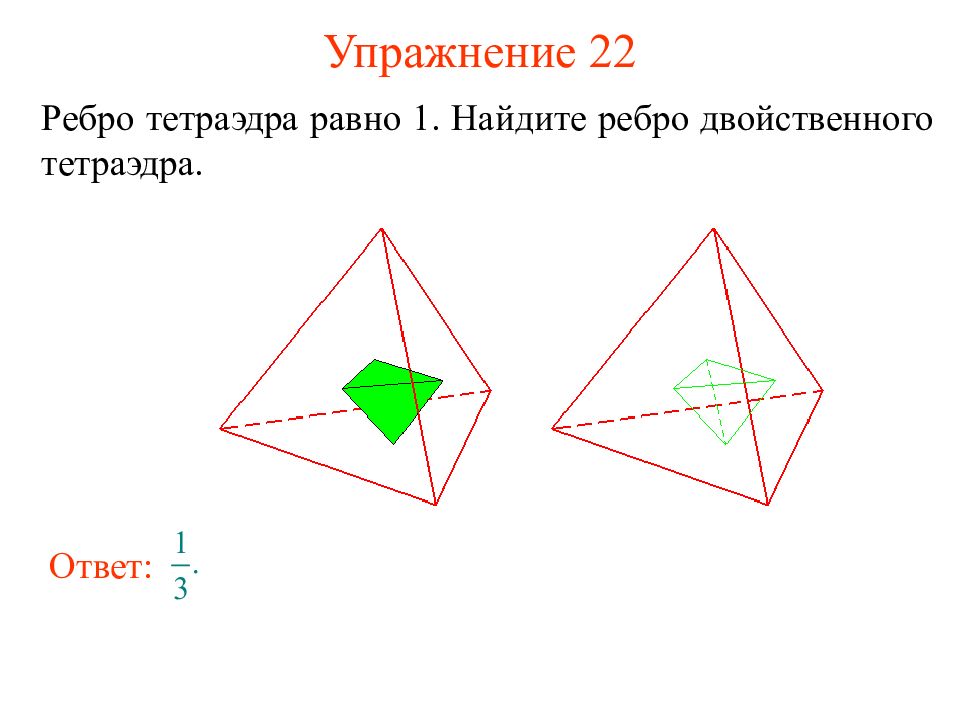
Слайд 33: Упражнение 22
Ребро тетраэдра равно 1. Найдите ребро двойственного тетраэдра. Ответ:
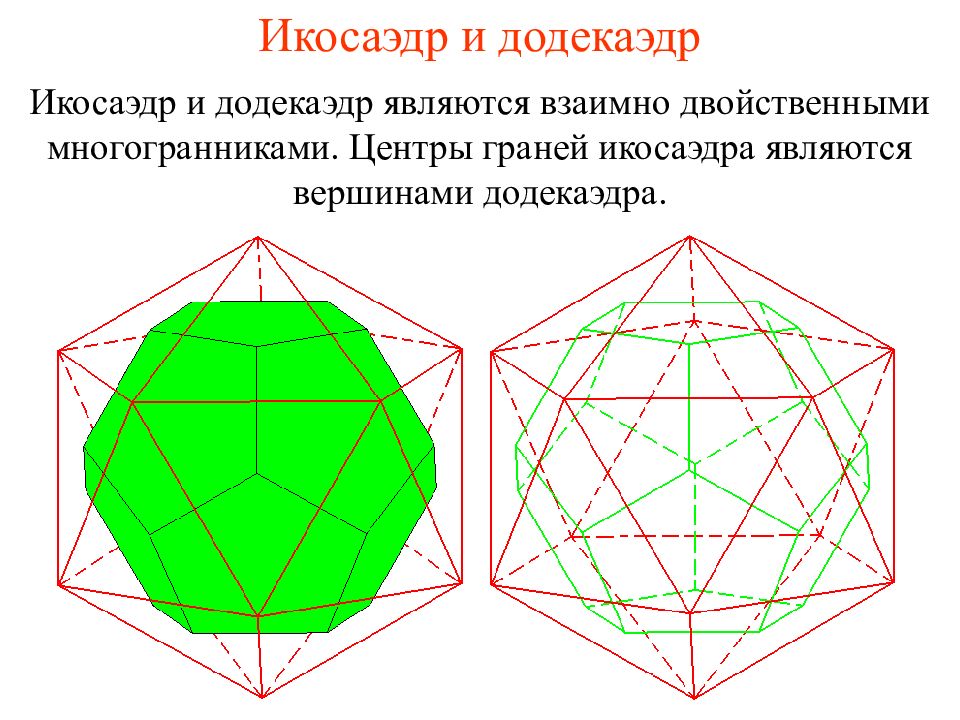
Слайд 34: Икосаэдр и додекаэдр
Икосаэдр и додекаэдр являются взаимно двойственными многогранниками. Центры граней икосаэдра являются вершинами додекаэдра.
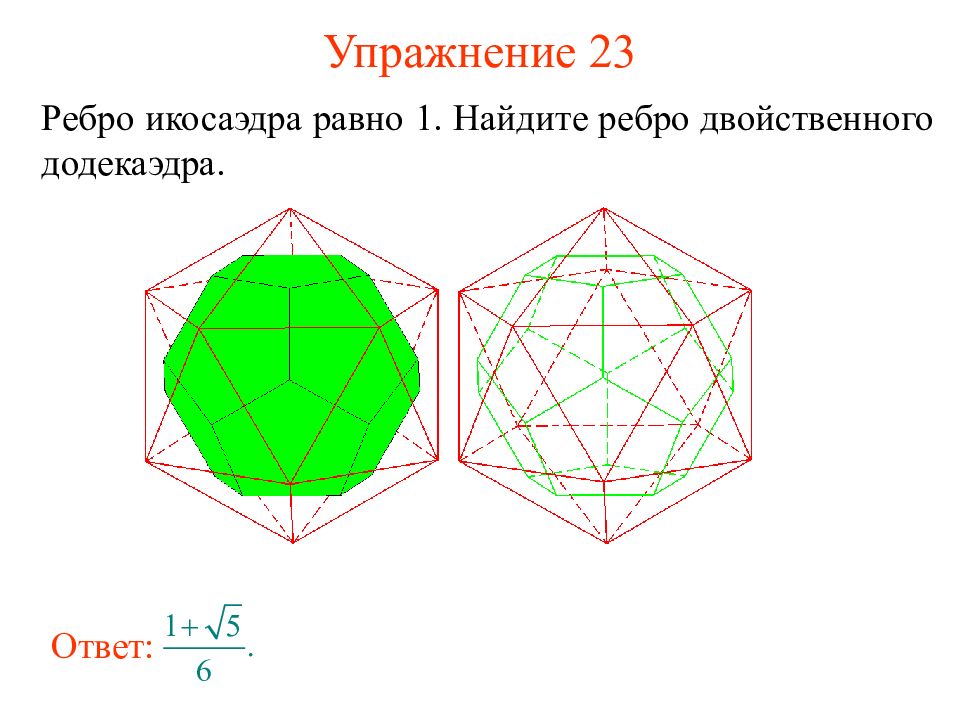
Слайд 35: Упражнение 23
Ребро икосаэдра равно 1. Найдите ребро двойственного додекаэдра. Ответ:
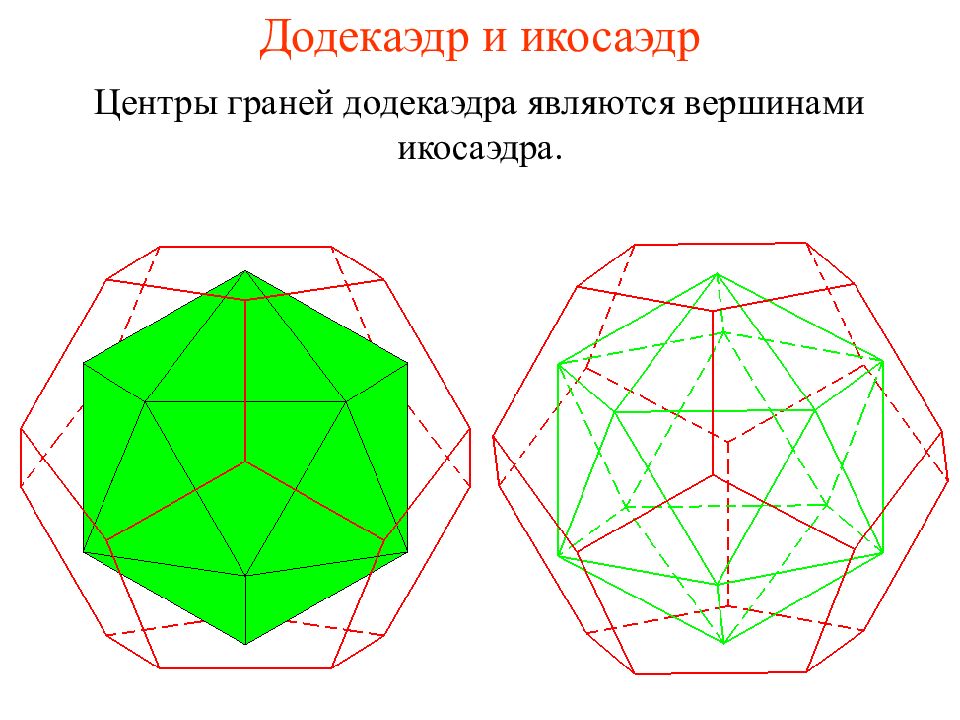
Слайд 36: Додекаэдр и икосаэдр
Центры граней додекаэдра являются вершинами икосаэдра.
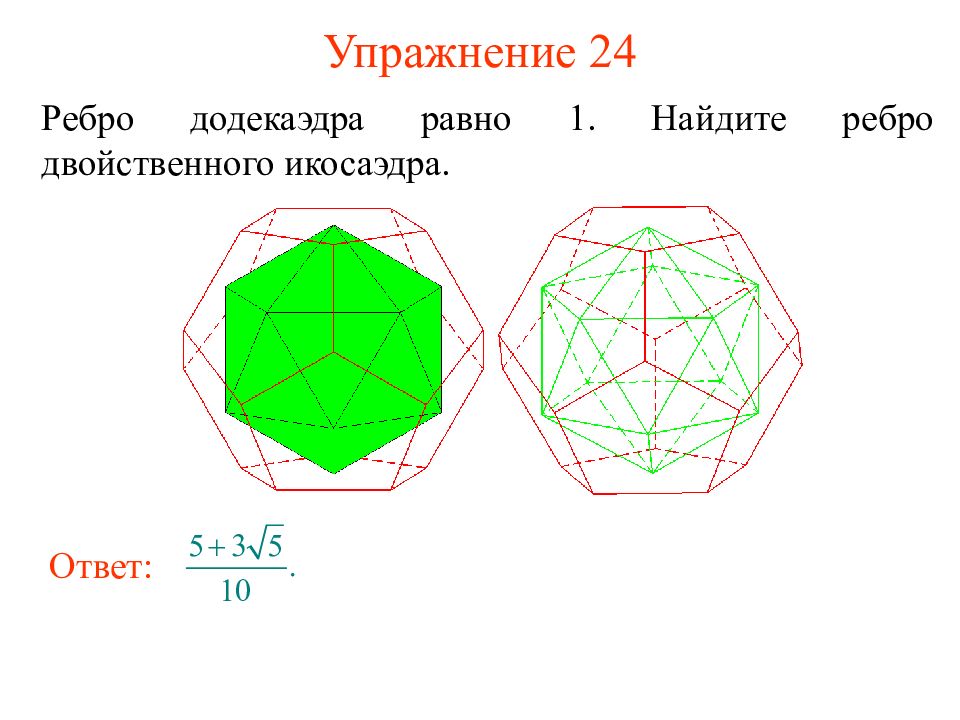
Слайд 37: Упражнение 24
Ребро додекаэдра равно 1. Найдите ребро двойственного икосаэдра. Ответ:
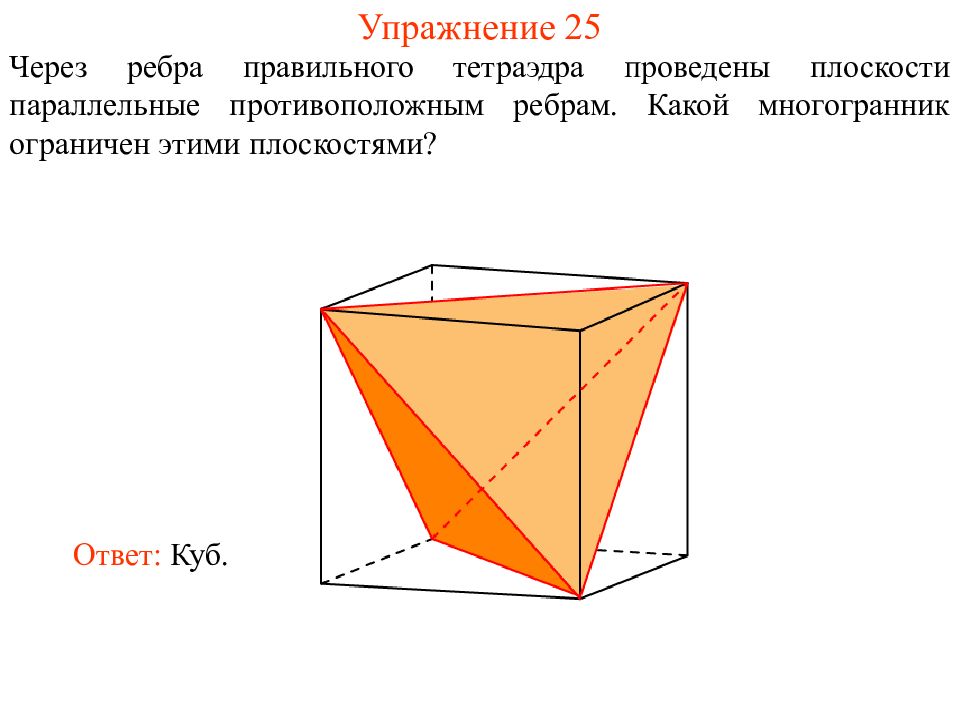
Слайд 38: Упражнение 25
Через ребра правильного тетраэдра проведены плоскости параллельные противоположным ребрам. Какой многогранник ограничен этими плоскостями? Ответ: Куб.
Слайд 39: Упражнение 26
Через середины двух ребер куба, выходящих из одной вершины, параллельно третьему ребру, выходящему из той же вершины куба, проведено сечение, отсекающее от куба треугольную призму. Такие же сечения проведены через все возможные пары середин ребер, выходящих из вершин куба. Опишите многогранник, который останется от куба в результате этих отсечений. Сколько у него вершин, ребер и граней? Какую форму имеют грани? Нарисуйте этот многогранник. Ответ: Полученный многогранник имеет 14 вершин, 24 ребра и 12 граней. Гранями являются равные ромбы.
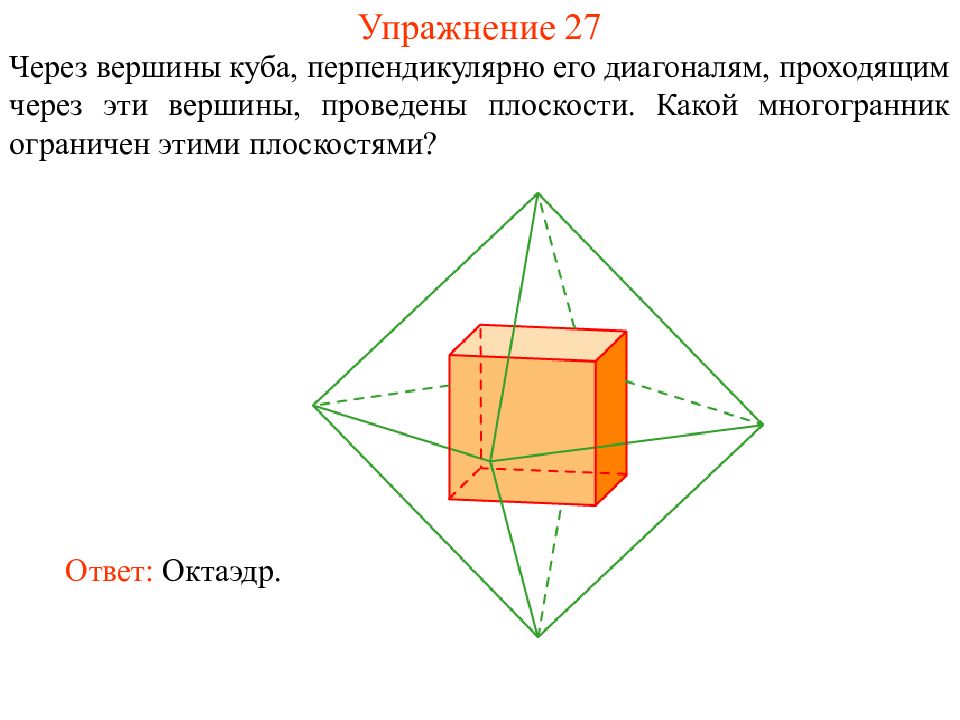
Слайд 40: Упражнение 27
Через вершины куба, перпендикулярно его диагоналям, проходящим через эти вершины, проведены плоскости. Какой многогранник ограничен этими плоскостями ? Ответ: Октаэдр.
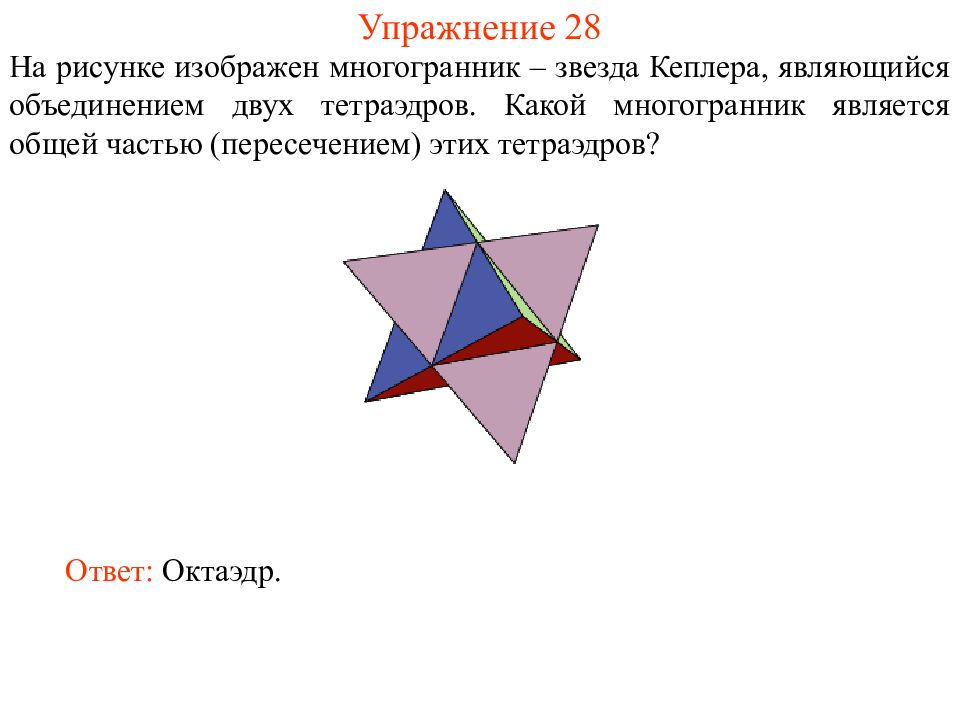
Слайд 41: Упражнение 28
На рисунке изображен многогранник – звезда Кеплера, являющийся объединением двух тетраэдров. Какой многогранник является общей частью (пересечением) этих тетраэдров? Ответ: Октаэдр.
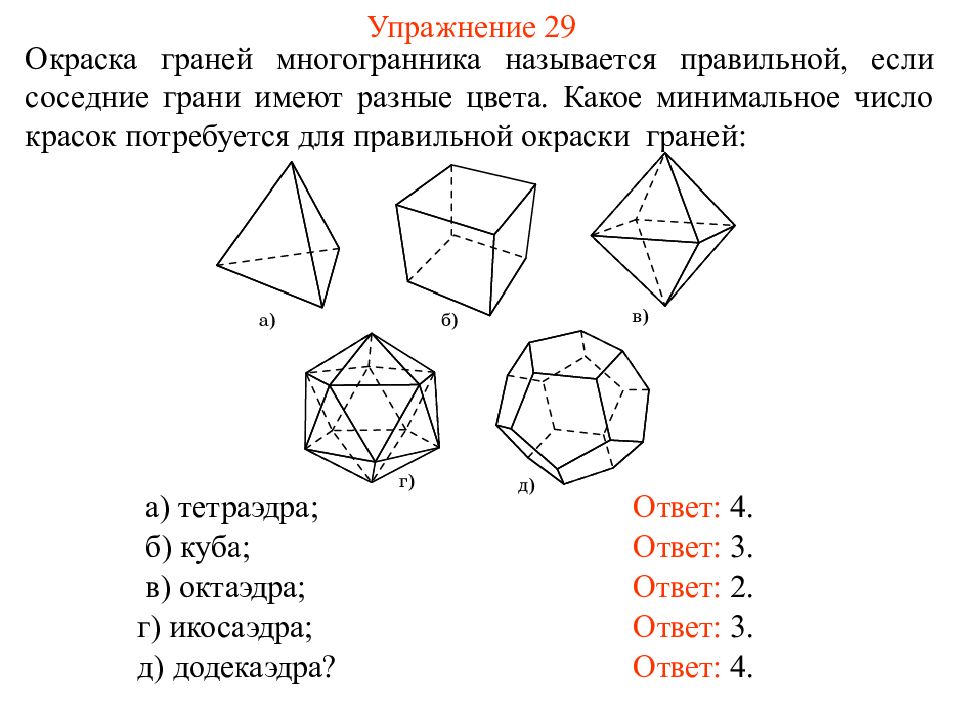
Последний слайд презентации: ПРАВИЛЬНЫЕ МНОГОГРАННИКИ: Упражнение 29
Окраска граней многогранника называется правильной, если соседние грани имеют разные цвета. Какое минимальное число красок потребуется для правильной окраски граней : Ответ: 4. а) тетраэдра; б) куба; в) октаэдра; г) икосаэдра; д) додекаэдра? Ответ: 3. Ответ: 2. Ответ: 3. Ответ: 4.