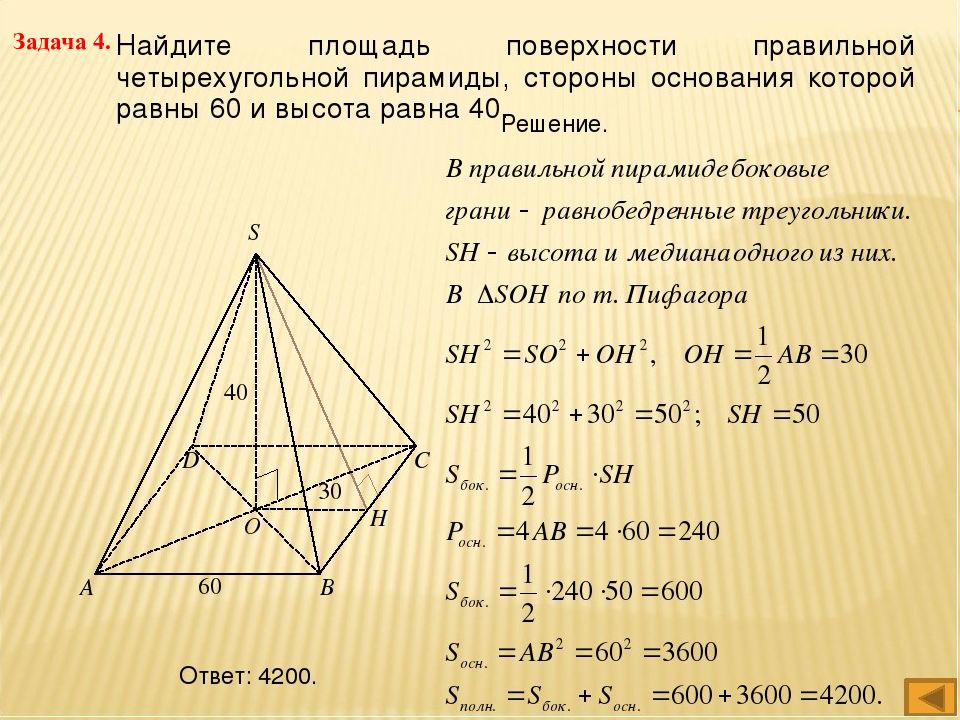
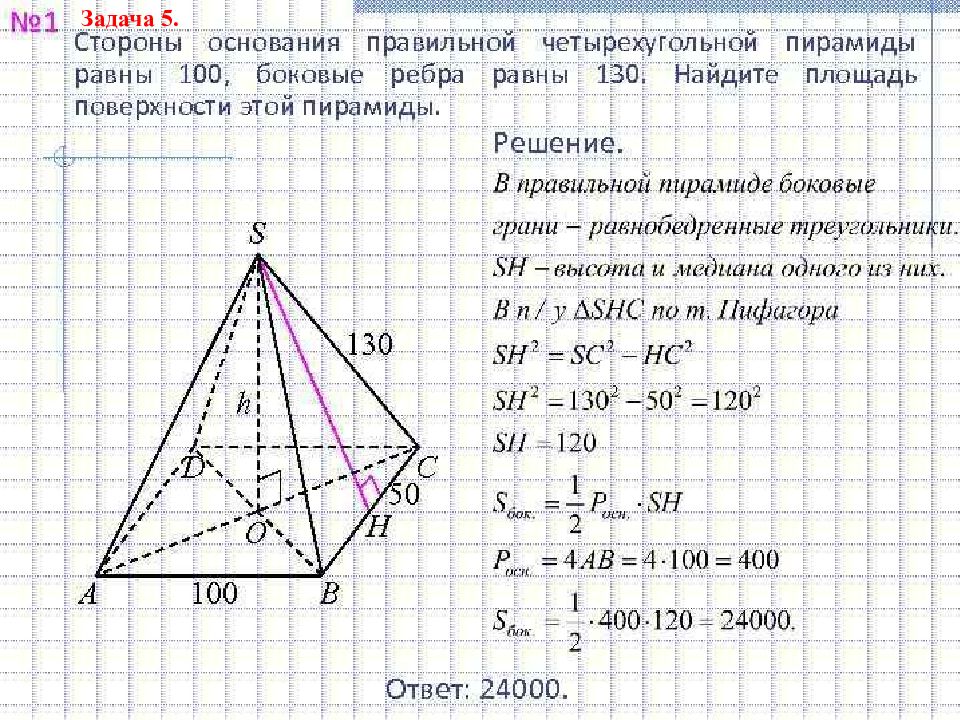
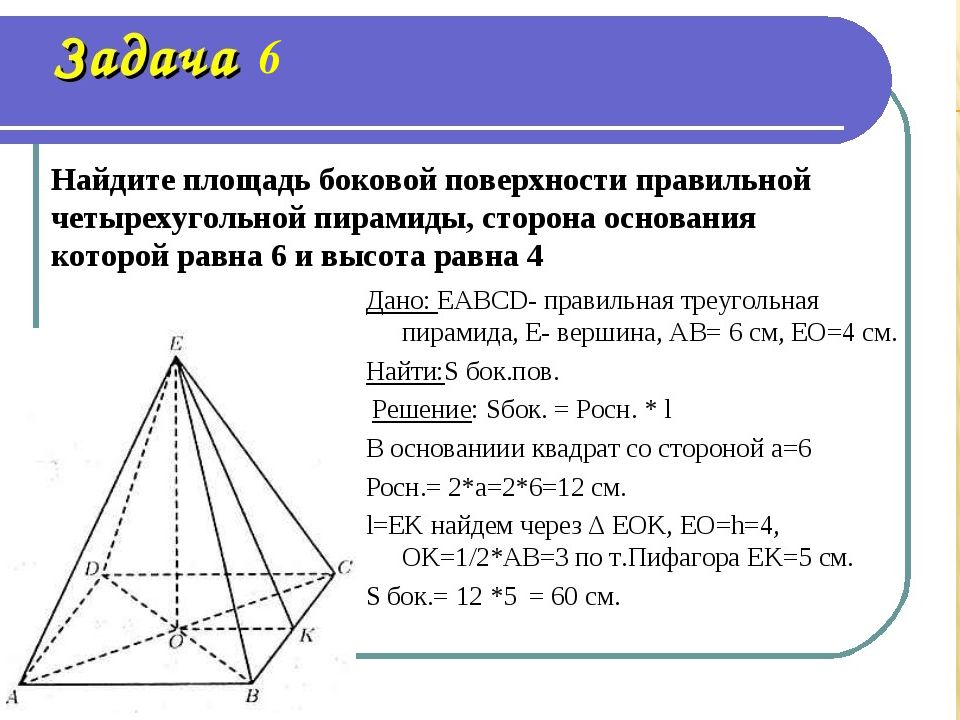
Первый слайд презентации: Площади боковой и полной поверхности пирамиды
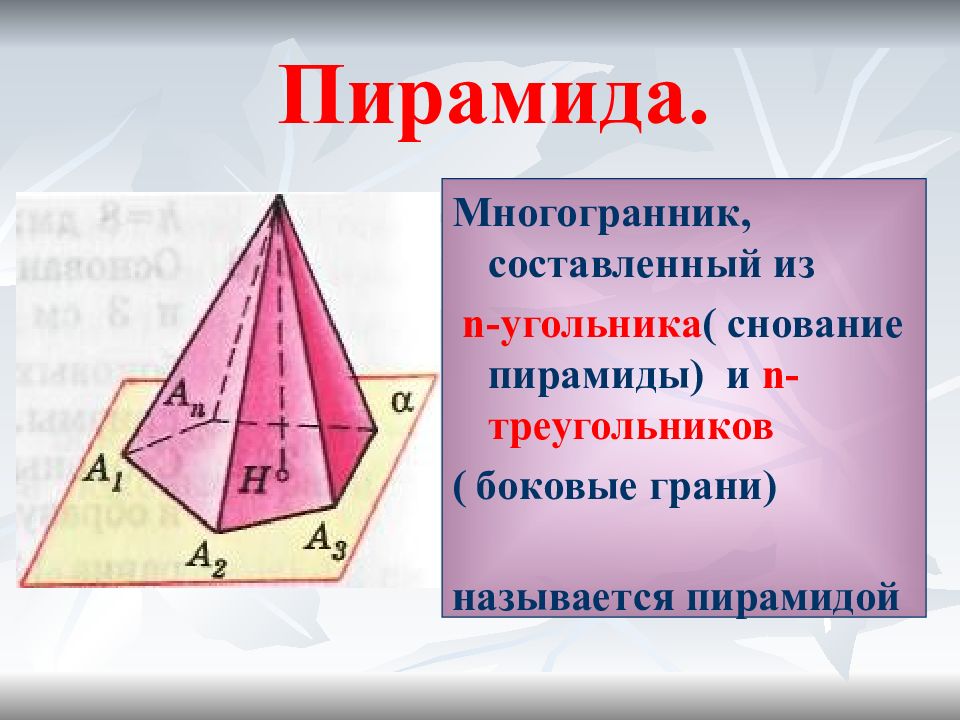
Слайд 2: Пирамида
Многогранник, составленный из n- угольника ( снование пирамиды) и n- треугольников ( боковые грани) называется пирамидой
Слайд 3: Правильная пирамида
Пирамида называется правильной, если ее основание- правильный многоугольник и вершина пирамиды проектируется в центр основания. В правильной пирамиде : все боковые ребра равны, все боковые грани- равные равнобедренные треугольники, все ее боковые ребра образуют с плоскостью основания равные углы.
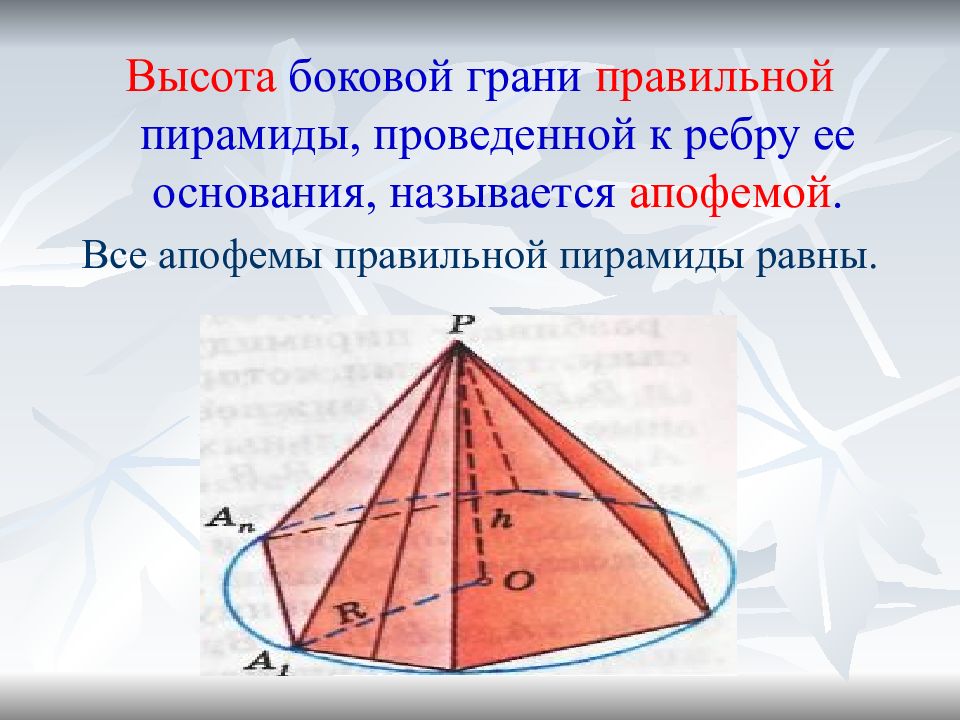
Слайд 4
Высота боковой грани правильной пирамиды, проведенной к ребру ее основания, называется апофемой. Все апофемы правильной пирамиды равны.
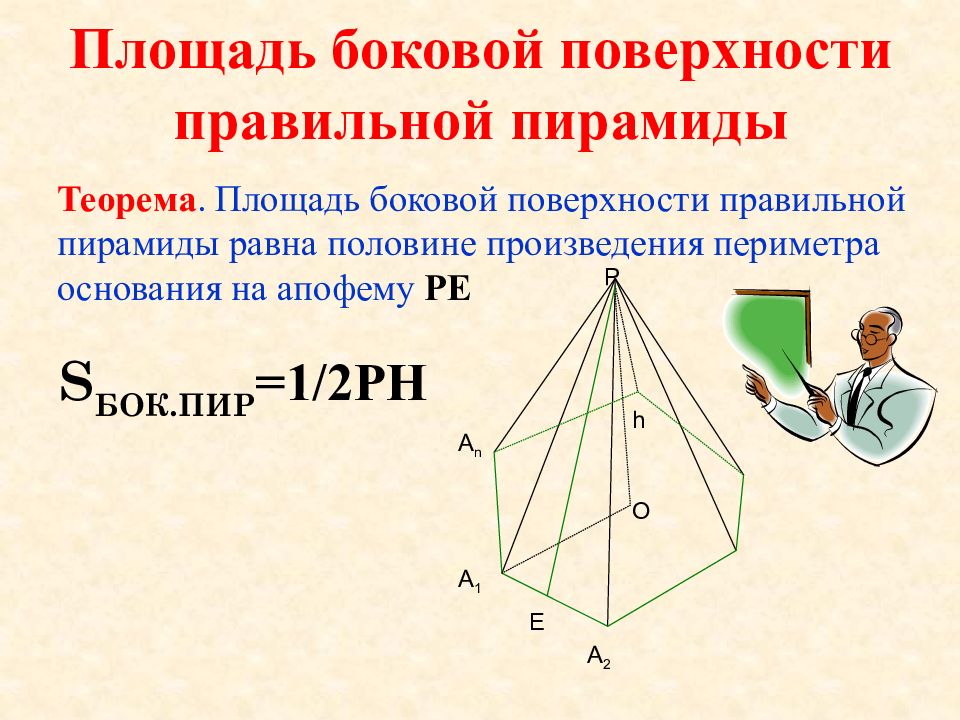
Слайд 5: Площадь боковой поверхности правильной пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему РЕ h A n A 2 A 1 O Е Р S бок.пир =1/2Р h
Слайд 6: Площадь полной поверхности пирамиды
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней (т. е. основания и боковых граней), а площадью боковой поверхности пирамиды – сумма площадей граней S полн = S бок + S осн
Слайд 7: ПОНЯТИЕ УСЕЧЕННОЙ ПИРАМИДЫ
Плоскость параллельная основанию пирамиды, разбивает её на два многогранника. Один из них является пирамидой, а другой называется усечённой пирамидой. Усеченная пирамида – это часть полной пирамиды, заключенная между её основанием и секущей плоскостью, параллельной основанию данной пирамиды
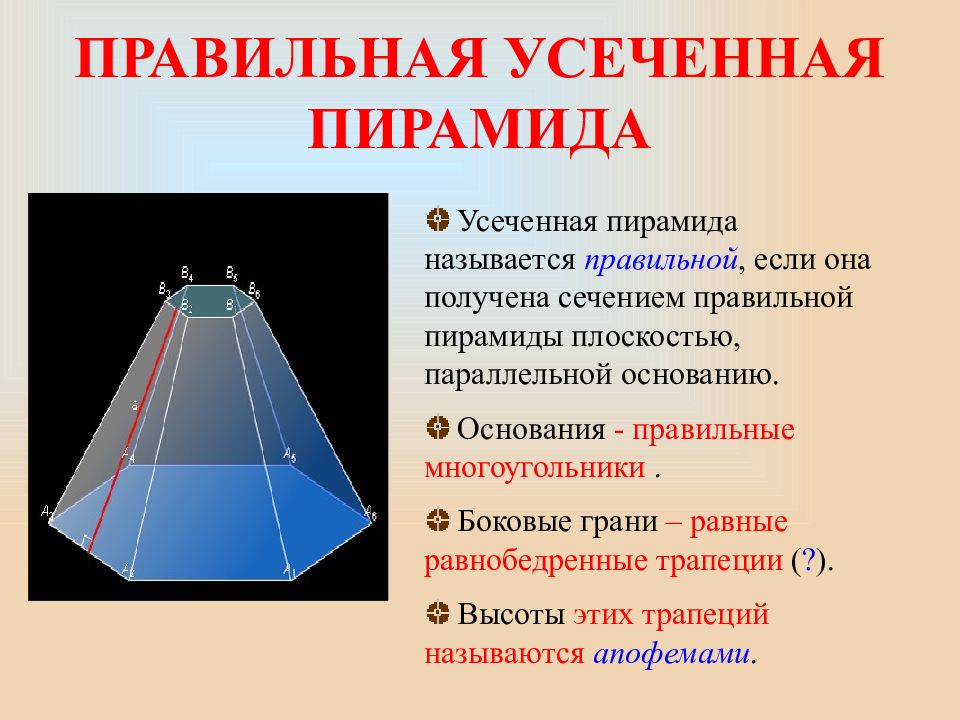
Слайд 8: ПРАВИЛЬНАЯ УСЕЧЕННАЯ ПИРАМИДА
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания - правильные многоугольники. Боковые грани – равные равнобедренные трапеции ( ? ). Высоты этих трапеций называются апофемами.
Слайд 9: ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему. ПЛОЩАДЬ ПОВЕРХНОСТИ УСЕЧЁННОЙ ПИРАМИДЫ S полн.усеч. = S бок + S верхн.осн. + S нижн.осн. S бок.усеч.пир =1/2(Р+ Р 1 )k Площадь полной поверхности правильной усечённой пирамиды равна сумме площади боковой поверхности и площадей 2-х оснований.
Слайд 10: Решение задач
Слайд 11
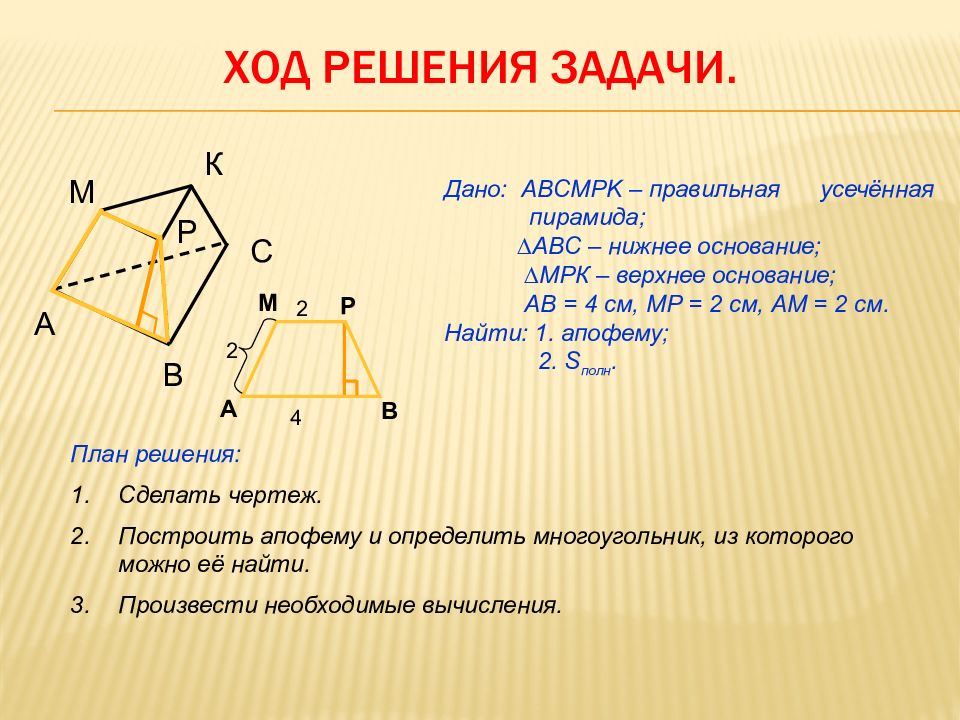
Найдите: 1. апофему пирамиды; 2. площадь полной поверхности. Задача 1. Стороны оснований правильной треугольной усеченной пирамиды равны 4 см и 2 см, а боковое ребро равно 2 см.
Слайд 12: Ход решения задачи
Дано: ABCMPK – правильная усечённая пирамида; ∆АВС – нижнее основание; ∆МРК – верхнее основание; АВ = 4 см, МР = 2 см, АМ = 2 см. Найти: 1. апофему; 2. S полн. План решения: Сделать чертеж. Построить апофему и определить многоугольник, из которого можно её найти. Произвести необходимые вычисления. А В С М Р К А В М Р 2 2 4
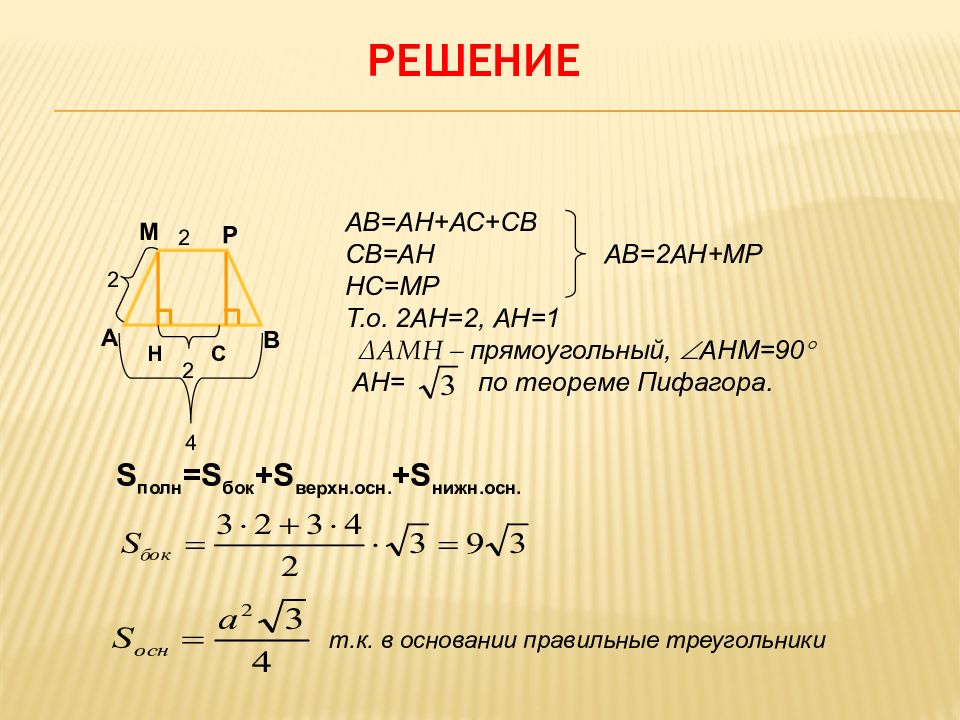
Слайд 13: РЕШЕНИЕ
А В М Р 2 2 Н С 2 АВ=АН+АС+СВ СВ=АН АВ=2АН+МР НС=МР Т.о. 2АН=2, АН=1 ∆АМН – прямоугольный, АНМ=90 АН= по теореме Пифагора. 4 S полн = S бок + S верхн.осн. + S нижн.осн. т.к. в основании правильные треугольники
Слайд 15
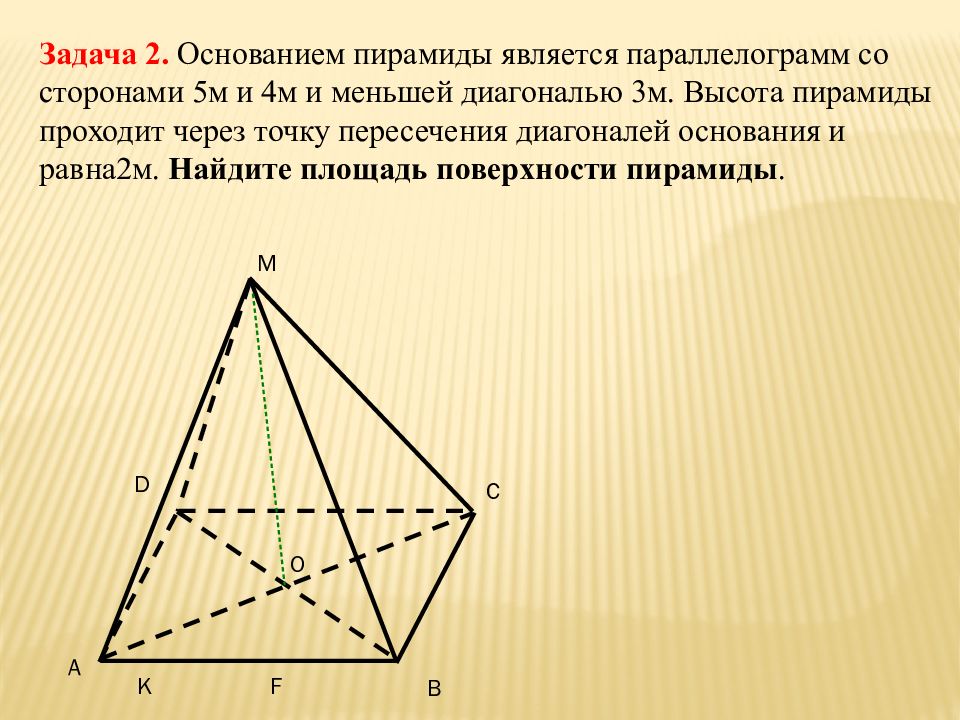
Задача 2. Основанием пирамиды является параллелограмм со сторонами 5м и 4м и меньшей диагональю 3м. Высота пирамиды проходит через точку пересечения диагоналей основания и равна2м. Найдите площадь поверхности пирамиды. А В С D M K F O
Слайд 16
А В С D M K F O Решение: Треугольник ABD – прямоугольный (4 2 +3 2 =5 2 ) Угол ADB равен 90 0. 1) AD и DO перпендикулярны, DO – проекция М D на АВС, следовательно AD и MD перпендикулярны ( по теореме о трех перпендикулярах) Следовательно MD высота ∆MAD. 2) ∆MDO: MD=√2 2 +1,5 2 = 2,5 3) ∆ADB: DK и AB перпендикулярны, рассмотрим S ADB : AB ·DK=AD ·BD,DK=2,4 м S бок = 2 S AMD +2S AMB =4 ·2,5+5 ·0,4·√34=10+2 √34 S осн =4 · 3=12 S пир =(22+2 √34 )м 2. ∆ MOF: OF║DK, OF= ½DK, OF= 1,2. MF=√MO 2 +OF 2 = 0,4√34.
Слайд 17
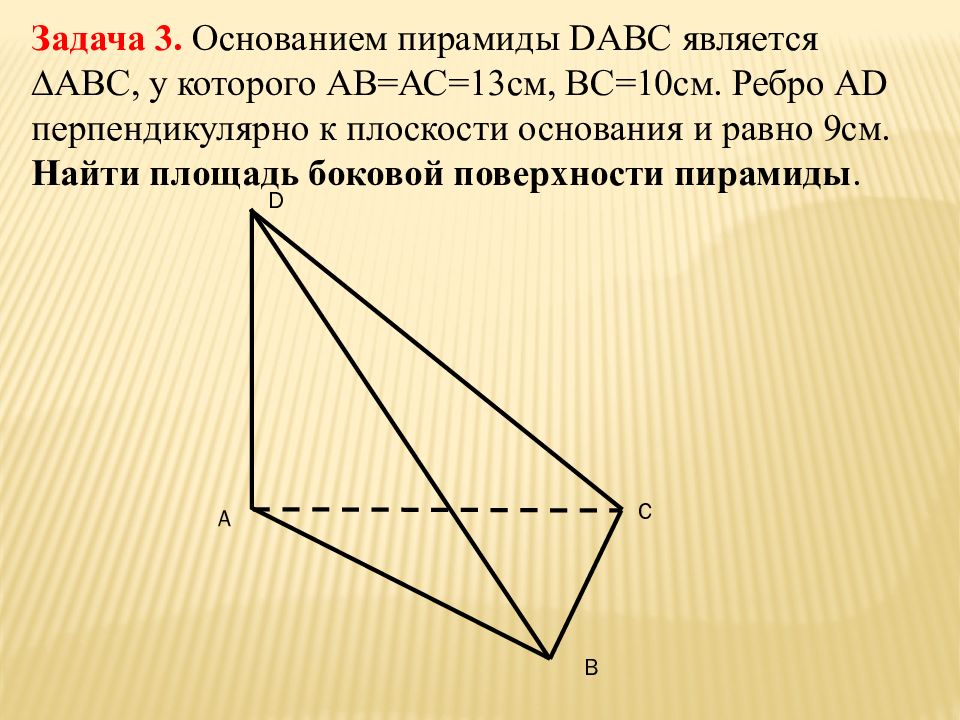
Задача 3. Основанием пирамиды DABC является ∆АВС, у которого АВ=АС=13см, ВС=10см. Ребро А D перпендикулярно к плоскости основания и равно 9см. Найти площадь боковой поверхности пирамиды. А В С D
Слайд 18
Решение: А С D В 1) Проведем АК перпендикулярно ВС К ВС и DK перпендикулярны (по теореме о трех перпендикулярах) DK – высота ∆ DBC. 2) ∆АВК: АК = √АВ 2 - BK 2 =√144=12 см 3) ∆ DAK : DK=15 см 4) ∆ ADB = ADC ( по двум катетам) S бок = 2 S ADB +S BDC S бок =2 ·½ · 13 · 9+ ½· 10 · 15 = 192см 2.
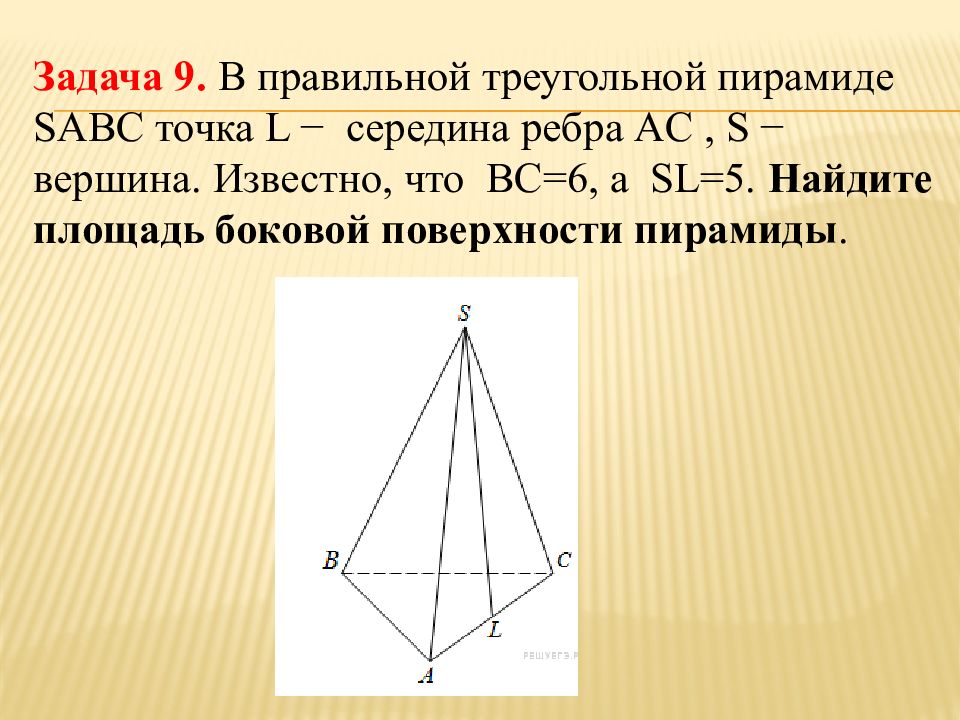
Слайд 25: Задача 9. В правильной треугольной пирамиде SABC точка L − середина ребра AC, S − вершина. Известно, что BC =6, а SL =5. Найдите площадь боковой поверхности пирамиды
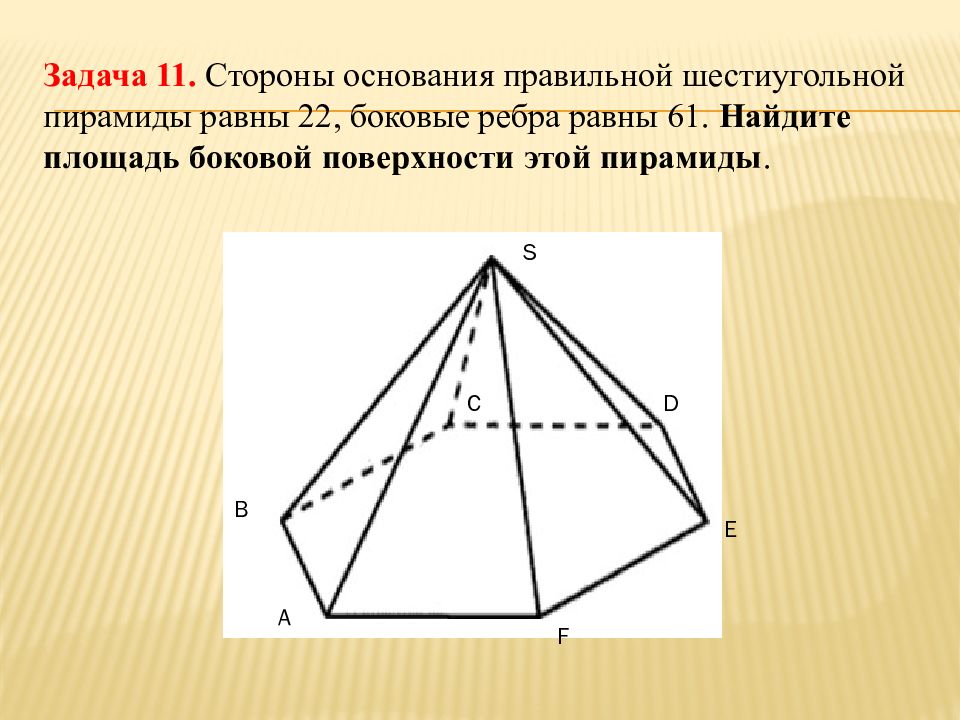
Слайд 28: Задача 11. Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды
А B C D E F S
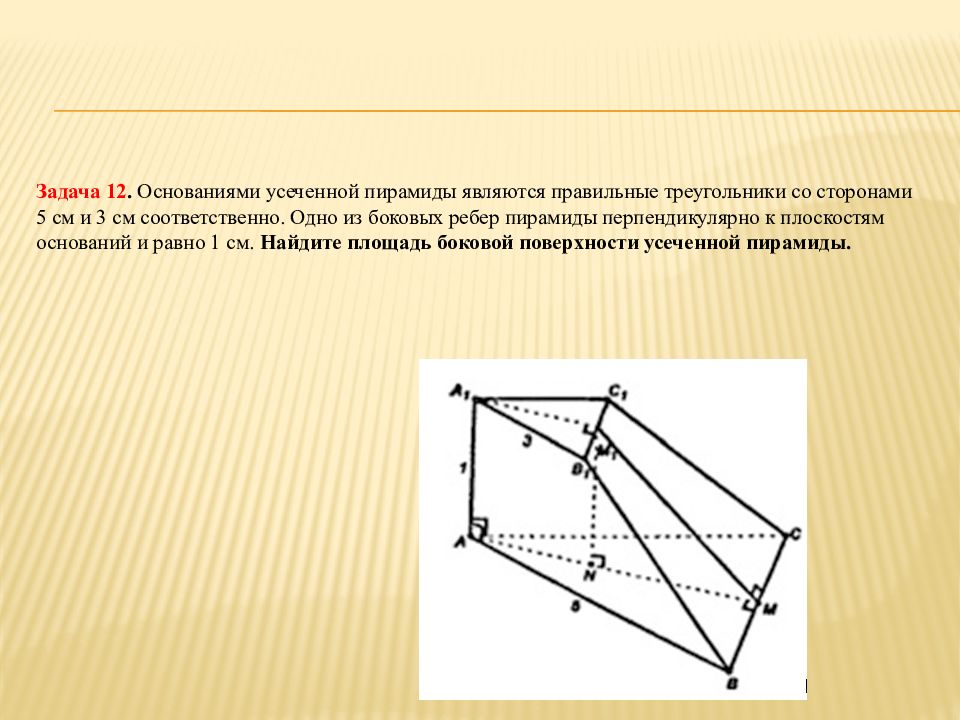
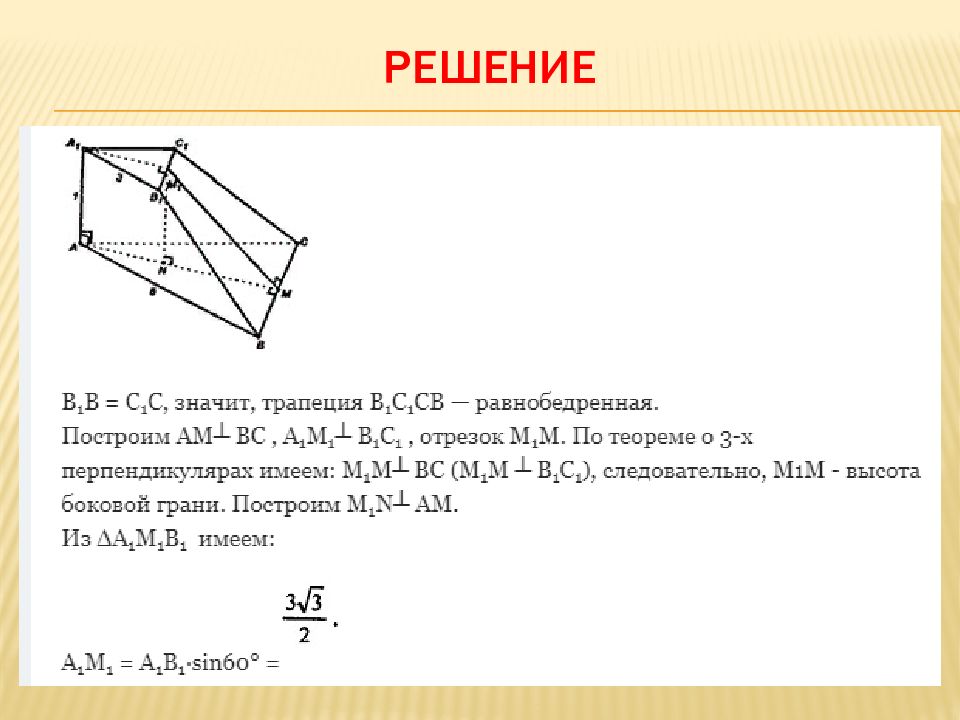
Слайд 30: Задача 12. Основаниями усеченной пирамиды являются правильные треугольники со сторонами 5 см и 3 см соответственно. Одно из боковых ребер пирамиды перпендикулярно к плоскостям оснований и равно 1 см. Найдите площадь боковой поверхности усеченной пирамиды
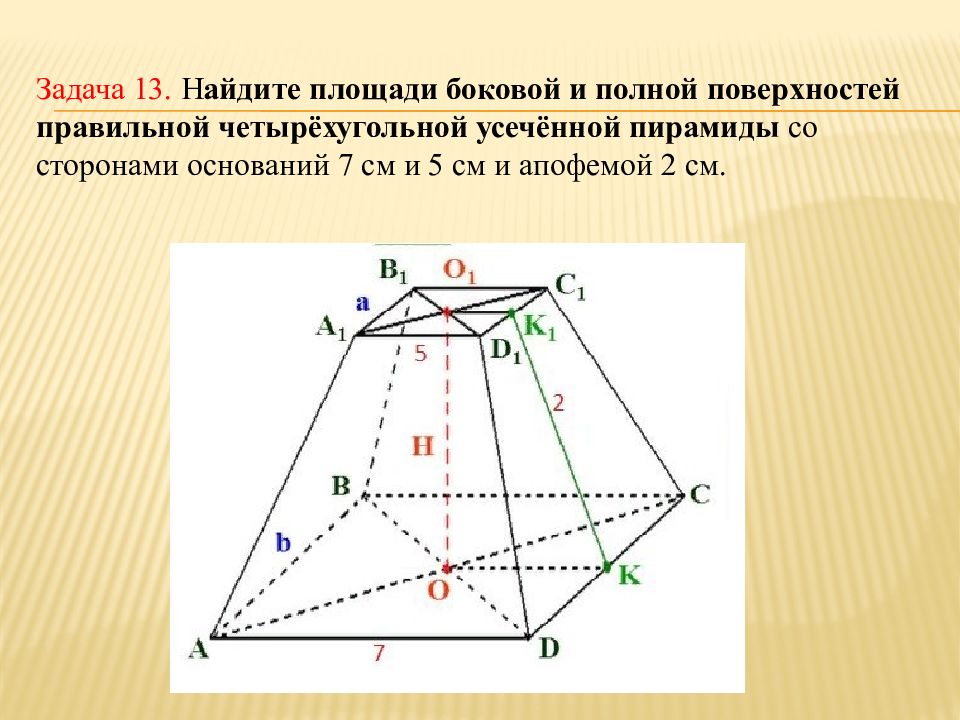
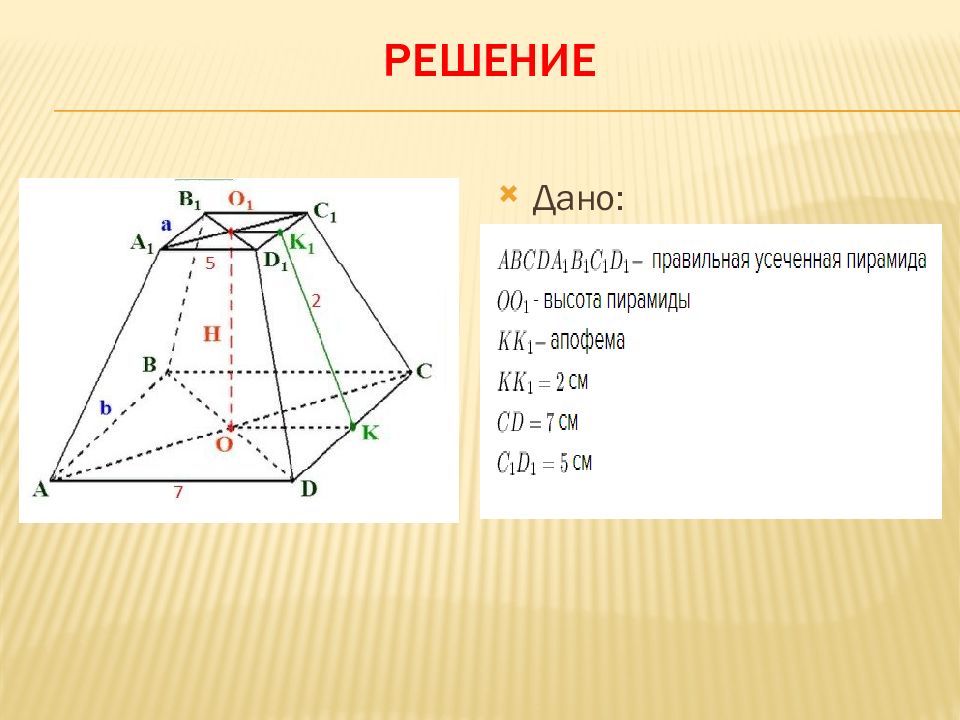
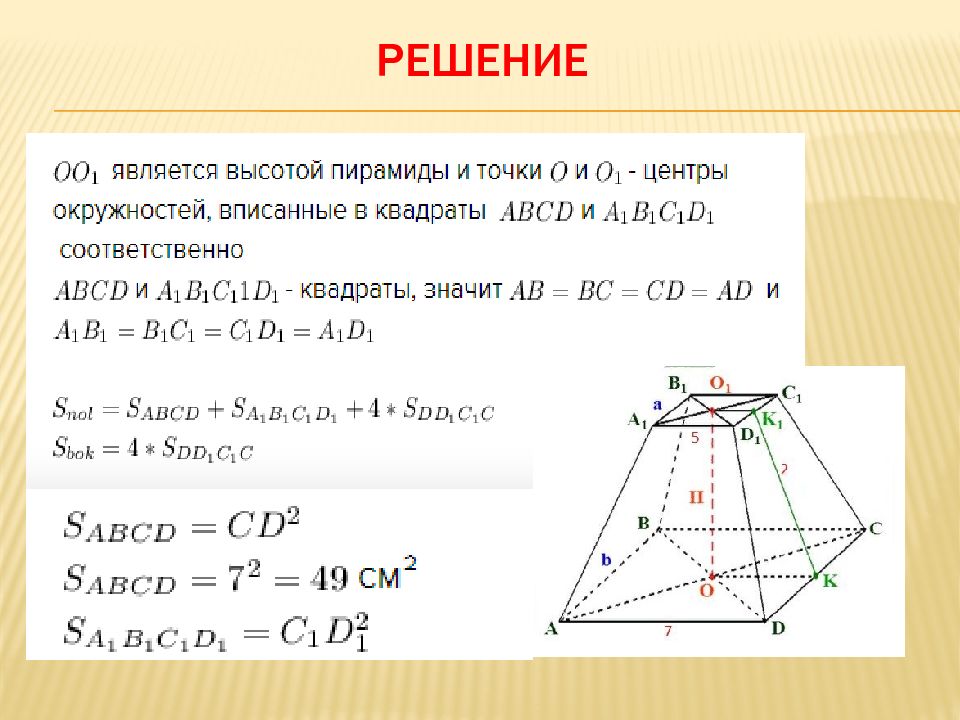
Слайд 34: Задача 13. Н айдите площади боковой и полной поверхностей правильной четырёхугольной усечённой пирамиды со сторонами оснований 7 см и 5 см и апофемой 2 см
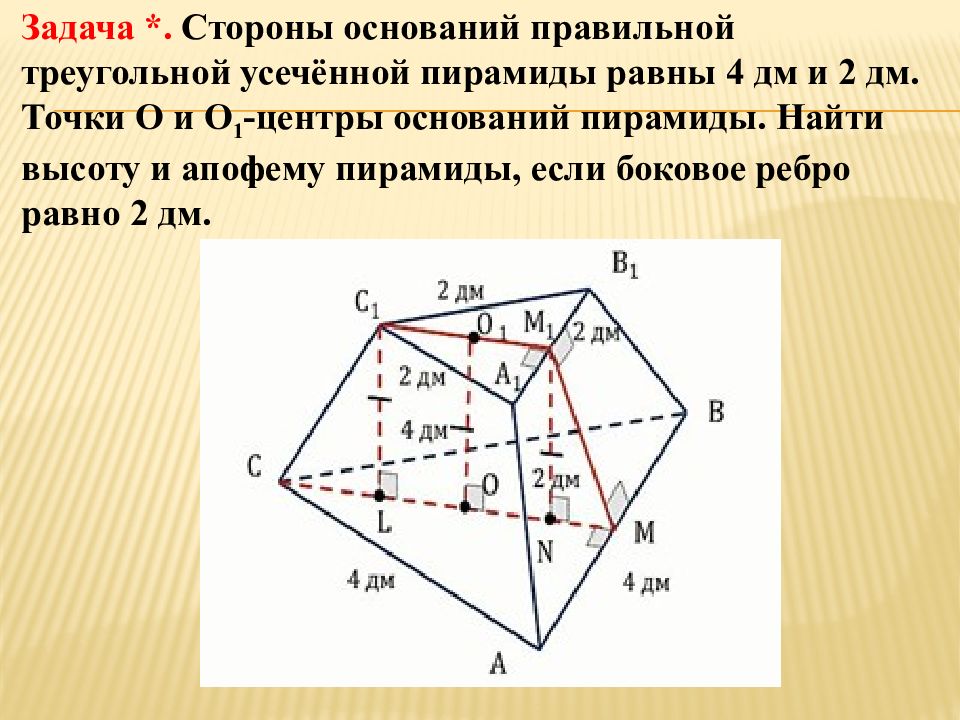
Слайд 39: Задача *. Стороны оснований правильной треугольной усечённой пирамиды равны 4 дм и 2 дм. Точки О и О 1 -центры оснований пирамиды. Найти высоту и апофему пирамиды, если боковое ребро равно 2 дм
Слайд 40: Решение
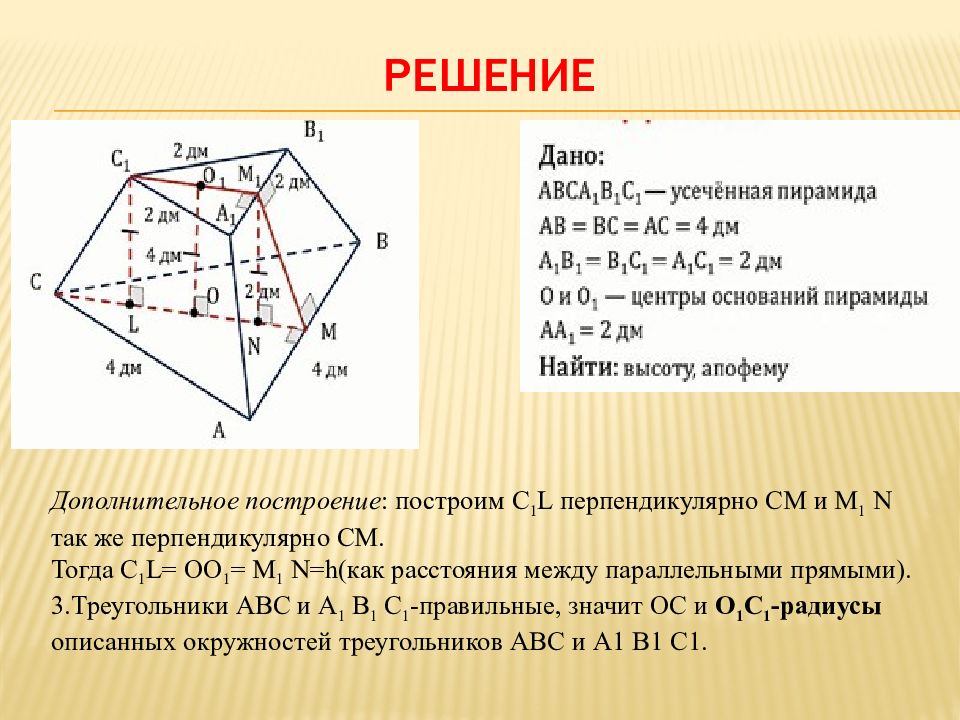
1.Дополнительное построение : построим СМ перпендикулярно АВ, С 1 М 1 перпендикулярно А 1 В 1 и соединим точки М 1 и М. По теореме о трёх перпендикулярах М 1 М перпендикулярен АВ(одновременно М 1 М перпендикулярна А 1 В 1 ), значит М 1 М- апофема. 2. Поскольку точки О и О 1 -центры оснований пирамиды, то ОО 1 -высота h.
Слайд 41: Решение
Дополнительное построение : построим С 1 L перпендикулярно СМ и М 1 N так же перпендикулярно СМ. Тогда С 1 L= ОО 1 = М 1 N=h(как расстояния между параллельными прямыми). 3.Треугольники АВС и А 1 В 1 С 1 -правильные, значит ОС и О 1 С 1 -радиусы описанных окружностей треугольников АВС и А1 В1 С1.
Слайд 42: Решение
4.Найдем длину отрезка СL как разность между длинами отрезков ОС и О 1 С 1 :